#snub cuboctahedron

[knotty-et-al]

Polytope info card of the Snub Cube

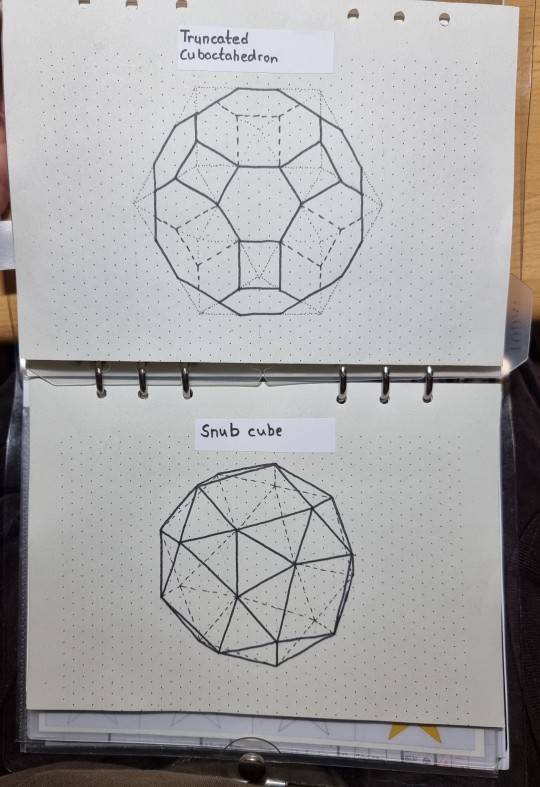
Today's shape was the archimedian solid "Snub cube".

The snub cube has 38 faces in total - 6 square faces and 32 triangular faces.

It has 60 edges and 24 vertices.

Each vertex is met by 4 triangle faces and 1 square face.

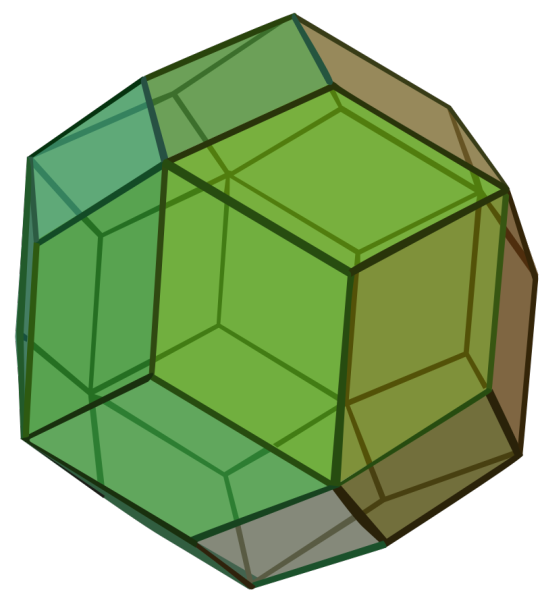
A snub cube is an alteration of a truncated cuboctahedron.

The drawing:

For the isometric projection drawing I started with a truncated cuboctahedron, and continued to alter the truncated cuboctahedron's octagonal faces into square faces.

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 5 (Third Place)

Propaganda

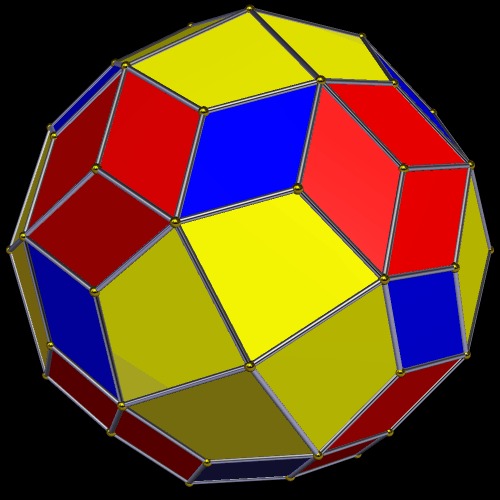
Snub Cube:

Also called the Snub Cuboctahedron

Archimedean Solid

Semiregular

Dual of the Pentagonal Icositetrahedron

It has 6 square faces, 32 regular triangular faces, 60 edges, and 24 vertices.

Chiral so it has two forms that are mirror images of each other.

Image Credit: Cyp

Rhombic Triacontahedron:

Also called the Triacontahedron

Catalan Solid

Dual of a quasiregular polyhedron

Dual of the Icosidodecahedron

It has 30 rhombic faces, 62 edges, and 32 vertices of two types.

One of the 9 edge-transitive convex polyhedra along with the 5 Platonic Solids, the 2 Quasiregular Convex Polyhedra, and the Rhombic Dodecahedron.

It has both the tumbling block quilt pattern and a five-pointed star on its surface.

Image Credit: Maxim Razin based on Cyp

[liminghin]

A Chart of my Polyhedra JSAB OC's

[snubcube]

day 1550 of pretending snapcube doesn't exist

[dailypolyhedra]

Polyhedron of the Day #171: Compound of two snub cubes

The compound of two snub cubes is a uniform polyhedral compound. It has 76 faces, 120 edges, and 48 vertices. It is also known as the disnub cuboctahedron. Its Bowers-style acronym is disco. Its Schläfli symbol is βr{4,3}. It is constructed by composing the two mirror image forms of the snub cube. It shares its vertex arrangement with a convex nonuniform truncated cuboctahedron. Its vertex figure is a mirror symetric pentagon. Its dual is the compound of two pentagonal icositetrahedra.

Image created using Robert Webb's Stella software, found at http://www.software3d.com/Stella.php.

[art-of-mathematics]

Drawing a snub dodecahedron (in isometric perspective) is quite lot of work, because I have to start with a dodecahedron (easy), then make an isocidodecahedron out of it (quite a lot of work) , and then make a truncated icosidodecahedron out of it (very much work) and then, after all these steps I can make the snub dodecahedron from this.

It is a similar procedure I used for drawing the snub cube:

Started with cube, then cuboctahedron, then truncated cuboctahedron, then snub cube.

[throwingmelons]

Oh snub cube/snub cuboctahedron, I know you're just a shape, but I love you so much.

This is a snub cube appreciation post. No snub cube hate is allowed here.

[kaishirase]

This model was designed by Alex Doskey using Great Stella. It was then exported to VRML format, which was used to build the physical model in a ZCorp stereolithograph machine. The model is only about 6 inches across, and has all regular non-intersecting faces.

Models by Adam Stolicki

Models by Adam Stolicki

Model by Adam Stolicki Model by Adam Stolicki Models by Adam Stolicki

Model by Adam Stolicki Model by Adam Stolicki Models by Adam Stolicki

Models by Giacomo Artoni

Hollow spherical model Stellation of Small Icosihemidodecahedron Stellation of Snub Cube Stellation of Great Dodecahemidodecahedron

Hollow spherical model

designed using this tutorial Compound of 6 Dodecahedra Stellation of Small Stellated

Truncated Dodecahedron Compound of 5 Octahedra

Models by Richard Stratton

Stellation of Great Ditrigonal Dodecicosidodecahedron Stellation of Small Icosihemidodecahedron Stellation of Snub Cube Stellation of Great Dodecahemidodecahedron

Stellation of Great Ditrigonal

Dodecicosidodecahedron Stellation of Small

Icosihemidodecahedron Stellation of Snub Cube Stellation of Great

Dodecahemidodecahedron

Models by Marc Picquendar

Stellation of Rhombic Triacontahedron Stellation of Rhombic Triacontahedron Small Snub Icosicosidodecahedron

Stellation of Rhombic Triacontahedron Final Stellation of Rhombic

Triacontahedron Small Snub

Icosicosidodecahedron

Compound of 5 Cubes Stellation of Truncated Octahedron Pentagonal Hexecontahedron Pentagonal Icositetrahedron

Compound of 5 Cubes Stellation of Truncated

Octahedron Pentagonal

Hexecontahedron Pentagonal

Icositetrahedron

Models by Robert Rech

Stellation of Great Ditrigonal Dodecicosidodecahedron Stellation of Small Icosihemidodecahedron

Stellation of Strombic Icositetrahedron Stellation of Triakisoctahedron

Models by Linda Zurich

Stellation of Cubitruncated Cuboctahedron Another stellation Stellation of Icosahedron Another stellation

Stellation of Cubitruncated

Cuboctahedron Another stellation Stellation of Icosahedron Another stellation

Models by Karlos Alonso Mediavilla

Compound of 5 Tetrahedra Compound of 3 Cubes Faceted Cube Compound of Dodecahedron and Great Dodecahedron

Compound of 5 Tetrahedra Compound of 3 Cubes Faceted Cube Compound of Dodecahedron

and Great Dodecahedron

Models by Steve Waterman

Waterman polyhedra

The first ten Waterman polyhedra in each of the three types available in Great Stella.

Models by Michael Barltrop

Compound of 15 Cuboids Compound of 4 Cubes Stellation of the Small Dodecahemicosahedron

Compound of 15 Cuboids Compound of 4 Cubes Stellation of the Small Dodecahemicosahedron

Monoacral stellation of Compound of 15 Cuboids Stellation of Small Dodecahemicosahedron Stellation of Great Dodecahemicosahedron

Monoacral stellation of

Compound of 15 Cuboids Stellation of Small Dodecahemicosahedron Stellation of Great Dodecahemicosahedron

A stellation Stellation of Small Stellated Truncated Dodecahedron

Stellation of the first Faceted

Rhombicosidodecahedron found in

Stella's Library Stellation of Small Stellated

Truncated Dodecahedron

Models by Keith Davison

See also: What people have to say about Stella.

[ohheyidothat]

A Snub disphenoid, Cuboctahedron, Enneagonal Prism, and a Disdyakis Triacontahedron!

Learning shapes and their names was for kindergarten omg. I didn’t realize people went ahead and named every possible shape they could think of. More coming.

[ecstatiqblr]

Strobl Snub Cuboctahedron for my boyfriend’s coworker.

[notreallyherehahaha]

In a kite-rhombus solid, or KRS, all faces are either kites or rhombi, and there are at least some of both of these quadrilateral-types as faces. I have found eight such polyhedra, all of which are formed by creating the convex hull of different Archimedean-Catalan base-dual compounds. Not all Archimedean-Catalan compounds produce kite-rhombus solids, but one of the eight that does is derived from the truncated dodecahedron, as explained below.

The next step is to create the compound of this solid and its dual, the triakis icosahedron. In the image below, this dual is the blue polyhedron.

The convex hull of this compound, below, I’m simply calling “the KRS derived from the truncated dodecahedron,” until and unless someone invents a better name for it.

The next KRS shown is derived, in the same manner, from the truncated tetrahedron.

Here is the KRS derived from the truncated cube.

The truncated icosahedron is the “seed” from which the next KRS shown is derived. This KRS is a “stretched” form of a zonohedron called the rhombic enneacontahedron.

Another of these kite-rhombus solids, shown below, is based on the truncated octahedron.

The next KRS shown is based on the rhombcuboctahedron.

Two of the Archimedeans are chiral, and they both produce chiral kite-rhombus solids. This one is derived from the snub cube.

Finally, to complete this set of eight, here is the KRS based on the snub dodecahedron.

You may be wondering what happens when this same process is applied to the other five Archimedean solids. The answer is that all-kite polyhedra are produced; they have no rhombic faces. Two are “stretched” forms of Catalan solids, and are derived from the cuboctahedron and the icosidodecahedron:

If this procedure is applied to the rhombicosidodecahedron, the result is an all-kite polyhedron with two different face-types, as seen below.

The two remaining Archimedean solids are the great rhombcuboctahedron and the great rhombicosidodecahedron, each of which produces a polyhedron with three different types of kites as faces.

The polyhedron-manipulation and image-production for this post was performed using Stella 4d: Polyhedron Navigator, which may be purchased or tried for free at http://www.software3d.com/Stella.php.

    Eight Kite-Rhombus Solids, Plus Five All-Kite Polyhedra — the Convex Hulls of the Thirteen Archimedean-Catalan Compounds In a kite-rhombus solid, or KRS, all faces are either kites or rhombi, and there are at least some of both of these quadrilateral-types as faces.

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 1

Propaganda

Truncated Octahedron:

Archimedean Solid

Semiregular

Dual of the Tetrakis Hexahedron

It has 8 regular hexagonal faces, 6 square faces, 36 edges, and 24 vertices.

A space-filling tessellation/honeycomb of Euclidean three-space.

Image Credit: Cyp

Snub Cube:

Also called the Snub Cuboctahedron

Archimedean Solid

Semiregular

Dual of the Pentagonal Icositetrahedron

It has 6 square faces, 32 regular triangular faces, 60 edges, and 24 vertices.

Chiral so it has two forms that are mirror images of each other.

Image Credit: Cyp

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 2

Propaganda

Sphere:

"Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space." — Wikipedia

Not a convex polyhedron.

Image Credit: Tumblr

Snub Cube:

Also called the Snub Cuboctahedron

Archimedean Solid

Semiregular

Dual of the Pentagonal Icositetrahedron

It has 6 square faces, 32 regular triangular faces, 60 edges, and 24 vertices.

Chiral so it has two forms that are mirror images of each other.

Image Credit: Cyp

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 4

Propaganda

Snub Cube:

Also called the Snub Cuboctahedron

Archimedean Solid

Semiregular

Dual of the Pentagonal Icositetrahedron

It has 6 square faces, 32 regular triangular faces, 60 edges, and 24 vertices.

Chiral so it has two forms that are mirror images of each other.

Image Credit: Cyp

Truncated Icosidodecahedron:

Also called the Rhombitruncated Icosidodecahedron, Great Rhombicosidodecahedron, Omnitruncated Dodecahedron, Omnituncated Icosahedron

Archimedean Solid

Semiregular

Dual of the Disdyakis Triacontahedron

It has 12 regular decagonal faces, 20 regular hexagonal faces, 30 square faces, 180 edges, and 120 vertices.

It has the most edges and vertices of all platonic and archimedean solids.

Of the vertex-transitive polyhedra, it fills up the most of the volume of the sphere it fits in (89.80%).

It is not actually the shape you get when you truncate an icosidodecahedron, although it is topologically equivalent.

It is the mod's favorite three-dimensional shape.

They made a void truncated icosidodecahedron and it's glorious. I had one for a while, it's hard to turn because of alignment issues, especially the decagonal sides. Fun puzzle tho, never did figure out how to permute the last layer...

Image Credit: @anonymous-leemur

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 3

Propaganda

Snub Cube:

Also called the Snub Cuboctahedron

Archimedean Solid

Semiregular

Dual of the Pentagonal Icositetrahedron

It has 6 square faces, 32 regular triangular faces, 60 edges, and 24 vertices.

Chiral so it has two forms that are mirror images of each other.

Image Credit: Cyp

Icosidodecahedron:

Archimedean Solid

Quasiregular

Dual of the Rhombic Triacontahedron

It has 12 regular pentagonal faces, 20 regular trianglar faces, 60 edges, and 30 vertices.

Vertex Transitive AND Edge Transitive

Image Credit: Cyp

[dailypolyhedra]

Daily Polyhedra Archive

(An ongoing list of polyhedra that have already been covered by this blog, mostly for my own convenience. This is a work-in-progress.)

Platonic solids

Cube

Dodecahedron

Icosahedron

Octahedron

Tetrahedron

Kepler-Poinsot polyhedra

Great dodecahedron

Great icosahedron

Great stellated dodecahedron

Small stellated dodecahedron

Archimedean solids

Cuboctahedron

Great rhombicuboctahedron

Icosidodecahedron

Rhombicosidodecahedron

Small rhombicuboctahedron

Snub cube

Snub dodecahedron

Truncated cube

Truncated dodecahedron

Truncated icosahedron

Truncated icosidodecahedron

Truncated octahedron

Truncated tetrahedron

Catalan solids

Deltoidal hexecontahedron

Deltoidal icositetrahedron

Disdyakis dodecahedron

Disdyakis triacontahedron

Pentagonal hexecontahedron

Pentagonal icositetrahedron

Pentakis dodecahedron

Rhombic dodecahedron

Rhombic triacontahedron

Tetrakis hexahedron

Triakis icosahedron

Triakis octahedron

Triakis tetrahedron

Prismatic polyhedra

Triangular prism

Pentagonal prism

Schönhardt polyhedron

Decagrammic antiprism

Square antiprism

Pyramidal polyhedra

Square pyramid

Hexagonal pyramid

Johnson solids

Square pyramid (J1)

Triangular bipyramid (J12)

Gyroelongated pentagonal rotunda (J25)

Square orthobicupola (J28)

Pentagonal orthobicupola (J30)

Elongated pentagonal gyrobicupola (J39)

Gyroelongated pentagonal cupolarotunda (J47)

Gyroelongated pentagonal birotunda (J48)

Triaugmented hexagonal prism (J57)

Augmented tridiminished icosahedron (J64)

Biaugmented truncated cube (J67)

Gyrate rhombicosidodecahedron (J72)

Snub disphenoid (J84)

Sphenomegacorona (J88)

Hebesphenomegacorona (J89)

Disphenocingulum (J90)

Bilunabirotunda (J91)

Triangular hebesphenorotunda (J92)

Near-miss Johnson solids

Edge-contracted icosahedron

Tetrated dodecahedron

Truncated triakis tetrahedron

Pentahexagonal pyritoheptacontatetrahedron

Rectified truncated icosahedron

Chamfered cube

Chamfered dodecahedron

Hemipolyhedra

Small dodecahemicosahedron

Tetrahemihexacron

Small icosihemidodecahedron

Zonohedra

Rhombic enneacontahedron

Bilinski dodecahedron

Truncated rhombicosidodecahedron

Rhombic icosahedron

Star polyhedra

Small snub icosidodecahedron

Rhombicosahedron

Great snub icosidodecahedron

Inverted snub dodecadodecahedron

Excavated dodecahedron

Great rhombic triacontahedron

Great triakis icosahedron

Great dirhombicosidodecahedron

Cubitruncated cuboctahedron

Quasitruncated great stellated dodecahedron

Uncategorised polyhedra

Chamfered icosahedron

Triamond stretched octahedron

Diminished rhombic dodecahedron

Császár polyhedron

Szilassi polyhedron

Biscribed orthotruncated propello octahedron

Rectified triangular prism

Escher's solid

Polyhedral compounds

Compound of five cubohemioctahedra

Compound of twenty octahedra

Compound of four cubes

Compound of two icosahedra

Compound of two great retrosnub icosidodecahedra

Compound of eight octahedra

Rhomboctahedron (compound of four triangular prisms)

Compound of five tetrahedra