#truncated cuboctahedron

[knotty-et-al]

Polytope info card of the Truncated Cuboctahedron

Today I finished this friend-shaped archimedian solid.

I drew the tiny drawing in the down right corner of the card and resized it with my printer.

The drawing:

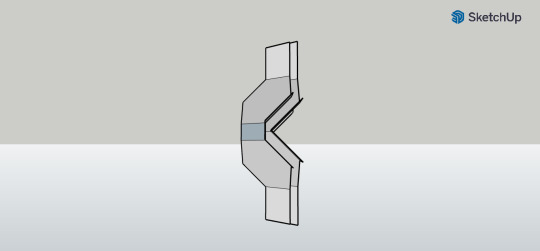
I drew this Truncated cuboctahedron in an isometric projection and used my beloved isometric dot paper.

To start with the truncated cuboctahedron I started to draw a cube (with pencil).

Then I altered the cube by drawing a cuboctahedron in it (with pencil as well). I truncated th vertices of the cube like in the depiction below:

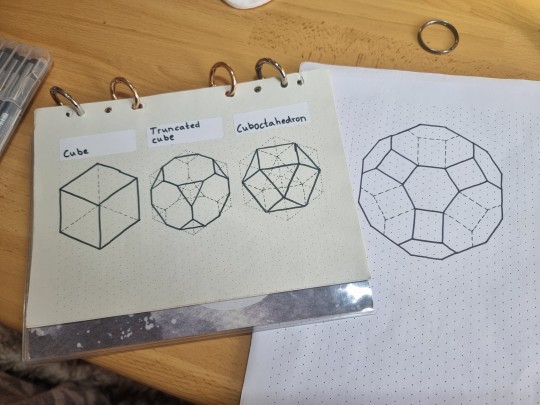
Then I altered the cuboctahedron drawing with another truncation - resulting in the truncated cuboctahedron shape.

[For clarification: I later erased the pencil lines of the cube and cuboctahedron, because it became messy and these lines were just there to help in the drawing process.

For the photo I laid pictures of a cube and cuboctahedron besides the truncated cuboctahedron drawing to show the similarity between these shapes - and present the principle of truncation visually.)

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 1

Propaganda

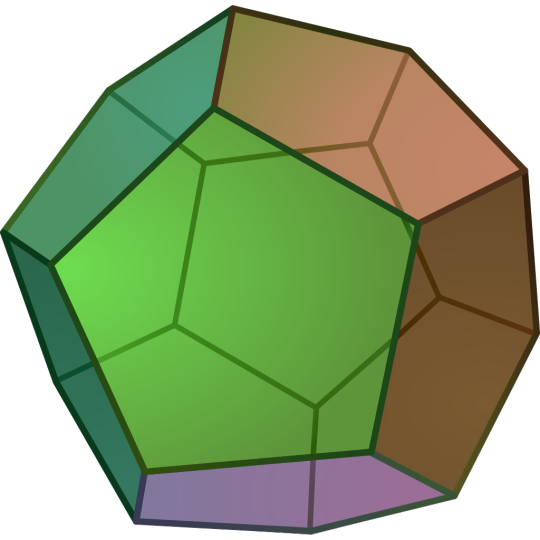
Regular Dodecahedron:

Also called the Pentagonal Dodecahedron

Platonic Solid

Regular

Dual of the Regular Icosahedron

It has 12 regular pentagonal faces, 30 edges, and 20 vertices.

Image Credit: Cyp

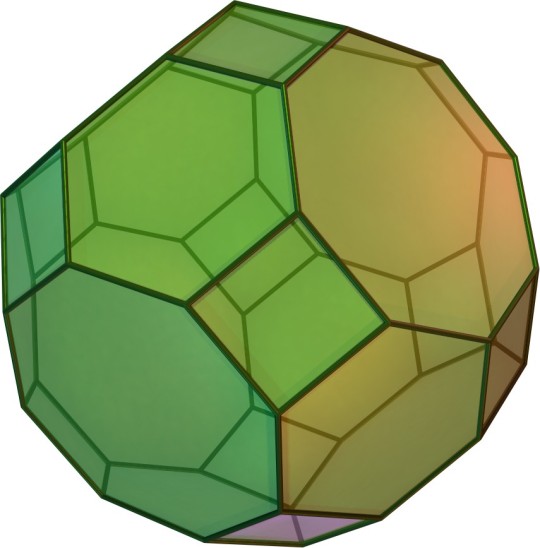
Truncated Cuboctahedron:

Also called the Great Rhombicuboctahedron

Archimedean Solid

Semiregular

Dual of the Disdyakis Dodecahedron

It has 6 regular octagonal faces, 8 regular hexagonal faces, 12 square faces, 72 edges, and 48 vertices.

Not actually the truncation of the cuboctahedron, although topologically equivalent.

Image Credit: Cyp

[geommatrix]

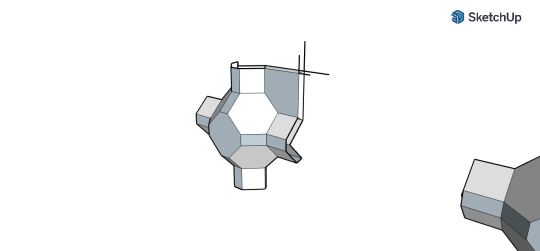
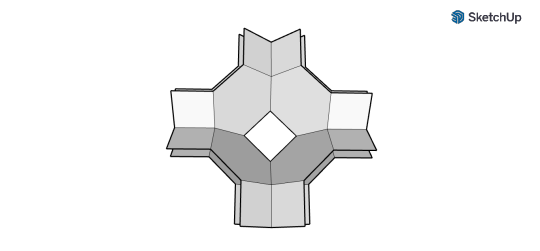
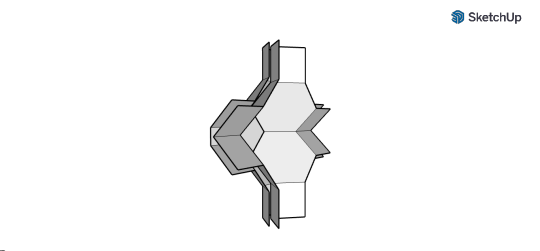
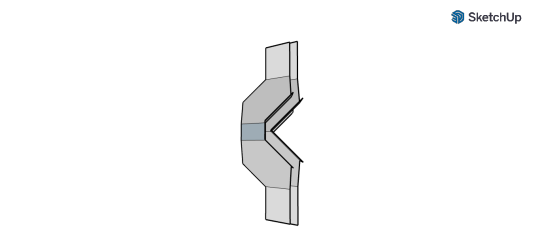
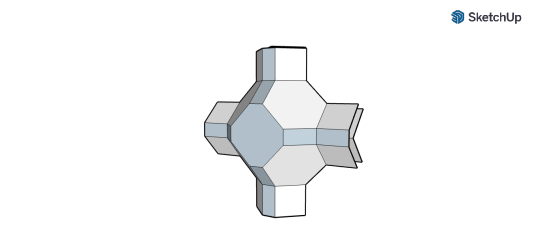
gmtrx truncated Cuboctahedron matrix

[dailypolyhedra]

Polyhedron of the Day #171: Compound of two snub cubes

The compound of two snub cubes is a uniform polyhedral compound. It has 76 faces, 120 edges, and 48 vertices. It is also known as the disnub cuboctahedron. Its Bowers-style acronym is disco. Its Schläfli symbol is βr{4,3}. It is constructed by composing the two mirror image forms of the snub cube. It shares its vertex arrangement with a convex nonuniform truncated cuboctahedron. Its vertex figure is a mirror symetric pentagon. Its dual is the compound of two pentagonal icositetrahedra.

Image created using Robert Webb's Stella software, found at http://www.software3d.com/Stella.php.

[art-of-mathematics]

Drawing a snub dodecahedron (in isometric perspective) is quite lot of work, because I have to start with a dodecahedron (easy), then make an isocidodecahedron out of it (quite a lot of work) , and then make a truncated icosidodecahedron out of it (very much work) and then, after all these steps I can make the snub dodecahedron from this.

It is a similar procedure I used for drawing the snub cube:

Started with cube, then cuboctahedron, then truncated cuboctahedron, then snub cube.

[i-am-thedragon]

@someniam

The offspring of a hexagonal prism and great rhombicosidodecahedron (which I will refer to from now as 'Grid', it's Bowers-style acronym) will likely inherit the hexagonal and tetragonal(square/rectangular) faces of its parents.

This could result in a truncated octahedron, or a truncated cuboctahedron. The latter also gains octagonal faces but is more visually similar to the Grid. Both are Archimedean solids like the Grid and bear a face count between that of both parents.

If not the above, the offspring could instead inherit the decagonal faces from the Grid and be a decagonal prism, resembling more their hexagonal prism parent.

These are the three most likely offspring from such a pairing. There's also the possibility of the offspring being the exact same shape as either parent, or being something else entirely depending on interference from recessive genetics.

To be honest, I couldn't come up with a lot for this pairing 😅

[robotblues]

A Space-Filling Pair of Polyhedra: The Cuboctahedron and the Octahedron There are only a few polyhedra which can fill space without leaving gaps, without “help” from a second polyhedron. This filling of space is the three-dimensional version of tessellating a plane. Among those that can do this are the cube, the truncated octahedron, and the rhombic dodecahedron. If multiple polyhedra are allowed in a space-filling pattern, this opens new possibilities. Here is one: the filling of space by cuboctahedra and octahedra. There are others, and they are likely to appear as future blog-posts here. Software credit: I made this virtual model using Stella 4d, polyhedral-manipulation software you can buy, or try as a free trial download, at http://www.software3d.com/Stella.php.

[kennedy-the-genderfluid-punk]

why do i have a cuboctahedron and two truncated icosohedra in my cells

biologists will be like this is a very simplified diagram of a mammalian cell

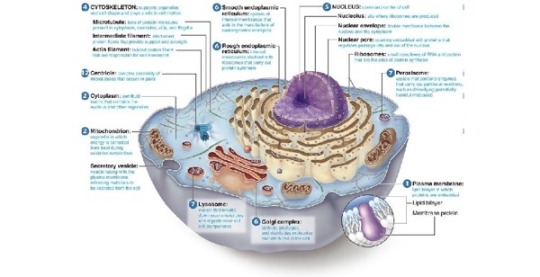
chemists will be like this is a molecule

[notreallyherehahaha]

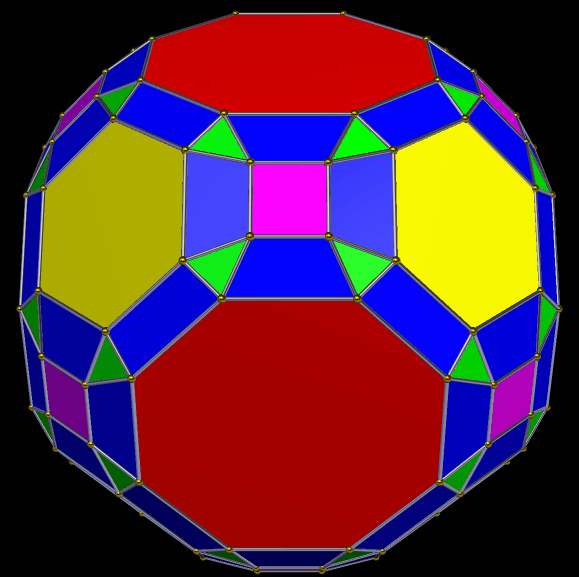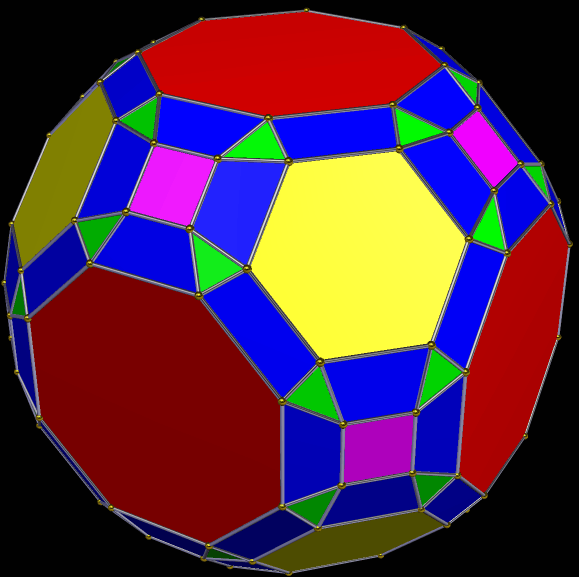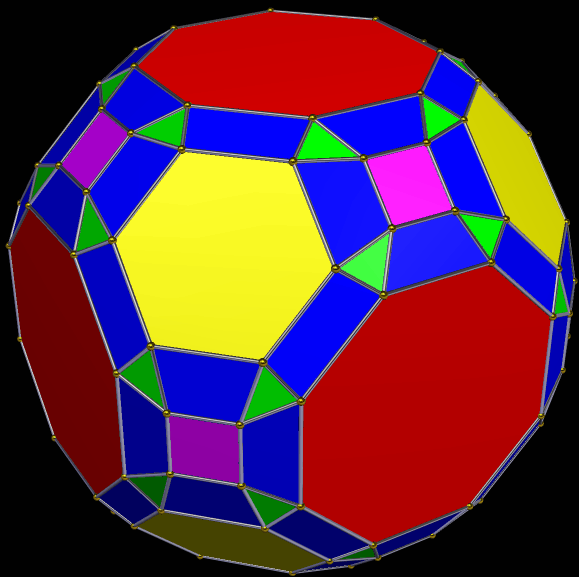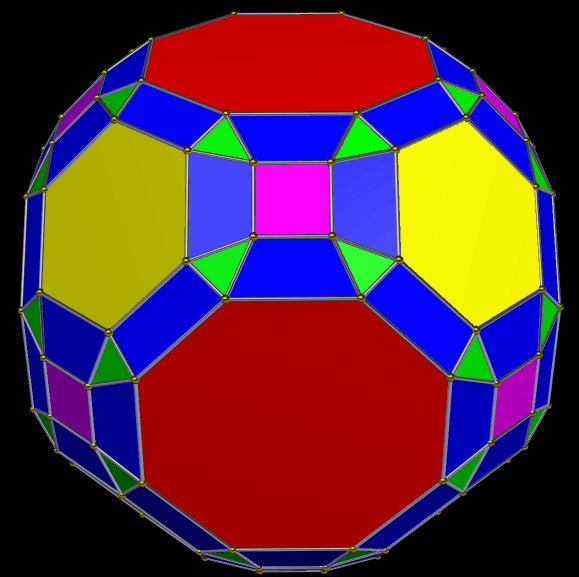
A Symmetrohedron Derived From the Great Rhombicuboctahedron, Which Is Also Known as the Truncated Cuboctahedron

This symmetrohedron has the six regular octagons, eight regular hexagons, and twelve squares of its “parent,” the great rhombicuboctahedron. It was modified by using the “morph duals at 50% by tilting to rectify” function, twice. This left the resulting polyhedron with additional faces: 72 trapezoids (24 each, of three types), and 48 scalene triangles. That’s 146 faces in all. I made it using…

[knotty-et-al]

Truncations of the cube

This is what I have done with my spare shape drawings...

Depicted are different truncations of the cube - and the cube itself.

The polyhedra are (from left to right and from top to bottom)

- Cube

- Truncated cube (Cube's vertices get cut off to one third of each edge.)

- Cuboctahedron (Cube's vertices get cut off to a half of each edge.)

- Rhombicuboctahedron (Cuboctahedron's vertices get cut off to a half of each edge.)

Truncated Cuboctahedron (Cuboctahedron's vertices get cut off to a third of each edge.)

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 1

Propaganda

Truncated Octahedron:

Archimedean Solid

Semiregular

Dual of the Tetrakis Hexahedron

It has 8 regular hexagonal faces, 6 square faces, 36 edges, and 24 vertices.

A space-filling tessellation/honeycomb of Euclidean three-space.

Image Credit: Cyp

Snub Cube:

Also called the Snub Cuboctahedron

Archimedean Solid

Semiregular

Dual of the Pentagonal Icositetrahedron

It has 6 square faces, 32 regular triangular faces, 60 edges, and 24 vertices.

Chiral so it has two forms that are mirror images of each other.

Image Credit: Cyp

[brightgreendandelions]

i do love the (not truncated, but rombic) cuboctahedron, maybe not as much as his sister, the elongated square gyrobicupola, but that's a lot of faces (26) to sew by hand. maybe i should find a friend with a sewing machine 🤔

i want to make a little polyhedron plushie!!

which polyhedra do you think will be more conducive to plushing? the easiest (i think) would be to make a (companion) cube, but i don't want to accidentally have a sphere 0_0

[curiosamathematica]

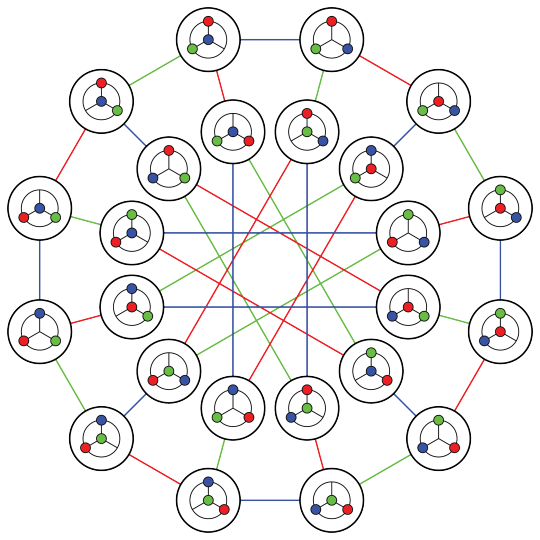
Imagine a simple sliding puzzle with three pieces on the vertices of a tetrahedron, that you can slide around along the edges. There are 24 possible game states. All moves in the game are recorded in the depicted graph, known as the Nauru graph.

Larger sliding puzzles with more “holes” can have even more interesting graphs. You can find a couple of examples here. There is among others a quite innocent-looking puzzle with five pieces and one hole, resulting in a subdivision of the truncated cuboctahedron with a total of 120 vertices!

[dailypolyhedra]

Polyhedron of the Day #117: Chamfered octahedron

The chamfered octahedron is a convex polyhedron. It has 20 faces, 48 edges, and 30 vertices. It is also known as the tritruncated rhombic dodecahedron. It is constructed by chamfering an octahedron (truncating its edges) or by truncating the order-3 vertices of a rhombic dodecahedron. Its dual is the triakis cuboctahedron.

Chamfered octahedron image created by T. Piesk, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=66347023