#volume and surface area of a sphere formula example

[faisalahamadibigcseexpert]

How to write an excellent IB Math SL IA?

Writing an excellent IB Math SL Internal Assessment (IA) requires a careful blend of mathematical rigor, clear communication, and personal engagement with the topic. The IA is a chance for you to showcase your mathematical understanding and problem-solving skills, while also demonstrating your ability to communicate your ideas effectively.

Here’s a step-by-step guide to help you write an outstanding Math SL IA:

1. Choose a Suitable Topic

Personal Interest: Pick a topic that genuinely interests you. The IA should reflect your curiosity and enthusiasm for mathematics, as this will come across in your writing. You can base it on real-life applications, a specific mathematical concept, or a personal project.

Mathematical Depth: Ensure the topic has enough mathematical complexity to allow for exploration and application of the required mathematical concepts (e.g., calculus, algebra, statistics, functions, geometry, etc.). Avoid topics that are too simple or too broad.

Manageability: Choose a topic that you can realistically explore within the time and scope of the IA. Don’t select something too complex that will be difficult to manage.

Example Topics:

Investigating the optimal dimensions for maximizing the volume of a box with a fixed surface area.

Modeling population growth using exponential functions.

Analyzing the relationship between two variables using linear regression and correlation.

Investigating the mathematics behind a particular game or sport (e.g., probability and statistics in soccer or basketball).

2. Formulate a Clear Research Question

Specific and Focused: Your research question should be clearly defined and focused. It should be something that can be explored mathematically with the tools at your disposal.

Inquiry-based: Frame your research question in a way that invites exploration and investigation. For example, rather than asking, "What is the volume of a sphere?" you might ask, "How does the volume of a sphere change as its radius increases?".

Example Research Questions:

How does the growth rate of a population in a certain city compare to the global average using exponential models?

How can the Fibonacci sequence be applied to optimize a given situation, such as a design for a plant growth model?

3. Plan Your Approach

Outline the Mathematical Methods: Before starting your investigation, plan what kind of mathematical tools and techniques you’ll need. This could include algebraic manipulation, statistical analysis, or the use of calculus.

Set a Structure: Organize your IA into a clear structure with logical steps. Typically, this would include:

Introduction: Define the problem or question you're investigating and explain why it’s relevant or interesting.

Mathematical Exploration: Apply the mathematics to explore the problem, including all relevant formulas, calculations, graphs, and analysis.

Reflection and Conclusion: Discuss your results, interpret the meaning of your findings, and consider limitations or improvements to the model.

4. Engage with Mathematics

Incorporate Mathematical Theory: Show a clear understanding of the mathematics you’re using. This means not just applying formulas, but also explaining the underlying principles and why the methods are appropriate for your problem.

Use Appropriate Techniques: Depending on your topic, this could involve algebraic manipulation, statistical tests, optimization, or differential equations. Be sure to demonstrate the use of at least two or three different mathematical concepts.

Show All Working: As you solve problems or conduct analysis, show all intermediate steps. The process is just as important as the final answer.

Use Technology Wisely: Tools like graphing calculators, Excel, or GeoGebra can help visualize data and solve complex problems, but ensure you explain how and why you’re using them.

5. Provide Evidence of Mathematical Rigor

Use Correct Notation: Consistently use proper mathematical notation throughout your IA.

Depth and Complexity: Go beyond basic computations. Show a higher level of understanding by exploring how different variables interact, comparing multiple methods, or analyzing data in depth.

Extend the Problem: If possible, extend your topic by considering different scenarios or using more advanced methods. This demonstrates your ability to think critically and explore the mathematics deeply.

6. Incorporate Graphs and Visuals

Graphs: Graphs are a vital tool for visualizing mathematical relationships. Use graphs to illustrate your findings, such as plotting functions, data sets, or optimization results.

Charts and Tables: Use these for displaying data and summarizing results in a clear and concise manner.

Visual Explanation: Use visuals to complement your mathematical reasoning, but ensure they are fully labeled and referenced in the text.

7. Reflection and Critical Thinking

Evaluate the Results: Reflect on the results you’ve obtained. Are there any anomalies or patterns that stand out? What do they tell you about the problem or model?

Limitations: Consider any limitations or assumptions in your work. For example, if you’re modeling real-world data, what factors might not have been considered in your model? What might change if you had more time or data?

Improvements: Discuss how the model or method could be improved or extended further. What would you do differently with more resources?

8. Write Clearly and Logically

Clear Structure: Follow the typical structure for an IA: Introduction, Exploration, Reflection/Conclusion. Ensure each section flows logically to the next.

Clarity and Precision: Write clearly and avoid unnecessary jargon. Your explanations should be precise, and your argument should be easy to follow.

Citations and References: If you use any external sources (like books, websites, or research papers), make sure to properly cite them. Use consistent citation methods, such as MLA, APA, or IB-specific guidelines.

9. Check the Criteria

Adhere to the IB Rubric: The IA is graded according to specific criteria. These include personal engagement, mathematical communication, use of mathematics, and reflection. Make sure that your IA addresses all of these elements thoroughly.

Proofread: Finally, proofread your IA for clarity, mathematical accuracy, and proper formatting. It’s also a good idea to have someone else read it for feedback.

10. Be Creative and Personal

Personal Engagement: The IB places a strong emphasis on personal engagement. Make sure your IA reflects your own interests, thoughts, and reflections. This could include choosing a topic you care about or reflecting on how you’ve learned from the process.

Originality: Try to bring something original to your IA, whether it’s a unique application of a mathematical concept or a new approach to solving a problem.

Example Structure of an IB Math SL IA

Introduction

Define the topic and research question.

Provide some background context and explain why the topic is interesting.

Mathematical Exploration

Discuss the methodology and mathematical concepts you will use to explore the problem.

Step-by-step explanation of the problem-solving process (including calculations, graphs, and analysis).

Reflection and Conclusion

Reflect on the results of your investigation.

Discuss any assumptions, limitations, and potential improvements.

Draw conclusions based on the findings.

References

Cite any sources, tools, or references used throughout the investigation.

Conclusion:

Writing an excellent IB Math SL IA involves selecting a topic that is both interesting and mathematically rich, applying appropriate mathematical techniques, and communicating your findings clearly. By ensuring that your IA is well-structured, mathematically rigorous, and reflects personal engagement with the topic, you’ll be well on your way to achieving a high mark.

[muveone]

How to calculate cubic feet?

Cubic feet are a unit of volume that is used to measure the space occupied by an object or a substance. It is commonly used in the United States, Canada, and the United Kingdom, especially for measuring the capacity of containers, rooms, appliances, and vehicles. Knowing how to calculate cubic feet can help you plan your move, pack your belongings, and estimate the cost of your removal service. In this article, we will explain how to calculate cubic feet using different methods and formulas.

Method 1: Using the dimensions of a rectangular object

The simplest way to calculate cubic feet is to use the dimensions of a rectangular object, such as a box, a crate, a fridge, or a sofa. A rectangular object has three dimensions: length, width, and height. To find the volume of a rectangular object in cubic feet, you need to multiply these three dimensions together. The formula is:

Volume = Length x Width x Height

For example, if you have a box that is 2 feet long, 3 feet wide, and 4 feet high, the volume of the box in cubic feet is:

Volume = 2 x 3 x 4

Volume = 24 cubic feet

If the dimensions of the object are given in inches, you need to convert them to feet first, by dividing them by 12. For example, if you have a fridge that is 36 inches long, 24 inches wide, and 60 inches high, the volume of the fridge in cubic feet is:

Volume = (36 / 12) x (24 / 12) x (60 / 12)

Volume = 3 x 2 x 5

Volume = 30 cubic feet

Method 2: Using the radius of a spherical object

Another way to calculate cubic feet is to use the radius of a spherical object, such as a ball, a globe, or a balloon. A spherical object has only one dimension: the radius, which is the distance from the center of the sphere to any point on its surface. To find the volume of a spherical object in cubic feet, you need to multiply the radius by itself three times, and then multiply the result by a constant number, which is 4.18879. The formula is:

Volume = 4.18879 x Radius x Radius x Radius

For example, if you have a ball that has a radius of 1 foot, the volume of the ball in cubic feet is:

Volume = 4.18879 x 1 x 1 x 1

Volume = 4.18879 cubic feet

If the radius of the object is given in inches, you need to convert it to feet first, by dividing it by 12. For example, if you have a balloon that has a radius of 6 inches, the volume of the balloon in cubic feet is:

Volume = 4.18879 x (6 / 12) x (6 / 12) x (6 / 12)

Volume = 4.18879 x 0.5 x 0.5 x 0.5

Volume = 0.5236 cubic feet

Method 3: Using the base area and the height of a cylindrical object

A third way to calculate cubic feet is to use the base area and the height of a cylindrical object, such as a can, a drum, or a pipe. A cylindrical object has two dimensions: the base area, which is the area of the circular base of the cylinder, and the height, which is the distance from the base to the top of the cylinder. To find the volume of a cylindrical object in cubic feet, you need to multiply the base area by the height. The formula is:

Volume = Base Area x Height

To find the base area, you need to use another formula, which is:

Base Area = 3.14159 x Radius x Radius

For example, if you have a can that has a radius of 0.5 feet and a height of 1 foot, the volume of the can in cubic feet is:

Base Area = 3.14159 x 0.5 x 0.5

Base Area = 0.7854 square feet

Volume = 0.7854 x 1

Volume = 0.7854 cubic feet

If the radius and the height of the object are given in inches, you need to convert them to feet first, by dividing them by 12. For example, if you have a drum that has a radius of 12 inches and a height of 36 inches, the volume of the drum in cubic feet is:

Base Area = 3.14159 x (12 / 12) x (12 / 12)

Base Area = 3.14159 x 1 x 1

Base Area = 3.14159 square feet

Volume = 3.14159 x (36 / 12)

Volume = 3.14159 x 3

Volume = 9.4248 cubic feet

[allmathtricks]

Volume and surface area of a three dimensional (3D) solid geometrical shapes.

[bscethereze-blog]

Nature of Mathematics

Hi there! Today we’re starting a new topic which Math is all around us! Yeah you read it it right. Everything we see in the world involves shapes.It is impossible to think of something without mathematics involve including technology,transport,money,electronics foods and many more. So What are shape? In Geometry, shape is a form or appearance of an object, As I did my research there is 2 types of shapes which two-dimensional that can be drawn in a flat surface examples are triangle and square or three-dimensional shapes which is a cylinder, rectangular prism and even sphere. As I look around I saw my mug just sitting in there and that gave me an idea the subject I would use in my blog. So as i do my research a mug is actually a three-dimensional you can move in from left to right, up and down,in and out.A three-dimensional shape like this is often called “volume”.If you start with circle and extend it along to a third dimension you now have 3D shape called cylinder you might have thought that we should call it a circular prism but technically prisms are shapes and are formed by extending one polygon and since we may have an idea that circle is not a polygon the resulting shape is not called prism,as what I remember there is a formula calculating this kind of 3D shapes which is you need to have is the are of a original 2D shape and multiply it by length or also called distance but in solving cylinder you need to solve the area of a circle is found by multiplying pi times its radius squared and once you know the area of a circle you now need it to  multiply that area by the length that the circle was extended. So that’s it for today guys I hope you learn something from me.Mwa

[ranvijay1singh]

What is the surface area of a sphere?

There are various geometrical figures that the students often come across. The sphere is one such concept that helps the students to learn and to compute the solutions as well.  

Few of the interesting facts that we all see is:

The geometrical shape of the sphere is always round and this can always be represented in the three dimensional space.

This is often defined as a flat figure as it does not have any sides and is a flat surface.

The volume of the sphere is calculated as 4/3 πr3

The volume of the sphere will always be equal to the surface area of the sphere and will be calculated by the formula 4πr2 

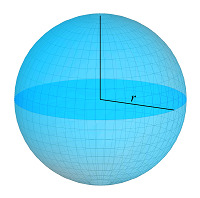
We can see the general representations of the sphere where we assume the distance from the center to the sides of the sphere as “R”.phere The other parameters are calculated based on the values.

Definition

In the geometrical applications, there are different other parameters also that we often see to define the sphere and the geometrical importance. So, a sphere is also defined as a geometrical round shape in three dimensional spaces. The sphere usually does not have any flat surface as we are not being able to define the sphere in terms of dimensions as in the length or breadth.

Unlike circle, that can also be explained in a plane shape or flat shape that is usually being defined in XY plane, in case of the sphere is defined in three dimensions, i.e. x-axis, y-axis and z-axis.

Important Facts:

A sphere is a symmetrical object that has all the dimensions defined in the same plane.

When we calculate the  surface points of sphere they are at equidistant from center

A sphere as a geometrical shape has only curved surface, no flat surface, no edges and no vertices.

Properties of a sphere

The sphere as a geometrical figure has few of the important features. These are also called attributes of sphere.

A sphere is a perfectly symmetrical shape that is represented in a 3D space.

It is not a polyhedron in nature.

All the points marked on the surface will be equidistant from the center.

The sphere does not have a surface of centers and will have a constant mean curvature

In case of the sphere there is a constant value for the width and circumference.

Shape of Sphere

The shape of a sphere is round where it does not have any faces. It should be noted that sphere is a geometrical three dimensional solid that have got curved surface. Like other solids, such as cuboid, cube, cone and cylinder, it does not have any flat surface or a vertex or an edge.

Now let us have a look at the real-life examples of sphere which are:

Basket balls

World Globe

Marbles

Planets

Moon

Equation of a Sphere

In the field of analytical geometry, if “r” is considered the radius, (x, y, and z) is said to be the locus of all points and (x0, y0, z0) is the center of a sphere, and then the equation of a sphere can be written as:

(x -x0)2 + (y – y0)2 + (z-z0)2 = r2

Formulas

As per statistics, the diameter is twice the radius. Therefore, diameter of a sphere is given as:

D = 2r units

Since we know that all the three-dimensional objects have the surface area and the volume, the surface area well as the volume of the sphere is explained so that we will be able to understand the system.

Surface Area of a Sphere

As the sphere is always represented in the 3D space, so a there is a mechanism to calculate the surface area... The formula of surface are is given by:

The Surface Area of a Sphere (SA) = 4πr2 Square units

Where “r” is considered the radius of the sphere.

Volume of a Sphere

This is so very important that we should be able to calculate the volume of the square as well.  This is often being defined as the amount of space occupied by the object three-dimensional object. The volume is to be calculated in many of the mathematical calculations as this will be able to give us the value addition and also the perfect representation on a scheduled space.

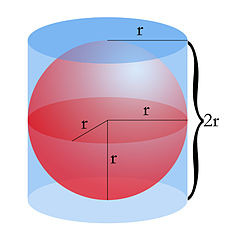
So, if we are to apply the Archimedes Principle, the volume of a sphere is given as,

The volume of Sphere (V) = 4/3 πr3 Cubic Units

The concepts are better explained in the online contents by

www.doubtnut.com It provides the latest materials to study along with online video tutorials that will help the students to understand the concept with ease. Moreover, there are doubts clearing sessions that are conducted that helps the students to identify their weakness and also build in the confidence. With their beautifully explained topics, Doubtnut are able to provide the students with the required materials to top up on their concept of learning and building in confidence.

[entrancei0012]

class 9 maths

The class 9 maths study material is available in PDF format which can be easily downloaded from our site. One can also access a very specific and examination focused strategy for class 9 maths by just simple signup at Entrancei. The sole idea has been to create a most accurate and detailed solution for class 9 maths that is free of cost. The experienced teachers at Entrancei have very extensively revealed the complete class 9 maths content. They have completely made sure all that is provided is important with respect to examinations. The class 9 maths solutions can be easily utilized for scoring good marks as one can reliably practice form them.

All the class 9 maths notes prepared as per the guidelines of CBSE Syllabus and guidelines. One can also go through test services for class 9 maths as it will help in gauging out the overall progress. The choosing union the class 9 maths optimum solutions helps in acing the students with the atmosphere of examination.

As general pattern, the class 9 maths should be taken very seriously as it helps in building strong concepts for further boards in 10th. The completecategorization of the syllabus of class 9 maths has been done in chapters, which helps students to easily go through it.

Ø  Chapter 1: Number systems

This chapter throws light upon number lines and how effectively they can be used. The class 9 maths solutions provided helps the students regarding laws of integral and rational powers of real numbers.

Ø  Chapter 2: Polynomials

The class 9 maths solutions to this unit give a vivid explanation about polynomials and their detailed terminologies. One will be acknowledged with various types of polynomials such as linear, Constant, quadratic and cubic polynomials.

Ø  Chapter 3: Coordinate Geometry

This chapters in class 9 maths help the students in understanding the concepts of Cartesian place and coordinates.

Ø  Chapter 4: Linear Equations in two Variables

This chapter in class 9 maths helps the students in understanding the equations presented in two variables. Plotting the equations on graph has been explained in a very detailed format in class 9 maths solutions provided.

Ø  Chapter 5: Introduction to Euclid’s Geometry

This chapter of class 9 maths throws minor lights upon how Indian history is associated with Geometry followed in the world. One will be explained regarding the geometry through axiom, Postulates, and Theorems of class 9 maths in detailed format.

Ø  Chapter 6: Lines and Angles

The chapter as lines and angles is generally asked as theorems and postulates in class 9 mathsexaminations. The level of difficulty is very minor compared to other units.

Ø  Chapter 7: Triangles

In this chapter of class 9 maths, you will study regarding the congruence of triangles and their associating theorems. This chapter of class 9 maths has various properties such as inequalities and properties in triangles.

Ø  Chapter 8: Quadrilaterals

This chapter of class 9 maths comprises of only one theorem as proof. Questions asked in this chapter are relatively very easy.

Ø  Chapter 9: Areas of Parallelograms and Triangles

One will be brought to the note of areas in geometrical shapes. The examples of the median can be used in various examples of this in class 9 maths of chapter.

Ø  Chapter 10: Circles

This chapter of class 9 maths gives brief insights about subtended angle chord, equal chords, Arc of the circle, cyclic quadrilaterals. This detailed solution of theorems based on triangles, Quadrilaterals, and circles are based in this chapter.

Ø  Chapter 11: Constructions

This chapter throws light upon bisecting and creating line segments to angles and lines. The student’sclass 9 maths would be learning the creation of triangles with different properties and different base angles.

Ø  Chapter 12: Heron’s formula

This chapter of class 9 maths comprises of only three exercises. This chapter givesan extension to the application of heron’s formula in polygons and quadrilaterals and triangles.

Ø  Chapter 13: Surfaces Areas and Volumes

The students need not be introduced with this topic as they well studied the mensuration in their earlier classes. One would be acknowledged with volumes of cubes, cylinders, spheres, cones, and the hemisphere’s in their class 9 maths syllabus.

Ø  Chapter 14: Statistics

The statistics chapter of class 9 maths is like a simple method of collection of data in different aspects. In total, this chapter of class 9 maths helps one to find the measure of central tendency, mean, median and mode of any raw data provided.

Ø  Chapter 15: Probability

With only about 1 exercise in class 9 maths, this chapter is very easy. This is based on observation and frequency of day to day examples.

 Why choose Entrancei

 There might be times when students are stuck with exercises, so there comes the team of Entrancei with an innovative solution to class 9 maths students. The students can any time give a call in order to get their doubts resolved associated with class 9 maths.

[ss1986us]

ncert solutions for class 9 maths

Brace up like scholars

https://www.entrancei.com/topics-topics-class-9-mathematics

 The class 9 maths study material is available in PDF format which can be easily downloaded from our site. One can also access a very specific and examination focused strategy for class 9 maths by just simple signup at Entrancei. The sole idea has been to create a most accurate and detailed solution for class 9 maths that is free of cost. The experienced teachers at Entrancei have very extensively revealed the complete class 9 maths content. They have completely made sure all that is provided is important with respect to examinations. The class 9 maths solutions can be easily utilized for scoring good marks as one can reliably practice form them.

While going through the maths subject Maths formula can help you a lot so do read and revise entire maths formula from entrancei.

All the class 9 maths notes prepared as per the guidelines of CBSE Syllabus and guidelines. One can also go through test services for class 9 maths as it will help in gauging out the overall progress. The choosing union the class 9 maths optimum solutions helps in acing the students with the atmosphere of examination.

As general pattern, the class 9 maths should be taken very seriously as it helps in building strong concepts for further boards in 10th. The complete categorization of the syllabus of class 9 maths has been done in chapters, which helps students to easily go through it.

Ø  Chapter 1: Number systems

This chapter throws light upon number lines and how effectively they can be used. The class 9 maths solutions provided helps the students regarding laws of integral and rational powers of real numbers.

Ø  Chapter 2: Polynomials

The class 9 maths solutions to this unit give a vivid explanation about polynomials and their detailed terminologies. One will be acknowledged with various types of polynomials such as linear, Constant, quadratic and cubic polynomials.

Ø  Chapter 3: Coordinate Geometry

This chapters in class 9 maths help the students in understanding the concepts of Cartesian place and coordinates.

Ø  Chapter 4: Linear Equations in two Variables

This chapter in class 9 maths helps the students in understanding the equations presented in two variables. Plotting the equations on graph has been explained in a very detailed format in class 9 maths solutions provided.

Ø  Chapter 5: Introduction to Euclid’s Geometry

This chapter of class 9 maths throws minor lights upon how Indian history is associated with Geometry followed in the world. One will be explained regarding the geometry through axiom, Postulates, and Theorems of class 9 maths in detailed format.

Ø  Chapter 6: Lines and Angles

The chapter as lines and angles is generally asked as theorems and postulates in class 9 maths examinations. The level of difficulty is very minor compared to other units.

Ø  Chapter 7: Triangles

In this chapter of class 9 maths, you will study regarding the congruence of triangles and their associating theorems. This chapter of class 9 maths has various properties such as inequalities and properties in triangles.

Ø  Chapter 8: Quadrilaterals

This chapter of class 9 maths comprises of only one theorem as proof. Questions asked in this chapter are relatively very easy.

Ø  Chapter 9: Areas of Parallelograms and Triangles

One will be brought to the note of areas in geometrical shapes. The examples of the median can be used in various examples of this in class 9 maths of chapter.

Ø  Chapter 10: Circles

This chapter of class 9 maths gives brief insights about subtended angle chord, equal chords, Arc of the circle, cyclic quadrilaterals. This detailed solution of theorems based on triangles, Quadrilaterals, and circles are based in this chapter.

Ø  Chapter 11: Constructions

This chapter throws light upon bisecting and creating line segments to angles and lines. The student’s class 9 maths would be learning the creation of triangles with different properties and different base angles.

Ø  Chapter 12: Heron’s formula

This chapter of class 9 maths comprises of only three exercises. This chapter gives an extension to the application of heron’s formula in polygons and quadrilaterals and triangles.

Ø  Chapter 13: Surfaces Areas and Volumes

The students need not be introduced with this topic as they well studied the mensuration in their earlier classes. One would be acknowledged with volumes of cubes, cylinders, spheres, cones, and the hemisphere’s in their class 9 maths syllabus.

Ø  Chapter 14: Statistics

The statistics chapter of class 9 maths is like a simple method of collection of data in different aspects. In total, this chapter of class 9 maths helps one to find the measure of central tendency, mean, median and mode of any raw data provided.

Ø  Chapter 15: Probability

With only about 1 exercise in class 9 maths, this chapter is very easy. This is based on observation and frequency of day to day examples.

 Why choose Entrancei

 There might be times when students are stuck with exercises, so there comes the team of Entrancei with an innovative solution to class 9 maths students. The students can any time give a call in order to get their doubts resolved associated with class 9 maths.

[maffsguru]

Surface areas and volumes of spheres | Year 10 Advanced | MaffsGuru.com

Download lesson notes and watch this video: https://www.maffsguru.com/

This video looks at the final section of the Year 10 textbook and covers the surface area and volume of a sphere (and hemispheres!). There are a number of worked examples which look at using the formulae to find the surface area and volume of spheres and hemispheres. I look at how to do this using pencil and paper methods as well as using the CAS.

#maffsguru #education #students #year9 #year9maths #school #mathematics #teaching #classroom #teachers #iteachmath #maths #onlinelearning #grade9maths #learnonline #mathsfun

[allmathtricks]

In this article provided formulas of Surface Area and Volume of a Sphere and a Hemisphere with examples.

[lovewimc]

center of mass physics

Center of mass Physics

Today our topic is center of mass Physics. This topic is very important to understand better Physics. Without understanding concept of center of mass Physics, It will not be easy for you to understand better Physics, So try to understand center of mass physics.

In previous post we have already study center of mass basic concept for continuous mass distributed body. You can refer previous post Center of mass formula .But here we will study center of mass for hollow and solid hemisphere with easy concept.   

(adsbygoogle = window.adsbygoogle || []).push({});

What is center of mass Physics ?

Center of mass of  a body is that point where whole mass of the body is concentrated it can lie within the body or outside the body depends upon the shape of the body.

Why need to study center of mass Physics ? 

In Practical every rigid body has some shape and size . If the body comes in motion then every point on rigid body have different velocity and acceleration. 

Suppose a rigid body of some mass m is rotating about its axis as well as translate. Every point on rigid body will have different velocity and acceleration.

It is really difficult to calculate velocity and acceleration of all point on rigid body.

Hence there is a single point where whole mass is concentrated is called center of mass and that point velocity and acceleration is consider as whole body velocity and acceleration.

Hence that special point is called center of mass.

We know that Newton's second law . Fnet = ma, p = mv. Here in this case "a" and "v"  is acceleration of center of mass  and "v" velocity of center of mass. If any body do combined motion rotational and translational then its path analysis will be easy, When we sit on center of mass and analyse body other particle motion.

Generally center of mass path is easy like (straight line, Circle, Projectile)       

Hence you can think the importance of center of mass.

Fnet  = ma equation has two important condition

Here "a" is acceleration of center of mass and m is a point mass.This is reason we need to study center of mass physics.

Practical uses and Application of center of mass Physics 

The center of mass plays an important role in astronomy. The barycenter is the point between two objects where they balanced each other. 

It is the center of mass where two or more celestial bodies orbit each other. When a moon orbits a planet or a planet orbits a star, both bodies are actually orbiting around a point that lies away from the center of the large bodies.

For example the moon does not orbit the exact center of the earth but a point on a line between the center of the earth and the moon, approximately 1710 km below the surface of the earth. Where their respective masses are balanced. This is the point about which the earth and moon orbits.

Automotive applications  engineers try to design sport car so that its center of mass is lowered to make the car handle easy.

Also uses in aeronautic, high jumping .

Now i think you have understand the importance of center of mass.

How to find hollow hemispherical center of mass ? 

                                                                (adsbygoogle = window.adsbygoogle || []).push({});

Center of mass hollow hemisphere

                                                                        From the figure it is clear that mass is distributed over the surface area of hollow hemisphere. One thing is clear that hollow hemisphere is symmetric about x axis means positive x axis (right side) and negative x axis (left side) mass distribution is same. 

Hence Xcm will no need to calculate it will be at origin for Xcm.

Along y axis its mass is different for different value of y.

Let total mass of hollow hemisphere is M and its radius is R, Now taking a elemental ring of mass dm, now the thickness of elemental ring will be Rdϴ as shown in figure.

Now the radius of elemental ring is Rcosϴ  as shown above figure. Now the Ring above the origin that is y = Rsinϴ as shown in figure.

Ycm  = ∫ ydm/∫dm  now put the value of y  =  Rsinϴ 

Now dm can't be integrated, Because  dm is not written in terms of y, Hence we need to find out the mass of elemental dm first.

So to find out the mass of elemental ring, we have to consider surface mass density. which is define as mass per unit surface area, It is denoted by 𝞼 .

Hence  𝛔  = M/A = M/2𝛑R²   Since mass is only distribute on surface area of hollow sphere 

So we can write 𝛔 =dm/dA or dm  = 𝛔dA.

Now we can calculate the area of elemental ring and it will be area .

of elemental circle of radius Rcosϴ and thickness Rdϴ.

Hence Area = 2𝛑Rcosϴ*Rdϴ So for elemental area  dA =   2𝛑Rcosϴ*Rdϴ  hence from here dm = 𝛔*2𝛑Rcosϴ*Rdϴ.

Now use the equation for Ycm  = ∫ ydm/∫dm  = ⎰Rsinϴ *𝛔*2𝛑Rcosϴ*Rdϴ/M 

Here ∫dm = M  since total mass is M.

(adsbygoogle = window.adsbygoogle || []).push({});

Ycm  = R³*𝛔*𝛑*1/M⎰2sinϴ*cosϴdϴ now putting value of 𝛔 and 2sinϴ*cosϴ = sin2ϴ then 

Ycm  = R³xM/2𝛑R²x𝛑/M⎰sin2ϴdϴ now take limit from 0 to 𝛑/2 total mass will be cover hence after simplification we will get .

                   𝛑/2 

Ycm  = R/2⎰sin2ϴdϴ

                  0

                               𝛑/2

Ycm  = R/2⎡-cos2ϴ/2⎤   now put the value we will get 

                                  0

 Ycm  = R/2 (2/2) = R/2  , Ycm = R/2 

Center of mass for solid hemisphere  

Solid hemisphere can be made by many hollow hemisphere so we will use this technique to find the center of mass for solid hemisphere.

                                                            This is 3-D because it is solid lets suppose an elemental strip is taken from origin at a r distance then just we have seen in case of hollow hemisphere its center of mass is at r/2 distance from origin.

Hence this elemental strip center of mass will be at r/2 distance from origin as shown above figure 

Now apply center of mass formula  Ycm  = ∫ ydm/∫dm .

Here it is clear y = r/2 

now this is solid so its mass density will be mass per unit volume and it is denoted by 𝛒 

  𝛒  = M/V  = M/(2x𝛑r³)/3 = 3M/2x𝛑r³  since half volume of solid sphere 

Ycm  =  ⎰r/2dm/⎰dm  = ⎰r/2dm/M  ⎰dm = M.

Since total mass is M

now for dm mass dm/dv  =𝛒  or dm  = 𝛒dv 

(adsbygoogle = window.adsbygoogle || []).push({});

now for dv  = Area x thickness  = 2𝛑r²xdr

dm  = 𝛒2𝛑r²dr  now put the value in above equation we will get 

Ycm  = ⎰r/2x𝛒2𝛑r²drx1/M  =  put  𝛒 = 3M/2𝛑r³

            R

Ycm = ⎰r/2*3M/2𝛑r³*2𝛑r²dr/M  after simplification and integration we will get 

           0

Ycm  =   3R/8 

Now we will continue in next post. I hope you have enjoyed learning Center of mass Physics .If you like comment and share thanks for learning and share.

Dated 3rd Nov 2018                                 

     via Blogger https://ift.tt/2qqPFkf

[racketnews]

Why are 2/3rds of US children ‘not proficient’ in math? Leading teacher demonstrates: texts LIE about ‘real-world math problems’, stupefy children to tune-out from counting what’s most important (like US .01% admitting they ‘lost’ $21 TRILLION of taxes)

*hyperlinks/videos live at source* hat tip: David Icke The US Department of Education reports that two-thirds of American school children are not proficient in mathematics (here, here). In 2016 I wrote an article series about public education that includes a section on math that documents: 1. Math texts lie about “real world math problems” with ridiculous and contrived word problems. 2. Math texts don’t even care to define mathematics or algebra. 3. Algebra 1 fail rates are up to 50% of students, and is connected to the above two points along with less than 1% of adults using algebraic formulas in work. The outcomes of such “education” include: 1. Americans concluding “math” is difficult and something to tune-out from; stupefying us from counting what’s most important in Life like US .01% “leaders” admitting they “lost” $21 trillion of our taxes (~$200,000 per average US household). Please pause to let that fact penetrate. 2. Training Americans as work animals to blindly obey a rogue state empire. 3. Americans blaming themselves as being “bad” at math, and too stupid to seriously engage in the numbers associated with competent citizenship. Math-hole Ph.D text author LIARS Those of us who apply mathematics to quantify reality, understand as comprehensively as possible what exists, and use math as a scorecard to upgrade real-world conditions abhor liars. Fraudulent data makes it impossible to understand the real world, misdirects our attention and work, and wastes valuable time. As you know, professionals quickly dismiss proven liars, and remove them from serious work. Again, look here for three examples of typical lying math word problems, that cannot be excused as anything but intentional lying with rejection to consult with anyone doing real-world work. Here are three more from the 1,200 page Algebra 1 text provided to my students. These are typical: From Module 14 Rational exponents and radicals, consider this claimed “real-world problem” on page 660: “The balls used in soccer, baseball, basketball, and golf are spheres. How much material is needed to make each of the balls in the table? The formula for the surface area of a sphere is 4????r2 and the formula for the volume of a sphere is V = 4/3????r3 . Use algebra to find the formula for the surface area of a sphere given its volume.” (table provided for the four balls’ volumes) Paraphrasing usual student observations: Oh my balls! Are these things empty of “material” and only have surface area?! This says the balls have nothing inside. Maybe the math-hole authors have the same problem of nothing inside their heads. Maybe so because they didn’t ask anyone who actually makes those balls. Golf balls are not spheres. It’s some other fucking shape with all those dimples. Not that this matters because I think the shit inside the ball is just as important as the outside cover for the ball to be any good for that sport. Yeah, we should just judge those balls by the cover and not look inside, just like we should ignore what’s inside our math book. People who use balls want to be good in those sports. Nobody good at those sports ever ever ever ever ever even thought of such a dumb-ass problem to waste their time. From Module 22 Using square roots to solve quadratic equations, consider this claimed “real-world problem” on page 894: “A contractor is building a fenced-in playground at a daycare. The playground will be rectangular with its width equal to half its length. The total area will be 5000 square feet. Determine how many feet of fencing the contractor will use.” Paraphrasing usual student observations: WTF (what the fence)? Just fence and no gates? Real contractors charge extra for gates ‘cuz they take more time. Are they going to throw the kids over the fence, dig a tunnel, or put slides over it for kids to get in and out? Where is the building where kids are inside??? The daycare isn’t connecting the fence to the building?! Nobody would do that. The kiddie cage the math-hole authors say is real isn’t at an existing daycare ‘cuz they’d already have a fence to keep the kids safe. Maybe a replacement fence would be real, but not this shit with a convenient 5,000 exact square feet that just happens to be a number that works evenly for a word problem about square roots. And anyway, if they know the area is 5,000, then they already know the width and length and don’t need to ask anyone. From Module 19 Graphing quadratic functions, consider this claimed “real-world problem” on page 1037 (with picture of a parabola): “Describe what the vertex, y-intercept, and endpoint(s) represent in the situation, and then determine the equation of the function. This graph models the depth in yards below the water’s surface (y-axis) of a dolphin before and after it rises to take a breath and descends again. The depth (d) is relative to time (t, in seconds as the x-axis), and t=0 when the dolphin reaches a depth of 0 yards at the surface.” Paraphrasing usual student observations: Wait. The math-holes say a dolphin swims up to zero to “take a breath.” The graph shows air as the positive numbers, and water in negative numbers. This means these dumb-x authors violate the definition of zero and don’t even notice :) No animal moves at perfectly constant speed in a perfect parabola. This is bullshit. So these authors find nothing in reality to show us other than these fake puzzles. Nice. The graph the math-holes give us show a speed of about 50 mph at 4 seconds before and after the fake “breath” where there’s no air. Is this a magic rainbow dolphin that’s the fastest in the universe? Will the magic dolphin be going 5,000 mph or so 10 seconds from the fake air? What’s an educated person to do? Call bullshit for what it is to expose liars, remove the liars, and rebuild with truth. Again, I wrote a series on the problem of bullshit public education. Next: see the bigger pattern of lies and empire, and remove those liars through lawful arrests: When Americans are told an election is defined by touching a computer screen without a countable receipt that can be verified, they are being told a criminal lie to allow election fraud. This is self-evident, but Princeton, Stanford, and the President of the American Statistical Association are among the leaders pointing to the obvious (and here, here, here, here, here, here, here, here, here, here, here, here, here, here, here, here, here, here, here). Again, no professional would/can argue an election is legitimate when there is nothing for anyone to count. The facts show Bernie Sanders won the Democratic Primary election, and claims by Democratic “leadership” of Russian election “meddling” are without factual documentation. US military now illegally occupy eight bases in Syria (and here), with escalating bombing of Syria and Iraq of over 4,000 bombs/month and over 84,000 since 2014. The US acknowledges ~500 civilian deaths from these bombs, with independent count of ~750 in just in June 2017. Among dozens of independent writers, I’ve documented that all “reasons” for wars on Iran, Syria, and Russia are easily proved lies (recently, here, here, here, and going back to 2005), with US Department of illegal Wars of Aggression (so-called “Defense”) claiming to have “lost” $65,000 for every US household. The US is a literal rogue state empire led by neocolonial looting liars. The history is uncontested and taught to anyone taking comprehensive courses. If anyone has any refutations of this professional academic factual claim for any of this easy-to-read and documented content, please provide it. Rogue state empire is the most accurate term to describe the US for the following reasons: People around the world view the US as the greatest threat to peace; voted three times more dangerous than any other country. The data confirm this conclusion: Since WW2, Earth has had 248 armed conflicts. The US started 201 of them. These US-started armed attacks have killed ~30 million and counting; 90% of these deaths are innocent children, the elderly and ordinary working civilian women and men. The US has war-murdered more than Hitler’s Nazis. The total deaths caused by rogue state empire for resource control (natural and human) in the last 20 years is ~400 million, more than all total wars and violence in all recorded Earth history. US ongoing lie-started and Orwellian-illegal Wars of Aggression require all US military and government to refuse all war orders because there are no lawful orders for obviously unlawful wars. Officers are required to arrest those who issue obviously unlawful orders. And again, those of us working for this area of justice are aware of zero attempts to refute this with, “War law states (a, b, c), so the wars are legal because (d, e, f).” All we receive is easy-to-reveal bullshit. The destruction of nearly all rights lawfully guaranteed in the US Bill of Rights within the US Constitution, and in Orwellian inversion of limited government. Corporate media are criminally complicit through constant lies of omission and commission to “cover” all these crimes. Historic tragic-comic empire is only possible through such straight-face lying, making our Emperor’s New Clothes analogy perfectly chosen. The top three benefits each of monetary reform and public banking total ~$1,000,000 for the average American household, and would be received nearly instantly. Please read that twice and imagine the connection between having a rogue state empire to enrich an oligarchy combined with internal financial manipulation to maximize those parasitical riches. Now look to verify for yourself. Iran has never threatened to “wipe Israel off the map” and only has IAEA-verified legal energy and medicine programs with nuclear materials. Trump and corporate media continues and escalates easily-verified lies to threaten more illegal war on Iran. Israel engages in lie-started and illegal War of Aggression on Gaza; ironically the largest concentration camp in world history. This is also easy to verify. Categories of crime include: Wars of Aggression (the worst crime a nation can commit). Likely treason for lying to US military, ordering unlawful attack and invasions of foreign lands, and causing thousands of US military deaths. Crimes Against Humanity for ongoing intentional policy of poverty that’s killed over 400 million human beings just since 1995 (~75% children; more deaths than from all wars in Earth’s recorded history). US military, law enforcement, and all with Oaths to support and defend the US Constitution against all enemies, foreign and domestic, face an endgame choice: Demand arrests, with those with lawful authority to enact it. An arrest is the lawful action to stop apparent crimes, with the most serious crimes documented here meaning the most serious need for arrests. Watch the US escalate its rogue state crimes that annually kill millions, harm billions, and loot trillions. In just 90 seconds, former US Marine Ken O’Keefe powerfully states how you may choose to voice “very obvious solutions”: arrest the criminal leaders (video starts at 20:51, then finishes this episode of Cross Talk): 3-minute video: Police, Military – Was your Oath sincere? I make all factual assertions as a National Board Certified Teacher of US Government, Economics, and History (also credentialed in Mathematics), with all economic factual claims receiving zero refutation since I began writing in 2008 among Advanced Placement Macroeconomics teachers on our discussion board, public audiences of these articles, and international conferences (and here). I invite readers to empower their civic voices with the strongest comprehensive facts most important to building a brighter future. I challenge professionals, academics, and citizens to add their voices for the benefit of all Earth’s inhabitants. ** Carl Herman worked with both US political parties over 18 years and two UN Summits with the citizen’s lobby, RESULTS, for US domestic and foreign policy to end poverty. He can be reached at Carl_Herman@post.harvard.edu Note: My work from 2012 to October, 2017 is on Washington’s Blog. Work back to 2009 is blocked by Examiner.com (and from other whistleblowers), so some links to those essays are blocked. If you’d like to search for those articles other sites may have republished, use words from the article title within the blocked link. Or, go to http://archive.org/web/, paste the expired link into the box, click “Browse history,” then click onto the screenshots of that page for each time it was screen-shot and uploaded to webarchive (blocked author pages: here, here). http://dlvr.it/QSlmDC

[omgchristine-blog1]

Volume formulas

     The formulas that we learned are for sphere, prisms, pyramids, and cone. It’s like the surface area but different formulas. The sphere formula is 4/3(pi)r^3. The formula for prisms is V=Ah.And, the formula for pyramid is 1/3ah. Finally, the formula for cone is (pi)r^2h/3.

   These were easy for me to solve for. Luckily, I didn’t have to use the quadratic formula for any of these. I understand how to solve these now because of ALL  the work and examples that was given to us. And, we didn’t have a choice but to do it so that we could get a grade. 

[dupont]

Think back to geometry class. Remember Pi? It’s still one of the most important mathematical constants around, and the history behind it might surprise you.

On March 14, mathematicians, physicists, students and teachers around the world will observe Pi Day, a celebration of what has become the most famous number in all of mathematics. Pi is the ratio of the circumference of a circle to its diameter, roughly 3.14. This ratio is true of any circle, no matter how big or small.

Pi is an essential component for the formulas that calculate the area of a circle or the volume of a cylinder, which, granted, none of us do very often. But there’s more. Want to know how much material it will take to manufacture a basketball? Pi is involved (in calculating the surface of a sphere). Need to plot the frequency of sound waves? Pi is involved (in measuring sine waves). Need to calculate the orbit of a satellite? You’ll need Pi.

Pi also appears in dozens of formulas that are not well known outside of mathematical circles, but are nonetheless important. “Whenever there’s something circular going on, or any type of periodicity, Pi is lurking around somewhere,” says Joseph Mazur, author of Enlightening Symbols, a Short History of Mathematical Notation. “It appears in very unexpected places. If you relate the actual length of a river — following the curves — to its length end-to-end as the crow flies — you get a number very close to Pi.”

“Just about everyone’s used Pi in calculations at some point,” says Gayle Gibson, Director of DuPont Engineering. She also says that DuPont engineers use it every day to help improve products and meet customer needs.

Ancient History

Pi has been around for a long time. There’s evidence that the Babylonians and ancient Egyptians were aware of Pi. The first formal approximation of its value was calculated by the famous Greek mathematician, Archimedes (287–212 BC).

Approximation is the key word here, as is clear from his method. First, he inscribed a regular polygon that fit as closely as possible inside a circle. Then he circumscribed another regular polygon that fit as closely as possible outside the same circle. Neither polygon would exactly represent the circumference of the circle, but he reasoned (correctly) that the circumference would lie somewhere in between. From this approach, he concluded that the value of Pi lies between 22/7 and 223/71.

With this method, it’s obvious that the more faces the two polygons have, the closer the approximation will be. Using two squares, for example, would not be nearly as accurate as using two octagons, and so on. With a geometrical approach, it’s possible to inscribe and circumscribe a circle with polygons that have many more faces — thousands, millions, even billions using a super computer — to get a closer and closer approximation.

Unfortunately for those who look to mathematics for the ultimate in precision, Pi is an irrational number. This means that, when expressed in decimals, it produces a string of digits that never ends, and never repeats any pattern in the unending string. With each decimal, you get closer to the truth, as it were, but you can never quite get there.

What’s in a Name?

Until relatively recently, 3.14159265359 was known only by a Greek name (Pi) that when translated, meant “the quantity which, when the diameter is multiplied by it, yields the circumference.” William Jones, a little-known math teacher in England, first proposed the name Pi in 1706. It became internationally accepted when one of the most famous mathematicians of all time, Leonhard Euler, began using it in 1737. Some Pi fans believe that the Greek letter Pi was chosen because it is the first letter of perimeter, but this is not certain.

The idea of a holiday to celebrate the world’s most well-known numerical constant was “invented” by Larry Shaw, a now-retired physicist at The Exploratorium, a science museum in San Francisco. What began as a modest march followed by the consumption of fruit pies, has become a holiday celebrated worldwide.

Although it seems that Pi will continue to reign supreme in the realm of special numbers, it does have one important challenger. That’s Tau, which is the ratio of a circle’s circumference to its radius, roughly 6.28. The use of this alternative was first proposed in the now famous article, “Pi Is Wrong,” published by University of Utah math professor Bob Palais in 2001. Tauists, as they call themselves, celebrate Tau Day on June 28 (6.28, of course). They offer persuasive arguments related to both the teaching and practice of math and engineering, but it’s unlikely they’ll ever succeed in toppling Pi from its throne.

For now, we’ll continue to celebrate Pi as the king of special numbers.