Don't wanna be here? Send us removal request.
Text
ART NOUVEAU & SUCESSION DE VIENA



HAZ ZOOM PARA VER MEJOR LA INFO:)
0 notes
Text
LA REVOLUCIÓN INDUSTRIAL Y SU RELACIÓN CON EL DISEÑO.

#REVOLUCIÓNINDUSTRIAL
0 notes
Text
Breve ensayo sobre el Juicio Crítico y la Crítica del Arte.
Empezando por lo que es, a mis palabras, el juicio crítico, sería aquella capacidad que tiene el ser humano, la virtud que hace que razonemos correctamente, esto nos hace ser un buen observador con disciplina lógica. Nos hace reaccionar de forma razonable frente a situaciones y conocer su realidad siguiendo reglas lógicas que permitan conclusiones válidas. Pese a ello, para tener un buen y válido juicio crítico, es necesario tener pleno conocimiento acerca de las cosas que engloban al elemento criticado, dado que si no se tuviera dicho conocimiento, el juicio carecería de valor y sería solamente un simple comentario u opinión.
La crítica de arte es un género, entre literario y académico e incluso periodístico, que hace una valoración estética sobre las obras de arte, artistas o exposiciones, en principio de forma personal y subjetiva, pero basándose en la Historia del arte y sus múltiples disciplinas.
La crítica, establece la relación entre obra y observador, a través de la mirada del crítico. Comienza en el momento en que miras una obra y decides si te gusta o no te gusta. En el momento en que se produce este acercamiento tus sentidos reaccionan, se activa tu curiosidad y empiezan las preguntas. Quieres saber más de la obra para averiguar por qué te gusta, o por qué no te gusta.
Si se tiene conocimiento de los métodos para la crítica del arte, por consiguiente sería mucho más práctico y eficaz la crítica sobre la obra, estos métodos pueden ser de acuerdo al enfoque que el crítico quiera dar, como son el método sociológico, método biográfico, método formalista, método iconográfico, método historicista, método de interpretación Artística, entre otros.

0 notes
Text
Estudio Sociológico sobre la Pintura de José Clemente Orozco, titulada "Desmembramiento"

En El desmembrado se representan las extremidades de un indígena decapitado durante una batalla, distinguiéndose una paleta de intensos colores. El artista subrayó las líneas diagonales que determinan la estructura de la composición y empleó gruesos empastes para perfilar los pies, las piernas, la cabeza y los miembros. El cuerpo descoyuntado simbolizaba la destrucción del mundo indígena. Cabeza flechada.
Se refiere a una consecuencia de la lucha armada de la conquista. Aquí se visualiza la cabeza de un hombre barbado y calvo, probablemente un español, atravesado por seis saetas en diversas partes de su rostro. La violencia explícita de la obra se acentúa gracias a su formato monumental y su paleta casi monocroma basada en tonos grises y azules. Ante la ausencia de elementos descriptivos, la mirada del espectador se concentra en el realismo y crueldad expresiva de esa escena.
0 notes
Text
El análisis del arte.
Introducción.
A lo largo de la historia han sido los numerosos textos que se han producido analizando y reflexionando sobre las diferentes expresiones artísticas
La valoración de una obra de arte exige el conocimiento de diferentes métodos, porque ningún método es capaz por sí mismo agotar los diferentes aspectos de las manifestaciones artísticas.
Desarrollo.
*Giorgio Vasari (1511-1574): tiene una aproximación critica a través del conocimiento de la biografía del artista. Método biográfico.
* Joachim Winckelmann (1717 - 1768): clasificó las obras de artes en estilos. Método historicista.
* Hyppolyte Tine ( 1828 - 1892): también clasificó las obras artísticas en estilos pero teniendo en cuenta su contexto. Método positivista.
* Aloïs Reigl (1858-1905), Heinrich Wölfflin (1864-1945) : estos dos concordaron que el estudio de la forma se constituye como elemento vertebrador del análisis. Metodo formalista.
* Wilhelm Worringer (1881-1965): centra su examen en el estudio y el análisis de las preferencias subjetivas hacia las formas. Empatía de percepción.
* Rudolr Arnheim (1904-2007): La composición es el elemento portador de significado en una obra de arte.
*Carl Gustav Jung (1875-1961): proceso de simbolización y la pervivencia de dichos símbolos en la mente del ser humano. Arquetipo.
* Erwin Panofsky (1982-1968): significación intrínseca de la imagen, analisis iconografico descriptivo, analisis iconografico interpretativo. Interpretación de la imagen.
* Arnold Hauser (1892-1978): el arte de asume una serie de funciones con expresiones de tipo: poder, ideologías, instrumentos de culto y ocio etcétera.
* Umberto Eco (1932- ): todo objeto artístico adquiere sentido a partir de una estructura comunicativa e interna. La capacidad comunicativa del lenguaje.
1 note
·
View note
Text
UNIDAD #4: Derivadas de una Función.
Comencemos explicando de forma sencilla qué es una derivada. Se entiende como la variación que experimenta la función de forma instantánea, es decir, entre cada dos puntos de su dominio suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales.
es una herramienta matemática para ello Isaac Newton desarrolló los principios del cálculo diferencial en su obra Methodus Fluxiorum et Serierum Infinitorum (1671). En ese trabajo, da los pasos precisos alrededor de los conceptos de función y de límite, que le permiten plantear matemáticamente cuando las cantidades varían infinitesimalmente y, de esta forma, describir el movimiento de un punto que traza una curva.
Derivada de una función en un punto
Dada una función f (x), y considerado un punto a de su dominio, se llama derivada de la función en ese punto, denotada como f ¿ (a), al siguiente límite:

Este límite también puede expresarse de las dos formas alternativas siguientes:

Interpretación geométrica de la derivada
La definición de derivada tiene mucho que ver con el concepto de variación instantánea. Teniendo en cuenta que el cociente:

expresa la pendiente de la recta que pasa por (a, f (a)) y (b, f(b)), es lógico pensar que si b y a están muy próximos entre sí, separados por un valor h que tiende a cero, esta recta se aproximará a la recta tangente a la función en el punto x = a.
Tal es la interpretación geométrica de la derivada de una función en un punto: coincide con la pendiente de la recta tangente a la función en dicho punto.

Derivadas laterales
Como sucedía con los límites, se pueden definir los conceptos de derivadas laterales de una función en un punto.
Dada una función f (x) y considerado un punto a de su dominio de definición, se define su derivada por la derecha, y se denota como f ¿ (a+), al límite siguiente:

Por su parte, la derivada por la izquierda de f (x) en el punto a, denotada por f ¿ (a-), se define como el siguiente límite:

Una función se dice derivable cuando tiene derivadas por la derecha y por la izquierda, y sus valores coinciden.
Aquí un vídeo:
youtube
Regla de los cuatro pasos: La derivada de una función también se puede obtener como el límite del cociente de incrementos, conocido como la regla de los cuatro pasos.
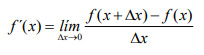
El procedimiento en este caso consiste en los pasos siguientes:

En la aplicación de esta regla, además de las operaciones de factorización que ya recordamos, será necesario utilizar el desarrollo de binomios como:

Y también recordar cómo racionalizar el numerador o denominador de una fracción. Veamos otros ejemplos para obtener la derivada de una función, aplicando esta definición de la regla de los cuatro pasos.
Ejemplo #1 Obtén la derivada de la función:

Solución:

Ejemplo #2 obtén la derivada de la función:
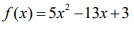
Solución:


Ejemplo #3 obtén la solución de la derivada:
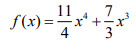
Solución:

youtube
0 notes
Text
calculo Unidad #3
Límite en un punto infinito: Decimos que el límite de f(x) cuando x tiende a más infinito (+∞) es L si la función toma valores cada vez más cercanos a L cuando x crece indefinidamente.Lo expresamos mediante
Limites de una funcion: Para la matemática, un límite es una magnitud fija a la que se aproximan cada vez más los términos de una secuencia infinita de magnitudes.
Se dice que una función f (x) tiene límite L en el punto x = a, si es posible aproximar f (x) a L tanto como se quiera cuando x se acerca indefinidamente a a, siendo distinto de a. En términos matemáticos, se expresa como:

Propiedades de los límites
Dadas dos funciones f(x) y g(x) que tienen límite en un punto a, se cumplen las siguientes propiedades:
El límite de la suma de ambas funciones es igual a la suma de los límites.
El límite de la diferencia se calcula como la diferencia de los límites.
El límite del producto de las funciones es igual al producto de sus límites.
El límite del cociente entre ambas funciones es igual al cociente entre los límites, siempre y cuando el límite del denominador sea distinto de cero.
El límite del producto de una constante por una función viene determinado por la multiplicación de la constante por el límite de la función.
Estas propiedades se expresan matemáticamente como sigue:

Ejemplo:
Consideremos la función f(x) = x 2. Para calcular su límite en el punto x = 2, damos a x valores cercanos a 2 por su izquierda y su derecha.
Por la izquierda:

Por la derecha:

Se observa que la función tiende a 4 por ambos lados de 2. Por tanto, su límite es 4:

Gráfica de la función:

Si la función tiende a puntos distintos por uno y otro lado del punto a, entonces no existe el límite de la función en dicho punto.
Observad que, normalmente, el límite de f(x) en el punto a coincide con su imagen, es decir, con f(a) . Para ser más exactos, esto ocurre en las funciones que son continuas en el punto a.
Un ejemplo de función discontinua es f(x) = 1/(x2) , cuyo límite cuando x tiende a 0 no coincide con f(0) porque la función ni siquiera está definida en dicho punto (no podemos dividir entre 0).
Límite en un punto infinito
Decimos que el límite de f(x) cuando x tiende a más infinito (+∞) es L si la función toma valores cada vez más cercanos a L cuando x crece indefinidamente.
Lo expresamos mediante
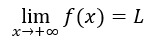
Análogamente, el límite de f(x) cuando x tiende a menos infinito (-∞) es L si la función toma valores cada vez más cercanos a L cuando x decrece indefinidamente.
Lo expresamos mediante
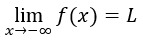
Ejemplos:
El límite de la función cuadrado es infinito:
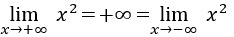
Y el límite de su inverso es 0:
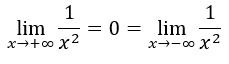
El límite es 0 porque un cociente positivo toma valores positivos más pequeños a medida que su denominador aumenta. Por tanto, cuando el denominador tiende a infinito, el cociente tiende a 0. Gráfica de la función:
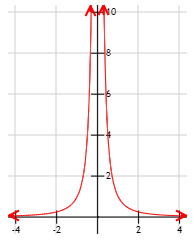

0 notes
Photo
Awesome picture👍👌👌

| Mirrored | Wind River Range, Wyoming.
5K notes
·
View notes
Photo

Quien no es capaz de tener defectos, no es capaz de tener humanamente grandes virtudes😇👀👏🙌🚫 📖📙💬Alessandro Verri💬 (en Córdoba, Veracruz)
1 note
·
View note
Photo

Quien no es capaz de tener defectos, no es capaz de tener humanamente grandes virtudes😇👀👏🙌🚫 📖📙💬Alessandro Verri💬 (en Córdoba, Veracruz)
1 note
·
View note


