existinglimits

[existinglimits]

A particularly fun equation

(x^2-5x+5)^(x^2-11x+30)=1

What I rather enjoy about this problem is that Wolfram Alpha doesn't get all of the solutions. While algorithms are powerful, they are not omnipotent.

And I don't mean just computer algorithms - I missed the same two solutions as Wolfram because I only used the standard approach - logarithms. (Luckily, getting something wrong makes it stick in my head better than getting something right, so this problem has lived in my brain rent free for over a month.)

Sometimes the thoughtful/creative/thorough application of more "basic" concepts is the way to go.

Hint:

What are three different cases where a^b = 1?

[existinglimits]

Limits & Indeterminate Forms (Part 2)

Let's explore an indeterminate form: ∞ / ∞

It helps to compare f(x) = 2x, g(x) = 5x, and h(x) = e^x.  These are all increasing (growing) functions. For all these functions, the limit as x approaches infinity is ∞.

Now, what happens if we take the limit as x approaches infinity of different ratios of these functions?

Lim_{x-->∞} (2x/5x) --> ∞/∞

Lim_{x-->∞} (5x/2x) --> ∞/∞

Lim_{x-->∞} (2x/e^x) --> ∞/∞

Lim_{x-->∞} (e^x/2x) --> ∞/∞

If we don’t do anymore work, then we get ∞/∞, but what does that mean? Especially since they are not all growing at the same rate, so they are approaching infinity at different rates.

∞/∞ is indeterminate, so we need to do more work. For some ratios (like 2x/5x and 5x/2x), you can do some simple or fancy algebra.

Algebra of the simple variety:

Algebra of the fancy variety:

For other ratios (like 2x/e^x), you’ll need to do something else.

If the numerator is approaching infinity faster, the function is sometimes called “top-heavy”.

If the denominator is approaching infinity faster, the function is sometimes called “bottom-heavy”.

If the numerator and denominator approach infinity at the same rate, the function is sometimes called “balanced”.

In most precalculus classes, it suffices to say that a ratio is top-heavy, bottom-heavy, or balanced. In most calculus courses, you’ll need to do something to show (if not prove) this. So, you’ll need some way to compare the rates of change so that you can determine whether the function in the numerator or the function in the denominator is approaching ∞ faster.

If you’ve taken calculus, what gives us the rate of change of a function?

(I'm making sure you think for a moment.)

For a function y = f(x), the rate of change of that function is given by its derivative: dy/dx = f'(x). So, you can take the derivative of the numerator and denominator separately to compare their rates of change. This is the idea behind L'Hôpital's rule, which is worthy of its own post.   

Questions to ponder:

Why doesn’t ∞/∞ = 1?

Are there any values that ∞/∞ couldn’t be equal to? Why or why not?

Related posts:

Part 1: ∞ - ∞

Rambling about infinity

[existinglimits]

Forgetting is part of learning

The Ebbinghaus Forgetting Curve "shows how information is lost over time when there is no attempt to retain it".

The cyclical process of learning, forgetting, and relearning has been shown to increase long-term memory. This is sometimes called "active recall" or the "testing effect".

This is also one of the reasons people will tell you not to cram. If you don't give yourself time to forget, then you aren't giving yourself time to relearn. So, the information is significantly less likely to stay in your long-term memory.

What is really, really important is creating a situation where you NEED to retrieve the information from you BRAIN.

You cannot have the answer immediately available in front of you.

Study tips

Flashcards

Sort the cards into two piles based on whether or not you know the answer.

Give yourself a moment to think before you flip the card over.

If you didn't confidently and completely know before looking, you don't know the answer.

Practice Problems

Attempt the problem WITHOUT looking at the answer.

If you get stuck, look at only the next step and copy it in a DIFFERENT COLOR. Then, see if you continue. Still stuck? Revel a tiny bit more of the solution.

Wait at least two hours, then redo any problems where you see something written in a different color.

Bonus Metacognition: Analyze the problems you got stuck on. Are there any types of problems you're struggling with? Are there any specific steps you're struggling with?

Make sure you're learning the information, not just where the information is stored. (aka: not what to google, not which page of the textbook, not which notebook, not which practice test, etc.)

[existinglimits]

[existinglimits]

Potential Infinity vs. Actual Infinity

One of the first ways to understand infinity is as a process. For example, if you keep on counting forever, then you will never run out of numbers. This is "potential infinity".

Humans are constrained by time, but infinity is not.

Consider writing the decimal approximations of 1/3, 2/3, and 3/3.

1/3 = 0.3333333333...

2/3 = 0.6666666666...

3/3 = 0.9999999999...

If you think of infinity as a process, then you think of 0.999... as continuously writing another 9. This is natural - we often think of numbers as the symbols that we write down to represent them.

We conflate the idea of a number with the numeral used to represent it.

(Math is Fun article on numbers vs. numerals)

More below the cut.

This never ending process of writing 0.999999999... indicates that there are infinitely many 9's. Since we can always write more, there will always be a 9 that hasn't yet been written.

Still, 3/3 = 1.

So, 0.9999999999... = 1

Which conflicts with the process understanding of 0.9999999999...

We are constrained by time, but infinity is not. We are constrained by numerals, but numbers are not.

Consider splitting a chocolate bar into thirds. Each piece is 1/3 of the chocolate bar. You wouldn't break off 0.3, then 0.03, then 0.003, then 0.0003.... and so on of the chocolate bar to combine them into 1/3 of the chocolate bar. You'd break off 1/3.

1/3 is not a process. All of those infinitely many 3's of the decimal representation are already there, we just can't write them all down.

3/3 is not a process. All of those infinitely many 9's of the decimal representation are already there, we just can't write them all down.

Going from a process oriented view of infinity to actual infinity is challenging, but I find that this connection helped me to begin that process. Something that is "infinite" in one sense, but has a concrete form.

I can see 1/3 of something and it isn't constantly growing in size by smaller and smaller amounts. I can see 3/3 of something and it isn't constantly growing.

The next step in understanding infinity to is accept that there are infinite sets (such as the set of all natural numbers). Then, it follows that there are different sizes of infinite sets (such as the size of the set of natural numbers vs. the size of the set of real numbers). So, there are different sizes of infinity.

A lot of this is from the melting pot of sources and experiences that is my brain, but I did reference wikipedia to make sure my brain wasn't being weird.

Wikipedia contributors. (2024, November 28). Actual infinity. In Wikipedia, The Free Encyclopedia. Retrieved 15:41, January 3, 2025, from https://en.wikipedia.org/w/index.php?title=Actual_infinity&oldid=1259986628

[existinglimits]

[existinglimits]

Property of Logarithms: log_b(mn) = ?

Video & Image without substitution highlights below.

[existinglimits]

Happy μ Year!

It's just a WIP, but I probably won't finish it. Happy New Year!

[existinglimits]

Learn your properties of logarithms

Just... just do it. Before you take calculus is best, but as soon as possible if you're in the middle of calculus.

You're not going to be able to do "logarithmic differentiation" if you aren't comfortable with log rules.

Below the cut are..

a link to Khan Academy Algebra 2 Unit 8: Logarithms

"Logarithms explained Bob Ross Style"

"What is the number 'e' and where does it come from?"

Link to Khan Academy Algebra 2 Unit 8: Logarithms

You can skip to "Properties of logarithms" if you're short on time, but most people who struggle with properties of logarithms do so because they don't understand logarithms.

Logarithms are the inverse of exponentials, so the rules are closely related but inverted. If you're REALLY struggling with logarithms, you may want to examine how comfortable you feel with properties of exponents.

Logarithms explained Bob Ross Style

What is the number "e"?

[existinglimits]

Limits & Indeterminate Forms (Part 1)

Let's explore an indeterminate form: ∞ – ∞

First, it is important to wrangle with the fact that while evaluating the “limit of a function” and evaluating “the function itself” feel similar for many functions, these are NOT always equivalent processes.

We can see this graphically.

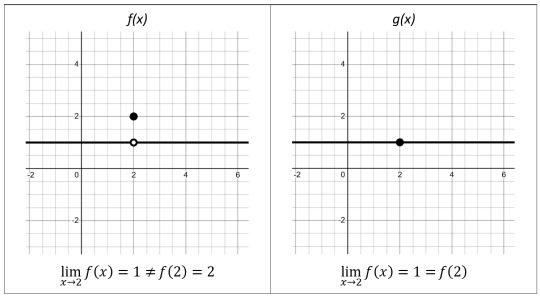
For f(x), f(2) does NOT equal the limit of f(x) as x approaches 2.

For g(x), g(2) DOES equal the limit of g(x) as x approaches 2

The result of evaluating a function isn’t quite as concrete as the result of evaluating a function because the function may not actually reach the result. This is particularly true for results of 0 and infinity.

On to the next point:

Not all infinities are the same size.

Let's examine two different functions: f(x) = 2x and g(x) = 5x.

The limit of f(x) = 2x, as x approaches infinity is ∞.

The limit of g(x) = 5x,  as x approaches infinity is ∞.

But what about the limit of [f(x) – g(x)] as x approaches infinity? Or the limit of [g(x) – f(x)] as x approaches infinity? They would both be ∞ – ∞ … but what is that? Zero?

While we use the same symbol for the different infinities… they are not the same. A little bit of algebra, combining like terms, can help us see that the limit of (2x – 5x) as x approaches infinity approaches negative infinity. While the limit of (5x – 2x) as x approaches infinity approaches positive infinity.

∞ – ∞ is said to be “indeterminate”.

We cannot determine the value through directly evaluating the limits. Instead, we need to do more work, namely algebra.

For calculus, it helps the relative sizes of infinities as the speed or slope of the function. The slope of g(x) = 5x is greater than the slope of f(x) = 2x, so g(x) approaches infinity "faster", so the limit of g(x) as x approaches infinity is "bigger".

"∞" is a bit of a catch all that becomes more and more nuanced as you continue through math. In calculus, it is frequently used to help us compare rates of change. Later, we compare the size of infinite sets (for example, are there more natural numbers or more real numbers?). Each person's individual understanding of infinity tends to mirror the development of our collective understanding throughout history.

Questions to ponder:

When is evaluating a limit the same as evaluating a function?

What might some other indeterminate forms be?

Is ∞ + ∞ indeterminate? Why or why not?

Is ∞ * ∞ indeterminate? Why or why not?

[existinglimits]

Evaluating Limits vs. Evaluating Functions (from graphs)

Let's pretend that you spilled juice on your textbook. Now you can't see what's going on when x = a. :(

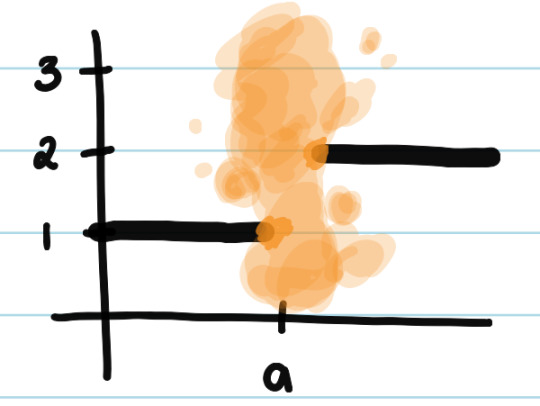
But, you can still try to make a guess based on what you can still see. There's more below the cut! :)

On the LEFT of the juice stain, it looks like f(x) is approaching 1. So, the limit of f(x) as x approaches a from the left is 1.

Now, let's look at the other side.

On the RIGHT of the juice stain, it looks like f(x) is approaching 2. So, the limit of f(x) as x approaches a from the right is 2.

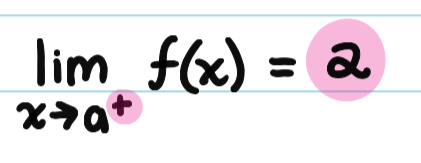
The limit of f(x) as x approaches a from the left (left hand limit, LHL) does NOT equal the limit of f(x) as x approaches a from the right (right hand limit, RHL).

The LHL =/= RHL, so we say that the limit Does Not Exist. Or, DNE for short.

But what is f(x) at x = a?? Unfortunately, the juice stain is in the way, so we can't make any definite conclusions about f(a). There could be a point at (a, any real number). Or even no closed point at all.

Here is a Desmos Activity with some simple practice problems to explore the difference between evaluating limits and evaluating functions.

Here's very similar problems as a doodle-y, handwritten worksheet & answer key. It is not screen reader friendly and looks like this:

I'm just experimenting and don't really know what I'm doing, so let me know if something helped or if you have questions.

[existinglimits]

You don't need to be good at something to enjoy it.

"Math is Hard. Unfortunately, people are just not that good at mathematics. While intensely enjoyable, it also requires hard work and self-discipline. I know of no serious mathematician who finds math easy. In fact, most … will confess as to how stupid and slow they are.

This is one of the personal hurdles that a beginning graduate student must face, namely how to deal with the profundity of mathematics in stark comparison to our own shallow understanding of mathematics.”

Garrity, T. A. (2021). All the math you missed: (but need to know for graduate school). Cambridge University Press.

My rambles under the cut.

This is part of the introduction to a book for people that want to go to GRADUATE school for MATH. People that are considered by most to be really good at math.

Part of the fun of math is that it is hard - the struggle, perseverance, discovery, and eventual understanding. If you find math hard, that's normal. Most anyone who loves math has been frustrated by it.

If you've cried over math, so have I. After many mornings of waking up with a solution that had eluded me the night before, I have learned that some things just need time to simmer in your subconscious. All those tear stained, incomplete proofs were necessary ingredients and experiences that my brain just needed time to digest.

Learning is weird. You need to give yourself as many opportunities and as much time as possible so that inspiration may strike.

You have to be okay with being "bad" at math if you want to be "good" at math. And you don't have to be good at something to enjoy it.