#math notes

[inbetweencoffees]

still doing maths

Not much to say in regards to my studying as I’m still working on calculus. Hoping to switch to algebra on Wednesday but we’ll see. Halfway through today’s to-do list/study plan, still have to reply to an email about my job interview next week. Other than that I’m an anxious mess. Might have to do with my exam results being published next week & the oral finals too but who knows. I’m hoping for things to get better soon.

[painted-lanes]

I forgot what his clothes look like

[snufflesarmy]

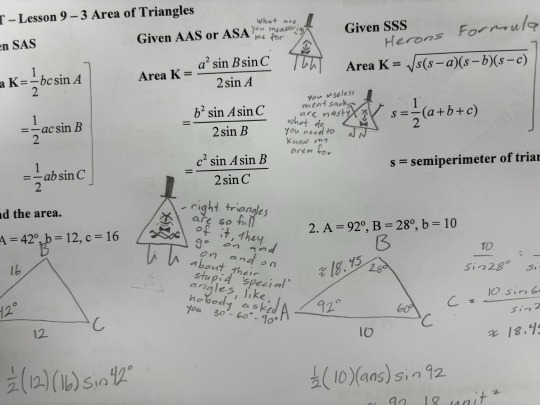
Math notes featuring a very disgruntled bill cipher

[sophiehatterirl]

For anyone wondering how to easily open up inserting an equation into Microsoft word all you have to hit is alt and =. It takes way less time to write out notes and make equations.

[themostofekramy]

12.1.2024

I have a final exam tomorrow, applied math, i studied a bit in the morning and i went to sleep after the Friday prayer, i’ll continue studying now till the exam, and oh boy do we have one long night ahead of us

[er-cryptid]

Adding Square Roots [Ex. 1]

Patreon

[lexusveryreal]

hm something something math something uhhh anyways william davis drawings

had to crop out the text on the right cuz no spoilers 😼

HUAHASHHHZZZ my only oc that i actually wrote abt and have fully fledged lore on and actually have a plot for 😭🙏

but he's so silly i love drawing him

bonus feature he's in the MIDDLE of the math notes

(next to another oc that may or may NOT be an alamo oc hmm idk)

[paledinosaurrebel]

I just realized I once again disappeared so just a random photo (hehe photo (this is funny because I am doing exercises about solar cells)) anyway messy and you can clearly see how motivated I was at the beginning and then I ran out of space and started colour coding. St least being a little kind to future me. It goes on over the next page also don't look to close I'm not entirely sure this makes any sort of sense.

Yay I'd lie and say I'll be be more active but maybe I'll go shopping ok my mutuals blogs:)

[ninjadoggo1]

More math notes

Angry noot

Nightmare sans- Jokublog

[then-ponder]

Physics questions so hard they make you question your understanding of integrating trivial functions, like y=mx +b. I mean what the fuck.

[chronicsstudyblr]

Tomorrow I have my first real maths test of the year.

The topic is linear functions, which I have been having trouble with since last year (not that I don’t have any problems with the other topics). But, since I’ve had this topic for so long, I’ve finally come to understand it a lot more. I’ve figured out the main reason as to why I couldn’t quite understand these functions; because I didn’t know what rate of increase really meant. That discovery helped significantly!

Yesterday and today I've tried to work my way through chapter two in Mønster 1P (Mønster=pattern, 1P is the shortened term for lower level maths). The number of math problems I've solved these two days, 12 (with subtasks A, B etc), is the equivalent of how many I would’ve solve last year in two weeks worth of math lessons. For that I am proud, even though the number is small.

I still have some time tomorrow to prepare, but for know I will relax, eat dinner, and sleep.

[inbetweencoffees]

Algebra🗒️

Literally stressing out because I have to be somewhat capable of doing algebra until wednesday and i still have too many things to cover. With my morning and late at night study sessions I’ve been more productive than doing anything in the afternoon but still- I’m losing most of sunday and almost the entire monday in study time because of the job interview…at least my cars oil is changed now and I can say that I’m somewhat understanding the math I’m doing- or at least I managed to answer my own questions :D

14 days till religion final, 17 days till math final

[nowtoboldlygo]

i passed fifth grade math <3

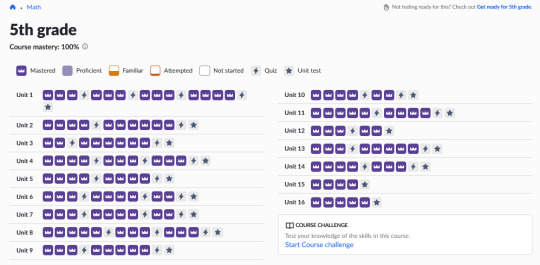
i've been abusing the start over feature a bit, especially for the quizzes. but the point isn't to get through the unit, the point is to have excellent foundational skills. so. keeping an eye out on that.

learned a new way to multiply multi-digit numbers, the "grid pattern"

definitely wouldn't have been able to write out a long division problem before this review. standard algorithm whomst?

still doing some multiplication table flashcards, and added in some long division worksheets for more practice problems than khan academy really offers. mathisfun.com offers several levels of difficulty.

[futurebird]

Starting two new notebooks today for calculus and geometry. Been hoarding these blanks for years. Time to fill ‘em up! I’m delighted with how perfect the “arthropod angel” stickers by @ketrinadrawsalot look on the marbled paper!

It’s the holy primordial soup!

[silenceitis]

An intuitive introduction to information theory, part 1

Motivation

Ok, let’s start with the basics; what exactly is information theory and why do we care about it?

As the name suggests, well, it’s the theory of information. More precisely, how do we “measure” how much “information” something has? What is the “best way” to represent this “information”? How can we communicate this “information”? How can we communicate information if there’s a chance some of it may be “lost” in transit?

As you may have guessed, this underpins many important technologies we all use today, such as digital communication and file compression.

All in all, it’s about developing a framework that allows us to quantify “uncertainty” and optimise communication.

Important ideas

Ok, so I’ve said the word “information” a lot. But what does this actually mean? Let’s think about the concept of surprise. If I told you “the sun will rise tomorrow”, you wouldn’t be very surprised would you? Or in other words, this statement wouldn’t give you much information. You are already pretty certain that the sun will indeed rise tomorrow. But what if I told you “your exam scheduled for 2 months time has been moved to tomorrow”? That would be pretty damn surprising right? Or, you could say it’s a very informative statement.

So, we can see that there is some relationship between the idea of surprise and the idea of information. Let’s try and describe this intuition a bit more precisely.

Clearly, how surprised we are about something is related to the probability of that thing happening. If I had a biased coin that had a 99% chance to land on heads, and 1% to land on tails, you’d be very surprised if I flipped a tails, and not very surprised at all if I flipped a heads. So surprise decreases as the probability of some event happening increases.

Further, if we have two completely independent things happening, it would make sense for our surprise to add. Going back to the same biased coin, suppose I flip it, and you feel whatever surprise you do about the result. If I flipped another biased coin at the same time, you would feel a certain amount of surprise about this too. But the amount of surprise you felt about the result of one of the flips wouldn’t change the amount of surprise you felt about the other, the two coins don’t affect each other do they?

And finally, if an event becomes slightly more likely, or slightly less likely, we would expect our amount of surprise to only change slightly too right? That is, the amount of surprise we feel about an event should depend continuously on the probability of the event.

If we denote s(A) to be our surprise for the event A, it turns out that S(A) = -log(p) satisfies all these properties, where p is the probability of A happening. Not only that, but this is actually the only function that satisfies these properties (up to our choice of base for the logarithm).

Ok, so we now have a sense of what we mean by surprise, and hence information, and an explicit function to calculate a numerical value representing this. But notice how to make use of this, we need to actually know what the outcome is. E.g. if I have a biased coin, you can’t tell me anything until I flip the coin and you interpret the result. But what if I have a coin and I haven’t flipped it yet? Based on the probabilities, we can work out how surprised we *expect* to be. Or in other words, on average, how surprised you will be.

This is exactly the concept of entropy!

Now, I’ve talked a lot about coin flips. You’re probably getting a bit bored of this. So let’s formalise things slightly. Suppose we now have a discrete random variable X, taking values in a set χ. As you may recall from any probability classes you’ve taken, the expected value of X can be calculated as

And we can calculate the expected value of a function of X as

Now, surprise is just a function of our random variable X, so we can use this formula to work out what entropy is! We will write entropy as H(X). Again, H(X) is just a value representing, on average, how surprised we are when we observe an event from X.

From this formula, we can say a few things about entropy.

Firstly, it it is always non-negative, which we expect; being “negatively surprised” about something doesn’t really make any sense right? So why would our average surprise ever be negative?

Furthermore, entropy is only zero when one of the probabilities in the sum is 1 (remember log(1) is zero, and probabilities sum to 1). Again, this makes sense. Our average surprise would only ever be zero if we were certain of what the outcome would be.

Ok great, we now know, given a random variable X, on average how surprised we will be. But what if we don’t actually know what the random variable X is? This happens all the time! In real life, we may be able to observe a random process, and hypothesise what we think the distribution is, but we may not know for certain. For instance, suppose I had a biased coin (yep, sorry, back to the coin again…), but I don’t tell you what the probabilities of landing on heads or tails are. You may take the coin, do a whole bunch of flips, and estimate the probabilities from your results. But your estimate is unlikely to be the true answer. We want to find a way to measure “how costly” it would be to use your estimate, rather than the true distribution. Or in other words, how much information we lose (or indeed surprise we gain) by using your estimate.

This leads us to the idea of divergence, a way of measuring how different two probability distributions are, by looking at the differences in entropy (aka surprise, aka information!) between the two.

Suppose we have a random variable with probability mass function p, on the set χ. But we want to encode X with a different pmf, q, also on χ. Then the average surprise when taking values from X and encoding with p (aka using p in our function S(A)) is just the entropy of X, H(X), as we discussed before.

And the average surprise when taking values from X but encoding with q (again, just using q in our surprise function) is

Notice how this is not quite the entropy of X, although it does look very similar. Our surprise has changed, as surprise is based on our “beliefs” of what the values of X will be, that is, it is based on our choice of encoding. But our “beliefs” do not change the actual probabilities of X taking particular values.

Hence, our divergence, written D(p || q), is just

However, the concept of divergence is not just used to compare how our guess for the distribution, q, compares with the true distribution, p. It can actually be used to compare how different *any* two distributions are, as long as they are both on the same set of values. More precisely, D(p || q) measures how different the two distributions are, *from the perspective of p*. I.e. we draw values from p, and measure how much more surprising that sample would be, on average, if it had come from q instead.

We do precisely the same thing as before, except instead of entropy, we have the slightly modified surprise function, as we did for q. Note that at no point have we made an assumption on what the actual distribution of X is here (which is why the sum is not the entropy of X, even if it looks very similar).

Now, as you may have noticed, what I said before hints at some asymmetry in the definition of divergence, and this is indeed the case. In general, D(p || q) is not equal to D(q || p)! If we think about the meanings of these two quantities, this makes sense. D(p || q) represents how “inefficient” it is to pretend that data from p came from q. Whereas D(q || p) represents how “inefficient” it is to pretend that data from q actually came from p. Intuitively, these are not the same thing.

Additionally, you may have noticed that the divergence can take the value infinity, when for some value of x, p is greater than zero, but q is zero. Intuitively, this means that q, the distribution you’re pretending the data came from, says that a certain event is impossible, but p says that this event *does* occur.

Ok, so now we’ve seen how we can “measure” how different one distribution is from another, which can be useful when we want to model an unknown distribution. But what if we don’t try to estimate our unknown distribution directly? Instead, we may be able to observe another random variable, and hypothesise that it may be able to tell us something about our unknown distribution.

This leads us to the idea of mutual information. How much does knowing Y tell us about X? Or in other words, how much is our uncertainty in X reduced by, if we also observe Y?

So really, we’re looking for a way of determining how much dependence there is between the two variables. If X and Y were independent, then knowing something about Y wouldn’t reduce our uncertainty in X. So we can measure how different the joint distribution of X and Y is, from the joint distribution if they were independent! This will give us exactly what we’re looking for; how “far” the joint distribution of X and Y is from being independent.

We can use our notion of divergence to calculate this! As you may recall, if X and Y are independent random variables, the joint pmf of X and Y is simply the pmf of X multiplied by the pmf of Y. So we just plug this into our divergence function, as below, writing I(X; Y) for the mutual information:

And with some rearranging and use of our previous definitions, we can get the following alternate forms for mutual information:

All of these definitions make it clear to us that mutual information is in fact symmetric, I.e. I(X;Y) = I(Y;X).

We can also see that mutual information is zero if and only if X and Y are independent, and that it is non-negative.

[themostofekramy]

4.1.2024

Not as productive as i wished for but thanks to god i did most of what i needed to do today easily, had a math session and studied calculus and app,revised and read some Quran, i even called for the start of prayer in the mosque 🕌

For some reason i’m starting to fall in love with math even more than i already am falling, the more you understand it the better you realize how beautiful it is