#(sqrt for the win)

[foobars-cool-car]

i dont typically have a lot of computer related feelings but the level of effort i need to put in to type 〉without having to copy/paste it from the internet is filling me with all consuming rage i fear.

[confidence-intervals-of-polls]

Hey there! Confidence Interval person here. Let's analyze this poll!

CHOOSE:

Our parameter, or p, that we're trying to estimate is the true proportion of all active [tumblr] users who say that they have cried over the death of a fictional character.

For this, we're going to use a 1-sample z-interval for p, and our confidence level will be 99.9%.

CHECK:

As before, trying to make an online poll random is extremely difficult due to voluntary response bias. As such, we will ignore the Random Condition, because if we took selection bias into account, nothing would go anywhere on here.

10% Condition: The average weekly active number of [tumblr] users is approx. 19.3 million. ~26,000 is most definitely less than 10% of the full population, and thus any dependence on responses is negligible in the sample.

Large Counts Condition: Our larger proportion is definitely over 10, but I hesitated to completely ignore this due to the landslide win, so I ran the calculations just to be sure.

n(0.937) = 24447.267 ≥ 10 ✅

n(1-0.937) = n(0.063) = 1643.733 ≥ 10 ✅

So we can assume the distribution is approximately normal.

CALCULATE:

The general formula for confidence intervals is point estimate ± margin of error, with the point estimate being our sample proportion and our margin of error being how much leeway we give the interval.

The specific formula for confidence intervals is: ˆp±z*sqrt((ˆp(1-ˆp))/n), where ˆp is our sample proportion, z* is our critical value (determined by our confidence level), and n is our sample size.

Now, we plug in our values and get: 0.937±3.291sqrt((0.937(1-0.937))/26091).

The rest is simply whittling it down to our two values that define the interval.

0.937±3.291sqrt((0.937(0.063))/26091)

0.937±3.291sqrt(0.059031/26091)

0.937±3.291sqrt(0.000002262504311)

0.937±3.291(0.00150416232)

0.937±0.00495019822

(0.93204980178, 0.94195019822)

CONCLUDE:

We are 99.9% confident that the interval between 0.932050 and 0.941950 (93.205% and 94.195%) captures the true proportion of all active [tumblr] users who have cried over the death over a fictional character.

EXTRA NOTES:

Finally I've done one where I don't immediately think I've made a mistake! These make much more sense than my other original values. Sorry for misleading some people!

TL;DR:

No significant evidence that the poll is inaccurate.

*This poll was submitted to us and we simply posted it so people could vote and discuss their opinions on the matter. If you’d like for us to ask the internet a question for you, feel free to drop the poll of your choice in our inbox and we’ll post them anonymously (for more info, please check our pinned post).

[linuxgamenews]

Survivor Challenge TD: Unleash Your Tower Defense Skills

Survivor Challenge TD the epic new tower defense games enters Early Access on Linux, Mac, and Windows PC. Thanks to the creative brilliance of developer SQRT Games. Which you can find on Steam with its 89% Positive reviews. Ever feel the thrill of a tower defense for Linux but wish you could pack all your firepower into one epic, unstoppable tower? That’s what Survivor Challenge TD is bringing to the table. It’s not just about placing towers anymore — it’s about crafting the tower, upgrading it to perfection, and also taking down waves of enemies like a pro. Let’s break it down!

Survive and Conquer

The Survivor Challenge TD  rules are simple: hold your ground. Waves of enemies are gunning for your tower, and it’s up to you to keep them at bay. The catch? You’re dealing with one tower. But you’ll upgrade, stack abilities, while combine elements to make it a tank. Survive the waves, and when the boss rolls in, show them who’s in charge. Beat the boss, and it’s game over for them!

Survivor Challenge TD - Early Access Trailer

Customize Your Power

Here’s where things get spicy. Since you don’t just play Survivor Challenge TD — you strategize.

Abilities Galore: Need more firepower? Maybe some AoE chaos? You’ve got abilities for that.

Elemental Combos: Think of it as the secret sauce. Combine elements to unlock extreme power-ups. Fire and ice? Sure. Lightning and earth? Why not!

Build Your Playstyle: Are you the slow but deadly type or an all-out DPS monster? Experiment with combos until you’ve got the ultimate Survivor Challenge TD setup.

Unlock and Dominate

Winning feels great, but unlocking new abilities and upgrades feels even better. Every level you complete isn’t just a victory—it’s also a step closer to a stronger tower and bolder combos. Plus, with elemental variants in play, the options for how you dominate are almost endless.

Why You’ll Like Survivor Challenge TD

If you’re into tower defense games but want something more hands-on and dynamic. Players already like the challenge of adapting strategies to different enemies and appreciate the variety of builds and abilities. The option to speed up gameplay is a welcome touch, though a higher speed would be great. With some tweaks — like more dynamic gameplay, better tutorials, and engaging progression — it could go from "spend an evening and forget" to a memorable hit. So, grab your gear, crank up those upgrades, and get ready to show the enemies who’s boss. While priced at $5.59 USD / £4.71 / 5,51€ with the 20% discount on Steam Early Access, until the 4th quarter of 2025. With support for Linux, Mac, and Windows PC.

[rotationalsymmetry]

Zero has a dramatic lead over -1 in Jan misali’s number tournament semi finals, understandable, and i is a little bit ahead of NaN. So, too early to call with 2 1/2 hours still to vote, but it seems like most likely we’ll have i vs 0.

Which is weird. In that a lot of these matchups have had some thematic resonance and I’m still sad we’re not getting one vs zero. But uh ok.

-1 vs i would have been really neat actually.

If we end up with NaN vs 0 that will be so terrible it almost wraps back around to awesome.

if i wins best number that'll be really cool though (yay imaginary numbers!) Just really epic. Possibly better than sqrt 2 but I really wish sqrt 2 was still in the running. I have mixed feelings about the idea of zero winning, obviously zero is a really big deal and deserves recognition but it also feels kinda nihilistic to have it win. Really? The best number is nothing at all? Why do we even bother with the rest then?

We really don’t have enough i propaganda yet. I can understand why, when you’re a serious math person you’ve encountered i long ago enough that you figure everyone knows what it is and it doesn’t need explaining, but also there’s so much to explain and enough of it’s really complex (heh) that it’s hard to tell where to even start.

[bayesic-bitch]

I disagree, both in theory and in practice. As a personal preference for one's own psychological reasons, this kind of risk aversion makes sense. But I don't think it follows from the way you've described expectation, and I think there are definitely situations where this kind of foundational risk aversion can lead to significantly worse outcomes. I'm not really trying to argue here, so much as to provide a different perspective.

My main issue here, is that this is not actually the definition of expected value. Expected value is defined as an integral over possible outcomes, not a limit. E[f(X)] = sum_x f(x) P(x), where P(x) is the probability of an outcome. The thing about limits of random variables is the law of large numbers, which is a consequence of the definition of expected values in some cases. However it only holds for distributions in which 1) variances are finite, and 2) all samples are independent and identically distributed. And many of the cases we care about in real life do not satisfy these properties. The view of expected value as an integral is more robust and general than viewing it as a limit, and it also does not require an event to b repeatable. This is especially true for Bayesian stats, where probabilities are not viewed as limits of repeatable processes either, but as statements of uncertainty. A Bayesian expected value is not not making a statement about a limit, but giving the average result if you consider all possible outcomes weighted by how probable they are to occur.

Ultimately though, I think what you're getting at here is really more about risk-aversion. Which is fine, and there are many situations where being risk-averse is beneficial. However again, risk aversion is not universally optimal. There are some problems that necessitate risk-seeking behavior to get good results. Here's one:

Assume you walk into a casino with 10 slot machines. Each play from a machine has a payout of +1 or -1. Whenever you start up a new slot machine you haven't played before, it secretly generates a random number between 0 and 1 to decide what its win rate will be, and then keeps that win rate forever. So if you start a new machine that generates a win rate of 0.4, you'll have a 40% chance of winning every time you play that machine for the rest of the game. You don't get to see the win rate though, you have to estimate it by trying the machine over and over and observing how oftSo while I definitely understand risk-aversion as a personal preference, I don't agree with the idea that this risk aversion is actually a direct consequence of the definition of expectation in the way youve described.en you win. Your goal is to maximize your total winnings over time.

On your view, after you've played a couple of machines and picked the one that has given you the best payout so far, it seems like you wouldn't want to play other machines. Starting a new machine is a non-repeatable event, and on average the new machine is going to have a worse payout then the best of the first n machines you've tried. However, the go-to algorithm for this problem is explicitly risk-seeking. It's called Upper Confidence Bound, and the idea is that you calculate the x% confidence bound (= mean(i) + sqrt(-log(1-x)/# times i has been played)) for every machine i, and then play the machine with the highest upper confidence bound. This explicitly favors machines with high variances over machines that you have a high certainty about. Moreover, this algorithm is guaranteed to be optimal up to a constant, and all other algorithms that are optimal must be risk-seeking to approximately the same degree.

I think that risk aversion is so common because taking a naively risk-averse strategy is often necessary for actual utility-maximizing action later. You generally want a high-probability guarantee that something will work out, because it makes planning easier later, and minimizes the impact of potential unknown factors that are difficult to evaluate. But this is only usually, not always beneficial, and I think it's worth considering when it does not follow our actual values. In particular, curiosity is a risk-seeking behavior, and something that I think is also essential for being well-adapted to the world. If we value curiosity about the world, then we are explicitly doing so against the value of risk-adversity.

I would very much like to see your expectation post, as I expect I will strongly disagree with it, and I think it might be a contributor to a lot of our disagreements. If you were gambling with small amounts of money, would you try to maximise something other than expected winnings?

Ok, I'll just talk about the expectation thing again here.

Right, so, for a random variable X, the expected value E(X) intuitively represents the value we would expect to get in the limit after sampling from X very many times and averaging out. But this limit is important—E(X) and the intuitive notion of "expectation" don't line up outside the limiting case.

For example, say someone offers you the following bet: they flip a coin with a 0.1 probability of landing on heads and a 0.9 probability of landing on tails. If it comes up heads, you get ten dollars. If it comes up tails, I pay them one dollar. The expected value of this bet is 0.1*$10 - 0.9*$1 = 10 cents. This means that, in the limit, if I take the bet n times, I can expect (in the intuitive sense) to make 10n cents. And so, if the guy offering this bet allows me to take it as many times as I'd like, the rational thing is to take it a bunch and make some money!

But if the guy only offers the bet once, then the limiting behavior does not come into play. It doesn't matter that if I took the bet a bunch of times I would make money in the limit, because we're not in the limit (nor an approximation of it)! If he offers the bet once, then I cannot in any intuitive sense "expect" to make ten cents. Rather, I expect, with a 90% probability, to simply lose one dollar.

If I take this bet once, the overwhelmingly likely outcome is that I'll just lose money and gain nothing. So I wouldn't take the bet! I think this is perfectly rational behavior.

I said this all to someone once and they said it had to do with the fact that the relationship between money and utility isn't linear, but it's not about that at all. Replace dollars with, idk, direct pleasure and pain units in the above bet and I would still act the same way. It's about E(X) measuring limiting behavior and thus primarily according with the intuitive notion of expectation only when you sample from X a large number of times.

[devoirat]

Devoir de Synthèse 1 Informatique 2ème Informatique

Exercice n°1 : (4 p)   Compléter « En pascal » le tableau suivant en mettant respectivement, pour chaque ligne, le nom de l’objet (résultat) correspondant, son type ainsi que sa valeur :   N° Expression en Pascal Objet Type Valeur 1 a := Ord(‘B’) ;       2 b := (Trunc (-6.56) +Round(1.49)) + Sqrt (Abs(-9));       3 c :=Upcase ( Chr (Ord (‘B’)) ;       4 d := ( ‘a’ = ’A’ ) ;       5 f := Copy ( ‘InterNet’, 6 , Long(‘car’) ) ;         6   Val ( ‘2èmeTI’, i , e ) ; i     e     7 f := Pos ( ‘pro’, ‘Professeur’) ;       8 g := ‘à˽˽page’ ; Insert (‘la˽’ , g , 3) ;         Exercice n° 2 : (3 p) En utilisant les fonctions et les procédures prédéfinies, écrire les instructions, en pascal, nécessaires pour aboutir aux résultats indiqués. - Ch : = ‘windows˽xp’; ………………………………………………………………..   ………………………………………………………………... ………………………………………………………………... ………………………………………………………………… - Ch : = ‘Bonneannée2016’ ; ……………………………………………………………….. ………………………………………………………………... - Ch1 : = ‘2ème ; Ch2 : = ‘Devoir’ ; Ch3 : = ‘Tech’;         A : = 2015 ; ……………………………………………………………….. ………………………………………………………………... ………………………………………………………………... Résultat : ch  =  ‘Win˽Xp’       Résultat : ch = ‘Bonne**année**2016’   Résultat : ch = ‘Devoir˽2ème˽Tech-2015’     Exercice N°3 : (6 p) Soit l’algorithme suivant : Travail demandé : - Dresser le TDO de cet algorithme : (2 pts)   OBJET NATURE / TYPE     - Traduire en pascal les instructions écrites en Gras et Italique (de N° 2 jusqu’ ‘à N°7) : (2 pts) ………………………………………………..……………………………………………………………… ……………………………………………………………………………………………………………….. ………………………………………………..……………………………………………………………… ……………………………………………………………………………………………………………….. ………………………………………………..……………………………………………………………… ……………………………………………………………………………………………………………….. - Exécuter cet algorithme dans le cas où ch = ‘’30+25*4’’ : (2 pts)   Exemple N° Instruction Ch1 x Ch2 y Ch3 z R         Ch=’’30+25*4’’ 2)               3)               4)               5)               6)               7)               8)                   Exercice N°4 : (7 p)   Vous avez tant rencontré ce type de message lors de la connexion à votre boite mail !! Cependant, l’objectif de notre exercice est de calculer puis d’afficher le pourcentage d’utilisation de la boite mail d’un tel utilisateur. Pour faciliter la tâche à celui-ci, on va lui demander de saisir deux données de types chaines: - Saisir, en premier lieu, une chaine « ch1 » (ne contenant pas d’espace) représentant l’espace déjà utilisé par les mails manipulés exprimé en MO. - Saisir, en deuxième lieu, une chaine « ch2 » (ne contenant pas d’espace) représentant la capacité totale réservée aux mails exprimée en GO. - Afficher le pourcentage « pc » d’utilisation de la boite NB : pourcentage d’utilisation, pc = (espace utilisé en GO/espace total en GO)*100 Exemple : Pour         ch1 =''1075.2MO'' &   ch2 =''15GO'' Le programme affichera :          ''Pourcentage d’utilisation est : = ''   7 sachant que ( (1075.2/1024)/15 )*100 = 7   Ecrire une analyse, un TDO et l’algorithme correspondant intitulé «Pourcentage » qui permet de saisir les deux chaines « ch1 » et « ch2 », de calculer et d’afficher le pourcentage « pc ». è Analyse : (4 pts) ……………………………………………………….………………………………………… ………….………………………………………………………….…………………………… …………….………………………………………………………….………………………… …………………………….……………………………………………………….…………… ……………………………….……………………………………………………….………… ……………………………….……………………………………………………….………… …………………………………………….…………………………………………………… ……………………………………………………………………….………………………… ……………………………….……………………………………………………….………… ……………………………….……………………………………………………….………… …………………………………………….…………………………………………………… ……………………………….……………………………………………………….………… …………………………………………….…………………………………………………… ……………………………………………………………………….…………………………   - Déduire le tableau de déclaration des objets (T.D.O) correspondant à cette è T.D.O : (1pt) OBJET NATURE/ TYPE     è Algorithme : (2 pts) ……………………………………………………….…………………………………………. ………….………………………………………………………….…………………………… ………………………….……………………………………………………….……………… ……………………………………….………………………………………………………… ………………………………………………………………….……………………………… ……………………………….……………………………………………………….………… …………………………………………….…………………………………………………… ……………………………………………………………………….………………………… ……………………………….……………………………………………………….………… ……………………………….……………………………………………………….………… …………………………………………….…………………………………………………… ……………………………………………………………………….………………………… ……………………………….……………………………………………………….………… …………………….………………………………………………………….………………… …………………………………….……………………………………………………….…… ……………………………………….……………………………………………………….… ………………………………………….………………………………………………………. …………………………………………………………………………………………………. ………………………………………………………………….……………………………… Read the full article

[wiresandstarlings]

I look for a picture of you to keep in my pocket, but I can’t find one where you look how I remember

A common problem in Bayesian inference is to determine how likely an outcome is. For example, when we flip a coin, how often will the coin land on heads? If we don't know anything about the coin, we'd start with the uniform distribution Beta(1,1). This means we think it's equally likely to land on heads or tails, but aren't confident. Then we'd flip the coin and if it lands on heads, we'd update our prior distribution to Beta(2,1). If it lands on tails, we'd update to Beta(1,2). A Beta(m,n) distribution has mean \(\frac{m}{m+n}\) and standard deviation \(\sqrt{\frac{mn}{(m+n)^2(m + n + 1)}}\) over the domain [0,1]. So if we get a heads, our prior distribution would be centered at \(\frac{2}{3}\) with standard deviation 0.236. This means that we think there's a \(\frac{2}{3}\) of getting a heads, but the real chance could easily be 0.4 or even 0.8 as well. If we flipped the coin 1000 times and got 500 heads and 500 tails, then our posterior distribution would be Beta(501,501). This has a mean of 0.5 and a standard deviation of 0.016. This means we're very confident that the coin has a 0.5 chance of landing on heads. It might be 0.49 or 0.51, but at this stage we're almost certain it's not 0.55. The bigger the numbers that parameterize our belief distribution are, the more confident we are that the mean of the distribution is the true mean.

I'm sweeping a bunch of math under the carpet here, but the underlying intuition is simple. The more we flip the coin, the more we know about it. And if you're not already familiar with Bayesian inference, this probably seems like an excessively elaborate formalization of a basic concept. However, Bayesian inference has one key insight. It cleanly demarcates our knowledge of the world into three components: our priors, our evidence, and our posteriors.

For example, with our coin-flipping exercise, we'd never start from an uninformed prior in practice. After all, flipping a coin is the canonical example of an uniformly distributed event with 2 outcomes. Even if we got 10 heads in a row, we'd dismiss that evidence as a freak accident. This is because we'd start from a distribution like Beta(10000,10000), making our posterior distribution Beta(10010,10000). So mean 0.5002, standard deviation 0.0035. We were confident the coin was fair before, and we're still confident the coin is fair.

I'm explaining all this because I want to discuss Bayesian inference in the context of opportunistic cheating in Magic. Some cheats are obvious and egregious, like mana weaving or stacking an opponent's deck while you're shuffling it. But the vast majority of cheats occupy a gray area where they could easily be honest mistakes.

The tricky thing about cheats of opportunity is that Magic is a complicated game that pushes on the limits of human cognition. With long tournaments, short lunch breaks that encourage skipping meals, grueling travel schedules, and loud, crowded convention centers, some mistakes and sloppiness are inevitable. Most of these mistakes will be detrimental, like missing triggers. Some will be beneficial, like miscounting how many damage an opponent's creatures deal. Asking whether someone is an opportunistic cheater is asking whether a disproportionate number of his mistakes benefit him.

This is where things get complicated, because the information stream on sloppiness is largely hidden and extremely biased. When our opponent makes a mistake that's in our favor, we either correct it and move on, if we need to in order to maintain the game state, or dismiss it, if it's something like a missed trigger. If someone misses a trigger on camera, it's a little embarassing but who really cares. However, when someone makes a mistake that's in her favor, we call a judge or start a witch hunt. Because of this, we only hear about sloppiness that could be construed as cheating, and never about sloppiness that definitely couldn't be.  

To compensate for this, we can consider the context of the alleged cheat or the rate at which a player makes beneficial mistakes. If a player makes a mistake that's in his favor in a game that he was certainly winning anyway, then it's not such a big deal. He doesn't have any real incentive to cheat, so he likely wasn't cheating. And if a player makes a serious error in her favor once every two or three years, then it's whatever. It's unlikely we'd hear about her so infrequently if she were actively looking for opportunities to cheat.  

However, even more than these proxies, we rely heavily on our priors. We “know a player is a good guy” or “have heard that so-and-so is shady.” When we trust a player, we're essentially assigning her a heavily informed prior that she's unlikely to cheat. Personally, I'd assign my best friends in Magic distributions like Beta(100,1000), where m = beneficial mistakes and n = detrimental mistakes, so that hearing any individual story of opportunistic cheating won't shake my faith in them very much. Not only that, because they're my friends, I'll hear about the judgment calls they get wrong, the triggers they miss, and the attack steps they forget, making my evidence much more complete. If I've heard someone is shady, then my prior will be something like Beta(20,30), so that any instance of opportunistic cheating greatly increases my suspicion of him.

Where things get really messy is when the biased information stream mixes with even uninformed priors. If I don't know a player, let's say because she’s from a different country and doesn’t speak English very well, then I'll start from an uninformed prior like Beta(1,1). That sounds equitable enough, but because I don't know anything about her and I'll only hear stories about mistakes that worked in her favor, I'll quickly come to the conclusion that she's a cheater, or at least likely to be cheating. Maybe I'll see her make a boneheaded mistake twice and hear about how she played an extra land four times, and then my posterior will be Beta (3,5). Despite extremely limited and incomplete information and no personal bias a priori, my posterior reflects a relatively strong belief that she's cheating.

I believe that the professional Magic community is seriously racist. We can just count the number of Asian, European, and Latin American players who are widely suspected of cheating against the number of Americans. Not necessarily out of any ill intent, but because most Magic players are American and will naturally give other Americans some benefit of the doubt, whereas they'll assign foreign players at best an uniform prior.

I felt compelled to write this because I'm frustrated by the Hall of Fame voting dialogue. I don't have a vote and I've always been an outsider to the professional Magic scene proper, so I don't have any real stake here, but I'm perplexed by how ready some people are to drag people they barely know through the mud. And I think people need to seriously consider if they're treating people from other countries, cultures, and backgrounds fairly.

[its-no-biggie]

yknow what, im not just gonna campaign in the tags for this one. do you know how mind blown i was when i first learned about imaginary numbers?? [hmmm. might have to start capitalizing i (the pronoun) to avoid ambiguity.]

one of the most beautiful things about math is that once you run into something that doesnt fit into the rules youve laid out, you MAKE NEW RULES. what happens in a system that only has natural numbers when you try to evaluate 5 - 7 ? "it doesnt work like that. you cant subtract a big number from a small number" -people who only use numbers for counting, probably. but MATHEMATICIANS are like, well, lets define a whole new set of numbers that work backward from 0, in the same way the naturals work forward from 0. then 5 - 7 = -2. [definitely not how this actually went down btw. just for illustrative purposes.] I mean, thats the reason -1 is still in this tournament! it defines a whole new set of numbers!

the imaginary numbers are just like that, except less useful, I guess? so theyre not taught until university. but they literally redefine how you see the number line! cause thats what the imaginary plane (edit: complex plane. cannot believe i forgot the name, can you tell i wrote this late at night lmao) is, its an extension of the number line. imaginary numbers, unlike what the name suggests, are not some nebulous, mysterious concept. its just a different type of number, with a unit defined by sqrt(-1). it completely changes how you think about numbers!

that kind of discovery..... that moment when a simple concept - I wonder what would happen if we defined sqrt(-1)? - opens up a whole new world of mathematics. its what makes me love math so much. there are truly endless possibilities, and its so much fun to stumble across some new field of math that you didnt even know existed, with its own rules and applications.

and thats really the spirit of this tournament, isnt it? most of my votes so far have been for numbers that come from entire fields or applications of mathematics that the average person hasnt even heard of, like the different types of infinities, or star, or the order of the monster group. because the joy of discovering a new subset of mathematics through a random number you found online is worth so much more to me than properties like how many factors a number has or how useful it is. [that being said, I did campaign hard for belphegors prime. its funny, sue me.] I mean, for some of those numbers, like aleph null and TREE(3), I can distinctly remember the first time I learned about them, and how exciting it was! sure, I've seen some interesting videos about tau and the golden ratio and any number of notable primes. but being introduced to an idea that breaks down your preconceived notions of what math is and how numbers even work..... that moment is priceless.

a vote for i is a vote for those discoveries. vote i

[also like. I know that i is currently winning. I just thought it was an obvious choice and its a surprisingly close race so I'm campaigning anyway]

Number Tournament: TWO vs THE IMAGINARY UNIT

[link to all polls]

2 (two)

seed: 3 (66 nominations)

previous opponent: pi

class: prime number

definition: a couple

[Wikipedia article]

i

seed: 11 (46 nominations)

previous opponent: e

class: imaginary

definition: up one unit from the origin

[Wikipedia article]

[aldridge]

Close tennis matches are long tennis matches

Last night, Emma Raducanu won her 19th and 20th consecutive sets at the US Open since the first qualifying round 18 days ago, and in doing so became Britain's first British woman to win a grand slam title since 1977.

It was also the first time I've watched a tennis match from first shot to last in quite a while – and probably the same for lots of other people too. And, of course, tennis scoring can be a bit complicated for the casual viewer. As someone I follow on Twitter wrote:

Whoever invented tennis scoring was definitely on acid.

— Hannah Al-Othman (@HannahAlOthman) September 11, 2021

This reminded me of a pretty famous maths problem: If you have a probability p of winning a point in tennis, what's the probability that you win a game?

Recall that a "game" is, starting from 0 ("love") the first person to 4 points (denoted, for obscure reasons, "15", "30", "40", "game"), but you must win by 2 clear points. To keep track of the two clear points, if the game gets to 40-40 (that is, 3 points each), that's called "deuce". The player who wins the next point has "advantage" ("Advantage Raducanu" or "Advantage Fernandez", calls the umpire); if they win the next point, they win the game, while if the opposing player wins the next point, it returns to deuce again.

(I say a "pretty famous" maths problem, because I remember coming across it a couple of times in my teens, probably in pop-maths books. Then in 2002, it was a question in my Cambridge entrance interview. I hadn't memorised the exact solution or anything, but I could remember enough of the general process to be able to work smoothly through to the solution without errors or needing help. I aced the question, and I got in. It's interesting to wonder in what ways my life might be different now if I hadn't come across this tennis problem before the interview. There's got to be at least a chance I wouldn't be a maths lecturer now without it.)

Game

What makes this an interesting maths problem is the "two clear points" rule, as tracked by deuce and advantage. This means that there's, mathematically speaking, no limit to how long a game might last: it could go deuce, advantage, deuce, advantage, deuce, advantage, ... (each advantage to either player) for an arbitrarily long time. (The second game of last night's Raducanu–Fernandez match had five deuces and five advantages before Raducanu broke serve.) So the non-boring part of the question is: Once you get to deuce, what then is the probability that you win the game?

Remember that p is the probability you win a point; it will be convenient to write q = 1 - p for the probability you lose a point. Let d be the probability you win the game starting from deuce. So from deuce, three things can happen:

You win the next two points, with probability p × p = p2. You then win the game.

You lose the next two points, with probability q × q = q2. You then lose the game.

You win one of the next two points: either win then lose or lose then win, with probability p × q + q × p = 2pq. You then return to deuce again, so your probability of winning the game is back to the d that you started with.

Putting all this together, we have

d = p2 + 2pqd.

We can then solve this for d, to get

d = p2 / (1 - 2pq) .

That solves the difficult/interesting part of the problem, Then it's straightforward but tiresome to turn this probability of winning a game from deuce into probability of winning the game from the start. A graph of the answer looks like this:

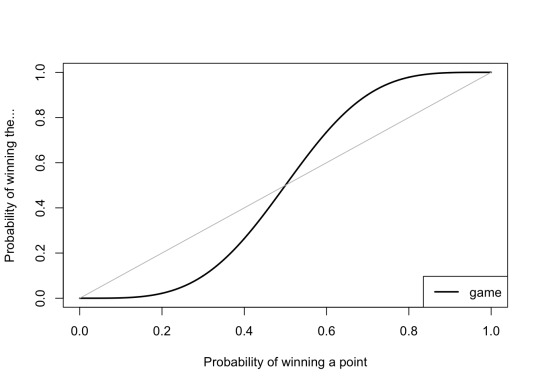
Note that having just a slightly better than 50:50 chance of winning each point gives you a much better than 50:50 chance of winning the whole game. For example, Raducanu won 54% of points last night (81 points out of 149), which would give you a 61% chance of winning each game – Raducanu actually won 63% of the games. (This is ignoring the very important issue of serving vs returning.)

Set and match

You can similarly stretch this out to a whole set, again ignoring serving/returning, which is again mathematically tiresome but not mathematically difficult. Here, the effect that a small superiority in winning points leads to a bit superiority in winning sets is even more pronounced.

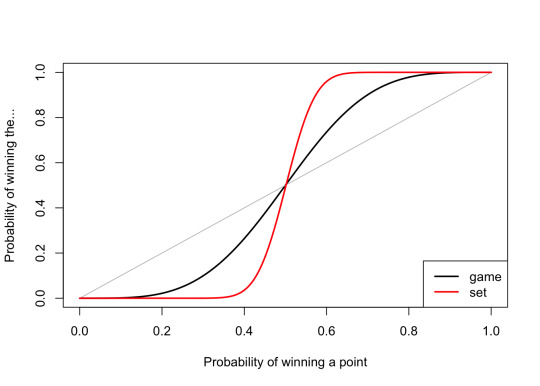
Unsurprisingly, for the whole match it's more extreme still – a 54% chance of winning a point gives you an 87% chance of winning the match, or 92% for a men's five-set match.

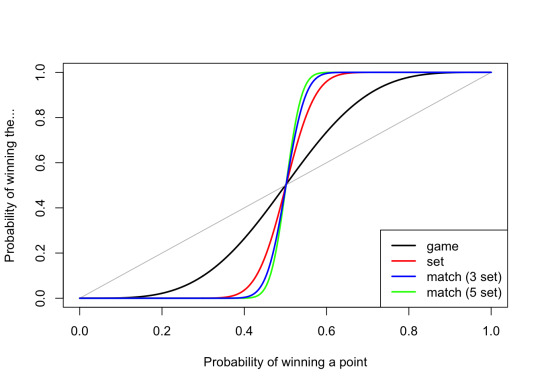
Close matches are long matches

So why bother with the complicated scoring. I guess the main reason is a sort of psychological one. A "first to 81 points" match would get pretty samey, and when one player is at 80 points to 68, it's pretty clear who's going to win. Instead we have the excitement of who's going to win this game, then who's going to win this set, as smaller bits of excitement within the match. It also gives a player that falls behind a chance to catch up – a 6–0 set loss is no worse that 7–6, so you pick yourself up, dust yourself off, and get started again.

But one other reason, is that ensures that matches where one player dominates are over very quickly, while tight balanced matches will go on for longer. This extends exciting close matches, and also makes it more likely that the genuinely better player will win. (A slightly worse player has more chance of snatching a lucky win in a shorter match.)

That picture shows the average number of games in a match. We see that close matches, where the probability of wining a point is close to 0.5, are the longest games, on average.

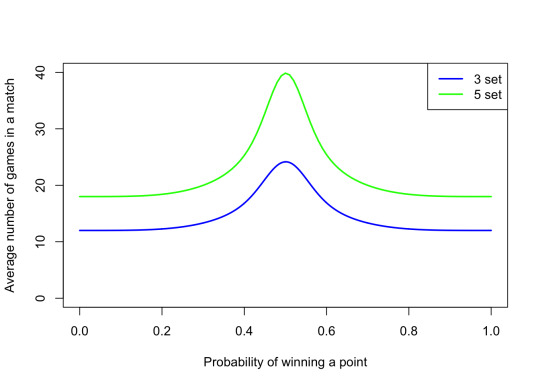
My own solution: Start playing a minimum number of points; maybe 100. From then, as soon as one player has scored n/2 + sqrt(n) points out of n, we say that they're two standard deviations above 50:50, reject the null hypothesis that p = 0.5, and declare them the winner. I don't think it will catch on.

[This article was helpful for cheacking my calculations.]

[rachelingly]

Learning (Day 7)

Mathematics

On April 12th, I improved my 3rd-grade math from 99% to 100%! My 4th-grade math improved from 92% to 95% and my trigonometry from 85% to 89%. When it comes to Trig, I just need to do a better job of checking my work and not second-guessing myself. 

But I find myself being super comfortable now with coordinates, radians, and degrees outside of the 1st quadrant. Like if you ask me what the cosine of 330 degrees is, I know it off the top of my head! (sqrt(3)/2, btw). It is such a win for me to become more and more comfortable with subjects that used to leave me in tears the first time around.

Russian

I did my Russian language lessons via Duolingo. I had started a free trial for the pro and it ended in the middle of my lesson! Honestly, I am considering getting it because I found the pronunciation to be very helpful for me. Anyways, I earned 102 XP on April 12th!

French

Per my last post, I decided to put Quantum Computing on the backburner. On April 12th, I took a trip to the library and found a French lesson book along with CDs! So it seemed only right to replace my quantum computing lessons with French. I did the first lesson and answered the grammar questions. I learned the verbs to be (être), to have (avoir), to visit (visiter), to speak (parler), and to study (étudier). I, also, learned their conjugations and did the exercises at the end. Honestly, I am finding it hard to suppress Russian and not replace the French pronouns with Russian ones. 

But this lesson was so much fun! Today, I listened to the corresponding audio on the way to work and repeated it for practice. You know how bad your pronunciation gotta be to think to yourself: "that is not what that man said" every time you repeat it back?

[argumate]

perhaps the score for each player is a tuple of:

number of proofs found

1 / sum of sqrts of proof lengths

number of valid lemmas proposed

1 / sum of winning proof lengths divided by lemma lengths

such that the winner is decided by whoever finds the most proofs, with tie-breaks decided by whoever found the shortest proofs, and any remaining tie-breaks decided by whoever proposed the most valid lemmas, and any remaining tie-breaks decided by whoever proposed the shortest lemmas with the longest proofs.

hopefully that would drive exploration in a profitable direction, then the only question is which formalism to start with, presumably one already well-understood like Horn clauses or something like that to see if it can rediscover a known algorithm like first order resolution.

okay so maybe this is the game:

N players, M rounds, N*M turns, each turn one player proposes a lemma and then all the players attempt to find a proof for it.

each player who finds a proof gains points inversely proportional to its length, encouraging shorter proofs.

the player who proposed the lemma also gains points proportional to the ratio of the lengths of it and its shortest proof, encouraging short lemmas that are difficult but possible to prove.

(the scoring must be balanced to ensure that players cannot get more points by cooperating to generate unnecessarily long proofs for simple lemmas!)

possibly players who propose lemmas nobody can prove will lose points? or lemmas that somebody can prove false, perhaps?

anyway at the end of the game the weakest players are culled and the strongest enthusiastically breed in the conventional fashion.

[gamingavickreyauction]

In defence of argument 1:

In my understanding, the word "consequentialism" means you have a function f: S -> X from states of the world to some linearly ordered set X. We'll assume X is the real numbers, because it would be pretty weird if it wasn't. Then the action you should take is the action that maximizes f(s). However, in reality, we don't know what effect our actions will have. Maybe that baby you saved will grow up to be turbo-Hitler. So we generally instead maximize the expected value of f(s). This move, or something like it, isn't really optional for consequentialists, because just about every practical problem is uncertain.

So does this approach fall foul of the stoolmakers? Assuming a utility of 1 if we get a stool and 0 otherwise, it needn't be the case that the expected benefit of each stoolmaker participating adds to 1. In fact, if each assumes all the others will definitely participate, each will conclude there is an expected benefit of 1 from their labour. So taking the expected utility of a vote isn't assuming additivity in a problematic way: we are adding up f(s), not adding up s.

So what is the expected benefit of voting? It's the expected benefit of the least bad option winning over the worst bad option winning per person, multiplied by the number of people, divided by the probability that your vote was pivotal. E(B) = bNp. Now, in a larger voting population, the probability of your vote being pivotal will be smaller, approximately inversely proportional to the number of people, so the large and small terms cancel out. The benefit of voting, in this analysis, is on the order of b.

But the sum of E(B) for each person needn't add to bN, so this isn't additive. In an election in a safe seat, for example, p will be far lower than 1/N. This suggests, for example, that the expected value of voting is much smaller in New York than in Wisconsin, for example, as your vote is much more likely to be pivotal if it's expected to be a close election.

Take a numerical example: lets say there are N people other than you (N is large), each with a 1/2 chance of voting for each option. This is a very close election. Then p is the probability of exactly N/2 votes being cast for your party. The number of votes for your party follows Bin(2N,1/2), so this is N choose N/2 *2^-N. Using Stirling's approximation this is 1/sqrt(Npi). And this is what everyone sees as the probability of their vote being pivotal. So it adds to more than 1- it isn't proportional to 1/N- and the bigger the election, the more important it is to vote, because the consequences scale up faster than the volitility scales down. I think this is counterintuitive because it is an unrealistically extreme example of a close election, but it illustrates that the expected utility argument isn't based on an assumption of additivity.

This agrees with my intuitions about when voting is valuable, and I think it agrees with most people's intuitions. Notably, if it could be known with certainty that your candidate was going to win anyway, or that your candidate was going to lose, the benefit of voting would also be 0. This special case resembles the Maxist analysis.

Now, it's not necessary to use the expected value, specifically, and Max has indicated in the past that they are critical of expected utility, though I don't think they ever laid out why. So there's a more general approach to rescue consequentialism from uncertainty:

A lottery assigns a probability of various events in S, so if S = {win the election, lose the election}, a lottery could be winning the election with probability 0.23 and losing with probability 0.77. We only need a function F: L(S) -> X that assigns lotteries over S to values in an ordered set, which we will assume is the real numbers, where the bigger F(l) the better.

We can make new lotteries by combining two lotteries, say l3 = p l1 + (1-p) l2. Suppose someone flips a coin, and if it lands heads, they give us lottery l; if it lands tails, they give us lottery n. This would be a new lottery, 1/2 l + 1/2 n. Presumably if we prefer lottery l to lottery m, we should also prefer flipping a coin and getting l on heads to flipping a coin and getting m on heads- otherwise our preference would depend on whether they flipped the coin before or after they asked what our preference is. So F should satisfy F(p l + (1-p) n) > F(p m + (1-p) n) if and only if F(l) > F(m). But other than that we have a lot of options other than the expected value, right? It turns out no, even with these minimal axioms, F must have the form of E(f(s)), or g(E(f(s))) for some strictly increasing g, and f some function S -> R. This is a variation on the Von Neumann Morgenstern theorem.

I've said this before but: as a strict consequentialist about ethics, I don't believe that voting matters because one's vote is almost sure to be inconsequential. This is not related to an larger sociopolitical convictions of mine, it's purely mathematical. People are already happy to acknowledge that (in the US, say) if you live in a state that always goes blue or always goes red, your vote doesn't actually have any effect. But this is true everywhere (except very small elections), it's just most obvious in these states.

Now, telling people to vote might well have an effect. If you have a large platform, and you say "go vote for candidate X!" and 1000 people do it, that might be enough to actually affect the outcome of an election. So I get why voting discourse is the way it is; advocating for others to vote is a very cheap action that might have a large effect size, so lots of people are going to do it. Turns out it can be rational to advocate for something that it is not in fact rational to do. This is pretty obvious if you think about it but for some reason people really don't like this idea.

Anyway, even though people know that their vote is not going to change the outcome of an election, they usually make one of two arguments that voting is rational, and these arguments are both bad.

The first is "if 1000 votes can have an effect, then one single vote must have 1/1000th of that effect, which is small but not zero!" or something like that. This follows from the false belief that effects are additive; i.e. that the effect of two actions is just the effect of one action "plus" the effect of the other. This is sort of patently nonsense because it's not clear what it means to "add effects" in the general case, but that's mostly a nitpick (people know roughly what they mean by "adding effects"). More important is that it's just wrong, and can be seen to be wrong by a variety of counterexamples. Like, to make up something really contrived just to illustrate the point: suppose you want to sit down on a stool. And there are no stools in town, but there are four stool-makers: three who make legs and one who makes seats. And none of them can build the stool on their own, each is only willing to make one part per stool. Maybe it's some sort of agreement to keep them all in business. Anyway, let's say you commission a stool, but the seat guy doesn't show, so you just end up with three stool legs. Does this allow you to "3/4ths take a seat"? Can you "take 3/4ths of a seat on this stool"? No, you can take zero seats on this stool, it's an incomplete stool. Effects are not additive! 1000 votes might sway an election, but that does not mean that any individual vote did so, and in particular if any one of those 1000 people chose not to vote it is very likely the election would have gone the same way!

The second bad argument goes like "if everyone thought like you, nobody would vote, and that would be bad!". This also fails in a simple logical way and a deeper conceptual way. The logical failure is just that the antecedent of this conditional is not true, not everyone thinks like me. And in fact, my choice to vote or not in itself has no impact on whether others think like me. Thus "if everyone else thought like that it would be bad" might be true but is irrelevant, you can't conclude anything about whether I should vote or not from it. Conceptually, I think this arises from this sort of fallacious conception of oneself not as a particular individual but as a kind of abstract "average person". If I don't vote, and I'm the average person, that basically means the average person doesn't vote! Which would be bad! But of course you are not the "average person", you are you specifically. And you cannot control the average person's vote in any way. Instead, the blunt physical reality is that you have a small list of options in front of you: vote for candidate 1, vote for candidate 2, ..., vote for candidate n, and I'm sure you can agree that in actual reality no matter which one you pick the outcome of the election is not likely to be changed. Your vote doesn't matter!

Now, I should say at the end here that I do in fact vote. I vote because I have a sort of dorky civics enthusiast nature, and I find researching the candidates and voting in elections fun and edifying. I vote for my own purposes! But I don't believe that it affects the outcome of things, which it plainly mathematically does not. I have no further opinions on voting discourse.

[mathematicianadda]

The Big Lock-Down Math-Off, Match 4

Welcome to the fourth match in this year’s Big Math-Off. Take a look at the two interesting bits of maths below, and vote for your favourite.

You can still submit pitches, and anyone can enter: instructions are in the announcement post.

Here are today’s two pitches.

Tom Edgar – Rayleigh cool pairs of sequences

Tom Edgar is a math professor at a small university in Washington State, and is currently the editor of the Mathematics Association of America’s undergraduate magazine Math Horizons. He’s @TedG on Twitter.

An Exercise. Let’s start with a really (or Rayleigh) neat exercise: pick your favorite irrational number larger than $1$ (okay, you can choose numbers that are probably irrational like $e+\pi$ or $e\cdot\pi$, but I assume you will pick $\sqrt{2},e,\pi$ or $\phi$ – just don’t pick a rational number.) Let’s call your number $x$. Then, compute the first few values in the following integer sequence.

\[ \left(\left\lfloor n\cdot x\right\rfloor\right)_{n=1}^{\infty} = \left(\left\lfloor 1\cdot x\right\rfloor,\left\lfloor 2\cdot x\right\rfloor,\left\lfloor 3\cdot x\right\rfloor,\left\lfloor 4\cdot x\right\rfloor,\ldots\right) \]

where $\left\lfloor y\right\rfloor$ is the floor function, or “round-down function,” which outputs the greatest integer less than or equal to the input $y$.

The resulting sequence forms an increasing list of integers, but some integers are missing: aha, a mystery! For instance, when we use $x=\sqrt{7}$, which is irrational since $\sqrt{p}$ is irrational for all primes $p$, we get the sequence

\[ \left(\left\lfloor n\cdot\sqrt{7}\right\rfloor\right){n=1}^{\infty} = ({\color{blue}2,5,7,10,13,15,18,21,23,26,29,31,34,37,\ldots}) \]

It looks like one or two integers are missing between each pair of consecutive entries in the list. But now, here’s the fun part! For the value $x$ you chose, compute the number $z=\frac{x}{x-1}$, which is also an irrational number larger than $1$, and construct the corresponding integer sequence for the value $z$:

\[ \left(\left\lfloor n\cdot z\right\rfloor\right){n=1}^{\infty} = \left(\left\lfloor 1\cdot z\right\rfloor,\left\lfloor 2\cdot z\right\rfloor,\left\lfloor 3\cdot z\right\rfloor,\left\lfloor 4\cdot z\right\rfloor,\ldots\right). \]

For example, when we do this with $x=\sqrt{7}$ so that $z=\frac{\sqrt{7}}{\sqrt{7}-1}$, we get the integer sequence

\[ \left(\left\lfloor n\cdot\frac{\sqrt{7}}{\sqrt{7}-1}\right\rfloor\right)_{n=1}^{\infty} = ({\color{orange}1,3,4,6,8,9,11,12,14,16,17,19,20,22,\ldots}). \]

Do you see what’s happened? Are you amazed? To make things just a bit clearer, let’s weave together the previous two integer sequences in increasing order:

\[ \color{orange}1,\color{blue} 2, \color{orange}3, 4, \color{blue}5, \color{orange}6, \color{blue}7,\color{orange} 8, 9, \color{blue}10, \color{orange} 11, 12, \color{blue}13, \color{orange}14, \color{blue}15, \color{orange}16, 17, \color{blue}18,\color{orange} 19, 20, \color{blue}21,\color{orange} 22, \color{blue}23,\color{orange} 24, \ldots \]

Every natural number appears once and only once! The choice of $x=\sqrt{7}$ is not special; this partitioning property will happen for any choice of irrational $x$ (the first linked video shows it happen for $x=\sqrt{2}$ and $x=e$). If you haven’t tried it yet, pick your favorite irrational and give it a go; you can use the commands

print([floor(n*pi) for n in [1..20]]) print([floor(n*pi/(pi-1)) for n in [1..20]])

in Sage to get the two sequences when $x=\pi$.

Beatty Sequences and Rayleigh’s Theorem. The sequences defined above, those of the form $a(n) = \left\lfloor nt\right\rfloor$ for fixed $t$, are known as Beatty sequences (due to a problem posed by Thomas Beatty in the American Mathematical Monthly in 1926). The associated theorem, stated below, is sometimes called Beatty’s theorem, but it was previously discovered by Lord Rayleigh, and as such is more appropriately known as Rayleigh’s theorem.

Theorem. Let $x>1$ be an irrational number, and let $z=\frac{x}{x-1}$. The two integer sequences $a(n)= \left\lfloor nx\right\rfloor$ and $b(n)=\left\lfloor nz\right\rfloor$ partition the natural numbers.

In other words, every natural number is either of the form $\left\lfloor nx\right\rfloor$ or $\left\lfloor \frac{mx}{x-1}\right\rfloor$, but no positive integer is of both forms; the two sequences are complementary (they may also be complimentary like those in figure 1).

Two complementary sequences

Intrigued? Explore what happens when $x$ is instead a rational number larger than $1$: are some numbers missing from the lists, or are there numbers that appear in both lists?

A full proof of Rayleigh’s Theorem can be found in many places (see [2] or even Wikipedia), but we might as well include the basic building blocks for readers who want to construct a proof themselves. The key is to make sure the sequences have no integers in common (no collisions) and that every integer appears in one sequence (no whiffs).

Let $x>1$ be a fixed real number, $z=\frac{x}{x-1}$, $a(n)=\lfloor nx\rfloor$ and $b(n)=\lfloor nz\rfloor$. The first key properties to check are that $\frac{1}{x}+\frac{1}{z}=1$, and that $nx$ and $nz$ are irrational for all positive integers $n$.

No collisions.

If we suppose that $a(n)=y=b(m)$ for some natural numbers $n,m$ and $y$ (so that $y$ would be in both sequences), then we conclude

\[ y< nx< y+1 \text{ and } y<mz < y+1. \]

Dividing the first inequality by $x$ and the second inequality by $y$ and investigating the integer sum $n+m$ allows us to obtain a contradiction.

No whiffs.

If we suppose $a(n)< y$, $a(n+1)\geq y+1$, $b(m)<y$, and $b(m+1)\geq y+1$ for some integers $n,m$ and $y$ (so that $y$ would be missing in both sequences) then

\[ nx< y \hspace{.5in} y+1< (n+1)x \hspace{.5in} mz< y \hspace{.5in} y+1< (m+1)z. \]

This time, use the previous inequalities to show that $y$ (an integer) lies strictly between $n+m$ and $n+m+1$, which is impossible.

A More General Result. It seems quite strange that two sequences generated by floor functions create a set of complementary sequences. You might wonder how easy it is to formulaically or systematically generate complementary integer functions in this way; luckily, many have investigated these objects. Lambek and Moser describe how, given any increasing integer sequence $f(n)$, we can construct two sequences $a(n)$ and $b(n)$ that partition the positive integers. To do this, they define

\[ f^\downarrow(n) = \big|{m\geq 1\mid f(m)<n}\big|, \]

so that $f^\downarrow(n)$ counts the number of outputs of $f$ strictly less than $n$. Computing $f^\downarrow(n)$ can be accomplished by counting the number of outputs on the graph of $f$ lying strictly below the line $y=n$.

Figure 2. Computing $f^\downarrow(5)$ (left) and $f^\downarrow(10)$ (right) when $f(n)=2n$.

For instance, if we let $f(n)=2n$ (the sequence of positive even integers) graphed in figure 2, then $f^\downarrow(5)$ counts the number of dots (outputs) strictly below the red dashed line at $y=5$ so that $f^\downarrow(5) = 2$. Similarly, the diagram on the right in figure 2 shows that $f^\downarrow(10) = 4$; there are $5$ dots below the dashed line at $y=10$.

Amazingly, by the Lambek-Moser theorem, the two sequences $a(n)=f(n)+n$ and $b(n)=f^\downarrow(n)+n$ are complementary. In our example using $f(n)=2n$, we get $a(n) =3n$ and $b(n)$ consists of all the integers congruent to $1$ or $2$ modulo 3 in increasing order.

We can apply the procedure above directly to the function $f(n) = \lfloor nx\rfloor-n$ to prove Rayleigh’s Theorem. Try this more general out for yourself: find the complementary sequences guaranteed by Lambek and Moser when $f(n) = n^2$ or $f(n)=n^3$, or when $f$ is your favorite increasing integer sequence!

Concluding Remarks. Finally, one way to attempt to understand a sequence $(a(n)){n=1}^\infty$ is to study the sequence of first differences, $(a(n)-a(n-1)){n=2}^\infty$. For the Beatty sequence for $x=\sqrt{7}$ that we investigated previously, the sequence of first differences starts

\[ 2, 1, 2, 2, 1, 2, 1, 2, 2, 1, 2, 2, 1, 2, 1, 2, 2, 1, 2, 1, 2, 2, 1, 2, 2, 1, 2,1,2,\ldots \]

Studying the first differences of Beatty sequences unlocks a large world of mathematical research connected to Sturmian words, Christoffel words, and Euclidean strings. The corresponding sequence when $x=\phi=\frac{\sqrt{5}+1}{2}$ has interesting connections to the Fibonacci numbers and the Beatty sequence for $\phi$ is used in the winning strategy or Wythoff’s game, a variation on Nim (for more on this game, see the wonderful video by James Grime and Katie Steckles, and a follow-up video by James Grime). These relatively unknown sequences unlock the door to many other interesting sequences related to the combinatorics on words.

PS. After recording the videos for this piece, I realized I am saying the name “Rayleigh” incorrectly – my apologies for this.

References

Samuel Beatty, Nathan Altshiller-Court, Otto Dunkel, A. Pelletier, Frank Irwin, J. L. Riley, Philip Fitch, and D. M. Yost. Problems and Solutions: Problems for Solutions: 3173-3180. Amer. Math. Monthly, 33(3):159, 1926.

Samuel Beatty, A. Ostrowski, J. Hyslop, and A. C. Aitken. Problems and Solutions: Solutions: 3177. Amer. Math. Monthly, 34(3):159–160, 1927.

J. Lambek and L. Moser. Inverse and complementary sequences of natural numbers. Amer. Math. Monthly, 61:454–458, 1954.

Fusible Numbers

Christian blogs at The Aperiodical, and collects his other doings at somethingorotherwhatever.com.

This is a puzzle that I’ve always enjoyed, not for the fun of solving it, but because of the unexpectedly deep answer to the question it makes you think of next.

At the end of the video I refer to these slides and this paper by Jeff Erickson and others.

So, which bit of maths made you say “Aha!” the loudest? Vote:

Note: There is a poll embedded within this post, please visit the site to participate in this post's poll.

The poll closes at 9am BST on Sunday the 19th, when the next match starts.

If you’ve been inspired to share your own bit of maths, look at the announcement post for how to send it in. The Big Lock-Down Math-Off will keep running until we run out of pitches or we’re allowed outside again, whichever comes first.

from The Aperiodical https://ift.tt/2KeuyeQ from Blogger https://ift.tt/3crswnI

[thisismyblogforwthicsinthep-blog]

Notes on Outline of Lecture of 17/2/2020

Tu toque ad hominemtu toque = “you also” in LatinExample:…..A parent says, don’t smoke, it’s unhealthy…..The kid says, “but you smoke”. . . . .“Practice what you preach!”. . . . .“So I don’t believe you!”What is a Logical Fallacy?

…..Literally, a reasoning mistake

…..Example:

. . . . .You say the square root of 100 is 10

. . . . .Someone wishes to argue otherwise

. . . . .They say you flunked arithmetic in 3rd grade

. . . . .People start to doubt that sqrt(100)=10!

. . . . .This is crazy, right?

. . . . .It happens all the time…

. . . . . . . just not as obviously

I like this example because you really do see this all the time like on social media, people calling each other out. 

you really do see  ad hominem argumentation in politics nowadays as well too. Most of running for office is just trying to dig up dirt on the opposite so you can attack their character and make yourself look better. 

Abusive ad hominem

Argue against something by attacking the person arguing for it

Amy Winehouse’s music sucks …..because she’s in the “27 club”

. . . . .logical fallacy? yes 

…..Jimi Hendrix’s music is great …..because he’s in the “27 club”

. . . . .logical fallacy? yes opinionated 

…..We shouldn’t do the project like Irving suggests …..because he’s totally uncool

. . . . .logical fallacy? yes attack on character. 

Tu toque ad hominem

tu toque = “you also” in Latin

Tu quoque, or the appeal to hypocrisy, is an informal fallacy that intends to discredit the opponent's argument by asserting the opponent's failure to act consistently in accordance with its conclusion.

Example:

…..A parent says, don’t smoke, it’s unhealthy

…..The kid says, “but you smoke”

. . . . .“Practice what you preach!”

. . . . .“So I don’t believe you!”

is there a logical fallacy there?  yes the kid is pointing out the failure of the parent so because they failed then it dosnt matter which in reality the parent is probably doing the right thing there. 

Scenario 1a (you are on the jury and the jury is discussing a verdict):

. . . “Take the defendant’s lawyer’s argument with a grain of salt – being paid to give a one-sided argument”

. . . . . .logical fallacy, or logically ok? logical fallacy, his job is to defend the guy and that is what he is paid to do, not because he just dosent want to. 

Summary:

. . . “ad hominem” means “to the man”

. . . it does not mean “invalid” or “valid”

. . . often it is an invalid/sneaky/sleazy argument trick

. . . . . . (remember its full name:

argumentum ad hominem)

. . . . . . ethical?

. . . sometimes it is logically reasonable

Circumstantial ad hominem argument

Saying that the arguer is biased, therefore the argument is invalid

subtype: conflicts of interest

“That’s just PR spin; they’re paid to say that”

. . . . .is that argument “to the man”?

. . . . .is it logically fallacious?

The American legal system

based on paying people to argue one side

it’s “adversarial”

Other countries have different approaches

Does the adversarial approach affect believability of the argument? yes because it may not even be about who was wrong or right in a case but who has more money and the better lawer who can deliver the most belibability in the court room wins, and really thats not how it should be. 

Can you think of a better method? level playing field on money used to higher lawyer. 

Guilt by association

(This example is not as current as it used to be but it illustrates the idea nicely):

“You want us to get out of Iraq? Well, Iran wants us to do that, too!”

…..“So we should not reduce troops”

. . . . .logical fallacy?

…..“So your argument is traitorous”

. . . . .logical fallacy?

…..“So your argument is wrong”

. . . . .logical fallacy?

see this all the time too. that first example is perfect too because it goes with all things such as social media, “oh you dont follow any religous pages, you must be none religous which is a shame” really dosnt do any justice at all because it could just not be true at all. 

[metastasiscreative]

OUR SQRT AD WINS BIG!

They said it was on-the-nose, but the good kind of on-the-nose. Like sunscreen.