#4-color theorem

[creamsicle-art]

Howdy yall! As you know things have been pretty shitty for transfems on this website (and world) lately. If maybe some of y'all would like to put your money where your mouth is, how about checking out (and maybe buying) some of my games such as...

4 Color Theorem, a puzzle game about coloring in maps.

Or Snowbird, a short platformer with some unique movement mechanics.

[rbrooksdesign]

"DMT-EDMT Series for December Geometry #30"

From another perspective...

Yesterday's post (#29)

The Butterfly Fractal 1 (BF1) is a fractal resulting from the simple doubling of quantity "1" -- 1 -- 1x2=2 -- 1x2x2=4. -- 1x2x2x2=8,...16--32--64...

When you lay it out into its "Butterfly-like" array, you can see that every "1" becomes a new source for the self-similar, re-iterative redundancy of the same "fractal" pattern within.

The BF1 pattern is repeated on both sides (of the "wings.”)

Today...

The central BF1 -- 1--2-- 4--8--16--32--64 in YELLOW is the key.

Yesterday (MULTI-COLOR butterfly) we showed it formed the two sides (wings) of the butterfly-like pattern.

It, in turn, informs the Mersenne Prime Square (MPS) -- (BLUE BF1 Columns) -- as the 127 BF1 Columns would actually form a true square if they were scaled down to equal the width.

Now, on the right, we have a "summary" of all that is going on in the figures on the left. It reveals 8 of the 10 ID parameters that ALL "containers" follow.

p=Prime, but it may be easier to think of it as the exponential power that 2 is raised to. (Reason: for some "containers" p is not prime, yet their pattern follows as though it was.) See below.

This "summary" pattern is EXACTLY the same for ALL SET 1 and SET 2 "containers" -- including the Mp-PN. This is a TRUE Mp-PN SET 1 "container."

Personally, the jump from the BF1 butterfly image to either of the MPS images is harder to keep straight until one remembers that the MPS presents the same information in 3 overlapping layers:

1. MPS = z² =127² = 16129

2. PN = xz = 64•127 = 8128, and, OC = yz = 63•127 = 8001, and, PN+OC = 8128+8001 = 16129

3. PNS = x² = 64² = 4096, and, OCS = y² = 63² = 3969, and, CR (Complement Rectangle) = xy = 64•63 = 4032, thus PNS + OCS + 2(CR) = 4096+3969+2(4032) = 16129=MPS.

Perfect Number Square (PNS) + CR = PN, and, ODD Complement Square (OCS) + CR = OC.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Math: Euclid-Euler Theorem = 2ᵖ⁻¹ (2ᵖ -1) = Perfect Number (PN) where 2ᵖ⁻¹ = x = 2⁶ = 64, and, 2ᵖ -1 = z = 127 = Mersenne Prime (Mp), as xz=PN.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

more...

[squareallworthy]

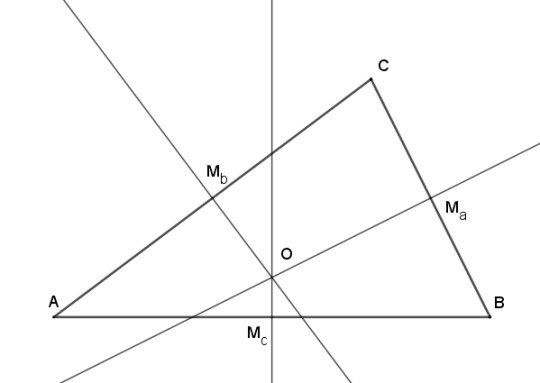
Triangle Tuesday 2: The circumcenter, pedal triangles, degeneracy, and what even is a triangle anyway?

The circumcenter is almost as simple an idea as the centroid, which we looked at before. To define it, you start the same way. Take triangle ABC, find the midpoints of the sides Ma, Mb, and Mc. Then instead of drawing lines to the midpoints from the vertices, draw perpendicular lines through the midpoints. These lines all coincide at a point O, which is the center of a circle that you can draw through the vertices. The circle is called the circumcircle, and that's why the point is called the circumcenter.

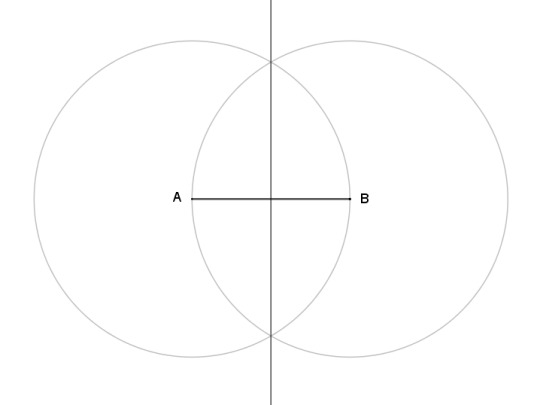
I say almost as simple, but in a sense the circumcenter is simpler than the centroid, because you could easily discover it by accident in the process of simply finding the midpoints. Drawing that perpendicular line, the perpendicular bisector, is the standard way of finding the midpoint of a line segment. It's covered all the way back in Book 1, Proposition 10 of Euclid's Elements, and it's simply this:

So if you find the midpoint of all three sides of a triangle with this method, you've already identified the circumcenter. But that doesn't prove that the perpendicular bisectors always coincide, nor that their point of crossing is the center of the circumcircle. For that, let's return to Euclid (Elements, book 4, proposition 5). Euclid's proof is very straightforward, and leads nicely into something interesting, so we'll follow that, but I will state the theorem differently.

Theorem: the perpendicular bisectors of a triangle coincide and their point of intersection is the center of a circle that meets all three vertices.

Let ABC be a triangle with midpoints of the sides Ma opposite A, similarly for Mb and Mc. Draw perpendiculars to sides AC and BC from their midpoints to meet at point O. Connect three segments from O to A, B, and C.

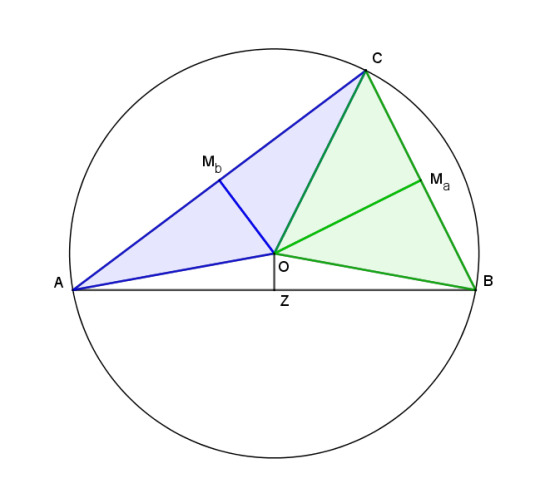
Consider the two blue triangles. Their sies AMb and CMb are equal, since Mb is the midpoint of AC. They also have OMb in common. Their angles at Mb are right angles, and therefore equal. So they have two sides and one angle the same, making them congruent, and therefore OA = OC.

The same argument applied to the green triangles shows that OB and OC are equal. By transitivity, OA = OB and O is equidistant from the three vertices. The radii of a circle are all equal, so a circle centered at O passing through A also passes through B and C.

Finally, draw a line from O perpendicular to AB. This creates two white triangles with sides OA and OB equal, side OZ in common, and equal right angles at Z. The two triangles are then congruent and the two sides AZ and BZ are equal. So Z is the midpoint Mc, showing that the perpendicular bisectors all meet.

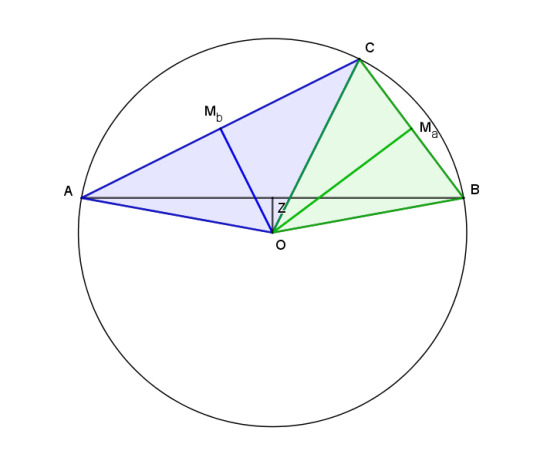
And the same argument works when ABC is obtuse. The circumcenter lands outside the triangle, and in this coloring the white triangles are no longer white, but all the relationships between the segments are the same.

(What Euclid didn't prove is that the perpendicular bisectors of AC and BC do in fact meet somewhere, that is, that they aren't parallel. It's not difficult, but I'm not going to prove that either, at least not yet, for reasons.)

Let's develop another idea. We located the circumcenter by drawing the perpendicular bisectors, but now consider doing this construction in reverse. That is, pick a point, and then draw perpendiculars to the three sides. The intersection of the perpendicular and the side is called the foot of that point with respect to that side. If you do that with with the circumcenter, the feet are of course the midpoints, but you can find the feet for any point.

And if we connect those three feet, we get a triangle. In this case, the medial triangle, which we have seen before. For a point in general, the triangle formed by its feet is called the pedal triangle of that point. ("Pedal" meaning "related to feet," and yes, that is why a lever operated with your foot is also called a pedal.)

So let's draw the pedal triangle for an arbitrary point, move it around, and see what happens. The point is going to sometimes be outside the triangle, but that's all right. With extended sides (dashed lines) we will still be able to draw a perpendicular to find a foot, no matter where the point is.

So there's something interesting -- the three feet become colinear and the pedal triangle flattens out into a straight line when the point is on the circumcircle. Does that always happen?

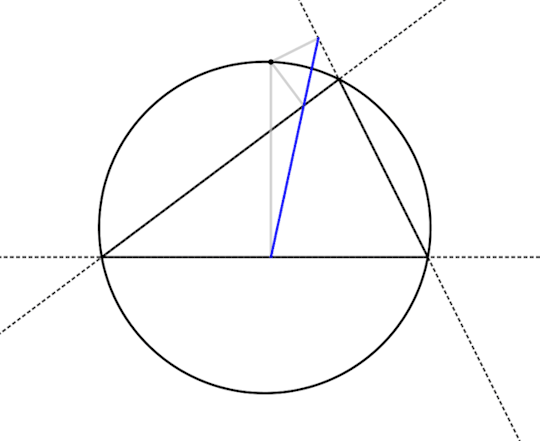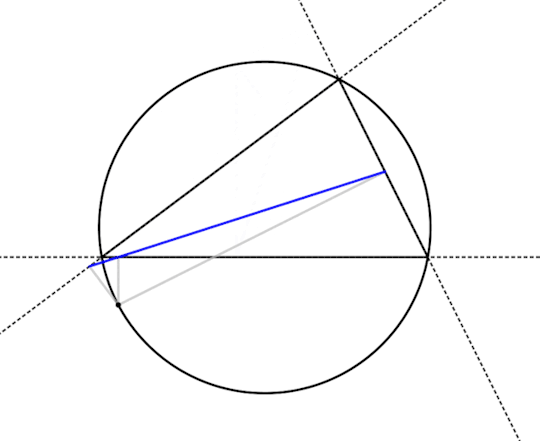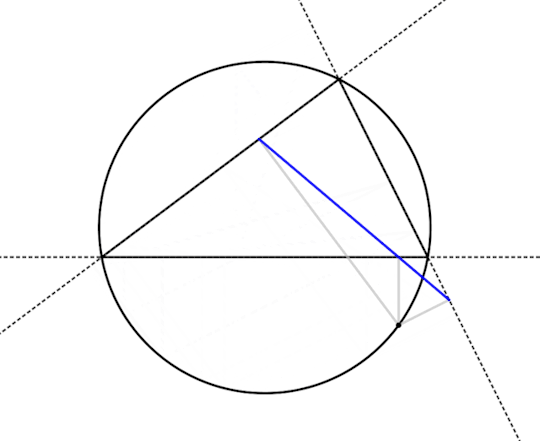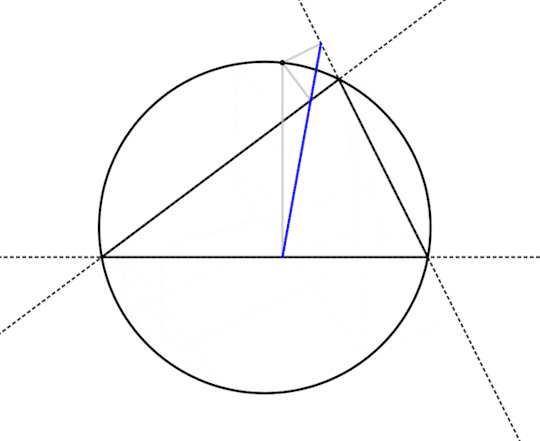
Looks like it does! So let's prove that. Below is a drawing of the flattened-out pedal triangle of a point on the circumcircle, all labeled up. I've also added a couple dashed lines to make following the proof easier. What we would like to show is that ∠JKP + ∠PKL = 180°.

We're going to extract some information from this drawing based on two facts: a) in a cyclic quadrilateral (meaning it has all vertices on the same circle), opposite angles sum to 180° and b) if two right triangles have the same hypotenuse, the triangles have the same circumcircle. I'm not going to prove either of those here because this post is long enough already, but both of these results follow straightforwardly from the inscribed angle theorem.

Theorem: For a point P on the circumcircle of a triangle ABC, the feet J, K, and L with respect to ABC are colinear.

Okay. PCBA is a cyclic quadrilateral, so

1) ∠BAP + ∠PCB = 180°.

And ∠BAP is the same as ∠LAP, so

2) ∠LAP + ∠PCB = 180°.

The two triangles AKP and ALP are right triangles with the same hypotenuse (the dashed segment AP), so all four points are on the same circle and ALKP is a cyclic quadrilateral. Therefore,

3) ∠LAP + ∠PKL = 180°,

4) ∠PKL = ∠PCB.

Quadrilateral PKCJ is also cyclic (again because of right triangles sharing the same hypotenuse), so

5) ∠JKP = ∠JCP

by the inscribed angle theorem. ∠PCB is supplemental to ∠JCP, so

6) ∠JKP = 180° - ∠PCB

and then combining 4) and 6),

7) ∠JKP + ∠PKL = ∠PCB + (180° - ∠PCB) = 180°,

which means that the pedal triangle of a point on the circumference of a circle is flattened to a line segment. Can we consider such a figure to be a triangle?

Now we can return to Euclid's omission in the existence proof of the circumcircle. Proving that the perpendicular bisectors aren't parallel is equivalent to proving that no two sides of a triangle are parallel, or that the three vertices of a triangle aren't colinear. Euclid didn't do that, but it's pretty simple, so he could have. And then he would simply have said that such an arrangement of line segments isn't a triangle. Modern geometers working with projective geometry can answer differently, and might say that this is a degenerate triangle, but we haven't gotten into that yet.

Let's do one more thing. We can extend the flattened line segment into a line, called the Simson line, after Robert Simson, who never wrote anything about it. It was actually discovered by William Wallace, but not named for him, because that's how things work in math.

The set of all Simson lines from all points on the circumcircle form an envelope in the shape of a deltoid, the Steiner deltoid, named for Jakob Steiner, who for all I can tell was its actual discoverer.

The deltoid is tangent to the sides of the triangle at three points where the Simson line coincides with the sides. I'll have more to say about this lovely deltoid later, but for now, please just enjoy this gif. It took me several hours to figure out how to make it, so if people reading this could spend a collective several hours staring at it, that would be great.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[charlesoberonn]

The Four Color Theorem is a theorem in Graph Theory which states that for every collection of contiguous non-overlapping regions on a plane, no more than 4 colors are required to color the plane so that no two adjacent regions share the same color.

Below are 108 examples I made in Photoshop:

[szimmetria-airtemmizs]

Here is a fun theorem: Consider 31 points evenly spaced on a circle, and color each of them arbitrarily blue or red. Then we can always find 5 points with the same color that divide the circle into arcs proportional to 1 : 2 : 4 : 8 : 16. The arcs need not be in the order suggested by the proportion. That is, 1 : 4 : 8 : 2 : 16 counts as a success!

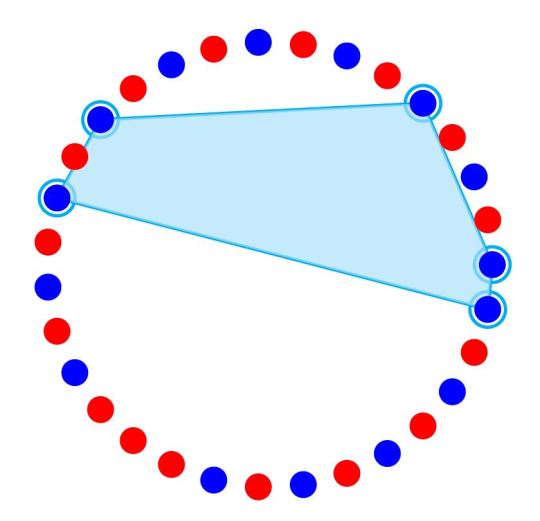
One of my favorite open problem is whether the generalization of this holds:

Stromquist's conjecture: For any k>= 3, consider (2^k)-1 points evenly spaced on a circle, and color each of them arbitrarily blue or red. Then we can always find k points with the same color that divide the circle into arcs proportional to 1:2:4: ... :2^(k-1), but not necessarily in this order.

I managed to prove this up to k=7 using a computer. Can you push it further?

[stencill]

4 color theorem pisses me off so bad. That should absolutely not work that way. God. Fuck i wish it was 5

[fittingoutjane]

One time I proved a theorem using colored chalk, and then said, "Did I prove a 4-color theorem?"

The other mathematician said, "No, Jane, you proved a theorem using 4 colors."

Kindergarten-level math research papers:

Field: Combinatorial Number Theory

Journal: Communications in Addition and Subtraction

Title: A Lower Bound on the Largest Natural number

Abbreviated Abstract: We prove a lower bound on the largest number. The proof proceeds in two steps: we begin with 1, and proceed by induction as until we lose count. We then add that number to itself. The main advance in the first step is to get a big number, and the second step notably avoids using multiplication (they don't teach that until 3rd grade).

Field: Topological Geometry

Journal: Advances in Nonlines

Title: The Four-Color Scribbles

Abbreviated Abstract: In this work we show a zoo of examples of nonlines (curves) with the unique property that they are either red, blue, orange, or purple, or some combination therein. The key idea is to use less colors rather than more, creating a clear and easy to follow proof. This provides a clear basis for simplifications to further work, such as scribbling with 5 colors.

Field: Playground Analysis

Journal: Slide Dynamics

Title: Sufficient Conditions to Yell Weeeeeee on Spiral Slides

Abbreviated Abstract: We identify sufficient conditions for a slide to cause joy. We identify a notion of a "fun slide," and prove that fun slides are a sufficient condition to make someone go Weeeee on a slide. We then verify a spiral slide is a fun slide, and provide numerous examples and non-examples (notably, a ramp is really not fun to slide down).

[linyihuite]

Wholesale customized size Irregular Perforated Gypsum Board

Gypsum Acoustics WELLYOUNG acoustic perforated gypsum board is designed on the basis of helholtz resonance theorem, After perforated, the holes, board and the wall make up of many resonant cavities, when air molecules pass the holes, the resonant cavities will consume large quantities of sound energy. Our high density gypsum panels come in a variety of perforations and sizes to meet your architectural sound absorption goals. They consume large quantities of ambient sound energy creating significantly quieter and more comfortable atmospheres for any space where quiet listening or learning environments are critical. 

FAQ Q1. Can I have a sample order for fiber glass ceiling tiles? A: Yes, we welcome sample order to test and check quality. Q2. What about the lead time? A:Sample needs 5-14 days, mass production time needs 2-4 weeks for order quantity more than Q3. Do you have any MOQ limit for fiberglass ceiling Panel order? A: Low MOQ, 50 sqm is available Q4. How do you ship the goods and how long does it take to arrive? A: We usually ship by sea. It usually takes 3-5 weeks to arrive. Q5. How to proceed an order for this Acoustic Panel? A: Firstly let us know your requirements or application. Secondly We quote according to your requirements or our suggestions. Thirdly customer confirms the samples and places deposit for formal order. Fourthly We arrange the production. Q6: Do you offer guarantee for the products? A: Yes, we offer 1- 3 years warranty to our products.

Features

Acoustic perforated gypsum board Light weight in unit acreage High edge rigidity Strong nail pull resistance Smooth,paintable surface NO visible joints and grid Sustainable,fully recyclable material Installs on any standard drywall suspension system Green environmental protection material

Application

WELLYOUNG Gypsum Perforated board is one of the best sound absorption products, it is widely used in Auditorium, office, cinema, church, hospital. School and so on.

Description

Perforated gypsum board Acoustic Board is a perforated 12.5mm gypsum board with air-cleaning effect including black or white acoustical EU standard Ahlstrom non-woven fabric on the back(special color when ordering).

Previous： New design Glass Fiber Sound Absorbing Drop

Next： Factory outlet Fiberglass Acoustic Ceiling Panels

[jonathankatwhatever]

It’s 21 Mar 2025, and I have nothing in mind and very little motivation, though I’m thinking of cleaning. I had one thought, which is that movement along the oK maps the flickering of the Triangular over gs, meaning the motion which surrounds movement along the szK, in complex space, and all the ways complex space relates to specific real points, like the way the Mandelbrot set maps what relates to and what doesn’t relate to a specified point and to a region of specified points. We discussed that, and it’s nice to see it connecting as a working piece. That is, this draws a region, which is also an orbit, for how to say this: when you take a number, a location, whatever and you square it, and then you add a value, and square that and repeat using the same value, then you get a dual, the dual of course, because you are literally taking a number and combining it repeatedly to make 2, to make 1+1, until it diverges, until the duality is to how that explosion disappears into infinity. You can trace that line in the infinities along the edges, so any larger steps, like orbits that barely stay in the region or which don’t, are still connected to any such region which is specified, because each process of counting to some larger number passes through the smaller ones, which means they cross over the infinities along the edge of the inclusion.

That’s interesting. This would be a neat test: you apply different sizes of the fixed point to see whether it’s likely to be cancerous because that is what is contained in the shape, color, edges, etc. Nice to find a real world example of the M-set in action. Those possibilities map to the gsPotential. I see this as if you’re going to play basketball, you tend to pick taller, meaning the game sets a basis. It gets a bit confusing at this point.

Okay or oK, which is what that means because it can be great or o that’s bad or I have to accept this or it’s going fine or it’s not and I’m saying it is, etc. This has to appear at the point of infinity, the one generated because (D3-4//4-3) can’t fully complete like squares can, which we see as modular forms being limited to squares, like in Fermat’s last theorem. The issue arises at (D2-3//3-2), which is like saying here’s your Irreducibles. You translate D2-3 as requiring an H/D and then ambiguous addition of either but not both of those to D3. It’s even harder going D3-2 because you have to take D3 apart and then assemble 2 pieces. This is necessary to avoid combining gsSheets to generate halves like 1.5. If we work with 1Space, we need a way to achieve those gsCompositions using 1Space, which means 1’s.

It really is as basic as that. We have ru1 and the various ways a ruler defines. In the case of (D2-3//3-2), you see the ruler needs to fit both ways, which is work. Now look at (D1-2//2-1), and the problem reduces to take 1 and double, take 2 and halve. The process doesn’t need memory since it begins with 1 and ends with 1 and maybe those are completely different 1’s. We can idealize this to SBE2, and thus we can insert a huge 1-0Segment separating the beginning 1 and the end 1. You see how basic this mechanism is? It’s inherent at a low level to how Things operate both in the immediate and over substantial gsProcess, which becomes time or distance, like you can be literally apart in time or distance or far apart in person while together.

Look at (D3-4//4-3): you can see the links we’ve discussed with D5 and D6 and D8, which takes us to CM64, which means you can see where distinct Things emerge out of connections, which we describe using CM36-28-36. One point I haven’t thought about in decades is that 28 has an orbit to 26 and 30. Those pathways become very interesting because that equates 2*13 and 3*10. The SBE*SBE3+1 makes sense: it it touches that End, then you’ve hit that match. The other End is 2*13, where 13 is 2, meaning it’s 2SBE2+1, so this counts as 4, which is IC, so we have the lower edge of that counting segment being the existence of what is counted to there. That reads as from here to here, with the tipping balance at 14 in duality to 28, meaning that’s D1-2 applied to make the ru1. And that makes an IC of 7’s, which are specified Hexagons, which are D6, which contain D3, and which specifically contain D3 within Hexagons along each 1-0Segment of the bT, so the entirety of what this has been typing about is those 3 as Triangular relating to the 4th. This idealizes to a lot of states, but of course as it layers and layers and layers, that is like a tube in which the result pops out, or like a lattice which generates a value at surface and values through pathways, etc. Or like current always being at the end you touch.

I think I’ll go clean. I’d like to make a visible difference here.

[nifglobal]

Best Interior Design Colleges in Mumbai: Courses, Placements, and More

Mumbai, the city that dreams, isn't just India's financial capital, but it is also an important hub for the creative industry, which includes interior and fashion. With a flourishing property market as well as a growing desire for beautiful spaces and spaces, working in interior design can be an ideal choice. Suppose you're in search of the best interior design institute in Mumbai. In that case, the following guide will assist you in exploring the best institutes, classes available, job opportunities, and the reasons why Mumbai is the perfect place to begin a career path within the field of interior design.

Why Choose Interior Design as a Career?

Interior design encompasses more than the mere decoration of a room and creating useful, secure, safe, and visually pleasing environments that increase your quality of life. As urbanization continues to grow and the changing styles of living, skilled interior designers are highly in demand in various industries which include commercial, residential hotel, retail, and hospitality.

When you enroll in the top interior design college located in Mumbai and you will have access to a structured course, real-world experience as well as industry contacts that will assist you in establishing a lucrative career.

Top Interior Design Institutes in Mumbai

Mumbai is the home of several top interior design Institute that provide specific courses designed to provide students with the appropriate abilities and expertise. Below are a few of the best interior design institute in Mumbai, which are distinguished due to their high-quality training, highly skilled faculty as well as a solid industry connection.

1. NIF Global - Leading Interior Design Institute in Mumbai

NIF Global is recognized as one of the most prestigious interior design institutes located in Mumbai providing the perfect mix of theoretical as well as practical experience. It provides students with practical training, real-time projects, and exposure to industry, which assist them in becoming skilled professionals.

Courses Offered:

Diploma in Interior Design

Advanced Diploma in Interior Design

Bachelor's Degree in Interior Design

Short-term Certification Courses

Key Highlights:

Industry-focused curriculum

Professional faculty who have many years of experience in the field

Placement assistance and internship

Modern infrastructure

2. Rachana Sansad School of Interior Design

The institute has set the standard for training in interior design over the last few years. The curriculum is structured and combines artistic and technical aspects.

Courses Offered:

Diploma in Interior Design

Bachelor's Degree in Interior Design

Why Choose Rachana Sansad?

An alumni-friendly network of strong strength

Learning through practical experience

Industry collaboration

3. JJ School of Arts - Department of Interior Decoration

The oldest and most well-known school, JJ School of Arts, has a broad Interior design course that focuses on expression through art as well as technical understanding.

Courses Offered:

Diploma in Interior Decoration

Key Benefits:

Expert faculty

Experience of the architectural and design heritage

Strong placement opportunities

4. Pearl Academy

Pearl Academy is known for its innovative approach to the field of design education. Pearl Academy offers specific Interior design classes that blend the latest technology and creativity.

Courses Offered:

Bachelor's in Interior Design & Styling

Diploma in Interior Design

Why Choose Pearl Academy?

International collaboration

Advanced design labs

Industry-driven curriculum

Course Structure and Specializations

Many of the top interior design institutes within Mumbai provide a variety of classes, ranging starting with diplomas to degrees. The typical curriculum includes:

The fundamentals in Design: Understanding color theorem, spatial planning as well as design concepts.

CAD and 3D Modeling: Learning software like AutoCAD, SketchUp, and 3ds Max for interior design.

Furniture Design: Making functional but attractive furniture pieces.

Textures and Material: Understanding different materials employed in interior design.

Acoustics and Lighting: Science behind the science of lighting and sound within an indoor space.

Project Management managing interior projects from beginning to end.

Green Design: Eco-friendly design strategies and green building principles.

A few institutes also provide the ability to specialize in luxurious commercial space, interiors as well as residential design, retail and hospitality interiors.

Placement and Career Opportunities

One of the most important aspects to consider when choosing the best interior design colleges in Mumbai is placement support. The top institutes are associated with respected interior design firms as well as architects and real estate agencies, making sure that students have the best exposure and opportunities for employment.

Career Options After Interior Design Courses

When they have completed an Interior design class, students are able to explore a range of options for careers, such as:

Interior Designers: Designing residential and commercial areas.

Furniture Designer: Making custom-designed furniture.

Designing Sets: designing sets and costumes for TV and film shows as well as events.

Exhibition designer: Working on trade fairs, art galleries, and exhibits.

Retail Designer: Interior design for malls and stores.

Interior Designer Freelance: Starting your own design and interior business.

Top Recruiters for Interior Designers in Mumbai

A number of renowned firms, as well as designers, recruit graduates from the top interior design institutes located in Mumbai. The top companies that recruit students are:

Livspace

Godrej Interio

Asian Paints (Sleek Kitchens)

Hafele India

Morphogenesis

Studio Lotus

Design Cafe

Why Study Interior Design in Mumbai?

Mumbai is the ideal city in which to study the interior design of a home for a variety of reasons:

Experience in a variety of Architecture: From colonial buildings to modern-day skyscrapers, Mumbai has an impressive history of architecture, which inspires designers.

A thriving design industry: Many top interior architects, designers, and design firms are based in Mumbai and offer students excellent networking opportunities and internships.

Cultural Hub: As a melting pan of different cultures, Mumbai offers a variety of styles for interiors that range from classic Indian style to modern minimalist.

Jobs Chances: With a booming property market and a growing demand for highly skilled interior designers will always be at an all-time high in Mumbai.

Conclusion

Picking the most reputable interior design institute located in Mumbai is vital to an enviable career in this industry. Institutions such as NIF Global, Rachana Sansad, JJ School of Arts as well as Pearl Academy provide high-quality education with hands-on instruction and great opportunities to get a job. If you have the proper knowledge and skills of the right people, you could make a successful career in the field of interior design. You can transform rooms into functional and artistic artworks.

If you're interested in designing beautiful spaces and creating spaces, then registering at any of Mumbai's most prestigious interior design institutes in Mumbai is the first move towards becoming a professional. Therefore, you should take your imagination to the next level and leave your mark on the realm of interior design!

[bobthecoolrock]

4 color theorem: there are at least 4 colors

Color theory: there are several colors

[4voicesstudio]

Animation and Educational Technology: How Visualization Helps Learning

Animation and Educational Technology: How Visualization Helps Learning

Animation is a powerful tool in educational projects that can make learning more engaging and effective. Visual elements help students retain information by demonstrating complex concepts in a visual way. In areas such as science, math, and language, animations can greatly enhance understanding of topics.

How does animation help students learn?

1. Visual: Animation visualizes abstract ideas, turning them into understandable images. This is especially useful in subjects where it is difficult to visualize the process, such as chemistry or physics.

2. Engagement: Dynamic and colorful animations can capture students’ attention and keep them interested throughout the lesson or learning material.

3. Accessibility: Animation can be used in online education, allowing students to study at their own time and pace. This is especially true in the era of distance learning.

4. Ease of perception: Animated materials help break information into small fragments that are easier to digest. This allows students to master new knowledge step by step without being overwhelmed.

5. Interactivity: Modern animations can be integrated into interactive platforms, allowing students to not only watch but also interact with the material, which contributes to a deeper understanding.

Examples of using animation in education

- Educational videos: Animation is widely used in the creation of educational videos that help explain topics from historiography to mathematical theorems.

- Game mechanics: Animation elements can be applied in educational games, which makes learning more fun and triggers motivation mechanisms in students.

- Multimedia presentations: Presentations with animated graphs and diagrams allow you to convey complex information to the audience in a more understandable format.

For inspiration and a professional approach to creating animated materials for educational needs, you can turn to animation studios such as https://4voices.studio/, which offer high-quality animation solutions for different needs.

You can check out the playlists designed by our visual artists on our channels:

https://www.youtube.com/@4VOICES.Studio

https://www.instagram.com/4voices.studio/

https://ru.pinterest.com/4voicesstudio/

In conclusion, animation is not just entertainment; it is a serious educational tool that can transform traditional teaching methods and make them more effective and attractive to students.

Animation and Educational Technology: How Visualization Helps Learning

[cristythedestroyer]

Ma.Cristel Mercado

2nd Year

Methods of Teaching Grammar

1. Diagramming sentences

Diagramming sentences is visualizing how to fit together the dilferent parts of a sentence. The subject of a clause goes in one slot, the verb in another, and so on. Words that modify another word are attached to the word they modify.

It helps students understand how a sentence works by breaking it down to the component pieces. It is like a puzzle which is not solved until all the parts are in the right place, and none are left over However, there has been a shift in the practice of diagramming.

3. Inductive Teaching

The main goal of he inductive teaching method is the retention of grarmmar concepts, with teachers using techniques that aro known to work cognitively and make an impression on students' contextual memory.

Scenario: A 5th-grade science class is learning about ecosystems and the relationships between living organisms and their environments. Instead of starting with definitions and theories, the teacher uses an inductive teaching approach to guide students toward understanding the concept of ecosystems.

4. Deductive Teaching

This type of teaching has many people rethink such methods, as more post-secondary level students are revealing sub-par literacy skills in adulthood. Deductive teaching melhods drive many students away from writing because of the tediousness of rote learning and teacher-centered approach.

Present the General Rule:

The teacher explains that this theorem applies to right-angled triangles, where (a) and (b) are the lengths of the two legs, and (c) is the length of the hypotenuse.

The teacher begins the lesson by writing the Pythagorean theorem on the board:

5. Interactive Teaching

This method allows teachers to tailor their lessons to the different learning styles of students. For instance, each student can be given a large flashcard with a word on it and the students, themselves, must physically arrange these into a proper sentence. Other games can include word puzzles or fun online quizzes.

Ask students to think about what they have learned.

Encourage them to make connections by answering these questions:

"How does evaporation occur in our environment?"

"What happens to water when it rains?"

"How can we conserve water in our daily lives?"

6. Functional-notional approach

When designing a lesson, teachers often choose real-world situation as their "notion, and choose corresponding functions to teach to prepare students to communicate in that situation in the lesson.

A lesson might be about how to buy something at a shop, in which case its notion is shopping and one of its functions might be asking prices. Functions often lend themselves naturally to specific grammatical patterns or common expressions.

7. Situational contexts

Fromkín, Rodman and Hyams (2011) sald context can be lingulstic and situational. Linguistic content is about the information that was formally written or spoken and situatlonal context is the general knowledge that a person has of the worid.

Someone is giving a speech in front of their entire school. They might rush their words more than they would in front of just their close friends because they are nervous about public speaking.

8. Using texts, stories, songs, and rhymes

There are different ways of using songs in the classroom. The level of the students, the interests and the age of the leamers, the grammar point to be studied and the song itself have determinant roles on the procedure. Apart from them, it mainly doponds on the creativity of the teacher. At the primary level of singing the song, the prosodic features of the language is emphasized. At the higher levels, where the practice of grammar points is at the foreground songs can be used with several techniques.

1. Text:

Book Chosen: Brown Bear, Brown Bear, What Do You See? by Bill Martin Jr. and Eric Carle.

Activity: The librarian reads the story aloud, showing the colorful illustrations. After each page, she asks the children, “What do you see?” encouraging them to predict the next animal.

2. Story: Short Storytelling

Story Chosen: An original short story about a friendly rabbit who goes on an adventure to find his missing carrot.

Activity: The librarian tells the story interactively, asking the children to make rabbit sounds whenever the rabbit is mentioned. She incorporates actions they can mimic, such as hopping.

3. Song: Sing-Along

Song Chosen: "Five Little Ducks."

Activity: The librarian leads the children in a sing-along, using hand motions to depict the ducks going out and the mother duck calling. After singing, she discusses the concept of counting and numbers.

4. Rhyme:

Rhyme Chosen: “The Itsy Bitsy Spider.”

Activity: The librarian introduces the rhyme using finger movements to illustrate the spider climbing up the spout. She encourages the children to join in, reinforcing vocabulary and movement.

9. PPP

A deductive approach often fits into a lesson structure known as PPP (Presentation, Practice,Production). The teacher presents the target language and then gives students the opportunity to practice it through very controlled activities. Presentation involves building a situation that requiresa natural and logical use of a new language. It is in the presentation stage that students krnow what they will learn and why. Practice involves testing the procedure so students can be familiar with the language. In this stage, students will be provided with activities that can make them use the new language. The production stage, being the most important stage, students here shall have made the transition from "learners" to becoming the presentation to help student communicate meaning using the new language.

Presentation

Introduce the Past Simple tense.

Activity: Begin with a brief explanation of the Past Simple tense using examples. You might present sentences like:

"I visited my grandparents last weekend."

"She watched a movie yesterday."

Practice: Provide gap-fill exercises where students complete sentences with the correct past tense form of the verb.

Example: "Last summer, we ______ (go) to the beach."

Production: Ask students to write a short paragraph about what they did last holiday. Encourage them to use as many past tense verbs as possible.

Modes of Teaching Grammar

1. Linguistic Mode

Students must be familar about the use of structures so that they will understand. Larsen-Freeman (2002, 2014) maintained that students must knaw about the use of structures that they will understand the consequences of thoir cholces because the grammatical system offers its users choices in how they wish to realize meanings and positions themselves ideologicaly and socially. Therefore, grammar teaching should not only for understanding the rules but also for inducing the of different sentence formations in different contexts.

A student enthusiastically presents their project on renewable energy to a group of judges and peers. They use clear speech, gestures, and visual aids to explain their findings and answer questions.

2. Story-telling mode

A grammar lesson is not completo without an application stage. Applicatlion is believed to require volume and repeition; that is, learners need to be given adequate opportunities to use the itens to be learnt as much as possible. Teachers should help learmers make he leap from form-focused accuracy to meaning-focused fluency after explicit ínstructions by providíng a variety of practice activities that will familiarize the learners with structure in contexts, giving practice both in form and communicate meaning.

The Monomyth method

During the journey, the lion cub finds some craxy friends and, in the end, he kicks the bad ones and marries a beautiful lioness. That here is an example of the Monomyth method - the hero leaves his home, he faces the unknown and after some adventures he has a good ending.

[hkayakh]

Funnily enough, this also has to do with map

Source: 4 color theorem

Stop Doing Borders

[petrichorsinestra]

Never expected to be tagged in one of these! I suppose I'll jump in :D

Last song: "Liquid Nights and Disco Lights" by Miracle of Sound. It's about the game Disco Elysium, or, out of context, generally trying to move on from your past mistakes and getting stuck wallowing in them. Highly recommend, as even without context it's an incredible song.

Favorite color: I love love love shades and hues of purple,,, Lavender is a favorite, but not the only one.

Last TV Series: I think I was about to finish Lycoris Recoil before I stopped. It's an anime about secret agent girls who operate undercover as high schoolers to keep society safe. Haven't quite finished it but it's got an interesting premise and the characters are super cute!

Sweet/Spicy/Savory: I love ice cream. A lot. I like spice when it's properly built into a dish, but the American use of spice as a physical challenge really doesn't appeal to me.

Relationship Status: Single and most likely aromantic. Please do not pursue me with that intent. Always love more friends, though!!

Last Thing I Googled: as I use DuckDuckGo as a regular browser, technically the answer would be "how to use Minitab with summarized data" but as far as my last web search goes, it was most likely "Nyquist theorem" from verify an answer after a final

People I want to get to know better: Just 4 tags here! 9 is too many for me lmao

@paladinia @sanguine-raven @violet-snail-girl @actualfactualrat

Nine people I'd like to get to know better

Tagged by @meghawhopp <33

Last song: Down by the River by Borislav Slavov from the Baldur’s Gate 3 Soundtrack (or more specifically the cover of Down by the River by Nerissa Ravencroft)

Favorite color: Blue and purple!

Last movie/TV show: Seinfeld, I’m currently on season four!

Sweet/spicy/savory?: I have a huge sweet tooth, so sweet things

Relationship status: Single

Last thing I googled: I searched up the show “Arthur” because I was trying to find that one meme where Buster was like “You really think someone would do that, just go on the internet and spread lies?”

Current obsession: Fragaria memories and tears of themis mostly^^

Tag Nine People: @kyaruun @xinieeee @deadmansbistro @florapot @hunita812 @scuffle-with-spirals @rexonalapis @maxellera @manicpixiedoomedgirl

[jonathankatwhatever]

It’s 19 Nov 2024. I’d like to begin with an update on my condition, which sounds more ominous than intended. Just this morning, I broke through the block preventing me from touching the wall. It’s now more clearly defined by lots more lavender, yellow, and orange. By defined, I mean the shapes and colors convey a wide variety of shapes and ideas, including how dimensionality functions, but in the general conception of swirls in and out of a general spot which actually emanates light because that is where the dark original layer is covered in a skin of white. It’s happy and absorbing.

I could talk for days about images. And I loved how my hands worked: the right hand, which tends to be careful and anxious gains confidence by thinking about the emotion being portrayed. Then it has a context in which it can focus without the anxiety produced by wondering if this is the correct path. The left hand is more artistically free and loves to take risks because it trusts what it sees in the moment.

I also wanted to mention that my gym work has progressed a lot. I have largely freed up the restrictions I can find in my arms and shoulders, even much of the distortion caused by my weird left hand grip: I pulled that out by mirroring the right hand grip back and forth until I found one which didn’t hurt and then I used that to pull and twist out the problem with the tensioning system we’ve developed. I love the dual cable cross; it really brings out my physical creativity.

My knee is improved. I use a variety of exercises, including a seated leg press machine with a twist. I put assist level weight on, meaning I can use one leg with the other as a stabilizer, meaning it’s near capacity but not quite, then press it out and then raise my hip to drive the weight all the way out straight. It’s a lot like doing a weighted push up stairs or a up a hill, with one leg and a stabilizer. Another favorite is a seated dip machine: I turn it into crunches by pressing the weight down, then allowing my shoulders to come up to my ears - and it is work to free that - and then down while leaning as far forward as possible, and then holding that. Release, repeat in various ways.

I made a note above about dimensionality so I would entirely lose the thread this morning. I’m a little wanderer no longer in a New England home.

It struck me while painting that the concepts of extensionality and I think it’s intensionality are labels for the process of Emanation and Inmanation. That means we’ve found a key notation part: these labels are gsProcess-related and thus describe the underlying phenomena differently than labels from disciplines like set theory. This was implanted in my brain, shall we say, last night when I heard then tried several times to repeat a gsProcess definition of a set as that which generates as Ends within the context. This morning that became the image receding and coming at you, and that immediately shifted to D-structure, and thus to the gsProcess of E & I because - and this was the cool part - the potential iterates bidirectionally, exactly in the D3-4//4-3 and D4-3//3-4 manner we’ve described. This means a set is that which generates within the potential, within that context, through this specific gsProcess.

This connects directly to the pairing conception of an End, and thus to the point at infinity and the hairy ball theorem, etc. in which the pairing is abstracted through Attachment, which is another way of saying the relationship Attaches because it is non-specified, which is of course IC, and IC is how we count along the szK. Or along the zSK. The Sisk and Zisk? I’m getting silly.

This expression, along with the demonstration of choice from yesterday, is something I’ve always dreamed of doing. The original set conception is that of a collection of things. We have now capitalized the Things, and that has added the structure which encloses and which generates sets and set theory.

What about the Continuum? I wanted to talk about that over the past 2 days when I was visualizing the real line as the szK. It’s actually the szK-zsK intersection where one of them is rotated to be 0, meaning there’s an I//I relationship, and the real line is this construction. The reason why is fascinating, if I can get it out: the actual real line is End to End, meaning for the Irreducibles to overlay perfectly, meaning to a value on the real line, including a repeating decimal, including a process that doesn’t repeat because it follows at least an algorithm which generates that specific value into the depth of the real line conception. You can see it right there in those last few words: the depth of the real line conception is the depth of the twist or the torsion from the surface to the hidden depth where all you see is the surface.

This is to me almost miraculous as a mathematical thought. Apply E&I. And I&E because it’s bidi too. Mind-blowing in a good way, which is how I’m painting the wall.

I think our best description of the CH now is that when you generate finite out of the infinite, it looks different than if you try to generate the infinite from the finite. One of the main tools by which the finite comes into existence is Regularization, because that expresses the constructions of D-structure as 1-0Segments, which means Ends in pairings, which then expresses as finite through the I//I process which relates potentials within contexts - imagine a potential surrounding a context which surrounds a potential, in each direction. This matches the delta-epsilon conception of a limit, which is at should be since we described above how that works.

To be more clear, when we say we have a limit, we are actually speaking of the gsProcess coming to that End, which is a pairing into or out of the projection where we imagine that End as being. Like here’s a dot and you can imagine there being an axis behind. And then when it’s a ball, the same true but in every single pairing so perhaps only in that pairing and no other. That’s the I//I process in a nutshell: this happens within the generated gsSpace in which D3-4//4-3 Things exist. In which we exist, as individuals and together.

Sometimes it takes me forever to get straightforward connections. I just remembered that we used to talk about how there is no excuse because it’s always up to you to do what you must do, that as much as one can connect, because of the visions of the wall of separation, we’re each always on our own. We can say now exactly why that is, that we are Things and Things exist in a series of specific relationships internally and in relation to the external world.

So I was only able to make an obvious connection to E&I and Boundary when I reached the point where E&I and Boundary coincide? How do they? Well, the basic series: the inverse, alternating series now goes around the perimeter so each step iteratively approximates the Boundary which arises when there are sufficient iterations. It isn’t a weakness of the method that it takes so long to generate significant digits: it’s a mark of the depth of the permutations which occur in a Boundary calculation. Think about the scaling of that: the vastness of the calculation internally is then transmitted from the inner edge, where it is far too much to grasp, and then it passes through filters to be read on the outside. That’s how context works. That’s how Things fit into the Eternal.

What does go around mean? That’s the szK//zsK relationship. Take one, say zsK as ordinal, then szK is cardinal, and since ordinal shrinks to cardinal, as in 1 or 0, a whole or a whole nothing, the bagel and the hole, and they shift and switch places. A crucial point is that only on the first move is there purity, meaning 1 and 0 are 1 and 0 from any spot at which they are measured, but they are measured within contexts so they’re never the 1 because the joining to that primal 1 is Triangular, in 1Space and not in 0Space. That expresses sets as the process which generates from that 1 or 0. I keep this trait, this hope, this state alive which did not originate within me but which is within me.

This explains a lot about the structures of reality. I mean the math. Example is that we can see each of us as within counts extending to us and from us and past us. This means we’re automatically within the realm of logarithms, because a log is inherently just a way of counting into the future from 1 to 2, meaning from whatever we are now and to whatever we will be. The log just counts the potential built into D-structure. You can see it reduce to classic examples like a tank being drained or a body coming to room temperature. The tank goes to whatever it will lose and the body goes to room temperature, meaning that’s the 2 count.

I think we can see something else: if you then take exponential, meaning 2^n, then you’re taking a context in which something is occurring that counts to 2 and enlarging that context. Maybe the difference is making a mountain out of a molehill is not the same as taking that process and making that whole thing bigger.

I need to take a break.