#Euler's Integer

[knightmareaceblue]

Cyberweek 2024 Day Five: Crossover

Pfft, I've been on an AvA kick recently, so I guess it's not too surprising that I chose this. On one hand, this crossover works well in theory. The stick figures are all fast, kinetic learners and really good at demonstrating their earned skills and knowledge.

On the other hand, the sheer tonal dissonance is hilarious.

[oqmemphis]

John Gabriel and Mathematical Ignorance

Have you ever watched a flat earth conspiracy video? If not, the usual format is pretty straightforward: the presenter rambles, unscripted and unedited, into a cheap microphone while using some shitty screen recording software to film themselves drawing lines on top of random jpegs in paint.net for five to ten minutes, before sitting back and proudly claiming that their unmatched genius has proven all human knowledge from the last several millennia to be hopelessly fraudulent.

John Gabriel is a flat earther for mathematics.

Mr. Gabriel writes and speaks at great length about an invention which he calls "the New Calculus", a theory most briefly described as an attempt to reformulate all of mathematics starting from (what he perceives to be) the base principles used by the Ancient Greeks. He believes that mathematics as a field of study has been practiced almost exclusively by idiots for approximately the last two thousand years, or nine hundred, or a hundred and fifty (the exact time at which things went to shit seems to vary a lot; he rejects much of Euler and Fermat, but also calls Cantor "the father of all cranks") and claims that only he can understand numbers "properly".

Whenever a popular maths YouTube channel makes a video about infinity (see Numberphile on -1/12 or Vsauce on transfinite ordinals), there are inevitably people in the comments arguing that the video's premise is misleading, wrong, unnecessary or incoherent, or that the concept of doing mathematics with infinite sets is fundamentally invalid. Mr. Gabriel takes this finitist view to its logical extreme.

In his 152-page tirade against modern academia, he argues that any "infinite process" is outright unmathematical and should not be allowed; his definition of "infinite process" includes convergent limits, such as the unending decimal expansion required to express irrational numbers. A significant basis of his work is that irrationals like π and √2 are not numbers, but rather "constants" or "incommensurable magnitudes". Why this is a useful distinction, given that these "constants" behave like numbers in nearly every regard, is never explained. He additionally claims that 0 is not only not a number, but is "not even required at all in mathematics". He spends the entire first half of the book re-deriving all of arithmetic and algebra based entirely on principles of Euclidean geometry, while repeating, mantra-like, that only integer ratios are numbers and that anyone who claims otherwise is an ignorant buffoon. I wonder if he writes RPF of himself throwing Hippasus into the sea.

He has then taken this idiosyncratic worldview as a starting point from which to reinvent calculus.

He is straightforwardly wrong.

Mr. Gabriel frequently complains that his critics mindlessly hurl insults at him without seriously engaging with his work, so as a show of absurdly generous good faith I will engage with it now. Any fellow masochists reading this are invited to take a look at Mr. Gabriel's manuscript - specifically his demonstration of how to take a derivative without the use of limits - and try and figure out where the problem is.

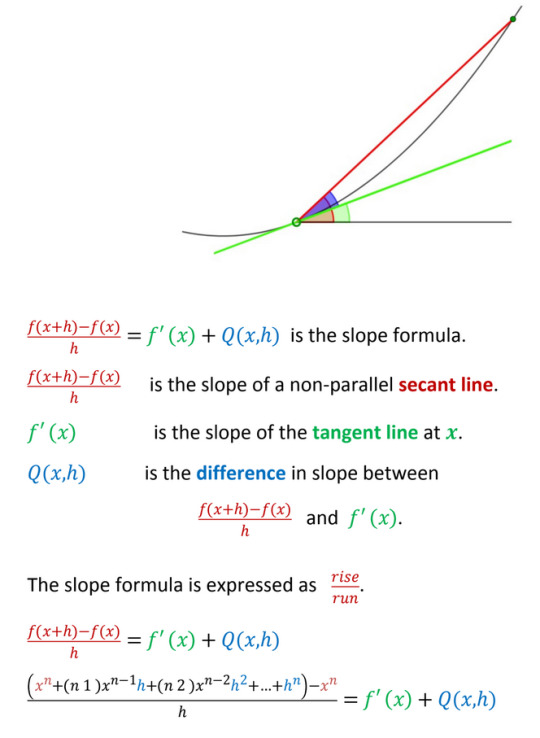
Ignoring Mr. Gabriel's apparent inability to find the subscript button in Microsoft Word, he has taken an nth-degree polynomial (which could contain many terms), and transformed it into a single term of degree n-1. This, you will be astounded to learn, is not the correct result when taking the derivative of anything more complicated than f(x) = x^p. Notably, he never attempts to do this.

In fairness, the above demonstration is not actually the New Calculus. Mr. Gabriel explains that he has helpfully preceded his earth-shattering revelations with a less rigorous, more geometrically-derived formulation. I'm sure we'll get some real mathematics in a minute.

What we get is him complaining that the Encyclopaedia Britannica does not provide sufficient intuition for the work of Newton and Leibniz, before claiming that his New Calculus is "the first and only rigorous formulation of calculus in human history". He uses this exact phrasing (or nearly) at least four other times in his PDF; if he is unhappy with the Britannica, I might politely advise him to try reading Roget's Thesaurus instead.

Finally, on page 120 of 152, we are given an explanation of the epiphany to which the entire monograph has been building.

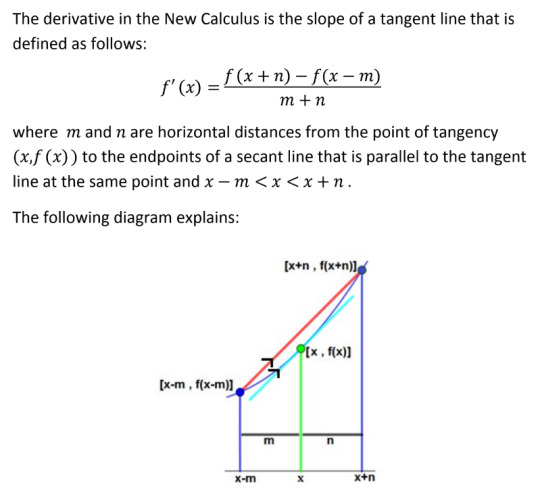
"Left as an exercise for the reader" is a phrase used by cowards (and to his credit, John Gabriel is not a coward), so I will point out the slight issue here: it is not possible to calculate values for m and n unless you already know the tangent slope. In his example of how to compute the derivative of sin(x), he expresses the function in its Taylor series form (so much for shunning infinite summations), and then simply replaces said series with the one for cos(x) without comment; he then manages to successfully determine his secant intersection values, and then calculates the value of the derivative function he just shoved into his pile of equations a few lines further up. Thus, his bafflingly circular logic is enabled almost invisibly.

This is it. This is all that this book is. John Gabriel's magnum opus, the thing he has been building up to for 119 pages amid paragraphs of bluster about the idiocy of irrationals and his own vaunted genius, is the ability to compute the derivative of a function as long as you know the derivative of the function. And as long as that derivative is not a zero found at one of the function's inflection points, because apparently that doesn't count as drawing a tangent line (for reasons that I'm sure are unrelated to the fact that Mr. Gabriel's secant method fails for such points).

I don't want to go deep into personal insults here - that's John Gabriel's job - but this is not useful mathematics. The logic is circular, the motivation is worthless, and it enables no new insights not already achievable with the current mainstream understanding of calculus. No statement is proven that has not already been shown to be true within the framework of Newton and Leibniz; there are only restatements of existing theorems based on the shaky-at-best logic of these new principles. So what is it for?

This is a question I kept coming back to while reading Mr. Gabriel's PDF. What is this for? What is gained by stubbornly insisting that π and e are not numbers, but rather "constants of incommensurate magnitude"? How does rejecting the usual definition of division as a multiplicative inverse in favour of some guff about "measuring in equal parts of an abstract unit" expand the horizons of mathematical knowledge? Of course, it doesn't.

John Gabriel, ultimately, is not important. There are thousands of other flat-earthers and similar grifters just as laughable as him, and to my knowledge there is roughly nobody who takes him seriously. (And if anyone does, the chance of some random guy on Tumblr convincing them otherwise is vanishingly small.) But I find his writing fascinating precisely because of the way in which he is wrong. He seems firmly rooted in the idea that mathematics is all discovery and no invention; that we can derive mathematical truths out of absolutely nothing. He rejects the notion of logical axioms as a starting point for derivation, instead seeking answers grounded in reality (by proxy, via "pure geometry"), and he is incensed when people ignore his demands.

But mathematics is not physics. Mathematical objects don't exist independent of their definitions, but they do exist independent of the real world. The rules of mathematics are defined by mathematicians only; if we want π to be a number, all we have to do is say "let π qualify as a number"; if we want to define an infinite sum as being equal to its limit, we can. If the rules disallow something, nobody can stop us picking different rules, reality be damned. John Gabriel has in fact done this too, even if he doesn't realise it - it's just that his starting axiom around which the rest of his theory is based is "I am the greatest mathematician in the world, and everyone who has come before me is a moron". I do not exaggerate when I say this; a pinned comment under one of his recent videos reads:

I, the GREAT JOHN GABRIEL explained why calculus works and I defined NUMBER correctly for the FIRST TIME in human history. For this, I am called a crank by your ignorant, incompetent and incorrigibly stupid mainstream math professors and teachers. I shall keep reminding students of your venom and your hatefulness towards me. You are vile, disgusting excuses for human beings. The longer you deny me as the greatest mathematician, the more shit will accumulate in your diapers.

If Mr. Gabriel objects to logical premises that are rooted in fiction, I have some suggestions for ideas he might want to discard.

[trivalentlinks]

does it ever strike you as weird that there are uncountably many real numbers, but only countably many can be named or precisely described in the english language in a finite amount of time?

obviously all rational numbers can be described in a finite amount of time

("53623562112541251251345146*10^2452/426257567257" is something you can say in a finite amount of time)

so can anything that can be built out of roots of integer polynomials ("algebraic numbers")

("square root of 7 plus 38 times the cube root of 17, divided by the seventh root of 2011")

but also there are lots of non-algebraic numbers that can be described in the english language in a finite amount of time

"the circumference of a circle divided by its diameter"

"euler's number"

"the limit of the series \sum 1/10^(n^3+n^n)" (probably, i don't actually know for sure that this one is non-algebraic, but it's definitely irrational)

"the fine structure constant" (i guess it's unknown whether this is rational or algebraic or anything)

but even with all this, we can name and describe so many numbers, not just all the (infinitely many) whole numbers, rational numbers, algebraic numbers, but so many more than that, and yet there's still way more that could never be named

like we can name all the stars, we can name every atom in the universe and infinitely more universes than that, but we can't name all the numbers between 0 and 1?

[aedislumen]

26 for the ask game （╹◡╹）

26. Forgotten hero everyone should know about

This could have been a perfect occasion to talk about Claude-Antoine Prieur again, but given that I plan to devote him many future posts on my blog, I thought it would have been more appropriate to use this ask to share my knowledge about an important and unfortunately still rather unknown STEM personality, who truly inspired me when I was a young student. I'm referring to Sophie Germain.

Born in Paris in 1776, Sophie was one of the rare mathematiciennes of the 18th-19th century. She had her first approach with mathematics during the days of the storming of the Bastille, when it was too dangerous for a young 13 years old girl to go outside. To pass the time, she turned to her father's library and a book named "Histoire des mathématiques" by Jean-Étienne Montucla captured her interest. The story of Archimedes narrated in the book fascinated her deeply, eventually leading her to start studying mathematics on her own through the works by famous mathematicians like Euler, Newton, Cousin. Her interest and dedication to the discipline was so strong, that during winter, when her parents denied her warm clothes and a fire in her bedroom to prevent her from studying she kept doing it anyway despite the cold; at the time maths wasn't considered appropriate as a studying discipline for a woman.

When the Polytechnic school opened in 1794, women couldn't attend, but the policy of the school allowed to everyone, who asked for them, notes of the lectures. She requested them under the pseudonym of Antoine-Auguste Le Blanc, a former student who had dropped out. Given that, as a student of the Polytechnic school, one was expected to send written observations about the lectures - a sort of homework - Germain wrote and sent hers to Joseph-Louis Lagrange, one of the teachers and renowned mathematician. The latter was so positively impressed by her essays that requested a meeting with the brilliant student LeBlanc, who unexpectedly had improved so much. She was then forced to reveal her identity. Lagrange was pleasantly surprised to realize Monsieur Le Blanc was in reality a young and talented woman and decided to support her, becoming her mentor.

One of her most noteworthy contribution to mathematics was in number theory, where she proved a special case of the so-called Last Fermat's Theorem (1), which has remained one of the hardest mathematical theorems to prove for more than three centuries and whose final proof was actually found only in 1994 by Andrew Wiles. Other important works of hers include treatises on elastic surfaces, one of which, Recherches sur la théorie des surfaces élastiques, awarded her a prize from the Paris Academy of Science in 1816.

Although she often faced prejudice for being a woman, Germain was praised and also supported by various well-known mathematicians of the time. Some of them include the aforementioned Lagrange, Legendre, who thanks to her work on the Fermat's theorem, was able to prove it for another special case; Cousin himself, Fourier, who managed to grant her the permission to follow the sittings held at the Paris Academy of science and last, but obviously not least, the great Gauss, who after Germain's death advocated for giving her an honorary degree in mathematics.

Notes

(1) In short, the Last Fermat's Theorem asserts that for n > 2 there are no integer solutions to the following equation:

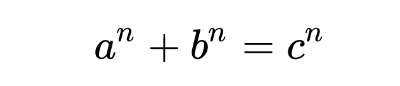
with a, b, c being positive integers. Sophie Germain proved the theorem for all numbers n equal to a prime p, so that 2p + 1 is also prime. The whole thing is much more complex that how I explained it, my aim was to write down a simple intoduction. If you want to read more about that I recommend you this link.

[admiral-crow-is-watching]

What part of maths letters commonly inhabit (Part I, Latin)

a,b,c: Some kind on constants. Could be anything.

A, B: probably set theory.

B: Could be open balls, could be a binomial distribution.

C: constants of integration in a normal font, complex numbers in blackboard font.

d, k, p, q: Dimensions of something or other

D: Could be another constant of integration, or possibly a domain of discourse if it looks fancy.

E: Expectation! You're doing probability.

e: Euler's number. Will not stop turning up absolutely everywhere.

e, g, h: Group theory or other algebra. You are unlikely to also see numbers.

f, F, g, G, h, H: The classic choice for functions.

H: Whatever this is is named after Hamilton.

i: square root of -1, complex numbers, right up there with e in turning up everywhere.

I: Indicator function, identity matrix, information. An underratedly versatile letter.

i,j,k: Another classic triple act. Could be either index variables or something three-dimensional, like unit vectors or quarternions.

K, M: upper bounds on some kind of modulus. Look for || everywhere.

L, l: Most likely likelihood functions from statistics.

m,n: Integers! Index variables, sequences, induction, these two have you covered.

M: Matrices, welcome to linear algebra.

N: Natural numbers in a fancy font, a normal distribution in a normal one.

O: either big O notation and you're doing computer science; or if it's blackboard font, you're doing octonions and may your gods go with you.

p, P, q: Probability theory, again.

P, Q: formal logic. Usually seen in conjunction with lots of arrows.

Q: Rational numbers, usually blackboard font, you are most likely in algebra.

R: Real numbers, you are in analysis.

r: Something has a radius. It could well be a very abstract multidimensional radius.

s: Possibly generating functions, especially in conjunction with F and G. Not one of the more common maths letters.

t, T: Something is happening over time.

v: Vectors are happening.

u, U: whatever this is, you're too deep.

w: Something in four variables is happening.

x,y,z: the classic variable set. unknowns, vectors, scalars, there's nothing this gang of three can't do.

Z: Integers in blackboard font; a standard normal distribution in a regular one.

[coraniaid]

top 5 mathematical identities :)

I wish Tumblr supported LaTeX.

OK, not trying to overthink this too much.

There are lots of fun identities involving binomial coefficients (or their q-analogs), or related integer sequences like the Catalan numbers and Motzkin numbers. But I think I have to go with the Chu-Vandermonde identity: who doesn't like a good convolution formula?

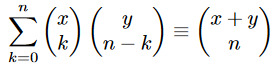
Of all the trigonometric identities I've ever had to learn, this is certainly not the most useful in practice or the hardest to prove or, arguably. the most inherently interesting either. I think the half-angle formula for tan is surprisingly pretty though.

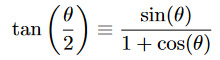
Let S be a finite set of real numbers. The maximum-minimums identity relates the largest element of this set to the smallest elements of every (non-empty) subset of S.

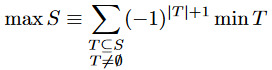
or, more concretely,

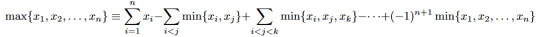
Perhaps not classically beautiful, but certainly enormously useful, the Sherman-Morrisson-Woodbury identity in linear algebra gives a formula for computing the inverse of a rank-k update of an invertible matrix by doing rank-k updates of the inverse of that original matrix. It's valid whenever the matrices are suitably conformable and when both the required inverses exist.

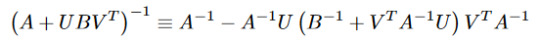
I feel like I have to include something due to Euler here, but -- rather than one of the famous ones involving π or anything to do with topology -- I'll go with some analytic number theory. The pentagonal number theorem gives a series expansion of the Euler function, valid for any complex x in the unit circle.

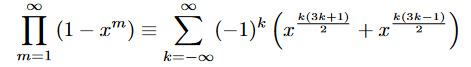
or, expanding both sides,

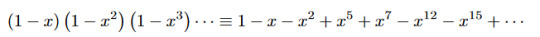
That takes us into the world of q-series and we can generalize it further to get Jacobi's triple product formula or various identities due to Ramanujan or MacDonald's identities for affine root systems or other increasingly exotic and strange things ... but this identity is the prototype for all of them.

[timeflow]

for the ask game!

n where n = inf A and A := {j∈ ℤ+ : ¬∃k ∈ℤ+ s.t. φ(k) = j}

assuming φ is euler totient function then I can check the cardinality of the multiplicative group of ℤ/kℤ and just go through the positive integers since I suspect it's probably either a really small number or it doesn't exist or it's an unsolved problem (either of these 2 cases would lead to me calling you names). φ(k)=1 and φ(k)=2 are obviously possible for k=2 and k=3 respectively, so I suppose φ(k)=3. 1,-1∈(ℤ/kℤ)* and 1≠-1 (since this would be k=2 which has φ(2)=1) so for the third element a such that (ℤ/kℤ)*={1,-1,a} you'd need a*a = 1, but since a is coprime with k you also need -a∈(ℤ/kℤ)*. this gives either -a∈{1,-1} at which point a∈{1,-1} which is a contradiction, or a=-a and 2a=0 which implies a divides k which is again a contradiction. so inf(A)=3, which means you have asked me:

3. Ever done any drugs?

no and I don't really intend to either

[kuroharukawada]

Okay, here's a super short FourX fic I write on the train today. It's written from X's POV

Just like Euler's identity

I never thought I would say this to myself, but I love you.

It's been so long since we've met for the first time but I still remember that day like it was yesterday. You helped me find my value, you gave me an identity, something that I can be. You were the first friend I ever made. Ever since I left The Expression Playground to look for a place where I was equal to others but never had a value I felt so lonely. Among the integers I felt small, weak, helpless. Noone really cared for a small, nameless variable I was before. But then you appeared in my life, you liked me, you wanted to spend with me. You introduced me to all of your amazing friends, everyone were so nice to me. But even among everyone else, you stood out. We've had so much fun everyday, I even forgot that I had a life before our meeting. Back home everyone were worried sick about me, especially Y and Z. But I didn't have to come back home, because you let me live with you, in your house.

Sometimes I wish I could come back to the past and tell you how much I love you now. But back then I was young, I barely understood the world around me. I didn't even realize you were always in love me, even when we were kids. But now that we went through so much together I finally understand why you always cared about me much than anyone else, even your own siblings.

Whenever I look at you, I feel my temperature rising, my heartbeat accerilating, my face turning deep orange. You make me so happy, even your simple presence in front of me. You're so amazing, so powerful, so charismatic, so... beautiful. Just like Euler's identity. I'm so happy that I can spend the rest of my eternal life with you. You're my everything, you're my value, Foury... ♡

[scarlet-lore]

So you guys are into integers, huh? Can I interest anyone in the ratio of the circumference and diameter of a circle? Perhaps an egg in these trying times?

I'm also a big fan of any number where if you use it as the base of an exponential function, its derivative is just the original function. How, bro??? Shout out to Euler for that one.

But hold the phone. What if we have numbers that when you multiply them with themselves, you only get negative numbers? Can you imagine it? Actually, I'd bet you can only imagine it, because to experience such a number in reality would add a sort of complexity to this imaginative plane. I digress.

[codingprolab]

CSCI 570 Homework 1

1. Arrange these functions under the Big-O notation in increasing order of growth rate with g(n) following f(n) in your list if and only if f(n) = O(g(n)) (here, log(x) is the natural logarithm1 of x, with the base being the Euler’s number e) : 2 log(n) , 2 3n , 3 2n , nn log(n) , log(n), n log(n 2 ), nn 2 , log(n!), log(log(n n )). 2. Show by induction that for any positive integer k, (k 3 + 5k)…

[amazingteamnames]

101 Best Math Team Names for US Students: Funny, Clever & Creative Ideas for Competitions

https://amazingteamnames.com/?p=2537 101 Best Math Team Names for US Students: Funny, Clever & Creative Ideas for Competitions Choosing the perfect math team name isn’t just about standing out—it’s about inspiring our team and making a statement before the competition even begins. A clever or bold name can spark excitement and boost our confidence every time we walk into a math meet. It’s our first chance to show off our team spirit and passion for problem-solving. We all know math can be tough but that doesn’t mean our team name has to be boring. With the right name we’ll capture attention and maybe even intimidate the competition a little. Let’s make sure our math team’s identity is as sharp and creative as our minds. Table of Contents Toggle Exploring Creative Math Team NamesHighlighting Punny Math Team NamesShowcasing Clever Math PunsSharing Witty Wordplay TeamsShowcasing Inspirational Math Team NamesEmphasizing Achievement and SuccessMotivating with Positive VibesFeaturing Pop Culture-Inspired Math Team NamesReferencing Movies and TV ShowsNodding to Famous MathematiciansCelebrating Classic Math Team NamesUsing Numbers and SymbolsLeveraging Timeless Math ReferencesOffering Subject-Specific Math Team NamesFocusing on Algebra and GeometryDiving Into Calculus and StatisticsSharing Funny and Quirky Math Team NamesDelivering Laugh-Out-Loud IdeasPresenting Lighthearted and Silly OptionsProviding Tips for Creating Unique Math Team NamesBrainstorming as a GroupUsing Online Name GeneratorsConclusionFrequently Asked QuestionsWhy is choosing a creative math team name important?What makes a math team name inspiring?How can we brainstorm unique math team names?Are funny or punny math team names a good idea?Should our math team name reference famous mathematicians?How do pop culture references enhance math team names?What are some examples of subject-specific math team names?How can we make sure everyone likes the chosen team name?Can we use online name generators for ideas?What’s the best tip for creating a memorable math team name? Exploring Creative Math Team Names Let’s jump right into ways we can brainstorm standout math team names together. First, we should think about what makes our team unique. Maybe we love tackling logic puzzles or get excited about outsmarting the competition. Something as simple as listing our favorite math topics—like calculus, geometry, or statistics—often sparks original ideas. Next, let’s look at clever wordplay. We could combine math terms with pop culture references. For example, names like “Alge-bros” and “Pi-thons” blend humor and math symbols, making our team feel both smart and approachable. Why not show off our competitive edge? Names like “The Integer-ators” or “Function Force” send a clear signal that we’re ready for any challenge. Picking strong vocabulary or action verbs helps us stand out to judges and rivals alike. If we want to inspire our team, we might use names that highlight our passion for problem-solving. “Equation Nation,” “The Riddlemeisters,” or “Prime Time” each suggest a love for math and a powerful team identity. We can also play with famous mathematicians’ names. Creating something like “Newton’s Nation” or “Euler’s Elite” connects us to history and adds an extra layer of cleverness. It helps to try rhymes or alliteration, too. Names such as “Decimal Dynamos” or “Sigma Squad” are catchy, easy to remember, and fun to cheer for at competitions. Let’s make sure we share ideas openly within our team before we decide. Gathering everyone’s input guarantees our name feels right for all of us. Once we agree, we’ll walk into every math event with confidence and a winning team spirit. Highlighting Punny Math Team Names Picking the right name can bond us as a team and show off our creative side. Math team names that mix math humor with wordplay not only make us stand out but can get everyone smiling before the competition even starts. Showcasing Clever Math Puns We see names like Alge-braic Avengers blending algebra with superhero energy, grabbing attention right away. Choosing something like Differential Ducks makes calculus sound fun and approachable, especially when we want to keep things light. Our pick of Integral Integers adds a clever twist, putting a fresh spin on mathematical basics. Sometimes, Pi-oneers gets chosen for its smart play on Pi and pioneers, united by that shared math passion. We could go for Sin-chronizers to cleverly tie together trigonometry and teamwork. Using Tangent Tacklers lets everyone know we’re ready to tackle tough problems. Whenever we want a laugh, Pie Charts Pirates or The Pi Rates bring playful pirate vibes into the math arena. Maybe we resonate more with Sum Like it Hot—it’s witty, memorable, and all about loving those sums. Sharing Witty Wordplay Teams Our team may even relate to Cos Ain’t Sin for its clever use of trigonometric concepts and a splash of attitude. Some of us enjoy the nod to statistics in The MAD Factors, where we mix mean and deviation for a creative punch. Prime Suspects instantly links us to number theory and adds a mystery twist. For a rebellious edge, Root Rebels shows off our ready-for-anything spirit. When we want to sound adventurous, Variable Vipers brings both math terms and flair. If pirates are more our thing, Polynomial Pirates invites both intrigue and challenge. Sometimes, a name like Quadratic Quizzers signals our quiz-ready confidence and love for equations. Our team could even be drawn to the rhythmic charm of Fibonacci Fiends, fueled by famous sequences and a bit of mischief. Each of these punny math team names gives us a unique way to celebrate what makes our group special—while never losing that mathematical flavor. Showcasing Inspirational Math Team Names Sometimes all it takes is an inspired team name to spark our drive and make us feel unstoppable before a big competition. Let’s explore two ways that math team names can capture achievement and motivation. Emphasizing Achievement and Success Calling ourselves the Derivative Dynamos signals to everyone that we excel with advanced calculus. We might go with Calculus Conquerors if we’re passionate about solving really tough problems. Taking on Euclidean Elites immediately sets a tone of geometric prowess. Algebra Alphas lets others know we’re ready to lead any algebraic challenge. Some teams select Geometric Geniuses when their specialty is angles and shapes. Equation Experts works well for those who want to showcase top-notch skills with any set of numbers and operators. Others choose Math Matrix to show how easily we navigate even the most layered problems. When we describe our team as Fibonacci Force, we let our admiration for mathematical sequences stand out. Gradient Guild carries a hint we’re prepared to tackle slopes and rates of change. Hypotenuse Heroes brings out our confidence with triangles and trigonometric ideas. Teams choosing Logarithm Legends love making log problems look easy. Naming ourselves Matrix Mavericks highlights our creative side with matrices. Prime Factors works best if we pride ourselves on unraveling the secrets of numbers. Team Name Achievement Area Derivative Dynamos Calculus Calculus Conquerors Advanced mathematics Euclidean Elites Geometry Algebra Alphas Algebra Geometric Geniuses Shape and spatial reasoning Equation Experts Problem-solving Math Matrix Complex problem navigation Fibonacci Force Mathematical sequences Gradient Guild Calculus, slopes Hypotenuse Heroes Trigonometry Logarithm Legends Exponential and log problems Matrix Mavericks Matrix algebra creativity Prime Factors Number theory Motivating with Positive Vibes Sometimes we want our name to boost not just skill, but also attitude and teamwork. Number Ninjas announces that our precision and strategy set us apart. If we want something with a touch of magic, Math Magicians brings out our flair for making math seem effortless. Calling ourselves Math Whizzes shows our confident speed with any problem thrown our way. Problem Solvers keeps things clear and lets everyone know we can tackle whatever challenge arises. Math Wonders hints at our curiosity and the awe we have for the subject. Logic Legends stands as a reminder that our critical thinking and teamwork make us strong competitors. Picking any of these names means we’re not just ready—we’re excited to show it. Team Name Positive Aspect Highlighted Number Ninjas Stealth, accuracy, and focus Math Magicians Fun, creativity, and charm Math Whizzes Speed, accuracy, and skill Problem Solvers Reliability and confidence Math Wonders Inspiration and curiosity Logic Legends Reasoning and smart teamwork Featuring Pop Culture-Inspired Math Team Names We love how a clever team name invites curiosity and sets us apart. Mixing math with pop culture always gives our group a fun, memorable vibe for competitions. Referencing Movies and TV Shows You’ll notice several of our favorites riff on familiar shows and blockbuster films. We call ourselves “The X-ecutors” when channeling the mystery of “The X-Files,” instantly sparking interest from anyone who hears it. Sometimes, we choose “Chaos Theorists,” drawing inspiration from chaos theory’s big Hollywood moments like “Jurassic Park.” Our moods change for each season—so when cryptic government secrets win the day, “Area 51” is just right, nodding to classic science fiction and conspiracy themes. We’ve also thrown “Think Or Sink” into the mix, hinting at the tense quick-thinking challenges from game shows and thrillers, reminding us how important fast math is under pressure. For those who enjoy witty puns and cinematic tech, “Pi-thons” gets laughs, cleverly blending Python programming, the famous movie snake, and, of course, the infinite pi. Nodding to Famous Mathematicians Sometimes, we go classic by saluting math icons with our team names. Whenever we want to bring some historical genius to the table, “The Turing Point” leads the charge—twofold, referencing Alan Turing and the crucial turning points in problem-solving (plus, a subtle nod to the hit film “The Imitation Game”). Feeling playful, we unite as “Algebros” for that brotherly team spirit, while celebrating the roots of algebra. If we’re inspired by mathematical depth, “Euler’s Disciples” instantly connects us to one of math’s greatest visionaries. Our “The Rational Radicals” persona pumps up the energy, where rational and radical mathematical ideas meet, showing we think way outside the box but know our foundational numbers. Each name keeps our legacy strong and our team identity sharp, making sure we honor the legends who shaped the math we love today. Celebrating Classic Math Team Names Sometimes a classic name says it all. We know that traditional math team names give teams an instant sense of belonging and pride, drawing on familiar concepts and revered mathematicians. Let’s explore some favorites that have stood the test of time. Using Numbers and Symbols Names built on numbers and mathematical symbols link directly to what we love about math. We see teams stand out with titles like The Prime Prodigies, spotlighting expertise in prime numbers—those indivisible and fundamental elements. Some groups opt for Quadratic Questers, creatively referencing their knack for solving quadratic equations and approaching every challenge head-on. It’s always fun to meet Radian Revolutionaries at tournaments, especially when we think about the way radians change our understanding of angles in trigonometry. Those of us who appreciate deep thinking tend to gravitate toward Logarithmic Leaders, a name that highlights the groundbreaking power of logarithms and exponential strategies. Other teams go for Integral Intelligentsia to show how thoroughly they approach every problem, embracing an all-encompassing problem-solving style. Math teams often inject even more playfulness when naming themselves. We love how Sine Wave Strikers brings the fundamental sin(x) into a bold, action-packed image. The clever team name Pi-thagorean Passers combines pi and the legacy of the Pythagorean theorem, blending two classic terms into one memorable label. Seeing Linear Linebackers on a roster always raises a smile, especially from those of us who connect linear equations to sports strategies. Some teams defend their turf as Differential Defenders, using the language of calculus to intimidate their competition. We can’t help but root for Vector Victors—their momentum reminds everyone that vectors can be both powerful and directionally inspiring. Leveraging Timeless Math References There’s a certain flair that comes with naming a team after legendary mathematicians or powerful math concepts. When we spot Golden Ratio Guardians at a contest, we know they value balance, symmetry, and that touch of mathematical perfection. Fibonacci Fanatics always give us a nod to the beauty hidden in nature’s favorite sequence, one that pops up everywhere from pinecones to financial models. We regularly run into Cartesian Coaches—named after René Descartes—and they always seem to master coordinate geometry challenges with confidence. Exact operations and processes also inspire great team names. Equation Experts instantly signal their problem-solving prowess, ready to tackle any formula thrown their way. Teams going by Function Fanatics stand out for their enthusiasm in unraveling the mysteries of mathematical functions and exploring their applications. Calling themselves Derivative Dynamos, some teams celebrate their calculus capabilities and their passion for change. Statistical Sages bring calm and wisdom to data interpretation, reminding us that deep understanding of probability and statistics can make all the difference during high-stress competitions. We love how these names connect us to math’s core ideas, the history we’re proud of, and the excitement we feel every time we face a new challenge. Offering Subject-Specific Math Team Names When we want to celebrate what makes our math team unique, going with a name that links directly to our favorite subject area adds extra flair and focus. Let’s explore some of the best subject-exact math team names for teams that love Algebra, Geometry, Calculus, or Statistics. Focusing on Algebra and Geometry We find Algebra teams often gravitate towards titles that reflect their knack for variables and equations. Names like Algebra Alliance, Algebra All-Stars, and Algebraic Avengers show unity and strength in problem-solving. Picking Algebra Brigade or Variable Voyagers (since variables are a core algebra concept) lets us stand out when tackling equations in any contest. Geometry squads get to take inspiration from shapes and space. Coming up with names like Geometry Guardians, Geometric Geniuses, or Angle Achievers captures our creative thinking for visual math challenges. Other clever options—Angle Artists and Shape Shifters—highlight our ability to approach geometric puzzles from every angle. Diving Into Calculus and Statistics For teams passionate about Calculus, using titles that honor advanced math makes a great statement. We love names like Calculus Crusaders and Calculus Crew for their team spirit. Inspired by calculus concepts, Derivative Dynamos and Integral Innovators point to our skills with rates of change and area under the curve. Function Fanatics works perfectly for teams that want to emphasize their understanding of math functions. Statistics-focused teams amp up their game with names that spotlight data and probability. We suggest Statistic Stars and Probability Powerhouses to broadcast our confidence in data analysis and chance. Choosing Probability Pros or Estimation Experts shows our analytical strength. Our data-driven identity stands out with a name like Data Dynamos that reflects our enthusiasm for crunching numbers and drawing solid conclusions. Sharing Funny and Quirky Math Team Names Sometimes, the best way to break the ice is with a math team name that makes everyone smile. Let’s make our team unforgettable with a little humor and a lot of creativity. Delivering Laugh-Out-Loud Ideas Everyone gets the giggles when we walk in as “The Mathemagicians,” ready to pull some numbers out of a hat. Nobody forgets “Pi Hard” or “Get Rich Or Pi Tryin’,” which always spark a chuckle from competitors and judges alike. Plenty of teams wish they’d picked “Numerator’s Gonna Numerate” or “How Can You Be So Obtuse?” for the quick wit in those names. Try “Live Free Or Pi Hard” to parody action movies or choose “Algebrains” if we want brainy and bold. Euler fans usually appreciate “Euler’s Disciples.” Whether we walk in as “Chaos Theorists” or “The Axiom Breakers,” clever math puns light up the room and set the tone for a fun battle of wits. Presenting Lighthearted and Silly Options Let’s keep things fun with team names like “Partial Fractions of Sanity” that show we’re not taking ourselves too seriously. We might become the “Odd Squad” or the “Denominator Dominators,” making math jokes right from the team roster. Some of us might love being the “Fractal Fanatics” or “The Lemma Llamas,” because everyone loves quirky mascots. “Sum It Up” wraps everything together if we like things simple and clever. If we want to bring a smile to every round, “Math Maniacs,” “So You Think You Can Add,” or “Pi-rate Ship” bring a playful twist. Whichever name we pick, our team’s humor will turn math contests into memorable events for everyone. Providing Tips for Creating Unique Math Team Names Let’s dig into actionable ways we can create an original math team name that fits our crew. Each method sparks creativity and helps us brainstorm something truly memorable. Brainstorming as a Group We always get the best ideas when everyone gets involved in the process. Gathering the whole team for a brainstorming session lets us bounce ideas off each other and riff on different suggestions until something sticks. Sometimes wild suggestions lead to brilliant names—imagine someone blurting out “Algebra Avengers” and that inspiring “Pi-thagorean Passers.” Encouraging everyone to share their perspectives helps us pick a name that genuinely reflects our identity and style. We also make sure the name fits our collective vibe, whether we love solving tricky calculus problems or enjoy a good, math-themed pun. Using Online Name Generators Sometimes we need a jump start, so using online name generators makes the process easier. These tools give us a stack of name ideas based on keywords like “math,” “pi,” or “integral,” which we can then tweak to match our team’s flair. Tweaking these suggestions allows us to mix in our favorite topics, inside jokes, or pop culture references, so we don’t end up with a name that sounds like everyone else’s. Checking these ideas against what’s already out there also helps us stay unique, original, and unmistakably us. Conclusion Choosing the right math team name is more than just a creative exercise—it’s a chance for us to showcase our team’s personality and passion for problem-solving. The perfect name can set the tone for our competitions and help us stand out in a crowd of talented teams. Let’s remember to have fun with the process and involve everyone in brainstorming. Whether we lean toward clever puns, pop culture references, or names that highlight our favorite math topics, the best name is one that brings us together and boosts our confidence. With a bit of creativity and teamwork, we’ll find a name that makes us proud to represent our love for math and our unique team spirit. Frequently Asked Questions Why is choosing a creative math team name important? A creative math team name boosts team spirit, confidence, and excitement. It helps your team stand out, makes a strong statement to competitors, and can foster a sense of unity and motivation before competitions. What makes a math team name inspiring? An inspiring math team name reflects your team’s identity, passion for problem-solving, and love for math. It often uses clever wordplay or references that resonate with members and celebrates teamwork, achievement, and creativity. How can we brainstorm unique math team names? Start by considering what makes your team unique, such as favorite math topics or shared interests. Use brainstorming sessions to gather input from everyone, try combining math terms with pop culture references, and experiment with alliteration or rhymes for catchy names. Are funny or punny math team names a good idea? Yes! Funny or punny names like “Pi Hard” or “Partial Fractions of Sanity” add humor, reduce pre-competition nerves, and make your team memorable. They create a fun, engaging atmosphere while showing off your creativity. Should our math team name reference famous mathematicians? Absolutely. Names inspired by legends like “Euler’s Disciples” or “The Turing Point” celebrate math history, reflect admiration for their contributions, and can motivate your team by honoring great minds. How do pop culture references enhance math team names? Blending math with movies or TV shows—like “The X-ecutors” or “Think Or Sink”—makes your team name memorable and fun. These references engage both team members and audiences by connecting familiar pop culture with math. What are some examples of subject-specific math team names? For Algebra: “Algebra Alliance” or “Algebra Alphas.” For Geometry: “Geometry Guardians.” For Calculus: “Calculus Crusaders” or “Derivative Dynamos.” For Statistics: “Statistic Stars” or “Probability Powerhouses.” How can we make sure everyone likes the chosen team name? Involve everyone in the naming process. Hold brainstorming sessions, vote on favorites, and ensure that the final choice reflects your team’s collective identity and enthusiasm for math. Can we use online name generators for ideas? Yes, online name generators can spark creativity by suggesting options you might not think of. Customize these suggestions to fit your team’s style for a truly unique and original name. What’s the best tip for creating a memorable math team name? Combine clever math references with humor or inspiration, and make sure the name resonates with the whole team. The best names are unique, catchy, and foster a strong sense of unity and pride. https://amazingteamnames.com/?p=2537 Amazing Team Names

[shalu620]

How to Learn Python Quickly and Effectively

Python is one of the most popular programming languages, known for its simplicity and versatility. Whether you're a beginner or an experienced developer, learning Python efficiently can open up many career opportunities. Here’s a step-by-step guide to mastering Python quickly and effectively. Considering the kind support of Python Course in Chennai Whatever your level of experience or reason for switching from another programming language, learning Python gets much more fun.

Start with the Basics

Before diving into complex topics, it’s essential to build a strong foundation. Begin by learning Python’s core concepts:

Variables and data types (strings, integers, lists, dictionaries)

Conditional statements (if-else, loops)

Functions and modules

Object-oriented programming (OOP)

Free resources like W3Schools, Python.org, and GeeksforGeeks provide excellent tutorials to get started.

Take Online Courses for Structured Learning

Enrolling in structured courses can accelerate your learning process. Some great online courses include:

Python for Everybody (Coursera – University of Michigan)

Complete Python Bootcamp (Udemy – Jose Portilla)

Python for Beginners (Codecademy)

These courses offer interactive lessons and projects to help reinforce your learning.

Practice Coding Every Day

Consistent practice is key to mastering Python. Solve coding problems daily on platforms like:

LeetCode

HackerRank

CodeWars

Project Euler

Practicing real-world problems improves problem-solving skills and coding speed.

Work on Real-World Projects

The best way to learn Python is by building projects. Start with small projects such as:

A simple calculator

A web scraper using BeautifulSoup

A personal expense tracker

A to-do list application

Building hands-on projects helps you understand Python’s real-world applications and boosts confidence. With the aid of Best Online Training & Placement Programs, which offer comprehensive training and job placement support to anyone looking to develop their talents, it’s easier to learn this tool and advance your career.

Learn Python Libraries for Your Field

Depending on your interests, focus on relevant Python libraries:

Web Development: Flask, Django

Data Science: NumPy, Pandas, Matplotlib

Machine Learning: TensorFlow, Scikit-learn

Automation & Scripting: Selenium, BeautifulSoup

Learning domain-specific libraries will make you job-ready in your chosen field.

Read Python Documentation and Books

Deepen your knowledge by reading Python’s official documentation and books such as:

Python Crash Course by Eric Matthes

Automate the Boring Stuff with Python by Al Sweigart

These resources offer practical exercises and real-world coding examples.

Join Python Communities and Forums

Being part of a coding community helps in learning and networking. Some great Python communities include:

Stack Overflow

Reddit’s r/learnpython

Python Discord and Slack groups

Engaging in discussions and solving others’ queries can reinforce your knowledge.

Contribute to Open Source Projects

Collaborating on open-source projects on GitHub helps you gain real-world experience. You’ll learn to work with a team, write clean code, and improve debugging skills.

Improve Debugging and Code Optimization Skills

Understanding debugging techniques is crucial for writing efficient code. Use Python’s built-in debugging tools like print(), pdb, and logging. Writing optimized and clean code enhances performance.

Build a Portfolio and Showcase Your Work

Employers value hands-on experience. Create a GitHub profile and upload your Python projects. If possible, build a personal website to showcase your coding skills and attract job opportunities.

Final Thoughts

The key to learning Python quickly is consistency, practice, and real-world application. Follow a structured learning approach, engage with the coding community, and work on projects. With dedication, you can become proficient in Python in just a few months.

[simknowsstuff]

Lagrange with single variable derivatives under d^3/dx^3, leibniz for everything else

Maybe Euler for non integer/variable derivatives and integrals

[tutoroot]

What are the Types of Real Numbers? 

The concept of real numbers has evolved over centuries. Ancient civilizations like the Greeks and Indians made significant contributions to the development of number systems. The formalization of real numbers, as we know them today, is attributed to mathematicians like Georg Cantor and Karl Weierstrass in the 19th century. 

Types of Real Numbers 

Real numbers can be broadly classified into two categories: 

1. Rational Numbers 

Rational numbers are numbers that can be expressed as a fraction, where both the numerator and denominator are integers, and 1 the denominator is not zero.    

Examples: 1/2, 3/4, -2/5, 0.5, 0.333… (repeating decimal) 

Decimal Form: Terminating or repeating decimals. 

2. Irrational Numbers 

Irrational numbers, on the other hand, cannot be expressed as simple fractions. Their decimal representations neither terminate nor repeat, extending infinitely without any discernible pattern. 

Examples: √2, √3, π (pi), e (Euler’s number) 

Decimal Form: Non-terminating and non-repeating decimals. 

Properties of Real Numbers 

Real numbers possess several fundamental properties: 

Commutative Property: For addition and multiplication, changing the order of the operands does not affect the result. 

Addition: a + b = b + a 

Multiplication: a * b = b * a 

Associative Property: For addition and multiplication, grouping the operands differently does not affect the result. 

Addition: (a + b) + c = a + (b + c) 

Multiplication: (a * b) * c = a * (b * c) 

Distributive Property: Multiplication distributes over addition. 

a * (b + c) = a * b + a * c 

Identity Property: 

Additive Identity: For any real number a, a + 0 = a. 

Multiplicative Identity: For any real number a, a * 1 = a. 

Inverse Property: 

Additive Inverse: For any real number a, there exists an additive inverse -a such that a + (-a) = 0. 

Multiplicative Inverse: For any non-zero real number a, there exists a multiplicative inverse 1/a such that a * (1/a) = 1. 

Real Numbers in the Real World 

Real numbers are ubiquitous in various fields of study and everyday life: 

Mathematics: 

Real numbers are fundamental to algebra, geometry, calculus, and other mathematical disciplines. 

They are used to define functions, solve equations, and analyze mathematical structures. 

2. Science: 

Real numbers are used to measure physical quantities like distance, time, mass, and temperature. 

They are essential in fields like physics, chemistry, and biology. 

3. Engineering: 

Engineers rely on real numbers to design and analyze structures, circuits, and systems. 

They are used in calculations involving force, stress, strain, and other engineering parameters. 

4. Economics: 

Real numbers are used to model economic phenomena, such as inflation, interest rates, and GDP. 

They are essential in financial analysis, investment decisions, and economic forecasting. 

5. Computer Science: 

Real numbers are used in numerical computations, computer graphics, and artificial intelligence. 

They are fundamental to algorithms and data structures. 

Real numbers are a cornerstone of mathematics and science, enabling us to quantify and analyze the world around us. By understanding the properties and applications of real numbers, we can unlock the power of mathematical reasoning and solve complex problems. Online maths tuition can help you grasp fundamental concepts from simple arithmetic to complex calculus. For personalised guidance and expert tutoring, please feel free to contact Tutoroot. They offer one-on-one tutoring sessions tailored to your specific needs, helping you easily grasp complex concepts. 

[acorgiirl]

Project Euler #3

It is the 3rd one and I'm already out of ideas of what to write in this preamble. So here we go (?)!

Links Project Euler: https://projecteuler.net/problem=3 HackerRank: https://www.hackerrank.com/contests/projecteuler/challenges/euler003

The prime factors of 13195 are 5,7,13 and 29. What is the largest prime factor of a given number N?

So with this there's a few ways I could go about doing this. Typically when dealing with primes, I like to collect a set of them using a sieve algoithm. But those tend to take up a lot of space. With the maximum N being up to 10^12, I don't wanna do that. So instead I'm going to check for 2 and then after that, only odd numbers. I'll be unnecessarily checking for a lot of composite numbers that way, but the way I'm going to do it, it'll be fine.

So according to the Fundamental Theorem of Arithmetic, every integer > 1 can be written as a product of primes. so in other words, every integer X > 1 can be written as X = P0 ^ k0* P1 ^ k1 * ... Pn ^ kn

where those P's are the prime factors and the k's are how many times that prime goes into X.

If you assume all those P's are ordered, where P0 is the smallest and Pn is the largest, this problem is just asking what is Pn. So what I'm going to do is whittle down X by dividing by numbers that go into it until nothing remains except 1. If I start from 2 then the last number I divided by must be the largest prime factor!

One other small optimzation. Lets look at the factors of 12: 1,2,3,4,6,12. The factor pairs are (1,12), (2,6),(3,4). I like to think of this as a see-saw. The left number is always <= the right number. So there's like this central pivot that separates the left numbers from the right numbers. And that would be when the left number == the right number. In other words, the square root of the number.

So to prevent me from checking every number from 3..N, I can actually shorten this to be every number from 3..√N. If I reach that point any my X > 1, then that means that X must be a prime itself. This is going to be a huge time save. For example, if N was 10,000, I'm saying I'd only have to check the first 100 numbers, which is 99% less than if I checked all 10,000.

Here's my code:

import sys t = int(input().strip()) for a0 in range(t): n = int(input().strip()) X = n last_prime = n while X%2 == 0: # first just check for 2 last_prime = 2 X //= 2 P = 3 while X > 1: if X%P == 0: last_prime = P while X%P == 0: X //= P if P*P > n and X > 1: #stop when P exceeds the square root last_prime = X break P += 2 print(last_prime)

And that's all test cases passed! Onto the next one!

[accidental-memory]

I am doing a thing called Project Euler, which is math challenges that require programming knowledge to solve. On the FAQ on the front page:

I've written my program but should it take days to get to the answer? Absolutely not! Each problem has been designed according to a "one-minute rule", which means that although it may take several hours to design a successful algorithm with more difficult problems, an efficient implementation will allow a solution to be obtained on a modestly powered computer in less than one minute.

I'm on problem 12, which boils down to: Find the first triangle number with more than 500 factors.

The wording makes it look very innocent. 500 isn't even that big a number compared to some of the problems you've done before this. Ha. Hahaha. I am not a data scientist lol, I'm just some guy fiddling around with Python

First part of the problem is how do you calculate a triangle number? This part's very easy. You can look it up but I actually derived the formula for all polygonal numbers about 6 years ago so I just know this already lol.

f(s,n) = ( (s-2)n^2 + sn + 2 ) / 2

where s is the number of sides in your polygon and n is the iteration when calling the first number, 1, the 0th number.

Since a triangle number means s=3, this in turn means the first coefficient will be s-2 = 3-2 = 1, so the first coefficient goes away and we get the formula for the nth triangle number:

(n^2 + 3n + 2) / 2

Second part is, count the factors of that triangle number. Okay...

Method 1: Divide that number by every positive integer less than or equal to itself, and count how many times you divide it evenly (i.e. have a remainder of zero)

This is pretty fast with small numbers but very quickly gets slowed down around the 500th triangle number when it's now trying to divide every new triangle number by thousands of numbers. So much for the "one minute rule" there.

Method 2: Find the prime factorization of the triangle number and use the exponents to calculate how many factors it has. (For example, the prime factorization of 50 is 5^2 X 2^1, so you multiply by one more than each of these exponents, 3X2 = 6, so 50 has 6 factors)

Great! ... But that means you have to generate prime numbers up to the square root of the number you're checking for. GENERATING PRIMES IS ALSO HARD.

To give you an idea of how it's going for me so far:

I ran method 1 for 5 hours and got to a number with 480 factors somewhere around the 5000th triangle number.

I'd been running method 2 for 4 hours so far and I was somewhere between the 400th and 600th triangle number so far. Definitely a no-go. Generating primes to check against is SO MUCH SLOWER, even though it enormously diminishes the number of things you're dividing the triangle number by to check for its prime factorization. Also method 2 took a lot more effort to code.

So now.. I'm kinda out of ideas except to keep my computer from going to sleep and just let it run all day while I'm at work using method 1. I'm sure that violates the "one minute rule" but if it works it works eh? -_-