#Samos is where pythagoras

[percy-ils]

being a Greek mythology fan while living in the exact places where the stories took place is insane. Ionia? just a few hours away, elementary schools take us to trips to see the big wooden horse. Symyrna? Literally my hometown. Ephesus? it's on the way to my summer house. Lesbos or chios? I can go there for a weekend getaway. Mount Ida? I almost fell into a creek there once. Samos? I can see it across the sea on a clear day. All the same with Pergamon and Halicarnassus and Dydma and a lot of other islands and places like it's all only a few hours away and I've been to almost all of them. legit the peak of being mythology fan

[factomaniac]

Math Madness #3: The Pythagorean Theorem Wasn’t Discovered by Pythagoras, and Other Facts About

a² + b² = c²

Thursday, 13 June 2024, Chicagoland, IL

Mesopotamian mathematics historians have established that, despite the name it is known by today, the Pythagorean Theorem was widely known in the Old Babylonian Empire existing from the 20th to the 16th Centuries BC, over 1,000 years before Pythagoras of Samos, the theorem’s namesake, was even born around the middle of the 6th Century BC in either the Greek island of Samos, or the city of Tyre in present-day Lebanon (Wikipedia “Pythogorean Theorem” 2024, Neugebauer 1969, Friberg 1981, Hørup 1998, Robson 2008, Wikipedia “Pythagoras” 2024, Porphyry 2014).

The Pythagorean Theorem asserts that in any right triangle, a triangle containing one right angle (an angle of 90°–ninety degrees–or π/2 radians), the area of a square where each side is the length of the triangle’s hypotenuse (the side of the triangle opposite the right angle) is equal to the sum of the areas of two squares where each side of each square is the length of each of the other sides of the triangle, which are perpendicular to one another.

By the way, the word hypotenuse comes from French, by way of Latin hypotenusa, ultimately originating from the Ancient Greek ἡ ὑποτείνουσα (“hē hypoteínousa”), meaning “the [side] stretched below [the right angle]” because, in Ancient Greek times, right triangles tended to be drawn with the right angle pointing upward, therefore, the hypotenuse appeared to be stretched below the other two sides forming the right angle (Wikipedia “Hypotenuse” 2024, Liddle, Scott, Jones 1940/Perseus Project 2024, Online Etymology Dictionary “Hypotenuse” etymonline.com 2024).

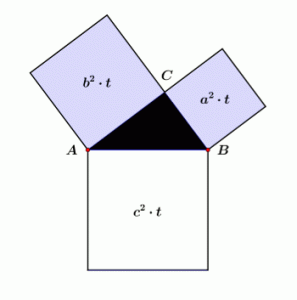
Although typically this theorem is typically stated as something like “the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides,” and written algebraically as a² + b² = c² today, in ancient times, it was originally construed geometrically with actual squares on the sides of the right triangle. Remarkably, thousands of geometric and algebraic proofs of the Pythagorean Theorem exist. One very simple modern geometric proof is below.

Besides serving visually as a proof of the Pythagorean Theorem, the above illustration also makes a good jumping off point for an algebraic proof of it as well. Referring to the second frame of the illustration with the c² square in the center, notice that the sides of the entire frame each measure a + b. Therefore, its area can be found by squaring this expression: (a + b)². Also notice how the area of the frame can be found by adding the area of the c² square itself to the areas of each of the four triangles, ½ab: c² + 4(½ab). The Pythagorean Theorem then pops out just by writing an equation that sets these two expressions as equal to one another.

(a + b)² = c² + 4(½ ab) → a² + 2ab + b² = c² + 2ab → a² + b² = c²

By the way, the equation of the Pythagorean Theorem can also be rearranged to find the length of one of the sides of a right triangle while knowing the length of the other two sides:

∵ a² + b² = c², c = √(a² + b²), a = √(c² - b²), b = √(c² - a²) (∵ symbolizes "because" and √(x) is "the square root of x").

Originally, Euclid proved this theorem by taking a right triangle with the right angle pointed upward and the hypotenuse as the base at the bottom and then, as I mentioned above, making squares off of all three sides of the triangle whose sides are the length of the respective triangle sides they are formed from.

Although I’m presenting what is essentially Euclid’s proof of the Pythagorean Theorem, I’m going to put my own spin on it in that I’m going to refer to the points, lines, and shapes in a way very different from how it is done in classical geometry. Because one thing I recall that I found confusing when learning classical geometry in primary and secondary school was the reference to shapes by the points that form their corners, such as referring to a shape as Triangle ABC—or worse △ABC—because it contains the points A, B, and C, or saying that one shape is congruent to another because they contain proportional sides that meet at points forming the same angles. I’ve always found the semantics and vocabulary of classical geometry baffling compared to, say, algebra or even calculus. Therefore, points will have miniscule Greek letters, the lengths of lines will be referred to using miniscule Roman letters, and the shapes are depicted with Roman numerals. (Please note that I will occasionally use traditional notation as well as my own notation in order to avoid confusion.)

First, we have Triangle I in dark grey (traditionally defined by points ϙ [qoppa, pronounced “COPE-ah”, an archaic Greek letter now only used as a numeral], α, and β, or symbolically as △ϙαβ) with sides of lengths a, b, and c, a is the length of the side of the triangle on the right side of the right angle, b is the length of the side on the right angle’s left side, and c is the length of the hypotenuse, in the style of the ancient Greeks, on the bottom of the triangle forming its base. Next, there are the squares in white (Squares II [□ϙηιβ], III [□αφγϙ], and IV [□βαδε]—see the uniting brace on the bottom of Square IV) formed from each of Triangle I’s sides, all of whose sides, by definition, are all the same exact length, and the same length as each of the sides of Triangle I from which they are formed.

Further, taking point ϙ, let’s draw a line segment straight down through Triangle I through point κ and all the way down through Square IV (□βαδε) to point λ, dividing the square into two rectangles, Rectangles V (▯καδλ) and VI (▯βκλε). Now, also in lighter grey, we have two larger non-right triangles, Triangles VII (△φαβ) and VIII (△ϙαδ), by drawing line segments from point φ to point β (line segment φβ, or φβ) and from point ϙ to point δ (ϙδ). Finally, also in lighter grey, we draw line segments from point α to point ι (αι) and from point ϙ to point ε (ϙε) to create another pair of smaller non-right triangles, Triangles IX (△αβι) and X (△ϙβε). (Usually, a line is placed above the endpoint letters to signify a line segment, but that type of font is not easily available on Tumblr, so I used crossout print instead.)

Note that the upper left corner of Square IV (angle βαδ, or ∠βαδ) and the lower left corner of Square III (∠φαϙ) both meet at point α and because they are both corners of squares are both right angles. So because Triangles VII and VIII have a common corner at point α, their angles both measure 90º (π/2 radians) plus the angle of the corner of Triangle I at point α (∠ϙαβ) and, therefore, both angles of the corners of Triangles VII (∠φαβ) and VIII (∠ϙαδ) that meet at point α are equal.

Because the side on the left of Triangle VII (φα) and the side on the top side of Triangle VIII (αϙ) both also lie on sides of Square III and both are of length b, and the bottom side of Triangle VII and the left side of Triangle VIII lie on sides of Square IV and both measure length c, and the angles of both triangles that meet at point α are equal, both Triangles VII and VIII are congruent to one another in that all their sides and all their angles are equal, and, therefore, we can assign the letter d to the length of the diagonal sides of both triangles.

Because the line starting at point ϙ going down to point κ and continuing down to point λ (ϙκλ) is a straight line parallel to left side of Square IV (αδ), that is (ϙκλ ‖ αδ), which is the same as the left side of Triangle VIII, measuring length c, and the top side of Rectangle V (αϙ) is parallel to its bottom side (δλ, or αϙ ‖ δλ), both each measuring length f, which is the height of Triangle VIII, therefore its area (½ cf) is half the area of Rectangle V (cf). By the way, if you would like to know the derivation of the triangle area formula, see my previous blog entry.

Further, since the line segment starting at point γ, on the right side of Square III, going to point ϙ and continuing to point β (γϙβ) is a straight line segment parallel to the left side of Square III (φα, or γϙβ ‖ φα), Triangle VII with a base of b and a height of c is half the area of Square III (½ bc = ½ b²), and is therefore, Triangle VIII with a base of c and a height of f is also half the area of Square III (½ cf = ½ b²), which is also half the area of Rectangle V (½ cf = ½ b²). Therefore, the areas of Square III and Rectangle V are equal (b² = cf).

Finally, since the line segment starting at point α, on the left side of Triangle I, going to point ϙ and continuing to point η, on the top side of Square II is a straight line segment parallel to the bottom of Square II (αϙη ‖ βι), Triangle IX has base and height a and, therefore, area ½ a², and the line segment starting at point ϙ, going through point κ and ending at point λ is a straight line segment parallel to the right side of Rectangle VI, Triangle X has base c and height g and, therefore, area ½ cg, and both Triangles IX and X are congruent to each other and, therefore, their areas are equal (½ a² = ½ cg) and, therefore, Triangle X is half of the area of Rectangle VI, and, therefore, both Square II and Rectangle VI have the same area (a² = cg). Therefore, Square IV has the same area as the sum of the areas of Squares II and III (a² + b² = c²). QED

But, as I said, there are thousands of proofs of the Pythagorean Theorem. Next time, we will cover one such proof recently discovered by two high school girls.

Works Cited:

Friberg, Jöran. "Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean Triples, and the Babylonian Triangle Parameter Equations." Historia Mathematica 8 (1981): 277-318.

Høyrup, Jens. "Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics." Homepage of Jens Høyrup of Roskilde University. Jens Høyrup. 1999. http://akira.ruc.dk/~jensh/Publications/Pythrule.pdf (accessed 2024).

Neugebauer, Otto. The exact sciences in antiquity (2nd ed.). Mineola, NY: Courier Dover Publications., 1969.

Wikipedia "Pythagoras" http://en.wikipedia.org/wiki/Pythagoras , (accessed 2024).

Wikipedia "Pythagorean Theorem" http://en.wikipedia.org/wiki/Pythagorean_theorem , (accessed 2024).

Coming soon: my new blog about Philosophy, Mythology, Religion, and Politics, also in Spanish and English. It's the Aristotelian, and it's available at the-aristotelian.tumblr.com

[iatrophilosophos]

@thesiltverses, have you read against his-tory, against leviathan by Freddy pearlman? Honestly I'd be shocked if you hadn't since it is very literally about the consumption of gods as tools in human hierarchy (among other things).

I've been thinking about the wound tree camp in reference to these passages:

"The once-free human being increasingly becomes what Hobbes will think he is. The armor once worn on the outside wraps itself around the individual’s insides. The mask becomes the individual’s face. Or as we will say, the constraint is internalized. The ecstatic life, the freedom, shrinks to a mere potentiality. And potentiality, Sartre will point out, is nothing."

"We do not learn of the revulsion or of the expectation of human renewal from the dancers themselves because ignorant armies, Cyrus’s foremost among them, break up the circles.

We learn from the children and grandchildren who have not themselves danced, but who have heard.

In China the visions of Zarathustra’s equally shadowy contemporary Lao Tze are gathered up in books and come to be known as The Way.

In India the visions of one called Gautama are collected and come to be considered by masked and armored as techniques for removing the mask and armor.

In Greece, echoes of the hopes stay with the women who continue to dance and who remember having seen a new Dionysus emerge from ashes. Echoes stay with musicians who gather with Pythagoras of Samos in order to renew the hopes.

The main outlines of what Turner will call “the crisis cult,” Christianity, precede it by twenty-five or thirty generations. And the main outlines of the inversion of the crisis cult also precede it, and by at least as many generations. The Persian Cyrus who wears the mantle of Zarathustra and the later Indian Ashoka who wears the mantle of Buddha are both forerunners of Constantine and the Popes."

"Now, in the days of Potifex Maximus Octavian, there is an even greater movement, both abroad and at home. What Turner calls “the crisis cult” is only one among many parts of this movement. Unfortunately for humanity and for nature, the crisis cult that will eventually father the Western Spirit takes root in a dark corner where light is expected to shine forth from Optimus Maximus, from the lightless abstraction of Leviathan itself.

The “crisis cult” does not spring out of the air but out of the attempts of human beings to disencumber themselves of the integument that dehydrates them. And it is not a “cult.” It is a living way that becomes da cult only when it is re-encased in the artifice’s integument."

If you have read it, I applaud the application of the concepts--but if not, then that's even more impressive.

Pearlman presents anti-civilization anarchy as the logical conclusion of criticisms of *gestures* all this shit; and as an explanation of why reformist political movements are so co-optable. In the bookclub we're currently reading AHAL in, we're asking the questions: is anti-civilization legitimately a less co-optable frame of critique? (Could we kill every god? Can we remove the armor, can we refuse to foster new gods?) What lessons can we take from the crisis cults? The silt verses and especially the wound tree camp is a really fantastic thought experiment as to how pearlmans concepts are lived through in the imperial core and splinter movements.

I don't have any answers or a neat question to tie it all together with, and I have to go work on the garden. I just wanted to say that the silt verses was really relatable and lovely to me and a lot of my friends who are trying to walk away from omelas, and that if it offered a spark to anyone else, pearlman is a pretty nice next step to dream and start moving. Here in the US, hurricane helene (very proximate to me) is viscerally introducing yet another wave of people to the fact that the grid is already collapsing under its own weight, and expectably a lot of the response is prioritizing buisness as usual for those at the top of the hill and sacrificing a lot of human beings to the foundations. I think in a time of disasters, art can--at least hopefully, sometimes--help us fight against the knee-jerk urge to reaffirm the system when it is in crisis by helping us to feel the horror of buisness-as-usual moreso than the fear of something else; and take those opportunities when we are forced to function outside of the grid to take more steps further away (community water catchment and filtration, composting toilets, continuing to build medical cohorts that can function as much as possible independently of global infrastructure and all the precarity and violence that entails) instead of clawing back in and throwing more bodies in the mud behind us. Dreaming through art also gives us--albeit imperfect--opportunities to iterate. As the world is rapidly deteriorating and we--as pearlman puts it--are trapped with the armor of internalized civility, the need to rapidly try on idea after idea to retain resilience (at least, i think so). I don't read much utopian fiction but Woman On The Edge of Time, a pulpy mad liberationist utopian sci-fi from the 70s (with some unfortunate 2nd wave feminist baggage :/) was a great exercise in this for me, because it provided a scattershot of ideas from "blindingly improbable considering the climate crisis" to "that seems decent" to "i would hate this immensely and would like to make intentional decisions about how I relate to people for whom this represents utopia." The silt verses also provided this to me (and, if it's not too much to say-- i enjoy and respect your work immensely, but I doubt we'd be great friends in an isolated compound :p)

But, art, philosophy, even just posting, whatever is a tool--it's up to us as an audience to engage with it as such, not only exercising media literacy (e.g. wondering if perhaps, when a work seems very heavy handed about a basic theme such as "capitalism bad", it may actually be taking that as a given to make deeper statements within the canon of works that all agree on "capitalism bad" 🙃) but deriving experimental lenses with which to view the world and bouncing ideas through the people around us to find affinity and tensions. As creators-- we have infuriatingly, beautifully limited control over if that actually happens. Wahooo

Woah that got long, sry lol!

Hello! Writing first to thank you for such an extraordinary creation - as a piece of writing and even more so in performance. Every episode manages to somehow build on and outdo the last; you navigated that transition from a smaller scale story of grisly mysteries and personal crises of faith to a grand scale of war, revolution and political satire with absolute aplomb, and never lost that throughline of exceptional characterisation and sharp writing, always steering to the most interesting conflicts. You are always very humble in your public comments, but I hope you allow yourself a little pride, because this is absolutely top notch stuff.

I was struck by Paige's final words, that she hopes what they left would be found 'flawed, inadequate, yearning'. As the show went on, I was surprised - in a good way - that the show's politics gradually crystalised into a full-on nihilist anarchism, something perhaps even along the lines of Monsieur Dupont. (Muna used the 'a' word in one of the Q&As but it was pretty evident even before that). Taking these gods as a metaphor for ideologies and social systems, the scope of it becomes pretty universal - and unsparing. And, equally, hard to answer.

I wondered when the Many Below/Wound Tree was introduced what answers they would find: what political movement could truly resist cooption or becoming its own horrible self-sustaining egregore. And in the end the answer you express I suppose is a negative one: that even Paige's god of victims is a tool, one that must eventually be discarded to go into some unknown place beyond it all (to walk away from Omelas), towards something that narrative fiction - as a form of the 'endless words' that are derided so much in the third season - can no longer address. Which I respect - to pose the question is vital, even if the tools can't reach any answers if they even exist.

I think this struggle exists in many stories that address themes of making a break from the rapacious society that created them (and take it seriously) - your Baru Cormorants and Mononoke-himes. We can describe the problem vividly, but since we do not have a counterexample to hand, any story we tell about ~what is to be done~ and what it will look like when it is feels like it will be just as hollow as the spins and angles and parasitic fantasies that so many characters advance in the Silt Verses. (How could there possibly be a time where it finally works out, after we have seen all this? But then, what are we living for?)

To try to make this a question and not a ramble, I wanted to ask - what do you see as the role of fiction in addressing the horrible machinery of this world? Is it enough to pose the question particularly sharply, skewer the bad and inadequate answers, and leave the readers/listeners to figure out how to make the killing of gods concrete? How do we punch through the bounds of it all being Content, another product to be bought and sold? What does it mean to sit here and fantasise about people making that revolutionary break when there is no revolution to be had?

I don't know what answer I'm hoping for here, but given the themes of the show, I feel like this must be a kind of thing you've thought about, and probably have a far more developed line of thought than I do. And if this is a bit too much to drop in your inbox on a Saturday morning, I will say again thank you for writing this story and all the actors for making it so strikingly concrete - it truly means a lot, and I will treasure it.

Hi, and thank you for listening and for a beautifully written and thoughtful ask! ('Horrible machinery of the world' stopped me dead in my tracks.) And I am very proud, genuinely.

I don't have a good enough answer to your questions, and for me a lot of TSV is very much about trying to figure those answers out, but let me try and sum up my perspective bit by bit.

Is it enough for fiction to pose the question, without also proposing the answer?

I don't think it's enough for fiction as a collective body of work.

I'd argue there's probably a tendency towards open-endedness and irresolution in these individual narratives simply because it feels like a more honest acknowledgement that in real life, the foe has yet to take a real body blow and will not go down easy; that the foe, in fact, is the marketplace for the work itself and ironically profits from the popularity of stories with easy heroic victories over villains who represent capitalism. That these stories inevitably become a pleasant consumable that serves our complacency within the belly of the beast, a kind of daily tonic to reassure us that good always triumphs and regular people always come out on top.

I also think that the sheer scale and scope of the topic creates its own challenges; you probably can't engage thoroughly enough with both the dystopian question and your ideas for a utopian answer all in a single story, without ultimately turning the latter into that false reassurance, a quick handwave of a happy ending.

You mention Omelas, and I think we could illustrate the problem by looking at how LeGuin handles her two successive masterpieces:

The Ones Who Walk Away From Omelas, which gives us the titular resource-rich u(dys)topia built on invisible suffering, and the dissidents who turn their backs on that world and walk out into the inhospitable wilderness in search of something better.

The Dispossessed, which as its premise gives us Anarres, an imperfect but sympathetic anarchist society whose adherents turned their backs on a neighbouring world of capitalist plenty to live out in the inhospitable wilderness in search of something better.

Anarres can very reasonably be viewed as LeGuin's direct answer to the question posed by Omelas, and she would have likely had it in her mind already as she wrote Omelas. But if the short story had ended with 'I hear that against all odds, the ones who walk away have successfully founded an anarchist utopia where hardship is everywhere but it's shared as equitably as possible. THE END', the amount of lazy shorthand and empty comfort involved in that happier ending would inevitably make it a dishonest and unserious offering.

Instead, Anarres is a starting premise to be interrogated at length over the course of a separate story, rather than a happy ending to simply reassure the reader that better things are possible - and even at the end of the novel LeGuin's unresolved questions are still very similar to the ones that we're left with in Omelas (and the same questions that I feel like we were knocking about in The Silt Verses, and which I guess you could argue are all lingering concerns at the end of Mononoke, as well): how and where can we find space to create and sustain a genuine alternative when the narrative environment of capitalism is so powerfully all-subsuming and constantly growing to fill the space? Do we need to disconnect entirely, vanishing as if dead? If we disconnect, how can we possibly survive and what inhumanities or ethical compromises will be required of us? If we do survive, is our isolationism a dereliction of human responsibility to those left behind?

All of which is to say that I think present-day fiction absolutely can make the attempt to meaningfully explore potential alternative-utopian solutions in more depth and with far more tangibility than we attempted with TSV - but that dystopian fiction like ours which concludes with the unexplored promise of a revolutionary utopia and the vague reassurance that the irrepressible human spirit will figure things out from here on out (Chewbacca gets a medal, everyone's in the streets wearing a Guy Fawkes mask) doesn't do much more than dramatically undermine its own goal of disrupting the audience's comfort.

That said, one of my big regrets this season was that we didn't succeed in more engagingly exploring and articulating the Woundtree camp's development into a flawed but functioning society in Dispossessed fashion ahead of the ending. That was my intention, but what quickly became clear was that in a dramatic format, with a limited cast, it was just endless static meeting-room scenes with Paige and Elgin discussing difficult responses to impossible challenges, while everyone else was out having dynamic and exciting adventures with lots of fun and exciting gods. Dystopias remain too entertaining for utopias' own good.

What do you see as the role of fiction in addressing the horrible machinery of this world?

I believe that absurdist horror fiction specifically, founded on the principle of 'people in a world that makes no sense, deluding themselves that it definitely does make sense' can play a very powerful role in that stated purpose.

Many horror traditions carry the baggage of inbuilt or inadvertent conservatism - the concept of a peaceable, passive, safe, middle-class Normality which is then disrupted by a terrifying outside threat (alien, ultra-foreign, ultra-low-class, underworldly, wild, etc). But absurdist horror very directly identifies Normality as the true source of our terror and very directly confronts our human response to it. It creates the right environment for us to ask all of the good questions. Isn't this an unsustainable nightmare we're living in? Why are we expending so much energy pretending it isn't? How do we get out and what do we do if we can't?

Probably the only listener reaction that's genuinely frustrated me about both of our shows is the folks who come away turning their noses up at the bluntness of that approach and acting like they've Solved The Art simply for figuring out where our broad sympathies lie. "Hm, just listened to The Silt Verses and I understood it at once; it's clearly trying to say that capitalism is bad. A little heavy-handed in its messaging for my liking, hm-hm!"

Not to go full Garth Marenghi, but for me the directness of the provocation and the obvious outrageousness of the nightmare is the point; it then allows us to go to places that other genres (or more understated critiques) generally can't.

How do we punch through the bounds of it all being Content, another product to be bought and sold? What does it mean to sit here and fantasise about people making that revolutionary break when there is no revolution to be had?

God, I don't know.

Maybe it means nothing; maybe we can't punch through; maybe there is no story unruly enough to be truly unco-optable, and therefore even the most radical fiction ultimately serves as a distraction, a placebo, a reassurance (that we are not alone, that better things are possible) which will impact the wider world more by keeping us subscribed to the Kindle app than by any action we might feel inspired to take.

Amazon is paying Boots Riley to make TV shows. Disney won much praise for delivering a revolutionary fantasy in a Star Wars shell. Apple is funding excellent, discomfiting and furious corporate satires about how we happily ignore invisible worker abuses for the sake of our own lifestyles, but they also cannot be considered accountable for the deaths of Congolese child-labourers in the global cobalt supply chain. The Dispossessed is in development as a limited series and the LeGuin estate are closely involved.

The master doesn't just own the tools, he's been buying up the guillotines as well.

What if, as with the unknowable nothingness outside of Omelas, the only art that cannot be reduced to product in net service of the status quo is the art that's so invisible and inaccessible and disconnected as to not exist at all? Does being relatively small and ramshackle really lend us any ideological purity, any genuine detachment? You can listen to The Silt Verses on Apple and Spotify and Amazon Music. Brought to you by Acast.

Chapter 36 with Dev and Seb was to a large extent intended as an articulation of that worry. To what extent can we still trust in the integrity of a sincere love story (one that we want to believe in) it if takes place in an insincere and predatory environment? Can any meaningful story be told honestly within such a space?

This stuff really worries me. I think it's probably right to worry. I don't know the answer. I do know that there are some folks for whom the show has made a tangible difference in terms of their life's direction, and that's a huge comfort to me.

There was someone who said it helped them find their faith, strangely and wonderfully. Someone else who said it contributed to their decision not to go down a more lucrative career path within what they view as an exploitative industry. (I hope they don't regret that decision; I hope it makes them happy.)

So there's something there. Maybe.

[psychreviews2]

The Presocratics: Pythagoras and Pythagoreans

Pythagoras of Samos

One of the most influential, and ironically, one of the most enigmatic Greek philosophers was Pythagoras. Why he was so influential was partly the large following that existed after his era. In A History Of Pythagoreanism, Carl A. Huffman says that "the historical Pythagoras may not be as important as the reactions to him."

As typical of pre-Socratic philosophers, there is little concrete evidence about the man himself. One is forced to focus on a mixture of truth and legend to get the full impact. For example, the Pythagorean theorem:

Pythagorean theorem, addition of volumes as an animation with alternating twist By Petrus3743 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=62590831

Historians debate on its origination and either conclude that it was used as far back as ancient Babylonia, 1,000 years before Pythagoras, or that it was discovered in many places independently. This isn't a new phenomenon for pre-Socratics, to have many discoveries attributed to them, and even more so for Pythagoras.

In McKirahan's works, Huffman, and also Kirk and Raven, Pythagoras was born on the island of Samos around the 6th century B.C. Tradition describes his father as a gemcutter or an engraver. He may have made travels to Egypt and learned astronomy and geometry there. In Babylonia he learned of mathematics and music. Eventually, he moved from Samos to Croton in southern Italy after escaping a tyrant named Polycrates. As legends of Pythagoras developed over centuries, his descriptions elevated to that of a charismatic leader or a deity. "When he disembarked in Italy and arrived in Croton...they were struck by his appearance: he had the look of a gentleman of liberal birth, with a gracious and orderly manner, voice and everything, and he seemed like someone well-travelled, naturally blessed by fortune and remarkably gifted in every way. Such an effect did he have on the city of Crotonians that when he had inspired the council of elder statesmen that was in charge of the city, by presenting a range of admirable ideas to them, the rulers then appointed him to deliver a youth mission program to the adolescents. And after that he was asked to address the children from the schools all congregated together, and then the women." Legends arose about Pythagoras in Croton including:

Killing a poisonous snake by biting it

A river hailed him by name

He made earthquake predictions

He could appear in two different places at the same time

He had a golden thigh

The people of Croton addressed him as Apollo from Beyond the North Wind

Around the time of his arrival in Croton, the people there had suffered a defeat in battle and were looking for a leader. Pythagoras influenced them and founded an influential cult that was philosophical, religious, but also political. He created a religious aristocracy based on a proto-communism where followers would have to give up their private property to join them. A form of tithing. The followers had duties based on their age group. Women were identified based on age, marriage, and if they had children. Men were classified based on the seasons. Penalties, fines, and if the story of Hippasus is correct, death would await those who divulged important Pythagorean principles. Worship of the Gods, moderation, silence, and purification were emphasized. As you can see, the modern-day doxing that people brandish everywhere in politics has always existed in one form or another.

The problem here, and even the problem today, is what is good leadership? The ancient Greeks had to feed just like we do, but populations are full of leaders and followers. Not everyone has the same energy or motivation to guide themselves. When leaders take charge, a lot of our feeding comes from them. Like a pet, an animal could do the difficult thing and provide its own feeding, or look to an owner to provide the feeding for free. The animal is freer, but also has more responsibilities in the wild. Conversely, the animal is less responsible, less free if its only source of feeding comes from an owner. Then how can it live if there are threats of abandonment? When the animal is finally domesticated, the skills to be able to live in the wild fade. Yet if there's still a little wildness left to direct one's own life, one can rebel against social controls and escape.

Philosopher Kings and Queens Today [Globalism vs Nationalism]:

Johnny Rotten 'Let me Finish!': https://youtu.be/v1uOwz_UrQ0

Nigel Farage - U.S. Election: https://youtu.be/fHiIQkDzqnQ

Trump YMCA Dancing Compilation: https://youtu.be/FBvoU-UiW84

"China ate your lunch Joe!" - 2020 Debate: https://youtu.be/KKwbWmWJ-ck

Justin Trudeau - Opportunity for a reset: https://youtu.be/n2fp0Jeyjvw

Prince Charles Says Pandemic a Chance to 'Think Big and Act Now’: https://youtu.be/BucTwPegW5k

China offers world its COVID QR code - The Register: https://www.theregister.com/2020/11/23/g20_leaders_meeting_tech_emphases/

Hillary Clinton "This would be a terrible crisis to waste": https://youtu.be/BMT05bpPb10

Tapper asks Gates when he thinks we'll be back to 'normal.' [2022]: https://youtu.be/dCt23D8VXpc

Humans are no different. Those at the top can easily exploit the production of others, regardless of whether one calls the system a "commune" or something else. If the leverage a leader has i.e. skills, advantages, and connections, it can make people tolerate their servitude. Then that friction from the power differential yields an abundance of goods for the leader. In the modern-day of representative democracies and lingering totalitarian states, the question is how accountable and responsible are our governments to the people? The debate involves many leaders in local, regional, and national governments. The next level beyond those is continental or global governances.

One of the two arguments is that governments that are close to the concerns of the governed work much more fairly than governments that are distant from sources of problems. The other argument is that there are people with a Philosopher King level of knowledge, that are capable of seeing the forest without getting lost in the trees in parochial concerns. Ultimately, the weak areas in any argument will be the level of corruption that discloses itself to the populace at any given time. The battle continues on how to live well along with others.

Despite the cult's attempts at being secretive, Pythagoras became famous and what is a common pattern throughout history is that when power shifts and consolidates, the public want to know more about you, and there's often a strong push back against inequities or claims of unfairness. What historians think is a conflation of many events into legend, tell the story of a Cylon who was rejected by the Pythagoreans, and who enlisted anti-Pythagorean support to destroy their community and end their influence. The sources vary wildly on how Pythagoras died. He was either killed, escaped and committed suicide, or starved to death.

Transmigration of the souls

According to tradition, Pythagorean principles were kept secret within the community and were never written down, but after Pythagoras died his ideas spread and likely went through many modifications. Pythagoras also left behind an impression on other pre-Socratic philosophers, and these were often negative in tone. Both Heraclitus and Xenophanes ridiculed his ideas.

"Pythagoras...practiced historical inquiry more than all other men, and making a selection of these writings constructed his own wisdom, polymathy, evil trickery." - Heraclitus.

"Now I will turn to another tale and show the way...Once they said that he was passing by when a puppy was being whipped, and he took pity and said: 'Stop, do not beat it; for it is the soul of a friend that I recognized when I heard its cry.'" - Xenophanes

"Much learning does not teach understanding, otherwise it would have taught Hesiod and Pythagoras, and also Xenophanes and Hecataeus." - Heraclitus

This provides clues to Pythagorean culture and their penchant for mixing mathematics with moral philosophy based on the transmigration of the souls, an idea possibly influenced by Pherecydes of Syros. Porphyrius described this transcendent belief. "...First, that he maintains that the soul is immortal; next, that it changes into other kinds of living things; also that events recur in certain cycles, and that nothing is ever absolutely new; and finally, that all living things should be regarded as akin. Pythagoras seems to have been the first to bring these beliefs into Greece."

Diogenes Laertius, in Lives of the Philosophers, recounts Pythagoras's purported past lives:

"Once he had been born Aethalides and was believed to be the son of Hermes. When Hermes told him to choose whatever he wanted except immortality, he asked to retain both alive and dead the memory of what happened to him...Afterwards he entered into Euphorbus and was wounded by Menelaus. Euphorbus [remembered] he had been born as Aethalides and received the gift from Hermes, and told of the migration of his soul and what plants and animals it had belonged to and all it had experienced in Hades. When Euphorbus died his soul entered Hermotimus, who, wishing to provide evidence, went to Branchidae, entered the sanctuary of Apollo, and showed the shield Menelaus had dedicated. (He said that when Menelaus was sailing away from Troy he dedicated the shield to Apollo.) The shield had already rotted away and only the ivory facing was preserved. When Hermotimus died, [the soul] became Pyrrhus the Delia fisherman, and again [he] remembered everything...When Pyrrhus died [the soul] became Pythagoras and remembered all that has been said."

The effect of these beliefs on followers was to create an ethical austerity based on the fear of harming reincarnated lives. Are you eating an animal that is a distant relative? How would you like being eaten? Increasing your purity, or decreasing it, could conceivably lead to better or worse future lives. "By contemplating the principle of order revealed in the universe - and especially in the regular movements of the heavenly bodies - and by assimilating himself to that orderliness, man himself was progressively purified until he eventually escaped from the cycle of birth and attained immortality."

Many superstitions developed from this belief in the transmigration of souls and added up to an ethical code of conduct. Here's a sample:

Vegetarianism.

Avoid butchers and huntsmen.

Do not eat beans. [This may have been due to people becoming ill with fava beans from southern Italy in particular.]

Sacrifice only inanimate things.

Sacrifice and worship without shoes on.

Cut not your finger-nails at a sacrifice.

Turn aside from highways and walk by footpaths.

Help a man who is loading freight, but not one who is unloading.

Speak not of Pythagorean matters without light.

Never step over a cross-bar.

When you are out from home, look not back, for the Furies come after you...

Do not wear a ring...

Disbelieve nothing strange about the gods or about religious beliefs.

Be not possessed by irrepressible mirth.

Like the Egyptians, do not bury the dead in woolen clothing.

Make your bed.

Mathematics

We can't attribute a unifying Pythagorean theory that encompasses mathematics and morality, but his later influences wrestled with both and broke into different groups. Kirk and Raven said that "after the death of Pythagoras, his school apparently split into two sects, one of which, the so-called 'Acousmatics' or 'Pythagorists', preserved the mystical side of his teaching, while the other, the 'Mathematicians', concentrated on the scientific side...Central notions, which held together the two strands that were later to fall apart, seem to have been those of contemplation, an orderliness found in the arrangement of the universe and purification."

With these rituals involving an element of measurement and music, it was possible to imagine limited notes on an unlimited scale, similar to Anaximander's bound and boundless. "The two most fundamental and universal of Pythagorean scientific doctrines are, first, the ultimate dualism between Limit and Unlimited, and second, the equation of things with numbers. What is required, therefore, is a plausible explanation of how these two doctrines, by no means obviously interdependent, should have occurred to Pythagoras or his followers. There seems no reason to doubt the tradition that Pythagoras himself discovered - probably by measuring the appropriate lengths of string on a monochord - that the chief musical intervals are expressible in simple numerical ratios between the first four integers. This single discovery would account naturally for all the most characteristic of Pythagorean doctrines. If the musical scale depends simply upon the imposition of definite proportions on the indefinite continuum of sound between high and low, might not the same principles, Limit and the Unlimited, underlie the whole universe? If numbers alone are sufficient to explain the 'consonances', might not everything else be likewise expressible as a number or a proportion? Moreover, since the first four integers contain the whole secret of the musical scale, their sum, the number 10 or the Decad, might well 'seem to embrace', as Aristotle puts it, 'whole nature of number' and so come to be regarded, as it certainly was, with veneration. It is not surprising, therefore, that both mathematics and music should have played from the outset so vital a part in Pythagoreanism."

As we can see, geometry also fits into the concept of bound and boundless by having limited objects in an unlimited space. The triangle could be used for counting, but the square or rectangle could be used to analyze odds and evens. The rectangle starting with an even number could predict successive even numbers. The square starting with one unit could predict the next series of odd numbers. Very easily, these unit-points could be used as measurements for physical matter. Kirk and Raven said that "these unit-points functioned also as the basis of physical matter: they were regarded in fact as a primitive form of atom. When, therefore, Aristotle speaks of number as, 'functioning as the material element in things', or when, as he often does, he asserts that the Pythagoreans regarded the universe as consisting of numbers, he means that concrete objects were literally composed of aggregations of unit-point atoms...[or] each object consisted of a definite number of unit-point-atoms."

The universe's beginning is tantalizingly described in the same way. "The Even was said to be 'taken in and limited by the Odd', so in 'the nearest part of the Unlimited was drawn in and limited by the first unit functioning as Limit."

Aristotle described the general Pythagorean view of the building blocks of the universe. "[They] thought that the limited and the unlimited and the number one were not some different natures, like fire or earth or anything else of this kind, but that the unlimited and number one for itself were the substance of the things of which they are predicated, and that for this reason also number is the substance of all things."

Using measurement, ritual, and purification influenced later Pythagoreans. Like in Zoroastrianism, it's quite easy to look at good measurements versus bad and to create mathematical ethics based on proportionality.

Alcmaeon

Pythagoras's influence of measurement and ethics continued with Alcmaeon of Croton who was born around the early 5th century B.C. Focusing on early biology and medicine, Alcmaeon looked at perception through the understanding of dualism.

"The majority of human affairs are in pairs."

This extended into his method of diagnosis. "Alcmaeon maintains that the bond of health is the 'equal balance' of the powers, moist and dry, cold and hot, bitter and sweet, and the rest, while the 'supremacy' of one of them is the cause of disease; for the supremacy of either is destructive. Illness comes about directly through excess of heat or cold, indirectly through [too much] or [too little] nourishment...Health on the other hand is the proportionate admixture of the qualities."

Pythagoreans and Aristotle

The difficulty with delineating what Pythagoras believed, since we have no original writings, is how reverence for him allowed followers to slip in their own beliefs, and by attributing these discoveries to Pythagoras, one could appeal to authority to gain followers. This was already a problem for Aristotle in his time, who did a review of Pythagorean beliefs which conflated different ideas that were probably associated with many different individuals. His survey is still helpful to see what these beliefs were even if attribution is impossible to determine.

One of the developments in mathematics was increasing the significance of the number one. Going from a breath of limit coming out of unlimited space was criticized by followers of Parmenides. The significance of the number one as an odd number increases when it is treated as a facilitator of both even and odd numbers, leaving the number three as the actual starting point of odd numbers.

"The first division of numbers that they make is into two classes, calling some even, some odd. Even numbers are those which can be divided into equal parts (e.g. 2 or 4), odd those which can be divided only into unequal parts (e.g. 5 or 7). Some held that the first of the odd numbers is 1. For even is the contrary of odd; [The number one] cannot be divided at all...If you add even to even, the whole is even; but add 1 to an even number and it makes the whole odd; whence it follows that 1 is not even but odd. Aristotle, however, in his work on the Pythagoreans, says that 1 partakes of the nature of both; for when added to an even number it makes it odd, when added to an odd, even - which would be impossible if it did not partake of the nature of both; and so, he says, it is called even-odd." For Kirk and Raven, finding a bridge between even and odd with the number 1 helps to counter Parmenidian criticisms of a limit coming out of an unlimited.

The value of number for the Pythagorean Philolaus is such that we cannot think or understand without it. "And all things that can be known contain number; without this nothing could be thought or known." Using numbers connected with abstract pictures Philolaus would map out the most basic perceptions of shapes that would register for us what kind of object is being displayed, almost like an early game of charades. "For the sake of argument let the definition of man be the number 250 and that of plant 360. Having settled that, he used to take 250 pebbles, some green, some black, others red and, in short, a variety of colours. Then he would smear the wall with unslaked lime and make a shaded drawing of a man or a plant; some pebbles he fixed in the drawing of the face, others in the hands, and others elsewhere, until he had completed the drawing of a man in the number of pebbles equal to the number of units which he claimed to define man."

Pythagoreans were also interested in astronomy and naturally used numbers to explain harmony. Part of the understanding of harmony for Pythagoreans came from harmonious musical intervals. Musical intervals involve proportion and for the cosmos to maintain harmony, planets would also need to retain harmonious proportions. For example on a musical scale, letters separate one octave (or 8 notes). Eg. On a C major scale: C D E F G A B C. On the same scale, a perfect 4th would be from C D E F G A B C, and a perfect 5th from C D E F G A B C. In mathematical proportions, the frequency ratios are 2:1 for an octave, 4:3 for a fourth, and 3:2 for a fifth. If you add 1 plus 2 for the octave plus 3 for a fifth and four for a fourth, you get the mystical 10.

Kirk and Raven connect both musical measurements with planetary ones by asking, "if numbers alone are sufficient to explain the 'consonances', might not everything else be likewise expressible as a number or a proportion?"

Octave intervals - Liberty Park Music: https://youtu.be/fV-p9n7upMc

The Very Best Explanation of Perfect 4th's and Augmented 4th's - Taylor Dietz: https://youtu.be/5Xm8qKMiWOQ

Perfect fifths - Piano Wallaby: https://youtu.be/x4Ah37OU9ps

When looking at the cosmos Pythagoreans like Philoaus would return to the mystical number 10, and try to fit it into the theory. "Philolaus places fire around the centre of the universe, and calls it the 'Hearth of the world', the 'House of Zeus', 'Mother of the Gods', 'altar, bond and measure of nature.' Then again there is another fire enveloping the universe at the circumference. But he says that the centre is by nature primary, and around the centre ten divine bodies dance, first the sphere of the fixed stars, then the five planets, next the sun, then the moon, then the earth, then the counter-earth..." Here we have a strange hearth-centred universe that everything orbits, including the sun, with a counter-earth to provide explanations for eclipses and also to provide the sacred number ten. The hearth here represents the important number one of limit versus unlimited.

Music and proportion complete their value in the cosmos and also within the body and mind. "The Pythagoreans, according to Aristoxenus, practised the purification of the body by medicine, that of the soul by music."

Later influences

Proportionality, mathematics, measurement, architecture, and lifestyle changes continued their influences throughout late-antiquity and into the renaissance. At these later stages of influence, one can see people picking and choosing which principles they wanted and mixing them with contemporary beliefs. For example, Milo of Croton, an athlete who styled himself as Heracles, led the battle of Crotonites against the Sybarites, wore a lion skin, and carried a club. Instead of being vegetarian, he was called by Aristotle "Big Eater" who ate 9 kg of meat and bread per day and drank ten litres of wine. Iccus of Tarentum, an Olympian victor, and teacher of gymnastics, instead led a life of moderation and sexual abstinence. His type of frugal meal was called by Greeks "an Iccus meal." The Pythagorean Archytas was an army commander and mathematician. He was also suspected of being an influence on Plato, so you can add philosophy to his resumé. Pythagoras's influences even include Copernicus, Newton, and writers such as Dante and Ovid. The ultimate influence of Pythagoras is for those who learn about the world but also go one step further to find the harmony that is being signaled to us, and to live according to those signals. If there are limits that come out of an unlimited, which limits are good for us and which are not?

Plato's test for leadership

Coming back to the question of what makes a good leader I think would naturally be answered by most people that a good leader is a catalyst for group success. Plato believed in a Philosopher King that had this ability to see the ultimate good and would himself refrain from what he called "appetitiveness." Appetites, cravings, and desires make for the cause of corruption, and any individual who has cravings, when they finally gain enormous power, will have strong impulses aiming to indulge. This was a concern for Plato, and one of his Pythagorean influences on his work may have come from Archytas, as described above.

A Pythagorean could be like a proto-Philosopher King for someone like Plato. A person who follows principles with a mathematical lens. To Plato, this leader would have a superior view of the whole of the city-state. Mathematical principles, principles that are harmonious with the universe would dictate that to the populace and make for a flourishing society. The problem he had was getting concepts into the soul of a learner. If it did not reach the stage of Understanding, meaning that quick flash of knowing that happens to people when they know many angles of a subject. They really know it. Plato listed those angles in 5 stages; stages that would be typical of someone learning mathematics.

"Everything that exists has three elements through which one must approach the knowledge of that thing; the fourth element is knowledge itself, and the fifth, one must posit, is that which is in fact knowable and true. The first of these is 'name,' the second is 'definition,' the third is 'image,' and the fourth is 'knowledge'...Eg. There is something called a circle, the name of which is the same thing I have just pronounced. Its definition is the second thing, and it is composed of nouns and verbs: 'that which is completely equal from every extremity to the middle' would be the definition of that thing that is called 'round,' 'spherical,' and 'circle.' The third element (the image) may be painted and expunged, lathed and destroyed, but the circle itself, which all these things represent, undergoes none of these changes, since it is something other than these things. The fourth element is knowledge and understanding and a true conception of these things. And since we must establish that these are all a single thing – something that resides not in sounds or shapes of bodies but within souls – it is clear that it differs both from the nature of the circle itself and from the three elements mentioned above. And of these, understanding comes closest to the fifth in likeness and affinity, while all the others remain quite far off..."

"And if we force someone to distinguish and explain the fifth, whoever is willing and able to upend the argument wins, and he makes the one who is offering a full interpretation through speech, writing, or actual answers appear, to most of his audience, to know nothing of the things about which he is trying to write or speak, since the audience is sometimes unaware that it is not the soul of the writer or speaker that is being refuted, but rather the nature of each of the four things, which is inherently flawed. Nevertheless, the thorough examination of all these problems, going up and down and over each one with great effort, imparts knowledge of a good thing unto a person of a good nature. If one’s nature is bad, however, as is the condition of most souls with respect both to learning and to what are called ‘morals,’ all these things wither and die...Whenever we look at a written composition, whether it be the laws of a lawmaker or anything else whatsoever, we must recognize that the author’s most serious ideas do not reside within this text, even if the author himself is serious, but that those ideas remain lodged in the most beautiful part of his soul."

The problem with theory is that it has to be tested by reality. In the controversial Seventh Letter, Plato recounted his disillusionment when he was requested to help free Sicily from a tyrannical government. "When I came I was in no wise pleased at all with 'the blissful life,' as it is there termed, replete as it is with Italian and Syracusan banquetings; for thus one's existence is spent in gorging food twice a day and never sleeping alone at night, and all the practices which accompany this mode of living. For not a single man of all who lives beneath the heavens could ever become wise if these were his practices from his youth, since none will be found to possess a nature so admirably compounded; nor would he ever be likely to become temperate; and the same may truly be said of all other forms of virtue. And no State would remain stable under laws of any kind if its citizens while supposing that they ought to spend everywhere to excess, yet believed that they ought to cease from all exertion except feastings and drinkings and the vigorous pursuit of their amours. Of necessity, these States never cease changing into tyrannies, oligarchies, and democracies, and the men who hold power in them cannot endure so much as the mention of the name of a just government with equal laws."

Plato worked with an ardent follower Dion to train the tyrant of Syracuse, Dionysius, to follow just laws instead of appetites, but at every turn his friend Dion would be accused of trying to usurp the throne. The problem that Plato had was that desires are also with the subjects of the tyrant and they benefit from the appetites of the leader, and in turn they benefit by how the leader provides for their appetites. Partly people can look at the motivations of others through the lens of their own desires with projection. If Dion was advising Dionysius, in the same manner as his followers, it would be a great temptation to usurp his power in their perspective and gain all the spoils. Also, any threat of self-discipline would be an immediate threat for those followers who love pleasure above all. On the other hand, with wisdom, many people learn to enjoy making decisions for oneself and hate dependency on tyrants. It's an acquired taste as Plato found out.

"Dion was an astute student of all things, including the arguments that I presented at the time, and he listened with such extraordinary acumen, like no other young man I’ve ever met, and he desired to live the remainder of his life differently from the majority of Italians and Sicilians, loving virtue more than pleasure or any other extravagance. As a result, he began to pass his time in a way that was obnoxious to those who were living according to the customs of the tyranny up until the death of Dionysius."

The accusations against Dion were believed and ultimately he was exiled and his property was sold to others. Plato was in a back and forth between himself and Dionysius, and after Dionysius cut the pay of his infantry, Plato was also made into a target of blame by them along with the tyrant. Plato eventually escaped with the help of Archytas. After all his trials and tribulations, he recommended what most advice-givers recommend, which is to not give advice to people who don't want to hear it. Unless leaders are able to govern themselves by crystallizing principles up to Plato's 5th level, they would have to put laws above themselves and role-model the correct behaviors for the rest of the population. Of course, any double-standards chip away at the motivation for anyone else to follow the rules.

New Jersey Governor Phil Murphy confronted while having dinner with his maskless family: https://dailycaller.com/2020/11/22/phil-murphy-new-jersey-covid-coronavirus-mask/

Whether there is a constitution to hold leaders accountable or not, Philosopher Kings ultimately have to internalize those behaviors against temptation. What people have to worry about is why people want power in the first place? That motivation there is often where the double-standards begin and conflict thereafter. Leaders love exclusivity and it's a major motivation for applying to powerful positions. Why take on more responsibility without more rewards? What hasn't changed since ancient times is the terror that people feel when acquiring money and positions. Personal political or philosophical opinions are often based on self-interest, and those who hold the purse strings have the freedom to disobey laws, and the power to make those dependent on them to obey under threat of coercion.

Plato said: "Neither Sicily, nor yet any other State—such is my doctrine—should be enslaved to human despots but rather to laws; for such slavery is good neither for those who enslave nor those who are enslaved...If the victors yield to the laws more than the vanquished do, then a refuge from all evil and a full share of salvation and happiness will be provided."

The Presocratic Philosophers - G.S. Kirk: https://www.isbns.net/isbn/9780521274555/

A History of Pythagoreanism - Carl Huffman: https://www.isbns.net/isbn/9781316648476/

Philosophy before Socrates - Richard McKirahan: https://www.isbns.net/isbn/9781603841825/

A Presocratic Reader - Richard McKirahan: https://www.isbns.net/isbn/9781603843058/

The Complete Pythagoras - Mohamed Amer: https://ia800704.us.archive.org/31/items/CompletePythagoras/CompletePythagoras.pdf

Plato at Syracuse - Various authors: https://www.isbns.net/isbn/9781316648476/

Plato, Epistles: Letter 7: http://www.perseus.tufts.edu/hopper/text?doc=Perseus:text:1999.01.0164:letter=7

Philosophy: http://psychreviews.org/category/philosophy03/

[forbidden-sorcery]

By the middle imperial period the legendary Pythagoras, supposedly a citizen of Samos under the tyrant Polycrates, whose supposed floruit was 535-522 BC, had himself come to be seen and projected as a full blown mage or sorcerer. Diogenes Laertius, for instance, writing in the early 3rd century BC, tells us both that he associated with Chaldeans and mages, and also that he learned the Egyptian language, descended into Egyptian crypts and (presumably in them) learned the secrets of the gods. Accordingly, representations of Pythagoras’ remote disciples in the imperial age also often project them as sorcerors, be it positively, negatively, or ironically.                Lucian has preserved for us a pair of Pythagorean portraits of particular interest. In his Philopseudes we meet Arignotus, who is a typical long-haired ascetic Pythagorean in appearance. He claims to have cleansed a haunted house owned by one Eubatides in Corinth of its occupying ghost. The house, as he tells the tales, has with its terrors driven away all who attempted to occupy it, and in consequence has long been unoccupied and derelict. On learning of this, Arignotus takes up his Egyptian spell-books and determines to spend the night in the house, despite attempts to deter him. He settles himself down to read by the light of his lamp in the largest room. In due course the ghost materializes, ready to attack. It is squalid and long-haired, and blacker than the dark. The ghost attacks Arignotus from all sides, transforming itself now into a dog, now a bull, now a lion. But Arignotus deploys against it his most blood-curdling Egyptian language spell and drives the ghost down into the ground into a corner of the dark room, noting the spot where it disappears. Against the expectation of those around he emerges safe and sound from the house in the morning. He goes straight to Eubatides with the news that the house is now purified of its terrors. He takes him and a large number of others back to the house and bids them to dig in the spot where he has seen the ghost go down. Some six feet under they find a mouldy and skeletal corpse. They take it out and give it proper burial elsewhere, thus laying to rest the unquiet spirit to which it had been giving rise.

Daniel Ogden - Night’s Black Agents: Witches, Wizards and the Dead in the Ancient World

[thesciencenut]

Continuation of the earlier post.

In the earlier post, I was talking about the great mathematicians of the world. In this post, I am gonna talk about - Archimedes and Pythagoras.

ARCHIMEDES

Archimedes was the most-famous mathematician and inventor in ancient Greece. Archimedes is especially important for his discovery of the relation between the surface and volume of a sphere and its circumscribing cylinder.He is known for his formulation of a hydrostatic principle (known as Archimedes’ principle) and a device for raising water, still used in developing countries, known as the Archimedes screw. Archimedes probably spent some time in Egypt early in his career, but he resided for most of his life in Syracuse, the principal Greek city-state in Sicily, where he was on intimate terms with its king, Hieron II. Archimedes published his works in the form of correspondence with the principal mathematicians of his time, including the Alexandrian scholars Conon of Samos and Eratosthenes of Cyrene. He played an important role in the defense of Syracuse against the siege laid by the Romans in 213 BCE by constructing war machines so effective that they long delayed the capture of the city. When Syracuse eventually fell to the Roman general Marcus Claudius Marcellus in the autumn of 212 or spring of 211 BCE, Archimedes was killed in the sack of the city.

TOP QUESTIONS

What was Archimedes’ profession? When and how did it begin?

What accomplishments was Archimedes known for?

What specific works did Archimedes create?

What is known about Archimedes’ family, personal life, and early life?

Where was Archimedes born? How and where did he die?

Study how turning a helix enclosed in a circular pipe raises water in an Archimedes screw

Study how turning a helix enclosed in a circular pipe raises water in an Archimedes screw

An animation of Archimedes screw.

Encyclopædia Britannica, Inc.

See all videos for this article

Far more details survive about the life of Archimedes than about any other ancient scientist, but they are largely anecdotal, reflecting the impression that his mechanical genius made on the popular imagination. Thus, he is credited with inventing the Archimedes screw, and he is supposed to have made two “spheres” that Marcellus took back to Rome—one a star globe and the other a device (the details of which are uncertain) for mechanically representing the motions of the Sun, the Moon, and the planets. The story that he determined the proportion of gold and silver in a wreath made for Hieron by weighing it in water is probably true, but the version that has him leaping from the bath in which he supposedly got the idea and running naked through the streets shouting “Heurēka!” (“I have found it!”) is popular embellishment. Equally apocryphal are the stories that he used a huge array of mirrors to burn the Roman ships besieging Syracuse; that he said, “Give me a place to stand and I will move the Earth”; and that a Roman soldier killed him because he refused to leave his mathematical diagrams—although all are popular reflections of his real interest in catoptrics (the branch of optics dealing with the reflection of light from mirrors, plane or curved), mechanics, and pure mathematics.

According to Plutarch (c. 46–119 CE), Archimedes had so low an opinion of the kind of practical invention at which he excelled and to which he owed his contemporary fame that he left no written work on such subjects. While it is true that—apart from a dubious reference to a treatise, “On Sphere-Making”—all of his known works were of a theoretical character, his interest in mechanics nevertheless deeply influenced his mathematical thinking. Not only did he write works on theoretical mechanics and hydrostatics, but his treatise Method Concerning Mechanical Theorems shows that he used mechanical reasoning as a heuristic device for the discovery of new mathematical theorems.

Get exclusive access to content from our 1768 First Edition with your subscription.

Subscribe today

His Works

There are nine extant treatises by Archimedes in Greek. The principal results in On the Sphere and Cylinder (in two books) are that the surface area of any sphere of radius r is four times that of its greatest circle (in modern notation, S = 4πr2) and that the volume of a sphere is two-thirds that of the cylinder in which it is inscribed (leading immediately to the formula for the volume, V = 4/3πr3). Archimedes was proud enough of the latter discovery to leave instructions for his tomb to be marked with a sphere inscribed in a cylinder. Marcus Tullius Cicero (106–43 BCE) found the tomb, overgrown with vegetation, a century and a half after Archimedes’ death.

sphere with circumscribing cylinder

sphere with circumscribing cylinder

The volume of a sphere is 4πr3/3, and the volume of the circumscribing cylinder is 2πr3. The surface area of a sphere is 4πr2, and the surface area of the circumscribing cylinder is 6πr2. Hence, any sphere has both two-thirds the volume and two-thirds the surface area of its circumscribing cylinder.

Encyclopædia Britannica, Inc.

Measurement of the Circle is a fragment of a longer work in which π (pi), the ratio of the circumference to the diameter of a circle, is shown to lie between the limits of 3 10/71 and 3 1/7. Archimedes’ approach to determining π, which consists of inscribing and circumscribing regular polygons with a large number of sides, was followed by everyone until the development of infinite series expansions in India during the 15th century and in Europe during the 17th century. That work also contains accurate approximations (expressed as ratios of integers) to the square roots of 3 and several large numbers.

On Conoids and Spheroids deals with determining the volumes of the segments of solids formed by the revolution of a conic section (circle, ellipse, parabola, or hyperbola) about its axis. In modern terms, those are problems of integration. (See calculus.) On Spirals develops many properties of tangents to, and areas associated with, the spiral of Archimedes—i.e., the locus of a point moving with uniform speed along a straight line that itself is rotating with uniform speed about a fixed point. It was one of only a few curves beyond the straight line and the conic sections known in antiquity.

On the Equilibrium of Planes (or Centres of Gravity of Planes; in two books) is mainly concerned with establishing the centres of gravity of various rectilinear plane figures and segments of the parabola and the paraboloid. The first book purports to establish the “law of the lever” (magnitudes balance at distances from the fulcrum in inverse ratio to their weights), and it is mainly on the basis of that treatise that Archimedes has been called the founder of theoretical mechanics. Much of that book, however, is undoubtedly not authentic, consisting as it does of inept later additions or reworkings, and it seems likely that the basic principle of the law of the lever and—possibly—the concept of the centre of gravity were established on a mathematical basis by scholars earlier than Archimedes. His contribution was rather to extend those concepts to conic sections.

Quadrature of the Parabola demonstrates, first by “mechanical” means (as in Method, discussed below) and then by conventional geometric methods, that the area of any segment of a parabola is 4/3 of the area of the triangle having the same base and height as that segment. That is, again, a problem in integration.

The Sand-Reckoner is a small treatise that is a jeu d’esprit written for the layman—it is addressed to Gelon, son of Hieron—that nevertheless contains some profoundly original mathematics. Its object is to remedy the inadequacies of the Greek numerical notation system by showing how to express a huge number—the number of grains of sand that it would take to fill the whole of the universe. What Archimedes does, in effect, is to create a place-value system of notation, with a base of 100,000,000. (That was apparently a completely original idea, since he had no knowledge of the contemporary Babylonian place-value system with base 60.) The work is also of interest because it gives the most detailed surviving description of the heliocentric system of Aristarchus of Samos (c. 310–230 BCE) and because it contains an account of an ingenious procedure that Archimedes used to determine the Sun’s apparent diameter by observation with an instrument.

Method Concerning Mechanical Theorems describes a process of discovery in mathematics. It is the sole surviving work from antiquity, and one of the few from any period, that deals with this topic. In it Archimedes recounts how he used a “mechanical” method to arrive at some of his key discoveries, including the area of a parabolic segment and the surface area and volume of a sphere. The technique consists of dividing each of two figures into an infinite but equal number of infinitesimally thin strips, then “weighing” each corresponding pair of these strips against each other on a notional balance to obtain the ratio of the two original figures. Archimedes emphasizes that, though useful as a heuristic method, this procedure does not constitute a rigorous proof.

On Floating Bodies (in two books) survives only partly in Greek, the rest in medieval Latin translation from the Greek. It is the first known work on hydrostatics, of which Archimedes is recognized as the founder. Its purpose is to determine the positions that various solids will assume when floating in a fluid, according to their form and the variation in their specific gravities. In the first book various general principles are established, notably what has come to be known as Archimedes’ principle: a solid denser than a fluid will, when immersed in that fluid, be lighter by the weight of the fluid it displaces. The second book is a mathematical tour de force unmatched in antiquity and rarely equaled since. In it Archimedes determines the different positions of stability that a right paraboloid of revolution assumes when floating in a fluid of greater specific gravity, according to geometric and hydrostatic variations.

Archimedes is known, from references of later authors, to have written a number of other works that have not survived. Of particular interest are treatises on catoptrics, in which he discussed, among other things, the phenomenon of refraction; on the 13 semiregular (Archimedean) polyhedra (those bodies bounded by regular polygons, not necessarily all of the same type, that can be inscribed in a sphere); and the “Cattle Problem” (preserved in a Greek epigram), which poses a problem in indeterminate analysis, with eight unknowns. In addition to those, there survive several works in Arabic translation ascribed to Archimedes that cannot have been composed by him in their present form, although they may contain “Archimedean” elements. Those include a work on inscribing the regular heptagon in a circle; a collection of lemmas (propositions assumed to be true that are used to prove a theorem) and a book, On Touching Circles, both having to do with elementary plane geometry; and the Stomachion (parts of which also survive in Greek), dealing with a square divided into 14 pieces for a game or puzzle.

Archimedes’ mathematical proofs and presentation exhibit great boldness and originality of thought on the one hand and extreme rigour on the other, meeting the highest standards of contemporary geometry. While the Method shows that he arrived at the formulas for the surface area and volume of a sphere by “mechanical” reasoning involving infinitesimals, in his actual proofs of the results in Sphere and Cylinder he uses only the rigorous methods of successive finite approximation that had been invented by Eudoxus of Cnidus in the 4th century BCE. These methods, of which Archimedes was a master, are the standard procedure in all his works on higher geometry that deal with proving results about areas and volumes. Their mathematical rigour stands in strong contrast to the “proofs” of the first practitioners of integral calculus in the 17th century, when infinitesimals were reintroduced into mathematics. Yet Archimedes’ results are no less impressive than theirs. The same freedom from conventional ways of thinking is apparent in the arithmetical field in Sand-Reckoner, which shows a deep understanding of the nature of the numerical system.

In antiquity Archimedes was also known as an outstanding astronomer: his observations of solstices were used by Hipparchus (flourished c. 140 BCE), the foremost ancient astronomer. Very little is known of this side of Archimedes’ activity, although Sand-Reckoner reveals his keen astronomical interest and practical observational ability. There has, however, been handed down a set of numbers attributed to him giving the distances of the various heavenly bodies from Earth, which has been shown to be based not on observed astronomical data but on a “Pythagorean” theory associating the spatial intervals between the planets with musical intervals. Surprising though it is to find those metaphysical speculations in the work of a practicing astronomer, there is good reason to believe that their attribution to Archimedes is correct.

PYTHAGORAS

Pythagoras of Samos[a] (c. 570 – c. 495 BC)[b] was an ancient Ionian Greek philosopher and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of Plato, Aristotle, and, through them, Western philosophy. Knowledge of his life is clouded by legend, but he appears to have been the son of Mnesarchus, a gem-engraver on the island of Samos. Modern scholars disagree regarding Pythagoras's education and influences, but they do agree that, around 530 BC, he travelled to Croton in southern Italy, where he founded a school in which initiates were sworn to secrecy and lived a communal, ascetic lifestyle. This lifestyle entailed a number of dietary prohibitions, traditionally said to have included vegetarianism, although modern scholars doubt that he ever advocated for complete vegetarianism.

In the next post, I will be talking about ramanujan and shakuntala devi.

Follow me, stay tuned, next post will be uploaded soon.

[doubtconnect]

Understanding Pythagoras Theorem: Unlocking the Mysteries of Triangles

Pythagoras Theorem has captivated mathematicians and scientists for centuries, shedding light on the interconnectedness of geometric shapes and offering practical applications in various fields. In this article, we embark on a journey to understand the enigmatic power of Pythagorean mathematics, exploring its applications, historical context, and significance in the modern world.

Have you ever wondered how the length of one side of a right-angled triangle relates to the other two?

How do we calculate the length of the hypotenuse when we know the lengths of the other two sides?

Enter Pythagoras Theorem, a mathematical gem discovered by the ancient Greek mathematician Pythagoras around the 6th century BCE. Let’s embark on a journey to understand this theorem, its applications, and the profound impact it has had on the world of mathematics.

The Pythagorean Formula: Unleashing the Power of Right Triangles

In the realm of right triangles, Pythagoras Theorem reigns supreme. This elegant formula states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. In mathematical terms, it can be expressed as:

a² + b² = c²

Here, ‘a’ and ‘b’ represent the lengths of the two legs of the triangle, while ‘c’ represents the length of the hypotenuse. This theorem provides a powerful tool for solving various geometric problems, enabling us to unlock hidden dimensions and relationships within triangles.

Powerful Technique For Understanding Heredity And Evolution Class 10th

Exploring Real-World Applications

Pythagoras Theorem, while seemingly abstract, finds practical applications in numerous fields. Let’s take a look at some real-world scenarios where this theorem comes into play:

1 Architecture and Construction: Architects and engineers rely on Pythagoras Theorem from towering skyscrapers to intricate bridges to ensure structural integrity. By calculating the diagonal distances, they can determine the lengths needed for beams, cables, and supports, making sure that buildings can withstand external forces.

2 Navigation and GPS: Pythagoras Theorem is at work in the realm of navigation. GPS systems utilize the theorem to calculate distances between satellites and receivers, enabling accurate positioning and providing directions for travelers worldwide.

3 Sports and Recreation: Ever wondered how far you hit that golf ball? Pythagoras Theorem can help! By measuring the horizontal and vertical components of the shot, the theorem can determine the distance covered.

Do 12th Marks Really Matter in Life? Unlocking the Truth & Debunking the Myth

Pythagoras and the Historical Significance

To truly grasp the significance of Pythagoras Theorem, we must delve into the historical context surrounding its discovery. Pythagoras, an ancient Greek philosopher, mathematician, and founder of the Pythagorean school, revolutionized the world of mathematics with his insights.

Born around 570 BCE on the island of Samos, Pythagoras left a lasting legacy that stretched far beyond numbers and shapes. His teachings encompassed a wide range of disciplines, including music, philosophy, and spirituality. The Pythagorean school, known for its emphasis on the harmony of numbers and the pursuit of wisdom, propagated Pythagoras’ theories and contributed to the development of mathematics.

Modern Applications and Advancements

Fast forward to the present day, and the impact of Pythagoras Theorem continues to reverberate in modern society. The fields of physics, engineering, and computer science owe much to this ancient mathematical principle. From designing circuit boards to analyzing data, the applications are boundless.

In physics, the theorem finds its way into various theories, such as the principles of electromagnetism and quantum mechanics. Engineers rely on Pythagorean mathematics when designing electrical circuits, optimizing fluid dynamics, and calculating structural loads. Furthermore, computer graphics and image processing heavily employ the theorem to render lifelike visuals and create realistic virtual worlds.

FAQs:

Q: Can Pythagoras Theorem be used in non-right triangles? A: No, Pythagoras Theorem specifically applies to right triangles, where one angle equals 90 degrees.

Q: Who is Pythagoras and why is he important? A: Pythagoras was an ancient Greek mathematician, philosopher, and founder of the Pythagorean school. He made significant contributions to mathematics, including the discovery of Pythagoras Theorem, which revolutionized geometric understanding.

Unveiling the Secrets of Pythagoras Theorem

Pythagoras Theorem remains a cornerstone of mathematical principles, enabling us to unlock the hidden dimensions of triangles and unravel the mysteries of space. Its real-world applications and historical significance continue to shape our modern world, showcasing the enduring power of mathematical discovery.

So, the next time you encounter a triangle, remember the words of Pythagoras and let this theorem guide you on a journey of exploration and understanding.

A guide to balancing school life and extracurricular activities

Why taking breaks is important for your academic success: The science behind rest and productivity

The Impact of Social Media on Students’ Academic Performance: An Analysis of Recent Studies

[madamlaydebug]

☆☆☆Stolen Legacy - The Egyptian Origins of Western Philosophy☆☆☆ Description Challenging the notion that civilization started in Greece, this uncompromising classic attempts to prove that the true authors of Greek philosophy were not Greeks but Egyptians. The text asserts that the praise and honor blindly given to the Greeks for centuries rightfully belong to the people of Africa, and argues that the theft of this great African legacy led to erroneous world opinion that the African continent has made no contribution to civilization. Quoting such celebrated Greek scholars as Herodotus, Hippocrates, Aristotle, Thales, and Pythagoras, who admit to the influence of Egyptian studies in their work, this edition sheds new light on traditional philosophical and historical thought. Originally published in 1954, this book features a new introduction. Description 'Stolen Legacy' is George G.M. James' attempt to show that the true authors of Greek philosophy were not the Greeks but the peoples of Egypt. Review "excellent book" -- roxanne warner "great book" -- luther warner The book is an attempt to show that the true authors of Greek philosophy were not the Greeks, but the people of North Africa, commonly called the Egyptians; and the praise and honor falsely given to the Greeks for centuries belong to the people of North Africa, and therefore to the African Continent. Consequently, this theft of the African legacy by the Greeks led to the erroneous world opinion that the African Continent has made no contribution to civilization, and that its people are naturally backward. This is the misrepresentation that has become the basis of race prejudice, which has affected all people of color. "The aim of the book is to establish better race relations in the world, by revealing a fundamental truth concerning the contribution of the African Continent to civilization. It must be borne in mind that the first lesson in the Humanities is to make a people aware of their contribution to civilization; and the second lesson is to teach them about other civilizations. By this dissemination of the truth about the civilization of individual peoples, a better understanding among them, and a proper appraisal of each other should follow. This notion is based upon the notion of the Great Master Mind: Ye shall know the truth, and the truth shall make you free. Consequently, the book is an attempt to show that the true authors of Greek philosophy were not the Greeks; but the people of North Africa, commonly called the Egyptians; and the praise and honour falsely given to the Greeks for centuries belong to the people of North Africa, and therefore to the African Continent. Consequently this theft of the African legacy by the Greeks led to the erroneous world opinion that the African Continent has made no contribution to civilization, and that its people are naturally backward. This is the misrepresentation that has become the basis of race prejudice, which has affected all people of color. For centuries the world has been misled about the original source of the Arts and Sciences; for centuries Socrates, Plato and Aristotle have been falsely idolized as models of intellectual greatness; and for centuries the African continent has been called the Dark Continent, because Europe coveted the honor of transmitting to the world, the Arts and Sciences. I am happy to be able to bring this information to the attention of the world, so that on the one hand, all races and creeds might know the truth and free themselves from those prejudices which have corrupted human relations; and on the other hand, that the people of African origin might be emancipated from their serfdom of inferiority complex, and enter upon a new era of freedom, in which they would feel like free men, with full human rights and privileges." ~ George G. M. James (Stolen Legacy) The Teachings of the Egyptian Mysteries Reached Other Lands Many Centuries Before It Reached Athens. "According to history, Pythagoras after receiving his training in Egypt, returned to his native island, Samos, where he established his order for a short time, after which he migrated to Croton (540 B.C.) in Southern Italy, where his order grew to enormous proportions, until his final expulsion from that country. We are also told that Thales (640 B.C.) who had also received his education in Egypt, and his associates: Anaximander, and Anaximenes, were natives of Ionia in Asia Minor, which was a stronghold of the Egyptian Mystery schools, which they carried on. (Sandford's The Mediterranean World, p. 195-205). Similarly, we are told that Xenophanes (576 B.C.), Parmenides, Zeno and Melissus were also natives of Ionia and that they migrated to Elea in Italy and established themselves and spread the teachings of the Mysteries. In like manner we are informed that Heraclitus (530 B.C.), Empedocles, Anaxagoras and Democritus were also natives of Ionia who were interested in physics. Hence in tracing the course of the so-called Greek philosophy, we find that Ionian students after obtaining their education from the Egyptian priests returned to their native land, while some of them migrated to different parts of Italy, where they established themselves. Consequently, history makes it clear that the surrounding neighbours of Egypt had all become familiar with the teachings of Egyptian Mysteries many centuries before the Athenians, who in 399 B.C. sentenced Socrates to death (Zeller's Hist. of Phil., p. 112; 127; 170-172) and subsequently caused Plato and Aristotle to flee for their lives from Athens, because philosophy was something foreign and unknown to them. For this same reason, we would expect either the Ionians or the Italians to exert their prior claim to philosophy, since it made contact with them long before it did with the Athenians, who were always its greatest enemies, until Alexander's conquest of Egypt, which provided for Aristotle free access to the Library of Alexandria. The Ionians and Italians made no attempt to claim the authorship of philosophy, because they were well aware that the Egyptians were the true authors. On the other hand, after the death of Aristotle, his Athenian pupils, without the authority of the state, undertook to compile a history of philosophy, recognized at that time as the Sophia or Wisdom of the Egyptians, which had become current and traditional in the ancient world, which compilation, because it was produced by pupils who had belonged to Aristotle's school, later history has erroneously called Greek philosophy, in spite of the fact that the Greeks were its greatest enemies and persecutors, and had persistently treated it as a foreign innovation. For this reason, the so-called Greek philosophy is stolen Egyptian philosophy, which first spread to Ionia, thence to Italy and thence to Athens. And it must be remembered that at this remote period of Greek history, i.e., Thales to Aristotle 640 B.C.- 322 B.C., the Ionians were not Greek citizens, but at first Egyptian subjects and later Persian subjects. A brief sketch of the ancient Egyptian Empire would also make it clear that Asia Minor or Ionia was the ancient land of the Hittites, who were not known by any other name in ancient days. According to Diodorus and Manetho, High Priest in Egypt, two columns were found at Nysa Arabia; one of the Goddess Isis and the other of the God Osiris, on the latter of which the God declared that he had led an army into India, to the sources of the Danube, and as far as the ocean. This means of course, that the Egyptian Empire, at a very early date, included not only the islands of the Aegean sea and Ionia, but also extended to the extremities of the East. We are also informed that Senusert I, during the 12th Dynasty (i.e., about 1900 B.C.) conquered the whole sea coast of India, beyond the Ganges to the Eastern ocean. He is also said to have included the Cyclades and a great part of Europe in his conquests. Secondly, the "Amarna Letters" found in the government offices of the Egyptian King, Iknaton, testify to the fact, that the Egyptian Empire had extended to western Asia, Syria and Palestine, and that for centuries Egyptian power had been supreme in the ancient world. This was in the 18th Dynasty i.e., about 1500 B.C. We are also told that during the reign of Tuthmosis III, the dominion of Egypt extended not only along the coast of Palestine, but also from Nubia to Northern Asia." ~ Mr. George G.M. James

[scientific-academia]

1.1 Musical Staves

Even individuals without a single minute of musical experience have seen how music is notated. Whether a simple, two-line tune or a complex, twenty-page symphony, the basis of most sheet music is the set of lines clustered into a repeated bar called a staff.

Photo from the collection of Brandon Giesbrecht.

A staff is constructed by five parallel lines called ledger lines which represent the positioning of musical notes on or between them. Non-pitched percussive instruments are non-standard and will be mentioned further along in the series. As instruments have different pitch ranges (for example, our recorder running from 523.25 to 3160 Hz), these five lines certainly aren’t enough to represent the large number of musical notes which are performed. To suggest whether, in general, lower notes are needed versus higher notes: we introduce clefs.

There are three clefs most commonly used today, called the G, F, and C clefs. These are shown in the same order below, but note that each clef has several sub-uses and so how far up or down on the staff will depend on its usage. As a counterexample: nowadays, the G clef is always the treble clef. Way back in the day though, it used to be shifted down one ledger line to act as the “French violin” clef. In either case, the central swirl of the G clef encircles the ledger line which denotes a tone called (unsurprisingly) G.

Where do the notes even come from, though? Confidently, we said last week that the tone produced by our soprano recorder at 523.25 Hz was the note “C”. Who decided?

Boethius, in the sixth century, used the first fourteen letters of the Latin alphabet (excluding J, which hadn’t been... invented yet) to represent the most commonly used tones of the period. As the range extended, and mathematician/philosopher types uncovered some of the nice relationships between notes, musicians decided to repeat the first seven letters instead. Finally, the C-first ordering of the letters arose from the usage of major and minor scales. But the names aren’t really important. Different cultures use different letters and symbols and produce similar results! How do we know that 523.25 Hz is the right frequency? Why not 520 Hz? Or even simpler at 500 Hz?

It’s, again, anticlimactic but the specific frequencies we use are really arbitrary. Slightly prior to 1834, Johann Heinrich Scheibler trekked from region to region in Europe measuring tuning forks (which were all a little or a lot different) with a device called the tonometer. His rough average of all these measurements? That a specific A note should be standardized to 440 Hz. Several meetings in several countries later, A = 440 Hz is here to stay. What matters most are the frequency differences between the notes, or intervals, and that’s where Pythagoras of Samos comes in.

Apocryphally, Pythagoras was strolling by a blacksmith’s shop one fine day and heard the pleasant ringing of two different sized hammers striking anvils. He determined that he only needed two ratios (2:1 and 3:2) to build a tuning standard. From this spilled forth all of the first ever documented tuning system. Skepticism towards the Cult of Pythagoras aside, much of what we now know about consonance, or how pleasing two sounds combined are to the ear, comes from the original system of Pythagorean tuning.

Construction goes as follows: Take some base frequency and multiply by 3/2. This produces a new tone which is consonant with the first. Repeat five more times and record these frequencies. Now return to the base and divide by 3/2 five times. These twelve notes occupy a larger range than most instruments can even reach and so we can use the other ratio to reduce all of the notes into a smaller range between the base frequency and the note exactly twice its frequency. This special higher limit is called the octave. An example for 440 Hz is provided below.

The asterisks following note names represent a modifier to the standard tone called an accidental. Specifically, sharps and flats. More on this will come later but for now, keep in mind that flats (♭) are lower in frequency and sharps (♯) are higher.

This isn’t the end of the story due to an unfortunate side effect. No whole number of multiples of 3/2 can ever fit between octaves of the same note. The mathematical phrase would be that 2^n =/= 3^m for any integer n,m > 0. This suggests that instead of eventually looping around to the same note, the tuning method produces a spiral, and conflicts with itself. 

As such, the original ratios from the Pythagorean system were altered again and again to eventually produce different tuning methods called temperaments which included the famous equal and well temperaments. A quick explanation of modern piano tuning can be found in a fun Minute Physics video by Henry Reich: “Why It’s Impossible to Tune a Piano”.

As we now have separation of octaves into twelve equal pieces, sharps and flats are used to denote a “half step” above and below the modified note, respectively. Using the piano as our model, a half step is the frequency distance between adjacent keys (e.g. B to C) while a whole step is twice the size and has a separating key (e.g. A to B).

Note that this suggests E♯ and F are the same frequency and therefore are the same note or D♯ is the same as E♭.

So a staff indicates the notes to be played throughout the work and the frequencies of these notes are now (more or less) standardized in Western music. The ledger lines and the spaces between the lines hold notes which increase in name alphabetically and then loop around every seventh letter. As closing remarks, we can present the first piece of sheet music for this series.

Note that the squiggle is called a quarter note rest, named after what it requires the musician to do (...sort of... just no noise, okay?) and the rectangle is a half note rest. Until a deeper discussion of rhythm and timing: they’re the same. Consider all notes and rests to take the same amount of time and ignore the vertical bars.

This shows eleven notes being played. The treble clef identifies the first six notes are G. There is also a B-flat and E-flat, and an F played at the end. From the above discussion, B-flat is at a frequency of 463.5 Hz. Also, the depicted E-flat is an octave below the one calculated and should therefore be half the frequency at 313.25 Hz in the Pythagorean tuning system. Have you identified which song the sheet music is for?

For Thought:

1) C clefs are often used for vocals. Given that we can shift clefs up and down on staves, where might a C clef be positioned for a soprano singer relative to a tenor singer? Given four vocal parts: soprano, alto, tenor, bass, which vocal parts would most likely share the same clef positioning?

2) We generated frequencies from the standard A = 440 Hz tone. Would a Pythagorean tuning scheme from one of the other calculated frequencies give the original A tone back? Generate equal temperament tuned notes from A and see if the C = 523.25 Hz note from last lecture appears.

3) Instruments can easily span more than a single octave in their range. As such, one needs to be able to distinguish between notes of the same name. A = 880 Hz is of the same pitch class (note name) and so we can distinguish this by saying that A4 = 440 Hz, and A5 = 880 Hz. In other words, there are three A notes lower than 440 Hz commonly in use. What would C = 523.25 Hz be then? What about the G emphasized by the treble clef?

4) Calculate the Pythagorean and equal temperament frequencies of the treble clef G. Sketch the fingering of this note on the soprano recorder and graph the waveform of the fundamental and first two overtones (integer divisions) with accurate labeling. What are these overtones in musical notation?

5) Offer an informal proof as to why there are no integer solutions larger than zero for the equation 2^n = 3^m.

Next Time: Scales

[historyofmathematics3-blog]

History of Mathematics

Without mathematics today, we would live an entirely different world. A way to truly be grateful of how mathematics has impacted our world is to understand how it effects our everyday lives. For a moment, imagine our world without it. What would that look like? We would have no concept of time, calendars, buildings, technology, transportation, recipes, and the list goes on. Take even one of these discoveries out of our lives and it would alter the world we live in dramatically.

The first examples of mathematics date back to 1750 BC from the Babylonians and Egyptians who used geometrical and algebraic equations. Of the two, the Babylonians were much more advanced. They used a base of 60 and calculations depending largely on tables. A whole papyrus of calculations exists of the Egyptian early mathematics. Mathematics is a science of structure order and relation that contributes to the evolution of counting and measuring. It has been made largely aware that mathematics has developed greatly from the 15th century. From this time to the late 20th century, developments in mathematics were largely situated in Europe and North America (Gray, J, Folkerts, M , Berggren, J, Knorr, W, Fraser, C, 2020).

One of the largest influences on mathematics was Archimedes, who was a Greek mathematician born in 287 BC. He developed many theories we learn today and was the foundation of many discoveries. He was born into an astronomer family, so from a young age he took a strong interest into studying science, mathematics, and politics. He was fascinated with mathematical equations and problem-solving. He is considered to be the father of mathematics as he made some great inventions regarding mathematics and science. He created a pulley system which was designed to help sailors move objects up and down that are heavy. He also created diverse mathematical ideas to solve problems along with the ‘method of exhaustion’ which assists in measuring the area of shapes. This assisted in the ability to quantify the value of PI. Although, out of all Archimedes achievements, his by far most outstanding discovery would be calculating the measurement of a circle. This method created a relationship between cylinders and spheres. Over his lifetimes he discovered various concepts, methods, and techniques. It is often said that today’s modern world would not be so developed without Archimedes (Toomer 2021).

There are many other great discoveries made by people in history such as Thales, Pythagoras of Samos, Zeno Democritus and many more. Pythagoras of Samons was a Greek philosopher and mathematician. He is well known for the discovery of Pythagoras’ Theorem, although have made other mathematical breakthroughs (Huffman 2005). The history of mathematics is important to understand as it details where our world began and what discoveries have been made to make the society we like in today. Without these people creating the mathematical breakthroughs they have, we would not have the life and resources we have today.

 References

Gray, J, Folkerts, M , Berggren, J, Knorr, W, Fraser, C, 2020 ‘Mathematics’, Encyclopedia Britannica, viewed 20th October 2021, <https://www.britannica.com/science/mathematics>

Toomer, G 2021, ‘Mathematics’ Encyclopedia Britannica, viewed 20th October 2021, < https://www.britannica.com/biography/Archimedes>

Huffman, C 2005 ‘Pythagoras’, Stanford Encyclopedia of Philosophy, viewed 21st October 2021 <https://plato.stanford.edu/entries/pythagoras/>

[image-transcribing-bot]

sd 88% M 2:56 AM Fuddling cups A fuddling cup is a three-dimensional puzzle in the form of a drinking vessel, made of three or more cups or jugs all linked together by holes and tubes. The challenge of the puzzle is to drink from the vessel in such a way that the beverage does not spill. To do this successfully, the cups must be drunk from in a specific order. Bridge-spouted vessel From Wikipedia, th ree encyclopedia A bridge-spouted vessel i a partcular design of ewer (ug or orgiating in antquty; there is ypicaly a connecting element between the spout and fling aperture, and the spout is a completely independent aperture from the usually smaller central tl opening. Early incidences ofthe bridge spouted vessel are found in Persia in the early Iron Age!" and on Crete. This type of vessel typically appears n the Bronze Age or earl Iron Age. A very early example of a bridge spouted boul has been recovered atthe ancient palace of Phaistos on Crete, dating tothe Bronze Age C! There is a diferent type, characteric of he pottery ofthe Nazca cuture of Pre-Columbian Per, where two spouts rsing vertcaly from the body ofthe vessel are Inked by a bridge that apparent also served as a caring handle See also. (eat) « Double spout and bridge vessel + Minoan pottery « Strupjar Dafamamnas v 2s 16t-century German stoneware ug & Pythagorean cup From Wikipedia, th ree encyclopedia A Pythagorean cup (also known as a Pythagoras cup, Greedy Cup, Tantalus cup or Koupa tis dikarasynis) is a practical Joke device in a form of a drinking cup, credited to Pythagoras of Samos #0 When itis fled beyond a certain point, a siphoning effect causes the cup to drain ts entre contents through the base Form and function. (ea) Cross secion o a Pinagorean cup being fled at .@ A Pythagorean cup looks lke a normal inking cup, except thatthe bov has a central column .. | 8, tis possible to dink all th fould nthe cup; butat C, in , gving t a shape lke a Bundt pan. The central column ofthe bois postioned directly the sphon efect causes the cup to drain over the stem of the cup and over the hole at the bottom ofthe stem. A small open pipe runs from this hole almost to the top of he central colum, where there is an open chamber. The chamber is connected by a second pipe to the bottom of the central column, where a hole n the column exposes the pipe to (he contents of the bou o the cup !" When the cup is fled, lquid rises through the second pipe up to the chamber at the top of the central column, folowing Pascal's principle of communicating vessels. As long as the level o the Hild does not ise beyond the level of te chamber, the cup functions as normal. Ifthe level rises furter, however, the Iquid splls trough the chamber into the frst pipe and out the bottom. Graviy then creates a siphon through the central column, causing the entre contents of he cup to be emptied trough the hole atthe bottom of the stem ) Some modem tolls operate on the same principle: when the water level in the bou rises high enough, a siphon is created. flushing the tolet toten reese. Cross secion ota a Pyinagorean cup Puzzle jug < A puzzle jug is a puzzle in the form of a jug, popular in the 18th and 19th centures, Puzzle jugs o vaying qualty were popula in homes and taverns

I am an image transcribing bot which uses Tesseract OCR to translate images to text. I'm far from perfect but I try my best! Most of you are welcome, friendly Human®. | PayPal | Patreon

i love humanity and our weird obsession with making drinking various liquids very hard to drink, for the fun of it

[msfitnic]

“We are all connected in the circle of life.” ~ King Mufasa
This legendary Disney king said it best, but some of us are not aware of it. Veganism has become a huge trend in today’s society. As a matter of fact, I was vegan (such labels are irrelevant) for 2 years before giving into meat (mostly chicken and fish). However, I must admit that veganism has its valuable qualities such as gaining more energy, feeling lighter, and having beautiful skin aka “The Vegan Glow”. Unfortunately, along with valuable qualities, there are some hinderances to transitioning in the lifestyle…and I blame the uber vegans. Uber vegans are such extremists. They are the ultimate Debbie Downers of the health community. Wait…did I just go there? Now, I’m being an extremist! Seriously, they are and I will explain how. Let’s start with the theory and belief behind the lifestyle.
Veganism is a leveled up form of vegetarianism. It consists of the concept of not eating as well as not using or wearing anything that includes an animal. As I’ve said, extreme. Vegetariansim has been around since 500 BCE, when it introduced by the Greek philosopher and mathematician Pythagoras of Samos. Later on, Buddhists, Hindus, and Jains adopted vegetarianism and acquired the belief that humans should not bring harm to other animals. It wasn’t until 1944 that the lifestyle was coined. Now, here we are with the extreme practice…
Again, veganism is a beneficial lifestyle in order to reset your body and your life. It makes you feel like a brand new being. However, it is some of the people who practice the lifestyle that gives it a bad reputation…the uber vegans. These are no ordinary vegans. They are usually on top of avoiding or using animal products. They don’t even consume white flour, white rice, white potatoes, and artificial sugar…well, according to Urban Dictionary. 
Besides their practice, the way of executing and “bringing awareness” to the masses is very aggressive and it offends me (not really, I’m being facetious). However, I’m serious about the aggressive statement. They can be very forceful…but not convincing. For instance, some vegans shame meat eaters for eating meat. As a matter of fact, they consider them barbarians.
Other than the lack of vegan restaurant options, vegans complain about the most trivial things. Of all things, I have an issue with the topic on bees. The controversy behind bees have been a hot topic in the health conscious community. Honey consumption is a NO when it comes to the vegan community. Most vegans believe that beekeeping is unethical and inhumane; this is where honey consumption is a problem. 
For bees, honey is the number one source of energy and they could starve without it. This is because honey has several micro-nutrients needed in order for bees to survive. So, when beekeepers remove honey from the hive and replace a sugar-substitute for the bees to consume, it makes the practice unethical. The sugar-substitute lacks the micro-nutrients found in honey, which makes the situation really bad for bees. Ok…I get it, but what does this have to do with humans consuming honey? The answer is endangerment and extinction. 
In beekeeping, honey bees are specifically bred in order to increase production. By doing this, the gene pool narrows due to increasing the susceptibility to diseases. To be honest, I also find this practice unethical, but honey is so delicious and it has several healing properties. However, I still believe that some vegans can go overboard with their beliefs. As a matter of fact, the argument tends to go left. 
For example, foods such as almonds, avocados, kiwi, butternut squash, and melon are not considered vegan due to the fact that they can’t exist without bees… OMG! Really?! So, this means since bees are gradually becoming endangered, more fruits are becoming non-vegan by principle…see why I find some of these principles ridiculous? There has never been an issue with consuming these foods…until now. Eventually, vegans will have to rely on air sandwiches and prana bites for sustenance. I guess it’s a good thing considering air is free. 
In all seriousness, veganism has become a very extreme practice to the point I just gave up and went back to meat (mainly fish and chicken). Again, veganism has its valuable qualities, but it became too overwhelming and frustrating to keep up due to revised principles and practices over time. Besides, King Mufasa says that we’re all connected into the circle of life. He says, “When we die, our bodies become the grass and the antelope eats the grass. What this Disney king means is that we should respect all creatures so that nature can follow its natural course. It’s a natural form of balance. I wonder has it occurred to vegans that the plants they consume were grown from animal manure? If they weren’t, how do you know? Most people don’t and I’m one of them. 
In conclusion, I think some vegans take things a little too far and make it almost unbearable for others to enjoy their lives. I believe we should live our best healthy lives, whether it’s plant-based or animal-based. The aggression needs to simmer down before I walk into a vegan restaurant with a cheeseburger in my hand…and I will eat it there!

[the-vegan-blr-blog]

Introduction:

The Purpose of My Blog:

In our society the majority of people consume meat. However, a large population of people identify as vegan. I will be going into depth on what are the struggles controversies, and judgments for people who identify as vegan. I will be researching on the controversies the vegan community face, from Italian lawmakers proposing to put parents into jail for making their child go on a vegan diet, to the challenges of being vegan and going against your culture’s norm. Before I discuss this, I want to first give a little history on veganism and where it originated from.

Brief Introduction to Veganism:

I learned from Time Magazine that World Vegan Day is on November 1st and for millions of people, this is a day of acknowledgment for people who do not eat meat. Not only do they not eat meat, but they don’t eat eggs, cheese, honey, whey(  liquid remaining after milk has been curdled and strained. It is a byproduct of the manufacture of cheese or casein and has several commercial uses) , or gelatin (a translucent, colorless, brittle, flavorless food ingredient that is derived from collagen obtained from various animal body parts). Or anything else that is made from or includes an animal. This also encompasses any clothing, objects, and accessories made from an animal. This includes leather, wool, pearls, and ivory piano keys.

Veganism is an extreme form of vegetarianism, and though the term was coined in the 20th century, the concept of not consuming animals can be traced back to ancient Indian and eastern Mediterranean societies. The Vegan Society informs us that the term veganism originated in England in 1944 by Donald Watson and six other non-dairy vegetarians, including Elsie Shrigley who was the co-founder of the vegan society.

Vegetarianism had been a topic since the 18th century but the idea of non-dairy vegetarian diets and lifestyles was still new. According to International Vegetarian Union vegetarianism was mentioned by the Greek philosopher and mathematician Pythagoras of Samos as early as around 500 BCE. Also, many followers of  Buddhism , Hinduism, and Jainism also advocated vegetarianism, believing that humans should not impose pain on other animals.

In the early stages the meatless lifestyle was not common in the west. When it was mentioned it was viewed as a temporary health diet for weight loss. However, Time Magazine shares that by 2005 there were around 250,000 self-identifying vegans in Britain and 2 million in the U.S.

In Conclusion:

I hope that during my journey of making this blog I will be able to dig deeper into the world of veganism. My intention is to shed light on a different side of veganism. When looking at other vegan blogs I saw a pattern that the blogs were either pro-veganism or anti-veganism. My goal is to discuss the culture and ethics of veganism and see whether we as a society are accepting or prejudice of this way of living.   

[meditationadvise]

5 Ways to Become 1% More Mindful Every Day

Great points are accomplished regularly in small actions, rather than in excellent jumps. It doesn't matter if your objective is extremely challenging, or if it is shateringly simple (like taking a seat to practice meditation everyday) and you just can not appear to do it. Effective as well as tranquil people have actually learned that large objectives take tiny, child actions to accomplish.

To show the relevance of little steps we could look to the mysterious means in which Michelangelo carved his sculptures. Michelangelo's buddy and biographer, Giorgio Vasari, defines a tedious approach the master artist used to carve identify of stone. Michelangelo laid his model for a project down in a box like a coffin. He after that filled up package up until the figure was immersed. The water was slowly permitted to leak out, or he eliminated it a little bit at time, to see which components of the figure would arise very first - like an archipelago peeping out from the sea's surface.

This is exactly how he would recognize which components to cut first in his stone block. In some cases it would certainly be a hip, other times it would certainly be a nose, or a shoulder. The approach was really imprecise, as well as took numerous hours of observation before he might also obtain to the task of sculpting a work of art out of marble or granite.

When we initially readied to a task - like sculpting a masterpiece out of rock - it could appear leviathan, impossible, even, but there is always a means. If we are aiming to develop even more mindfulness in our actions, words as well as acts, it doesn't take place over night. There are little steps we can take though, that will certainly finish in an outright master work. Right here they are:

1. If You Aren't sure Where to Start, Simply Dive In

You might make use of the sheer number of mindfulness techniques and also practices as a way of procrastination if you really desired to. One might invest years researching the different wisdom traditions (yoga exercise, tai chi, qi gong, Zen, focusing prayer, chanting, transcendental meditation, and so on) to find to a particular practice, but deliberate, nonjudgmental understanding of our moment-to-moment experience could be practiced right now. Just pick one technique, and also do it each and every single day. Establish an alarm on your cellular phone. Write yourself a note and stick it in your purse to advise on your own, or put a rubber band around your wrist as well as each time you see it, do the method. If you aren't sure where to start, simply dive in. Don't allow lack of knowledge be a reason to keep mindfulness at bay. You can constantly learn as you go.

2. Don' t Allowed Your Faith Quit You from Being Even more Mindful

According to Jon Kabat-Zinn, a Jewish-born, Harvard graduated microbiology Ph.D. that as soon as instructed at the College of Massachusetts Medical Center, and later on ended up being a student of the Zen Buddhist monk, Thich Nhat Hanh - Buddhist meditation is not a faith. Neither is Vipassana from old India. Exactly what prevails to all types of mindfulness is that they are a method to focus our interest, cultivate recognition, and also pay more attention to our inattention.

You could be Christian, Buddhist, Jain, Hindu, Muslim, Jewish, also atheist, as well as still method mindfulness. If you require to wed your mindfulness practice with your current religious ideas, that's o.k., but do not allow your spiritual background stop you from taking little actions every day.

If you are Christian, your mindfulness method could merely be, "Thank you, God." If you are Buddhist, it could be a five-minute incantation of the concept, "Om Peanut Padme Hum", which means imply, the gem is in the lotus (the 3rd eye.) If you are Hindu, you could simply sit silently and claim, 'Om Gum tissue Ganapatayei Namah,' which equates to 'I acquiesce the elephant-faced divine being (Ganesh) that is capable of getting rid of all barriers. I wish blessings as well as security.' Every one of these rules have vibrational power, and have been confirmed to alter your mind in incremental steps.

3. Move Into Challenges As opposed to Away From Them

By exercising mindfulness, we are much better able to removal right into difficulties and also discover how you can overcome them rather of shy away from them. Scientific research as well as imaging of the minds of meditators has actually located that an electrical change takes place in mind function, believed to reflect the growing of an "technique state," in which we approach, instead of away from, a tough exterior situation or inner psychological function such as an idea, feeling, or memory. Naturally, this could become a basis for durability in human beings.

When something disturbing, testing, or complicated shows up in your life, this is the excellent time to exercise mindfulness. Anyone could do a fundamental breathing reflection, at virtually any type of time, no issue where they are, or who they are with. The breath allows area in the nervous system, heart, and also brain to ensure that we could see things from a various perspective compared to before we began to breathe deeply and also with even more conscious interest. Just attempt it, as well as you'll be blown away by the advancing impacts of this basic practice.

4. If You Desired a Different Outcome, You Have to Do Something Different

How a lot of us long for more clam, even more happiness, even more tranquility, more success, more love, and so on in our lives? We long for these points like they are in some far-away desire. This mindset maintains us from taking obligation for our own actions. A desire is a great place to start, yet this need has to convert right into activity. Again, these activities can be little, they do not need to be monumental, once taken, as well as done once more and time and again, the results could be profound.

Mindfulness farming is an activity, or set of actions. Do not' wait around for more happiness, or a far better world. The adjustment absolutely does start with you - simply like Gandhi suggested.

Once you have a mindfulness technique developed you could see that you get even more maded with much less effort, yet it does certainly take effort when you initially venture making change.

https://youtu.be/xnLoToJVQH

5. If All Else Stops working, Listen to Conscious Music

Mainstream songs adjustments your resonance - were you aware? Not all of it is developed to boost you and assist you attach to Source.

One of the 'tricks' of the universe, is the innovative application of audio regularities. John Worley Keely discovered this creative use musical regularities in the late 19th century as well as accomplished outstanding tasks that opposed traditional physics as well as confounded the academicians of his day.

If you happen to listen Bob Marley on your iPod or songs player, then you'll probably be changed right into dizzying degrees of happiness. He was recognized to videotape his music in regularities that remained in placement with the Schumann Resonances - electro-magnetic waves that exist in the room in between the surface area of the earth as well as the Ionosphere - 7.83, 14.3, 20.8, 27.3 as well as 33.8 Hz. They are claimed to be the heartbeat of mom earth.

Many classic authors did the very same. Gregorian incantations, and also most old songs was tuned to positively influence our resonances. Pythagoras of Samos recognized that playing songs which was lined up with the beautiful bodies, might heal us from some of one of the most dire physical and also psychological problems. This is not real of a lot of modern music.

The easiest method to inform if songs is healing our harming you, is to observe exactly how it makes you really feel. Does it create you to ignore or tune up? Pick your songs accordingly, when you have no various other time to exercise mindfulness, a minimum of your mind is being modified by the positive as well as powerful impact of sound.

By practicing these tiny actions - transforming your thoughts and actions by 1% everyday, gradually you'll accumulate to a 100% modification. Since's something to obtain delighted about!

[julianworker]

Samos – 2 Walking around the ancient harbour of Pythagorio, parts of which are 2,600 years old, the visitor soon comes to a statue of Pythagoras, who was born i the area around 574 BCE.

[sciencespies]

Is maths real? That's actually a much smarter question than you might think

http://sciencespies.com/physics/is-maths-real-thats-actually-a-much-smarter-question-than-you-might-think/

Is maths real? That's actually a much smarter question than you might think

While filming herself getting ready for work recently, TikTok user @gracie.ham reached deep into the ancient foundations of mathematics and found an absolute gem of a question: “How could someone come up with a concept like algebra?”

She also asked what the ancient Greek philosopher Pythagoras might have used mathematics for, and other questions that revolve around the age-old conundrum of whether mathematics is “real” or something humans just made up.

Many responded negatively to the post, but others – including mathematicians like me – found the questions quite insightful.

Is mathematics real?

Philosophers and mathematicians have been arguing over this for centuries. Some believe mathematics is universal; others consider it only as real as anything else humans have invented.

Thanks to @gracie.ham, Twitter users have now vigorously joined the debate.

If she’s asking how we uncover mathematical truths, are those truths real or constructed etc indicates she likely got an A in algebra without even trying

— Lauren Pleska 🏳️‍🌈 (@RadFemme74) August 28, 2020

can we blow this one up instead of the one where i sound stupid hashtag math isn’t real pic.twitter.com/HuaEDwqXXP

— gracie cunningham | BLM (@graciegcunning) August 27, 2020

For me, part of the answer lies in history.

From one perspective, mathematics is a universal language used to describe the world around us. For instance, two apples plus three apples is always five apples, regardless of your point of view.

But mathematics is also a language used by humans, so it is not independent of culture. History shows us that different cultures had their own understanding of mathematics.

Unfortunately, most of this ancient understanding is now lost. In just about every ancient culture, a few scattered texts are all that remain of their scientific knowledge.

However, there is one ancient culture that left behind an absolute abundance of texts.

Babylonian algebra

Buried in the deserts of modern Iraq, clay tablets from ancient Babylon have survived intact for about 4,000 years.

These tablets are slowly being translated and what we have learned so far is that the Babylonians were practical people who were highly numerate and knew how to solve sophisticated problems with numbers.

Their arithmetic was different from ours, though. They didn’t use zero or negative numbers. They even mapped out the motion of the planets without using calculus as we do.

Of particular importance for @gracie.ham’s question about the origins of algebra is that they knew that the numbers 3, 4 and 5 correspond to the lengths of the sides and diagonal of a rectangle. They also knew these numbers satisfied the fundamental relation 3² + 4² = 5² that ensures the sides are perpendicular.

The Babylonians did all this without modern algebraic concepts. We would express a more general version of the same idea using Pythagoras’ theorem: any right-angled triangle with sides of length a and b and hypotenuse c satisfies a² + b² = c².

The Babylonian perspective omits algebraic variables, theorems, axioms and proofs not because they were ignorant but because these ideas had not yet developed. In short, these social constructs began more than 1,000 years later, in ancient Greece.

The Babylonians happily and productively did mathematics and solved problems without any of these relatively modern notions.

What was it all for?

@gracie.ham also asks how Pythagoras came up with his theorem. The short answer is: he didn’t.

Pythagoras of Samos (c. 570-495 BC) probably heard about the idea we now associate with his name while he was in Egypt. He may have been the person to introduce it to Greece, but we don’t really know.

Pythagoras didn’t use his theorem for anything practical. He was primarily interested in numerology and the mysticism of numbers, rather than the applications of mathematics.

The Babylonians, on the other hand, may well have used their knowledge of right triangles for more concrete purposes, although we don’t really know. We do have evidence from ancient India and Rome showing the dimensions 3-4-5 were used as a simple but effective way to create right angles in the construction of religious altars and surveying.

Without modern tools, how do you make right angles just right? Ancient Hindu religious texts give instructions for making a rectangular fire altar using the 3-4-5 configuration with sides of length 3 and 4, and diagonal length 5. These measurements ensure that the altar has right angles in each corner.

Big questions

In the 19th century, the German mathematician Leopold Kronecker said “God made the integers, all else is the work of man”.

I agree with that sentiment, at least for the positive integers – the whole numbers we count with – because the Babylonians didn’t believe in zero or negative numbers.

Mathematics has been happening for a very, very long time. Long before ancient Greece and Pythagoras.

Is it real? Most cultures agree about some basics, like the positive integers and the 3-4-5 right triangle. Just about everything else in mathematics is determined by the society in which you live.

Daniel Mansfield, Lecturer in Mathematics, UNSW.

This article is republished from The Conversation under a Creative Commons license. Read the original article.

.fb_iframe_widget_fluid_desktop iframe width: 100% !important;

#Physics