#rational root theorem

[math-journal2]

<— Unit 21: Part 5 —>

Possible Zeros w/o calculator

*good to know but it’s impractical if you got 8 or 9 possible zeroes to eliminate. If possible, graphing calculator

Page 51

[experiment, ignore it]

Page 56

[anocana]

so:

we can get the negative numbers from a non-negative number system (usually integers from natural numbers) by appending an abstract element, say x, with the equation x+1=0. having done so, we can write x as -1.

we can get the complex numbers from the real numbers by appending an abstract element, conventionally i, with the equation i*i = -1. we generally leave i as a letter instead of calling it a unary operation of 1.

in between these two, we need to define the rationals and the reals. which we can't really do by appending an abstract element. why not?

adding -1 closes the numbers under addition because 1 is the multiplicative identity and multiplication distributes over addition, so for any a, a(-1)+a = a(-1+1) = 0a = 0.

adding i closes the reals under polynomial roots because of the fundamental theorem of algebra which has a very complicated proof.

so there's not really a unified reason why adding these elements closes the numbers under some operation. each individual case where this happens has its own reason, but these reasons seem basically arbitrary to one another, so no reason to expect a priori that another closure has a single (or finite number of) associated abstract element(s)

[future-math]

Factoring polynomials using Rational Root Theorem

Don't forget to comment or ask me your questions!

[jonathankatwhatever]

Continuing. Unity. Roots of unity. I’m seeing all the concepts coming together rapidly. What was that label? The unification of the selves. At the time I think that developed in relationship to what I saw in you as a multitude which didn’t connect or rather which connected over what I now see a 1-0Segment of identifications. That is what constructs True to the identity of you, revealing to me the mathematics which Attaches at every count along the szK. That even relates to the idea Newton grappled with that mass goes to the center line at scale, which Einstein then described, which Gödel tried to encapsulate, which we can explain as the force of resolution along the szK in the gsProcess of gsConstruction. Using these concepts, we can firmly establish the existence of Things.

That may have been a bit much. I was trying to summon the memory of the labeling of identity, with one leading to True and the other leading to a specific form of contradiction, one in which trust evaporates and all results disappear because they would then be constructed on only one side of a 2:1, and there’s something hidden in that which I can now sense. The words suggest that this construction, the idea of rationalizing in which one side is held constant, is valuable up to the (1-0-1//0-1-0) limit, which is the edge of the label flip. That means what? I took it then as meaning you act outwardly an internal flip of gender identity, so you would be ultra female and ultra male, in the familiar construction of unmixed within the same space, which is a nice way of saying each connection is 1 and 0 so the gsProcesses distinguish one from the other in each threading of identity, even though the same pieces may assemble in either identity because those would share a great deal.

That conception has driven all the change in me. All the effort I expend. Chasing the Truth.

I find it extremely interesting that it was only days ago that I finally realized the words I was hearing about a different form of mission failure could represent your perspective, which identified then a sensible difference in knowledge. One reason that’s interesting is I’ve long discussed and we’ve examined the way roles complement. That regularly works itself out in Storyline, from the highly romantic to the minutely detailed. A making of 1. We know why that happens.

I have about 10 minutes. One approach is to look at the development in math into the conception of analytic, meaning coming to an End, involving complex numbers. We tend to think of that as ‘in the complex plane’ but I think it’s easier to grasp if you say ‘from the complex plane’ because the visible results, meaning those where the complex part is 0i, kinda like Oi-vey, come from or out of complexity.

So Riemann gets a lot of credit. Along with Dirichlet because the idea of epsilon-delta inverts the idea of an analytic End to what can be stated about that End, which is that there’s always an epsilon smaller because you can define that process and we treat that process as the End. Again, it helps to see that process coming at us rather than away from us. Like a speed limit can be seen as speed up to or as pressure to slow down to, depending on the context and your choice of perspective within that context.

For some reason, the mean value theorem came to mind. Yes, we can demonstrate there’s a line Between results. It’s there in the drawings because there must a branching at a root. Oh, think about that for a second. Treat Ends as roots. Which fits because they are. That models along an Extent and in comparison along a 1-0Segment of Extents. Wow.

[piatosniathenie]

Math Reflection 🌸 __________________

Upon my entry here to Pisay, I quickly learnt that the math I’d be learning would be more advanced in comparison to my friends in DepEd. Now, as a freshie who was in the seventh grade who was adjusting to both Pisay and dorm life, it was still quite alright since most topics were ones that I was already familiar with thanks to my former elementary coach. My grades were still thriving like they were before, but midway through, they started dropping little by little. So, my head may have internalised the saying that I was so smart in math that I was smarter than them in the subject and I got too prideful that I stopped doing math exercises during the pandemic. I understand now that it was quite naive of me to think that I was that smart in math that I no longer needed to practice solving and that I can understand concepts within the drop of the hat. I forgot the entire reason why I got good at math in the first place back in elementary: practice, practice, and even more practice. Eight hours a day for five days a week for three months for four years straight and that doesn’t even include summer training sessions for competitions and Saturday MTG sessions, all of which were just dedicated to learning mathematics. Now, you may ask what my point is in all of this. The aforementioned was just to give you a background of how it now leads to my Math 3 learning journey, or more specifically, the second quarter portion. So, yeah, that was just the prologue! Now, here’s the actual story that will talk about the stepping stones I had to get through during the second quarter of this school year!

Transitioning from Math 2 which was our introductory course to LETV, quadratic equations, functions, and of course, graphs ✨. We were taught the basic concepts which were essential as they would all be built up in the coming year levels. By the end of Math 2, I had better learning habits than I did at the beginning of it and was practicing more (minus the days I felt like I was at an all-time low and had no motivation to do anything) but hey, at least they improved and it paid off since my grades became higher(ish) (shout out to ma’am for helping me and making us create outlines for the topics!! mwa mwa). The ninth grade soon rolled along and we were back to refreshing former topics that we were taught in our earlier years and of course, they were more difficult than we remembered. First quarter was fine (ignoring the FAs I got embarrassingly low scores on due to my lack of practice and rush cramming. Not a good habit, I’m very much aware). We went through angles, geometry, reruns of the midpoint formula, and more. 

Finally, here we are at the second quarter and wow, I don’t think I’ve disliked graphs more than I do now, more specifically transformations. I apologise, that was blunt, but I will explain more into that in the later paragraphs. In the beginning, it was fine since it was just division with polynomials, factor theorem, and remainder theorem. Sounds nice, right? They were fairly easy topics that anyone could grasp quickly and were just a refresher from grade 7. After the two week break/suspension, we were taught rational root theorem and Descartes’ rule of signs. Again, easy enough topics once you get the hang of it and practice a lot, which I did during the break. The topics I mainly struggled with were functions mainly due to the fact that it required knowing how to interpret graphs (my Achilles’ heel 😭), but more on that later on. Before I knew it, we were taking our first long test of the quarter. Did I cram? Yes. The result you may ask? I failed miserably. An astounding ten out of thirty. Thankfully, our teacher was kind enough to give us another long test to make up for it so the majority of us wouldn’t fail. Again, I reviewed/crammed, but I had a better understanding of the topics this time after we went over our mistakes in the first LT. When the scores were revealed, I surprisingly got a 20 out of 30 in spite of me not reviewing as much as I was supposed to. Then again, the concepts were familiar and were easy to grasp and it just required comprehension. I will not forget what my teacher said as he gave me my score: “Wow, nagreview talaga ‘to,”. Sir, alam mo po ba na natulog lang ako for the entire lunch break before the LT. Hihi, I’m sorry, but thank you for the retake!! 

Afterwards, we mainly focused on transformations for the remainder of 2024. Now, despite the amount of exercises given to us and the numerous sessions we had on GeoGebra, I still did not have a good grasp on it as much as our other lessons. Everyone else said that it was one of the easiest, but I don't know. I guess I’m not as “literate” as others when it comes to graphs or my mind simply didn’t process it. Either way, I should practice on it. However, when it comes to the ones I was proficient with and a topic that I will want to carry with me for the rest of my life is the division of polynomials. It was quite relaxing in a way and I enjoyed doing it inspired me to exercise my basic arithmetic skills every once in a while.

Learning all of these lessons was certainly not an easy feat for me to do due to the other requirements and lessons I had to focus on as well which usually did not leave me enough time to concentrate on solely math. I have my friends to thank for teaching me at midnight and between classes, especially in transformations >.<. Shout out kay Joseph for being my math tutor since grade 7. Sir Joseph, thank you for not giving up on our batch no matter how hard-headed and stubborn we are and for always diligently giving us the resources we need to review. Lastly, Pia, I am begging you to do more math exercises if you want your grades to go up. Go back to your former learning habits and just keep on practicing, I swear that’s the only way you’ll go back to being your former self from elementary (don’t forget rest). Mwa!

[thewestcoastmathtutor]

Rationalize the Denominator without Multiply. with a Root or Conjugate| The Westcoast Math Tutor

Rationalize the Denominator without Multiply. with a Root or Conjugate| The Westcoast Math Tutor https://www.youtube.com/watch?v=Gqq0HJ1hIXA This video shows how to rationalize the denominator without multiplying the denominator with a root or with a conjugate. 🔔 Join The Westcoast Math Tutor to watch more content on High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ✅ Stay Connected To Me. 👉 Facebook: https://ift.tt/sp2wn1K ✅ For Business Inquiries: thewestcoastmathtutor@gmail.com ============================= ✅ Recommended Playlists: 👉 Decimal to Fraction https://www.youtube.com/watch?v=3J8Dnl0wLQE&list=PLPSu23Z8U7JG3C22WEiDhDf2bBXZ2yQJK 👉 Improper Fraction to Mixed Number https://www.youtube.com/watch?v=VvL7fXAYtHg&list=PLPSu23Z8U7JG0ErjzsUGv6KfDThOE7SxO 👉 Linear Equation https://www.youtube.com/watch?v=UUeuIQ6bUxU&list=PLPSu23Z8U7JGhun3PPquRpkjrMdNFAggz&pp=iAQB ✅ Other Videos You Might Be Interested In Watching: 👉 Evaluating Logarithms https://www.youtube.com/watch?v=ve9BMVUC6fE 👉 Exponential to Logarithmic Form & Logarithmic to Exponential Form https://www.youtube.com/watch?v=KbEULbAjvtI 👉 Logarithms Easy ! 2 Explanations https://www.youtube.com/watch?v=77msni1vacc 👉Boundedness Theorem, 2 Examples https://www.youtube.com/watch?v=NWPFmBmu380 ================================ ✅ About The Westcoast Math Tutor: Hello Friends! I’m The Westcoast Math Tutor, and with this channel, I will provide tutorial videos to better your understanding of different high school math topics. Once in a while, I will also make other interesting math videos outside of high school math topics. If you have any questions, please ask me in the comments. This channel is what I’ve been doing for you. If you want to do something for me, hit the bell button, like, and share. Thanks for watching, and happy learning, everyone! ✅For Appointment and Business inquiries, please use the contact information below: 📩 Email: thewestcoastmathtutor@gmail.com 🔔Subscribe for more High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ================================= #logarithmroots #inverseproperty #logarithmbasics #logarithmtutorial #mathexplained #logarithmproblems Disclaimer: I do not accept any liability for any loss or damage incurred by you acting or not acting as a result of watching any of my publications. You acknowledge that you use the information I provide at your own risk. Do your research. Copyright Notice: This video and my YouTube channel contain dialogue, music, and images that are the property of The Westcoast Math Tutor. You are authorized to share the video link and channel and embed this video in your website or others as long as a link back to my Youtube Channel is provided. © The Westcoast Math Tutor via The Westcoast Math Tutor https://www.youtube.com/channel/UCqP_EgHF0TGr65xMEcFPcjA September 22, 2023 at 08:38AM

[weirdvic]

Oh I have a good one!!! This might be the worst proof ever designed so proceed with caution.

Suppose that there exists x rational such that x^3 = 2. Then x^3 = 1^3 + 1^3. This contradicts Fermat's last theorem!!!! Hence the cubic root of two is irrational.

I did warn you...

I sort of want to start a mathematics competition to find the most elaborate possible proofs of simple mathematical theorems. For instance, could one deploy a spectral sequence to show that the Euclidean division algorithm works? That is the sort of reckless fun I want to see in the world.

[math-journal2]

<— Unit 20 — Unit 21 Poly — Unit 22 —>

Unit 21: Poly Functions Zeros

Part 1 —>

Remainder Theorem

#1

Factor Theorem

#1

Rational Zero Theorem

#1

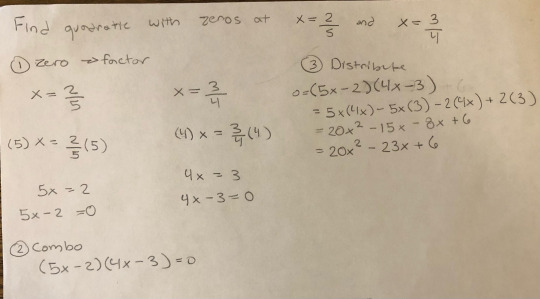
Page 52

[scientific-academia]

1.1 Musical Staves

Even individuals without a single minute of musical experience have seen how music is notated. Whether a simple, two-line tune or a complex, twenty-page symphony, the basis of most sheet music is the set of lines clustered into a repeated bar called a staff.

Photo from the collection of Brandon Giesbrecht.

A staff is constructed by five parallel lines called ledger lines which represent the positioning of musical notes on or between them. Non-pitched percussive instruments are non-standard and will be mentioned further along in the series. As instruments have different pitch ranges (for example, our recorder running from 523.25 to 3160 Hz), these five lines certainly aren’t enough to represent the large number of musical notes which are performed. To suggest whether, in general, lower notes are needed versus higher notes: we introduce clefs.

There are three clefs most commonly used today, called the G, F, and C clefs. These are shown in the same order below, but note that each clef has several sub-uses and so how far up or down on the staff will depend on its usage. As a counterexample: nowadays, the G clef is always the treble clef. Way back in the day though, it used to be shifted down one ledger line to act as the “French violin” clef. In either case, the central swirl of the G clef encircles the ledger line which denotes a tone called (unsurprisingly) G.

Where do the notes even come from, though? Confidently, we said last week that the tone produced by our soprano recorder at 523.25 Hz was the note “C”. Who decided?

Boethius, in the sixth century, used the first fourteen letters of the Latin alphabet (excluding J, which hadn’t been... invented yet) to represent the most commonly used tones of the period. As the range extended, and mathematician/philosopher types uncovered some of the nice relationships between notes, musicians decided to repeat the first seven letters instead. Finally, the C-first ordering of the letters arose from the usage of major and minor scales. But the names aren’t really important. Different cultures use different letters and symbols and produce similar results! How do we know that 523.25 Hz is the right frequency? Why not 520 Hz? Or even simpler at 500 Hz?

It’s, again, anticlimactic but the specific frequencies we use are really arbitrary. Slightly prior to 1834, Johann Heinrich Scheibler trekked from region to region in Europe measuring tuning forks (which were all a little or a lot different) with a device called the tonometer. His rough average of all these measurements? That a specific A note should be standardized to 440 Hz. Several meetings in several countries later, A = 440 Hz is here to stay. What matters most are the frequency differences between the notes, or intervals, and that’s where Pythagoras of Samos comes in.

Apocryphally, Pythagoras was strolling by a blacksmith’s shop one fine day and heard the pleasant ringing of two different sized hammers striking anvils. He determined that he only needed two ratios (2:1 and 3:2) to build a tuning standard. From this spilled forth all of the first ever documented tuning system. Skepticism towards the Cult of Pythagoras aside, much of what we now know about consonance, or how pleasing two sounds combined are to the ear, comes from the original system of Pythagorean tuning.

Construction goes as follows: Take some base frequency and multiply by 3/2. This produces a new tone which is consonant with the first. Repeat five more times and record these frequencies. Now return to the base and divide by 3/2 five times. These twelve notes occupy a larger range than most instruments can even reach and so we can use the other ratio to reduce all of the notes into a smaller range between the base frequency and the note exactly twice its frequency. This special higher limit is called the octave. An example for 440 Hz is provided below.

The asterisks following note names represent a modifier to the standard tone called an accidental. Specifically, sharps and flats. More on this will come later but for now, keep in mind that flats (♭) are lower in frequency and sharps (♯) are higher.

This isn’t the end of the story due to an unfortunate side effect. No whole number of multiples of 3/2 can ever fit between octaves of the same note. The mathematical phrase would be that 2^n =/= 3^m for any integer n,m > 0. This suggests that instead of eventually looping around to the same note, the tuning method produces a spiral, and conflicts with itself. 

As such, the original ratios from the Pythagorean system were altered again and again to eventually produce different tuning methods called temperaments which included the famous equal and well temperaments. A quick explanation of modern piano tuning can be found in a fun Minute Physics video by Henry Reich: “Why It’s Impossible to Tune a Piano”.

As we now have separation of octaves into twelve equal pieces, sharps and flats are used to denote a “half step” above and below the modified note, respectively. Using the piano as our model, a half step is the frequency distance between adjacent keys (e.g. B to C) while a whole step is twice the size and has a separating key (e.g. A to B).

Note that this suggests E♯ and F are the same frequency and therefore are the same note or D♯ is the same as E♭.

So a staff indicates the notes to be played throughout the work and the frequencies of these notes are now (more or less) standardized in Western music. The ledger lines and the spaces between the lines hold notes which increase in name alphabetically and then loop around every seventh letter. As closing remarks, we can present the first piece of sheet music for this series.

Note that the squiggle is called a quarter note rest, named after what it requires the musician to do (...sort of... just no noise, okay?) and the rectangle is a half note rest. Until a deeper discussion of rhythm and timing: they’re the same. Consider all notes and rests to take the same amount of time and ignore the vertical bars.

This shows eleven notes being played. The treble clef identifies the first six notes are G. There is also a B-flat and E-flat, and an F played at the end. From the above discussion, B-flat is at a frequency of 463.5 Hz. Also, the depicted E-flat is an octave below the one calculated and should therefore be half the frequency at 313.25 Hz in the Pythagorean tuning system. Have you identified which song the sheet music is for?

For Thought:

1) C clefs are often used for vocals. Given that we can shift clefs up and down on staves, where might a C clef be positioned for a soprano singer relative to a tenor singer? Given four vocal parts: soprano, alto, tenor, bass, which vocal parts would most likely share the same clef positioning?

2) We generated frequencies from the standard A = 440 Hz tone. Would a Pythagorean tuning scheme from one of the other calculated frequencies give the original A tone back? Generate equal temperament tuned notes from A and see if the C = 523.25 Hz note from last lecture appears.

3) Instruments can easily span more than a single octave in their range. As such, one needs to be able to distinguish between notes of the same name. A = 880 Hz is of the same pitch class (note name) and so we can distinguish this by saying that A4 = 440 Hz, and A5 = 880 Hz. In other words, there are three A notes lower than 440 Hz commonly in use. What would C = 523.25 Hz be then? What about the G emphasized by the treble clef?

4) Calculate the Pythagorean and equal temperament frequencies of the treble clef G. Sketch the fingering of this note on the soprano recorder and graph the waveform of the fundamental and first two overtones (integer divisions) with accurate labeling. What are these overtones in musical notation?

5) Offer an informal proof as to why there are no integer solutions larger than zero for the equation 2^n = 3^m.

Next Time: Scales

[presumenothing]

so satisfying to whack things with intellect. gotta flex em neurons

[locally-normal]

Reminds me of the good old proof that for n>2, the nth root of 2 isn't rational: suppose it were, then (a/b)^n = 2 for some integers a,b, so, a^n = 2b^n = b^n+b^n which by Fermat's last theorem is a contradiction.

Reblog with your favorite massively overpowered proof

Hydrogen bomb vs. coughing baby: graphs and the Yoneda embedding

So we all love applying heavy duty theorems to prove easy results, right? One that caught my attention recently is a cute abstract way of defining graphs (specifically, directed multigraphs a.k.a. quivers). A graph G consists of the following data: a set G(V) of vertices, a set G(A) of arrows, and two functions G(s),G(t): G(A) -> G(V) which pick out the source and target vertex of an arrow. The notation I've used here is purposefully suggestive: the data of a graph is exactly the same as the data of a functor to the category of sets (call it Set) from the category that has two objects, and two parallel morphisms from one object to the other. We can represent this category diagrammatically as ∗⇉∗, but I am just going to call it Q.

The first object of Q we will call V, and the other we will call A. There will be two non-identity morphisms in Q, which we call s,t: V -> A. Note that s and t go from V to A, whereas G(s) and G(t) go from G(A) to G(V). We will define a graph to be a contravariant functor from Q to Set. We can encode this as a standard, covariant functor of type Q^op -> Set, where Q^op is the opposite category of Q. The reason to do this is that a graph is now exactly a presheaf on Q. Note that Q is isomorphic to its opposite category, so this change of perspective leaves the idea of a graph the same.

On a given small category C, the collection of all presheaves (which is in fact a proper class) has a natural structure as a category; the morphisms between two presheaves are the natural transformations between them. We call this category C^hat. In the case of C = Q, we can write down the data of such a natural transformations pretty easily. For two graphs G₁, G₂ in Q^hat, a morphism φ between them consists of a function φ_V: G₁(V) -> G₂(V) and a function φ_A: G₁(A) -> G₂(A). These transformations need to be natural, so because Q has two non-identity morphisms we require that two specific naturality squares commute. This gives us the equations G₂(s) ∘ φ_A = φ_V ∘ G₁(s) and G₂(t) ∘ φ_A = φ_V ∘ G₁(t). In other words, if you have an arrow in G₁ and φ_A maps it onto an arrow in G₂ and then you take the source/target of that arrow, it's the same as first taking the source/target in G₁ and then having φ_V map that onto a vertex of G₂. More explicitly, if v and v' are vertices in G₁(V) and a is an arrow from v to v', then φ_A(a) is an arrow from φ_V(v) to φ_V(v'). This is exactly what we want a graph homomorphism to be.

So Q^hat is the category of graphs and graph homomorphisms. This is where the Yoneda lemma enters the stage. If C is any (locally small) category, then an object C of C defines a presheaf on C in the following way. This functor (call it h_C for now) maps an object X of C onto the set of morphisms Hom(X,C) and a morphism f: X -> Y onto the function Hom(Y,C) -> Hom(X,C) given by precomposition with f. That is, for g ∈ Hom(Y,C) we have that the function h_C(f) maps g onto g ∘ f. This is indeed a contravariant functor from C to Set. Any presheaf that's naturally isomorphic to such a presheaf is called representable, and C is one of its representing objects.

So, if C is small, we have a function that maps objects of C onto objects of C^hat. Can we turn this into a functor C -> C^hat? This is pretty easy actually. For a given morphism f: C -> C' we need to find a natural transformation h_C -> h_C'. I.e., for every object X we need a set function ψ_X: Hom(X,C) -> Hom(X,C') (this is the X-component of the natural transformation) such that, again, various naturality squares commute. I won't beat around the bush too much and just say that this map is given by postcomposition with f. You can do the rest of the verification yourself.

For any small category C we have constructed a (covariant) functor C -> C^hat. A consequence of the Yoneda lemma is that this functor is full and faithful (so we can interpret C as a full subcategory of C^hat). Call it the Yoneda embedding, and denote it よ (the hiragana for 'yo'). Another fact, which Wikipedia calls the density theorem, is that any presheaf on C is, in a canonical way, a colimit (which you can think of as an abstract version of 'quotient of a disjoint union') of representable presheaves. Now we have enough theory to have it tell us something about graphs that we already knew.

Our small category Q has two objects: V and A. They give us two presheaves on Q, a.k.a. graphs, namely よ(V) and よ(A). What are these graphs? Let's calculate. The functor よ(V) maps the object V onto the one point set Hom(V,V) (which contains only id_V) and it maps A onto the empty set Hom(A,V). This already tells us (without calculating the action of よ(V) on s and t) that the graph よ(V) is the graph that consists of a single vertex and no arrows. The functor よ(A) maps V onto the two point set Hom(V,A) and A onto the one point set Hom(A,A). Two vertices (s and t), one arrow (id_A). What does よ(A) do with the Q-morphisms s and t? It should map them onto the functions Hom(A,A) -> Hom(V,A) that map a morphism f onto f ∘ s and f ∘ t, respectively. Because Hom(A,A) contains only id_A, these are the functions that map it onto s and t in Hom(V,A), respectively. So the one arrow in よ(A)(A) has s in よ(A)(V) as its source and t as its target. We conclude that よ(A) is the graph with two vertices and one arrow from one to the other.

We have found the representable presheaves on Q. By the density theorem, any graph is a colimit of よ(V) and よ(A) in a canonical way. Put another way: any graph consists of vertices and arrows between them. I'm sure you'll agree that this was worth the effort.

[mthevlamister]

Let's Discuss Gödel's Incompleteness Theorems

Second big math post! I may keep doing this as I prolong writing!

This series of posts is also called "I put all my money into learning mathematics and its explorers, now you have to deal with it."

Background Info:

Statement: a sentence that either always true or always false [3 is rational is a true statement]

In contrast to this, an Open Sentence: a sentence that uses variables that does not have a clear truth/false indicator [x = 3. How do I know that? X doesn't always equal 3].

Formalist: a mathematician who believes that we create math. It's like a game of chess. We make the rules.

Platonist: a mathematician who believes math exists beyond us. We cannot create math. We can only discover it's true nature.

So, let's get into it.

There are two theorems by Gödel that discuss incompleteness.

The first is as follows: Any consistent formal system F within which a certain amount of elementary arithmetic can be carried out is incomplete; i.e., there are statements of the language of F which can neither be proved nor disproved in F.

The second is: For any consistent system F within which a certain amount of elementary arithmetic can be carried out, the consistency of F cannot be proved in F itself.

Let's break down the thought process of these.

When we have a statement, we know the rules listed above. However, will we always find a proof for it? Sure, I could prove that the square root of thirteen is irrational [very fun proof if you ever want to look into it], but will I find a proof of why the grass in my yard is green? It's a true statement. My grass is very green, but I can't really prove it [maybe I can! I'm lazy].

And will there be a contradiction? Yes, the grass is green now, but what happens when the amount of sunlight changes? Are some bits yellow? Are my color-rods just dogshit? What about when the grass isn't there? Is it still green?

I can't prove that my grass' color will never lead to a contradiction! It very well could! One day, in one hundred years, maybe grass will change to be a different shade! My proof is now contradicted because of future events, but I don't know that at the moment.

Now there are two types of mathematicians: platonists and formalists. If you're like me, you may wish to say you're a mix. That it's a game we can play, but we didn't invent it. That being said, I'm a platonist for sure, but that's besides the point. My point is that this theorem follows the platonist imo. There are statements that exist that we cannot prove, whether true or false, but they exist freely without us showing the truth.

I. Adore. Math.

[topoillogical]

for math ask meme: 19 (*not* 18), 49, 53, 57

19.How did you solve it [a good math problem you've solved recently]?

Talking with friends was definitely a huge part of solving it, both in the sense that they were able to act as rubber ducks / sounding boards and that they were able to provide important insight. 

In terms of the mental path that I took to solving it, the first step was finding intuitive characteristics that distinguished each space. One space was clearly different from the other two because it was compact, and a friend of mine helped me prove that it was the unique compact space satisfying the properties.

The intuitive characteristic that distinguished the remaining spaces was the reach of open neighborhoods around a special point. In one space, these neighborhoods were short and close to the special point, whereas in the other space, any open neighborhood around the special point contained points arbitrarily far away along the number line. In order to put these into words, I called the spaces "Daddy shortfingers" and "Daddy longfingers", with the "fingers" here being the open neighborhoods.

Upon describing daddy shortfingers and longfingers to a different friend in this way, he quickly realized that shortfingers was locally compact while longfingers wasn't, which was a really neat way of formalizing my idea of them being different based on the length of these metaphorical fingers. Given this categorization, I was able to use methods similar to the one I used for a compact space to show that daddy shortfingers was the unique locally compact space satisfying the properties, and daddy longfingers was the unique non locally compact such space. It was SO satisfying. 

49. What’s your favorite number system? Integers? Reals? Rationals? Hyper-reals? Surreals? Complex? Natural numbers?

Probably the complex numbers! It's kind of cliché, but they're popular for a reason. Algebraic completeness is an absolutely delicious property -- especially if I'm doing anything linear algebra related, I will choose to work in the complex over the reals any day. 

In analysis they behave beautifully too; complex analysis is an absolutely gorgeously simple subject where all the gnarly little sticky points in real analysis melt away. And also you can calculate infinite sums using residues!

53. Do you collect anything that is math-related?

I SORT OF collect math books! I always keep my textbooks and when I go to a book store, the first place I go (and where I usually buy from) is the math section -- these purchases may be pop math books, and I have SEVERAL of these (just books describing cool uses of math, or cool math problems, the weirdest mathematicians and theorems, etc), or they may be more academic (I once impulse purchased a copy of La Geometrie just because it had a beautiful split-page format of the original French with a modern English translation).

57. What inspired you to do math?

My entire childhood and teenage years, basically. I was incredibly lucky to be not only recognized as a gifted child but also given accommodations for this, meaning that I had access to more advanced content than my peers, and later, that I was placed in a program with similarly gifted children and given advanced curriculum. This meant that the way math was taught was often different from the standardized bullshit criticized in A Mathematician's Lament, and I was able to really appreciate and dig into it.

One thing that stands out from childhood as being important to my mathematical development is that when I was very small, pre-kindergarten, my mom taught me multiplication using cut out paper squares. She then taught me cubes and cube roots with sugar cubes, so for example I could multiply 2 x 5 x 7 by making a 5 x 7 grid of cubes, and then putting another layer on top (and then compute the answer by counting them if I so desired), or I could make a 3 x 3 x 3 cube and conclude that 3^3 was 27 and that 3 was the cubed root of 27. This was an EXTREMELY basic understanding of multiplication, as I only understood the geometric rules. Still, it was a formative memory to tiny little 3 year old me, so much so that I still remember how I enjoyed it and how it sparked my interest in math. 

Later, in middle school, I had a particularly great 7th grade teacher, who posed the problem to us of creating every number between 1 and 100 using only 4 4s, and some basic operations. The problem was so fun to work on that I worked on extensions of it for a couple years afterwards. In high school my 10th grade math teacher was particularly lovely, and I had a teacher for both 9th and 12th grade who was just so overwhelmingly organized that class was an absolute delight (polished powerpoints, good homework and tests which you'd get back the next day, etc). This culminated in 12th grade me ONLY enjoying math class, partially because of the organization and sense that the class made, and partially because I just loved the subject and also found it the easiest. That then led to 12th grade me ONLY SHOWING UP to math class and skipping all my other classes, so when it came time to pick a major on my university applications the choice was obvious. I could literally only be fucked to do math. Therefore, I must major in math.

As I've gotten older, I've gotten more competent at stuff like organization and motivation, and I can show up to classes that aren't math and am even double majoring in psychology. But I just have this intense passion for math that never goes away, and that's why I stay. It's not the only thing I am able to do any more, and it's certainly not the easiest. But I LOVE it, you know?

Thank u for the questions btw!

[phantom-does-a-thing]

i want to talk to you about the pythagoreans because they are fucking insane

so they believed that all math was rational and that every single thing on earht could be descirbed/expressed rationally. there were no imaginary numbers adn there was no such thing as an irrational number (like w square roots in the denominator)

but they discovered the Pythagorean theorem

which disproved that belief

because unless it's a pythagorean tripple (like 345) there gonna be an irrational number in there (like a 30 60 90)

so they hid this. they didnt tell the rest of their world about their discovery because to them it was essentially blasphemy

until this one guy is like "yall are ridiculous. people deserve to know this"

so he tells the world

and they fucking kill him.

also they didnt eat beans because to the pythagoreans they "looked like fetuses" so they couldnt eat beans.

absolutely bonkers

Idk, they should've kept it a secret I feel like that dude had it coming to him. If it weren't for him I wouldn't have to be learning about freaking radicals and stuff in school. That's the one part about algebra that I hate.

I respect their decision not to eat beans because beans taste bad, but their reasoning is yknow. I won't say it but I'm thinking it. Fetuses hm.

Irrational numbers and imaginary numbers deserved to stay hidden away tbh

[asqtbg05-blog]

January 4, 2021

I woke up very early today at 4:30 A.M. I pray first then i start using my phone. I watch videos to waste some time. I ate breakfast early so I won’t be late for my online class. We do an activity in our ESP class about how we celebrate the Christmas and New Year despite of this Pandemic we are experiencing. I ate my lunch 30 minutes before my next class. We studied about rational root theorem in our math class. I’m doing my diary a few minutes before 8 P.M. and I still have a lot school works to do and I still have to do my devotion. I wish Tomorrow I’ll be faster doing my school works. This is the first day of continuing the classes  and I’m adjusting again. I am thankful for the year that passed, My family are healthy and is very well. I am hoping that 2021 will be a better year for all of us.

[thewestcoastmathtutor]

How to Rationalize the Denominator of a 3rd Root | The Westcoast Math Tutor

How to Rationalize the Denominator of a 3rd Root | The Westcoast Math Tutor https://www.youtube.com/watch?v=X_tqzahPKFU This video shows how to rationalize the denominator of a 3rd root. 🔔 Join The Westcoast Math Tutor to watch more content on High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ✅ Stay Connected To Me. 👉 Facebook: https://ift.tt/AEfyb2V ✅ For Business Inquiries: thewestcoastmathtutor@gmail.com ============================= ✅ Recommended Playlists: 👉 Decimal to Fraction https://www.youtube.com/watch?v=3J8Dnl0wLQE&list=PLPSu23Z8U7JG3C22WEiDhDf2bBXZ2yQJK 👉 Improper Fraction to Mixed Number https://www.youtube.com/watch?v=VvL7fXAYtHg&list=PLPSu23Z8U7JG0ErjzsUGv6KfDThOE7SxO 👉 Linear Equation https://www.youtube.com/watch?v=UUeuIQ6bUxU&list=PLPSu23Z8U7JGhun3PPquRpkjrMdNFAggz&pp=iAQB ✅ Other Videos You Might Be Interested In Watching: 👉 Evaluating Logarithms https://www.youtube.com/watch?v=ve9BMVUC6fE 👉 Exponential to Logarithmic Form & Logarithmic to Exponential Form https://www.youtube.com/watch?v=KbEULbAjvtI 👉 Logarithms Easy ! 2 Explanations https://www.youtube.com/watch?v=77msni1vacc 👉Boundedness Theorem, 2 Examples https://www.youtube.com/watch?v=NWPFmBmu380 ================================ ✅ About The Westcoast Math Tutor: Hello Friends! I’m The Westcoast Math Tutor, and with this channel, I will provide tutorial videos to better your understanding of different high school math topics. Once in a while, I will also make other interesting math videos outside of high school math topics. If you have any questions, please ask me in the comments. This channel is what I’ve been doing for you. If you want to do something for me, hit the bell button, like, and share. Thanks for watching, and happy learning, everyone! ✅For Appointment and Business inquiries, please use the contact information below: 📩 Email: thewestcoastmathtutor@gmail.com 🔔Subscribe for more High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ================================= #logarithmroots #inverseproperty #logarithmbasics #logarithmtutorial #mathexplained #logarithmproblems Disclaimer: I do not accept any liability for any loss or damage incurred by you acting or not acting as a result of watching any of my publications. You acknowledge that you use the information I provide at your own risk. Do your research. Copyright Notice: This video and my YouTube channel contain dialogue, music, and images that are the property of The Westcoast Math Tutor. You are authorized to share the video link and channel and embed this video in your website or others as long as a link back to my Youtube Channel is provided. © The Westcoast Math Tutor via The Westcoast Math Tutor https://www.youtube.com/channel/UCqP_EgHF0TGr65xMEcFPcjA September 12, 2023 at 09:32AM