#bigotime

[latextestblog]

\(\LaTeX\) test post \(\iddots\cal R \frak g \mathbb{R}\;\;\bigotimes^n_{i=1}\mathscr{V}_i\) \[J:=\int_0^1 \left(\frac \pi 4+\arctan t\right)^2\cdot \log t\cdot\frac 1{1-t^2}\; dt =-\frac 1{64}\pi^4\] \begin{xy}\xymatrix{ 0 \ar@{=}[d] \ar@{->}[r]^{0} \ar@{->}[rd] & A \ar@{->}[r]^{i_1} \ar@{->}[d] \ar@{->}[rd] & B \ar@{->}[r]^{j_1} \ar@{->}[d] \ar@{->}[rd] & C \ar@{->}[r]^{0} \ar@{->}[d] \ar@{->}[rd] & 0 \ar@{=}[d] \\\\ 0 \ar@{->}[r]^{0} & D \ar@{->}[r]^{i_2} & E \ar@{->}[r]^{j_2} & F \ar@{->}[r]^{0} & 0 }\end{xy}

guess all commutative diagrams and music notation will have to be shitty png's for now

$$\begin{aligned} K &= \int_0^1\arctan^2 t\cdot\log t\;\left(-\log\frac {1-t}{1+t}\right)’\; dt \ &= \underbrace{\int_0^1\arctan^2 t\cdot\frac 1t\cdot \log\frac {1-t}{1+t}\; dt}_{=2K\text{ (why?)}} \ &\qquad\qquad+ \underbrace{\int_0^12\arctan^2 t\cdot\frac 1{t+t^2}\cdot \log t\cdot \log\frac {1-t}{1+t}\; dt}_{=-K\text{ (why?)}} \ . \end{aligned}$$

\(\text{Lorem ipsum \verb!\ \\ \\\ \\\\! dolor sit amet, consectetur adipiscing elit}\), sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. \begin{verbatim}Nullam non nisi est sit amet facilisis magna.\end{verbatim} Dictum fusce ut \verb!placerat! \(\verb!orci nulla \ \\ \\\ \\\\ !\). Ipsum dolor sit amet consectetur adipiscing elit duis tristique sollicitudin. \(\displaystyle\int_0^{2\pi} x^2\; \cos x \cdot\operatorname{Li}_2(\cos x)\; dx\) Ultricies mi eget mauris pharetra et ultrices neque. Mollis nunc sed id semper. Laoreet sit amet $ 64\int_0^1 \left(\frac \pi 4+\arctan t\right)^2\cdot \log t\cdot\frac 1{1-t^2}\; dt =-\pi^4$ cursus sit amet dictum. Amet massa vitae tortor condimentum lacinia quis. Egestas sed sed risus pretium quam vulputate dignissim suspendisse in. Ut porttitor leo a diam sollicitudin tempor. Interdum velit euismod in pellentesque massa placerat.

Auctor elit sed vulputate mi. Vitae semper quis lectus nulla at volutpat. Odio tempor orci dapibus ultrices. \(\lim_{x \to 0+}(2\sin \sqrt x + \sqrt x \sin \frac{1}{x})^x\) Ornare suspendisse sed nisi lacus sed viverra. Maecenas volutpat blandit aliquam etiam erat velit scelerisque. Suspendisse in est ante in nibh mauris cursus.

\[ \lim_{x \to 0+}\left(2\sin \sqrt x + \sqrt x \sin \frac{1}{x}\right)^x \ = \exp \left(\lim_{x \to 0+} x \ln\left(2\sin \sqrt x + \sqrt x \sin \frac{1}{x}\right)\right) = \exp\left(\lim_{x \to 0+} \frac {\ln \left(2\sin \sqrt x + \sqrt x \sin \frac{1}{x}\right)} {\frac 1 x}\right) = \exp \lim_{x \to 0+} \dfrac {\dfrac {\cos \sqrt x} {x} + \dfrac {\sin \dfrac 1 x} {2 \sqrt x} - \dfrac {\cos \dfrac 1 x} {x^{3/2}}} {- \dfrac {1} {x^2} \left(2\sin \sqrt x + \sqrt x \sin \frac{1}{x} \right)} \]

tikz-cd commutative diagram

\[\begin{tikzcd} {\displaystyle{\mathcal P(n)\odot\left(\bigodot_{i=1}^n \mathcal{P}(m_i)\right)\odot\left(\bigodot_{i=1}^n\left(\bigodot_{j=1}^{m_i} \mathcal{P}(l_{i_j})\right)\right)}} & {\displaystyle{\mathcal P(n)\odot\left(\bigodot_{i=1}^n \mathcal{P}(m_i)\odot\left(\bigodot^{m_i}_{j=1}\mathcal{P}(l_{i_j})\right)\right)}} \\ & {\displaystyle{\mathcal P(n)\odot\left(\bigodot_{i=1}^n \mathcal{P}(l_i)\right)}} \\ {\displaystyle{\mathcal P(m)\odot\left(\bigodot_{i=1}^n\left(\bigodot_{j=1}^{m_i} \mathcal{P}(l_{i_j})\right)\right)}} & {\mathcal{P}(l)} \arrow["s", from=1-1, to=1-2] \arrow["{\gamma\odot\mathrm{id}}"', from=1-1, to=3-1] \arrow["\gamma"', from=3-1, to=3-2] \arrow["{\displaystyle{\mathrm{id}\odot\left(\bigodot_{i=1}^n\gamma\right)}}", from=1-2, to=2-2] \arrow["\gamma", from=2-2, to=3-2] \end{tikzcd}\]

amscd commutative diagrams (they don't work here lol)

\[\begin{CD} S^{{\mathcal{W}}_\Lambda}\otimes T @>j>> T\\ @VVV @VV{\mathrm{End} P}V\\ (S\otimes T)/I @= (Z\otimes T)/J \end{CD}\]

\begin{CD} A @>a>> B\\ @VVbV @VVcV\\ C @>d>> D \end{CD}

\begin{CD} A @<<< B @>>> C\\ @. @| @AAA\\ @. D @= E \end{CD}

shitty png

music

\begin{music} \parindent10mm \instrumentnumber{1} % a single instrument \setname1{Piano} % whose name is Piano \setstaffs1{2} % with two staffs \generalmeter{\meterfrac44} % 4/4 meter chosen \startextract % starting real score \Notes\ibu0f0\qb0{cge}\tbu0\qb0g|\hl j\en \Notes\ibu0f0\qb0{cge}\tbu0\qb0g|\ql l\sk\ql n\en \bar \Notes\ibu0f0\qb0{dgf}|\qlp i\en \notes\tbu0\qb0g|\ibbl1j3\qb1j\tbl1\qb1k\en \Notes\ibu0f0\qb0{cge}\tbu0\qb0g|\hl j\en \zendextract % terminate excerpt \end{music}

array commutative diagram without hacks

\[\begin{array}{ccccccccc} 0 & \xrightarrow{i} & A & \xrightarrow{f} & B & \xrightarrow{q} & C & \xrightarrow{d} & 0\\\ \downarrow & \searrow & \downarrow & \nearrow & \downarrow & \searrow & \downarrow & \nearrow & \downarrow\\\ 0 & \xrightarrow{j} & D & \xrightarrow{g} & E & \xrightarrow{r} & F & \xrightarrow{e} & 0 \end{array}\]

array commutative diagrams with hacks from StackExchange (they don't work here lol)

$$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} 0 & \ra{f_1} & A & \ra{f_2} & B & \ra{f_3} & C & \ra{f_4} & D & \ra{f_5} & 0 \\ \da{g_1} & & \da{g_2} & & \da{g_3} & & \da{g_4} & & \da{g_5} & & \da{g_6} \\ 0 & \ra{h_1} & 0 & \ra{h_2} & E & \ra{h_3} & F & \ra{h_4} & 0 & \ra{h_5} & 0 \\ \end{array} $$

\[\newcommand{\ra}[1]{\kern-1.5ex\xrightarrow{\ \ #1\ \ }\phantom{}\kern-1.5ex} \newcommand{\ras}[1]{\kern-1.5ex\xrightarrow{\ \ \smash{#1}\ \ }\phantom{}\kern-1.5ex} \newcommand{\da}[1]{\bigg\downarrow\raise.5ex\rlap{\scriptstyle#1}} \begin{array}{c} 0 & \ra{f_1} & A & \ra{f_2} & B & \ra{f_3} & C & \ra{f_4} & D & \ra{f_5} & 0 \\ \da{g_1} & & \da{g_2} & & \da{g_3} & & \da{g_4} & & \da{g_5} & & \da{g_6} \\ 0 & \ras{h_1} & 0 & \ras{h_2} & E & \ras{h_3} & F & \ras{h_4} & 0 & \ras{h_5} & 0 \\ \end{array}\]

xy-pic commutative diagram Due to rich text editor shenanigans, \(\backslash\backslash\mapsto\backslash\), even in \verb, but not in the hashtags. Putting these xy-pic's in the title causes it to duplicate the entire title in the post body.

\begin{xy} \xymatrix { U \ar@/_/[ddr]_y \ar@{.>}[dr]|{\langle x,y \rangle} \ar@/^/[drr]^x \\\\ & X \times_Z Y \ar[d]^q \ar[r]_p & X \ar[d]_f \\\\ & Y \ar[r]^g & Z } \end{xy}

[kazexmoug-blog]

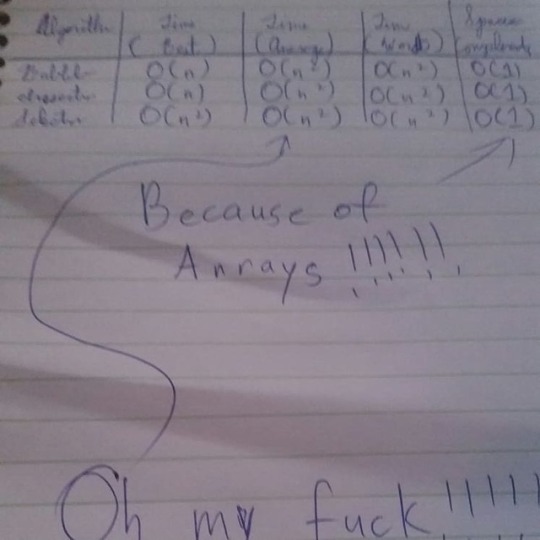
When your average case is also your worst case and you actually know what it means.......THANKS ARRAYS LOL!!!!!! #coding #datastructuresandalgorithms #learningtocode #computerscience #sortingalgorithms #timecomplexity #bubblesort #insertionsort #selectionsort #bigotime #computerscienceisfun #learningsomethingnew #learningtoimprove #selftaughtcoder #kazexmoug #learningtech #timecomplexity #spacecomplexity #runtimes #algorithms #softawareengineering #mathisfun #computerscienceforeveryone #codingmakesmehappy #mathisnotscary #teachyourselfcode #algorithmanalysis #gettingoutofmyhead #criticalthinking #entryleveltech https://www.instagram.com/p/Bz3ONFXpZYe/?igshid=ibaa3jipzdz

[shengshampoo]

藉由 MathJax使用 LaTeX語法編寫數學公式教程

藉由 MathJax使用 LaTeX語法編寫數學公式教程

致敬轉載翻閱臨摹的資料來源，內容：

MathJax使用LaTeX语法编写数学公式教程

如何插入公式

LaTeX的數學公式有兩種： 行中公式和獨立公式。 行中公式放在文中與其它文字混編， 獨立公式單獨成行。

行中公式可以用如下兩種方法表示： \(Math Formulas\)　 或　$Math Formulas$ 獨立公式可以用如下兩種方法表示： \[Math Formulas\] 或　$$Math Formulas$$

例子：

語法：

$[J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma (m + \alpha + 1)} {\left({ \frac{x}{2} }\right)}^{2m + \alpha}]$

數學輸出顯示：

$[J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m! \Gamma (m + \alpha + 1)} {\left({ \frac{x}{2} }\right)}^{2m + \alpha}]$

語法：

When $a \ne 0$, there are two solutions to \(ax^2 + bx + c = 0\) and they are $$x = {-b \pm \sqrt{b^2-4ac} \over 2a}.$$

數學輸出顯示：

When $a \ne 0$, there are two solutions to \(ax^2 + bx + c = 0\) and they are $$x = {-b \pm \sqrt{b^2-4ac} \over 2a}.$$

如何插入公式大括號

語法 1：

$$ f(x)=\left\{ \begin{aligned} x & = & \cos(t) \\ y & = & \sin(t) \\ z & = & \frac xy \end{aligned} \right. $$

數學輸出顯示： $$ f(x)=\left{ \begin{aligned} x & = & \cos(t) \ y & = & \sin(t) \ z & = & \frac xy \end{aligned} \right. $$

語法 2：

$$ F^{HLLC}=\left\{ \begin{array}{rcl} F_L & & {0 < S_L}\\ F^*_L & & {S_L \leq 0 < S_M}\\ F^*_R & & {S_M \leq 0 < S_R}\\ F_R & & {S_R \leq 0} \end{array} \right. $$

數學輸出顯示：

$$ F^{HLLC}=\left\{ \begin{array}{rcl} F_L & & {0 < S_L}\\ F^*_L & & {S_L \leq 0 < S_M}\\ F^*_R & & {S_M \leq 0 < S_R}\\ F_R & & {S_R \leq 0} \end{array} \right. $$

如何輸入上下標

^ 表示上標， _ 表示下標。 如果上下標的內容多於一個字符， 要用 {} 把這些內容括起來當成一個整體。 上下標是可以嵌套的， 也可以同時使用。

語法：

$x^{y^z}=(1+{\rm e}^x)^{-2xy^w}$

數學輸出顯示：

$x^{y^z}=(1+{\rm e}^x)^{-2xy^w}$

如果要在左右兩邊都有上下標， 可以用\sideset命令。

語法：

$\sideset{^1_2}{^3_4}\bigotimes$

數學輸出顯示：

$\sideset{^1_2}{^3_4}\bigotimes$

語法：

$$\max_{k}$$

數學輸出顯示：

$$\max_{k}$$

語法：

$$\mathop{argmax}_{K}$$

數學輸出顯示：

$$\mathop{argmax}_{K}$$

如何輸入括號和分隔符

() 、[] 和 | 表示自己， {} 表示 {}。 當要顯示大號的括號或分隔符時， 要用 \left 和 \right 命令。

語法：

$f(x,y,z) = 3y^2z \left( 3+\frac{7x+5}{1+y^2} \right)$

數學輸出顯示：

$f(x,y,z) = 3y^2z \left( 3+\frac{7x+5}{1+y^2} \right)$

有時候要用 \left. 或 \right.進行匹配而��顯示本身。

語法：

$\left. \frac{ {\rm d}u}{ {\rm d}x} \right| _{x=0}$

數學輸出顯示：

$\left. \frac{ {\rm d}u}{ {\rm d}x} \right| _{x=0}$

如何輸入分數

語法：

$\frac{1}{3}$

數學輸出顯示：

$\frac{1}{3}$

語法：

$1 \over 3$

數學輸出顯示：

$1 \over 3$