#borsuk-ulam

[mapsontheweb]

The Borsuk-Ulam Explorer.   Just think what a coincidence it would be if the earth was exactly the same temperature at two point opposite each other on the surface? Similarly for another measurement like pressure. Yet thanks to algebraic topology we know not just that such pairs of points must exist at all times, but at least one pair must have both the same temperature and pressure.  Use the

Borsuk-Ulam Explorer

to see for yourself…

[trendydigests]

How to Cut a Ham Sandwich and Other Math Tricks

Have you ever wondered how to cut a ham sandwich into two equal parts with one slice? Or how to find a point on a sphere that has the same temperature as its opposite point? Or how to fold a protein or control a robot using polygons? If you are curious about these questions, you might be interested in learning about the Borsuk-Ulam theorem, a mathematical theorem that has many surprising and…

[jonathankatwhatever]

This AMT was intense. I made a ton of mental notes to type out and can’t remember any of them.

The typing appears back to normal, which is a relief. Had to restart the app a few times.

I saw my fear in light of something called the Borsuk-Ulam Theorem, which relates pairs over a dimensional enclosure, meaning over a Euclidian space within an n-sphere.

My intense fear that somehow I’m wrong, that this can’t be happening, that there must be something crucial I’ve missed, that I’ve either been misled or have misled myself, that I’m delusional in the bad sense, that I’m being betrayed, that maybe I don’t know the real mission and I’m being used. Those all align on the fear axis. That axis can’t go away because it contains its own positives, meaning it pairs in 1-0Segments over the 1-0Space (which may be a better name than 0Space). Fear that I’m not doing enough is an obvious example. Fear for everything that happens with regard to you. Fear of unknowns.

And it isn’t that there’s a single voice which stretches 0-1-0 over the enclosed dimensional space. No, it’s more that there are baubles, those dimensional bubbles which connect on a counting string, which connect over the 1-0Space. They lie on the counting string which connects the polar Ends. And the string they connect across is the 1Space counting, meaning the gs processes that say this is the same over this extent.

I’m not sure how best to say that all the mathematics has come together. All the visions seem to have clear, proven analogues. e eyboard acting up again .

——

Trying again. Nope. Need to use onscreen keyboard. Yuck.

Just looked at L-functions again. Made sense with the injection model. I looked at Dirichlet characters and that connects injection to the modularity of the identity functions we describe.

[auroral-melody]

bonus ask: infodump about the most obscure math thing you can think of off the top of ur head

this isn’t obscure but it IS really cool

borsuk-ulam theorem, or “meterologist’s theorem”: if you look at earth, there are always two points across from each other (”antipodal”, think north and south poles) that have the same temperature/pressure/humidity/whatever you’re measuring, as long as whatever you’re measuring is continuous.

it has to do with the Intermediate Value Theorem. if you don’t know anything about calculus, it basically means “if i have a line between 1 and 5, somewhere on that line is a 4″. it’s one of those math theorems that’s feels A Bit Obvious but it’s important to establish ok. basically, if things don’t suddenly jump/teleport, we can say this.

okay, let’s get into the why! pick two points on earth, call em a and b. they’re opposite each other.

now move them along any path you like (as long as they stay antipodal) so that they get to the other point. the temperatures HAVE to cross, and that’s where they’re equal!

to put it another way, more mathematically: make a function f, where

f = the temp at a - the temp at b.

ignore my ms paint drawing of the earth and the fact that those AREN”T the north and south poles

the order here matters which you subtract. it flips to the negative when you’ve moved to the other point. now, f is a continuous function (we’re assuming the earth’s temperature doesn’t Suddenly Jump, so we can apply the IVT), so f hits every point in between 30 and -30 if you go between them like in the gif above.

so, when you look at f on one point, you’re positive. then you travel t the other point and check, and it’s negative. at some point there, it crossed zero! at that point, the temperatures were equal.

0 = temp of a - temp of b

temp of b = temp of a

now, if you do this infinitely many times, you end up with a band of points that have antipodal equal temperatures, because blah blah continuity, basically. if you do this same process with pressure, but this time only measuring on those points / following that band --

you’ll find a point with the same temp and pressure :)

references i stole these explanations and gifs from:

https://brilliant.org/discussions/thread/borsuk-ulam-theorem-the-global-version/

http://mathforum.org/library/drmath/view/54746.html

[bsdndprplplld]

8 V 2022

I am on my way home from a math conference, the first one in which I participated actively – I prepaired the talk about the Borsuk-Ulam theorem

my lecture was centered around the connection between the classic "continuous" BUT and its combinatorial analog: Tucker's lemma

I wanted to talk about this because I was amazed at how cool and "versatile" this theorem is. there is a whole book about its applications and generalizations, which is btw very well-written, I highly encourage everyone to read it:

my presentation went well, although after practicing it for about a week the topic seemed really fucking boring to me, no wonder

other than that I have another recommendation to make. do you also hate how messy multivariable calculus is? I do. calculations and technical definitions everywhere, and at the end everything comes down to calculating the determinant of some jacobian. bluh. I stumbled upon a book that describes everything from a sort of algebraic perspective, smells a little bit like category theory too. very clean, very satisfying to read:

I have been studying covering spaces recently and I can give some dope motivation for learning about the structure induced by the covering mapping:

I will never forget that the homomorphism induced by the covering projection is injective

that would be it for my mathemathical life. my personal life, which is still closely connected to math, brings me some psychological progress. I no longer get stuck in loops of "oh I'm so bad at math. maybe I'm not? I got a good grade from X. ah but I got a shit grade afterwards". it might be because I didn't fall on my face for a while now, only decent grades, good ideas, a good presentation, this is correct. but I also do not negotiate with myself that this is supposed to be proof that I'm good enough, I just stopped paying attention to these and focused on math instead. and paradoxically when I stopped caring about being good at math I was rewarded with getting better at math???

a coincidence,

a pleasant one, nonetheless.

anyway I will have to take a fall at some point, unavoidable. and it will be the final test of my progress, becauase I used to get very elevated in my sense of self-worth after receiving a single good grade among trash ones and now I'm just ok. not the god, just ok. but back then, at some point I would no longer be god, I would get smacked in the face by some "proof that I'm actually trash" and that would be a fall from a significant altitude. so I'm hoping that the fall will also be less painful now

I think the biggest change I made was giving up, I abandoned all hope. nooow here is the moment when people interrupt me with "nooo that's horrible don't give up you're a great person you just have to notice that"

fuck off you don't understand shit

I'm doing better now precisely because I stopped hoping that one day I'll stop feeling worthless, that one day something great will happen that will prove once and for all that I'm meant for something great. I can't stand this anymore, I am disgusted by the fact that deep down I still believe that I'm supposed to be the best and that I can't enjoy anything unless I am winning. I want to puke when I'm reminded that everything I do serves the purpose of winning the negotiations I have with myself about what my actual value is

my self-hatred runs much deeper now than ever before and I have no more patience for self-victimization, no more room for "allowing myself to feel". fuck off, all I feel is rage. I want to be able to do things without the prospect of a reward, my goal is to enjoy things, not the sense of being good at doing things

so that's what I'm doing, I made peace with the fact that I will probably never feel good about myself and that I have no chance at achieving the greatness I crave. and I must say I started respecting myself more, turns out I am actually able to do things without the promise of being the best at them, the vision of bringing value to the world motivates me. and fuck the western culture with its oh you must love yourself you are a great person. no, you don't have to do that and you have no way of knowing what kind of person you are, nobody has ever defined it in a strict formal sense, people just use this phrase to trigger the feel-good in others

I am aware that all of this sounds really bad, but I don't care, it works. and my math will be better like that because now that I stopped crying over being trash I have more time to study

I just hope that the fall won't be as painful

[lolt64]

firmly dont believe the borsuk-ulam theorem. wont even capitalize it

[hollowlunerfang]

Liked on YouTube: Who (else) cares about topology? Stolen necklaces and Borsuk-Ulam https://youtu.be/FhSFkLhDANA

[natedlock]

Just some more math from the ol’ youtube channel

[hippasos]

In George Orwell's distopian novel "Nineteen Eighty-Four" the author describes a world divided into three pieces by totalitarian or authoritarian states which are always fighting against each other. The people living in the state "Oceania" are under constant surveillance by televisions and have to worship the great "Big Brother" whose existence is not even clear. The protagonist tries to escape from the system to get privatcy, but in the end he becomes a part of the omnipresent system after a brain-washing and loves the "Big Brother". Well, that's a nice story, but why is it a part of the series "math explains world"? Last time we had the Borsuk-Ulam-theorem. It gives an awsome application in this context. :) Let's consider the map of Orwell's distopian world.

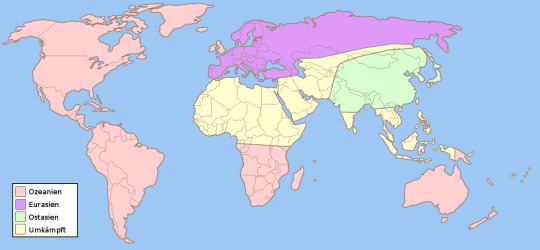
There are three countries: Oceania, Eurasia and Eastasia. Now we wounder, if there is a pair of antipodal points, s.t. one of the teritories of the countries includes this pair of points! Further more we wounder, if this is always the case. So is it possible, that there exists a pair of antipodal points, s.t. in any constellation of divisions of the world into three teritories this pair is included in one of the teritories?

The answer is YES!!! :D You can use any division into three pieces, but there is always a pair of antipodal points in one of the three teritories. OK, to be mathematically correct, the division of the 2-Sphere (notation: S^2), which is in our case just the surface of the earth, into three sets has to be, s.t. this sets are closed. This means: If we consider the boundaries of the sets, then their boundaries have to be in each set they're belonging to (see: https://en.wikipedia.org/wiki/Closed_set). Further more there have to be exactly three teritories (not 4 like in the picture). The lemma is the following:

Whenever S^2 is expressed as the union of three closed sets C1 , C2 and C3, then at least one of these sets must contain a pair of antipodal points {x,−x}.*

The question is: Why?

Proof: Let's consider S^2 as a subspace of the IR^3 and let d be the distance from one point of the 2-sphere to an other point on this sphere by going a path on the sphere. This is just the distance you know in real life. If you go from your home to an other city by car and you can drive just the linear distance, then you are not going the direct way, but a way which is determined by the curvature of the earth which we can approximate by a 2-sphere. We now define three distance functions, D_i: S^2 --> IR for i = 1,2,3 mapping a point x to the distance of this point to C_i, i.e. D_i(x) = inf_{y in C_i}(d(x,y)). What is this cruel map describing? The inf (read: Infimum) of something searches for the smallest value of d(x,y) by varying the point y in C_i. These D_i are continuous. Now consider the map f: S^2 --> IR^2 with f(x) = (D_1(x), D_2(x)). We sayed that this lemma comes from the Borsuk-Ulam-theorem. So we will use it here. By the theorem there exists a point x, s.t. f(x) = f(-x), i.e. D_1(x) = D_1(-x) and D_2(x) = D_2(-x). If D_1(x) = D_1(-x) = 0, then x and -x are in C_1. Similarly for D_2. But if they are both D_1(x) and D_2(x) not 0, then x and -x must belong to C_3.

That's the proof. Q.E.D.

Next time we will discuss the structure of the universe. See you then!

*Source: Hatcher, Allen (2001): Algebraic Topology, URL: http://www.math.cornell.edu/~hatcher/

Source of the pictures: wikipedia.

[curiosamathematica]

It's been a while! This time, I'll present you Tucker's lemma, a combinatorial lemma which is analogue to the perhaps more famous Borsuk-Ulam theorem.

The latter states that every continuous function from an n-sphere into Euclidean n-space maps two opposite points to the same point. You can interpret this as follows for n=1: there are always two location on the Earth's equator with exactly the same temperature. Opposite points on a sphere are called "antipodal". For n=2, Borsuk-Ulam guarantees the existence of antipodal points on the Earth with equal temperature and barometric pressure.

Now, let's dive into the discrete analogue of Borsuk-Ulam. Consider a circle and add an even number of points, say 2n, on the boundary, with the restriction that every point must have an antipodal ally. Next, add as many points in the interior as you wish, without restriction. Divide the circle into triangular regions by connecting the points willingly. Finally, label the points with numbers from the set {-2, -1, 1, 2}. Antipodal points must have opposite labels, but you're free to choose the inside labels.

However, despite your liberty in this process, Tucker's lemma states you can always find a line segment in this configuration whose endpoints have opposite labels! In the example above, the dashed segment is the one we're looking for. Just as the Borsuk-Ulam theorem, you can generalize this to higher dimensions, cf. Wikipedia. 

[hippasos]

M.E.W.: Bursuk-Ulam

Let's start the topic "math explains world" (M.E.W.) with a result from Algebraic Topology. In its mathematical formulation the theorem looks not very interesting:

If f: S^2 ---> IR^2 is continuous, then there exists a pair of antipodal points x and -x, s.t. f(x) = f(-x), where S^2 denotes the 2-sphere (something which we can imagine as the surface of a ball) and IR^2 is the real number plane.

This theorem is the so-called Borsuk-Ulam-theorem. Stanisław Marcin Ulam, who also was involved in the early development of nuclear weapons, assumed that this theorem might be correct. Karol Borsuk, a Polish mathematician, proved 1933 the theorem.

But why should we be interested in such a boring thing from the last century? Well, I can reassure you, it's not that boring. ;-)

The application of this theorem implies a result which is really mindblowing. Let us consider temperature and pressure on earth. We can imagine the S^2 to be the surface of the earth. Antipodal points on earth are just points which lie on opposite sides of the S^2, like the north and south pole. There is a nice antipodal map on http://www.antipodesmap.com/, which helps to find antipodal points on earth. For example an antipodal point to Berlin would be somewhere in the south-west of New Zealand.

The map f could be a function that assigns points of the earth to a pair of two values, temperature and presssure. If we can assume that this map is continuous, then the theorem says that there is always a pair of antipodal points on earth, which has the same temperature and pressure. Think about this! o.O

But why should this statement true? I will explain it.

!!! WARNING: The following section is written for freaks and nerds who are really interested in the idea of the proof. If you are not of this type, then you should skip the following. ;-) !!!

I will give only the idea of the proof by several pictures. This is not really mathematically correct, but intuitive. Proof: In Algebraic Topology the term of covering spaces is connected with this theme (it's also connected with the term of the fundamental group). What is a covering space? We only have to know what is the covering space of the S^1 (unit circle or 1-sphere) to proof the theorem. The so-called universal covering of the S^1 is a map from p: IR ---> S^1 which has the following properties and is shown in the modified picture from Hatcher's Algebraic Topology book (2001, p. 29).

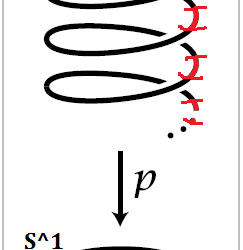
A small (open) neighbourhood U (in red) of an arbitrary point of the S^1 has a bunch of corresponding (open) neighbourhoods in IR (also in red), s.t. we can map them to the first neighbourhood by p and p induces a homeomorphism from one of the neighbourhoods to U, this means that the neighbourhoods are really “similar” to the neighbourhood U. In the following proof we can assume that p(t) = e^(2 pi i t) (cf. https://en.wikipedia.org/wiki/Euler%27s_formula). The proof follows Hatcher’s proof (2001, p. 32,33). Now we are well prepared for the proof. We prove the theorem by assuming the contrary and leading it to a contradiction (https://en.wikipedia.org/wiki/Proof_by_contradiction).

Let's suppose that such a map exists, but has no point x, s.t. f(x) = f(-x). Then we can define the function g: S^2 ---> S^1 with g(x) = (f(x) - f(-x))/|f(x) - f(-x)|. We can calculate just by inserting -x in the formular, that g(-x) = g(x). We call the equator loop (cf. picture down) y: [0,1] ---> S^2, where we choose x_0 as the basepoint of the loop, i.e. 0 and 1 get mapped to x_0 in S^2.

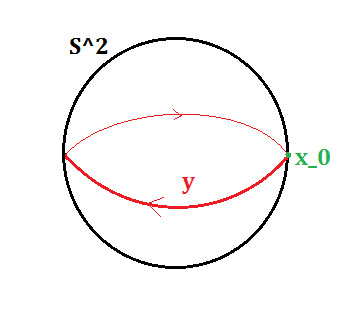
This is indeed a loop, because it starts and ends at the same basepoint x_0. The composition g*y given by g*y(x) = g(y(x)) is a map from [0,1] to S^1 which starts and ends at the same point, hence a loop in S^1.

Since we know that a neighbourhood of a point in S^1 has a bunch of neighbourhoods in IR by the property of the covering space, we can construct a unique path in IR by lifting pieces of the loop g*y in S^1 by this lifting-property of the covering space to IR. This path is unique, if we fix basepoints, i.e. we map 0 in IR to 1 in S^1 by p. (Rmk.: Consider that 1 is in S^1, because we are working in the complex plane. If you are not firm working with complex numbers, just read (1,0) instead of 1 and consider the real number plane IR^2.) We can construct this lifting of the loop in finitely many steps (by compactedness). We call this lifting G*Y which is just a path from [0,1] to IR. So we have G*Y: [0,1] ---> IR. Now we can compare loops in S^1 with paths in IR. An example of the path G*Y in IR (in blue) is given by the following picture:

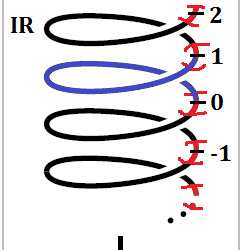
The corresponding loop at the base S^1 is also coloured blue (modified picture from Hatcher, 2001, p. 29).

Let's consider the difference d: [0,1/2] ---> IR given by

d(t) = G*Y(t) - G*Y(t + 1/2) = G(Y(t)) - G(Y(t+ 1/2)).

This difference is just the difference of antipodal points in S^1 in terms of the difference of the corresponding paths in IR. We know, if we go once around the circle S^1, i.e. we have a loop starting and ending at 1 in S^1 (see Rmk. before), then we go from 0 to 1 in IR, like we see it in the picture. If we go 1/2 of the way of the loop g*y in S^1, then we have two antipodal points z and -z in S^1. Now we consider p: IR ---> S^1 given by p(t) = e^{2 pi i t}. Any two antipodal points z and -z in S^1 give integers x in p^{-1}(z) and x' in p^{-1}(-z) which differ just by a number of the form "n + 1/2" where n is an integer. Looking at the preimage p^{-1}(z) or p^{-1}(-z) means just looking at the bunch of points in IR above the points z and -z. But being something of the form "n + 1/2 = (2n + 1)/2 = odd integer/2" means just that the difference

d(t) = G*Y(t) - G*Y(t + 1/2) = q/2, where q is an odd integer.

But then

    G*Y(1) - 0 = G*Y(1) - G*Y(0) = G*Y(1) - G*Y(1/2) + G*Y(1/2) - G*Y(0)     = (G*Y(1) - G*Y(1/2)) + (G*Y(1/2) - G*Y(0)) = q/2 + q/2 = q.

So G*Y(1) = q not equal to 0 and this means that G*Y starts in 0 and ends in q. But this is a contradiction, because y is homotopic to the constant loop c that stays for its whole interval [0,1] at one point (i.e. c(t) = x_0), i.e. we can deform y in S^2 continuously to a point, like in this picture:

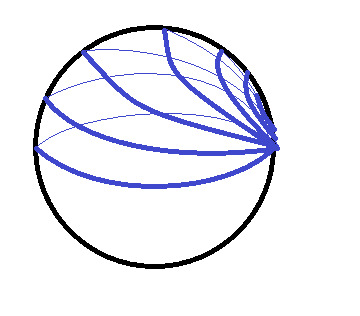
But then g*y is homotopic to a constant loop, hence G*Y, too. But we saw that G*Y doesn't stay at one point, but goes from 0 to q. So it can't be the constant loop. CONTRADICTION!

Q.E.D.

Next time we will look at an interesting consequence of the theorem, which has something to do with a division of the world. But this will not be written before next month. See you then!

Sources:

First picture: https://de.wikipedia.org/wiki/Karol_Borsuk#/media/File:Borsuk.jpeg, https://de.wikipedia.org/wiki/Stanis%C5%82aw_Marcin_Ulam#/media/File:Stanislaw_Ulam_ID_badge.png

Second picture: https://de.wikipedia.org/wiki/Erde#/media/File:The_Earth_seen_from_Apollo_17.jpg

Third and fifth picture: Modified pictures from

Hatcher, Allen (2001): Algebraic Topology, URL: http://www.math.cornell.edu/~hatcher/