#orthocenter

[squareallworthy]

Triangle Tuesday 3: The orthocenter, the Euler line, and orthocentric systems

Previously, we have looked at two different ways to mark a point in a triangle. First, we drew cevians (lines from the vertices) to the midpoints of the sides and found that they all cross at a point, which is the centroid. Then we tried drawing perpendiculars to the sides from the midpoints, and those all met at the circumcenter. And you could do this with any point on the side of a triangle -- draw a cevian to it, or a perpendicular from it, and see what happens.

This time, though, we're going to do both. That is, we're going to work with the cevians that also form perpendiculars to the sides. These are the altitudes, which run from a vertex to the nearest point on the opposite side, called the foot of the altitude. The three altitudes all meet at a point H, and that's the orthocenter. (The letter H has been used to mark the orthocenter since at least the late 19th century. I believe it's from the German Höhenschnittpunkt, "altitude intersection point.") Anyway, let's prove that the orthocenter exists.

Theorem: the three altitudes of a triangle coincide.

Here's a very simple proof that the three altitudes coincide. It relies on the existence of the circumcenter, which we already proved before. Given a triangle ABC, draw a line through A parallel to the opposite side BC. Do the same at B and C. These lines cross at D, E, and F and form the antimedial triangle (in blue).

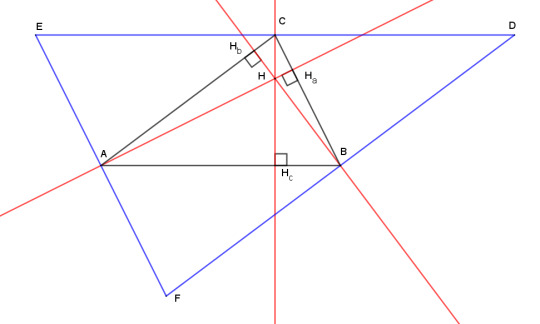
Then the altitudes of ABC are also the perpendicular bisectors of DEF. We proved before that perpendicular bisectors all meet at a point, therefore altitudes do as well.

That was easy. Let's do it again, but in a different way. It's not quite as simple, but it includes a large bonus.

Theorem: the three altitudes of a triangle coincide at a point colinear with the circumcenter and centroid, and GH = 2 GO.

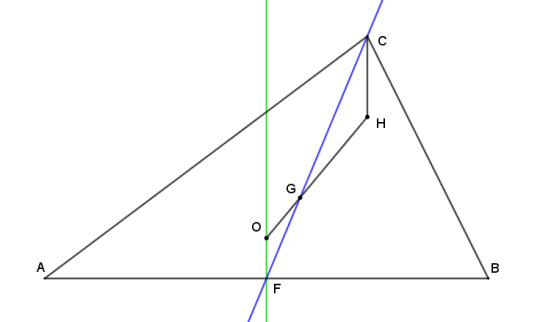
Let's take triangle ABC, and let F be the midpoint of side AB. Then mark two points that we already know, the circumcenter O and the centroid G. We'll also draw the median (green) and the perpendicular bisector (blue) that run through F, leaving the other ones out to avoid cluttering the picture.

We already know from our look at the centroid that G cuts segment FC at a third of its length, so GC = 2GF. Let's extend segment OG in the direction of G by twice its length out to a point we'll label H, so that GH = 2GO.

Now consider the two triangles GOF and GHC. By construction, their two blue sides are in the ratio 1:2, and the same for their two black sides. They also meet in vertical angles at their common vertex G. So by side-angle-side, the triangles are similar, and it follows that HC is parallel to OF, and therefore perpendicular to AB. So H lies on the altitude from H to side AB.

By analogous construction, we can show that H also lies on the other two altitudes. So not only have we proved that the altitudes coincide, but also that O, G, and H all lie on a line, and furthermore that G is located one third of the way from O to H, in any triangle.

This proof is due to Leonard Euler, and the line OGH is called the Euler line. Not only these three points but many others as well fall on this line, which we will get to later on.

Let's look at some more properties of the orthocenter and the feet of the altitudes. I'm just going to look at the case of an acute triangle for now, and show how this extends to the obtuse case later.

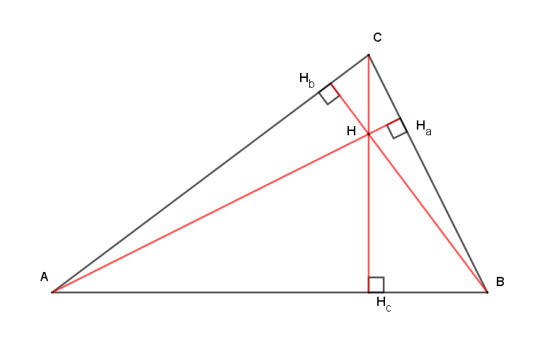
Theorem: two vertices of a triangle and the feet of the altitudes from those vertices are concyclic.

Proof is easy: the two right triangles AHcC and AHaC share segment AC as a hypotenuse. Therefore AC is a diameter of the common circumcircle of AHcC and AHaC (following from Thales's theorem).

(Incidentally, look at the angle formed by the blue segment and the altitude CHc. It subtends the same arc as angle CAHa, so (by the inscribed angle theorem again) they must be equal. That's not a part of this theorem, so just tuck that fact away for a moment.)

Theorem: a vertex, the two adjacent feet of the altitudes, and the orthocenter are concyclic.

Same idea, but now the right triangles are AHcH and AHbH, and AH is the diameter of the common circumcircle.

(And incidentally, look at the angle formed by the new blue line and the altitude CHc. It subtends the same arc as HbAH, which is same angle as CAHa. So those angles must be equal too. Since both angles between a blue line and the altitude CHc are equal to the same thing, they are equal to each other. Again, not a part of this theorem, just something I wanted to note.)

So those are some interesting concyclicities, but now let's look at the pedal triangle of the orthocenter, which is called the orthic triangle.

Oh, hey, it's made up blue lines, just like the ones we were talking about. And we proved that the two longest blue lines make equal angles with the altitude between them. By symmetry, we can prove the same thing about all the angles made by the blue lines. So that means

Theorem: two sides of the orthic triangle make equal angles with the altitude between them.

Another way to say this is that the altitudes are the angle bisectors of the orthic triangle. And I admit that was kind of a roundabout way to introduce the orthic triangle, but I think it makes the proof of this property easier to follow.

Two other properties of the orthic triangle immediately follow from this:

In an acute triangle, the inscribed triangle with the shortest perimeter is the orthic triangle

and

In an acute triangle, the orthic triangle forms a triangular closed path for a beam of light reflected around a triangle

which are two ways of saying the same thing.

But those two properties only hold for acute triangles. What happens to the orthic triangle in an obtuse triangle? Let's push point C downward to make triangle ABC obtuse and see what happens. To make things clear, I'm going to extend the sides of ABC and the altitudes from line segments into lines. Here's the before:

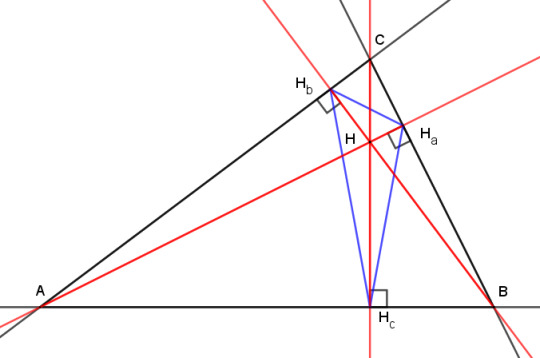
And here's the after:

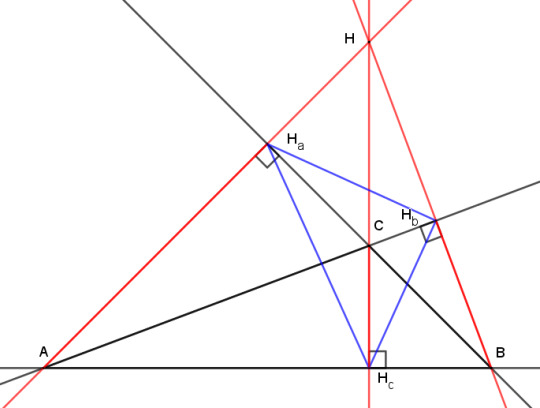
The orthocenter has moved outside of triangle ABC, and two of the altitudes have their feet on extensions of the sides of ABC rather than on the segments AC and BC. The orthic triangle now extends outside ABC, and certainly isn't the inscribed triangle with the shortest perimeter any more.

But look at it another way. We now have an acute triangle ABH, and the line HHc is an altitude of both the obtuse triangle ABC and the acute triangle ABH. Meanwhile, lines AC and BC have become altitudes of ABH.

So what we have is essentially the same acute triangle with two swaps: point C trades places with H, and Ha trades places with Hb. That means that our two theorems about concyclic points morph into each other as triangle ABC switches between acute and obtuse. Here's an animation to show the process:

And this is why I didn't bother with the obtuse case above -- each theorem of concyclicity is the obtuse case of the other.

So if we can just exchange the orthocenter with one of the vertices, what does this mean for their relationship? If you are given a group of vertices and lines, how can you tell which one is the orthocenter and which one are the vertices? Well, you can't.

Theorem: Given an acute or obtuse triangle ABC and its orthocenter H, A is the orthocenter of triangle BCH, B is the orthocenter of ACH, and C is the orthocenter of ABH.

The proof comes from consulting either of the "before" and "after" figures above. Take any three lines that form a triangle, red or black. The other three lines are then the altitudes of that triangle. The three feet are where a red and black line meet perpendicularly, so they are the same for all four possible triangles, which means all four share the same orthic triangle.

(Of course, if ABC is a right triangle, then we get a degenerate case, as you can see from the gif at the moment when C and H meet.)

Such an arrangement of four points is called an orthocentric system. Of the four points, one is always located inside an acute triangle formed by the other three, and it's conventional to label the interior one H and the others ABC.

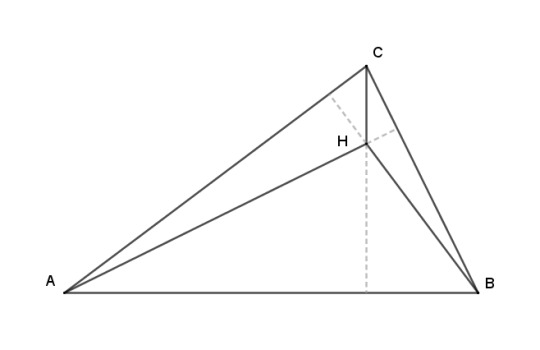
Orthocentric systems pop up all over the place in triangles, so expect to see more of them as we go along. Now, let me do one little lemma about altitudes, and then I'll show something cool about orthocentric systems.

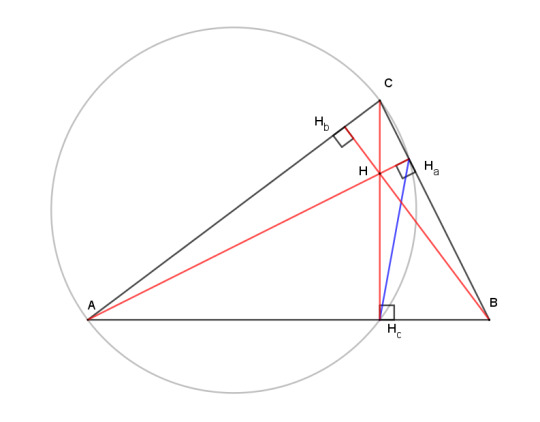
Lemma: the segment of an altitude from the orthocenter to a side of the triangle is equal to the extension of the altitude from the side to the circumcircle.

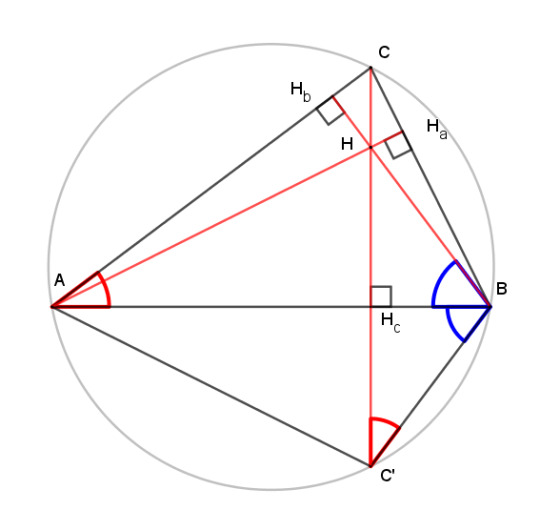
We can show this with just a little shuffling of angle identities. Extend altitude CHc to meet the circumcircle at C'. The angles CAB and CC'B, labeled in red, subtend the same arcs, so they are equal. Triangle ABHb is a right triangle, so angle HbBA, in blue, is complementary to it. The same is true for the right triangle C'BHc, so the two angles labeled in blue are equal. Then by angle-side-angle, triangles BHcH and HHcC' are congruent, and segment HHc = HcC'.

By the same argument, we can show that triangle AHHc is congruent to AC'Hc, which leads us into the next bit.

Theorem: all the circumcircles of the triangles of an orthocentric system are the same size.

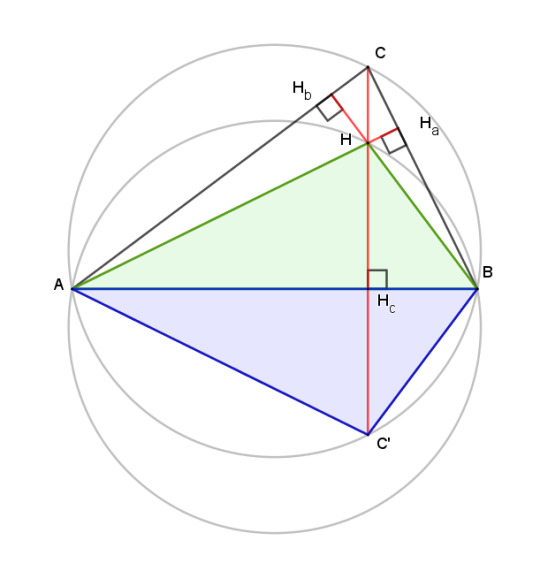
The blue triangle has the same circumcircle as triangle ABC. From the foregoing, the blue and green triangles are congruent. Therefore their circumcircles are the same size as well. The same argument works for ACH and BCH.

So here is an orthocentric system with its four circumcircles.

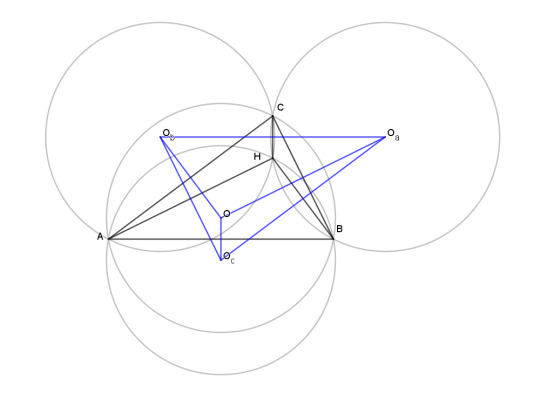
The four circumcenters O, Oa, Ob, and Oc form another orthocentric system, congruent to the first one.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[frostymilkshakerage]

Man. First time I watched? I was 13. Stayed up late to watch the episode I had heard so much about. Didn't emotionally recover til I was...how old am I now? Oh wait. HAVEN'T EVEN DONE THAT YET

Crazy to think that a decade ago today, the greatest, most important and most memorable episode of Gravity Falls aired.

Not What He Seems is a timeless episode that every fan, new or old, remembers watching for the first time. It was a moment no one will ever forget!

There's few shows that can reach the level of importance and level that Gravity Falls did. And few shows can even say they have a single episode within them that reached the same level of iconic status that Not What He Seems did. It was a game changer episode for so many reasons. Nothing like it will likely ever happen again. It was a once in a generation episode and moment.

As a reminder, the ENTIRE script to Not What He Seems is public and available to be read by any fan!

What's more, In the lead up to the episode, Disney XD shared 3 audio recordings of Grunkle Stan thinking to himself while locked up. Back in 2020 I refound them and made a video of it!

Here's to 10 years of Gravity Falls' greatest episode!!

[nyancrimew]

what if i told you about Euler's Line? it's a line that goes through every type of center a triangle has, from the circumcenter to the orthocenter, the centroid, even the nine-point center!! it's actually a really cool property triangles have. i would recommend u read more into this its a quite interesting topic and very deep. if u wanna learn more about this u should search up "among us impostors kissing red sus" on duck duck go images

wow that's so cool let me duck duck go images that real quick- hm this is awakening something in me, triangles are so cool

[sybaritick]

when you're teaching, and especially if you're trying to explain a concept to an individual student, how do you maintain a positive and supportive tone? i'm curious because i'm a TA and i worry that i don't come across as intended when i'm trying to help students

hmm, good question. I do work with students one on one a lot, though they are often middle school students (ages maybe 9-15) which might be a little different.

for teaching I'm lucky that a sort of talkative positive personality comes naturally to me, I am a yapper. and I think being generally friendly (asking a student about how their soccer tournament went or if they did anything interesting over a long weekend) helps to make people feel a bit more at ease than jumping right to "good morning! Let's find the slant asymptote of this function." i have talked to students about Forza Motorsport and Minecraft and sewing plushies and nuclear power plants and chess, just whatever happens to interest them, and maybe I'm wrong but I think this actually helps. But with college students this may not be as relevant/important.

Emphasizing that it's OK and normal to make mistakes or not understand things (and modeling this by, if you goof in front of them which will inevitably happen occasionally like mixing up the orthocenter and centroid of a triangle, taking it in stride.) Gently redirect self-deprecating remarks (if they say they're terrible at math or they're stupid) by saying they're not and the whole point is for this to be challenging. Doing hard things is the way to get better at them!

Occasionally I have had frustrating students (people who are totally distracted, don't seem to care about the material even slightly, don't understand and also don't ask any questions even after i explain it as best i can repeatedly, etc) and this is probably the hardest situation to keep the positive and supportive tone in. I try to explain it a different way if I can (eg, if there's both an algebraic and a geometric explanation, I switch). Sometimes, the best I can do is move on to something else/take a break and hope that coming back to it later with fresh eyes will help because it often does. Remind them this isn't an emergency if they don't understand the material Right Now. I give extensions very freely (glad the school I teach at promotes this) and regularly say if you don't get it, that's OK, take your time, talk to other students and other instructors if you need to, etc. Don't stay up until 2am finishing this assignment, get a good night's sleep and finish it tomorrow.

I know a lot of this is probably either obvious or only makes sense for younger children, but I hope at least some piece of it is relevant! good luck with the TA'ing is it math or CS?

[gaylilgremlin]

It's soon midnight here and I swear after the fucking finals I'll never look at a math example again

I do not care what a centroid is

Or an orthocenter

Or how to do standard deviation

My eyes hurt and I never wanted to murder a triangle more

[enky-the]

three vowels are overrated, two vowel systems are way more interesting!!

inside me there are two wolves. one wants to create the most elaborate and overcrowded vowel system you've ever seen. the other thinks it's time to give a more conventional system a try.

[perdvivly]

Nothing, what’s an orthocenter with you?

[luicosas]

Watching some computer vision lectures recently and learned this cool 3 point perspective fact:

The orthocenter of the 3 vanishing points is where the center of projection is - for normal cameras this is around the center of the image +- some manufacturing errors.

I can finally explain why some of my 3 point perspectives feel weird. For example, looking at this picture from

Its orthocenter is outside the frame which makes it seem the bottom of the image was cropped out. Triangulating vanishing points is one of the ways to detect if a photo has been cropped.

* This assumes the 3 vanishing points are from a cube, 90 90 90 degrees. The principle of projection can also be calculated from the vanishing points of other shapes but it becomes more mathy.

[medical-fitness]

Is Surgery Necessary for Carpal Tunnel Syndrome in Lahore?

Carpal tunnel syndrome (CTS) is a common condition that can cause significant discomfort, making daily activities challenging. If you're experiencing symptoms like tingling, numbness, or pain in your hands and fingers, you might wonder if surgery is your only option for relief. This article explores the available carpal tunnel syndrome treatments in Lahore, whether surgery is necessary, and the associated costs.

Orthocenter, a trusted name in orthopedic care, provides expert solutions for carpal tunnel syndrome cure, ensuring patients receive the best treatment tailored to their needs.

Understanding Carpal Tunnel Syndrome

Carpal tunnel syndrome occurs when the median nerve, which runs through a narrow passageway in your wrist (the carpal tunnel), becomes compressed. This can result from repetitive hand movements, wrist injuries, or underlying health conditions like arthritis or diabetes.

Common symptoms include:

Tingling or numbness in the thumb, index, and middle fingers.

Weakness in the hand, making it difficult to grip objects.

Pain that may radiate up the arm.

Early intervention is crucial to prevent the condition from worsening.

Non-Surgical Carpal Tunnel Syndrome Treatments in Lahore

Surgery is not always the first line of treatment for carpal tunnel syndrome. Several non-surgical methods can provide relief, particularly in the early stages:

1. Wrist Splints

Wearing a wrist splint at night can keep your wrist in a neutral position, reducing pressure on the median nerve.

2. Physical Therapy

Specific exercises can help stretch and strengthen the wrist and hand muscles, alleviating symptoms.

3. Medications

Over-the-counter anti-inflammatory medications, like ibuprofen, can reduce swelling and relieve pain.

4. Corticosteroid Injections

In some cases, a doctor may recommend corticosteroid injections to reduce inflammation around the median nerve.

At Orthocenter, specialists focus on providing non-invasive carpal tunnel syndrome treatments in Lahore whenever possible, prioritizing patient comfort and recovery.

When Is Surgery Necessary?

Surgery is typically considered when non-surgical treatments fail to provide relief or if the condition is severe. Signs that surgery may be necessary include:

Persistent numbness or weakness in the hand.

Worsening symptoms despite trying non-surgical methods.

Evidence of nerve damage through diagnostic tests like nerve conduction studies.

Carpal tunnel release surgery is a relatively simple procedure that involves cutting the ligament pressing on the median nerve. This can be performed through:

Open Surgery: A small incision is made in the palm to access the carpal tunnel.

Endoscopic Surgery: A smaller incision is used, and a camera guides the surgeon.

Both methods are effective, and recovery typically takes a few weeks to a few months.

Carpal Tunnel Syndrome Treatment Cost in Lahore

The cost of carpal tunnel syndrome treatment in Lahore depends on several factors, including:

Type of Treatment: Non-surgical options like splints or physical therapy are more affordable than surgery.

Surgical Method: Endoscopic surgery may be slightly more expensive than open surgery due to the equipment used.

Hospital Facilities: High-quality facilities, like those at Orthocenter, may offer advanced care at competitive rates.

Orthocenter is known for providing transparent and affordable carpal tunnel syndrome treatment costs in Lahore, ensuring patients receive excellent care without financial stress.

Why Choose Orthocenter for Carpal Tunnel Syndrome Treatment in Lahore?

Orthocenter is a leading provider of orthopedic care, offering advanced and personalized treatment options for carpal tunnel syndrome. Here’s why it stands out:

Experienced Specialists: A team of highly skilled doctors ensures accurate diagnoses and effective treatments.

State-of-the-Art Facilities: Equipped with modern technology for both non-surgical and surgical solutions.

Patient-Centered Approach: Orthocenter prioritizes patient comfort, providing customized care plans.

Affordable Pricing: Competitive rates make quality treatment accessible to everyone.

Take Control of Your Hand Health Today

If you’re struggling with carpal tunnel syndrome, it’s essential to seek timely treatment to avoid long-term complications. Surgery is not always necessary, and many patients find relief through non-surgical methods.

Orthocenter, with its experienced specialists and advanced care, is a trusted choice for carpal tunnel syndrome treatment in Lahore. Schedule a consultation today to explore your options and take the first step toward a pain-free life!

FAQs About Carpal Tunnel Syndrome Treatment in Lahore

Q1: Is surgery the only carpal tunnel syndrome cure?

No, surgery is not the only cure. Non-surgical treatments like splints, therapy, and medications can be effective, especially in the early stages. Surgery is recommended for severe or unresponsive cases.

Q2: How much does carpal tunnel syndrome treatment cost in Lahore?

The cost varies based on the treatment type and facility. Non-surgical methods are more affordable, while surgical options depend on the technique used. Orthocenter offers competitive pricing for all treatments.

Q3: How long is the recovery time after carpal tunnel surgery?

Recovery typically takes 4–6 weeks for light activities and up to 3 months for complete recovery, depending on the severity and surgical method.

Q4: Are there any risks associated with carpal tunnel surgery?

As with any surgery, risks include infection, scarring, or nerve damage. However, these are rare, and experienced surgeons at Orthocenter minimize such risks.

Q5: Can carpal tunnel syndrome come back after treatment?

While recurrence is uncommon, it can happen. Maintaining good wrist posture and avoiding repetitive strain can help prevent it.

[squareallworthy]

Reverse unpopular opinion ask meme: Irregular polygons

Irregular polygons are awesome. You can do so much more with them, in so many areas, but I'm going to limit myself to talking about just two of them: tiling and triangle centers.

(Did you think I was going to be all snobby toward my irregular friends and give them only grudging approval? Heck no, I love those guys! And so by the rules of the meme I get to infodump about the things I love, so this may be long but you asked for it.)

Let's first talk about covering the plane with copies of a single shape -- a monohedral tiling. And for now, let's restrict ourselves to periodic tilings. All triangles and all non-self-intersecting quadrilaterals tile the plane periodically, so that's not very interesting. All you have to do is place one polygon and then make copies by rotating 180 degrees around the midpoints of the sides.

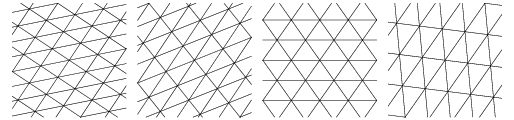
With five sides, things become more complicated, because regular pentagons don't tile by themselves, but there are fifteen ways an irregular pentagon can periodically tile the plane. Here are four of them that were discovered in 1976 and 1977 by Marjorie Rice, an amateur mathematician.

There are three types of monohedral periodic convex hexagonal tilings.

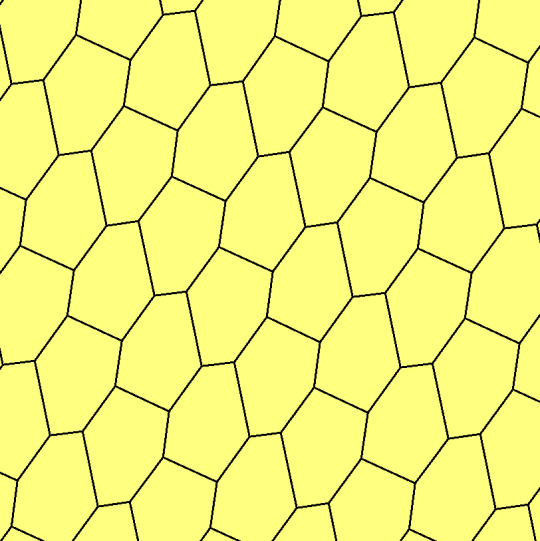
For polygons with seven or more sides, there are no monohedral periodic tilings using a convex prototile , but there are periodic tilings for nonconvex polygons of any size. Some of them are quite famous.

Most of Escher's work in his Regular Division of the Plane series uses shapes with curves as well as straight sides, so they don't show polygon tilings, strictly, but the patterns do point toward complex tilings that are visually pleasing.

Irregulars can tile aperiodically, too. Here's a pentagon tiling with 6-fold rotational symmetry. It can be extended infinitely, and tilings can be constructed with pentagons for n-fold symmetry of any n>2.

Going back to non-convex shapes, here's the Voderberg tile, an enneagon that forms a spiral tiling. Notably, one copy of the shape can be completely surrounded by two others.

And of course I can't go without mentioning the tiling news of the century: "Tile (1,1)", aka the Hat, aka the T-shirt, a tridecagon (and polykite) that can tile the plane but only aperiodically. IDK if you follow polygon news but this was huge.

Okay, enough about tilings. With tilngs it's pretty easy to get what's going on just by looking at them, but my next topic, triangle centers, requires a bit more explanation. Also there's a bit of jargon, but I will try to keep it simple.

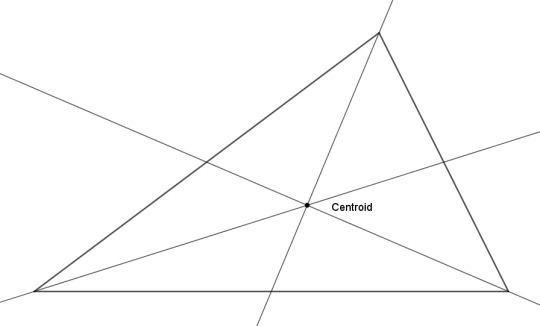
Take an arbitrary triangle ABC. Where is its center? One way you might define it is to find the midpoint of each side and draw a line to it from the opposite vertex. Each line divides the triangle in half, and these three lines (the medians) all cross at a point, the centroid. This works for any triangle, no matter its shape. The point marks the center of gravity of the area of the triangle, and also the center of gravity of its vertices. Based on that, you could consider this the center of the triangle.

Or you could work with angles instead of sides. Draw lines from each vertex that divide the angles in half (the angle bisectors). These all meet at a point called the incenter, which marks the center of the largest circle that fits inside the triangle. To put it another way, it's the point that is equidistant from all three sides. That's another point you could call the center of the triangle.

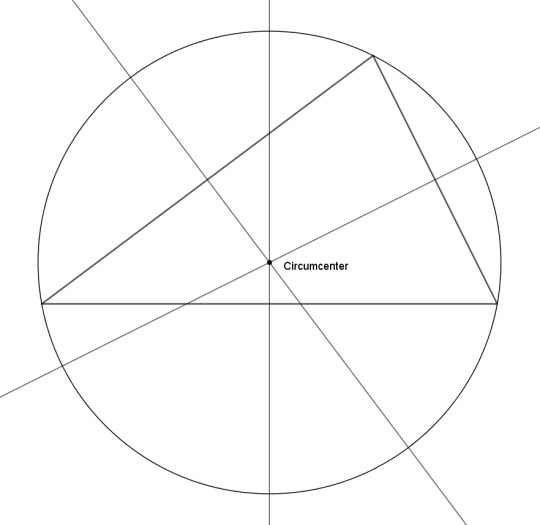
Or, how about a circle around the triangle instead? From the midpoints of the sides, draw the perpendicular bisectors. Again, they all intersect at a point, the circumcenter, which is the center of the circle that passes through the vertices -- the point that is equidistant from all three of them. So you could also call that the center of the triangle.

Or how about drawing perpendicular lines from the sides again, but having them pass through the opposite vertices (the altitudes)? They coincide at a point called the orthocenter. Isn't that neat? Yet another point we could call the center of the triangle.

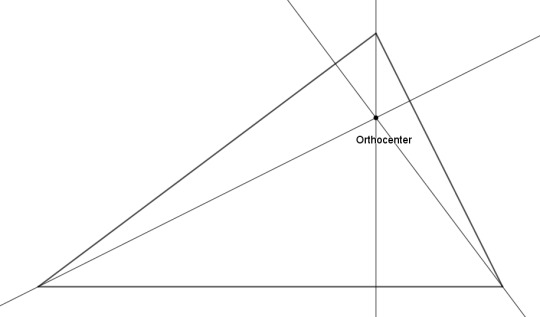
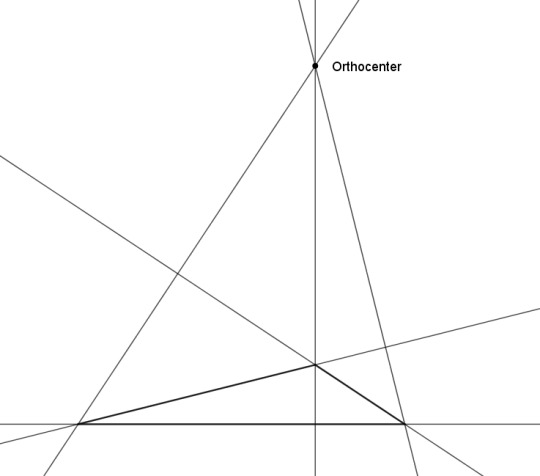
But wait -- can we? For an obtuse triangle, the circumcenter and the orthocenter are going to lie outside the triangle. (For the orthocenter of an obtuse triangle, you have to extend each side into a line, and draw the altitude as a perpendicular to that.) Being outside a thing is really not what we have in mind when we talk about the center of the thing. Should we care about that?

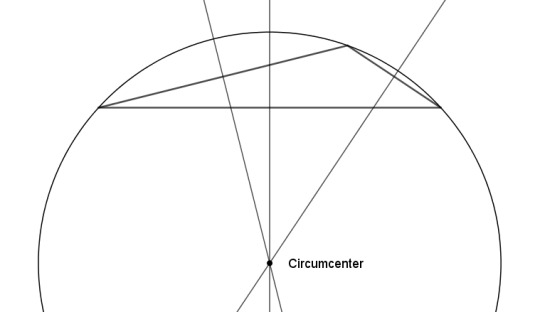
Maybe not. Check this out. We'll go back to the circumcircle, and draw tangents to it at the three vertices. The three tangents form the tangential triangle (in blue), which we'll call A'B'C', where A' is opposite A, and so on with B and C. Now draw the circle that passes through A, A', and the circumcenter, and do the analogous construction for B and C (in red). The three circles coincide in two places: the circumcenter and another point called the far-out point. And as the name suggests, this is usually well outside the triangle, even for acute triangles.

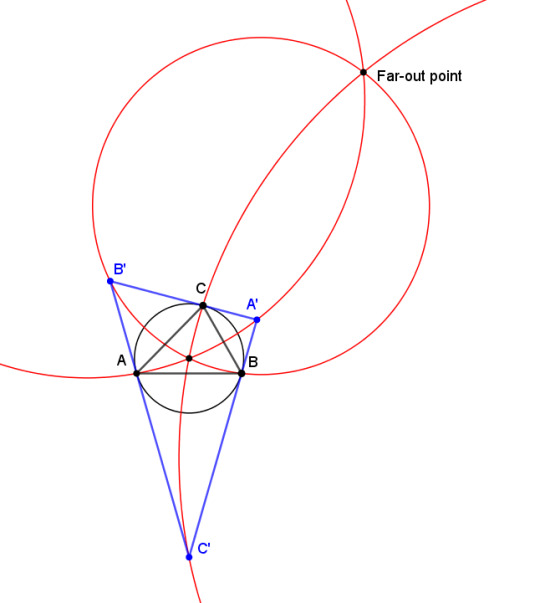
There's no reasonable way to call this point the center of the circle. But so what? I just love the fact that the three circles line up like that. I no longer care about finding "the" center of the triangle. I no longer care that "center" is rather a misnomer for many of these points. I just think it's neat that you can draw these constructions on ordinary aysmmetrical triangles and they keep all converging on one point. Want more? Reflect the medians across the angle bisectors, and they all meet at the symmedian point. Or connect the vertices of the tangential triangle with the intersections of the medians and the circumcircle. Those lines meet at the Exeter point. Or, from each vertex, draw the line that splits the perimeter of the triangle in half. These are called the splitters, and they meet at the Nagel point. And on and on and on.

You can simply wander around a triangle, connecting things that relate somehow to vertex A, then do the equivalent thing for B and C, and stumble upon new centers. And there are tens of thousands of these things, constructed with straightedge and compass or by other methods. And there are so many ways to enjoy these things. You can page through the enormous collection and get a kind of stamp-collecting satisfaction just looking at their variety and knowing that they exist. Or you can appreciate the proofs that show that the constructions really do specify a unique point. Or proofs that show that a point constructed to have one property has a surprisingly different property. Or you can notice that the points fall into certain families and appreciate the connections between them. (For instance, the centroid, circumcenter, orthocenter, far-out point, and Exeter point, among others, all happen to lie on the same line, the Euler line.) Or you can convert the points to trilinear coordinates, manipulate them algebraically, and get to know them that way.

But to appreciate them at all, you need to work with irregular triangles. Because here's the thing: in an equilateral triangle, all these points collapse to the same point. Everything simplifies to a single center, and the incredible wealth of invisible structure that teems inside every ordinary triangle is gone.

You have finally found "the" center, but at what cost? Symmetry is death. Only through asymmetry will the vast truth of the triangle be revealed to you.

And those are just a few of the reasons irregular polygons are cool!

[my-perspective-corner]

Advanced setup.

Let's try and tackle this thing:

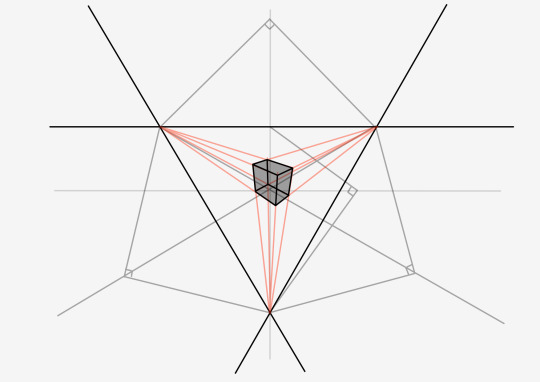
In the basics part 3, I covered a technique for finding vanishing points on the horizon. Here's a summary:

To find a vanishing point you simply need to position your eye at the station point, and look at an angle that is parallel to the lines you want to find a vanishing point for. If you want to find a vanishing point for lines that move straight up, you look straight up. If you want to find a vanishing point for lines that move straight forwards, you look straight forwards, and so on. Whatever point you are looking at on the canvas when you do this is where that vanishing point should be. However, this requires us to measure angles in 3d space above our canvas, which can be a bit difficult. So to make it easier we can rotate the station point around the horizon until it is flat with the canvas. allowing us to easily draw and measure angles from it.

This works well when the horizon crosses the station point. But when it doesn't (like in three point perspective) you'll bump into a problem. If you look at a side view you'll see why.

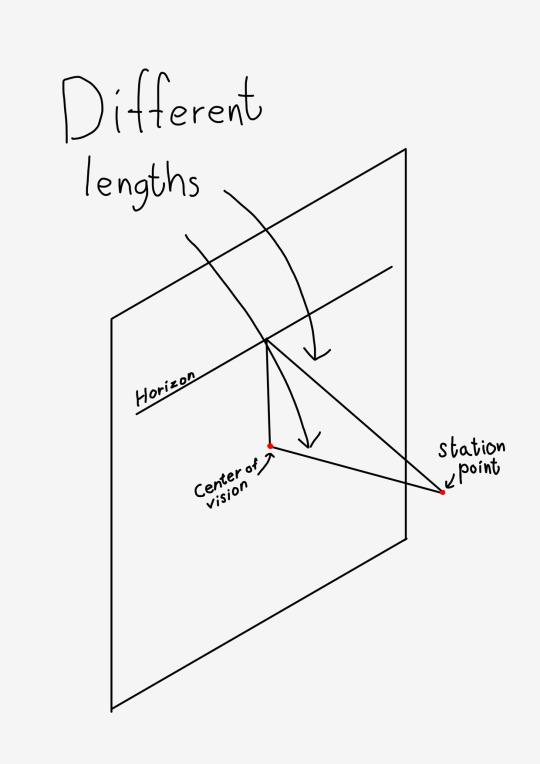
When the horizon line does not cross the center of vision then we can no longer use the distance between the station point and the canvas to find how far below the horizon our station point should be after being rotated. The distance and therefore our vanishing points will always be off. There are two ways to solve this. The first one is to use the pythagorean theorem. The second one is to do some more rotating. 

If we take the picture above and rotate it to the side first, basically rotating the station point twice, then we can easily measure the distance between the station point and the horizon on our canvas.

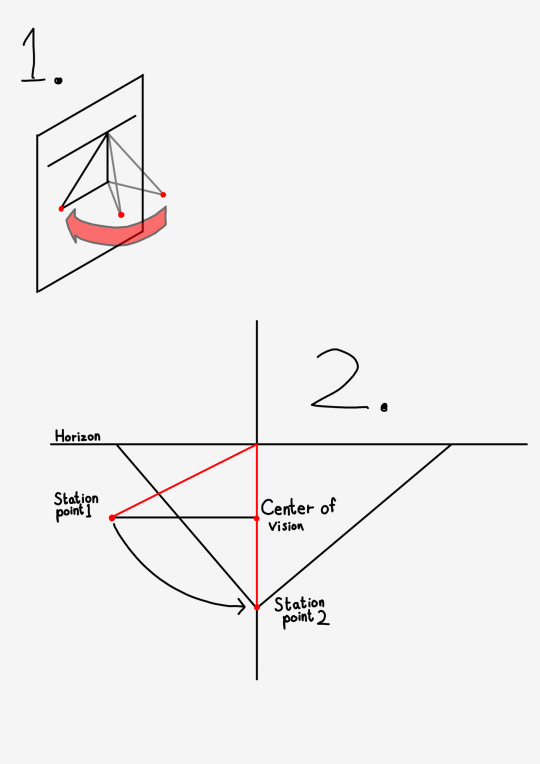
(note: It doesn't matter which direction you rotate the station point. It won't change the location of the vanishing points. Which direction I rotate them in depends on whether I want to prioritize saving space or reducing clutter.)

Once we've done this, we can also use this vertical station point to find the third vanishing point. The third vanishing point is always perpendicular to the ground, so all we need to do is add a line that is perpendicular to the line moving towards the horizon to our vertical station point.

And that's really most of it. As long as the initial station point you rotate is rotated around the center of vision, and the distance between them is the same, then any vanishing point you find using them will always feel like they are in the same 3d space, allowing you to rotate things however you want.

However, when most people use this type of setup they will usually want to find diagonal vanishing points for vertical surfaces. And to do that we’ll need to do some more rotating.

First you'll need to find the horizons for these vertical surfaces. That's the easy part, you just need to draw straight lines through all vanishing points.

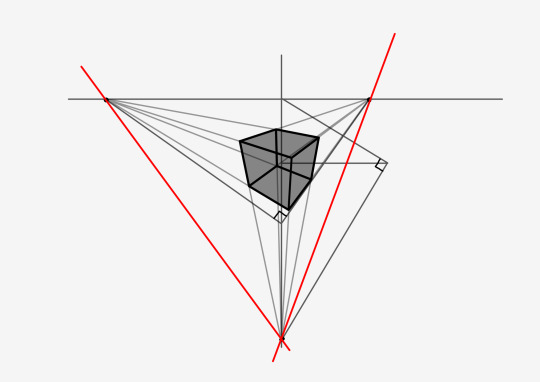
Now we’ll need to rotate the station point around them. The best way I can describe how to do that is to first rotate the canvas so that one of these new horizons is horizontal, and then do the same things you did with the first horizon.

The first step in doing this is to add what I've heard some people refer to as the gravity line. It is the line that you draw from the horizon that the station point will be on after being rotated. I think the best way to understand it is to imagine the gravity line as the shadow of the station point as it is being rotated.

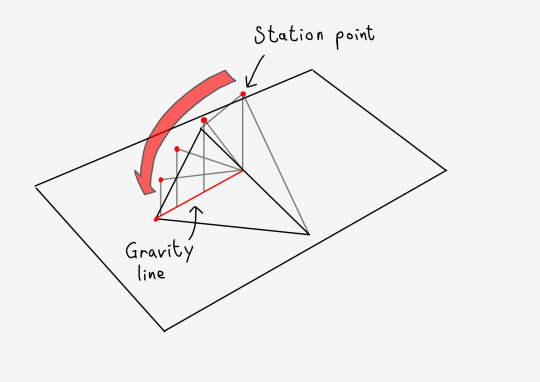
This gives it two properties that you'll need to keep when drawing it for other horizons in order to make sure everything is consistent: It will always start on top of the center of vision, and it will always be perpendicular to the horizon it is being rotated around.

Luckily these are pretty easy to draw due to an interesting phenomenon that occurs when all vanishing points are set up properly. That being that the center of vision will always be in the orthocenter of the three vanishing points.

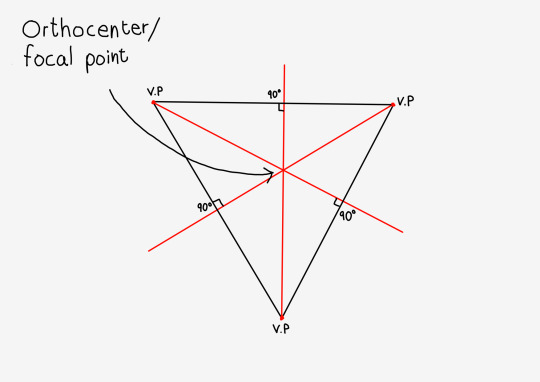
This means that to set up the gravity lines, all you need to do is draw a line from a vanishing point through the center of vision, and it will always cross the horizon opposite to it at a 90 degree angle.

Next you'll need to find where in the gravity line the station point is. There are multiple ways of doing this. One comes from remembering that all vanishing points we currently have are 90 degrees apart from each other. So you'll just need to find where on the gravity line two lines drawn from each vanishing point on it’s horizon meet at 90 degrees. You can either mess around with a set square for a while, or you could draw some circles. Turns out that if you draw two lines from opposite ends of a circle towards any point on its edge then they will always meet at 90 degrees.

If you use the halfway point between the two vanishing points as a center, and the distance between it and the vanishing points as a radius, and draw a circle, then that circle will always intersect the gravity line where the station points should be.

However, the easier and more common technique comes from remembering that, as the station point is rotated around different axes, so are the lines connecting it to vanishing points. All lines that connect different station points to the same vanishing point will always be the same length. So instead of finding the halfway point between two vanishing points, you can just find a vanishing point, take the distance between it and any station point it is connected to, and draw a circle with that radius around the vanishing point.

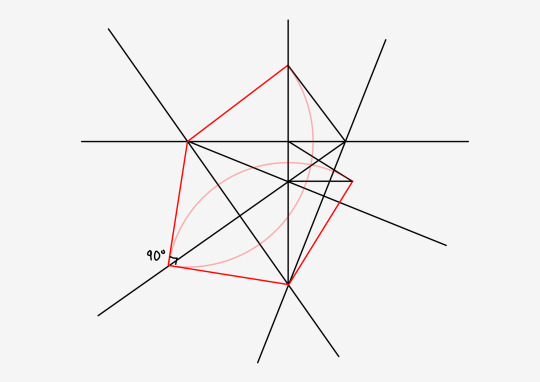
When done correctly with all three horizons, you should be able to rotate every station point around their horizon, and have all of them meet at the same point directly above the center of vision.

Once you've completed a full setup you can find diagonal vanishing points for all surfaces.

Realistically, you probably won't draw this too often. At least not a full one. Perfect perspective is not something people tend to look for in art nowadays, making this level of precision unnecessary. The method I described at the top of this post for how to eyeball the locations of vanishing points will probably be enough for most drawings. Unless you are trying to show off some advanced perspective then close enough is good enough. I barely draw this in full. However, I do often draw it in parts. Whether it's just the two first station points to set up three point perspective, or if it's just rotating the station point around one horizon for a wall so I can find some diagonals. You technically don't even need to find all three diagonal vanishing points to draw a perfect cube, you just need two of them, and the rest will kinda just fall into place. I want people to understand the theory because that is more useful than just memorizing what lines to draw where. I don't want you to view this as a bunch of steps to get one final setup. I want you to look at each step as its own technique that you can use when you need it, because it is by taking this apart that you'll get most use out of it.

[the-depression-gremlin]

tyy for the tag!!!

last song: Rainbow Factory by WoodenToaster

fav color: black, purple, or blue

last movie/show: the tv series Bones (crime show lover)

s/s/s: sweet!

last googled: how to find an orthocenter of a triangle from coordinates (honors geometry is kicking my ass and im a little stupid)

current obsession: Voltron Legendary Defender (lance my pookie)

last book: Warrior cats: The Silent Thaw (all of my old obsessions are back)

looking forward to: the end of this fucking school year i hate this place

@pikamiii @back-on-my-autistic-bullshit @mushed-kid

:)))

Get to know me/People to know better

thank you so much for tagging me @cosmmicdancer :)

last song: bobby sox by green day, I think

favorite color: yellow or a yellowy orange

last movie/tv show: the OA

sweet/savoury/spicy: I need a perfect balance between sweet and savoury/spicy, because of the tism, but my wife would say its definitely sweet

last thing i googled: bahnstreik 2024 (hello fellow germans)

current obsession: moral panics and everything surrounding them

last book: currently reading stone butch blues

looking forward to: my wife getting their passport and moving in with me after almost 4 years of long distance <3

tags: @leaskisses444, @signforsign, @starsendlessly, and @amarettofemme and @sunkissedbutch, because we recently became mutuals and you seem like darlings :)

(absolutely no pressure to participate )

[sciencesolutions]

[zhampres]

another one