#python program to check armstrong number | Explore Tumblr posts and blogs

souhaillaghchimdev · 2 months ago

Text

Python: 100 Simple Codes

Python: 100 Simple Codes

Beginner-friendly collection of easy-to-understand Python examples.

Each code snippet is designed to help you learn programming concepts step by step, from basic syntax to simple projects. Perfect for students, self-learners, and anyone who wants to practice Python in a fun and practical way.

Codes:

1. Print Hello World

2. Add Two Numbers

3. Check Even or Odd

4. Find Maximum of Two Numbers

5. Simple Calculator

6. Swap Two Variables

7. Check Positive, Negative or Zero

8. Factorial Using Loop

9. Fibonacci Sequence

10. Check Prime Number

===

11. Sum of Numbers in a List

12. Find the Largest Number in a List

13. Count Characters in a String

14. Reverse a String

15. Check Palindrome

16. Generate Random Number

17. Simple While Loop

18. Print Multiplication Table

19. Convert Celsius to Fahrenheit

20. Check Leap Year

===

21. Find GCD (Greatest Common Divisor)

22. Find LCM (Least Common Multiple)

23. Check Armstrong Number

24. Calculate Power (Exponent)

25. Find ASCII Value

26. Convert Decimal to Binary

27. Convert Binary to Decimal

28. Find Square Root

29. Simple Function

30. Function with Parameters

===

31. Function with Default Parameter

32. Return Multiple Values from Function

33. List Comprehension

34. Filter Even Numbers from List

35. Simple Dictionary

36. Loop Through Dictionary

37. Check if Key Exists in Dictionary

38. Use Set to Remove Duplicates

39. Sort a List

40. Sort List in Descending Order

===

41. Create a Tuple

42. Loop Through a Tuple

43. Unpack a Tuple

44. Find Length of a List

45. Append to List

46. Remove from List

47. Pop Last Item from List

48. Use range() in Loop

49. Use break in Loop

50. Use continue in Loop

===

51. Check if List is Empty

52. Join List into String

53. Split String into List

54. Use enumerate() in Loop

55. Nested Loop

56. Simple Class Example

57. Class Inheritance

58. Read Input from User

59. Try-Except for Error Handling

60. Raise Custom Error

===

61. Lambda Function

62. Map Function

63. Filter Function

64. Reduce Function

65. Zip Two Lists

66. List to Dictionary

67. Reverse a List

68. Sort List of Tuples by Second Value

69. Flatten Nested List

70. Count Occurrences in List

===

71. Check All Elements with all()

72. Check Any Element with any()

73. Find Index in List

74. Convert List to Set

75. Find Intersection of Sets

76. Find Union of Sets

77. Find Difference of Sets

78. Check Subset

79. Check Superset

80. Loop with Else Clause

===

81. Use pass Statement

82. Use del to Delete Item

83. Check Type of Variable

84. Format String with f-string

85. Simple List Slicing

86. Nested If Statement

87. Global Variable

88. Check if String Contains Substring

89. Count Characters in Dictionary

90. Create 2D List

===

91. Check if List Contains Item

92. Reverse a Number

93. Sum of Digits

94. Check Perfect Number

95. Simple Countdown

96. Print Pattern with Stars

97. Check if String is Digit

98. Check if All Letters Are Uppercase

99. Simple Timer with Sleep

100. Basic File Write and Read

===

#ebook

0 notes

juliebowie · 11 months ago

Text

Introduction to Armstrong Number in Python

Summary: Discover the concept of Armstrong Numbers in Python, their unique properties, and how to implement a program to check them. Learn about basic and optimised approaches for efficient computation.

Introduction

In this article, we explore the concept of an Armstrong Number in Python. An Armstrong number, also known as a narcissistic number, is a number that equals the sum of its own digits, each raised to the power of the number of digits.

These numbers are significant in both programming and mathematical calculations for understanding number properties and algorithmic efficiency. Our objective is to explain what an Armstrong number is and demonstrate how to implement a program to check for Armstrong numbers using Python, providing clear examples and practical insights.

Read: Explaining Jupyter Notebook in Python.

What is an Armstrong Number?

An Armstrong number, also known as a narcissistic number, is a particular type of number in which the sum of its digits, each raised to the power of the number of digits, equals the number itself. This property makes Armstrong numbers unique and exciting in mathematics and programming.

Definition of an Armstrong Number

An Armstrong number is defined as a number equal to the sum of its digits; each raised to the power of the total number of digits. For example, if a number has 𝑛 digits, each digit d is raised to the ��th power and the sum of these values results in the original number.

Explanation with a Simple Example

Consider the number 153. It has three digits, so we raise each digit to the third power and sum them:

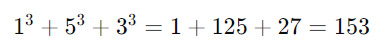
Since the result equals the original number, 153 is an Armstrong number. Another example is 370:

Difference Between Armstrong Numbers and Other Numerical Concepts

Armstrong numbers are distinct because they involve the specific property of digit manipulation. Unlike prime numbers, which are based on divisibility, or perfect numbers, which relate to the sum of divisors, Armstrong numbers focus solely on digit power sums. This unique characteristic sets them apart from other numerical concepts in mathematics.

How to Determine an Armstrong Number?

To determine whether a number is an Armstrong number, we need to verify if the sum of its digits, each raised to the power of the number of digits, equals the number itself. This concept may seem complex at first, but with a clear understanding of the process, it becomes straightforward.

Let's break down the steps and explore the mathematical method used to identify Armstrong numbers.

Mathematical Formula

The formula to check if a number is an Armstrong number is:

Here, d1,d2,…,dm represent the digits of the number, and 𝑛 is the total number of digits.

Step-by-Step Breakdown

Determine the Number of Digits: First, find the total number of digits, nnn, in the given number. This is crucial as each digit will be raised to the power of nnn.

Extract Each Digit: Extract each digit of the number. This can be done using mathematical operations like modulus and division.

Raise Each Digit to the Power of nnn: For each digit, calculate its power by raising it to nnn.

Sum the Powered Digits: Add the results of the previous step together to get the sum.

Compare the Sum with the Original Number: Finally, compare the sum with the original number. If they are equal, the number is an Armstrong number.

Example Calculation

Let's determine if 153 is an Armstrong number:

Number of digits (n): 3

Extracted digits: 1, 5, 3

Raised to the power of n:

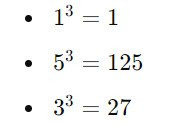
Sum of powered digits: 1+125+27=1531

Comparison: The sum, 153, equals the original number, confirming that 153 is an Armstrong number.

This systematic approach helps in accurately identifying Armstrong numbers, making the concept both interesting and accessible.

Also Check: Data Abstraction and Encapsulation in Python Explained.

Armstrong Number Algorithm

An Armstrong number, also known as a narcissistic number, is a number that is equal to the sum of its own digits each raised to the power of the number of digits. To determine if a number is an Armstrong number, we follow a specific algorithm.

This section outlines the steps involved and discusses the efficiency and complexity of the algorithm.

Outline of the Algorithm

To check if a number is an Armstrong number, follow these steps:

Determine the Number of Digits:

First, calculate the number of digits (n) in the given number. This step helps in raising each digit to the appropriate power.

Calculate the Sum of Digits Raised to the Power of n:

For each digit in the number, raise it to the power of n and sum these values. This step involves iterating through each digit, performing the power operation, and accumulating the results.

Compare the Sum with the Original Number:

Finally, compare the calculated sum with the original number. If they are equal, the number is an Armstrong number.

Key Steps in the Algorithm

Extracting Digits: We extract each digit from the number, which can be done using modulus and division operations.

Power Calculation: Raise each extracted digit to the power of the total number of digits.

Summation: Accumulate the results of the power calculations to form the total sum.

Comparison: Compare the accumulated sum with the original number to determine if it is an Armstrong number.

Efficiency and Complexity

The Armstrong number algorithm is efficient for small to moderately sized numbers. The primary operations involve basic arithmetic, such as modulus, division, and exponentiation, making the algorithm computationally light. The time complexity is O(d), where d is the number of digits in the number.

This is because the algorithm processes each digit exactly once. For large numbers, the time complexity may increase, but it remains manageable due to the simplicity of the calculations involved.

Implementing Armstrong Number in Python

To determine whether a number is an Armstrong number, we need to implement a straightforward approach in Python. Armstrong numbers, also known as narcissistic numbers, are numbers that equal the sum of their own digits each raised to the power of the number of digits.

Here, we’ll explore a basic implementation in Python and discuss how to optimise it for better performance.

Basic Implementation

Let’s start with a simple Python program to check if a number is an Armstrong number:

Explanation of the Code:

Function Definition: The function is_armstrong_number takes an integer number as its parameter.

Convert Number to String: We convert the number to a string using str(number) to easily access each digit.

Count Digits: We determine the number of digits using len(digits).

Initialise Sum Variable: We initialise sum_of_powers to zero to accumulate the sum of each digit raised to the power of num_digits.

Calculate Sum of Powers: We loop through each digit in the string, convert it back to an integer, raise it to the power of num_digits, and add it to sum_of_powers.

Check Armstrong Condition: Finally, we compare sum_of_powers with the original number to determine if it is an Armstrong number.

Optimised Approach

While the basic implementation is easy to understand, it may not be the most efficient for larger numbers. Here are some optimisations:

Use List Comprehension: Python’s list comprehension can make the code more concise. Here’s an optimised version:

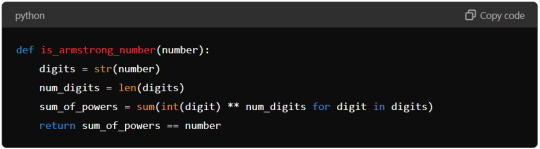
This version uses a single line to calculate sum_of_powers using list comprehension, making the code more compact and potentially faster.

2. Precompute Powers: For very large numbers, precomputing powers for digits (0 through 9) and reusing them can reduce computation time.

3. Avoid String Conversion: If working with extremely large numbers, you might want to avoid converting numbers to strings repeatedly. However, this is a trade-off between readability and performance.

By employing these optimisations, you can enhance the efficiency of the Armstrong number checking algorithm, especially for larger inputs.

Frequently Asked Questions

What is an Armstrong Number in Python?

An Armstrong Number in Python is a number that equals the sum of its digits each raised to the power of the number of digits. For example, 153 is an Armstrong Number because 1^3+5^3+3^3=153.

How can I check for an Armstrong Number in Python?

To check for an Armstrong Number in Python, calculate the sum of each digit raised to the power of the total number of digits. If this sum equals the original number, it’s an Armstrong Number.

What is the efficiency of the Armstrong Number algorithm in Python?

The Armstrong Number algorithm in Python is efficient for small to moderate numbers with a time complexity of O(d), where d is the number of digits. The primary operations include basic arithmetic and exponentiation.

Further See: Understanding NumPy Library in Python.

Conclusion

In this article, we've explored Armstrong Numbers in Python, highlighting their unique property of being equal to the sum of their digits raised to their respective powers. We demonstrated how to implement and optimise a Python program to check for Armstrong Numbers. Understanding this concept and its implementation enhances both mathematical knowledge and programming skills.

#Armstrong Number in Python #Armstrong Number #Python

0 notes