#set builder notation

[math-journal2]

<— Unit 🍑— Unit 13 — Unit 14 —>

Precalculus

Unit 13: Inequalities

Part 1 —>

Review: Unit 2 pg2 / Unit 2 pg4 / Unit 4 pg9

Set Builder Notation

Inequality —> SD

Inverval Notation

Inequality —> IN

Absolute Value Inequality

Number Lines

Domain & Range

Page 38

[notarealwelder]

Let's talk about Axiom Schema of Replacement.

To start from the beginning: what's ZFC for?

Whenever we're doing any kind of math, we want to say that things exist. To build objects from nothing or from other objects, to use obviously definable functions, to locate subobjects with properties, and to.....not really care about proving their....fairly obvious existence.

ZFC gives us tools for exactly that! It claims existence of all kinds of things. —well, ok, really it claims existence of exactly one kind of thing — sets — but most anything can be encoded as a set, and by golly there are sets in ZFC.

Now, some amount of design went into ZFC, and its axioms are, to an extent, individually ≈compact in ≈scope of objects they provide, and all have a ≈well-defined purpose. There's Pair if we want to build a set by concretely pointing at its objects; there's Union when we want, well, a union over a collection; there's Infinity when we're not satisfied with finite objects; there's Powerset when we want e.g. functions to exist as first-class objects.

However: while these axioms are very generally useful, they're not very suited to constructing.....objects of specific weird shapes. To get these, we want the full expressive power of first-order-logic formulas, and therefore, Axiom Schemas.

ZFC has two.

---

Axiom Schema of Restricted Comprehension (also: of Specification) is probably extremely familiar! It's the axiom that validates the set-builder notation, { x ∈ A | φ(x) }; it lets us take any set and acquire its subset filtered by any formula. Very useful! However, it's only usable if we can construct an overset that definitely contains everything we need. What if we can't?

Concrete example: let ω be the name of the standard countable set, and consider iterated powersets of ω: ω, 𝓟(ω), 𝓟(𝓟(ω)), ..., 𝓟ⁿ(ω), ... . Is there a union of all of these? Union would give us that if we managed to construct the set {ω, 𝓟(ω), 𝓟(𝓟(ω)), ..., 𝓟ⁿ(ω), ...}, but, while all individual 𝓟ⁿ(ω) definitely exist by iterated application of Powerset, it's not clear how'd we collect them all into a set.

---

On a completely unrelated topic¹, let's talk about two concepts of a function.

(¹ blatant lie)

One way to define a function is to exhibit a set that represents it, i.e. contains pairs (x, y) with x ∈ X and y ∈ Y, and also exactly one such pair for every x from X.

Another way to define a function is through a predicate. if we imagine a 2-variable formula φ(x, y), for which our ambient theory proves ∀ x. ∃! y. φ(x, y) — that, for any value of the first-argument `x` exactly one value `y` of the second-argument satisfies φ — then it's reasonable to say that φ defines a function! We can, in principle, plug any given `x` into the proof of ∀ x. ∃! y. φ(x, y), and extract the `y` that the proof demonstrates, linked to `x` fairly functionally.

It's easy to see that any set-function can be converted into a formula-function: if we're given an f : X → Y, then φ(x, y) := (x,y) ∈ f trivially "defines" the same "function" as f!

To convert a functional predicate into a set-function, we'll need the Axiom Schema of Replacement.

---

Slightly simplifying, Axiom Schema of Replacement says:

- given a formula φ(x,y),

- a codomain X from which we'll pull x-arguments to φ,

- and a proof that this formula is in fact functional on X,

- there exists the set Y collecting all the `y`s that satisfy φ for `x`s from X.

Or, formally: ∀ X. [∀ x ∈ X ∃! y. φ(x, y)] ⟹ ∃ Y ∀ y. [y ∈ Y ⟺ ∃ x ∈ X . φ(x, y)].

(In fact, φ is allowed to have other free variables, and also to depend on X, but, eh, details.)

With that, we can convert formulas into functions! Take a φ and a codomain X; acquire the domain Y via Replacement, construct the product X×Y the usual way, then filter it via Comprehension to {(x,y) ∈ X×Y | φ(x, y)}, and there we have it.

To answer our previous question: the union of 𝓟ⁿ(ω) certainly exists! we can construct a formula φ(n, S) that's satisfied exactly when S = 𝓟ⁿ(ω), then acquire the image of ω under φ via Replacement, and union over the resulting { 𝓟ⁿ(ω) | n ∈ ω }.

(There's a trick to constructing that φ, but that's a topic for another post.)

[project-m-a-m-i]

Rule Section B: Cards

Cards are the primary means of playing a run through any rendition of Project M.A.M.I or existing deck-builder game, each with their own unique set of abilities to advance through the game. Depending on the format you use, cards are often played using an energy or mana system that limits how many you play in a turn before being discarded. Cards are usually drawn at the start of an encounter and at the start of the player’s next turn. All player actions are denoted by them, although the diversity of deck-builders can often make them VERY hard to translate into being playable in another game. That’s where I come in. As such, the term “card” will fall under one of these sub-classes:

Unit: An extra combatant with their own stats and abilities that can change the flow of the game, either considered an ally, enemy, or neutral. When the HP of a unit reaches 0, it is considered “dead” or “destroyed” and usually removed from the field to a “graveyard pile” separate from a discard pile. Unlike Leaders, a dead unit doesn’t necessarily mean your run is over unless extra applicable rules state so.

Champion: A unique unit that has special rules, abilities, passives, upgrades, and stats that set it apart from other units. Only one copy of a Champion can appear in your deck or on your side of the field at a time. Letting a Champion die sometimes puts the player at a disadvantage, although strategies differ.

Action: Often considered things such as “attacks”, “skills”, “spells”, and “tricks” among other things, these cards have an immediate effect on the game once played successfully before being moved to the discard pile.

Passive: A card that applies an extra rule to the game once played successfully. Passives persist from the moment they’re played until the end of the combat encounter.

——————————

Sub-Rules

Keywords: Keywords are common words that are used over multiple cards that indicates a specific overarching rule to be followed.

Equipment: A card/rule modifier that can be applied to cards between encounters in a run to change their rules and/or stats. Their length can range from specific actions, a number of turns, or even an entire run.

Modifier: A sub-type of passive or action that applies or changes extra rules to PART of the field, sometimes considered to apply a status effect. Modifiers persist from the moment they’re played until they expire or removed by other rules.

Energy/Mana/Resources: A measurable, finite resource that allows you to play cards once spent. Most formats utilize energy or other exterior limits in some way to limit the amount of cards you can play in a turn, although it can regenerate in different ways depending on your rule sheet.

Category: A notation that limits which decks a card can be played in unless overridden by another rule. Oftentimes, categories indicate that cards are exclusive to specific Leaders.

Class: A sub-classification for a given card which bears no immediate effect, but may trigger other rules and card abilities/text.

Tokens: Tokens are cards and units created by other cards or rules. They do not start in your deck at all.

——————————

Recorded Categories:

(None Yet)

[samanthablake02]

Perfect Your Craft: Learning Advanced Kotlin Programming by 2025

Late 2024 industry reports indicate that applications with robust architectures and asynchronous capabilities experienced a 30% increase in user engagement. Merely understanding Kotlin basics is no longer sufficient for excelling in modern Android and backend programming. To thrive, developers must master advanced Kotlin techniques, including Domain Specific Languages (DSLs), Coroutines, and architectural patterns, to build scalable, maintainable, and performant applications. For any android app development company, investing in these advanced skills is now essential to staying competitive and delivering top-tier solutions.

Revealing the Potential of Kotlin DSLs: Designing Beautiful APIs

Why Adopt Kotlin DSLs?

Enhanced Readability: DSLs enable code that resembles declarative statements, making it accessible to domain-specific users.

Rapid Development: DSLs abstract complex functionalities, allowing developers to focus on domain logic.

Modularity: DSLs promote separation of concerns, localizing changes within specific domains for streamlined maintenance.

Simplified Interfaces: DSLs provide intuitive syntax, hiding underlying complexity and aiding in complex rule implementations.

Key Techniques for DSL Development

Define Your Domain: Clearly identify the tasks or setups the DSL will simplify.

Create Intuitive Syntax: Use Kotlin features like lambdas with receivers, infix notation, and extension functions to design elegant DSL structures.

Iterative Growth: Start with a minimal set of features and expand incrementally, ensuring focus and usability.

Prioritize Developer Experience: Incorporate clear error messages, comprehensive documentation, and engaging examples for seamless adoption.

Common DSL Design Mistakes to Avoid

Overcomplication: Avoid overly broad or complex DSLs lacking domain focus.

Inconsistent Syntax: Ensure coherent syntax throughout to maintain usability.

Poor Documentation: A well-documented DSL is essential for developer understanding and application.

Neglecting Performance: Always consider the performance implications of using DSLs.

Kotlin Coroutines: Mastering Asynchronous Programming

The Beauty of Kotlin Coroutines

Simplified Code: Coroutines make asynchronous code appear sequential, improving readability.

Lightweight Execution: Coroutines are far lighter than threads, enabling thousands to run with minimal overhead.

Structured Concurrency: Coroutines streamline management and cancellation of asynchronous tasks.

Seamless Integration: Coroutines integrate with popular Android libraries like Retrofit and Room.

Essential Coroutine Practices for 2025

Master Suspend Functions: Understand how suspend modifies non-blocking functions.

Learn Coroutine Builders: Familiarize yourself with launch, async, and runBlocking, each serving unique purposes.

Understand Contexts and Dispatchers: Explore Dispatchers.IO, Dispatchers.Main, and Dispatchers.Default for optimized thread execution.

Utilize Kotlin Flows: Handle asynchronous data streams effectively with Kotlin Flows.

Common Coroutine Challenges

Avoid Blocking Main Threads: Steer clear of runBlocking in production environments.

Implement Lifecycle-Aware Scopes: Use viewModelScope or lifecycleScope to manage coroutine lifecycles on Android.

Handle Exceptions Gracefully: Use try-catch blocks and supervision strategies for robust error management.

"Kotlin Coroutines represent a fundamental shift in how developers approach asynchronous programming. Their elegance and power are essential tools for modern Kotlin development." — Competent Kotlin Developer, 2024

Architectural Patterns: Methodical Kotlin Applications

Kotlin Architectural Paradigms for 2025

Model-View-ViewModel (MVVM): A pillar of Android development that decouples UI from business logic for better maintainability.

Clean Architecture: Modular, framework-agnostic design promoting testability and scalability.

Model-View-Intent (MVI): A reactive paradigm leveraging immutable states and unidirectional data flow for predictable UIs.

Benefits of Modular Applications

Faster Build Times: Modular code speeds up builds significantly.

Code Reusability: Modules enhance collaboration and feature delivery.

Streamlined Gradle DSL: Kotlin’s Gradle DSL simplifies building and managing modular projects.

Important Factors Influencing Architectural Decisions

Architectural decisions are influenced by several key factors that impact the scalability, maintainability, and testability of applications:

Application Complexity: MVVM is ideal for simpler applications, while Clean Architecture or MVI suits more complex projects.

Team Size: Larger teams benefit from modular architecture as it facilitates concurrent development and reduces merge conflicts.

Testability: Patterns emphasizing decoupling and pure functions—like Clean Architecture and MVI—are particularly helpful for applications requiring extensive testing.

Scalability Needs: Applications anticipating significant growth require modularity and loose coupling to ensure robust scaling.

Avoiding Architectural Anti-Patterns

Massive Activities/Fragments: Avoid overloading Activities or Fragments with too much logic. Delegate responsibilities to ViewModels or other architectural components.

Minimize Tight Coupling: Reduce dependencies between modules and components. Use dependency inversion techniques to decouple high-level modules from low-level implementations.

Layer Ignorance: Ensure clear layers in your architecture—separation between presentation, domain, and data layers is essential for maintainability.

Common Questions

What Are the Main Advantages of Domain-Specific Languages (DSLs)? DSLs enhance domain focus, improve developer efficiency, and simplify code readability.

How Do Kotlin Coroutines Simplify Asynchronous Operations? Coroutines replace callbacks with sequential, readable synchronous-like architectures, simplifying asynchronous code.

Why Does Kotlin Project Architectural Pattern Selection Matter? As application complexity increases, architectural patterns ensure maintainability, scalability, and robustness.

Which Kotlin Features Benefit MVVM Implementation? MVVM naturally aligns with Kotlin’s data classes, coroutines, and flows, enhancing asynchronous operations and data handling.

What Mistakes Should Developers Avoid With Kotlin Coroutines? Prevent stalling main threads, avoid coroutine leaks, and implement proper exception management for stable program behavior.

Recommendations

Learning advanced Kotlin programming is vital for creating innovative, high-performance applications as we move toward 2025. By investing in knowledge of DSLs, coroutines, and strong architectures, developers can lead Kotlin development and deliver exceptional software solutions.

Action Steps:

Experiment with DSL Design: Develop domain-specific languages tailored to your project’s needs to boost clarity and efficiency.

Dive Into Coroutines and Flows: Deepen your understanding of asynchronous programming to optimize app responsiveness and scalability.

Investigate Architectural Patterns: Explore architectural frameworks suited to your application’s requirements for better scalability and testability.

Share Knowledge: Collaborate with fellow developers to learn, exchange ideas, and refine advanced Kotlin practices together.

Elevate your Kotlin proficiency today! Embrace advanced programming techniques to fully utilize Kotlin’s capabilities and stay ahead in creating outstanding applications. Let’s pave the way for innovative software solutions in 2025 and beyond.

[class11maths]

Master Chapter 1: Sets from Class 11 Maths with Ashish Sir in this detailed lecture! This video provides step-by-step solutions for NCERT Exercises 1.1 & 1.2, ensuring a solid understanding of Sets and their types.

🔹 Key Concepts Covered: ✔️ Meaning of Sets & Different Forms (Roster & Set Builder Notation) ✔️ Special Types of Sets (Null, Finite, Infinite, Equal Sets) ✔️ Complete Solutions for NCERT Exercise 1.1 & 1.2

[speedywonderlandtrash]

Class 9 general math chapter 2 exercise 2.1 solution : part 1

Class 9 general math chapter 2 exercise 2.1 solution

Set: A set is defined as a well-defined collection or assembly of objects from the real or conceptual world. Typically, sets are denoted by uppercase English letters such as A, B, C, ... , X, Y, Z. Each object or member of a set is called an element of the set. For example, if B = {a, b}, then a and b are elements of set B. Methods of Representing a Set: A set can be represented primarily by two methods: 1. Roster (Listing) Method 2. Set-builder Method 1. Roster Method: In this method, all elements of the set are explicitly listed and enclosed within curly braces { }. If there are multiple elements, they are separated by commas. For example: A = {a, b}, B = {2, 4, 6}, C = {Niloy, Tisha, Shuvra}, etc.

2. Set-builder Method: In this method, all elements of the set are not explicitly listed; instead, a common property that defines the elements is specified. For example: A = {x : x is an odd natural number}, B = {x : x is one of the top five students in grade nine}, etc. Types of Sets: Finite Set: A set in which the number of elements can be counted is called a finite set. Infinite Set: A set in which the number of elements cannot be counted is called an infinite set. Empty Set: A set that contains no elements is called an empty set. The empty set is denoted by Φ. Venn Diagram: John Venn (1834-1883) introduced a method of representing sets using diagrams. In this method, the sets under consideration are depicted using various geometric shapes in a plane, such as rectangular, circular, and triangular regions. These diagrams are known as Venn diagrams, named after John Venn. Subset: Any set that can be formed from the elements of a given set is called a subset of that set Annual exam preparation for class nine Proper Subset: If B is a subset of A and A has at least one element that is not in B, then B is called a proper subset of A, and it is written as B ⊆ A. For example: A = {3, 4, 5, 6} and B = {3, 5} are two sets. Equality of Sets: Two sets are considered equal if they contain the same elements. For example: A = {3, 5, 7} and B = {5, 3, 7} are equal sets, written as A = B. Difference of Sets: The set that is formed by removing the elements of one set from another set is called the difference of sets. Universal Set: In practical discussions, all sets under consideration are subsets of a particular set, called the universal set. For example: If A = {x, y} is a subset of B = {x, y, z}, then B is the universal set relative to A. Complement of a Set: If U is the universal set and A is a subset of U, then the set containing all elements not in A is called the complement of A. The complement of A is denoted by Ac or A´. Mathematically, Ac = U A. Union of Sets: A set formed by combining all elements of two or more sets is called the union of the sets. Intersection of Sets: A set formed by the common elements of two or more sets is called the intersection of the sets. Suppose A and B are two sets. The intersection of A and B is denoted by A ∩ B and is read as "A intersection B." In set-builder notation, A ∩ B = {x : x ∈ A and x ∈ B}. Disjoint Sets: If two sets have no elements in common, they are called disjoint sets. Power Set: The power set of a set A is denoted by P(A). Ordered Pair: An ordered arrangement of two elements, where one is designated as the first position and the other as the second, is called an ordered pair. Cartesian Product: The set of all ordered pairs formed by the elements of any two sets A and B is called their Cartesian product. Relation: If A and B are two sets, then a non-empty subset R of the Cartesian product A × B is called a relation from set A to set B. Function: If two variables x and y are related in such a way that for any value of x, there is only one corresponding value of y, then y is called a function of x. Domain and Range: For any relation, the set of the first elements in its ordered pairs is called its domain, and the set of the second elements is called its range. Suppose R is a relation from set A to set B, meaning R ⊆ A × B. The set of the first elements in the ordered pairs of R will be the domain of R, and the set of the second elements will be the range of R. The domain of R is denoted by dom R, and the range by range R. Graph of a Function: The visual representation of a function is called its graph. Graphs play an essential role in clarifying the concept of functions. Two perpendicular intersecting straight lines are called coordinate axes, and the point where they intersect is called the origin. Perpendicular Axes: In a plane, two straight lines XOX´ and YOY´ are drawn intersecting each other perpendicularly. The horizontal line XOX´ is called the x-axis, the vertical line YOY´ is called the y-axis, and their intersection point O is called the origin. Coordinates: The signed numbers representing the perpendicular distances from any point in the plane to the axes are called the coordinates of that point. Creative Question - 1 Given: ƒ(x) = x² + 4x + 3 A = {x ∈ Ι : x is an odd number and x B = {x ∈ Ι : x is a divisor of 21} C = {x ∈ Ι : x is a multiple of 7 and x Solve the following: a. Find the value of ƒ(−1). 2 b. Show that if the number of elements in A is n, then the number of elements in P(A) is 2ⁿ. 4 c. Prove that A × (B ∩ C) = (A × B) ∩ (A × C). 4 Creative Question Solution: (a)Given, ƒ(x) = x² + 4x + 3 So, ƒ(−1) = (−1)² + 4 × (−1) + 3 = 1 − 4 + 3 = 0 (Answer) **(b)** Given, A = {x ∈ Ι : x is an odd number and x So, A = {1, 3, 5} Subsets of A: {1}, {3}, {5}, {1, 3}, {1, 5}, {3, 5}, {1, 3, 5}, and Æ (empty set) Thus, P(A) = {{1}, {3}, {5}, {1, 3}, {1, 5}, {3, 5}, {1, 3, 5}, Æ} The number of elements in set A is 3, and the number of elements in its power set P(A) is 8, which is equal to 2³. Thus, if the number of elements in set A is n, the number of elements in P(A) is 2ⁿ, as shown. (c) Given, B = {x ∈ Ι : x is a divisor of 21} = {1, 3, 7, 21} and C = {x ∈ Ι : x is a multiple of 7 and x = {7, 14, 21, 28} Now, B ∩ C = {1, 3, 7, 21} ∩ {7, 14, 21, 28} = {7, 21} Left Side: A × (B ∩ C) = {1, 3, 5} × {7, 21} = {(1, 7), (1, 21), (3, 7), (3, 21), (5, 7), (5, 21)} Right Side: A × B = {1, 3, 5} × {1, 3, 7, 21} = {(1, 1), (1, 3), (1, 7), (1, 21), (3, 1), (3, 3), (3, 7), (3, 21), (5, 1), (5, 3), (5, 7), (5, 21)} A × C = {1, 3, 5} × {7, 14, 21, 28} = {(1, 7), (1, 14), (1, 21), (1, 28), (3, 7), (3, 14), (3, 21), (3, 28), (5, 7), (5, 14), (5, 21), (5, 28)} (A × B) ∩ (A × C) = {(1, 7), (1, 21), (3, 7), (3, 21), (5, 7), (5, 21)} Therefore, A × (B ∩ C) = (A × B) ∩ (A × C) Question -2 g(x) = and h(t) = are two algebraic expressions. a. Find the values of g(0) and h(1). 2 b. Find the value of . 4 c. Prove that = . 4 Solution for Question 2 (a) Given, g(x) = So, g(0) = = = = -1 (Ans.) and h(t) = h(1) = = = = 3 (b) Similar to Example 24 from Exercise 2.2 in the textbook. (c) Given, h(t) = So, h = = and h() = = = = Therefore, (Proved) Read the full article

[textileebook]

Discrete Mathematics with Applications, 5th Edition PDF by Susanna S Epp

Discrete Mathematics with Applications, Fifth Edition By Susanna S. Epp Contents: Speaking Mathematically 1 Variables 1 Using Variables in Mathematical Discourse; Introduction to Universal, Existential, and Conditional Statements The Language of Sets 6 The Set-Roster and Set-Builder Notations; Subsets; Cartesian Products; Strings The Language of Relations and Functions 15 Definition of a…

[lilith-hazel-mathematics]

Agreed with prev, "N◃G" basically means N is a divisor of G, implying N is smaller than G, hence N<G, or rather N⊂G. They all have the same kinda shape <,◃,⊂

Related fun fact: the divisor relation on the integers forms a partial order, but for some stupid reason it's denoted by |, the symmetrical vertical bar. Instead, I use ◃ with an underline to denote the divisor relation, and without the underline it denotes strict divisor.

In addition to being more readable, there's also no notational overlap. By contrast, the "|" is sometimes used in set builder notation, and it's also identical to absolute value bars; try parsing {n | |n| | m}, the set of signed divisors of m. Please join me in normalizing usage of ◃ to denote the divisor relation.

we need an equivalent for "> eats the bigger number" for semidirect products. the side with the bar acts on the side without, but idk a good mnemonic for that.

the best i can come up with is thinking of the bar as a weapon one side is using to attack the other but i dont think thats the best aesthetically lol

[yurimysterycult]

is there some way you can define an 'operator' (i cant think of a better word) which gives the diagonal of a set, {(a,a) | a ∈ X}? or the identity function X -> X as a set? you can notate the latter as id_X (subscript) but can you make that id itself a mathematical object?

i dont think it would be a function, since the domain would have to be the set of all sets right? which doesnt exist / isnt a set

this is all because im doing combinatorics and im thinking that the space of 2-permutations of a set Y is equal to Y^2 \ id_Y... but writing it like that feels insane and i dont really like using set builder notation either

[math-journal2]

Set Builder v Interval Notation

[lurking-latinist]

It is that!

Specifically, it's a math textbook (or rather a series of math textbooks - Algebra is followed by Trigonometry and then Calculus) by Douglas Downing, in which you learn the subject by following along with the adventures of a group of characters who are themselves learning and applying the subject. They are the royal court of a(n extremely math-oriented) fantasy kingdom called Carmorra: the King, Marcus Recordis the scribe, Professor A. A. A. Stanislavsky, Gerard Macinius Builder, and Alexanderman Trigonometeris, the Royal Keeper of the Triangles (I'm sure you can guess in which volume he was introduced). Also sometimes, but not always, a nameless first-person narrator who was shipwrecked on Carmorra's coast and lost their memory, but occasionally has flashes of insight that supply the real-world names for calculus concepts.

It was extremely formative to me at an early age--much earlier than when I actually fully understood the math. I liked to read the adventures, and I followed what I could of the math; I skimmed and accepted the rest rather as I now skim and accept all the sailing in the Aubrey-Maturin books. But in rereading it now, I'm struck by the fact that, unlike what you might expect, the adventure and the math aren't two different, how shall I say, modes. It's not as if for a few pages you have exciting dragon battles, and then they stop and multiply binomials. Rather, the adventure is the discovery of math.

Sometimes this is a bit contrived--the heroes' recurring opponent is a cackling villain called the Gremlin who often sets them math challenges, and sometimes this is merely in the nature of a dare or threat--"If you can't take this derivative within twenty-four hours, I will drop this maiden over the side of a cliff" sort of thing (that's not a specific book example, I don't think there are any distressed maidens). But often the Gremlin's threats merely add a level of excitement to actual real-world math applications: "I have destabilized this bridge and you have to use calculus to fix it!" And then the characters are working together to reason towards the math concepts they need to apply. And you the reader are doing the same. Often the Gremlin isn't even involved, and they've just decided, for instance, that they want to throw a party and they need to calculate the ratio between one ingredient and another ingredient in the food.

BUT! I think a particular part of the appeal for me, as well as the educational value, is the group of characters that are doing this. It would be very, very different if it were a solo adventurer. The group of characters not only models mathematical discovery and learning; they model collaboration, and they each represent a different approach to math and a different role in the process of discovery and learning. (And one of my particular buttons to push is stories where each team member has a specific role and they work together; which is why I love this so particularly.) It would be easy for them to just be identical puppets mouthing mathematical ideas to each other, but in fact they each have a different personality that a student reading the book might be able to relate to or learn from.

Recordis, for instance, the Royal Scribe, is organized and conservative. He loves charts and tables and having everything written down neatly; he loves double-checking things; he doesn't mind brute force derivations (until they involve too much writing, when he'll suggest notation shortcuts). He doesn't like unnecessary innovations, and often voices the skepticism someone might have about a new idea--which is great, because it means the characters get to test that idea and prove it stands up. (Although he's completely incapable of coping with imaginary numbers, and faints away every time they're mentioned, which is the book's Watsonian excuse for not covering complex numbers in much depth. The Doylist reason is of course that it's only an introductory textbook.)

The Professor is in many ways Recordis' opposite. She's always eager to push things further and extend ideas. She can be more theoretically minded, and other characters find practical applications for things she's just worked out are possible. Because of this, she's also the most likely to realize that a concept they discovered in one domain is applicable to other areas, often remembering ideas from previous chapters or even books. She has the most "academic" approach to mathematical discovery.

The King, fitting to his status, tends to be the leader of the group, and often synthesizes others' approaches. He keeps an eye on the shape the investigation is taking and how it's getting them closer to their goal. He often mediates disputes between rival strategies, which I think is a great thing to model for high school and college students who might be using these books, personally. He's also depicted as concerned about his subjects' welfare, which is nice.

Builder isn't always present at the Royal Court, but as his name suggests, he's responsible for practical, hands-on implementation of their mathematical discoveries. He's often assisted by a friendly, childish giant (one of the series' fantasy elements) called Pal, whose massive strength and short attention span account for the sometimes peculiar conditions and constraints of word problems.

Trigonometeris of course is mainly in the foreground inhis own book, although he continues to appear in Calculus, usually as the spokesman of the trigonometric functions. He's characterized more by this specialist subject matter than by any particular approach, but I love him a lot. His introduction in Trigonometry as the despondent inventor of the Adjustable Triangle (which turns out to be a device illustrating triangles on the unit circle--hence trigonometry...), desperate to demonstrate its usefulness to anything and everything, is very endearing, especially as he is actually able to make it that useful!

And then, of course, there's the evil Gremlin--"the archenemy of the people of Carmorra--the Spirit of Hopelessness and Impossibility!" as he is described in Trigonometry. Which is the best description of a villain in anything, ever. He has magic powers and a cool, evil cape. He is, of course, always defeated in the end!

There are delightful illustrations too--here's one, from Trigonometry:

It's a really cool book series if you're interested in math, pedagogy, math pedagogy, or teams of character archetypes working together. Or if you want to understand me psychologically, I guess. And I am nominating it for Yuletide. I want fic where they discover other things.

Oh, and they're all on the Open Library at present.

if not stopped I may make a post on character dynamics in the Algebra the Easy Way series

[dailyadventureprompts]

Saw your thing about the compass home base on my dashboard, and I immediately gave a follow after looking at your other stuff :D any chance you can do a druid themed home?

Player Home: Two-Goats Lookout

"I'll admit, it took me a while to find this place: Not only is it out of the way, I thought the notation on my map was warning me to beware a pair of angry ungulates guarding the pass" -Barnabus Blythe, Coachman

Setup: Built half way up a rolling mountain on foundations set down by a barbarian warlord, this walled outpost overlooks a vast landscape of rolling foothills and plunging valleys  along the kingdom’s border. Serving both as shelter for travelers and staging ground for expeditions into the wild frontier, this forester’s fortress could act as a thriving home for a party focused on exploration and facing the challenges of the wilderness. 

Adventure Hooks: 

As it guards an important mountain pass, Two-Goats Lookout could be a good place for a first-time party to meet: drawn from local trappers, caravan travelers, and soldiers shipped out to the boonies to defend the kingdom’s furthest border. Hunting dangerous wildlife, protecting the footholds of civilization, and escorting foreign traders to and from nearby settlements can all provide a great backdrop for early adventures, to say nothing of the various caves and ruins scattered throughout the landscape waiting to be explored. 

The party might first learn of the lookout while hunting a dangerous outlaw, who retreats to the disused outpost after kidnapping the scion of a noble house for ransom. After the brigands are dealt with, the innocent is returned, the party may realize mid-way through their looting that they’re now in possession of a reasonably established (if somewhat bloodstained) keep. Why not invest a bit of their looted spoils and hard-won reward and see about turning this into their personal clubhouse? 

Alternatively, if the party were of an outlaw bent themselves, Two-Goats Lookout would provide an excellent hidden base from which to plot their attacks against a corrupt administration overseeing the local townships. Mostly forgotten though it might be, It’d be the perfect place to add a few fortifications, perhaps start assembling a band of merry individuals who also share the party’s problems with authority. 

It’s not uncommon for nobles to be put into the position of having to reward groups of adventurers for their vital service in preserving the order of their realms. While some of these sellswords are professional and well composed enough to earn themselves a place at court, most mercenaries are about as crass and volatile as a powderkeg with political opinions. In this latter case, standing operating procedure is to load them down with gold or shiny weapons and hope they go away, but if the vagabonds DO want land, perhaps a fortress far, far, FAR, away from their benefactor’s own could do the trick? 

Accommodations & Upgrades: 

Though already sitting on enough stock and provisions to last out the winter or repel a marauding band of ogres, the Lookout has a long way to go before being truly self sufficient. Architects can be hired to make repairs and additions, artisans to craft gear from abundant local resources. Perhaps they should go about seeking some followers to fill the lookout’s many unused buildings. 

A small temple to Erathis, the Lawbearer was built by one of the Lookout’s previous owners, but anyone who goes to pray there can tell that the shabby little shrine has something off about it.  The temple was actually built in a space considered sacred by the fortress’s original barbarous inhabitants, and the builder presumed to consecrate it in the name of his patron without asking either goddess.  This has left the outpost in a sort of spiritual limbo between the domains of the goddess of law, and the goddess of the wilds, Melora.  Rededicating the temple to either goddess could provide numerous blessings, With the Lawbearer granting safer roads and surer walls/ tools, and the Wildmother blessing the surroundings with bountiful game and favorable weather. Doing so would require some meditating, and perhaps acting as go-betweens to appease both gods. 

Traveling about the hinterlands and befriending local traders is sure to give the party insight into sources of natural resources, as well as merchants willing to invest in some new ventures: after a year or two of good work the party might end up owners of a mine or lumbermill, a great source of downtime funds. 

Further Adventures:

A series of odd occurrences among villages in the foothills leads the party to discover that a nearby peak contains a band of darkelf bat-riders, hunters and isolationists who aren’t above a little light caravan-raiding now and again. Maybe the party should make nice with their new neighbors before the two encampments come to blows. 

After a series of inexplicably prismatic clouds begin raining random objects through the valley, the party is sent to investigate and discovers a rogue alchemist who’s set up shop (quite literally) on top of a nearby mountain after levitating his house away to escape his debts. 

A series of clever passages connect most of Two-Goats Lookout’s buildings for ease of travel through the winter, but beneath these lays a blocked off series of chambers known as “The Deep Cellars”. Dating back to the time of the warlord, these chill dungeon chambers connect to a series of long buried caverns, and may infact contain the warlord’s final horde.  

While the Deep Cellars do contain the horde, it is locked behind a curse-warded door that can only be opened by a key taken by the warlord to his tomb, a tomb that exists somewhere out across the mountains or down into the foothills. Perhaps the party can decipher the clues left within the caverns ( and do a little research on history) and discover just where this tomb might lay. 

Art

[transgenderer]

talking about math can be frustrating sometimes because like. english grammar is not set theory, to the point where soetimes you just have to grab a piece of paper and write what you mean in set builder notation, which feels very silly

[jmarsreb-blog]

Sets (pt. 1)

Sets are the building blocks for mathematics, and so it seems fit to start there. We think of a set as a collection of (distinct) objects.

The classic examples of sets are just $X = \{1,2\},$ the natural numbers $\mathbb{N}$ which consists of all numbers greater than 0, and the integers $\mathbb{Z}$ which consist of all whole numbers. A natural example is also $\emptyset$, which is known as the empty set, or the set which contains no elements.

Sets are natural objects, but the definition I gave isn’t quite a good one. We’ll leave the ambiguity there for now, but we may come back to more rigorous set theory later. (One may wonder; is the set of all sets which do not contain themselves a set?)

There are some natural operations we want to do with sets. For example, if I want to combine sets, I can take the union of them. That is, if $A$ and $B$ are sets, the union of the sets $A \cup B$ is the collection of elements which is either in $A$ or $B$. We’ll generally write this as

$$ A \cup B = \{x \ : \ x \in A \text{ or } x \in B\}.$$

Translating this, this says that $A \cup B$ is the collection of elements $x$ such that $x$ is in $A$ or $x$ is in $B$. We read the colon as “such that” and what follows are the conditions for the elements in the set. This is sometimes referred to as set builder notation.

Pictorially, we can think of a union as the blue shaded region in the following picture:

Another thing we may want to do is look at the elements which are contained in two given sets, $A$ and $B$. This is referred to as the intersection, and we formally write this as

$$ A \cap B = \{ x \ : \ x \in A \text{ and } x \in B\}.$$

Pictorially, we have the intersection is the blue shaded region in the following:

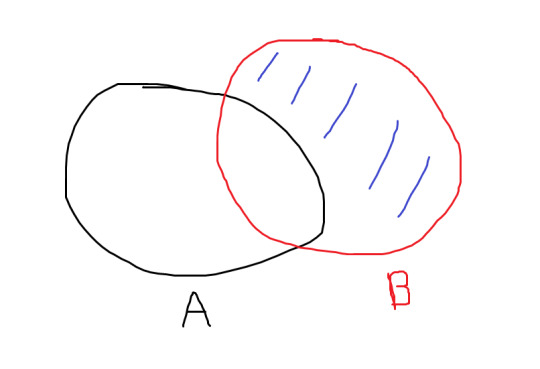
Sometimes we wish to look at elements which are in one set but not the other. This is referred to as set minus. That is, if $A$ and $B$ are sets, the set minus of them is

$$ B - A = \{x \ : \ x \in B \text{ but } x \notin A\}.$$

Again, we can think of this pictorially, where the elements in $B-A$ are the blue shaded region:

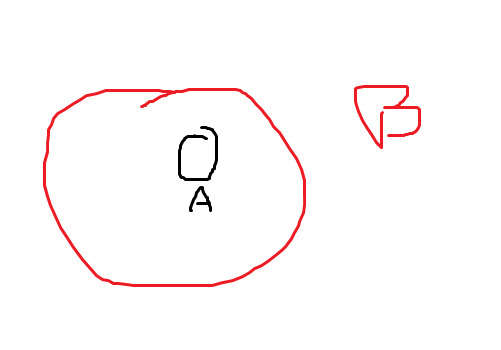
We say that $A$ is a subset of $B$ if we have that, for all $x \in A$, $x \in B$. That is, all of the elements which belong to $A$ also belong to $B$. One should have the following picture in their head:

We say that two sets are equal if $A \subseteq B$ and $B \subseteq A$, and we write it as $A = B$. You can think of this as saying that they share all of the same elements.

If we have some universal set $X$, we often write the complement as $A^C$, which is understood to be the set of elements which are not in $A$. We can also think of this as $X - A$.

Remark: If $A, B \subseteq X$, then we can think of $B - A$ as $B \cap A^C$.

A nice exercise is to verify when associativity (that is, parentheses don’t matter), commutativity (order doesn’t matter), and distributivity apply when using parentheses and intersections/unions. For example, we have that

$$ A \cup (B \cup C) = A \cup B \cup C,$$

which gives us associativity for unions, and we have

$$ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) $$

which gives distributivity between unions and intersections.

One special relation we have is called deMorgan’s laws. These state the following; let $\{E_i\}$ be a countable (we’ll come back to this later, for now just think finite) collection of sets, then we have

$$ \left( \bigcup_i E_i \right)^C = \bigcap_i E_i^c$$

and

$$ \left( \bigcap_i E_i \right)^C = \bigcup_i E_i^c.$$

Proof: To prove this in the finite case, it suffices to do it for two sets. So lets say we have $E_1, E_2$ are sets. Taking $x \in (E_1 \cup E_2)^C$, we see that this says that $x \notin E_1 \cup E_2$. In other words, $x$ is not in $E_1$ or $E_2$. But this is the same as saying that $x$ is not in $E_1$ and it is not in $E_2$, or $x \in E_1^c \cap E_2^c$. Hence, $(E_1 \cup E_2)^C \subseteq E_1^C \cap E_2^C$.

Now, take $x \in E_1^C \cap E_2^C$. Then in the same way we’ve done above, we have that $x$ is not in $E_1$ and it is not in $E_2$, but this is the same as saying $x$ is not in $E_1$ nor $E_2$, which comes out to $x \notin (E_1 \cup E_2)^C$. So $E_1^C \cap E_2^C \subseteq (E_1 \cup E_2)^C$, and we have equality. The argument when we flip intersection and union is the same.

Why was doing it for two sets sufficient? Say we have sets $E_1, \ldots, E_n$, and we want to figure out

$$ \left( \bigcup_{i=1}^n E_i \right)^C.$$

We can rewrite the inside as

$$ \left( \bigcup_{i=1}^{n-1} E_i \cup E_n \right)^C.$$

Now, using what we’ve just shown, we know it holds for two sets, so we get that this is equal to

$$ \left( \bigcup_{i=1}^{n-1} E_i \right)^C \cap E_n^C.$$

We can then continue this way until we get the desired result. This is the essence of induction, which I won’t go into yet.

Another important trick is to “disjointify” sets. We say that two sets $A$ and $B$ are disjoint if $A \cap B = \emptyset$; that is, they do not share any elements. A disjoint union is a union of sets which are disjoint. The reason this is important is for notions of size; for now, staying in the realm of finite sets, we say that the size or cardinality of a set is simply the number of elements in that set. So if $X = \{1,2\}$, then the size, denoted by $|X|$, of $X$ is simply 2. When we have a disjoint union, we get to add up the sizes of the sets to get the size of our union; when we do not have a disjoint union, this is not the case.

For example, let $X = \{1,2\}$, $Y = \{2,3\}$ and $Z = \{3,4\}$. Then $X \cap Y = \{2\}$, which is not the empty set, and so these are not disjoint. We have $X \cup Y = \{1,2,3\}$, which has three elements. So $|X \cup Y| \neq |X| + |Y|$ in this context. On the flip side, we have $X \cap Z = \emptyset$; these sets are disjoint. So taking their union, we have $X \cup Z = \{1,2,3,4\}$, which has size 4, and so we do have $|X \cup Z| = |X| + |Z|$. In some sense, it is easier to calculate the size of the union provided our sets are disjoint.

To transform a union into a disjoint union, we can rewrite it as $A \cup B = A \cup (B-A)$. If $A \cap B = \emptyset$, we see that $B - A = B$, so $A \cup B$ remains the same. Generally, we see that $A \cap (B-A) = \emptyset$, so these are indeed disjoint sets. As such, we now get that we can calculate $|A \cup B| = |A| + |B-A|$. To verify this, taking our prior example, we have $|X| = 2$, $Y-X = \{3\}$, and so $|Y-X| = 1$. Hence, $|X| + |Y-X| = |Y \cup X|$.

Finally, one last operation we can do to sets is the Cartesian product. If $A$ and $B$ are two sets, we define the Cartesian product to be the set of all ordered pairs $(a,b)$ so that $a \in A$, $b \in B$. That is,

$$ A \times B = \{(a,b) \ :  \ a \in A, b \in B \}.$$

For finite sets, one may ask again what the size of this set is. Here, we see that size acts multiplicatively; $|A \times B| = |A| \cdot |B|$. To see this in a small setting, take $X$ and $Y$ from prior. Then

$$X \times Y = \{(1,2),(1,3),(2,2),(2,3)\}.$$

So we see that $|X \times Y| = 4 = |X| \cdot |Y|$.

To finish, let’s examine the powerset of a set. The powerset of a set, let’s say $X$, denoted by $\mathcal{P}(X)$, is the collection of all subsets of $X$. For example, if $X = \{1,2\}$, then

$$\mathcal{P}(X) = \{\emptyset, \{1\}, \{2\}, \{1,2\}\}.$$

If we again think about size, we can note that there is a nice combinatoric way of figuring out the size of the powerset of a finite set. Say we have $n$ elements in our set; then each subset of $n$ either contains that element or it doesn’t. So we have two options for each element, and as a result we see that $|\mathcal{P}(X)| = 2^{n}$.

[textileebook]

Discrete Mathematics with Applications, Metric Version, 5th Edition PDF by Susanna S Epp

Discrete Mathematics with Applications, Metric Version, Fifth Edition  By Susanna S. Epp Contents: Chapter-1 speaking mathematically 1 Variables 1 Using Variables in Mathematical Discourse; Introduction to Universal, Existential, and Conditional Statements The Language of Sets 6 The Set-Roster and Set-Builder Notations; Subsets; Cartesian Products; Strings The Language of Relations and Functions…