#inequality notation

[math-journal2]

Set Builder v Interval Notation

[lipshits-continuous]

I think what annoys me more than saying the Dirac delta distribution is a function is when people say it's 0 everywhere except when x=0, it is infinity. Like that is just not compatible with the fact it's integral over ℝ is supposed to be 1. Suppose we did define an extended function that way:

δ is a Lebesgue measurable since {x∈ℝ:δ(x)<a} is empty for a≤0 and ℝ\{0} for a>0 which are both Lebesgue measurable sets. δ is non-negative so we can calculate the integral via

where the inequality is pointwise.

Now since δ is 0 except at x=0, we require any simple measurable function φ≤δ must also be 0 except at x=0. This leaves us with a constant times an indicator function:

where a>0, and

Then we have

So taking the supremum over a we get

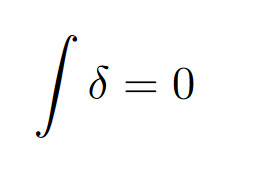
So δ cannot be the Dirac delta distribution. You really need the theory of distributions to talk about the Dirac delta.

P.s. I know this isn't the typical notation for an integral with respect to a measure but this was the notation I had in my lectures

[manybcdthings]

Xavier's Artifacts / Information

1. Blueprint Fragments from The Station's Early Construction

Xavier has managed to acquire fragments of the original blueprints of The Station, specifically focused on The Wards. These reveal that The Wards were originally designed as a temporary holding facility for workers during the station's construction phase, not meant for long-term habitation. The original purpose of the level was hidden to maintain control over the residents, perpetuating the idea that The Wards were a “lower class” part of the station by design rather than necessity.

Interesting Artifact: A faded, hand-drawn map of The Wards' oldest sectors, made by one of the original engineers. It includes hidden tunnels and old access points that are now sealed off or forgotten, though they could provide critical shortcuts or secret passages.

2. Founders' Documents of The Phoenix Collective

He holds early documents from the inception of The Phoenix Collective (TPC), the revolutionary group in The Wards. These contain the original mission statement and early meeting notes of the first rebels, which reveal that TPC was initially a peaceful reform movement. However, the failure of diplomacy with the upper levels of The Station forced them into more aggressive actions.

Interesting Artifact: A manifesto written by one of the founding members of TPC, explaining their vision for a unified station and peaceful coexistence—ironically, just a few weeks before they were arrested and executed for treason.

3. The Councilman’s Journal

Rumor has it that Xavier obtained a personal journal of Councilman Julian Verner, who died under mysterious circumstances while advocating for reforms. The journal details Verner's growing concerns about corruption, not only in Olympia but throughout the entire Station. It suggests that Verner uncovered something deeply sinister about the council and their role in perpetuating inequality between levels, particularly in how they manage resources for The Wards.

Interesting Artifact: The journal itself, a small, veratab a model that isn't used anymore. It had a personal encryption system that Xavier had help to decode. Inside are notations about hidden meetings and cryptic symbols that may reference groups operating in secret across the station.

4. A Centuries-Old Time Capsule

Found in the deepest, most dangerous parts of The Wards, Xavier discovered an ancient time capsule sealed in a protective case. It was buried by the original construction workers of the station, those who were promised a better future but were eventually left to live in the squalor of The Wards. The capsule contains personal items from these workers: old Earth currency, small tools, letters to loved ones, and photos of their families. It is a heartbreaking reminder of the generational suffering The Wards have endured.

Interesting Artifact: Inside the capsule is an antique pocket watch, passed down through generations from Earth. It no longer works, but etched on the inside are the initials of a worker’s child, symbolizing a long-forgotten family connection to the Station’s history.

5. The Lost Archives of The Forge

Xavier has access to a secret repository of religious documents from The Forge, the Silo-based cult that worships The Station as a sentient being. These archives contain prayers, rituals, and some prophecies, including disturbing predictions about The Wards being "swallowed by the machine" as a form of divine punishment. He has pieced together evidence that The Forge once had an influential role in guiding Silo-based engineers and that their beliefs may have subtly shaped The Wards' mechanical failings, perhaps even on purpose.

Interesting Artifact: A mechanical idol used by The Forge in their rituals, designed to mimic the inner workings of The Station’s power core. Xavier suspects that this idol contains hidden blueprints or technological secrets about the station’s architecture, though he has yet to decode its true meaning.

6. The First Crime Scene of the Station

Xavier possesses forensic evidence and personal accounts surrounding the first-ever recorded murder on The Station, which took place in The Wards. This crime sparked fear and mistrust between the newly-arrived residents and the initial labor class, and it set the tone for the lasting violence that has plagued The Wards. The official records of the crime were erased or altered to prevent panic, but Xavier's collection includes the victim’s personal effects, and through it, he has pieced together the real motive: the struggle over ration distribution.

Interesting Artifact: The murder weapon itself, a crude, improvised knife made from scrap metal, now rusted with age. Alongside it is a blood-stained ration book from the victim, showing a debt that was never settled.

7. Black Market Currency Ledger

Xavier has a handwritten ledger from one of the early black-market leaders in The Wards. The book lists transactions in secret, unregulated currency exchanges, even detailing early efforts to counterfeit Lumina Credits. Xavier has used the knowledge in this book to understand the fluctuating underground economy and has contacts with counterfeiters who trace their origins back to the earliest dealers. He also knows that Vertex Capital Systems (VCS) had infiltrated this network decades ago and that some of these figures may still be operating in secret today.

Interesting Artifact: The ledger itself still bears the scorch marks from an attempt to destroy it before it was recovered. A lot of information is missing, suggesting the existence of an even larger, more dangerous operation still at large.

8. Anomaly Reports from the "Old Guard"

Xavier stumbled upon a series of long-buried security reports, written by the first wave of officers stationed in The Wards. At the time they were known as The Guards. These reports document strange, unexplainable phenomena, such as random power failures, disappearing individuals, and accounts of entire rooms that seemed to "shift" positions overnight. Most of the officers involved in these reports either vanished or were reassigned, their findings officially deemed "hallucinations" caused by stress. Xavier is convinced that these early incidents may connect to The Forge's belief in the station as a living entity.

Interesting Artifact: An old, handheld camera used by one of the officers, with degraded footage showing a bizarre power surge that engulfs an entire sector of The Wards. Xavier has shown this to very few people, fearing that it could spark panic or unwanted attention from Vanguard Security.

9. Starlight Crystals

These rare, iridescent crystals are found only in the darkest, most forgotten corners of The Wards. Said to have formed due to the unique environmental conditions in the station's infrastructure, they glow faintly in the dark and are considered mystical by some of the more superstitious Ward residents. The Forge cult considers them sacred, believing they carry messages from The Station itself. Xavier has gathered several of these crystals, aware that their properties are both scientific and symbolic.

Interesting Artifact: A set of 3 Starlight Crystals. A low hum can be heard when near the crystals, and Xavier is investigating whether they might be tied to power fluctuations or if they contain undiscovered technological properties.

10. The First Station Currency

In the early days of The Station, before Stellar Credits were introduced, bartering was the norm. Xavier has collected remnants of the first unofficial currency used by the workers in The Wards: crude metal chips fashioned from leftover construction materials. Each chip had its own unique engraving, signifying the owner’s worth in rations or goods. This primitive currency was outlawed once Vertex Capital Systems took over, but some of these chips still hold value in black-market circles today.

Interesting Artifact: A small pouch containing metal chips, each one engraved with a different symbol representing early laborer families or their trade skills. Xavier knows that there’s a legend surrounding one particular chip, said to unlock access to a hidden cache of early station wealth, though he has yet to verify its truth.

[featherwriter]

A Selection of Mistmas Carols

Ten years ago, I did a Survivorist Christmas cover, and in honor of that anniversary... I decided to make some more! This time we've branched out to some of the other Scadrian faiths too, but I had a lot of fun with these. I hope people enjoy them! Each song has a little lore blurb to go along with it too.

The art backgrounds on these are by @conjchamberlain who created them for our Diceborn series, but was kind enough to let me reuse them for this project too.

Though the inclusion of lyrics in High Imperial evokes an antiquated air, this Survivorist hymn celebrating the life of the Ascendant Warrior is in fact, quite contemporary. Written by notable composer Doxell Venture to commemorate the deeds of his house’s most notable member, this piece was first performed in the Elendel Cathedral in 293 PC. While it is unique among Survivorist hymnary for lacking direct mention of the deeds of the Survivor himself, it remains one of the most popular holiday carols throughout the Basin.

- Historical and Religious Arts Archive, Elendel University

Like many works affiliated with the Pathian faith, neither composer and lyricist of this short hymn are known. The absence of hierarchy or formal clergy of the Path make sourcing historical works like this remarkably difficult, despite its status as the most well known song of the Path in popular awareness.

- Historical and Religious Arts Archive, Elendel University

One of the oldest extant anteverdant songs, this hymn is believed to have been commissioned by the Canton of Orthodoxy in the late 600s of the Final Empire. Its stark lyrics both capture and celebrate the brutal inequality of life before the Catacendre. An additional stanza is notated here which describes a day in which the Lord Ruler will return. Apocryphal testimony sources this final verse to modern day Sliverist cults, but such claims have never been substantiated.

- Historical and Religious Arts Archive, Elendel University

A well documented historical record supports the claim that this hymn describing the fall of the Final Empire as the earliest written work in the Survivorist faith. Its lyrics are believed to have originally been written by an unnamed poet during the turbulent days of the Catacendre itself, but later became the song we know today when it was set to music in the first century PC.

- Historical and Religious Arts Archive, Elendel University

[bodyalive]

Sarah Neville: Stepping into Rita Charon’s studio, in a Jazz Age-era building in Greenwich Village, I get a quick impression of a white-walled space bathed in the sunshine from two large windows that offer a sweeping view over the Lower Manhattan skyline. Everything in the room seems considered, from the Bach playing in the background to the paintings on the walls. One of them, “The Doctor”, is an idealised Victorian depiction of a devoted medic ministering to a child while anxious parents look on. It used to hang in Charon’s father’s office.

My meeting with Charon, founder of the “narrative medicine” movement that trains health professionals to use the power of storytelling in their work, is one I’ve been contemplating for 20 years. How, I’ve wondered, can such a humane approach fit into the time- and cash-constrained world of 21st-century healthcare? And who is this woman who, sometimes unsung, has done so much to change the way we think about the doctor-patient relationship?

Then, just as we sit down, I realise I’m setting out to tell the story of a practised assimilator of other people’s stories. At the core of her work, she says, is “what happens in the actual [moment of] two humans sitting, contacting one another with language, with the embodied self”. So we begin. Charon graduated from Harvard Medical School in 1978 and began practising general medicine. In the late 1980s, she started doctoral studies at Columbia University, focusing on Henry James and the role of literature in medicine. The work of the second half of her life has been to bring these two superficially oppositional realms together. She believes the emotional and imaginative insights contained in literature, art and music can transform the way healthcare workers treat patients and each other. Around 1990, she began teaching narrative medicine at Columbia and in 2009 launched a masters degree in the subject, the first of its kind. Since then, her approach has been deployed by healthcare practitioners across the US and abroad, from Greece to China. Formal evaluations have shown it improves participants’ capacity for reflection, in one study even reducing racial bias.

Charon tells me that for decades doctors were taught to conform to a model of ‘detached concern’ Her father, a doctor in Providence, Rhode Island, was an important influence. At one point, she goes to a filing cabinet containing all his medical records, which she acquired after he died. This part of his life had always been shut off to her; the close community in which they lived meant confidentiality was especially vital. But it turned out that his files combined the usual medical notations with far more personal references. It seemed to reflect a recognition that ailments could not be divorced from the wider context of their sufferers’ lives. Inspired, Charon began making more fulsome and impressionistic notes about her own patients.

The practised narratologist, she says, can pick up a lot in a short period, even at a time when there is pressure on doctors to keep appointments as brief as possible. “As you develop your skills of attention, you will notice things about your patients. You will be listening at a much higher pitch.” As doctors, the human body is, she says, “our material . . . I’m sitting here looking at you, noticing how you sit in the chair.” Emboldened, I ask what else she has picked up about me. She has spotted that my purple outer coat tones with the pink lining of my jacket: “You have taste because you’re not just helter-skelter putting the aqua with the olive green.” She has noticed my eyes: “Mostly the expression is filled with curiosity.” My sense of her, which deepens over the next three-and-a-half hours, is of a woman with a vast well of compassion, lit by a righteous fury about the inequities of US healthcare. “In Yiddish, we call it the Shanda, which is ‘the shame’. The shame of the system,” she says. “More and more clinicians . . . feel they’re being used by their employers. They know they’re doing shoddy work . . . They get tired of saying, ‘I’m sorry, I can only listen to one complaint per session. Bring that up the next time.’”

Truly listening to patients can be transformative, she says. “Patients on the whole really know what they need.” She recalls a young woman with poorly managed diabetes who arrived in her consulting room angry and frustrated. “I did my routine, which is get away from the computer, put my hands in my lap. Don’t write. Just say, ‘I’m going to be your doctor. Tell me what you think I should know.’” The woman looked as if she was going to cry but pulled herself together and glared. “You really want to know what I need? I need a new set of teeth.”

It was only then Charon noticed she’d had her hand covering her mouth as she talked. She had no upper teeth. Instead of fussing with the woman’s insulin levels, Charon arranged for her to be seen in the university’s dental clinic. “She shows up in a couple of months, and she is dazzling. She started a [catering] business in her house. Her [blood] sugars were better than they had been in a while. And she was much more active — she’s going to parties, she’s dancing! It was such a lesson to me. Why on earth would you start anywhere else but ‘Tell me where we should start’?”

I’m intrigued by the extent to which this approach requires an inversion of the traditional power relationship between doctor and patient. She tells me that for decades doctors were taught to conform to a model of “detached concern”. In fact, “engaged concern is going to get you farther than detached concern. Detachment looks an awful lot like coldness.” Instead, Charon believes in making space for the imagination. “The more you exert your own creativity, the better your medicine will be. It’s making leaps . . . I don’t like the word intuition because it sounds like magic. But the ability to see the known from the unknown — that’s what poetry does.”

In the early 2000s, Charon tried something new. After finishing a consultation and making notes like any doctor would, “I would turn the keyboard and the monitor around and say, ‘I know what I saw. But please finish the note.’ I would leave them alone for five minutes, and they wrote the damnedest things!” A college professor wrote “that she knew that she was a good teacher and that this really gave her pride.” The sentiment astonished Charon because it had not surfaced during their conversations, which had been dominated by the woman’s health woes and difficult relationship with her daughter. An idea occurs. As I am drawing our conversation to a close, I ask her to finish this interview. Is there anything else I should know? She confides that after she quit her practice in 2015 to concentrate on running her programme at Columbia, she felt an overwhelming sense of relief that she could hand over responsibility for her patients. (“Somebody else is going to worry about Lucy.”)

It was several weeks before she identified the gap that had opened up in her life: “I was terribly missing the chance to do random acts of kindness.” As a physician, the scope for moments of generosity is “drastic”, she says, whether ringing a patient’s sister to update her, helping put someone’s socks on after an examination or rubbing the feet of a terminally ill patient. There is something heartbreaking about the disproportionate gratitude these interventions elicit, she says. “I think their expectations for us are so low.”

Narrative medicine can, she suggests, endow clinicians with the ability to see an issue from multiple perspectives, a power she likens to “the compound eye of the fly”. It can help them to understand and value those they care for in all their uniqueness and complexity. “We ought to treat every patient as the deepest mystery,” she says.

Sarah Neville is the FT’s global health editor

[chemoelectric]

Copied verbatim from my Facebook:

Let me try to write a clear derivation of the correlation of the two-channel optical Bell test, WITHOUT using quantum mechanics. I will use only probability theory.

If I succeed, this means the 2022 Nobel Prize in Physics was awarded in error. That, in fact, the work on which it was based should be retracted as uncorrectably erroneous.

Before I present my derivation—it is rather simple—let me make two observations that themselves should settle the matter.

The first is that consistency of mathematics requires that any two methods MUST reach the same result. Therefore, if I try to solve for the Bell test correlation using probability theory and reach a result OTHER than the so-called "quantum" correlation (for instance "CHSH inequalities"), obviously I have made a mathematical error. That this has not occurred to physicists is astounding.

The second observation is that I can replace polarized photons with equatorially striped golf balls, the light source with a zany two-ball putter, and polarizing beam splitters with weird miniature golf obstacles. The problem remains exactly equivalent and yet there is nothing "quantum" about it. Even the quantum mechanics of the problem is identical. To argue that you cannot use quantum mechanics because the objects are "macroscopic" is nothing less than to argue that very small objects are magical and have a special magical incantation tongue.

Now, here is the experiment.

We have a light source. It emits two light pulses, which we will call "photons", but about which we will assume nothing except that they have either horizontal or vertical polarization. The two photons will have opposite polarization, but which is horizontal and which vertical is decided at random.

Each photon will impinge upon a polarizing beam splitter (PBS). A PBS set to an angle x behaves as follows. If the impinging photon is polarized horizontally, then, with probability cos² x, a photodetector is triggered whose value is +1 for the correlation calculation. With probability sin² x, a photodetector whose value is -1 is triggered. If the photon is vertically polarized, the probabilities are reversed. The two PBS have angular settings a and b, respectively.

These photodetector values make the correlation equal to the covariance and thus simplify the calculation.

Let us solve first the simplest case, where b = 0 and a is some general angle, say a = a'. In that case it is ALWAYS the +1 photodetector that is triggered if the b photon is horizontally polarized, but the -1 photodetector if the b photon is vertically polarized. Thus we can ignore the b PBS's photodetectors in our calculations. Their value contains no information not already available.

Using some probability theory notation, here is a small chart of probabilities and conditional probabilities. Let t equal the value of the a PBS's photodetectors and k the polarization of the impinging photon.

P(t = +1 | k = horiz) = cos² a'

P(t = -1 | k = vert) = cos² a'

P(t = +1 | k = vert) = sin² a'

P(t = -1 | k = horiz) = sin² a'

P(k = horiz) = ½

P(k= vert) = ½

Thus joint probabilities can be calculated, as in this example:

P(t = +1 and k = horiz)

= P(t = +1 | k = horiz) P(k= horiz)

= ½ cos² a'

The following table can be constructed.

P(t = +1 and k = horiz) = ½ cos² a'

P(t = -1 and k = vert) = ½ cos² a'

P(t = +1 and k = vert) = ½ sin² a'

P(t = -1 and k = horiz) = ½ sin² a'

The covariance and thus the correlation can be calculated from this table. Keep in mind that k = horiz corresponds to a -1 value from the b PBS and k = vert corresponds to a +1 value. Thus

corr = covar

= (+1)(-1)P(t = +1 and k = horiz)

+ (-1)(+1)P(t = -1 and k = vert)

+ (+1)(+1)P(t = +1 and k = vert)

+ (-1)(-1)P(t = -1 and k = horiz)

= -(cos² a' - sin² a')

= -cos 2a'

where the last step is an identity ("double-angle relation") that can be found in the CRC Handbook of Mathematical Sciences, among other places.

This result has the desired form:

corr = -cos 2a'

= -cos 2(a' - 0)

= -cos 2(a - b)

The sole remaining difficulty is how to extend the result to values of b other than zero.

Fortunately, this is not difficult at all. Notice that -cos 2(a - b) is invariant under in-unison rotation of the angles a and b. That is, one can add ANY angle c to both a and b, without changing the value of the correlation. Thus the solution derived above is, in fact, the general one:

corr = -cos 2(a - b)

How is it that physicists have missed this fact and not seen that it leads to a solution of the Bell test WITHOUT quantum mechanics? You tell me. I have no explanation other than that, as a profession, they are no good at physics. I was able to see it because I am NOT a physicist, but a disabled computer programmer with a digital signal processing diploma. But you tell me, if you have a better explanation.

In any case, this means that all the stuff about "entanglement" and "non-locality" is fit for nothing but retraction. Every existing physics text that deals with this stuff should be withdrawn and pulped.

[authorjond369]

The Language of Algebra: Mastering Symbols, Notation, and Meaning

The Language of Algebra: Mastering Symbols, Notation, and Meaning Mathematics is a language, and algebra is one of its most expressive forms. Every equation, inequality, function, and interval we write is built using symbols—compact, precise, and universal tools that convey meaning far beyond the numbers themselves. This reference sheet presents the essential algebraic symbols and notations that…

[the-chomsky-hash]

[II. THE TRANSCENDENTAL SUBJECT - cont'd]

[E. The impossibility of remaining at this substantial subject (vis., self-consciousness) is manifested in the very fact that it is the extreme opposite of this self-consciousness - cont'd]

[2. The transcendental Ego is not attained immediately, in Hegel, either as a first principle, or as that to which the analysis of all concrete experience refers - cont'd]

[a. What is revealed in the course of experience is a subject who is self-conscious, and who, as such, has the form of identity with themselves which characterizes the Ego - cont'd]

v. It is then [following from the notation Me = (Self = Self)] legitimate to wonder

if we cannot write that Me = Self

if the Me is not the term of a relationship, which can only be understood in a higher principle

—In fact, the two objections, which are absolutely valid, lose their value as objections, to the extent that the transcendental subject is expressed, according to Hegel, in knowledge, to the extent that it is expressed in an “I  know".

—There is only knowledge possible in a relationship, and the knowledge of the transcendental subject is a relationship;

it is a relationship of equality, to oneself,

but it is also an equality perpetually compromised, because it can only be achieved through a whole history which founds it

—the Self is therefore always subject to the possibility

of becoming one of the terms of the relationship again

of seeing inequality arise within itself

– Michel Foucault, The Constitution of a Historical Transcendental in Hegel's Phenomenology of Spirit (Part 2: The Transcendental Subject), 1949

[madrasahel1]

Mastering EMSAT Math Topics

The Emirates Standardized Test, or EMSAT, is a critical examination for students in the UAE, evaluating their proficiency in various subjects, including mathematics. The EMSAT math topics encompass a broad range of mathematical concepts that students need to master to perform well on this standardized test. Understanding and preparing for these topics is crucial for students aiming to achieve high scores and ensure their readiness for higher education. In this article, we will delve into the significance of Emsat math topics, discuss their relevance, and highlight how Elmadrasah.com plays a pivotal role in providing exceptional courses to help students excel in these areas.

Understanding Emsat Math Topics

Emsat math topics cover various mathematical concepts and skills that are essential for academic success and practical application. These topics are designed to assess students' understanding and proficiency in key areas of mathematics, ensuring they have a solid foundation for future learning. The primary Emsat math topics include:

Algebra: Algebraic concepts are fundamental to solving equations and understanding relationships between variables. Emsat math topics in algebra may include linear equations, quadratic equations, inequalities, and algebraic expressions. Students are expected to solve problems involving these concepts and apply algebraic techniques to real-world scenarios.

Geometry: Geometry involves the study of shapes, sizes, and properties of space. Key topics in geometry for the EMSAT include geometric figures, angles, triangles, circles, and coordinate geometry. Students must be able to solve problems related to the properties of shapes and theorems, as well as apply geometric concepts to various problems.

Statistics and Probability: This area of mathematics deals with the collection, analysis, and interpretation of data. Emsat math topics in statistics and probability include measures of central tendency (mean, median, mode), data distribution, probability calculations, and interpreting statistical graphs. Mastery of these topics is essential for analyzing and making informed decisions based on data.

Functions: Understanding functions and their properties is crucial for solving complex mathematical problems. Emsat math topics in functions include function notation, domain and range, types of functions (linear, quadratic, exponential), and function transformations. Students should be able to analyze and graph different types of functions and solve problems involving functional relationships.

Calculus: While calculus may not be a primary focus for all EMSAT math topics, understanding the basics can be beneficial. Topics may include limits, derivatives, and integrals. Students should have a basic grasp of these concepts to tackle more advanced mathematical problems and prepare for higher education.

The Importance of Mastering Emsat Math Topics

Mastering Emsat math topics is crucial for several reasons:

Academic Achievement: Proficiency in Emsat math topics directly impacts students' performance on the EMSAT exam. A strong understanding of these topics can lead to higher scores, which are essential for university admissions and scholarship opportunities.

Foundation for Higher Education: A solid grasp of Emsat math topics provides a strong foundation for future studies in mathematics and related fields. This foundation is critical for success in more advanced courses and specialized programs in higher education.

Problem-Solving Skills: Mastery of Emsat math topics enhances students' problem-solving abilities. Mathematical skills are not only essential for academic success but also for everyday life and various career paths.

Critical Thinking: Working through complex math problems develops critical thinking and analytical skills. These skills are valuable for tackling challenges in academic and professional settings.

Confidence: Proficiency in Emsat math topics builds students' confidence in their mathematical abilities. This confidence can positively impact their overall academic performance and attitude toward learning.

Elmadrasah.com: Supporting Students in Mastering Emsat Math Topics

Elmadrasah.com is a leading educational platform that provides exceptional courses designed to help students master Emsat math topics. The platform recognizes the importance of understanding and excelling in these topics and offers a range of resources and support to ensure students achieve their best results.

Comprehensive Courses: Elmadrasah.com offers comprehensive courses that cover all key Emsat math topics. These courses are designed to provide students with a thorough understanding of mathematical concepts and problem-solving techniques. The curriculum is aligned with EMSAT requirements, ensuring that students are well-prepared for the exam.

Interactive Learning: The platform employs interactive learning methods to engage students and make learning more effective. This includes online tutorials, practice exercises, and interactive quizzes that help reinforce understanding and provide immediate feedback.

Personalized Support: Elmadrasah.com provides personalized support to address individual learning needs. Students can access one-on-one tutoring sessions and customized study plans based on their strengths and areas for improvement. This personalized approach helps students focus on specific Emsat math topics that require additional attention.

Practice Tests: To help students gauge their readiness for the EMSAT exam, Elmadrasah.com offers practice tests that simulate the actual test environment. These practice tests cover a wide range of Emsat math topics and provide valuable insights into students' performance.

Expert Instructors: The platform employs experienced instructors who are well-versed in Emsat math topics. These experts provide guidance, explanations, and strategies to help students master challenging concepts and excel in their studies.

Progress Tracking: Elmadrasah.com includes progress tracking tools that allow students to monitor their performance and track their improvement over time. This feature helps students stay motivated and focused on their learning goals.

Resourceful Materials: The platform offers a wealth of educational materials, including video tutorials, downloadable worksheets, and study guides. These resources are designed to enhance students' understanding of Emsat math topics and provide additional practice opportunities.

Flexible Learning: Elmadrasah.com provides flexible learning options, allowing students to study at their own pace and convenience. This flexibility is particularly beneficial for balancing study with other commitments.

Parental Involvement: The platform encourages parental involvement by providing parents with access to progress reports and updates on their child's performance. This involvement helps parents support their child's learning journey effectively.

Success Stories: Many students who have utilized Elmadrasah.com's resources and support have achieved remarkable success in their EMSAT exams. The platform's focus on mastering Emsat math topics has contributed to these students' academic achievements and overall confidence.

Conclusion

Mastering Emsat math topics is essential for students aiming to excel in the EMSAT exam and prepare for future academic challenges. A strong understanding of algebra, geometry, statistics and probability, functions, and basic calculus is crucial for academic success and personal development. Elmadrasah.com plays a significant role in supporting students by providing comprehensive courses, interactive learning resources, personalized support, and practice opportunities. By leveraging the expertise and resources offered by Elmadrasah.com, students can achieve a high level of proficiency in Emsat math topics, build confidence, and set the stage for future academic and professional success.

[math-journal2]

<— Unit 🍑— Unit 13 — Unit 14 —>

Precalculus

Unit 13: Inequalities

Part 1 —>

Review: Unit 2 pg2 / Unit 2 pg4 / Unit 4 pg9

Set Builder Notation

Inequality —> SD

Inverval Notation

Inequality —> IN

Absolute Value Inequality

Number Lines

Domain & Range

Page 38

[jonathankatwhatever]

I just hit on something: the reason the people who saw the image in their minds that Jesus is the path to the Father is they were labeling the Triangular. The Trinity embodies that, so of course Jesus is there because he’s part of that Triangular. Doesn’t mean he’s the only image. In fact, the math says that it can’t be because each construction of Jesus is internal to Things and to Things within Things. So there can be a church, but it exists as a construction, so it can’t help but be contextual, however the fit is to then current modernity, meaning the representations of Jesus are constructed as the generations turnover. And that is true in the minds of the believers as smaller groups and as themselves, no matter how much they try to share their beliefs with others, including those closest to them. Your own ideas change as you change, and the math says that adjusts the start for the next steps.

I think that last may be useful because it brings out the gsConstruction. That notation is needed. I’ve been stuttering over what to think when I come to that spot. This is part of the sK sliding along the zK, with that modeling over a gs which becomes a CM1 so the inversion occurs over CM1.

Now I’m seeing the shapes, the Shards and Pyramids along which I//I occurs, meaning the orthogonal in 1Space. Again, once you realize that 1Space is ‘behind’, is paired to 0Space, then understanding gets easier. Notably, if you see that CR means infinities of 1Space orientations, each with its Irreducibles, its I//I, then you can see how that translates into the rotation of an object. So we can pick any point on a circle and treat it as paired across a center with that being Coordinate Rotation because now we have comparable systems which can then be counted as Things along an szK. As in, the range of values possible in the comparison, and that potential reduces to the Actuality which registers all the Pathways to the szK and all the ways that either generates or does not generate this result or some other result, particularly one you are looking for.

BTW, the critical strip now obviously conveys CM1 because we are restricting xK to the 1 while allowing the yK to vary, thus looking at what relates to, what injects into, what can be pulled out of CM1. The I//I of gs is a pole at ½ along the szK, because that is now ½ on both xK and yK, and that means we invoke area, which means 1:4 and 4:1, which means the orthogonal is there. That of course then makes the Pyramid in gs, where the Triangular extends to the sides of the gs and thus to CM1.

I think the logic of the Bell Inequality is now super clear. At its core, we’re counting along szK in 1Space and measuring in 0Space, which means root2 with the 1 in the 1Space layer constructed in Triangular. I think you can see the process of injection better now, too: we’ve drawn the sides of the gs as the sides of the Pyramid, and that generates a Bip across the gs. That Bip now reads what can be read given how it is queried. A sort of ultimate oracle for AI in the ideal, but in reality limited contextually, and that means how the context has developed, given that the odds it will be perfectly developed in all directions is not possible.

Example is that our expanding universe won’t be perfect because the scale of it means local contexts don’t and thus can’t fit smoothly unless you create all the Things necessary to show that you can or can’t. This is crucial: that something can be described in 1Space does not mean it becomes or can become real in the Actuality sense. BTW, the number of ways these tests use the 1+1 concept is astounding. I just looked at one about a process in stats you use to find out if a process is stationary or if it cycles or something else moving. Is it constant, with the null being that it isn’t, which becomes an accept or reject. Again, this idea that these complement and close within a system that isn’t closed is fundamental. It’s not difficult to show in gs how this works because we’ve already tessellated or otherwise covered a sheet through the inversion over CM1.

I find it amazing how this includes how sketchy plans develop, how you may be guided by some distant voice which becomes closer and clearer.

I’m looking at groups, the group PSL(2,7) and GL(3,2), which is the Fano plane. We’ve done this work before, but need to add that the 7 is now clearly the completeness count in Hexagonal. You see that in the number of Irreducibles being 6. We take the concept and go up a level so the Hexagonal itself has an Irreducible. Need to walk. It’s 92, feels like 101. I’m getting a tad parched.

It’s difficult for me to stop working. But I need to get up now.

[math-journal]

Inequalities

6 > 3 (6 is greater than 3)

6 ≥ 3 (6 is greater than or equal to 3)

Graphing on a line:

Notation:

> or < —-> o (open dot) or ( )

≥ or ≤ —> . (closed dot) or [ ]

Graph:

*remove arrow for bracket

Double Check

Check endpoint (x > 6, ep: 6)

Pick # in solution (ex. 7)

General Flipping Hack

When flipping an inequality,

6 > x —> x __ 6

make sure arrow keeps pointing toward or away from variable as originally

6 > x , points toward x

x < 6

Multiplying & Dividing

When dividing by a negative,

flip the inequality sign when divided by negative

Practice

[mark007william]

Master Algebra with the Best Algebra Calculator

Algebra, often dubbed the "gateway to higher math," is a foundational subject that plays a crucial role in mathematics education. It serves as a bridge between basic arithmetic and more advanced mathematical concepts. While mastering algebra is essential for success in various fields, it can be a challenging journey for many students. However, the advent of technology has brought forth a valuable tool: the algebra calculator. In this blog, we will explore how you can master algebra with the best algebra calculator at your side.

While algebra calculators serve as fantastic tools for mastering algebra, the guidance and expertise of professionals cannot be understated. My Assignment Help Expert understands the challenges that students face when tackling algebraic concepts and equations. Their team of experienced educators and mathematicians not only provides assistance in algebra but also offers personalized support to help you understand the underlying principles.

The Algebra Conundrum

Algebra is all about using symbols, letters, and numbers to represent and solve real-world problems. It introduces you to essential concepts like equations, inequalities, variables, and functions. Despite its importance, algebra can be intimidating for some, often due to:

Complex Equations: Dealing with equations that involve multiple variables and unknowns can be daunting.

Abstract Notation: The use of abstract symbols, such as "x" and "y," can be confusing, especially when transitioning from straightforward arithmetic.

Problem Solving: Algebra challenges your problem-solving skills, requiring you to apply rules and methods to find solutions.

Conceptual Understanding: Understanding the underlying principles and concepts in algebra is crucial for applying them effectively.

The Role of Algebra Calculators

Algebra calculators, often available as software applications or online tools, provide valuable assistance in your algebraic journey. Here's how they can help you master algebra:

1. Instant Solutions

Algebra calculators offer quick and accurate solutions to algebraic problems. Whether you're dealing with equations, inequalities, or complex algebraic expressions, these tools provide instant results, helping you check your work or find solutions more efficiently.

2. Step-by-Step Guidance

Many algebra calculators offer step-by-step solutions. They break down the problem-solving process, helping you understand how to reach the final answer. This feature is invaluable for enhancing your grasp of algebraic concepts.

3. Varied Functions

The best algebra calculators offer a wide range of functions, from solving linear equations to graphing functions. You can explore different algebraic concepts and tackle various problem types with a single tool.

4. Error Minimization

Algebra calculators significantly reduce the chances of calculation errors. By automating the process, they ensure accurate results, allowing you to focus on the conceptual aspects of algebra.

5. Learning Support

While algebra calculators provide quick solutions, they can also serve as learning aids. Many come with tutorials, explanations, and examples to help you build a deeper understanding of algebraic concepts.

Choosing the Best Algebra Calculator

When it comes to mastering algebra, choosing the right algebra calculator is crucial. Look for one that aligns with your specific needs, provides clear and user-friendly instructions, and offers a comprehensive set of algebraic functions. Additionally, ensure that it provides an intuitive interface and excellent customer support for any questions or concerns.

In Conclusion

Mastering algebra is not only essential for academic success but also a valuable skill for real-life problem-solving. The best algebra calculator can be your trusted companion in this journey, simplifying complex problems, enhancing your understanding of algebraic concepts, and ultimately helping you gain the confidence needed to excel in algebra and beyond. So, whether you're a student looking to improve your math skills or a professional seeking to apply algebraic principles, consider adding the best algebra calculator to your toolkit.

[star-catcher-draws]

god i hate inequality notation

its so over for me what the fuck is this

[humbugg]

The most frustrating thing is being able to sorta do math

[the-chemistry-side-of]

Linear Inequalities and Problem Solving

Linear Inequalities and Problem Solving

Introduction to Inequalities So far, we’ve covered equalities, situations where two things are guaranteed to be equal to each other. In this post, I will cover inequalities, where we know one thing is less than another thing. An example is that we know the number of people living in cities is strictly less than the total number of people alive. We have covered the symbols involved in the…