#zero integer
Explore tagged Tumblr posts
Text
Ok so I was thinking, what if the secret way to defeat 2763 is something really stupid and unexpected, like having to embarrass yourself in front of a whole lot of people, Zero could easily achieve this by playing all of those embarrassing tapes in front of everyone to see and hear for example (2763 kidnapped a lot of numbers and would be with them as well) or something else like get rejected by your crush, or even have a very romantic moment with your crush, but live, like if 2763 reads your mind and finds out embarrassing memories and other things about you it doesn't work, only if it happens live, and then 2763 is defeated by dieing of cringe unironically or something. Like their secret weakness is live cringe.
(And it just doesn't work the same, or at all when they read minds/memories, only when the cringe is happening live, like Zero would still be embarrassed live if they showed the tapes to everyone even if the tapes aren't being performed live. And it would also depend if 2763 finds it cringe, like if Zero gets rejected live, or on the opposite end of the spectrum manages to kiss Fifteen live, if 2763 finds those things cringe in any way then that would also work, since being humiliated in public, being rejected, and couples kissing, are all things that could make a bystander of such events feel an incredibley crushing cringe)
This is not very likely since usually in the subscriber specials we learn how the algebraliens work, but it would make for a very good story that would be very dramatic and have a very big emotional impact. Also it would be funny to be able to say that 2763 died of cringe.
#bfdi#xfohv#subscriber specials theory#2763 theory#zero integer#zero algebralien#my theory#my theories#bfdi tpot#2763 bfdi#zero bfdi#bfb#2763 xfohv#2763 spoilers#xfohv theory#bfdi theory#subscriber specials#2763's weakness#the secret way to defeat 2763#the way Zero could defeat 2763
25 notes
·
View notes
Text

#the power of two#tpot#x finds out his value#xfohv#daily one integer#one tpot#one xfohv#zro xfohv#zero xfohv
599 notes
·
View notes
Text
quick doodles



#object shows#Bfdi#battle for dream island#battle for bfdi#battle for bfb#The power of two#tpot#tpot two#two tpot#two integer#two bfb#bfb two#bfdi two#two bfdi#four bfb#bfb four#bfdi four#four bfdi#algebraliens#fifteen x zero#fifteen xfohv#Xfohv fifteen#xfohv#zero xfohv#xfohv zero#x finds out his value#Object show#Object show community
351 notes
·
View notes
Text
me about act 3 jessie: Zero Pussy did that to her
#have any of you seen the twitter post that said incels do have sex but they still consider themselves incels because SOME women deny them#i'm thinking of that#zero pussy except she is getting pussy at a rate of nonzero positive integer
14 notes
·
View notes
Text
Since that post is around again, please repeat after me:
Zero is a number.
Numbers don’t work like colours.
Zero is a number, not a lack of number or a “tint” or a “shade” some other type of bs.
#tumblr math#odd numbers post#the part about zero not being a number haunts me#the rest of the mistakes is challenged in the post#but i dont remember this one being corrected#zero is a number#also its even ig#who cares#mathematicians sure dont#they dont really use odd or even#they just say 2k or 2k+1#where k is an integer#or something
3 notes
·
View notes
Text
bold of you to assume zero is a number
if a number divided by itself is always equal to 1, surely this holds true for 0/0 as well
#zero is like. a Vibe#zero is a concept#an un-number#go define the integer set from scratch out of curly braces and never a zero shall ye find
13K notes
·
View notes
Text
Dump



0 notes
Text
i am suffering
#trying to do to the password assignment problem set that asks for an input and checks if it has:#a lowercase letter‚ an uppercase letter‚ a number and a symbol.#if one is absent it spits an error message‚ and if they are all given it says it is a valid password.#my thought process was to make integers named lower‚ upper‚ number and symbol#then‚ for as long as there is a character in the given string‚#it takes a given character from the string‚ and uses a switch function to add 1 to one of the aforementioned integers depending on what sort#of character it is.#if it's lowercase‚ it adds 1 to the integer lower‚ etc.#and then at the end it checks if all the integers are above zero. if yes‚ it's valid. if no‚ it's invalid.#so i wrote something simple with that logic to emulate that.#except! when i try to compile it‚ my program gives the error message that 'expression is not an integer constant expression' on the line#that checks if given character is lowercase.#i think it's a problem with the ctype library because im not good with it yet.#im looking at the manual pages for ctype.h provided by cs50 but it is giving me net zero information im understanding nothing#what is this! what am i looking at#why won't you understand what i mean when i say 'islower'#i don't want to manually go ''int c > 64 | int c < 90'' it'll take off points for design...#agh! agh. god#🌙rambling#im taking a break this is enough for today.
0 notes
Text
Algebraliens
Algebraliens are funny things but I suppose it's no shock that they exist! If we can have living objects, we can have living math.
They are all eccentric and on some level, quite chaotic. Some algebraliens are a dim sort of chaotic and others thrive off of chaos.
Algebraliens come in many shapes, sizes, and colors. They also have skin. They prooobably have blood and muscle too. I considered bones, but...

These things have no bones.
Gender is NOT a thing to Algebraliens!! They simply don't have it. They vibe with pronouns, though. (Remember: pronouns ≠ gender) You'll find that Algebraliens may have preferred pronouns but they are generally chill-- you may get gently told about the preferences but that's as far as most go.
Some confirmed pronouns--
Zero - He/they (the one with the hat!)
One - She/they
Two - They/them
Four - He/they
Five - He/they
Six - He/she/they
Seven - They/them
Eight - They/he
Nine - Any/all
Ten - They/It
Fourteen - He/him
Fifteen - She/her
Two Thousand, Seven Hundred, Sixty-Three(2763 from here on out) - It/its
X - They/any
-
ADAPTATIONS!
Heat Resistance - An algebralien is able to withstand incredibly high temperatures and lava. Somehow. X can be seen during the challenge to find their emeralds drifting through lava(likely unharmed due to their power) and Two, during the 2763000 subscriber special, merely had their skin burnt by lava.
Durability & Invulnerability - Algebraliens have skin that is difficult to penetrate. They're quite malleable. You are going to need tremendous force and effort to pierce their skin and make them bleed. They're also just... really difficult to kill.
I don't know what this is called - Your biggest concern as an algebralien would be dehydration although you could go an extended period of time without water and even longer without food. An algebralien not eating or drinking enough will eventually start to feel the side effects.
-
If an algebralien does not take care of themself, there are consequences.
The aforementioned side effects include worse physical health but also weakened power.
-
POWERS!
You could say the adaptations mentioned above are powers but! By algebralien standards, they aren't.
It's not known where powers originate from, nor is it known why/how it exists-- but it does. The current power scale between algabraliens looks something like this:
2763 > Two > One > Four and X > Literally everyone else
2763 and Two would be on the same level if it weren't for 2763's natural ability to suppress algebralien power. The further away an algebralien is from 2763, the more their power returns.
One is just below Two. She plans to change that, though.
Four and X are the embodiment of algebralien chaos.
-
EVERY algebralien has their own little pocket dimension.
They can project or transport themselves into their pocket dimension and powerful algebraliens like Four can transport items into their dimension. They also have total control over their domain-- and I mean total. They can shape it to their will, break the laws of physics, and bend its reality. This does mean an algebralien can trap another in their domain if they play their cards right.
The algebraliens who live primarily at the Equation Playground have doorways to their pocket dimensions that connect to the Playground in case of emergency. These doorways can be used, destroyed, materialized and dematerialized, ecetera, all depending on what the user wants.
-
FUSION!!!
By adding or multiplying, integers can fuse together or unfuse. It takes a lot of willpower from one side to keep from unfusing if the other is against it.
By subtracting, you can whittle a number down to smaller numbers. They have to be manually added together again to refuse and act as a hive mind.
You can kill an integer by division if you use a zero. However, trying to divide powerful integers by zero will instead leave their soul/spirit inside of the zero instead.
Any symbol or object can be used for this process as long as at least one integer is involved.
75 notes
·
View notes
Text
Great explainer! Very meta point though - isn't this sort of a cyclical way to define a hole, at least to someone who wants to insist that a straw has two holes?
In essence, we're finding holes by taking non-bounding loops (great), and saying two loops bound the same hole if they bound some other 2-simplex. Which like. is kinda what the debate is about.
Idk, find it slightly easier to see in the manifold. H_1 is generated by embedded S¹s, modulo the relation that the boundary of a pair of pants is zero, and an the boundary of an annulus=straw is zero. So a straw only having one hole is part of the definition of homology.
Why Straws Have One Hole: An Introduction to Homology Part 2
In this post I'll discuss simplicial complexes and how we can use them to make our test for holes simpler and motivate the definitions for simplicial homology! The post is more technical but I have tried to motivate each step.
Simplicial Complexes:
A common theme in topology is to build up our spaces from smaller, simpler spaces. One way of doing this is to use simplices! These are generalisations of triangles to all dimensions:
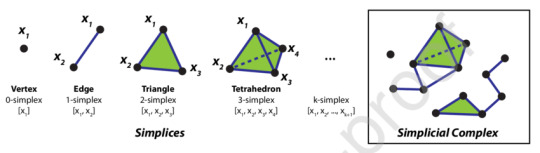
Image is taken from here
An n-simplex has n+1 verticies and is denoted by its vertices in square brackets: <e₀,...,eₙ>. A simplicial complex is made by gluing simplices together such that the intersection of two simplices is also a simplex that is included in the complex. We also require that any n vertices can define at most one n-simplex in the complex. If some vertices e₀,...,eₙ in a simplicial complex, K, define an n-simplex <e₀,...,eₙ> that is in K, we call <e₀,...,eₙ> an n-face of K.
An example of a simplicial complex is a square where each vertex of the square is a 0 simplex and each edge is a 1-simplex. If instead we considered a solid square, we wouldn't automatically get a simplicial complex because the 2 dimensional part isn't made up of 2-simplices. We fix this by adding an addition 1-simplex bewteen one pair of diagonal points which gives us a simplical complex with four vertices, five 1-simplices and two 2-simplices:

We can construct a great number of spaces using simplices! This construction is only up to homeomorphism but that's all we care about! A simplicial complex that is homeomorphic to a space is called a triangulation of that space. Importantly we can triangulate a straw:

This is the simplest triangulation because having fewer simplices would lead to us having different simplices described by the same vertices.
Simplicial Homology
So why do we care about triangulations? The key here is to notice that the boundary of an n-simplex is a simplicial complex made up of (n-1)-simplices. For example, the boundary of a 2-simplex is a simplicial complex made of three 1-simplices. The idea is to modify our test to only involve simplices because then we only have to check finitely many things! This is where things start to get a bit more technical but I will try my best to motivate each step!
Firstly, we need to introduce a convention in the way we describe simplices. We pick an order for the vertices in our complex to be listed, e.g. for the triangulation of the straw we could pick the order a,b,c,d,e,f. Then any time we write a simplex we must list the vertices in that order. For example, with the order above, <a,b,d> is how we describe the left most 2-simplex. The reason we need this is we are about to start thinking about simplices in a more abstract way and we need a systematic way of writing them.
Now for arguably the weirdest (but most powerful) step. We want a way to talk about the boundary of a simlicial complex as one object and we want a way to say when a particular simplicial complex has no boundary. The motivation for this is we want to talk find the analogue of a loop that we can use to test for holes, that is we want a one dimensional object that doesn't have a boundary. Since we eventually want to count things, it might be prudent to somehow assign numbers to things. As mentioned above, the boundary of an n-simplex can be thought of as the union of (n-1)-simplices and unions of sets are kind of similar to a kind of sum. The idea is to talk about "sums" of simplices. It doesn't really make sense to add simplices but we can sort of just fudge it. This fudging is known as "formal sums" and this is when we say "okay, we don't know what a sum of these things actually is but we study it anyway".
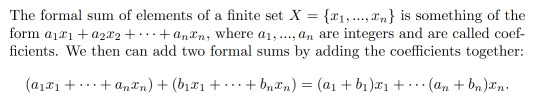
We say the elements of X generate these formal sums.
We then consider the set Cₙ(K) of all the formal sums of n-simplices in a simplicial complex K and we call it the nth simplicial chain group of K and we call elements of Cₙ(K) n-chains. We say that the rank of Cₙ(K) is the number of elements of X. Note that the sum or difference of two chains is again a chain.

The rank of C₂(K) is 1 and the rank of C₁(K) and of C₀(K) is 3.
We can now also give meaning to a simplex that is written in a different order to our chosen order. Given an ordered list of vertices, we can swap two elements around to get a different ordered list. If n is the number of swaps it takes to get an ordered list of vertices into our chosen order, we say that the simplex with vertices written in a different order is equal to the element of Cₙ(K) given by (-1)ⁿ times the simplex with the vertices written in our chosen order.

Now we want to figure out how to represent the boundary as a map from Cₙ(K) to Cₙ₋₁(K) since the boundary of an n-simplex is made up of (n-1)-simplices.
The full representation of this map is a bit detailed so I will stick to the case when n is less than or equal to 2 since that's all we need. The definition of this boundary map only depends on what it does to the simplices because it comes from considering their boundaries. So we will say that the boundary map applied to a formal sum is just the formal sum of the map applied to each simplex, for example

where ∂ is denotes the boundary map. So we just need to define ∂ on simplices.
To motivate the definition, we consider a 2-simplex <x,y,z> with the order x,y,z. Starting at x, we can think of the boundary as a loop that goes from x to y, then from y to z then from z back to x:

So we could represent the boundary as the formal sum <x,y>+<y,z>+<z,x>. Then written in our chosen order, the boundary is <x,y>+<y,z>-<x,z>. That is ∂(<x,y,z>)=<y,z>-<x,z>+<x,y>. In the first term, we remove the first vertex, in the second term we remove the second vertex and multiply by -1, and in the third term we remove the third vertex and multiply by -1 twice. So it would seem sensible to that the pattern here is the nth term in the boundary of a k-simplex is the simplex where the nth vertex is removed and we mutlipy by (-1)ⁿ⁻¹.
So the boundary of a 1-simplex <x,y> is <y>-<x>. But the boundary of a 0-simplex is always 0 since 0-simplices are just points and have no boundary!
We also have that the boundary of the boundary of a 2-simplex is 0. This makes intuitive sense since the boundary itself has no points at the edge of it but we can show this still works in our abstraction to formal sums:
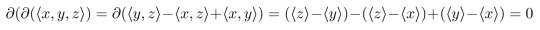
Now we have two special types of formal sums: those that have no boundary and those that are the boundary of something else. We call an n-chain that has no boundary an n-cycle and we call an n-chain that is the boundary of an (n+1)-chain an n-boundary. We can extend the first above argument to show that boundaries are always cycles, i.e. the boundary of a boundary is always 0. 1-cycles are what replace loops in our earlier test, that is we want to find 1-cycles that aren't 1-boundaries! An obvious yet important example of a boundary is 0, 0 is the boundary of 0 (we'll use this fact later). Two other important facts are the sum of n-cycles is also an n-cycle and the sum of n-boundaries is also an n-boundary. If c and c' are both cycles, then ∂(c+c')=∂c+∂c'=0+0=0 and if c=∂b anf c'=∂b', then c+c'=∂b+∂b'=∂(b+b').
Let's take a step back to summarise what we have so far. We have found a test for holes in a space but it didn't really allow for easy calculation of the number of holes in a space. So we restricted our view to simple spaces and have found a way of abstractly representing the building blocks of those spaces. This abstraction has allowed us to reframe our test for holes into a purely algebraic question!
But how can we be sure this test still works? Let's consider a circle. Using our first test, we can just take a loop around the circle. Then this loops isn't the boundary of anything since it bounds a disc of the same radius but this disc isn't part of the circle. So the circle has a hole. Now we triangulate the circle using three vertices and 3 edges, i.e. a triangle. If we label the vertices as <x>, <y> and <z> we already know an example of a cycle: <y,z>-<x,z>+<x,y>. Even though this calculation was done for a 2-simplex, it only involves the 1-simplices so it is valid in this situation too! But in this case, we don't have any 2-simplices in our space so this cycle can't be the boundary of anything! Conversely, suppose we get a positive result using our simplicial hole test, i.e. we've found a cycle that isn't the boundary of anything. Then we can construct a loop in the space using this cycle and this loop wouldn't be the boundary of anything so the first test would also be positive!
The final step that actually lets us count things is to define the homology groups! What we want to do is find cycles that aren't boundaries. Algebraically, we do this by considering cycles to be "the same" if their difference is a boundary. That is, we say two n-cycles c and c' are homologous if there is some (n+1)-chain b such that c-c'=∂b. We have that all n-boundaries are homologous to each other. Say both c and c' are n-boundaries and that b and b' are (n+1)-chains such that c=∂b and c'=∂b', then c-c'=∂b-∂b'=∂(b-b'). The since b and b' are (n+1)-chains, b-b' is an (n+1)-chain so c and c' are indeed homologous. In particular, 0 is a boundary so every boundary is homologous to 0. So now suppose that c is a cycle that is homologous to 0, then there exists an (n+1)-chain b such that c-0=∂b. So c=∂b and hence c is also an n-boundary. This means that a cycle is a boundary if and only if it is homologous to 0. So now if we want to find cycles which aren't boundaries, we look for cycles which aren't homologous to 0.
We define the homology class of a cycle c to be the set of all the cycles which are homologous to c and we denote it [c]. For example, the homology class of 0, [0], is the set of all boundaries! We can also define a notion of addition of homology classes: [c]+[c']=[c+c']. That is, the sum of two homology classes of two cycles is the homology class of their sum. We call the set of all homology classes of a cycles of a simplicial complex K, the (first) homology group of K and write H₁(K). If H₁(K) only has one element, i.e. H₁(K)={[0]} every cycle must be a boundary and K would have no holes. But if K has a hole, H₁(K) would have more than one element.
We are actually now quite close to being able to count the number of holes a space has! Let's come back to the example of a circle. Intuitively, a circle has 1 hole and we've already seen that we have one cycle which isn't a boundary: <y,z>-<x,z>+<x,y>. But by the way we defined the boundary, we also have that
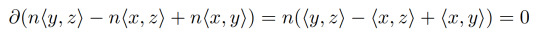
for any integer n. So for any non-zero integer n, we can find a cycle that is not a boundary. In particular, if m doesn't equal n, then n(<y,z>-<x,z>+<x,y>) is not homologous to m(<y,z>-<x,z>+<x,y>) since their difference is (n-m)(<y,z>-<x,z>+<x,y>) which is not a boundary unless n-m=0, which is not the case here since n doesn't equal m. Moreover, I claim that any cycle in a circle must be of this form. Remember, this cycle represents the loop going around the triangulation of the circle once. The only way we can get loops in the circle are obtained by going around the circle a whole number of times (where going in the opposite direction gives us a "negative" loop). Any other path you try to take will end up with not having the same start and end point and so would have a boundary! So there is a homology class of the circle for each integer. Moreover, adding these cycles represents going around a loop n+m times so adding the homology classes together is somehow the same as the regular addition we know for the integers! In formal terms, we say that H₁(circle) is isomorphic to the integers. Like how homeomorphism is the notion of "the same" for topologists, isomorphism is the notion of "the same" for algebrists! The important part of this is that all of the homology classes can be expressed as an integer multiple of [<y,z>-<x,z>+<x,y>] just like how an integer can be thought of as an integer multiple of the number 1. In this sense, we say that [<y,z>-<x,z>+<x,y>] generates H₁(circle), i.e. H₁(circle) has 1 generator. This cycle came about as a loop around the hole in the circle so it is sensible to guess that the number of generators corresponds to the number of holes!* This is how we will go about showing that a straw has 1 hole in the next part! That is, we shall figure out what the first homology group of a straw is and find out how many generators it has!
*technically, we actually count the free generators of H₁ since the torsion elements represent something else but it won't matter for what we're doing. Alternatively, we could have defined homology over a field to get vector spaces which naturally don't have any torsion but this doesn't feel quite as natural as doing homology with integral coefficients.
#also for simplicial homology its not that hard to say what “formal sums” are#its just an assignment of an integer to each n-simplex#possibly modulo the condition that only finitely many are non-zero#maths
26 notes
·
View notes
Text
Kinknuary Day 22: Spanking
Pairing: Kep1er Xiaoting x Male Reader
Word Count: 4,956
[Kinknuary Masterlist]
--------------------------------------

--------------------------------------
“Don’t you want to take me somewhere else more than this?”
“I actually just want to go home now, Xiaoting—I’m pretty tired…”
“Aw, come on—please? Just one more then we’ll go home…”
Of course, Xiaoting won’t end a day without a good note because she detests anything that’ll make her feel bored or even the simplest hint of discontentment and you won’t dare to disappoint her. Sometimes, life doesn’t go the desired path they want them to and that’s being sampled on her right now, and you won’t let her selfish wants be your burden in the long run.
“Aren’t you even feeling tired, Xiaoting?” Your tone laces a hint of discomfort as she seems to be much more invigorated than you even though you’ve mostly spent the whole day shopping and attending such an incredible party you’ve ever gone to.
“Not really, but please—”
“Okay, okay…” You break her constant plea with a single proposition: a classic game of rock, paper and scissors and whoever wins, will mark both of your fates—it’s quite a simple game but unable to be rejected as Xiaoting agrees about that, and you smiled because of her sudden agreement.
“Just once, okay?”
“Alright…” Xiaoting sounds pretty defeated even though it hasn't started yet because the pessimistic side of hers says that she may end up losing and it will deeply make her disappointed and knowing how well she will think, you curl up a smirk as this is the moment of truth.
Counting down up to the lowest possible integer, you could feel the tension on Xiaoting’s eyes, laced with anticipation and the desire to win as she wanted herself to be fully-redeemed on peak-happiness but it’s like, you can clearly read her mind through that serious gaze of hers as you curl up a smirk after utter ‘zero’ and guess what, all became too ambitious for someone who desired something truly at its best.
It wasn’t really the best, for Xiaoting as you landed ‘rock’ front of her which made her gasp in defeat as it’s too late, with even half a second to spare and cheat, she panicked and managed to land a ‘scissor’ and with that little game, you knew who’s victorious and it’s goddamn you.
“I hate this game! It’s unfair!!” Xiaoting whines and as expected, she rants out how rigged that game could be and how you “cheated” to get that desired prize as she frowns in front of you, her pouty yet disappointed expression still exuding such beauty that no one can come close.
“How is it unfair? You even switched it up at the last second and ended up losing? Just accept your defeat—”
“Ughh, fine! Fine, I will…” Xiaoting brushes off your further continuation of fighting how she’s on the wrong side as she doesn’t want to hear anything that would just make things worse—it’s like she’ll lose anything of our decision, probably a good night’s rest at her place, especially with you on her side. Knowing that investing onto another argument or another plea won’t make anything better since a deal is a deal and you’re just going to wait for time to tell the fate you have in store with and knowing how Xiaoting will take your upcoming proposition wholeheartedly, then it’ll be just only a matter of time before it all unveils onto that anticipated abyss of wonders and desires.
---
It never gets old between the both of you and the fact that you’ve been holding this for a while now is surprising, knowing how insatiable Xiaoting can be at an times you lay your eyes on her as her vixen-like aura and her seductive nature is enough to make you lure in to your deepest desires, and it’s being fulfilled with multiple, sloppy kisses on her lips. You chase your delightful moments in every kiss that you make up with her, as much as the lustful need in you every time you tangle your tongue on hers as you went deeper, and Xiaoting, pulling out as she’s running out of breath due to our audacious nature and aggressive actions towards her.
“Why would you pull out, babe? Am I too much for you to handle?”
“Not reall—ahh, ohh… right t-there…” Maybe you’re right or you could lean onto the opposite, knowing that the culprit would be the lack of oxygen would let those speculations set aside onto the correct verdict. You know how your lips are one of her ultimate weaknesses out of the many things you can elaborate as you let her know how your stupendous skills can make a girl like her fall under your spell within just mere seconds. You latch onto her deep, sharp collar bones that you always love worshiping, knowing how perfectly sculpted those are like the rest of her body, deemed to be drooled on a praised by only you—you could be just the luckiest menace of them all, being gifted with such an angel being close to the epitome of perfection, from head to toe. You keep peppering that porcelain skin of hers with multiple kisses, running your lips down to her neck as she moans almost-inaudibly and incredibly sultry, voicing out her deep satisfaction towards your expertise.
“Oh god—you k-kiss me so well—oh, so good!”
Hearing her constant compliments on your actions, you continue to pepper her with intimate kisses until you pull out right after, hearing her soft whimpers needing your lips to be attached onto her skin as soon as possible but you had enough, for now.
“Isn’t my baby needy for me?” Your eyes demanded an answer escaping her lips right away, wanting her to unleash that living submissiveness inside her and you’ll do it slowly, knowing how the beast inside her will be a little challenging to tame.
“Y-Yes…”
She’s succumbing onto that state slowly as her eyes glistening with need and her soft, needy tone is enough of an evidence, luring her into falling under your spell and will not make her escape out of it. With her needy pleas and her body grinding greedily against yours, wanting to feel your touch, you can’t seem to be convinced as there’s few elements that’s lacking from her constant pleas. “Yes what, baby?”
“Yes, please…” With Xiaoting’s constant pleas, you can’t help but just fulfill her needs right at this moment but you need to unlock that beast inside of you with the magical word that will turn her world upside-down.
“You’re getting there, baby~” You tease her porcelain skin with a gentle swipe of your fingers, running it down her neck and then up to her toned midriff, which you always love kissing and worth worshiping until the end of time. Xiaoting knows that she needs to crack the code within you, and with a clever mind and taking a few seconds of the clock for her to think about what could make that happen, she finally thought of that forbidden word and it’s only a matter of time until~
“Yes I am, daddy.”
You never expected her to fail in any kind as she’s cognizant as the way she is and it’s always impressive to see and even hear it all with utmost sincerity and need. With your face still inches away from her, such eye contact would let the other succumb onto the endearing stare of the other yet you’ll change that, more likely, a commanding one as you live up with that, wanting Xiaoting to strip her clothing in front of you with class and skill like nobody can achieve. Maybe, you haven’t seen anyone become on par with her skills, let alone surpassing her and you’ll keep it that way—it’s way phenomenal seeing Xiaoting doing the things she’s great at and you won’t even bother thinking of another woman to do it for you. With her seductive gaze inviting you to strip her clothing with her, you wouldn’t skip that opportunity as you do so, slowly removing the fur-like sleeves on her arms but before you completely strip it off her, you take some time to commend her flawless figure and her outfit perfectly complimenting each impeccable feature she has.
“Thanks, d-daddy—really l-loved this one…”
“You know, as much as I want this on you, this would be better on the floor.”
Xiaoting’s lips curled up a sinister smirk as she invited you to make that “wish” of yours come true, and it wouldn’t take up much of your time until it became accomplished. She would aid herself for you to be comfortable, leaning onto you as she gives you such inviting and sultry moans, making yourself get riled up for her and you love it but you wouldn’t be fazed with that as you continue stripping her. Her hands wouldn’t be idle as she pulled her pants, down to her ankles and then onto the floor with a swift motion and god, those scrumptious, milky thighs on your sight is tempting to be voraciously kissed as hunger took over you yet you continue your work and with her top off, her slender, hourglass figure is now within your eyes to be blessed and you couldn’t ask for more because of it.
Xiaoting is a work of art, sculpted by the gods to perfection as you’re the lucky man to handle and appreciate this masterpiece, maybe even use it until her legs give out—a sullied goddess, in your own books.
“God, you’re fucking hot, Xiaoting—oh gosh…” You can’t believe your eyes as it takes numerous gazes throughout her perfect figure, eyeing every inch and drooling on it like it’s a five-course meal—maybe it may lie down onto the scope of similes but metaphorically, she’s always the main course and you would love to devour her like a predator hungry for its prey. With her last bits of defense still within her body, concealing her true beauty, you asked Xiaoting if you can strip it off her and without any hesitations, she nodded as she’s been longing for this for a while now.
“You really love my body so much, hm, daddy?” Xiaoting doesn’t even need to ask you about that because she already knows what your answer will be and it’s always readable, your eyes glistening with hunger over her is enough evidence.
Still busy admiring her scrumptious body and her drooling all over it, it took you seconds before you could respond as you flash a smile at her, making her feel delighted and truly loved by you. “Of course, baby—I love it all but daddy’s getting impatient…”
Xiaoting runs her finger onto your clothed chest, up towards your shoulders as she rests her arms on it, and then utters such a seductive invitation letting you know how it’s going to start. “Have your way with me, daddy—I’d love what you’ll make me do…”
And as always, Xiaoting never laid a better invitation than that and she never fails to make you amazed and aroused. With all of that foreplay coming into its denouement, you commanded Xiaoting to get onto the bed as her naked body is now on display, ready to get used as she gets on all fours.
“This is going to be fun…”
---
“Count.”
“Y-Yes, daddy…”
It’s maybe a newly profound kink of him, and maybe even you, considering that as you're guilty as he probably likes how your thighs jiggle with his mighty palm striking onto your butt with the force of a truck, and you love it. He knows how you love it so much, your eyes won’t even deny letting him know about that and under his own control, you completely submit yourself and let him have his way with you.
“Don’t hold back, baby—let it all out and count, do you understand?”
You nod frantically, not wanting to disappoint him as you wiggle your ass in front of him, inviting him to do the honors of the actions he’s been longing to do—
*loud smack* “O-One…”
It was just the first one and it’s already rocking your world, sending your arousal up to the sky as his smacks are pleasurable, making your sensitivity peak at its finest. You could feel yourself getting wet with the thought of his hands spanking your butt harshly until it’s red as a tomato while ramming your tight cunt down and you can’t wait for it to happen.
*another loud smack* “Two—oh god…”
Another one emanates around your ear as the crisp of its pristine sound sends your libido skyrocketing, probably filling the urge of him using you but you can sense and know how he won’t just pull the trigger this easily—the both you wanted this on the first place: you wanting this for a long time now and gains gratification from it and lastly, him wanting to tease you and there’s no better way to do that with his palm printed onto your milky buttcheeks, going to be redder than a tomato.
*another loud smack* “T-Three… That feels so g-good…”
It may feel redundant but you love every second of it and will not even feel the hint of being tired of it because of his harsh actions—you wanted the pain anyways, as he knows how you derive pleasure from his spanks and the discordant sounds of it increasing your libido onto the roof, and makes you even wetter by multiple barrages of it.
*another loud smack* “F-Four—f-fuck, daddy…”
This time, it was way harder than the rest as you whimper in pain again because of his harshness, but gaining that genuine gratification as you love the pain and the pleasure mixing all up together—you’re maybe a masochist because of how you derive intense pleasure, and you know he’s here to fulfill that at all costs. Even though you can’t catch a glimpse of the hot sight of him doing such sinful things to you, you can’t still brush the fact that your imagination reaches the furthest of its limits, capable of formulating the filthiest thoughts known to mankind.
*another loud, harsh smack* “Five—o-ohh… too g-good—ahh~”
You keep voicing your own satisfaction alongside your ragged breaths between random intervals that puts him onto authority to further smack you until your butt is scarlet red but you can sense that he has better options in mind, the feral beast inside him wanting to be unshackled from its restraints, and you’d be the guest to let it be a wish come true.
“Such a good girl for me, hm?”
You know he’s growing impatient, and you can sense it igniting in his eyes and you wouldn’t dare to let him wait for another move preceding what he could command you.
“Yes, daddy—” Your sultry voice invites him into falling down to his own, carnal desires and you know he wouldn’t make the both of you wait for nothing as every second should be treasured. “—now will you fuck your good girl?”
It’s up to him to write your fate, and you’ll just relax yourself and find out what it would be…
---
It does tempt you into fulfilling her needs and it’s just a single strand before you break your shackling confines, and it wouldn’t be long until you reach your primal desires. It wasn’t your cup of tea to tease into oblivion but if she wanted that then so be it as foreplay plays an impressive role on someone’s anticipation and her desires running like a roller coaster, all opting for the chase of fun and the freakiest frustrations of not being attended.
“Put it in, daddy—please, ohh!”
Of course, another tease makes her weak, whimpering in need as she tightly grabs the bed sheets for a leverage to fight the profound pleasure that she's not experiencing. You continue swiping your finger onto her heated core as she cries in response, and it further skyrockets once you start stimulating her clit and with her small sounds being the fuel on your unstoppable lust, you won’t let her wait for more as you gave what she truly deserves.
With your hands caressing the soft, silky skin of hers, you grab her hips and position yourself into a state of bliss and within a single second, it all went uphill as you could just hear each other’s groans emanating the wonders of such a great commencement of sex. You deliver shallow and leisure thrusts, aiming to just make her anticipate and savor every second of that blithe that she always loved. You continue peppering her neck with constant pecks as you muster such a sluggish pace, making her feel loved as you worship her and make her know how much you adore her.
“You l-love kissing me, daddy?”
You smile at her question, and you know that she already has the knowledge about that question, but you would love to let her know about everything you love about her, more likely, verbally. “Of course, baby—how could I not adore every inch of your perfect body?”
Well, she’s not egoistic but she knows how perfect she is in your eyes and that’s something that always wanted to hear, as it boosts her confidence in a great percentage and makes her feel the utmost care by you. Maybe the slow and redundant foreplay was getting on your nerves longer than you expected as you wanted to ruin her and Xiaoting herself would love the thought of that.
Maybe it won’t rely onto the cloud of thoughts as it’s now ascending into reality, pacing faster into a moderate speed where she constantly whimpered in need, your constantly ramming cock into her tightness becoming too much for her and of course she would request for an element to be added for the better experience for both parties.
“Spank my ass while you f-fuck me, daddy—oh god!”
Now averting your hands onto different places: your left hand swiftly fondling her perky breasts for better stimulation and your other hand already finding its way onto smacking that soft flesh in front of you, the rippling of it and the sound it reverberates around the room makes such an arousing sight that it further thrust you into her rapidly as she recoils a little from your harshness.
Who would have thought that a modest, sophisticated girl like her is invested in such a sinful, cruel act? Well, it wasn’t emanating from her aura totally but you know how she subconsciously knows how hot and captivating of a woman she is—you’re glad that she’s yours and you’re the only one to have a sight of her alluring masterclass. Maybe it’s a faux conception knowing that Xiaoting doesn’t exude such hotness if she’s always being a little “puffball”, as you call her, but her other side is nothing compared to this and god, the next thing you’ll know is that you’ll be just riled up for her that the both of you will succumb to each other’s needs and be the freakiest creatures known to mankind.
If it wasn’t always the case about the latter, then you don’t know what is because the both of you prove your points about that title.
Harsh spanks add up to the sea of cacophonous sounds that lingers around your ear, further fueling you to bring such hard poundings in aims to totally let her succumb to submission, and you’re nearing that goal with all of the stimulation you’re doing on her. Every whimper she exclaims with the pain you’re bestowing her just makes the sight rapidly hotter but you know it wasn’t enough until her cheeks are scarlet red so you muster a new pattern of thrusting between spanks and using the other hand as a leverage by grabbing her hips harshly. The constant rhythm of your hips gradually increases over time, and so is your harsh treatment towards her but you want to add an incredible twist that will elevate the experience even more.
Xiaoting lets out series of cries as you pound her into the mattress, her arms able to give out with how much you’re treating her and then suddenly, you slow down immediately, catching her off-guard and for her to recovering a little as you’re selfless—you wanted her to savor every moment whenever possible and not want her to reach her high too quickly even though you know how your cock can make her do that in a few minutes. With your sudden impeding, you could take a closer attention to admiring her scrumptious backside and the sexiest curves of her hourglass figure that you can drool on for days and won’t get tired of. This is also an exceptional time to let your hands be berserk and give her harsh barrages of spanks that makes her even wetter and even more whimpers that lets your cock twitch because of how soft and arousing her tone is.
“P-Please fuck me h-harder, daddy–oh gosh, s-so good!!”
Another resonating smack lingering around her ears as you’re a little infuriated with her pleas, making her writhe a little and cry in need of a better pace. “Don’t tell me what to do, baby…”
Her tightness is nearly suffocating but you don't care, not when a hot sight is just right in front of you as you resume on your frantic pace, making her moan uncontrollably to the point that she almost screams and it’s deafening but angelic. With all of the constant stimulation of your hands throughout her body and the pain you’re bringing in with such onslaught of smacks, it wouldn’t be surprisingly to know if Xiaoting is going to reaching her high sooner than you expected as the constant constricting of her pussy and the juices seeping out of it are enough evidences to set herself near to the promised land. Now with her buttcheeks red with your hand printed on it, you gave her a small break and continue to double your efforts on pounding her tight cunt, letting her know how she’s going to be having the paramount orgasm of her whole life and with a shuddering response escaping her lips, you knew it’s deemed to come into an end.
“Shit—daddy, I’m gonna c-cum so soon!!”
She wanted this for so long and you wouldn’t dare to put it in a halt and gave the reward that Xiaoting absolutely deserves. “Then cum, baby—cum all over my cock—”
It all went onto that singular point of bliss, releasing deafening screams of pleasure as she lets everything out around your ravaging length and with Xiaoting aiming to further elevate her orgasmic trance, she requested you still fuck her senseless on her orgasm as you do so, making her a wild, mindless mess just capable of uttering such sinful sounds. With your ruthless pace, Xiaoting kept whimpering on how she wants you to treat her harsher as you fulfill her wants, further hammering her tightness with such thrusts mustered to the highest velocity possible and with spanks with a force of a truck. After such breathtaking thrusts and a breakneck pace, you instantly calmed down the feral beast inside of you and gave her a leverage to recover, thrusting with such a sluggish pace as she catches her breath due to her orgasmic high.
“Daddy, t-that was—”
“Good? Yes, baby, I know—” You lean down to kiss her beautiful neck, and then course your way near her ear and continue her sentence. With your lips still worshiping the porcelain skin of hers, you let her know how great the experience was and showered her with compliments that definitely stroked her ego. “—because honestly, you felt great around my cock, baby…”
Xiaoting lets out needy whimpers—maybe even possibly smiling because of your compliments—as you stroke her hair to make her feel your touch, your hips now ensuing a moderate pace, pumping into her but this time, it’s all full of affection and love and dismissing the harshness and greed like from earlier. Knowing yourself would be near your own high too, you wanted to save the best for the last as you warn Xiaoting that you’re going to pull out and let herself switch into a different position.
“Baby, turn around for me so I can fuck you while seeing your beautiful face.”
It was straightforward and she obliges immediately without any questions and even with the hint of frustration laced on her emotions, it wouldn’t be long until you reward her with something exceptional as now is the time for another side of bliss. As she spun her figure around gracefully, her hands grabbed your shoulders as you immediately didn’t waste any time teasing her and plunged your length deep inside her and god, she’s still as tight as earlier and you wouldn’t complain about that because that’s what makes every second worth cherishing.
Your hands then coursed down on her waist, caressing it as your touch makes her writhe a little and it didn’t bother you, continuing onto your desired precedence to reach your ultimate high. You pump your hips in her with aims to make her feel the utmost pleasure and how much you love her and with Xiaoting’s cleverness and the heat rising up onto its maximum scope, her hands didn’t become idle and pulled your head towards her, initiating into a heated kiss. It was full of hunger and lust as the both of you kept on chasing the higher authority, battling for the dominant control over the other person as drool inevitably seeped out of your mouths with your tongues dancing around gracefully. The kiss eventually gets sloppier and more heated and so are your ramming thrusts, pistoning onto a velocity unable for anyone to comprehend and it wouldn’t take long before you achieve your long-anticipated high with that familiar tingle in your loins.
Wanting to savor the last moments before your peak, you initiated a new rhythm as you gave up on a ridiculous pace in exchange for more powerful thrusts, as every time you do it, her thighs jiggle like jelly and that’s why you love such slow-paced thrusts that aims to strike harder—maybe the accumulation of such force on hammering her tight cunt is wonderful and it wouldn’t be long until you achieve something that you’ve been longing for.
“Aren’t y-you close, daddy?”
You chase your breath as you became too focused on peppering her neck with kisses and fucking her into oblivion that it took your seconds before you responded back, “I’m pretty close, baby—”, and instantly you kissed her lips again as you looked at her endearingly, full of fervor as you muttered such saccharine-filled words, “—I love you so much…”
That made Xiaoting realize how sincere everything was and she always knew it, but she never felt this much adrenaline and affection as she can’t help but smile sincerely as you continue hammering her and chasing that peak of yours. “I love you too, daddy—more than anything in this world.”
You pulled Xiaoting into another heated kiss as you buried your entire length in this, filling her up to the hilt as she let out muffled moans onto your lips but didn’t let herself faze on her grand prize, continuing on deepening the torrid kiss. You fill her up as you grab her waist tightly, almost forming into an embrace in order for a better leverage on dumping everything inside her. You groan between your heated kisses with Xiaoting as everything is just now in a complete state of bliss, every spurt worth treasuring as the constriction of her walls makes the pleasure worth your while and maybe even extending your orgasm. When you feel that everything has been toned down, you then palm her shoulders and pulled out slowly, Xiaoting catching her breath because of such a heated kiss initiated by you and god, what an incredible it is to see her pussy full of your cum, and some of it dripping and onto the sheets they stain—you suppose you would need a new mattress considering how much she spurted ner nectar all over the place and maybe, that would be the case.
“Ohh, it’s s-so much, daddy…” Xiaoting moans in satisfaction as she can feel the warmness of your seed that fills every inch of her velvety walls, and some are even seeping out of her lips. She took this as an opportunity to scoop out a sample and tasted it and as expected, she was delighted to let her taste buds orchestrate the final verdict of its delectability. “It’s salty and sweet—I love it, daddy…”
You smile because of her satisfaction being voiced out verbally, and with that, it makes you feel that everything was worth both your whiles and there’s nothing you could ask for more when it’s already been fulfilled.
“You felt so good, baby and—” You caressed Xiaoting’s cheeks and looked at her endearingly again, feeling affectionate and thankful with the greatness she's bestowed you and being such a good girl for you. “—glad you loved me filling you up.”
“I love your harshness too, daddy—everything is just perfect…” It’s a little surprising that she can still articulate words that she shouldn’t but she got stamina for days so her recovery would be pretty quick. You know the night’s getting older but you know there’s more ways to enjoy everything you could think of but for now, a good night’s rest would not be bad as you can feel your drowsiness slowly taking over you until—
*notification pops up*
Yujin’s gonna see you tomorrow and you’re fucked up…
Well, was this all a mistake? You’d consider this as one but maybe this won’t be and all you can do is to prepare onto something that’s the last thing you want to deal with—her.
799 notes
·
View notes
Text
I drew my Zero, One and Two gijinka's digitally



Also here's Zro in his eldritch form, One with her cape and witch hat, and a less eldritch version of Two:



Also sorry for not posting in a very long time, I've got no reason for that and it will happen again :)))
#my art#fanart#artists on tumblr#digital art#bfdi#bfdi:tpot#algebralien art#algebraliens#zero integer#one integer#two integer#zro bfdi#zro xfohv#zero algebralien#one algebralien#two algebralien#humanized#eldrich forms#zero#one#two#subscriber specials#art#gijinka#bfb#osc art#zero bfdi#one bfdi#two bfdi
13 notes
·
View notes
Text
An international team of physicists has successfully measured the size of a certain type of neutrino to a certain degree. In their paper published in the journal Nature, the group describes experiments they conducted that involved measuring the radioactive decay of the element beryllium. Neutrinos are subatomic particles with a mass very close to zero. They also have a half-integer spin and rarely react with normal matter. To date, three kinds of neutrinos have been identified, each by association with an electron, muon or tau particle. Physicists have become more interested in neutrinos over the past several years because it is thought better understanding them may lead to a better understanding of why there is more matter than antimatter in the known universe.
Continue Reading.
98 notes
·
View notes
Note
what's the 3-dimensional number thing?
Well I'm glad you asked! For those confused, this is referring to my claim that "my favorite multiplication equation is 3 × 5 = 15 because it's the reason you can't make a three-dimensional number system" from back in this post. Now, this is gonna be a bit of a journey, so buckle up.
Part One: Numbers in Space
First of all, what do I mean by a three-dimensional number system? We say that the complex numbers are two-dimensional, and that the quaternions are four-dimensional, but what do we mean by these things? There's a few potential answers to this question, but for our purposes we'll take the following narrative:
Complex numbers can be written in the form (a+bi), where a and b are real numbers. For the variable-averse, this just means we have things like (3+6i) and (5-2i) and (-8+3i). Some amount of "units" (that is, ones), and some amount of i's.
Most people are happy to stop here and say "well, there's two numbers that you're using, so that's two dimensions, ho hum". I think that's underselling it, though, since there's something nontrivial and super cool happening here. See, each complex number has an "absolute value", which is its distance from zero. If you imagine "3+6i" to mean "three meters East and six meters North", then the distance to that point will be 6.708 meters. We say the absolute value of (3+6i), which is written like |3+6i|, is equal to 6.708. Similarly, interpreting "5-2i" to mean "five meters East and two meters South" we get that |5-2i| = 5.385.
The neat thing about this is that absolute values multiply really nicely. For example, the two numbers above multiply to give (3+6i) × (5-2i) = (27+24i) which has a length of 36.124. What's impressive is that this length is the product of our original lengths: 36.124 = 6.708 × 5.385. (Okay technically this is not true due to rounding but for the full values it is true.)
This is what we're going to say is necessary to for a number system to accurately represent a space. You need the numbers to have lengths corresponding to actual lengths in space, and you need those lengths to be "multiplicative", which just means it does the thing we just saw. (That is, when you multiply two numbers, their lengths are multiplied as well.)
There's still of course the question of what "actual lengths in space" means, but we can just use the usual Euclidean method of measurement. So, |3+6i| = √(3²+6²) and |5-2i| = √(5²+2²). This extends directly to the quaternions, which are written as (a+bi+cj+dk) for real numbers a, b, c, d. (Don't worry about what j and k mean if you don't know; it turns out not to really matter here.) The length of the quaternion 4+3i-7j+4k can be calculated like |4+3i-7j+4k| = √(4²+3²+7²+4²) = 9.486 and similarly for other points in "four-dimensional space". These are the kinds of number systems we're looking for.
[To be explicit, for those who know the words: What we are looking for is a vector algebra over the real numbers with a prescribed basis under which the Euclidean norm is multiplicative and the integer lattice forms a subring.]
Part Two: Sums of Squares
Now for something completely different. Have you ever thought about which numbers are the sum of two perfect squares? Thirteen works, for example, since 13 = 3² + 2². So does thirty-two, since 32 = 4² + 4². The squares themselves also work, since zero exists: 49 = 7² + 0². But there are some numbers, like three and six, which can't be written as a sum of two squares no matter how hard you try. (It's pretty easy to check this yourself; there aren't too many possibilities.)
Are there any patterns to which numbers are a sum of two squares and which are not? Yeah, loads. We're going to look at a particularly interesting one: Let's say a number is "S2" if it's a sum of two squares. (This thing where you just kinda invent new terminology for your situation is common in math. "S2" should be thought of as an adjective, like "orange" or "alphabetical".) Then here's the neat thing: If two numbers are S2 then their product is S2 as well.
Let's see a few small examples. We have 2 = 1² + 1², so we say that 2 is S2. Similarly 4 = 2² + 0² is S2. Then 2 × 4, that is to say, 8, should be S2 as well. Indeed, 8 = 2² + 2².
Another, slightly less trivial example. We've seen that 13 and 32 are both S2. Then their product, 416, should also be S2. Lo and behold, 416 = 20² + 4², so indeed it is S2.
How do we know this will always work? The simplest way, as long as you've already internalized the bit from Part 1 about absolute values, is to think about the norms of complex numbers. A norm is, quite simply, the square of the corresponding distance. (Okay yes it can also mean different things in other contexts, but for our purposes that's what a norm is.) The norm is written with double bars, so ‖3+6i‖ = 45 and ‖5-2i‖ = 29 and ‖4+3i-7j+4k‖ = 90.
One thing to notice is that if your starting numbers are whole numbers then the norm will also be a whole number. In fact, because of how we've defined lengths, the norm is just the sum of the squares of the real-number bits. So, any S2 number can be turned into a norm of a complex number: 13 can be written as ‖3+2i‖, 32 can be written as ‖4+4i‖, and 49 can be written as ‖7+0i‖.
The other thing to notice is that, since the absolute value is multiplicative, the norm is also multiplicative. That is to say, for example, ‖(3+6i) × (5-2i)‖ = ‖3+6i‖ × ‖5-2i‖. It's pretty simple to prove that this will work with any numbers you choose.
But lo, gaze upon what happens when we combine these two facts together! Consider the two S2 values 13 and 32 from before. Because of the first fact, we can write the product 13 × 32 in terms of norms: 13 × 32 = ‖3+2i‖ × ‖4+4i‖. So far so good. Then, using the second fact, we can pull the product into the norms: ‖3+2i‖ × ‖4+4i‖ = ‖(3+2i) × (4+4i)‖. Huzzah! Now, if we write out the multiplication as (3+2i) × (4+4i) = (4+20i), we can get a more natural looking norm equation: ‖3+2i‖ × ‖4+4i‖ = ‖4+20i‖ and finally, all we need to do is evaluate the norms to get our product! (3² + 2²) × (4² + 4²) = (4² + 20²)
The cool thing is that this works no matter what your starting numbers are. 218 = 13² + 7² and 292 = 16² + 6², so we can follow the chain to get 218 × 292 = ‖13+7i‖ × ‖16+6i‖ = ‖(13+7i) × (16+6i)‖ = ‖166+190i‖ = 166² + 190² and indeed you can check that both extremes are equal to 63,656. No matter which two S2 numbers you start with, if you know the squares that make them up, you can use this process to find squares that add to their product. That is to say, the product of two S2 numbers is S2.
Part Four: Why do we skip three?
Now we have all the ingredients we need for our cute little proof soup! First, let's hop to the quaternions and their norm. As you should hopefully remember, quaternions have four terms (some number of units, some number of i's, some number of j's, and some number of k's), so a quaternion norm will be a sum of four squares. For example, ‖4+3i-7j+4k‖ = 90 means 90 = 4² + 3² + 7² + 4².
Since we referred to sums of two squares as S2, let's say the sums of four squares are S4. 90 is S4 because it can be written as we did above. Similarly, 7 is S4 because 7 = 2² + 1² + 1² + 1², and 22 is S4 because 22 = 4² + 2² + 1² + 1². We are of course still allowed to use zeros; 6 = 2² + 1² + 1² + 0² is S4, as is our friend 13 = 3² + 2² + 0² + 0².
The same fact from the S2 numbers still applies here: since 7 is S4 and 6 is S4, we know that 42 (the product of 7 and 6) is S4. Indeed, after a bit of fiddling I've found that 42 = 6² + 4² + 1² + 1². I don't need to do that fiddling, however, if I happen to be able to calculate quaternions! All I need to do is follow the chain, just like before: 7 × 6 = ‖2+i+j+k‖ × ‖2+i+j‖ = ‖(2+i+j+k) × (2+i+j)‖ = ‖2+3i+5j+2k‖ = 2² + 3² + 5² + 2². This is a different solution than the one I found earlier, but that's fine! As long as there's even one solution, 42 will be S4. Using the same logic, it should be clear that the product of any two S4 numbers is an S4 number.
Now, what goes wrong with three dimensions? Well, as you might have guessed, it has to do with S3 numbers, that is, numbers which can be written as a sum of three squares. If we had any three-dimensional number system, we'd be able to use the strategy we're now familiar with to prove that any product of S3 numbers is an S3 number. This would be fine, except, well…
3 × 5 = 15.
Why is this bad? See, 3 = 1² + 1² + 1² and 5 = 2² + 1² + 0², so both 3 and 5 are S3. However, you can check without too much trouble that 15 is not S3; no matter how hard you try, you can't write 15 as a sum of three squares.
And, well, that's it. The bucket has been kicked, the nails are in the coffin. You cannot make a three-dimensional number system with the kind of nice norm that the complex numbers and quaternions have. Even if someone comes to you excitedly, claiming to have figured it out, you can just toss them through these steps: • First, ask what the basis is. Complex numbers use 1 and i; quaternions use 1, i, j, and k. Let's say they answer with p, q, and r. • Second, ask them to multiply (p+q+r) by (2p+q). • Finally, well. If their system works, the resulting number should give you three numbers whose squares add to 15. Since that can't happen, you've shown that the norm is not actually multiplicative; their system doesn't capture the geometry of three dimensions.
#math#numbers#human interaction#this took the better part of a day to write oops#although to be fair I haven't exactly been focused#Also hi Pyro! Welcome.#that silly fast food emoji post went wild#I've gotten 30 followers just from that one post#which isn't that many in objective terms but like it's 40% of my current count so#hello everyone#I might start reblogging things again now
299 notes
·
View notes
Text
So what's up with dividing by zero anyways - a ramble on algebraic structures
Most everyone in the world (at least in theory) knows how to add, subtract, multiply, and divide numbers. You can always add two numbers, subtract two numbers, and multiply two numbers. But you must **never** divide by zero... or something along those lines. There's often a line of logic that leads to dividing by zero leading to "infinity," whatever infinity means, unless you're doing 0/0, whatever that means either. Clearly this is a problem! We can't have such inconsistencies in our fundamental operations! Why aren't our top mathematicians working on this?
So, that might be a bit of an exaggeration: division by zero isn't really a problem at all and is, for all intents and purposes fairly well understood, but to see why we'll have to take a crash course through algebra (the field of math, not the grade school version). Sorry for those of y'all who have seen fields and projective space before, not much to gain out of this one.
Part I: In the beginning, we had a Set.
As is true with most things in math, the only structure we start with is a set. A set isn't useful for much; all we can do with a single set is say what elements are and aren't in the set. Once you have more than one set, you start getting interesting things like unions or intersections or functions or Cartesian products, but none of those are _really_ that useful (or at least necessary) for understanding algebraic structures at the level we need, so a single set is what we start with and a single set there will be. The story then goes as follows: on the first day the lord said "Let there be an operation!" and it was so. If you want to be a bit of a nerd, a (binary) operation on a set A is formally a map * : A x A -> A, but for our purposes we just need to know that it matches the standard operations most people know (i.e. addition, subtraction, multiplication, but not division) in that for any two numbers a and b, we can do a * b and get another number. Of course, once again this is not very helpful on its own, and so we need to impose some more conditions on this operation for it to be useful for us. Not to worry though, these conditions are almost always ones you know well, if not by name, and come rather intuitively.
The first structure we'll discuss is that of a monoid: a set with an operation that is associative and has an identity. Associativity simply means that (a * b) * c = a * (b * c), and an identity simply means that we have some special element e such that a * e = e * a = a. For two simple examples and one nonexample, we have the natural numbers (with 0) under addition is a monoid: 0 + a *= *a *+ 0 = *a, and any two natural numbers add to another natural number; the integers under multiplication is a monoid: 1 * a = a * 1 = a, and any two integers multiply to another integer; and the integers under subtraction is not a monoid, since subtraction is not associative (a - (b - c) =/= (a-b) - c). In both of these examples, the operation is commutative: in other words, a * b = b * a for every a and b. There are plenty of examples of operations that are not commutative, matrix multiplication or function composition probably being the most famous, but for the structures we're going to be interested in later operations are almost always commutative, so we can just assume that from the start.
Of course, you might wonder where subtraction comes from, if it doesn't fit into a monoid structure (and in particular isn't associative). Not to worry! We can simply view subtraction as another type of addition, and our problems go away. In particular, we add the condition that for every a, we have an inverse element a⁻ ¹ (or -a if our operation is addition) such that a * a⁻ ¹ = a⁻ ¹ * a = e. For fans of universal algebra, just as a binary operation can be thought of as a function, the inverse can be thought of as a function i : A -> A that sends each element to its inverse. This forms a structure we know as a group. While none of the above examples form a group, one of them can be naturally extended to a group: if we simply add negative whole numbers to natural numbers, we get the group of integers over addition, where for any integer a, we have its inverse -a where a + -a = 0. In particular, the subtraction a - b is just a + -b = -b + a, where -b is the additive inverse of b. As we will soon see, division can also be thought of in a similar way, where a/b = a * /b = /b * a where /b is the multiplicative inverse of b. As a side note, the examples above are very specific types of monoids and groups which turn out to be quite far from the general ideas that monoids and groups are trying to encapsulate. Monoids show up often in computer science as they're a good model for describing how a list of commands affects a computer, and groups are better thought of as encapsulating symmetries of an object (think of the ways you can rotate and reflect a square or a cube).
Part II: So imagine if instead of one operation, we have... two...
If you've ever taken introductory algebra, you've probably never heard of monoids and only done groups. This is partially because monoids are much less mathematically interesting than groups are and partially because monoids are just not as useful when thinking about other things. For the purposes of this post, however, the logical steps from Set -> Monoid -> Group are surprisingly similar to the steps Group -> Ring -> Field, so I've chosen to include it regardless.
Just as we started from a set and added an operation to make a monoid, here we start from an additive group (i.e. a group where the operation is addition) and add another operation, namely multiplication, that acts on the elements of the group. Just like in the monoid, we will impose the condition that multiplication is associative and has an identity, namely 1, but we also impose the condition that multiplication meshes nicely with addition in what you probably know as the distributive properties. What we end up with is a ring, something like the integers, where you can add, subtract, and multiply, but not necessarily divide (for example, 2 doesn't have a multiplicative inverse in the integers, as a * 2 = 1 has no solutions). Similarly, when we add in multiplicative inverses to every nonzero element, we get a field, something like the rational numbers or the real numbers, where we can now divide by every nonzero number. In other words, a ring is an additive group with a multiplicative monoid, and a field is an additive group with a subset that is a multiplicative group (in particular the subset that is everything except zero). For those who want to be pedantic, multiplication in a ring doesn't have to be commutative, but addition is, and both addition and multiplication are commutative in a field. A full list of the conditions we impose on the operations of a monoid, group, ring, and field can be found here).
So why can't we have a multiplicative inverse to 0 in a field? As it turns out, this is because 0 * a = 0 for every a, so nothing times 0 gets you to 1. There is technically a structure you can have if 0 = 1, but it turns out there's only the one single element 0 in that structure and nothing interesting happens, so generally fields specifically don't allow 0 = 1. Then, what if instead we relaxed the condition that 0 * a = 0? Similarly, it turns out that this isn't one of the fundamental conditions on multiplication, but rather arises from the other properties (a simple proof is a * 0 = a * (0 + 0) = a * 0 + a * 0 implies 0 = a * 0 - a * 0 = a * 0 + a * 0 - a * 0 = a * 0). If we were to relax this condition, then we lose some of the other nice properties that we built up. This will be a recurring theme throughout the rest of this post, so be wary.
Part III. We can't have everything we want in life.
While all the structures so far have been purely algebraic and purely algebraically motivated, the simplest way to start dividing by zero is actually "geometric," with several different ways of constructing the same space. The construction we'll use is as follows: take any field, particularly the real numbers or the complex numbers. We can always take the cartesian product of a field K with itself to form what's called affine space K^2, which is the set of ordered pairs (a,b) for a, b in K. As a side note, the product of groups, rings, or fields has a natural definition of addition or whatever the underlying group operation is by doing it componentwise, i.e. (a,b) * (c,d) = (a * c, b * d), but our operations will not coincide with this, as you'll see soon. This affine space is a plane - in fact, when we do this to the real numbers, we get the Cartesian plane - within which we can construct lines, some of which we get by considering the set of points (x, y) satisfying the familiar equation y = mx + b for some 'slope' m and 'intercept' b. In particular, we want to characterize all the lines through the origin. This gives us all the lines of the form y = mx, as well as one additional line x = 0. This is the basic construction of what we call the projective line, a space characterizing all the lines through the origin of affine 2-space. The geometric picture of this space is actually a circle: the bottom point representing the number 0; the left and right halves representing negative and positive numbers, repsectively; and the top point representing the number "infinity."
There are a few ways of describing points on the projective line. The formal way of doing so is by using what are called homogenous coordinates. In other words, for any nonzero point (a,b) in affine space, it is surely true that we can find a line through the origin and (a,b). In particular, if a is not zero, then this line takes the form y = (b/a) x where the slope is b/a. Furthermore, any two points (a,b) and (c,d) can actually sit on the same line, in particular whenever c = ka and d = kb for some number k. Thus, we can define homogenous coordinates as the set of points [a : b] for a, b in our field where [a : b] = [ka : kb] by definition, and the point [0 : 0] is not allowed as it doesn't specify any particular line (after all, every line passes through the origin). As is alluded to above, however, this means that whenever a =/= 0, we can take k = 1/a to get [a : b] = [1 : b/a], in other words characterizing each line by its slope. Furthermore, whenever a = 0, we can take k = 1/b to get [0 : b] = [0 : 1]. In other words, the projective line is, as we informally stated above, equivalent to the set of slopes of lines through the origin plus one other point representing the vertical line, the point at "infinity." Since slopes are just numbers in a field, we can add, subtract, multiply, and divide them as we normally do with one exception: the slope of the lines containing [a : b] for any a =/= 0 is b/a, so clearly the line with infinite slope consisting of points [0 : b] implies that b/0 should be infinity. Voila! We can divide by zero now, right? Well... there are two loose ends to tie down. The first is what infinity actually means in this case, since it is among the most misunderstood concepts in mathematics. Normally, when people bandy about phrases such as "infinity isn't a number, just a concept" or "some infinities are different from others" they are usually wrong (but well meaning) and also talking about a different kind of infinity, the ones that arise from cardinalities. Everything in math depends on the context in which it lies, and infinity is no different. You may have heard of the cardinal infinity, the subject of Hilbert's Hotel, describing the size of sets and written primarily with aleph numbers. Similarly, you may also have heard of the ordinal infinity, describing the "place" in the number line greater than any natural number. Our infinity is neither of these: it is to some extent an infinity by name only, called such primarily to take advantage of the intuition behind dividing by zero. It's not "greater" than any other number (in fact, the normal ordering of an ordered fields such as the real numbers breaks down on the projective line), and this is a consequence of the fact that if you make increasingly negative and increasingly positive slopes you end up near the same place: a vertical line. In other words, "negative infinity" and "positive infinity" are the same infinity.
The second loose end is that defining our operations this way is actually somewhat algebraically unsound, at least with respect to the way we think about operations in groups, rings, and fields. As mentioned above, the operation of addition can be lifted to affine space as (a,b) + (c,d) = (a+c,b+d). However, this same operation can't really be used for homogenous coordinates, since [1, 0] = [2, 0] as they lie on the same line (the line with slope 0), but [1, 0] + [1, 1] = [2, 1] while [2, 0] + [1, 1] = [3, 1], and [2, 1] and [3, 1] are not the same line, as they have slopes 1/2 and 1/3, respectively. Dividing by zero isn't even needed to get weirdness here. Luckily, we can simply define new operations by taking inspiration from fractions: b/a + d/c = (bc + ad)/ac, so we can let [a : b] + [c : d] equal [ac : bc + ad] (remembering that homogenous coordinates do to some extent just represent the slope). Luckily, multiplication still works nicely, so we have [a : b] * [c : d] = [ac : bd]. Unluckily, with these definitions, we no longer get a field. In particular, we don't even have an additive group anymore: [a : b] + [0 : 1] = [0 : a] = [0 : 1], so anything plus infinity is still infinity. In other words, infinity doesn't have an additive inverse. Furthermore, despite ostensibly defining infinity as 1/0, the multiplicative inverse of 0, we have that [1 : 0] * [0 : 1] = [0 : 0], by our rules, which isn't defined. Thus, 0 still doesn't have a multiplicative inverse and 0/0 still doesn't exist. It seems like we still haven't really figured out how to divide by zero, after all this. (Once again, if you want to read up on the projective line, which is a special case of projective space, which is a special case of the Grassmannian, in more depth.)
Part IV: I would say wheels would solve all our problems, if not for the fact that they just make more problems.
At this point, to really divide by zero properly, we're going to need to bite the bullet and change what dividing really means. Just as we can think of subtraction as adding the additive inverse (i.e. a - b = a + -b where -b was a number), we can start thinking of division as just multiplying by... something, i.e. a/b = a * /b, where /b is something vaguely related to the multiplicative inverse. We can already start doing this in the projective line, where we can define /[a : b] = [b : a], and it works nicely as [a : b] * [b : a] = [ab : ab] = [1 : 1] whenever neither a nor b is zero. This lets us rigorize the statements 1/infinity = 0, infinity/0 = infinity, and 0/infinity = 0, but doesn't really help us do 0/0 or infinity/infinity. Furthermore, note that because 0/0 =/= 1, /[a : b] isn't really the multiplicative identity of [a : b], it's just the closest we can get.
Enter the wheel! If 0/0 is undefined, then we can simply... define it. It worked so nicely for adding in infinity, after all - the picture of the point we added for infinity is taking a line and curling it up into a circle, and I like circles! Surely adding another point for 0/0 would be able to provide a nice insight just as turning a line into the projective line did for us.
So here's how you make a wheel:
You take a circle.
You add a point in the middle.
Yeah that's it. The new point, usually denoted by ⊥, is specifically defined as 0/0, and really just doesn't do anything else. Just like for infinity, we still have that a + ⊥ = ⊥ and a * ⊥ = ⊥ for all a (including infinity and ⊥). It doesn't fit into an order, it doesn't fit in topologically, it is algebraically inert both with respect to addition and multiplication. It is the algebraic formalization of the structure that gives you NaN whenever you fuck up in a calculator and the one use of it both inside and outside mathematics is that it lets you be pedantic whenever your elementary school teacher says "you can't divide by zero" because you can go "yeah you can it's just ⊥ because i've been secretly embedding all my real numbers into a wheel this whole time" (supposing you can even pronounce that).
Part V: So what was the point of all this anyways
The wheel is charming to me because it is one of the structures in mathematics where you can tell someone just asked a question of "what if this was true," built some space where it was, and just started toying with it to see what happens. It's a very human and very beautiful thing to see someone go against conventional knowledge and ask "what breaks when you allow 0/0" even if conventional knowledge does tend to be right most of the time. In this sense, perhaps the uselessness of the wheel is the point, that even despite how little ⊥ does from a mathematical lens, some people still took the time to axiomatize this system, to find a list of conditions that were both consistent and sufficient to describe a wheel, and genuinely do actual work seeing how it fits in within the universe of algebraic structures that it stays in.
While a wheel may not be used for much (it might be describable in universal algebra while a field isn't, though I'm not too well versed in universal algebra so I'm not actually entirely sure), every other structure discussed above is genuinely well studied and applicable within many fields inside and outside of math. For more viewpoints on what the projective line (and in general the projective sphere) is used for, some keywords to help you on your way are compactification of a set if you care about the topological lens, the real projective line or the Riemann Sphere if you care more about the analysis side, or honestly the entirety of classical algebraic geometry if that's your thing.
Another structure that might be interesting to look at is the general case of common meadows, an algebraic structure (M, 0, 1, +, -, *, /) where the condition of / being involutive (i.e. /(/x) is not always x) is relaxed, unlike a wheel where it is always involutive. Note that these structures are called meadows because the base structure they worked on is a field (get it? not our best work I promise mathematicians are funnier than this). These structures are at the very least probably more interesting than wheels, though I haven't checked them out in any amount of detail either so who knows, perhaps there isn't much of substance there either.
132 notes
·
View notes
Note
Hey Red, I'm trying to build a better understanding of mathematics, because to my mind math has always been a collection of arcane sigils that I had to memorize to pass tests in school. I must know how these sigils came to be and why they mean what they mean. Are there any resources you recommend I use in my pursuit of these secrets? Please and Thank You 🙏
It's good you described math as something you "build," because I think that's the best analogy possible.
Mathematics, in its purest form, involves no memorization. Math is the process of taking a very small number of established truths and defined operations that preserve truth, and using those operations on your established truths to expand your space of known truths. As long as you start from a point of truth and only use operations that preserve truth, you will derive truths. If you understand the base principles from which a branch of math is constructed, you can rederive it from first principles. Memorization is easier, but you can rederive it.
For instance, we can start with two things, the number "1" and the operation "+". 1 means "a single thing" and + means "put them together." If those two concepts exist, then we also have 2, 3, 4, and every other positive integer, because we can derive them by using + on as many 1s as we want. If we drop a rock on an empty patch of ground, and then drop a rock on that same patch of ground, that patch of ground now has two rocks on it.
If we include within the definition of "+" that there exists an identity value 0, and every value has an inverse that when added to it produces zero, we also get 0 and all the negative integers, producing the group of integers. Every integer can be expressed using nothing but the number 1, the + operation, and its inverse - if we're feeling spicy.
If we decide to add another truth-preserving operation, "*", with identity value 1 and the same kind of inverse property that "+" has, we rederive every rational number. Every number in this field of rational numbers can be described as a combination of 0s and 1s using only + and * and their inverses; truthful objects combined in truth-preserving operations. We started from the truth and we used it as our only building material to create something equally truthful.
We can memorize a multiplication table, but multiplication is just iterated addition. If we forget, we can just do the addition again.
Algebra is a simple rearrangement of a simple beginning math problem by way of other truth-preserving operations. When you're starting out, you might expect to see something like
3 + 5 = ?
Algebra starts when we replace "?" with a placeholder, "x". This is just a change of terminology. It preserves truth.
3 + 5 = x
This isn't what most algebra problems look like, though. Most basic algebra problems look more like
3x + 7 = 31
But these two formulae are the same, because we can turn one into the other through operations that preserve truth.
3x + 7 = 31 -> subtracting the same value from both sides of the equation is an operation that preserves truth. We subtract 7 from both sides, getting
3x = 24 -> dividing both sides of the equation by the same value is also an operation that preserves truth. We divide both sides by 3, getting
x = 8 -> addition is associative, so we can break 8 up however we want if we do
x = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = (1 + 1 + 1) + (1 + 1 + 1 + 1 + 1) = 3 + 5
Solving an algebra problem is the process of breaking down the things that make it complicated using the truth-preserving operations that defeat them. Added values can be subtracted. Multiples can be divided. Exponents can be root'd.
We understand what it means to put a placeholder in a math problem. We realize, by the same token, we can put in more than one placeholder, if we want. This gives us problems that don't have single numerical solutions, but spaces of solutions. Consider
2*x = ?
We do what we did before, replacing that "?" with something that means the same thing. We use a different letter to avoid confusion.
2*x = y
Now we have multivariable algebra. Instead of getting hard numbers for both variables, we have pairs of numbers. If we pick an x, we get a y. If we pick a y, we get an x. The relationship between the values is clearly defined; x will always be y/2. If x is 3, y is 6. If x is -1.8, y is -3.6.
Now for the sake of convenience, we create shorthand - another change of terminology that preserves truth. We come up with a term that describes this relationship between x and y. We decide to call y a "function."
y = f(x) = 2*x
A function is what we're calling one half of an equation; what goes on the other side of the equals sign. It's just a rename, like when we turned ? into x. It preserves truth.
The trick at this stage is that every element of this seeming increasingly complexity is actually an attempt to make the process simpler as we handle more and more things. We don't technically need any numbers other than 0 and 1 if we're just dealing with rational numbers. We could write 378/5 with nothing but 1s and +, -, * and /, but by god we wouldn't want to. We could write [x^3 + 2x + 5] as ?*?*? + ? + ? + 1 + 1 + 1 + 1 + 1 and it would mean the same thing. The shorthand and symbols get dizzying if you lose track of what they mean, but when you remember what they mean, you understand why you need them.
Any piece of mathematical shorthand basically means "for this thing we're talking about, this set of things is known to be true." We can rederive those things if we need to, but the shorthand is there to help us avoid doing it unnecessarily. We call the integers a group because that means it has an associative operation that is invertible and has an identity element that, when used in the operation, leaves the operated-on value unchanged. We don't want to write that out every time we use + or remember what 0 means, but we can if we have to.
Calculus is where most people think math turns into wizardry, but derivatives and integrals are just another pair of inverse functions like + and - or * and /, and the building block of this branch of math is the derivative. Any formula for a derivative can, in a pinch, be rederived by calculating the difference quotient (f[x+h]-f[x])/h as h approaches 0. If f(x)=x^2, we may memorize that its derivative f'(x)=2x, or we may calculate
[f(x+h) - f(x)]/h =
([x+h]^2 - x^2)/h =
(x^2 + 2xh + h^2 - x^2)/h =
(2xh + h^2)/h = 2x + h
And the limit of this as h->0 is 2x.
Everything in math can be broken down to first principles. Everything. Sometimes it's very hard to figure out what tool you need to break it down to its next stage of simplification, but it was built from first principles and it can be broken down the same way. If it isn't making sense, break it down with truth-preserving methods until it does - even if you have to go all the way back to zeroes and ones.
617 notes
·
View notes