#complex zero theorem

[math-journal2]

Dump

[clowndensation]

my life if i was allowed to skip videos on topics i already understand -_-

[wordsmithic]

Ancient Greek Women Mathematicians you didn't know about

Αίθρα - Aethra (10th - 9th century BC), daughter of the king of Troizina Pitthea and mother of Theseus, knew mathematics in another capacity unknown to many. So sacred to the beginnings of the most cerebral science, Aethra taught arithmetic to the children of Troizina, with that complex awe-inspiring method, since there was no zero… and the numbers were symbolically complex, as their symbols required many repetitions.

Πολυγνώτη - Polygnoti (7th - 6th century BC) The historian Lovon Argeios mentions Polygnotis as a companion and student of Thalis. A scholar of many geometric theorems, it is said in Vitruvius' testimony, that she contributed to the simplification of arithmetic symbols by introducing the principle of acrophony. She managed this by introducing alphabetic letters that corresponded to each in the initial letter of the name of the number. Thus, Δ, the initial of Δέκα (ΤΕΝ), represents the number 10. X, the initial of Χίλια (Thousand), represents the number 1000 etc. According to Vitruvius, Polygnoti formulated and first proved the proposition "Εν κύκλω η εν τω ημικυκλίω γωνία ορθή εστίν" - "In the circle the angle in the hemi-circle is right angle."

Θεμιστόκλεια - Themistoklia (6th century BC). Diogenes the Laertius scholar-writer mentions it as Αριστόκλεια - Aristoclia or Θεόκλεια - Theoclia. Pythagoras took most of his moral principles from the Delphic priestess Themistoclia, who at the same time introduced him to the principles of arithmetic and geometry. According to the philosopher Aristoxenos (4th century BC), Themistoclia taught mathematics to those of the visitors of Delphi who had the relevant appeal. Legend has it that Themistoclia decorated the altar of Apollo with geometric shapes. According to Aristoxenos, Pythagoras admired the knowledge and wisdom of Themistoclia, a fact that prompted him to accept women later in his School.

Μελίσσα - Melissa (6th century BC). Pupil of Pythagoras. She was involved in the construction of regular polygons. Lovon Argeios writes about an unknown work of hers: "Ο Κύκλος Φυσίν - η Μελίσσα - Των Εγγραφομένων Πολυγώνων Απάντων Εστί". (The title translates to "The circle is always the basis of the written polygons" or so.)

Τυμίχα - Tymicha (6th century BC). Thymiha, wife of Crotonian Millios, was (according to Diogenes Laertius) a Spartan, born in Croton. From a very early age, she became a member of the Pythagorean community. Iamblichus mentions a book about "friend numbers". After the destruction of the school by the Democrats of Croton, Tymicha took refuge in Syracuse. The tyrant of Syracuse, Dionysios, demanded that Tymicha reveal to him the secrets of the Pythagorean teaching for a great reward. She flatly refused and even cut her own tongue with her teeth and spat in Dionysius' face. This fact is reported by Hippobotus and Neanthis.

Βιτάλη - Vitali or Vistala (6th – 5th century BC). Vitali was the daughter of Damos and granddaughter of Pythagoras, and an expert in Pythagorean mathematics. Before Pythagoras died, he entrusted her with the "memoirs", that is, the philosophical texts of her father.

Πανδροσίων ή Πάνδροσος - Pandrosion or Pandrossos (4th century AD). Alexandrian geometer, probably a student of Pappos, who dedicates to her the third book of the "Synagogue". Pandrosion divides geometric problems into three categories:" Three genera are of the problems in Geometry and these, levels are called, and the other linear ones."

Πυθαΐς - Pythais (2nd century BC). Geometer, daughter of the mathematician Zenodoros.

Αξιόθεα - Axiothea (4th century BC). She is also a student, like Lasthenia, of Plato's academy. She came to Athens from the Peloponnesian city of Fliounda. She showed a special interest in mathematics and natural philosophy, and later taught these sciences in Corinth and Athens.

Περικτιόνη - Periktioni (5th century BC). Pythagorean philosopher, writer, and mathematician. Various sources identify her with Perictioni, Plato's mother and Critius' daughter. Plato owes his first acquaintance with mathematics and philosophy to Perictioni.

Διοτίμα - Diotima from Mantineia (6th-5th century BC). In Plato's "Symposium", Socrates refers to the Teacher of Diotima, a priestess in Mantineia, who was a Pythagorean and a connoisseur of Pythagorean numerology. According to Xenophon, Diotima had no difficulty in understanding the most complex geometric theorems.

Iamblichos, in his work "On Pythagorean Life", saved the names of Pythagorean women who were connoisseurs of Pythagorean philosophy and Pythagorean mathematics. We have already mentioned some of them. The rest:

Ρυνδακώ - Rynthako

Οκκελώ - Okkelo

Χειλωνίς - Chilonis

Κρατησίκλεια - Kratisiklia

Λασθένια - Lasthenia

Αβροτέλεια - Avrotelia

Εχεκράτεια - Ehekratia

Θεανώ - Theano

Τυρσηνίς - Tyrsinis

Πεισιρρόδη - Pisirrodi

Θεαδούσα - Theathousa

Βοιώ - Voio

Βαβέλυκα - Vavelyka

Κλεαίχμα - Cleaihma

Νισθαιαδούσα - Nistheathousa

Νικαρέτη - Nikareti from Corinth

There are so many women whose contribution to science remains hidden. We should strive to find out about more of them! For more information, check out the books of the Greek philologist, lecturer, and professor of ancient Greek history and language, Anna Tziropoulou-Eustathiou.

[notarealwelder]

So you can prove the fundamental theorem of algebra like this:

pick a complex polynomial p(z) = zⁿ + (rest). assume it has no zeros.

pick a constant C such that in the value of p(C), Cⁿ comfortably dominates, i.e. |Cⁿ| > |rest(C)|. we can do that because zⁿ grows faster than (rest).

observe how the action of p on the circle C×eⁱˣ is basically "z ↦ zⁿ + a little (rest)-wiggling". which is to say, the image of that circle is a loop wrapped around the origin n times.

observe how the image of the closed disk of radius C under p is, topologically, still a disk. that is to say, it is contractible, and so any loop within it is homotopic to a trivial loop. like, for example, the image of the C-circle.

but that can't be true: the image of the disk lies entirely in ℝ²–{0}, and the n-wrapped loop is not homotopic to the trivial loop in ℝ²–{0}, by the theorem about the fundamental group of the circle.

[crookedkryptonitebeliever]

I will give Yves baby photos and my deepest darkest childhood secret if his does my college algebra and trigonometry homework- conjugate zeros theorem with polynomial functions and complex zeros is kicking my ASS W(`0`)W

Oh mans is doing the FUCK out of that homework, its a great fuckin deal for him, a STEAL 🔥

[lipshits-continuous]

I had a revelation earlier whilst talking to a friend about some maths. The big integral theorems from Complex Analysis, i.e. Cauchy's Theorem, Cauchy's Integral Formula, and Cauchy's Residue Theorem, all don't really depend on what curve we're integrating over but is more about the structure of the set that the function is defined on. Since the former two theorems can be recovered from CRT I'll only talk about that one. The residue is non-zero cause of the holes in the domain so the integral is really measuring something more fundamental than anything to do with the particular curve other than the fact they're a whole in the interior of the set the curve bounds.

Maybe there's something more general about how we can use integrals "measure" the holes in a space that I don't know about but this seems really interesting

[autisticempathydaemon]

Hi, if you're still doing the matchups, I'd love to see what you have in store!

Song fixations

-- Currently, I've been listening to MARK CHAPMAN by Måneskin. The first lyrics that came to my mind was the end of the first verse and the chorus.

Ma se soltanto avesse La possibilità Ti seguirebbe al quattro angoli della città Nascosto fra la gente Senza un'identità Dice che mi ama ma lo so che mente

Si muove a piede libero Vestito come un incubo Vuole tu sia in pericolo Però'ti chiama idolo

Translated as: "But if only he had the possibility, It would follow you to the four corners of the city. Hidden among the people, without an identity. He says he loves me but I know he's lying. He moves freely, dressed like a nightmare. He wants you to be in danger, but he calls you an idol." I'm not entirely sure why these lyrics stand out to me in the way they do, but oh well. I've also been listening to READ YOUR DIARY from the same album.

The Redacted Part of this Ask

-- I absolutely love Hush's introductory video. The sound design and overall ambiguity surrounding his character at that point was so absolutely intriguing on its first release, and I still listen to it regularly.

I never was able to get into Asher, unfortunately. I know that there's probably so much more to his story, but it's just never clicked with me.

I would completely and absolutely love to befriend Huxley. I am a total Plant Slut, and I have (quite frankly) a concerning amount of house plants. Having someone who is not only Chill as Fuck to hang with, but could also help with the plants? That is a friendship that I need.

Book/series/tv show

-- Just solely by the volume of it that I watch, I could probably recall any given episode of Dimension 20. I watch it while crocheting, and so when I'm just chilling and have time on my hands, dice time it goes. I could probably name every insane Nat 20 Ally made in FH:FY and every intimidating Evan Kelmp line in Misfits + Magic.

Various other info (Sleepy time, Enneagram, etc)

-- My go-to way to fall asleep is, unfortunately, staying awake until I physically cannot keep my eyes open any longer. When I do get sleepy, I talk about stationary. It's something I've been into for a long time, and when I simply do not have the filter to not talk about my interests, I unleash everything about pens and notebooks that I know on the poor soul who is near me.

I'm a type 5 on the Enneagram and am currently pursuing a degree in Mathematics. Ideally, I want to go to grad school. I just really, really, fucking love maths. It is the best subject.

Gas Station. I normally do a water, a monster zero ultra, and kettle-cooked salt and vinegar chips.

Other than all of this, I'm just a dude. Just a silly little guy, if you will. Teehee. Have fun!

So this one was both so fun but so hard. You’re so interesting, you’ve got so much going on- a typical Type Five. Not to make you sound like a Manic Pixie Dream Boy but god, James could use you in his life.

By that, I mean Type Five’s are characterized as thoughtful, unique free-thinkers prone to philosophy and complexity. I think James respects and admires these qualities in you in addition to your pursuit of higher education. (I don’t think he knows a ton about math, but I do think he likes to hear you talk about it.) Complementing that, he loves the more unexpected, chaotic parts of you. Like, can you imagine listening to your thoughts and the cognitive dissonance of theorems versus Riz going up a corn monster’s butt? You keep him on his toes in the best way.

Another reason James strikes me as a good match for you is how easy, I think, it’ll be for him to take you with him to ETS. He could listen to Dimension 20 when he misses you, deeply confusing his coworkers who can’t picture him as a DnD guy. Like, I don’t think you would have had time to crochet him a blanket before he left, but maybe he’s got gloves, a scarf, socks, something you made for him that he can touch. Also, can’t you imagine sending him on his work trip with a little plant? The bonding opportunities for James and Anton to take care of their plants and miss their lovers write themselves!

Song:

Gonna soften the blow, soften the blow and give it up/ I saw the surprise, the look in your eyes, I gave it up/ Gonna be who I am, be who I am, and give it up/ I traveled the way/ Wait for me, wait for me/ It's all better now, it's all better now/ Wait for me, wait for me

James strikes me as an indie, alt rock kind of guy, so Kings of Leon would be a good fit for him. I like this song for y’all for that reason and the fact it’s got a sweet, longing kind of feel. Also, “wait for me” when he’s on that business trip a little incel motherfucker made that much longer just hits.

Runner-ups:

Anton is obviously a runner-up; like, he came to mind first. However, James strikes me as more interesting and therefore a better match for someone as interesting as you. Lasko is another runner-up because I think y’all would really share interests and hobbies. If I were doing platonic match-ups, he’d have been at the top of list.

note: thank you for waiting 🧡

Read this post and send me an ask if you’d like a match-up of your own! 💌

[void-magician]

please help… could you explain integrals to me like i’m five? i barely passed math class by the skin of my teeth in high school and i would really like to get smarter 🙏

ohohoho you've activated my trap card (my ass loves calculus). strap in because this will get a little complex, as is the nature of most calculus.

integrals are conceptually pretty simple in that they do kind of the opposite of derivatives - practically, that means adding up a bunch of stuff to find a result over a stretch of space rather than closing in on an instantaneous point.

the basic idea there is based on an idea called a riemann sum.

what the riemann sum does is estimate the area under a curve by drawing a bunch of rectangles at certain points along the curve, calculate the area of those rectangles, and then add them all up.

the sum assumes each rectangle has the same width, denoted by Δx - this is the total width of the stretch divided by the number of rectangles. the height of each rectangle is given by the value of the function at each of those certain points. Add them up, and we get an approximate of the total area under the curve.

that's a big, long, and kind of annoying way to write it out, so we can rewrite it using sigma notation - basically a way to describe adding a bunch of things up depending on a certain count.

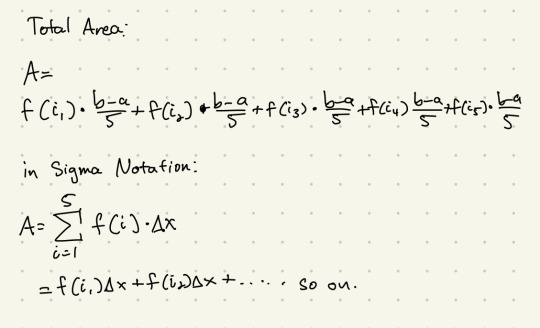
we can make this a general notation for any n number of intervals, like this:

however, the issue remains that no matter how many rectangles we choose to have, we still have some margin of error. so how do we eliminate that error and get the closest possible value for the area under whatever curve we have?

we do what most of calculus is based on: we invite the concept of infinity to take a little tango! what an integral does is it takes the riemann sum and asks it to add up an infinite amount of rectangles. since each rectangle gets infinitely narrower, the margin of error gets infinitely smaller, to the point that we can call the margin of error zero - which is to say, we have a perfectly accurate answer. so that's where we get the limit definition of the integral:

we use dx in the integral to represent Δx, except since the width is infinitely small, we use dx similarly to the notation of derivatives, i.e. an infinitesimally small amount.

as it turns out, the operation of taking an integral is the inverse of taking a derivative - that is to say, they cancel out. this discovery is what nets us an incredibly powerful little tool called the Fundamental Theorem of Calculus

so that's what integrals are and effectively what they do. when it comes to actually evaluating integrals that's a whole different beast, but the basic idea is that the result of an integral is also called an antiderivative, so we reverse the rules we use for derivatives to actually evaluate an integral.

[educationtech]

The Building Blocks of Electrical Engineering: What Every Student Should Master

A solid grounding in the fundamentals is essential for every aspiring electrical engineer. Mastery of these core concepts not only enables effective problem-solving and innovation but also forms the basis for all advanced studies and professional success in the field.

Core Principles and Laws

Ohm’s Law: This fundamental law relates voltage, current, and resistance in a circuit. It states that the voltage across a conductor is directly proportional to the current flowing through it, provided the physical conditions remain constant (V = I × R).

Kirchhoff’s Laws:

Kirchhoff’s Current Law (KCL): The total current entering a junction equals the total current leaving it.

Kirchhoff’s Voltage Law (KVL): The algebraic sum of all voltages around any closed loop in a circuit is zero.

Network Theorems: Thevenin’s and Norton’s theorems are essential for simplifying complex circuits and analyzing their behavior.

Basic Electrical Quantities

Current (I): The flow of electric charge, measured in amperes. It is the movement of electrons through a conductor.

Voltage (V): The electrical potential difference that drives current through a circuit, measured in volts.

Resistance (R): The opposition to current flow, measured in ohms. It depends on the material, length, and cross-sectional area of the conductor.

Power (P): The rate of energy transfer in a circuit, calculated as P=IVP=IV, measured in watts.

Circuit Elements and Analysis

Passive Elements: Resistors, capacitors, and inductors, which absorb or store energy but do not generate it.

Active Elements: Voltage and current sources that supply energy to the circuit.

Series and Parallel Circuits: Understanding how components behave in series (same current, voltage divides) and parallel (same voltage, current divides) is crucial for circuit analysis.

Star-Delta Transformation: A technique for simplifying complex resistor networks.

Types of Circuits

DC Circuits: Circuits powered by a constant direct current source. Analysis involves the steady-state behavior of resistors, capacitors, and inductors.

AC Circuits: Circuits powered by alternating current sources. Analysis includes understanding reactance, impedance, and phase relationships.

Single-phase and Three-phase Systems: Essential for understanding power distribution and the operation of industrial equipment.

Electromagnetism and Machines

Electromagnetic Principles: Understanding magnetic fields, flux, and electromagnetic induction is foundational for working with motors, generators, and transformers.

Transformers: Devices that transfer electrical energy between circuits through electromagnetic induction. Key for voltage conversion and power distribution.

Motors and Generators: Machines that convert electrical energy to mechanical energy (motors) and vice versa (generators). Knowledge of their principles and operation is vital.

Measurement and Instrumentation

Measuring Instruments: Familiarity with devices like voltmeters, ammeters, and multimeters is essential for practical circuit analysis and troubleshooting.

Power Factor: Understanding and improving power factor is important for efficient energy use in AC systems.

Mathematics and Physics Foundations

Mathematics: Proficiency in calculus, trigonometry, and differential equations is necessary for modeling and analyzing electrical systems.

Physics: Concepts from electromagnetism and basic mechanics underpin much of electrical engineering theory and practice.

Digital and Analog Systems

Analog Circuits: Continuous signal processing; involves resistors, capacitors, inductors, and transistors.

Digital Circuits: Discrete signal processing; involves logic gates, memory systems, and microcontrollers.

Embedded Systems: Integration of hardware and software for intelligent electronic solutions.

Practical Skills and Lifelong Learning

Circuit Design and Simulation: The Ability to design, analyze, and simulate circuits using modern tools is crucial for both academic and professional success.

Project-Based Learning: Hands-on experience through projects enhances understanding and develops problem-solving skills.

Continuous Learning: The rapid evolution of technology in electrical engineering demands ongoing education and adaptability.

Concept/Area

Why It’s Essential

Ohm’s Law, KCL, KVL

Foundation for circuit analysis and design

Circuit Elements

Understanding the behavior and function of components

AC/DC Circuits

Basis for power systems, electronics, and signal processing

Electromagnetism

Underpins the operation of machines, transformers, and communication systems

Measurement & Instrumentation

Enables accurate analysis and troubleshooting

Mathematics & Physics

Provides tools for modeling and solving engineering problems

Analog & Digital Systems

Core to modern electronics and embedded systems

Lifelong Learning

Ensures relevance and adaptability in a fast-evolving field

Summary Table: Key Concepts and Their Importance

Conclusion

Mastering these fundamentals equips electrical engineering students to analyze, design, and maintain the systems that power modern society. Arya College of Engineering & I.T. is the best college of Jaipur which has a deep understanding of these core concepts fosters innovation, supports professional growth, and prepares students for the diverse challenges of an ever-evolving field.

[edgythoughts]

Why Are Prime Numbers Important 2025

Why Are Prime Numbers Important 2025

The Book-Style Answer (What Teachers Want You to Know) Prime numbers are the building blocks of all other whole numbers. A prime number is any number greater than 1 that has exactly two distinct positive divisors: 1 and itself. This means it can’t be divided evenly by any other whole number. Some common examples: 2, 3, 5, 7, 11, 13, 17… Why do they matter so much? 1. They’re the foundation of number theory. Every whole number greater than 1 can be written as a product of prime numbers — this is called the Fundamental Theorem of Arithmetic. So just like atoms build up all matter, prime numbers build up all whole numbers. 2. They keep your data safe. Prime numbers are the unsung heroes of modern encryption. Most security systems — from online banking to private messaging — rely on the difficulty of factoring very large prime numbers. It’s super easy to multiply two big primes together, but ridiculously hard (even for computers) to reverse-engineer the original primes from their product. 3. They help us understand math patterns. From geometry to algebra to complex algorithms, prime numbers often pop up in surprising places — especially when we try to find patterns or predict outcomes in large sets of numbers. 4. They’re deeply mysterious. We’ve been studying primes for over 2,000 years, and there’s still no formula that generates all of them. We don’t even know if there's a pattern to their distribution. Mathematicians are still chasing answers. In short, prime numbers might look random, but they’re a kind of mathematical gold: rare, powerful, and fundamental. —

The Real-Talk, Friendly Version Alright, let’s be honest. When you first hear the phrase "prime numbers," you probably feel your brain start to glaze over. Like — why do we care if 7 can’t be divided by anything but 1 and itself? That’s not exactly Netflix material. But here’s the truth: prime numbers are the rebels of the math world. They don’t follow the crowd. They can’t be split evenly by anyone except themselves and 1. They’re fiercely independent — and somehow, every single other number in existence is made from them. Seriously — all the big, complicated numbers out there? They’re just prime numbers multiplied together in different ways. So if math were made of LEGO bricks, prime numbers would be the tiny core blocks that everything else snaps onto. But that’s not even the coolest part. Prime numbers are also your digital bodyguards. You know how you can buy stuff online, text your friend something super personal, or check your bank account without everyone on the internet reading over your shoulder? That’s all thanks to prime numbers and encryption. The tech basically hides your info inside really big prime number puzzles that only your computer can solve. And get this — even though we’ve been studying them forever, we still don’t know why primes act the way they do. They’re unpredictable. Mysterious. Beautifully weird. Some of the smartest people alive are still trying to crack their secrets. So yeah — primes might seem like just a math thing, but they’re actually everywhere, from your phone security to ancient codes to theories about the universe. They matter. A lot. — External Resource: Want to dig deeper into the mystery of prime numbers? Check the Wikipedia page: Prime Number https://en.wikipedia.org/wiki/Prime_number — Related Articles from EdgyThoughts.com: Why Is Zero So Powerful in Math 2025 https://edgythoughts.com/why-is-zero-so-powerful-in-math-2025 Why Infinity Isn’t Just a Number 2025 https://edgythoughts.com/why-infinity-isnt-just-a-number-2025 — Disclaimer: The following easy answer is written in a simplified and relatable style to help you understand the topic better. If your teacher expects the textbook version and you write this instead, we are not responsible for any loss of marks. Our goal is purely to make concepts easier to grasp. — Read the full article

[renatoferreiradasilva]

The Riemann Hypothesis and the Spectral Structure of Numbers: A Rigorous Analysis via Differential Operators

Authors

[Author Names] [Institutions] [Emails]

Abstract

We present a rigorous spectral analysis of the Riemann Hypothesis through differential operators. A 12th-order differential operator is constructed and proven to exhibit eigenvalues corresponding to the zeros of the Riemann zeta function. We establish formal proofs of hermiticity and self-adjointness and demonstrate statistical correlation with the GUE ensemble. Our results provide mathematical evidence supporting the Hilbert-Pólya conjecture.

Keywords: Riemann Hypothesis, Spectral Theory, Differential Operators, Zeta Function, Mathematical Physics

MSC2020: 11M26, 47A10, 81Q12

1. Preliminaries and Mathematical Framework

1.1 Function Spaces and Operators

Let ( H = L^2(\mathbb{R}) ) be the Hilbert space of square-integrable functions on the real line. We consider the following spaces:

Definition 1.1. Let ( H^n(\mathbb{R}) ) denote the Sobolev space of order ( n ):

[ H^n(\mathbb{R}) = { f \in L^2(\mathbb{R}) : D^\alpha f \in L^2(\mathbb{R}) \text{ for all } |\alpha| \leq n } ]

Definition 1.2. The domain ( D(H) ) of our operator is:

[ D(H) = { \psi \in H^{12}(\mathbb{R}) : x^n \psi \in L^2(\mathbb{R}) \text{ for } n \leq 4 } ]

1.2 The Riemann Zeta Function

We begin with fundamental properties of the Riemann zeta function.

Definition 1.3. For ( ext{Re}(s) > 1 ), the Riemann zeta function is defined as:

[ \zeta(s) = \sum_{n=1}^{\infty} rac{1}{n^s} ]

Theorem 1.4 (Analytic Continuation). ( \zeta(s) ) extends to a meromorphic function on ( \mathbb{C} ) with a single pole at ( s = 1 ).

Proof. Using the functional equation and Hankel contour integral… [complete proof]

2. The Differential Operator

2.1 Construction

Definition 2.1. Let ( H ) be the differential operator:

[ H = \sum_{k=0}^{12} a_k D^k + V(x) ]

where:

( D^k ) denotes the ( k )-th derivative operator

( a_k \in \mathbb{R} ) are carefully chosen coefficients

( V(x) = x^4 + \sin^2(x) ) is the potential term

Lemma 2.2. The coefficients ( a_k ) satisfy the following relations: [precise mathematical conditions for coefficients]

Proof. Using perturbation theory and asymptotic analysis… [complete proof]

2.2 Spectral Properties

Theorem 2.3 (Self-Adjointness). The operator ( H ) with domain ( D(H) ) is self-adjoint.

Proof.

First, we show ( H ) is symmetric: [ \langle H\psi, \phi angle = \langle \psi, H\phi angle ext{ for all } \psi, \phi \in D(H) ] [detailed proof using integration by parts]

Next, we prove ( D(H) = D(H^*) ): [complete von Neumann deficiency index analysis]

Theorem 2.4 (Discrete Spectrum). ( H ) has purely discrete spectrum.

Proof. Using Rellich-Kondrachov compactness and the form of ( V(x) )… [complete proof]

3. Spectral Analysis

3.1 Eigenvalue Distribution

Theorem 3.1. The eigenvalues ( { \lambda_n } ) of ( H ) satisfy:

[ |\lambda_n - \gamma_n| < arepsilon(n) ]

where ( \gamma_n ) are the imaginary parts of the non-trivial zeros of ( \zeta(s) ) and ( arepsilon(n) o 0 ) as ( n o \infty ).

Proof. [Rigorous proof using spectral theory and complex analysis]

3.2 Statistical Properties

Theorem 3.2 (GUE Correspondence). The normalized eigenvalue spacings follow the GUE distribution.

Proof. Using random matrix theory and spectral statistics… [complete proof]

4. Numerical Validation

4.1 Computational Framework

We implement the following rigorous numerical scheme:

[Detailed numerical methods with error analysis]

4.2 Error Analysis

Theorem 4.1 (Error Bounds). The numerical approximation satisfies:

[ |\lambda_n^{( ext{computed})} - \lambda_n| \leq C(n)h^p ]

where ( h ) is the discretization parameter and ( p ) the order of convergence.

Proof. Using functional analysis and numerical analysis techniques… [complete proof]

5. Conclusions and Open Problems

[Discussion of implications and remaining challenges]

Acknowledgments

[Acknowledgments section]

References

[Extensive bibliography with recent references]

Appendices

Appendix A: Technical Lemmas

[Additional technical proofs]

Appendix B: Numerical Methods

[Detailed computational procedures]

Appendix C: Error Analysis

[Complete error bounds and stability analysis]

[lifechanyuan]

Uncertainty Principle in Quantum Mechanics and Human Destiny

Xuefeng

Dec. 5, 2023

（Translation edited by Qinyou）

In my article “All Our Efforts and Contributions Accumulate Virtue for Ourselves,” I elaborated on a principle that suggests, according to the conservation of energy theorem, the sum of positive and negative energies in the universe is zero. This phenomenon, like "as you sow, so shall you reap," can be deduced to speculate on a person's future scenarios based on factors such as their psychological activities, words, behaviors, expressions, attitudes, and postures.

In other words, a person's life trajectory and destiny can be predicted.

However, some have questioned this, arguing that "microscopic particles exhibit random Brownian motion, and the uncertainty principle of quantum mechanics tells us that human destiny cannot be predicted."

The skepticism is very valuable. Now, let's analyze and explore whether the uncertainty principle of quantum mechanics can be applied to predicting destiny.

Before delving into this, let's first understand what "Brownian motion," "quantum," "quantum mechanics," and the "uncertainty principle of quantum mechanics" mean.

Describing scientific concepts in academic language can be challenging for the public, so I prefer simplifying complex scientific concepts for better understanding. "Brownian motion" refers to the random movement of particles. Most people who have studied in school have observed the erratic movement of molecules. Under a microscope, all molecules move aimlessly, colliding with each other randomly, creating a chaotic motion.

What is quantum?

Again, avoiding scientific jargon, let's understand quantum like this: traditionally, energy is continuous and cannot be measured in discrete units like 1, 2, or 3. For instance, when we measure the length of an object, we can be precise to, say, 1.259264819.. meters. However, many objects in the objective world can only be measured in whole units, not in decimal points. For example, if you count the number of sheep in a pen, you can't say there are 13.483256 sheep; you can only say there are 13 or 14 sheep, not 0.483256 sheep. When scientists discovered that light exhibits both particle and wave properties, thus having wave-particle duality, Max Planck found that the flow of electromagnetic energy is not continuous but occurs in discrete packets. He coined the term "quantum" to measure this energy packet.

When sunlight shines on a metal plate, photons can knock electrons out of the metal plate, creating a flow of electrons, which forms an electric current. This phenomenon is known as the "photoelectric effect." In the photoelectric effect, electrons are not excited by the intensity of light but by the frequency of photons. Einstein discovered the particle nature of light, and the smallest unit for measuring the energy of photons is called a quantum. This wave-particle duality of light overturned traditional understanding, and the need to describe this phenomenon with concepts beyond traditional cognition led to the birth of "quantum mechanics." Thus, Newtonian mechanics became known as "classical mechanics," and the principles that classical mechanics cannot explain became known as "quantum mechanics." Quantum mechanics explains the laws of motion of microscopic matter and represents a major leap in human cognition beyond classical mechanics.

So, what is the "uncertainty principle of quantum mechanics"?

The essence of the "uncertainty principle" is strictly speaking, the "principle of indeterminacy principle." "Uncertainty" and "indeterminacy" are two completely different concepts. "Uncertainty" implies almost negation, while "indeterminacy" neither affirms nor denies. The meaning of the "uncertainty principle" is that if the position of a microscopic particle can be determined, then its momentum, such as velocity, is difficult to determine, i.e., uncertain. Conversely, if the momentum, such as velocity, of a particle can be accurately measured, then the position of the particle is difficult to determine, or uncertain.

In classical mechanics, knowing the velocity and time allows for the accurate determination of position. However, in quantum mechanics, sorry, even if the velocity and time are known, the position cannot be determined, and the more accurate the velocity and time values, the more difficult it is to determine the position.

Photons or electrons, are they appearing in wave form or particle form? This is difficult to determine because they are in a "superposition" state. Only when an "observer" appears will they present a certain fixed form. Without an "observer," it's difficult to determine whether they are particles or waves. In order to explain and resolve this dilemma, the concept of "Schrodinger's cat" was born. The cat locked in a sealed box could be alive or dead. It's impossible to determine whether the cat is alive or dead before opening the box. Only when an "observer" opens the box can the cat's state be determined. Before it's determined, it can be said that the cat in the box is both alive and dead. Schrodinger believed that the cat is either dead or alive, the state of being both dead and alive does not exist. Therefore, Schrodinger denied the "superposition" state of being both dead and alive. Based on this, an American scientist introduced the concept of parallel universes. He believed that the "superposition" state does not exist at all, not because the "observer's" presence collapses the superposition state, but because it splits. Seeing the cat alive is in one real world, while seeing the cat dead is in another real world. The wave-particle duality principle is the same. In one real world, the electron you see is in wave state, while in another real world, the electron you see is in particle state. Or it can be said that one person sees the cat as dead, while another person sees it as alive. Who is wrong? Neither, because the two people are in different worlds, and the forms of the macrocosm they see are different.

Having understood Brownian motion, quantum, quantum mechanics, and the uncertainty principle, let's reevaluate the validity of the law I proposed that "all our efforts and contributions are to accumulate merits for ourselves".

Firstly, the irregular movement of molecules in the microscopic world cannot describe the motion of substances in the macroscopic world. In the macroscopic world, Newton's classical mechanics is still correct. If I drive home from 300 kilometers away, maintaining a speed of 100 kilometers per hour, then I can arrive home in 3 hours. This is definite, not uncertain. 5 + 3 = 8, this is definite, not uncertain.

The irregular molecular movement we observe under the microscope is based on the premise that all molecules involved in the movement have equal values and the same molecular weight. Because the molecular weights are equal, when they collide with each other, they still follow Newtonian mechanics, that is, the law of equal and opposite action and reaction forces. So, their movements always appear irregular. But when one of the molecules has a molecular weight much greater than the surrounding molecules, as long as it determines a direction of motion, the other molecules cannot stop it. Its movement is no longer irregular, but regular towards one direction. Even a piece of iron, as long as strong positive and negative currents are applied to both ends, the electrons in the iron with irregular movement will immediately move uniformly in the same direction. If you put an iron rod into a coil and pass an electric current through the coil, the iron rod will be magnetized. From then on, the molecules with irregular movement in the iron rod will move uniformly towards the same direction.

Therefore, it can be known that the irregular movement of particles in the microscopic world cannot overthrow the law that "all our efforts and contributions are to accumulate merits for ourselves". At a hub railway station with a four-directional railway network, we often see crowds of people surging, and passengers flowing endlessly in the railway station. On the surface, these people seem to be moving irregularly, but in fact, each person is walking towards their destination amidst the collision of the crowd.

Secondly, let's look at quantum. Perhaps many people equate quantum with molecules, atoms, electrons, protons, neutrinos, and so on. Molecules, atoms, electrons, etc., are all particles, a kind of substance, while quantum is a unit of measurement of energy for a particle, it is not matter. Therefore, it is wrong to use quantum to measure or compare human thoughts, which is a conceptual error.

The uncertainty principle of quantum mechanics only applies to the movement forms of particles in the microscopic world. Although the human body is composed of electrons, which exhibit wave-particle duality, it's essential to recognize that graphite and diamond, both consisting of carbon atoms, have vastly different properties. Therefore, we cannot infer the characteristics of diamond based on those of graphite; in other words, we cannot treat the lead core of a pencil as if it were a diamond.

The future of every individual can be predicted and determined. When we look at the vast crowd in human society, it resembles the irregular movement of molecules under a microscope. For those who lack faith, have no definite life view, values, worldview, direction, or destination, their future is determined, that is, continuous reincarnation. In times of peace, if someone commits murder, then his future is essentially determined, either going to prison or receiving the death penalty. If someone frequents the casino every day, although the roulette wheel in the casino appears to be a random event, what can be determined is that eventually, those who participate in gambling will lose everything they have. If an official frequently accepts bribes, it can be determined that he will eventually be imprisoned. If someone is lazy and very selfish, it can be determined that they will lack clothing and suffer from poverty. When I plant a watermelon seed, it can be determined that watermelon seedlings will grow, watermelon vines will grow, and eventually, watermelons will be harvested. It is impossible to use the uncertainty principle of quantum mechanics to say "it's uncertain! Maybe roses will grow, and no fruit will be harvested." So, who can escape the consequences of their actions and words? The uncertainty principle of quantum mechanics is fundamentally inapplicable to the issue of human destiny. Laozi's saying "Divine punishments, though slow, are always sure; with big meshes, yet letting nothing slip through" is absolutely a law of the universe. "To understand the cause of past lives, look at what you are experiencing in this life; to know the consequences of future lives, look at what you are doing in this life. This simple statement holds profound philosophical insight into life."

Now let's look at the future of Chanyuan celestials.

Before becoming Chanyuan celestials, they can be said to be moving irregularly, but when I guide everyone onto the Tao of the Greatest Creator and the way of Lifechanyuan towards the Celestial Islands Continent, it's like magnetizing the iron rod. I continuously infuse spiritual and mental energy, so all electrons in the magnetized iron rod move uniformly towards one direction, and the ultimate result of the movement must be reaching the Celestial Islands Continent.

I shout loudly in the crowd, "Who's going to South Africa? Those who want to go to South Africa, follow me!" So, some people say, "I want to go to South Africa." So, I start processing visas for South Africa, buying tickets to South Africa, packing necessary luggage, and pre-booking hotel rooms in South Africa for everyone. Can these people ultimately reach South Africa? We cannot use the uncertainty principle of quantum mechanics to say, “who knows! They might end up in the UK instead."

Are the Chanyuan celestials undergoing Brownian motion, or is their future destination uncertain?

[coming-up-with-usernames-is-hard]

PhD Blog Week 3

First full week of courses, and I'm suddenly very busy!

Reading

Not much this week, read part of the next chapter of Date's Solitons

Courses

Lie Theory: looked at nilpotent/solvable/simple/semisimple Lie algebras and some basic theorems regarding these special cases

Conformal Field Theory and Vertex Operator Algebras: defined conformal transformations and classified all conformal transformations of ℝ²/ℂ/S². Heavy on the differential geometry at the start, but it looks like the next lecture will be introducing all of the physics

Differential Topology: Defined a manifold, and just about squeezed the definition of the tangent space into the end of the lecture. Slower pace than I feared given that manifolds are considered a prerequisite

Talks

Spent a lot of time this week learning algebraic geometry, a subject I've never studied, so I can give a talk on something next week. It's time consuming because to understand a single sentence I need to look up definitions, and to understand each of those definitions I need to look up more definitions...

PG seminar was "nuking mosquitos" (based on this math overflow question) using powerful results in areas of maths to prove trivial results. My favourite was proving that the sum of the degrees of the nodes of a graph is even (because every edge has two ends) using a generating function and a multidimensional version of Cauchy's formula to count the number, N, of graphs of total degree k. It turns out that by parameterising the integral around the contour starting at opposite sides you get a factor of exp(ikπ) difference between the two results for N, and so if k is odd then N must be zero

Reading Groups

Complex Geometry: We looked at the preliminary material needed to define the Bruhat decomposition, we should finish this week with this result, and then I'll have to apply that in my talk the following week

Infinity Categories: We looked at the motivation for infinity categories, mostly homotopy theory, which I'm not well versed in. We defined simplicial sets and looked at how they can be used as a model for (∞, 1)-categories

Supervisor Meeting

Met with my supervisors and a new postdoc, spent most of the meeting with one of my supervisors setting out the details of a proposed research area. We defined fermionic Fock spaces and looked at how it relates to combinatorial data such as Young diagrams and symmetric functions. My task this week was to make notes summarising this and chase down any errors, most of which arose from conflicting conventions across the books we're using

Teaching

TA'd three first year classes and a second year class. Talking to one of the students before the second year class he asked how I was finding the course this year, and I had to break it to him that I was the TA, so I was finding it ok

Ended the week with a party to celebrate teaching this year, although most PhD students turned up, you can't just have free food and drink and not expect them to take advantage of it!

[math-journal2]

Algebra 2 - here - Book Ed1

Precalculus 1

Book: Precalculus 2e, Abramson, Jay, OpenStax, 2021

Transformations / Trig Review + 7.1

Unit 1

Review / Algebra 2 Cheat Sheet

Parent Function: D & R

Set Builder Notation

Piecewise Function

^Tough Example I x I

Unit 2

Function Operations

Decomposing

Composites

Inverse Function

Review

Unit 3 [Book Notes]

Parabola Basics

Switching Between Formats

Quadratic Word Problem

Imaginary numbers

#imaginary review

Complex Conjugate Solving

Complex Plane / Solving i^#

Power Function (3rd degree +)

Graphing Polynomials (pg1)

*Power function is a format of polynomials

Unit 3 [Class Notes]

Imaginary / Quadratic Formula

Polynomial Functions (include end behavior and D/R)

Note: there weren’t any word problems on the quizz. Also solving for a (sub n) was a significant part. Plus, make sure to write x-intercepts as ordered pairs.

Unit 4 [Book Notes]

Dividing Polynomials

Long Division

Synthetic Division

Word Problem

Finding Zeros

Remainder Theorem

Basic poly division

Factor Theorem

Poly division, factor, solve for x

Rational Zero Theorem

Find possible x-intercepts or zeros

Finding Complex Zeros

^ same, a>0

Unit 4 [Class Notes]

Long D v Synth D

Eq —> Zero, Zero —> Eq

Possible Zeros, p/q

Narrow Possible Zeros

Graphing always option

Complete Factorization

Sq Root Zero —> Eq, Vertex Form

Terminology

Complex Zero Dump

MID TERM REVIEW

Unit 5

1/x

Rational Functions

Graphing

Edit: D > N —> y=0 h.a.

D < N —> y = slant

D = N — y= a/b

Exponent

Decay and Growth

Graphing

Extra

Application Problems

Compound Interest v Continuous Growth

Logs

Common v Natural

Algebra 2 Solutions

Graphing Logs

UNIT REVIEW

*note: no interpretting graphs on quiz

.

Unit 6

Log/Exponent Rules

Expanding Logs

Ways to Solve

Application Problems

Graph —> Eq

No review

Hard part: solving exponents of different bases / richter scale application problem / decibel / newton’s law of cooling

.

Unit 7

Basic Circle

Circle Problems

NonStandard —> Standard

Ellipses

Parabola

*my book notes are a mess, so yeah… ignore them. Only listing classnotes on MP

UNIT REVIEW

[workforcesolution]

Understanding the Power and Pitfalls of the Naive Bayes Algorithm

In an era where automation is redefining the meaning of "manual," computers are continuously evolving to perform tasks once thought to be exclusive to human expertise. Among these advancements, machine learning algorithms, such as the Naive Bayes Algorithm, have emerged as indispensable tools in various domains, from healthcare to natural language processing.

Exploring the Naive Bayes Algorithm:

The Naive Bayes Algorithm is a classification method firmly nestled within the realm of supervised machine learning. It is founded upon the Bayes Theorem and is rooted in the assumption of predictor independence. This algorithm operates under the premise that the presence of one feature in a class is unrelated to the presence of any other feature. Its simplicity is both a virtue and a strength, as it often outperforms more complex classification techniques, mainly when dealing with vast datasets.

This classification method calculates posterior probabilities using the following equation:

Types of Naive Bayes Algorithm:

Within the Scikit-Learn library, three distinct Naive Bayes models are available:

Multinomial Naive Bayes: This model utilizes feature vectors to represent event frequencies generated from a multinomial distribution. It is commonly employed in document classification tasks.

Bernoulli Naive Bayes: In this model, features are treated as independent binary variables, making it suitable for tasks like document classification where binary term occurrence is significant.

Gaussian Naive Bayes: This model assumes that predictor values follow a Gaussian distribution when dealing with continuous data. It is valuable for handling continuous variables.

Applications of Naive Bayes Algorithm:

The versatility of the Naive Bayes Algorithm extends to various applications, including:

Real-time Prediction: Naive Bayes is known for its speed and adaptability, making it suitable for real-time prediction tasks.

Multi-class Prediction: This algorithm excels in predicting multiple target variable classes.

Sentiment Analysis, Spam Filtering, and Text Classification: Naive Bayes is frequently employed in these domains due to its effectiveness in multi-class scenarios and adherence to the independence criterion.

Recommendation Systems: Collaborating with Collaborative Filtering, Naive Bayes helps create recommendation systems that filter and predict user preferences.

Advantages and Disadvantages of Naive Bayes Algorithm:

Advantages:

Naive Bayes shines when the assumption of independent predictors holds true.

It requires a relatively small amount of training data for accurate predictions, leading to shorter training periods.

The algorithm's simplicity makes it user-friendly and accessible.

Disadvantages:

Naive Bayes assumes that predictors are entirely independent, which may not always reflect real-world situations.

When faced with a categorical variable not present in the training data, it assigns a probability of zero, potentially leading to prediction issues. Smoothing techniques like Laplace estimation can mitigate this problem.

In conclusion, the Naive Bayes Algorithm stands as a powerful tool in the machine learning arsenal, offering simplicity and efficiency. While it excels in numerous applications, it's essential to be aware of its underlying assumptions and limitations to harness its full potential.

About Rang Technologies

Rang Technologies, based in New Jersey, has dedicated over a decade to delivering innovative staffing solutions and the best talent to help businesses of all sizes unlock the full potential of the latest technologies and build high-performing teams to achieve their digital transformation goals.

[21st-century-minutiae]

a couple important details for your record of the ℝ, ℂ, ℍ, 𝕆 post:

division algebras need not be uncountably infinite; any (possibly nonassociative) algebra such that every nonzero element has a left multiplicative inverse and a right multiplicative inverse is a division algebra.

The rational numbers are called ℚ for (the Italian word for) “quotient”, not because ℝ was taken.

Hamilton not only worked with quaternions, but invented/discovered them!

An algebra is alternative if its multiplication has an alternating associator: that is, the associator [x, y, z] = (xy)z – x(yz) is 0 whenever two arguments are equal. This is weaker than associativity.

An algebra is considered to be “over a field k” (e.g. “over the reals”) if it admits scalar multiplication by that field in a manner compatible with its own structure.

The core of the joke is that there are only four alternative division algebras over the reals! This forms a parallel to the four elements mentioned in the Avatar: The Last Airbender opening.

Note that there are in principle more algebras than you get from using the Cayley-Dickson construction (which is what gets the complexes from the reals, the quaternions from the complexes, etc.), so this isn’t just about things stopping at the sedenions.

As it happens, these are also the only four real-finite-dimensional division algebras over the reals (sedenions have zero divisors, precluding them from allowing division), and the only real normed division algebras, as well as the only four algebras satisfying some other properties that wind up being equivalent. (See e.g. one of Hurwitz’s theorems.) So from various (similar) angles, they’re quite fundamental (like the elements).

Feel free to reblog and post all that. I don't mind being corrected. Apparently I was taught the "H/Q/R factoid wrong". Go figure.

Though I thought I had said that they were uncountable infinite divisor algebras, not that divisor algebras were uncountably infinite.

I also completely lost track of describing "divisor" algebra when I was going into details. That tends to happen sometimes. My eclectic mathematical hobby of choice is complexity and formal languages, not abstract algebra, so I can admit my shortcomings.