#Euler-Lagrange Equation

[virtual-bunny]

“ HEY NERDY BOY ! ”

random headcannons about nerdjo because he turns me on

pairings: nerd! gojo x chubby fem! reader

WARNINGS: SMUT but not too detailed, some body image issues, probably some writing errors :3

a/n: i might come back every now and then if a new idea pops up in my head hehe

ARTIST CREDS: @/N06ARA ON TWITTER

✧ nerdjo who can almost cry over how beautiful he thinks you are

✧ nerdjo who stammers over his words when you wear shorts that squeeze your thighs just right

✧ nerdjo who clings onto your body and inhales your scent and gets a boner instantly as he grips your love handles

✧ nerdjo who slouches so you can give him a kiss, his glasses slidding down his nose bridge as your lips touch his cheeks, his cheek warm from him being flustered, and when you pull away, nerdjo’s eyes are almost crossed eyed as he sighs deeply

✧ nerdjo who uses your tummy as a stress ball when you sit next to him while he does his physics homework

✧ nerdjo who lays on your tummy as you play with his hair while he sleeps, saliva spilling from the side of his mouth

✧ nerdjo whose so head over heels for you that he begs you to let him carry your books and backpack so he can trail behind you to see the way your ass and thighs jiggle

✧ nerdjo who helps you with your homework and pinches your cheek, side or thighs whenever you get something wrong

✧ nerdjo who holds onto your stomach when you’re riding him, his face flushed and glasses crooked as he looks up at you with drunken eyes

✧ nerdjo who stumbles to catch up to you because he was too caught up watching you walk infront of him

✧ nerdjo who rolls his eyes when his jock friend geto teases him when he sees that gojo isn’t paying attention to lecture “she’s got you wrapped around her finger doesn’t she?” “wrapped around her thighs” nerdjo sighs without a second thought

✧ nerdjo who likes to put his hands around your tummy and gently squeeze it whenever you two are watching tv and you’re sitting between his legs

✧ nerdjo who fivershly pumps his cock at the thought of your round body jiggling when you ride him, or when you laugh, or when you walk

✧ nerdjo who makes snarky comments at you when you try to show him that “you’re way smarter than he is”

✧ nerdjo who reads out his physics notebook out loud just to make you mad because you hate physics

✧ nerdjo who goes all red whenever he brings you gifts on his way to your dorm

✧ nerdjo who doesn’t like going outside and rather stay home watching Teen Titans but still does because he knows you like to go out on dates

✧ nerdjo who used to bite his pencils out of habit but now bites your chubby hands if you’re sitting next to him as he does his homework or helps you with yours

✧ nerdjo who has to assure you he loves you and thinks you’re as beautiful as “The Euler-Lagrange Equation” (you have no idea what this means)

✧ nerdjo who puts his hands under your stomach, thighs and boobs to keep them warm

✧ nerdjo who bores you to death as he talk about quantum physics but you don’t say anything because you find it cute the way he sometimes spits by accident when he rambled and how his glasses slowly fall when’s he’s making movements as he talks

✧ nerdjo who likes to prove you wrong whenever you try to be a “smarty pants”

✧ nerdjo who softens when you go up to him while he was working on a project and tell him you’re worried about him because he looks like he hasn’t slept in three days

✧ nerdjo who mutters to himself in class when a stupid frat guy tries to answer the professors question, obviously saying the wrong answer but clearly only doing it to get laughs out of everyone. “what an idiot.” gojo grits to himself

✧ nerdjo who looks seriously shocked when he’s helping you with your homework and you get the wrong answer even though the right answer is CLEARLY right in front of your eyes “love… you seriously don’t know the answer…?”

✧ nerdjo who spends HOURS in the library to a room all by himself, books, papers, pens and pencils all scattered around the table while trying to get his work done, his hair messy and eyebrows furrowed, but when you text him saying you were gonna drop off food for him, his whole demeanor turns soft and giddy thinking about how he’s gonna be able to see you

✧ nerdjo who if he’s not doing homework or reading, is playing or watching digimon in your dorm, explaining everything he possibly can so you can catch up to the lore (you stopped listening a long time ago)

✧ nerdjo who doesn’t really talk much in class but when he does, the professors have to cut him off because gojo can talk for HOURS

✧ nerdjo who makes you sit on his lap as he codes on his computer

✧ nerdjo who can solve a rubix cube in a minute and always does when you ask him to (for your own entertainment)

✧ nerdjo whos into physics and computer science

✧ nerdjo who awkwardly puts his arm around your shoulder when the two of you are walking back to your dorm (he nearly trips)

✧ nerdjo who when you tell him a fun science fact, crosses his arms, leans back on the couch and goes “well ACTUALY-“ it’s too late to stop him, he’s already yapping to you on how the fact is wrong

✧ nerdjo who starts looking stupid now because you two have a class together when the new semester started and he can’t concentrate at all because he’s too concentrated looking at YOU

✧ nerdjo who tries to be freaky by putting his shaky hand on your upper thigh but you smack it away and he gives you a sad puppy look as he fixes his glasses, you swear you could see tears forming in his eyes

✧ nerdjo who runs to you when he finishes a prototype for whatever sciencey class he has and with full confidence says “you’re looking at the new science prodigy babe!” “uh huh” you say

✧ nerdjo who goes to the library again to study, he’s so stressed but he’s glad you came along, that’s until you went under the desk he was sitting at, undoing his belt and pulling down his pants and boxers JUST barely, hes literally gripping onto the table, face flushed hair messy crooked glasses and chest heaving trying so hard not to make it obvious you have his dick in your mouth

✧ nerdjo who makes you tag along with him to the nearest store to get the newest Digimon cards

✧ nerdjo who makes you gasp when you turn around for one second and look back to see him fighting a literal ten year old for a box set of Digimon cards

✧ nerdjo who doesn’t show you memes, but shows you reddit posts that you have no interest in looking at

✧ nerdjo who makes you sit on his face, but not to eat you out, but so your thighs can squish his face. he says that “it de-stresses him” and when you go to complain he says “it’s scientifically proven that it does”

✧ nerdjo who SOMETIMES is a cocky asshole in class, and when an acquaintance of yours who’s also in gojos’s class tells you how much of an asshole your boyfriend is, you straighten nerdjo up by riding his face nonstop to the point he’s crying because HE’S not getting any action

✧ nerdjo who you convince that overstimulating him will “de-stress him” and “make him focus better” so when you tied him up in your bed with a vibrator wrapped on the head of his cock, he’s whining, crying, squirming, eyes rolled all the way to the back of his head and pleading you to “let him do anything to you” (when you finally let him cum he tells you the next day that his focus is 97.56% better than it was the day before)

✧ nerdjo who’s so competitive when the two of you play video games he forgets you’re his GIRLFRIEND and is brutal with the insults when you loose

✧ nerdjo who’s actually really strong and likes to carry you around your dorm or outside when the two of you go for a walk. and even though you’re protesting and telling him you “don’t wanna hurt him” all nerdjo says is “just cause i’m smart doesn’t mean i’m not strong”

✧ nerdjo who likes to suck your clit while gripping your tummy

✧ nerdjo who likes to grip your fupa cause he’s weird like that

✧ nerdjo who ANALYZES your pussy and your actions whenever he’s fingering you or fucking you so he can make you feel better for the next time you two fuck (you always have a stronger orgasam each time after the other)

✧ nerdjo who bites his nails and gets told off by you (he immediately begs for your forgiveness)

✧ nerdjo who kisses your tummy whenever he lays down on your lap and turns his head so he’s looking up at you and says “you’re the most angelic thing i’ve ever seen, you know that?” he sighs contently while pushing his glasses up and giving you the stupidest toothy smile

[greenouillee]

tumblr should let me use LaTeX commands so i can inflict mathematics onto people directly like boo! euler-lagrange equation upon ye

[rottenpumpkin13]

Sorry...I noticed we didn't write the last thing Zack Googled.

Zack's Search History:

• How to swallow materia and not die

• Hairstyles chicks dig

• Is it offensive to call women chicks?

• Hairstyles women find respectable

• Does Sephiroth wear a wig

• Yearly income of a honeyboy at the honeybee inn

• honeybee inn application

• How to hypothetically blow up a mako reactor

• Euler-Lagrange equation and how it can be used to solve for the stationary action in variational calculus

• am i gay quiz

• does it count as murder if it’s technically a summon doing the killing

• where to buy a black market Masamune replica

• cute tonberry dance videos

• how to kiss a boy

• How to break the news to someone that you borrowed their sword and took it on a mission to prove that it can be used effectively and not be damaged, but then you lost it and now you cant find it and not die

[mathematics-official]

For the math asks: 57, 68, and 72

(Idk if this is how I’m supposed to ask them, so ignore this if not)

57. I was just kinda created like this, idk what to tell you -_-

68. In a way, I already have all of mathematics on my "skin" :3

72. Yeah I like that part of me :3

57. I think I started math because it was unambiguous, beautiful, and I had a gift :]

68. Yes, some day I want Euler's equation (in my pfp) and Euler-Lagrange equation

72. Yeah they're awesome!

[aedislumen]

26 for the ask game （╹◡╹）

26. Forgotten hero everyone should know about

This could have been a perfect occasion to talk about Claude-Antoine Prieur again, but given that I plan to devote him many future posts on my blog, I thought it would have been more appropriate to use this ask to share my knowledge about an important and unfortunately still rather unknown STEM personality, who truly inspired me when I was a young student. I'm referring to Sophie Germain.

Born in Paris in 1776, Sophie was one of the rare mathematiciennes of the 18th-19th century. She had her first approach with mathematics during the days of the storming of the Bastille, when it was too dangerous for a young 13 years old girl to go outside. To pass the time, she turned to her father's library and a book named "Histoire des mathématiques" by Jean-Étienne Montucla captured her interest. The story of Archimedes narrated in the book fascinated her deeply, eventually leading her to start studying mathematics on her own through the works by famous mathematicians like Euler, Newton, Cousin. Her interest and dedication to the discipline was so strong, that during winter, when her parents denied her warm clothes and a fire in her bedroom to prevent her from studying she kept doing it anyway despite the cold; at the time maths wasn't considered appropriate as a studying discipline for a woman.

When the Polytechnic school opened in 1794, women couldn't attend, but the policy of the school allowed to everyone, who asked for them, notes of the lectures. She requested them under the pseudonym of Antoine-Auguste Le Blanc, a former student who had dropped out. Given that, as a student of the Polytechnic school, one was expected to send written observations about the lectures - a sort of homework - Germain wrote and sent hers to Joseph-Louis Lagrange, one of the teachers and renowned mathematician. The latter was so positively impressed by her essays that requested a meeting with the brilliant student LeBlanc, who unexpectedly had improved so much. She was then forced to reveal her identity. Lagrange was pleasantly surprised to realize Monsieur Le Blanc was in reality a young and talented woman and decided to support her, becoming her mentor.

One of her most noteworthy contribution to mathematics was in number theory, where she proved a special case of the so-called Last Fermat's Theorem (1), which has remained one of the hardest mathematical theorems to prove for more than three centuries and whose final proof was actually found only in 1994 by Andrew Wiles. Other important works of hers include treatises on elastic surfaces, one of which, Recherches sur la théorie des surfaces élastiques, awarded her a prize from the Paris Academy of Science in 1816.

Although she often faced prejudice for being a woman, Germain was praised and also supported by various well-known mathematicians of the time. Some of them include the aforementioned Lagrange, Legendre, who thanks to her work on the Fermat's theorem, was able to prove it for another special case; Cousin himself, Fourier, who managed to grant her the permission to follow the sittings held at the Paris Academy of science and last, but obviously not least, the great Gauss, who after Germain's death advocated for giving her an honorary degree in mathematics.

Notes

(1) In short, the Last Fermat's Theorem asserts that for n > 2 there are no integer solutions to the following equation:

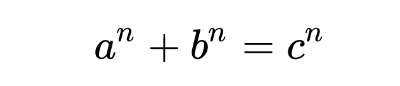
with a, b, c being positive integers. Sophie Germain proved the theorem for all numbers n equal to a prime p, so that 2p + 1 is also prime. The whole thing is much more complex that how I explained it, my aim was to write down a simple intoduction. If you want to read more about that I recommend you this link.

[minmin-vs-physics]

wow emergency post but veritasium posted a video on Hamilton's Principle, and it's a brilliant video as always.

im glad they made a video on this bc the principle of least action is one of my favourite things ever, but it's not very glamorous, so i don't think it gets adequate appreciation outside physics.

anticlimactic but, my favourite undergrad physics class was lagrangian and hamiltonian mechanics. it's an unassuming class, but i think there's a lot to learn from it. after all, the machinery introduced in the class like lagrangians are used everywhere from quantum field theory to general relativity.

BUT, veritasium explains much better than i ever can. highly recommend.

i cannot articulate the beauty of the Euler-Lagrange equations. maybe ill do a post on it sometime.

[motsimages]

I am reading The Fabric of Civilisation, and it speaks about how intertwined fabrics and science and humanities are and today I am translating about a knitting machine and it mentions the Lagrange-Euler equations, and I don't know what that is but I remember the chapter about maths and looms and how it actually is harder than it seems and very mathematical and I don't know. This machine that I can't even imagine is suddenly more interesting.

[visual-calc]

Trick or treat !!!!!!!

- homoskedasticity anon

(Also dunno if my ask the other day got eaten by tumblr. If it did then this sign off will not make much sense lmao)

You get the Euler-Lagrange equation! One of Euler’s other results, and fantastically useful for figuring out the equations of motion of complicated systems. Not so spicy on its own, but the mathematics can get quite complicated in a hurry when applying it.

[dat-physics-gal]

I cast the Euler-Lagrange equation! A powerful divination, that can predict trajectories of anything you want: objects, phenomena, stock prives, etc.

[mathemadept]

Pre Christmas Exam Vibes

Academic, Physics (Classical Mechanics): Basic Lagrangian Overview

NB: none of this should be taken as any type of academic resource, I'm still just in my second year of a 4 year theoretical physics degree. The information in this post might have errors, if there are glaring mistakes I'd appreciate any feedback.

The latex wont display correctly unless you read the post from here

Exams are just around the corner, days are getting shorter, and there's still so much revision left for me to do by the end of this week. The intensity and density of material this term is much greater than last year. Even though one can't truly devise a measurement of intensity, it definitely feels like there has been a geometric increase. So far this semester I have taken classes in 4 subjects from the school of physics and 3 from the school of mathematics.

I have a feeling the majority of my time until the day exams start is going to be spent self learning material I may have missed in lectures throughout the semester. As a STEM student, the only way to truly improve is to do as many practise problems as you can. I know this. I am fully aware of this fact. Nevertheless I find it increasingly difficult to initiate studying.

I'm procrastinating at the moment so this post is just going to be a small info dump of some ACM.

Advanced Classical Mechanics and the Lagrangian

so far this year the most difficult subject I've had to wrap my head around has been Advanced Classical Mechanics. The course this semester has consisted mostly of an introduction to the Lagrangian formulation of classical mechanics, a surprisingly old study but with many innovations in the field having occurred only during the 20th century. Noether's Theory, which connects symmetries in the Lagrangian with conservation laws, is perhaps the most glaring example of the modern developments that took place during the beginning of the last century.

The maths involved in the course is pretty simple/ rudimentary, just some basic linear algebra for harmonic oscillators and some single and multivariable calc ( all stuff covered last term). The most difficult part of ACM so far has just been how different it is to Newtonian mechanics. In some sense the mathematical formalism makes it easier: there is less to remember and the majority boils down to constructing a valid expression for the lagrangian, but it takes more creativity to analyse a question correctly.

It is interesting to note that Lagrangian mechanics is a more fundamental idea/representation of the universe than Newtonian physics, in fact The entirety of Newtonian dynamics can be seen as a specific case of the more general Lagrangian formulation. I say this as the concept of the Lagrangian is not restricted to macroscopic dynamical systems but also extends to relativistic and quantum mechanical interactions.

Lagrangian Mechanics

Lagrangian mechanics, whose basis lies in the principle of least action, is such an incredibly powerful tool. It has honestly become one of my favourite concepts in physics so far due to its simplicity, generality and conceptual beauty. With the Lagrangian and implementation of the Euler Lagrange equation you can derive the equations of motion of a system, combining with noether's theory we can also find conserved quantities of the system. Of course, the most difficult part of the Lagrangian mechanics is finding the Lagrangian associated with a particular system.

what is the Lagrangian anyways?

any physical system has an associated function called the Lagrangian which can be expressed as the difference between the kinetic and potential energy of the system. More formally, the Lagrangian is the function between two points in the co-ordinate space such that the action, defined as $S=\int_{t_1} ^{t_2}f(\vec{q}, \dot{\vec{q}},t)\operatorname{d}t$ is stationary. In other words, the Lagrangian,$L$, is a function of $q,\dot{q},t$ such that the variation of the action is 0. Mathematically, this can be expressed as $$\delta S= \delta \int_{t_1} ^{t_2}L\operatorname{d}t=0$$

It is also found that for a specific system, the Lagrangian is the same as the difference between the kinetic and potential energies of the system. $$ L = T-V $$

In nature, all systems seek take the path of least action from one point of their configuration space to another. The Lagrangian is only a specific case of a variational calculus problem where the quantity to be minimised was the action and the variable of integration is time. The same principle can be used to find a function that minimises any quantity with respect to some boundaries that are kept fixed. Good examples of the more general variational problems/principle (is/ can be used to find) the equation of the brachistochrone, the curve which allows for the fastest descent of a ball acting only under gravity, or the surface of a bubble. In each case the "action" (the quantity to be minimised) is different. For the brachistochrone the action takes the form of time, representing the time of descent from some initial point $(x_i,y_i)$ to some other final point $(x_f,y_f)$. In the case of a bubble or film of soap around a wire mesh, the quantity to be minimised is the potential energy.

Euler Lagrange Equation and Equations of Motion

Once the Lagrangian is determined for a system with coordinates $\vec{q} = (q_1,q_2,\dots,q_n)$, we can use the Euler Lagrange equation to determine the equations of motion of the system.

the derivation for the Euler lagrange equation is straightforward but lengthy so I will simply state the equation without the derivation. Explicitly, the Euler Lagrange equation for a Lagrangian, $L$ with generalised co-ordinates $q$ is given by

$$\frac{\partial L}{\partial q} = \frac{\operatorname{d}}{\operatorname{d}t} \frac{\partial L}{\partial \dot{q}}$$

where the partial derivative $\frac{\partial L}{\partial \dot{q}}$ is called the conjugate $q$ momentum, $p_q$.

there is of course so much more to cover in Lagrangian mechanics, but this post is already getting quite long. I might make another post later and continue with some more basic concepts. For now, though, I am signing off.

[miguelmarsmars]

November 25th, 2023. Postales desde el limbo.

Markers on paper. 18×13 cm.

Euler-Lagrange Equation

Sierpiński Carpet

Physics of the Universe

[cant-afford-lobotomy]

Image description: A set of images on a white background with overlaid black sans-serif text. Above, the title reads "Come study PHYSICS" "totally a real science and (clumsily underlined in red) not magic!" The exclamation point is clumsily added in red. "we have..."

The top left image is of a glowing radioactive rock. The text reads "Glowing death aura rock", which is scribbled out in red. Then "radioactive isotopes (has the power to level entire cities but ITS NOT MAGIC)".

The top right image consists of the circuit diagram for a full bridge rectifier, the Euler-lagrange equation, and a vector calculus identity. The text reads "THEY ARE NOT RUNES SHUT UP".

The bottom left image is of an apple on a metallic plate, hovering above a base with a wire coming from it. Overlaid white text reads "it's not levitation it's [gap] uhhhh magnets".

The bottom middle image is a monochrome image of a man standing next to two metal hemispheres, about the size of a large melon - the demon core experiments. Bold red text reads "NOT a real demon" and "we are NOT SUMMONING DEMONS".

The bottom right image is of a glass device. It is bulb shaped, and largest at its top. It has many cylindrical glass projections from its bottom, which are brightly glowing blue. The main bulb also glows blue, though more dimly. It is in a dark room and has many wires protruding from it. It is a mercury arc rectifier. White overlaid text reads "what the fuck".

[truphysics]

D'Alembert's Principle

Introduction D’Alembert’s principle, named after French mathematician and physicist Jean le Rond d’Alembert, is a fundamental concept in classical mechanics. This principle extends the Newtonian mechanics to systems with constraints and allows the derivation of the equations of motion for complex systems in a generalized and systematic way. Basic Statement D’Alembert’s principle states that…

[mathematical-cheese]

What if I just dont square these trinomials

[bubbloquacious]

I feel like to lean into my theme I should learn more about minimal surfaces

[dat-physics-gal]

These are the kind of shit i might've had to calculate the motion of in theoretical mechanics. Getting war flashbacks to Lagrangians together with weird constraints trying to get solveable Euler-Lagrange equations.

The physics of balancing toys 🙃