#Principal Axis Theorem

[andranikfakirian]

Project "CompMath.AstrophysicsODEs": Early Projects, Part 2

Let's continue the series of Early Projects. The next one was from the sphere of analytical mechanics. The task was to simulate the rotational motion of bodies using quaternions. Quaternions make it possible to describe such motions quite succinctly in formulas. Special attention should be paid to modeling the Dzhanibekov effect, aka Tennis racket theorem.

P.S.: Below is a test of the operation of this simulator with a spin of the simple screw around its axis.

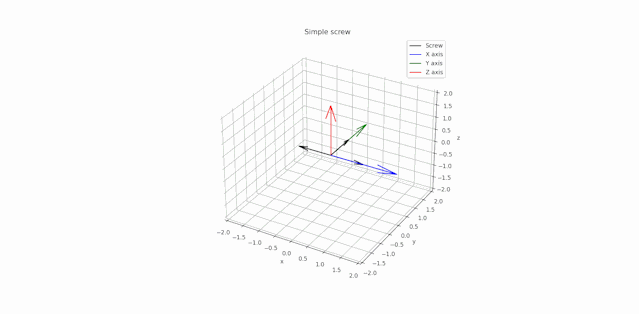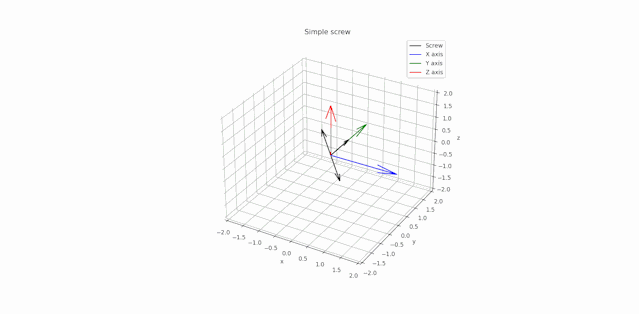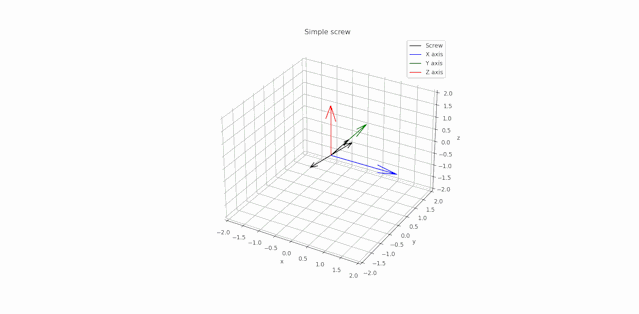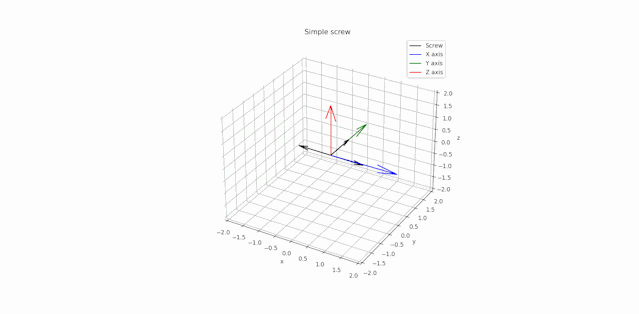
P.S.2: Here is a simulation of the Dzhanibekov effect. As it can be seen when the body have three distinct principal moments of inertia, rotation around one of the principal axes (associated with the second-order inertia moment) unstable. That's why the wing screw turns over.

[speedywonderlandtrash]

Class 8 math chapter 6 MCQ and one word questions

Class 8 math chapter 6 MCQ and one word questions

  Class 8 Math Chapter 6 Questions, Chapter 6 Math MCQ for Class 8, One-Word Questions Class 8 Math, Class 8 Math Chapter 6 MCQ, Math Chapter 6 Class 8 Questions MCQ questions 1. What is the horizontally placed number line on graph paper called? a) x-axis b) y-axis c) Base d) Hypotenuse 2. What is the vertically placed number line on graph paper called? a) y-axis b) x-axis c) Hypotenuse d) Base 3. What is the intersection point of the x-axis and y-axis called? a) Common point b) Origin c) Overlapping point d) None of the above 4. What is the first part of the coordinates of a point called? a) Abscissa b) Hypotenuse c) Base d) Both b and c 5. Which of the following points lies on the x-axis? a) (0, 1) b) (1, 0) c) (0, -1) d) (-1, 0) 6. If A(2, 3) is a point, what is its abscissa? a) 5 b) 1 c) d) 2 7. What is the ordinate of point P(5, 4)? a) 9 b) 4 c) d) 2 8. Among the points A(3, 2), B(2, 3), C(0, 4), and D(-3, -3), which is farthest from the origin? a) D b) B c) C d) A 9. Who introduced the method of representing a point's position using coordinates? a) Euclid b) Newton c) Leibniz d) René Descartes Class six || Exercise 1.1: Part - 3 10. Into how many parts can the xy-plane be divided? a) 2 b) 3 c) 4 d) 6 11. In which quadrant is the point (1, -4) located? a) First b) Second c) Third d) Fourth 12. In which quadrant is the point (-2, -3) located? a) First b) Second c) Third d) Fourth 13. What is the value of y in the second quadrant? a) Zero

b) Positive c) Negative d) None of the above 14. Which formula is used to calculate the distance between two points? a) Pythagoras theorem b) Newton’s formula c) René Descartes' formula d) None of the above Class 8 Math MCQs and Short Questions, Chapter 3 15. What is the distance between the points (1, 2) and (1, 0)? a) 2 units b) 2√2 units c) 3 units d) None of the above 16. What is the distance between the origin and the point (4, 0)? a) 2 units b) 4 units c) 3 units d) None of the above 17. What is the absolute value of the difference in abscissas for points (-1, 2) and (-3, 6)? a) -4 b) 2 c) 3 d) -3 18. If the difference in abscissas is 4 and the difference in ordinates is 6, what is the distance between the two points? a) 10 units b) 5√2 units c) √52 units d) 2 units 19. What is the midpoint of the points (x₁, 0) and (x₂, 0)? a) b) c) d) 20. What is the midpoint of the points (2, 0) and (6, 0)? a) (2, 0) b) (3, 0) c) (4, 0) d) (1, 0) 21. What is the abscissa of the midpoint of the points (-4, 0) and (6, 0)? a) 1 b) 2 c) d) -5 22. What is the coordinate of the midpoint between the origin and the point (0, -6)? a) (0, -3) b) (0, -6) c) d) None of the above 23. What is the midpoint of the points (-2, -3) and (1, 5)? a) b) c) d) 24. What is the ordinate of the midpoint of the points (-2, 4) and (4, 6)? a) -2 b) 2 c) 5 d) -5 25. What is the phenomenon of rising or falling with respect to a plane called? a) Incline b) Slope c) Both a and b d) Coordinate 26. The ratio of vertical distance to horizontal distance is called— a) Incline b) Coordinate c) Both b and d d) Overlapping line 27. The vertical distance of the upper end of a ladder is 3 units, and the horizontal distance of the lower end is 4 units. What is the slope of the ladder? a) b) 1 c) d) 4 28. Which of the following indicates the slope? a) b) c) d) Both b and c 29. What is the formula for calculating the slope using coordinates? a) b) c) d) 30. If the difference in ordinates is -8 and the difference in abscissas is 4, what is the slope of the straight line? a) -16 b) -2 c) -2 d) 2 Class 8 math profit and principal creative and one word question  31. What is the slope of the straight line formed by the origin and the point (2, 3)? a) b) c) 6 d) -3 32. What is the slope of the straight line passing through the points (-2, 5) and (1, -4)? a) -3 b) 3 c) d) 1 33. With which axis is the slope considered inclined? a) x-axis b) y-axis c) Both axes d) Both a and c 34. Which of the following is the equation of a line parallel to the x-axis? a) x = 1 b) x = 0 c) y = 2 d) y = 0 35. What is common about the points on a straight line parallel to the x-axis? a) Unequal b) Equal c) Positive d) Negative 36. If the ordinates of points are equal, with which axis will the line be parallel? a) x-axis b) y-axis c) Axis line d) Both a and c 37. What type of line is y = 3? a) Parallel to the y-axis b) Parallel to the axis line c) Parallel to the x-axis d) Both a and c 38. Which pair of points forms a straight line parallel to the x-axis? a) (-3, -3), (7, -3) b) (3, -3), (4, 4) c) (4, -6), (7, -3) d) (7, 4), (7, 7) 39. Which of the following is the equation of a straight line parallel to the y-axis? a) x = -2 b) y = 3 c) x = 0 d) y = 0 40. What is common about the abscissas of the points on a straight line parallel to the y-axis? a) Positive b) Negative c) Equal d) Unequal 41. If the abscissas of multiple points are equal, with which axis will the straight line be parallel? a) x-axis b) y-axis c) Axis line d) None of the above 42. What will be the equation of a straight line formed by five points with the same abscissa, x = -1? a) Parallel to the x-axis b) Parallel to the axis line c) Parallel to the y-axis d) None of the above 43. Which pair of points forms a straight line parallel to the y-axis? a) (4, 4), (7, 7) b) (-3, 3), (4, 4) c) (4, -6), (4, -7) d) (4, 9), (0, -7) 44. What is the equation of the straight line passing through the points (-1, 4) and (3, 1)? a) 3x + 4y + 13 = 0 b) 3x - 4y + 13 = 0 c) -3x + 4y - 13 = 0 d) 3x + 4y - 13 = 0 45. If the slope of a straight line is 𝑚 = − 2 m=−2 and it passes through the point (1, 4), what is the equation of the line? a) -2x + y + 6 = 0 b) 2x - y - 6 = 0 c) 2x + y + 6 = 0 d) 2x + y - 6 = 0 46. What is the coordinate of the intersection point of two equations? a) (6, 5) b) (5, 6) c) (6, -5) d) (-5, 6) 47. At what point does the second equation intersect the x-axis? a) (6, 0) b) (11, 0) c) (0, 6) d) (0, 11) one-word questions Question 1: What is the horizontal straight line drawn on graph paper called? Answer: x-axis. Question 2: What is the vertical straight line drawn on graph paper called? Answer: y-axis. Question 3: What is the intersection point of the x-axis and y-axis called? Answer: Origin. Question 4: What can we accurately determine using the Cartesian coordinate system? Answer: The position of various objects. Question 5: What is the mathematical method called that represents the position of a point relative to the origin using its distance and angle? Answer: Coordinate geometry. Question 6: Who introduced the coordinate system? Answer: René Descartes. Question 7: What is another name for the Cartesian coordinate system? Answer: Rectangular Cartesian coordinates. Question 8: What is the nature of numbers on the left side of the x-axis from the origin? Answer: Negative. Question 9: What is the ordinate of any point on the x-axis? Answer: Zero. Question 10: What is the abscissa of any point on the y-axis? Answer: Zero. Question 11: What is the abscissa of the origin? Answer: 0 (Zero). Question 12: Into how many parts is the xy-plane divided? Answer: Four parts. Question 13: What are the signs of the abscissa and ordinate in the first quadrant? Answer: Positive. Question 14: What is the nature of the abscissa, x, in the second quadrant? Answer: Negative. Question 15: What is the nature of the abscissa, x, in the third quadrant? Answer: Negative. Question 16: What is the nature of the ordinate, y, in the fourth quadrant? Answer: Negative. Question 17: Which formula is used to calculate the distance between two points? Answer: Pythagoras’ theorem. Question 18: What is the formula for calculating the distance between two points? Answer: Question 19: What is the distance between the points (3, 4) and (9, 7)? Answer: units. Question 20: What is the distance between the points (4, 6) and (-8, 4)? Answer: units. Question 21: What is the distance between the points (0, 0) and (3, 4)? Answer: 5 units. Question 22: What is the midpoint of the line segment joining the points (5.5, -5.5) and (-6.5, 6.5)? Answer: (-0.5, 0.5). Question 23: What is the formula for calculating the abscissa of the midpoint of two points located on the x-axis? Answer: The sum of the abscissas ÷ 2. Question 24: What is the midpoint of two points located on the x-axis? Answer: Question 25: What is the formula for calculating the midpoint of any two points? Answer: Question 26: What is the midpoint of the points (x₁, y₁) and (x₂, y₂)? Answer: Question 27: What is the midpoint of the points (4, 6) and (-8, 4)? Answer: (-2, 5). Question 28: What is the phenomenon of gradually rising or falling with respect to a plane called? Answer: Slope. Question 29: What is the ratio of vertical distance to horizontal distance called? Answer: Incline. Question 30: What is the inclination of a straight line with respect to the positive direction of the x-axis called? Answer: Slope. Question 31: What is the change in vertical distance corresponding to one unit of horizontal movement called? Answer: Slope. Question 32: What is the slope of the straight line passing through the points (0, 0) and (4, 0)? Answer: 0. Question 33: With which axis is the slope considered inclined? Answer: x-axis. Question 34: Based on position, how can the slope be categorized? Answer: Positive or Negative. Question 35: What is the slope of the line passing through the points (3, 0) and (0, 4)? Answer: . Question 36: What is common about the ordinates of all points on a straight line parallel to the x-axis? Answer: Equal. Question 37: If the ordinates of the points on a straight line are equal, with which axis will the line be parallel? Answer: x-axis. Question 38: If points with the same ordinate are sequentially connected, what kind of line is obtained? Answer: A straight line parallel to the x-axis. Question 39: The line y = 3 is parallel to which axis? Answer: x-axis. Question 40: What is common about the abscissas of all points on a straight line parallel to the y-axis? Answer: Equal. Question 41: If the abscissas of the points on a straight line are equal, with which axis will the line be parallel? Answer: y-axis. Question 42: If points with the same abscissa are sequentially connected, what kind of line is obtained? Answer: A straight line parallel to the y-axis. Question 43: The line x = a is parallel to which axis? Answer: y-axis. Question 44: If the slope is unknown, how many points are required to determine the equation of a straight line? Answer: Two. Question 45: What is the equation of the straight line passing through the points (x₁, y₁) and (x₂, y₂)? Answer: . Question 46: What is the equation of a straight line with slope m passing through the point (x₁, y₁)? Answer: Question 47: What is the equation of a straight line with slope 2 passing through the point (0, 1)? Answer: Read the full article

[penguin-ghost]

Week 4 - Running out of title ideas

It's almost the-mid semester break...??? This week has been a very meh week for me... I was rejected from my 2nd dream university (in the UK) and so I will probably (read: almost definitely) just do my undergrad in Sydney. To my surprise, I actually wasn't all that upset (?) just because so many people deferred from last year and the offer rate for my subject dropped to 10%. It’s really an incredibly tough year for applicants, especially international applicants. Oh well, life is life. Let's get back to uni life in Sydney.

Physics

We finally started learning something entirely new! Rotation of rigid bodies with angular versions of displacement, velocity and acceleration. I love the symmetry between the regular equations and the angular ones, there's something so satisfying about them. I also happened to really enjoy this week's lab, although it basically involved throwing my phone into the air 👀. Anyhow, it was interesting to find out that the phone cannot stably rotate about its x-axis (which is explained by the Tennis racket theorem).

Understanding the material has been relatively easy, but tackling problems is another story. Sometimes it is difficult to know what principals/laws/approaches to apply. I guess it all takes practice. Although I must admit, Physics often makes one feel intellectually incompetent.

Reality, Ethics and Beauty

We wrapped up the module on metaphysics, and it ended with a bang (at least for me). We discussed the two main approaches to mental states and consciousness: Dualism and Materialism along with their sub-categories.

I also picked a question for my essay: it's about free-will and higher order desires.

Next week begins the ethics part of the course, and there is substantially more reading to be done. But overall, I'm surprised by how little reading we actually do as Phil majors...

Linear Algebra

Began studying matrices and things... but so far, the content is still a rather boring... Fingers crossed 🤞🏻 things get more interesting when it comes to eigenvalues.

Calculus of One Variable

Compared to Linear Algebra, this class is significantly harder (and feels more rigorous), which also makes it much more fun. We spent a while formally defining limits with the epsilon-delta definition. It did take some time to digest although it does make intuitive sense.

p.s. I think this is actually my favourite class(?)

Introduction to Programming

What the hell.

I was pretty satisfied with my progress after the Monday lectures on lists and arrays. Then I attended my tutorial on Wednesday and my confidence level dropped straight into a deep abyss (I still haven't finished the exercises 😢). 

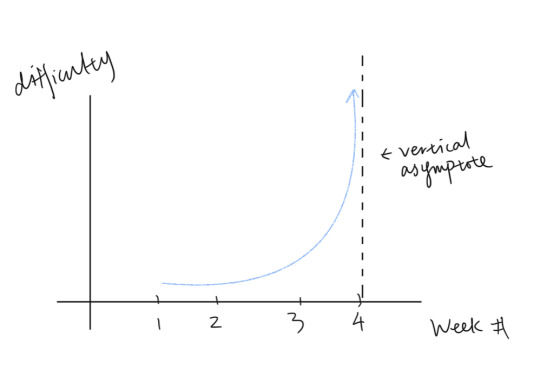
On the other hand, it feels great when I finish writing a program THAT WORKS. It's a pretty addictive feeling actually 🤦🏻‍♀️

I also tried to learn Vim, although I'm not using Vim to code yet, I am getting familiar with the keybindings in VS code (via the Vim extension). And it definitely speeds things up. I'm hoping to make the full transition during the mid-semester break, or some time in the holidays when I have more time to properly learn it.

p.s. we got our first assignment and the instruction is so damn long.

[thesciencenut]

Continuation of the earlier post.

In the earlier post, I was talking about the great mathematicians of the world. In this post, I am gonna talk about - Archimedes and Pythagoras.

ARCHIMEDES

Archimedes was the most-famous mathematician and inventor in ancient Greece. Archimedes is especially important for his discovery of the relation between the surface and volume of a sphere and its circumscribing cylinder.He is known for his formulation of a hydrostatic principle (known as Archimedes’ principle) and a device for raising water, still used in developing countries, known as the Archimedes screw. Archimedes probably spent some time in Egypt early in his career, but he resided for most of his life in Syracuse, the principal Greek city-state in Sicily, where he was on intimate terms with its king, Hieron II. Archimedes published his works in the form of correspondence with the principal mathematicians of his time, including the Alexandrian scholars Conon of Samos and Eratosthenes of Cyrene. He played an important role in the defense of Syracuse against the siege laid by the Romans in 213 BCE by constructing war machines so effective that they long delayed the capture of the city. When Syracuse eventually fell to the Roman general Marcus Claudius Marcellus in the autumn of 212 or spring of 211 BCE, Archimedes was killed in the sack of the city.

TOP QUESTIONS

What was Archimedes’ profession? When and how did it begin?

What accomplishments was Archimedes known for?

What specific works did Archimedes create?

What is known about Archimedes’ family, personal life, and early life?

Where was Archimedes born? How and where did he die?

Study how turning a helix enclosed in a circular pipe raises water in an Archimedes screw

Study how turning a helix enclosed in a circular pipe raises water in an Archimedes screw

An animation of Archimedes screw.

Encyclopædia Britannica, Inc.

See all videos for this article

Far more details survive about the life of Archimedes than about any other ancient scientist, but they are largely anecdotal, reflecting the impression that his mechanical genius made on the popular imagination. Thus, he is credited with inventing the Archimedes screw, and he is supposed to have made two “spheres” that Marcellus took back to Rome—one a star globe and the other a device (the details of which are uncertain) for mechanically representing the motions of the Sun, the Moon, and the planets. The story that he determined the proportion of gold and silver in a wreath made for Hieron by weighing it in water is probably true, but the version that has him leaping from the bath in which he supposedly got the idea and running naked through the streets shouting “Heurēka!” (“I have found it!”) is popular embellishment. Equally apocryphal are the stories that he used a huge array of mirrors to burn the Roman ships besieging Syracuse; that he said, “Give me a place to stand and I will move the Earth”; and that a Roman soldier killed him because he refused to leave his mathematical diagrams—although all are popular reflections of his real interest in catoptrics (the branch of optics dealing with the reflection of light from mirrors, plane or curved), mechanics, and pure mathematics.

According to Plutarch (c. 46–119 CE), Archimedes had so low an opinion of the kind of practical invention at which he excelled and to which he owed his contemporary fame that he left no written work on such subjects. While it is true that—apart from a dubious reference to a treatise, “On Sphere-Making”—all of his known works were of a theoretical character, his interest in mechanics nevertheless deeply influenced his mathematical thinking. Not only did he write works on theoretical mechanics and hydrostatics, but his treatise Method Concerning Mechanical Theorems shows that he used mechanical reasoning as a heuristic device for the discovery of new mathematical theorems.

Get exclusive access to content from our 1768 First Edition with your subscription.

Subscribe today

His Works

There are nine extant treatises by Archimedes in Greek. The principal results in On the Sphere and Cylinder (in two books) are that the surface area of any sphere of radius r is four times that of its greatest circle (in modern notation, S = 4πr2) and that the volume of a sphere is two-thirds that of the cylinder in which it is inscribed (leading immediately to the formula for the volume, V = 4/3πr3). Archimedes was proud enough of the latter discovery to leave instructions for his tomb to be marked with a sphere inscribed in a cylinder. Marcus Tullius Cicero (106–43 BCE) found the tomb, overgrown with vegetation, a century and a half after Archimedes’ death.

sphere with circumscribing cylinder

sphere with circumscribing cylinder

The volume of a sphere is 4πr3/3, and the volume of the circumscribing cylinder is 2πr3. The surface area of a sphere is 4πr2, and the surface area of the circumscribing cylinder is 6πr2. Hence, any sphere has both two-thirds the volume and two-thirds the surface area of its circumscribing cylinder.

Encyclopædia Britannica, Inc.

Measurement of the Circle is a fragment of a longer work in which π (pi), the ratio of the circumference to the diameter of a circle, is shown to lie between the limits of 3 10/71 and 3 1/7. Archimedes’ approach to determining π, which consists of inscribing and circumscribing regular polygons with a large number of sides, was followed by everyone until the development of infinite series expansions in India during the 15th century and in Europe during the 17th century. That work also contains accurate approximations (expressed as ratios of integers) to the square roots of 3 and several large numbers.

On Conoids and Spheroids deals with determining the volumes of the segments of solids formed by the revolution of a conic section (circle, ellipse, parabola, or hyperbola) about its axis. In modern terms, those are problems of integration. (See calculus.) On Spirals develops many properties of tangents to, and areas associated with, the spiral of Archimedes—i.e., the locus of a point moving with uniform speed along a straight line that itself is rotating with uniform speed about a fixed point. It was one of only a few curves beyond the straight line and the conic sections known in antiquity.

On the Equilibrium of Planes (or Centres of Gravity of Planes; in two books) is mainly concerned with establishing the centres of gravity of various rectilinear plane figures and segments of the parabola and the paraboloid. The first book purports to establish the “law of the lever” (magnitudes balance at distances from the fulcrum in inverse ratio to their weights), and it is mainly on the basis of that treatise that Archimedes has been called the founder of theoretical mechanics. Much of that book, however, is undoubtedly not authentic, consisting as it does of inept later additions or reworkings, and it seems likely that the basic principle of the law of the lever and—possibly—the concept of the centre of gravity were established on a mathematical basis by scholars earlier than Archimedes. His contribution was rather to extend those concepts to conic sections.

Quadrature of the Parabola demonstrates, first by “mechanical” means (as in Method, discussed below) and then by conventional geometric methods, that the area of any segment of a parabola is 4/3 of the area of the triangle having the same base and height as that segment. That is, again, a problem in integration.

The Sand-Reckoner is a small treatise that is a jeu d’esprit written for the layman—it is addressed to Gelon, son of Hieron—that nevertheless contains some profoundly original mathematics. Its object is to remedy the inadequacies of the Greek numerical notation system by showing how to express a huge number—the number of grains of sand that it would take to fill the whole of the universe. What Archimedes does, in effect, is to create a place-value system of notation, with a base of 100,000,000. (That was apparently a completely original idea, since he had no knowledge of the contemporary Babylonian place-value system with base 60.) The work is also of interest because it gives the most detailed surviving description of the heliocentric system of Aristarchus of Samos (c. 310–230 BCE) and because it contains an account of an ingenious procedure that Archimedes used to determine the Sun’s apparent diameter by observation with an instrument.

Method Concerning Mechanical Theorems describes a process of discovery in mathematics. It is the sole surviving work from antiquity, and one of the few from any period, that deals with this topic. In it Archimedes recounts how he used a “mechanical” method to arrive at some of his key discoveries, including the area of a parabolic segment and the surface area and volume of a sphere. The technique consists of dividing each of two figures into an infinite but equal number of infinitesimally thin strips, then “weighing” each corresponding pair of these strips against each other on a notional balance to obtain the ratio of the two original figures. Archimedes emphasizes that, though useful as a heuristic method, this procedure does not constitute a rigorous proof.

On Floating Bodies (in two books) survives only partly in Greek, the rest in medieval Latin translation from the Greek. It is the first known work on hydrostatics, of which Archimedes is recognized as the founder. Its purpose is to determine the positions that various solids will assume when floating in a fluid, according to their form and the variation in their specific gravities. In the first book various general principles are established, notably what has come to be known as Archimedes’ principle: a solid denser than a fluid will, when immersed in that fluid, be lighter by the weight of the fluid it displaces. The second book is a mathematical tour de force unmatched in antiquity and rarely equaled since. In it Archimedes determines the different positions of stability that a right paraboloid of revolution assumes when floating in a fluid of greater specific gravity, according to geometric and hydrostatic variations.

Archimedes is known, from references of later authors, to have written a number of other works that have not survived. Of particular interest are treatises on catoptrics, in which he discussed, among other things, the phenomenon of refraction; on the 13 semiregular (Archimedean) polyhedra (those bodies bounded by regular polygons, not necessarily all of the same type, that can be inscribed in a sphere); and the “Cattle Problem” (preserved in a Greek epigram), which poses a problem in indeterminate analysis, with eight unknowns. In addition to those, there survive several works in Arabic translation ascribed to Archimedes that cannot have been composed by him in their present form, although they may contain “Archimedean” elements. Those include a work on inscribing the regular heptagon in a circle; a collection of lemmas (propositions assumed to be true that are used to prove a theorem) and a book, On Touching Circles, both having to do with elementary plane geometry; and the Stomachion (parts of which also survive in Greek), dealing with a square divided into 14 pieces for a game or puzzle.

Archimedes’ mathematical proofs and presentation exhibit great boldness and originality of thought on the one hand and extreme rigour on the other, meeting the highest standards of contemporary geometry. While the Method shows that he arrived at the formulas for the surface area and volume of a sphere by “mechanical” reasoning involving infinitesimals, in his actual proofs of the results in Sphere and Cylinder he uses only the rigorous methods of successive finite approximation that had been invented by Eudoxus of Cnidus in the 4th century BCE. These methods, of which Archimedes was a master, are the standard procedure in all his works on higher geometry that deal with proving results about areas and volumes. Their mathematical rigour stands in strong contrast to the “proofs” of the first practitioners of integral calculus in the 17th century, when infinitesimals were reintroduced into mathematics. Yet Archimedes’ results are no less impressive than theirs. The same freedom from conventional ways of thinking is apparent in the arithmetical field in Sand-Reckoner, which shows a deep understanding of the nature of the numerical system.

In antiquity Archimedes was also known as an outstanding astronomer: his observations of solstices were used by Hipparchus (flourished c. 140 BCE), the foremost ancient astronomer. Very little is known of this side of Archimedes’ activity, although Sand-Reckoner reveals his keen astronomical interest and practical observational ability. There has, however, been handed down a set of numbers attributed to him giving the distances of the various heavenly bodies from Earth, which has been shown to be based not on observed astronomical data but on a “Pythagorean” theory associating the spatial intervals between the planets with musical intervals. Surprising though it is to find those metaphysical speculations in the work of a practicing astronomer, there is good reason to believe that their attribution to Archimedes is correct.

PYTHAGORAS

Pythagoras of Samos[a] (c. 570 – c. 495 BC)[b] was an ancient Ionian Greek philosopher and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of Plato, Aristotle, and, through them, Western philosophy. Knowledge of his life is clouded by legend, but he appears to have been the son of Mnesarchus, a gem-engraver on the island of Samos. Modern scholars disagree regarding Pythagoras's education and influences, but they do agree that, around 530 BC, he travelled to Croton in southern Italy, where he founded a school in which initiates were sworn to secrecy and lived a communal, ascetic lifestyle. This lifestyle entailed a number of dietary prohibitions, traditionally said to have included vegetarianism, although modern scholars doubt that he ever advocated for complete vegetarianism.

In the next post, I will be talking about ramanujan and shakuntala devi.

Follow me, stay tuned, next post will be uploaded soon.

[dreamonengineering]

The tennis racket theorem or intermediate axis theorem is a result in classical mechanics describing the movement of a rigid body with three distinct principal moments of inertia. Credit to @nasa Follow for more! Follow→ @dream_on_engineering @dream_on_engineering @dream_on_engineering #Project #Engineering #Electrical #Electronics If you are the copyright owner of this video and would not like to have this content featured on this channel, direct message us to have us remove it. #Tech #Dreaminengineering https://www.instagram.com/p/B_txg4aJtil/?igshid=ghknww1j77da

[longlistshort]

This is the last weekend (5/25/19) to see Vanessa German's excellent sculpture exhibition, $LANG: Short Language in Soul, at Gavlak Los Angeles.

From the press release-

$LANG is German’s first solo exhibition in Los Angeles, the artist’s native city, and her first with Gavlak. The exhibition features a body of work created by German during her recent month long residency at Aguacate in Puerto Vallarta, Mexico. Though assembled in Mexico, many of the found objects incorporated in the sculptures were sourced from the artist’s current neighborhood of Homewood in Pittsburgh, Pennsylvania - the historic black neighborhood whose residents are often faced with systemic, institutionalized racism, and violence in their daily lives.

A self-trained “citizen artist,” German explores the power of art and love as a transformative force in the dynamic cultural ecosystem of communities and neighborhoods. As the founder of the ARThouse, a community arts initiative in her own neighborhood ravaged by gun violence, German’s art extends to helping local children heal through art  making. Recently recognized as the 2018 recipient of the Don Tyson Prize, the majority of German’s $200,000 grant is going toward opening a Museum of Resilience to honor the neighborhood's large population of black single mothers. Her spoken-word performance art, influenced heavily by hip-hop, opera and the long tradition of Negro spirituals, calls attention to the epidemic of racially charged violence and advocates for compassion and empathy in daily  life. Similarly, German’s sculptural work blends spirituality, beauty, and femininity to focus  on empowering black women and girls. In a transformative way, the artist hopes that her work gives a space for positive and inclusive manifestations of love and awareness.

Born in Wisconsin, German moved to Mid-City Los Angeles at seven months old along with her five siblings and mother, Sandra German, a fiber artist and quilter. “We were makers as a way of life. We were raised by making something,” German explains about her formative years. The multi-media works assembled for $LANG explore her lived experience growing up black in Los  Angeles and how the power of art kept her alive. German writes:

As a strange, dirty, round, nappy black girl in Los Angeles, never really smelling good, or looking hair-combed & pressed, i was always inventing things that i deeply, profoundly believed had power. People made fun of me for this. i wrote poems to cure cancer. i drew and drew and drew and drew and refused to pick my pencil up from the paper until i’d driven any thought of disbelief from my mind. i was furious with these thoughts of creativity and power; that i was alive and could make *things that had the power to do *something. i believed this like a deep, deep fire. It kept me alive.

On view in the gallery are a series of 15 mixed-media assemblage sculptures using vintage tennis rackets, titled from the specific branding text on each. German’s use of rackets stems from Intermediate axis theorem, or tennis racket theorem, an effect in classical mechanics defining the  movement of a rigid body with three distinct principal moments of inertia. German explains: “Here in this work is the rigid body (black femaleness) reckoning with three distinct principal moments of inertia: Americanness; the aesthetics  of femininity (body and sex and identity), Blackness and the value in the striations of the known and unknown, and Love & Creative Power.” German utilizes historically black found objects such as hair weave and cowrie shells to adorn her hand painted portraits of black women, creating majestic and empowered presentations of a community so commonly subjected to violence and oppression in American society.

Also on view are five of German’s signature sculptures of which she refers to as “power figures,” or “tar babies.” Created by sculpting and hand painting large figures, adding a wide range of materials from feathers, glitter, seashells, plastic toys, bottle caps, vintage products, and fabric found from both Homewood and her travels. These female figures are based on traditional Congolese Nkisi Power Figure sculptures, which create protection, fend off evil spirits, and punish wrongdoers. German’s rococo meets folk power figures confront the violence of white supremacy and racism. German describes her process of assembling these sculptures as wholly spiritual.

[architectnews]

Theorem Winery, Calistoga, California

Theorem Winery, Californian Building Development, CA Commercial Development, USA Architecture Project, Images

Theorem Winery in Calistoga

Jun 25, 2021

Design: Richard Beard Architects

Location: Calistoga, California, USA

Theorem Winery

Theorem Winery is located west of downtown Calistoga, California, within the Diamond Mountain appellation in Napa Valley. Eschewing the ubiquitous large winery venues focused on handling hundreds of guests at one time, Theorem is designed as an intimate, bespoke experience where hospitality reigns supreme.

The 60-acre complex features a cluster of late-19th century structures originally built by Beverley Cole as a country retreat to escape the fog of San Francisco (Cole is noted for establishing what would become the University of California/San Francisco Medical System).

The property includes a small schoolhouse and a distinguished Greek revival cottage known as the Cole House, which was restored and remodeled by Richard Beard prior to master planning the property for the new winery. The winery is designed to complement the restored historic structures, taking inspiration from the vernacular agricultural buildings found on site and in the region. Clad in dark-toned materials to visually recede into the surrounding landscape, the complex takes second seat to views of Mount St. Helena to the north and vineyards to the south.

Modest in scale, the 8,977-square-foot venue is coupled with a carefully orchestrated guest experience, which begins as guests pass through an exterior arbor/trellis. Daylight, and its manipulation, becomes an important element in stripping away the world beyond and enabling guests to become fully emerged in the wine experience. The trellis and welcome/reception area serve as the first step in lowering light levels to allow visitors’ retinas to adjust. From there, guests walk down a mirror-lined staircase to the darker subterranean barrel room where the tasting journey begins.

Exposed, vertically oriented, board-formed concrete walls wrap the space: its raw, unfinished nature recalling the nascent wine resting in adjacent barrels. The area is marked by a simple table and a pair of bronze wings affixed to the wall; the wings serving as a popular photo/social media location. Next, guests are escorted to any number of tasting sites within the complex: in front of the schoolhouse, at the lookout point, under the barn trellis, or in the fermentation room.

The two-story building, featuring dark roofing and siding, is a steel structure with a cross-axis floor plan. Axial vistas allow for views from and through the winery facility. Large, solid oak sliding barn doors provide full closure when desired. Steel-framed glass doors and windows fill the interior spaces with natural light, reducing the need for supplemental lighting in the fermentation room and visually connecting interior spaces to the natural surroundings. The roof of the primary fermentation room features a continuous monitor to provide ample daylight into the structure.

Below-ground barrel storage provides improved, at-grade access for wine production and a cool, consistent temperature in which to mature wine. Additional areas include the crush pad, various storage rooms, a full restroom, and a laboratory/office. Production capacity is 8,412 cases. Tasting and tours are by appointment only and limited to just a few people at a time. With wine and landscape taking center stage, Theorem Winery provides an intimate and nuanced experience that is simultaneously familiar and timeless.

Theorem Winery in Calistoga, California – Building Information

Design: Richard Beard Architects Richard Beard Architects project team Richard Beard, Principal Katherine Schwertner, Project Manager Bruno Lopez-Moncada, Project Architect

Project team Richard Beard Architects (architecture and site master planning) Nicholas Vincent Design (interior design) Finley Construction (contractor) Applied Civil Engineering (civil engineer) Blasen Landscape Architecture (landscape architecture) ZFA Structural Engineers (structural engineer) TEP Engineers (mechanical and plumbing Engineers) Refrigeration Technology Inc (refrigeration engineer) Hiram Banks Lighting Design (lighting engineer)

Materials/Fabricators Soule Building Systems (prefabricated steel structure) Milgard Ultra Series (fiberglass windows) Crown Industrial (fabricator for custom oak sliding doors and all exterior metal doors) Heath Ceramics (bathroom tiles) Vibia (production room chandelier) John Pomp (custom Tasting Room chandelier made of Jules glass) FSB (door hardware) Reclaimed walnut (custom shelving made with walnut from the site) Reception desk (custom-designed bar with painted white oak, leather panels, and Calacatta stone top) Chandelier (hand-cast, sculpted glass crystal chandelier on blackened steel frame) Bar stools (custom, bleached Walnut and Bronze adjustable bar stools with leather seats) Cabinet (Viennese Secessionist Cabinet with Brass hardware and inlays, circa 1900) Shelves (custom copper floating shelves)

Photography by Paul Dyer

Theorem Winery in Calistoga images / information received 250621>

Location: Mar Vista, Marin County, North California, USA

Californian Buildings

San Francisco Architectural Designs – chronological list

San Francisco Architectural Tours by e-architect

HillSide House in California, Mill Valley Design: Zack de Vito Architecture photo : Bruce Damonte, Bruce Damonte Photography HillSide House in Mill Valley

San Francisco Architecture Studios – architecture firm listings on e-architect

Big Ranch Road Retreat in the Napa Valley Design: WDA (William Duff Architects) photograph © Matthew Millman Photography Napa Valley Barn Renewal

Hanover Page Mill Associates, LLC, Stanford Research Park, Palo Alto Design: Form4 Architecture photo courtesy of The Chicago Athenaeum Hanover Page Mill Palo Alto Building

The Italian Swiss Colony Building Lobby Architects: jones | haydu photograph : Matthew Millman The Italian Swiss Colony Building Lobby

California Loft Residence

American Houses

San Francisco Architecture

Californian Architects

American Architecture

American Architect

Comments / photos for the Theorem Winery in Calistoga design by Tim Gorter, Architect USA page welcome

The post Theorem Winery, Calistoga, California appeared first on e-architect.

[siva3155]

300+ TOP ANTENNA Interview Questions and Answers

ANTENNA Interview Questions for freshers experienced :-

1. What is An Antenna? Antenna is a transition device or a transducer between a guided wave and a free space wave or vice-versa. Antenna is also said to be an impedance transforming device. 2. What is Meant By Radiation Pattern? Radiation pattern is the relative distribution of radiated power as a function of distance in space .It is a graph which shows the variation in actual field strength of the EM wave at all points which are at equal distance from the antenna. The energy radiated in a particular direction by an antenna is measured in terms of FIELD STRENGTH. (E Volts/m) 3. What is Radiation Intensity? The power radiated from an antenna per unit solid angle is called the radiation intensity U (watts per steradian or per square degree). The radiation intensity is independent of distance. 4. Define Beam Efficiency? The total beam area (WA) consists of the main beam area (WM) plus the minor lobe area (Wm). Thus WA = WM+ Wm. The ratio of the main beam area to the total beam area is called beam efficiency. Beam efficiency (SM) = WM / WA. 5. What is Directivity? The directivity of an antenna is equal to the ratio of the maximum power density P (q,f)max to its average value over a sphere as observed in the far field of an antenna. D = P (q,f)max / P(q,f)av. Directivity from Pattern. D = 4p / WA. Directivity from beam area (WA). 6. What are The Different Types Of Aperture? Effective aperture. Scattering aperture. Loss aperture. Collecting aperture. Physical aperture. 7. Define Different Types Of Aperture? Effective aperture (Ae): It is the area over which the power is extracted from the incident wave and delivered to the load is called effective aperture. Scattering aperture (As): It is the ratio of the reradiated power to the power density of the incident wave. Loss aperture (Ae): It is the area of the antenna which dissipates power as heat. Collecting aperture (Ae): It is the addition of above three apertures. Physical aperture (Ap): This aperture is a measure of the physical size of the antenna. 8. What is Aperture Efficiency? The ratio of the effective aperture to the physical aperture is the aperture efficiency. i.e Aperture efficiency = hap = Ae / Ap (dimensionless). 9. What is Meant By Effective Height? The effective height h of an antenna is the parameter related to the aperture. It may be defined as the ratio of the induced voltage to the incident field.i.e H= V / E. 10. What are The Field Zones? The fields around an antenna may be divided into two principal regions. Near field zone (Fresnel zone) Far field zone (Fraunhofer zone)

ANTENNA Interview Questions 11. What is Meant By Polarization? The polarization of the radio wave can be defined by direction in which the electric vector E is aligned during the passage of atleast one full cycle.Also polarization can also be defined the physical orientation of the radiated electromagnetic waves in space. The polarization are three types. They are Elliptical polarization ,circular polarization and linear polarization. 12. What is Meant By Front To Back Ratio? It is defined as the ratio of the power radiated in desired direction to the power radiated in the opposite direction. i.e FBR = Power radiated in desired direction / power radiated in the opposite direction. 13. What is Antenna Efficiency? The efficiency of an antenna is defined as the ratio of power radiated to the total input power supplied to the antenna. Antenna efficiency = Power radiated / Total input Power. 14. What is Radiation Resistance ? The antenna is a radiating device in which power is radiated into space in the form of electromagnetic wave. W’ = I2 R Rr = W’/ I2 Where Rr is a fictitious resistance called called as radiation resistance. 15. What is Meant By Antenna Beam Width? Antenna beamwidth is a measure of directivity of an antenna. Antenna beam width is an angular width in degrees, measured on the radiation pattern (major lobe) between points where the radiated power has fallen to half its maximum value. This is called as "beam width" between half power points or half power beam width.(HPBW). 16. What is Meant By Reciprocity Theorem? If an e.m.f is applied to the terminals of an antenna no.1 and the current measured at the terminals of the another antenna no.2, then an equal current both in amplitude and phase will be obtained at the terminal of the antenna no.1 if the same emf is applied to the terminals of antenna no.2. 17. What is Meant By Isotropic Radiator? A isotropic radiator is a fictitious radiator and is defined as a radiator which radiates fields uniformly in all directions. It is also called as isotropic source or omni directional radiator or simply unipole. 18. What is Gain? The ratio of maximum radiation intensity in given direction to the maximum radiation intensity from a reference antenna produced in the same direction with same input power. i.e Maximum radiation intensity from test antenna (G)= Maximum radiation intensity from the reference antenna with same input power. 19. What is Self Impedance? Self impedance of an antenna is defined as its input impedance with all other antennas are completely removed i.e away from it. 20. What is Mutual Impedance? The presence of near by antenna no.2 induces a current in the antenna no.1 indicates that presence of antenna no.2 changes the impedance of the antenna no.1. This effect is called mutual coupling and results in mutual impedance. 21. What is Meant By Cross Field? Normally the electric field E is perpendicular to the direction of wave propagation. In some situation the electric field E is parallel to the wave propagation that condition is called Cross field. 22. What is Axial Ratio? The ratio of the major to the minor axes of the polarization ellipse is called the Axial Ratio (AR). 23. What is Meant By Beam Area? The beam area or beam solid angle or WA of an antenna is given by the normalized power pattern over a sphere. WA = ò ò4p Pn ( q,f ) dW Where dW = Sin q dq.df 24. What is Duality Of Antenna? It is defined as an antenna is a circuit device with a resistance and temperature on the one hand and the space device on the other with radiation patterns, beamangle, directivity gain and aperture. 25. State Poynting Theorem? It states that the vector product of electric field intensity vector E and the magnetic filed intensity vector H at any point is a measure of the rate of energy flow per unit area at that point. The direction of power flow is perpendicular to both the electric field and magnetic field components. 26. What is Point Source? It is the waves originate at a fictitious volume less emitter source at the center ‘O’ of the observation circle. 27. What is Meant By Array? An antenna is a system of similar antennas oriented similarly to get greater directivity in a desired direction. 28. What is Meant By Uniform Linear Array? An array is linear when the elements of the array are spaced equally along the straight line. If the elements are fed with currents of equal magnitude and having a uniform progressive phase shift along the line, then it is called uniform linear array. 29. What are The Types Of Array? Broad side array. End fire array Collinear array. Parasitic array. 30. What is Broad Side Array? Broad side array is defined as an arrangement in which the principal direction of radiation is perpendicular to the array axis and also the plane containing the array element. 31. Define End Fire Array? End fire array is defined as an arrangement in which the principal direction of radiation is coincides with the array axis. For end fire array δ = - β d where β = 2Π / λ and d = distance between the elements. 32. What is Collinear Array? In this array the antenna elements are arranged coaxially by mounting the elements end to end in straight line or stacking them one over the other with radiation pattern circular symmetry. Eg. Omnidirectional antenna. 33. What is Parasitic Array? In this array the elements are fed parasitically to reduce the problem of feed line. The power is given to one element from that other elements get by electro magnetic coupling. Eg. Yagi uda antenna. 34. What is The Condition On Phase For The End Fire Array With Increased Directivity? When δ = - β d, produces maximum field in the direction φ = 0 but dies not give the maximum directivity. It has been shown by Hansen and woodyard that a large directivity is obtained by increasing the phase change between the sources so that δ = - (βd + π / n ). This condition will be referred to as the condition for increased directivity. 35. Explain Array Factor? The normalized value of the total field is given by, E = ( 1 / n) ( sin (n Ψ / 2) / sin ( Ψ / 2) ) The field is given by the expression E will be referred to as array factor. 36. Define Beam Width Of Major Lobe? It is defined the angle between the first nulls (or) it is defined as twice the angle between the first null and the major lobe maximum direction. 37. List Out The Expression Of Beam Width For Broad Side Array And End Fire Array? For broad side array the expression for beam width between the first nulls is given by, BWFN = ( ( + / -) 2 λ / n d ) For End fire array the expression for beam width between the first nulls is given by, BWFN = ( ( + / -) 2 ( 2 λ / n d ) )1/2 38. Differentiate Broad Side And End Fire Array? In Broad side array antennas are fed in phase δ = 0, where as in end fire arrays the antenna elements are fed out of phase i.e. δ = - β d. In broad side array the maximum radiation is perpendicular to the direction of array axis, where as in case of end fire array the maximum radiation is directed along the array axis. 39. What is The Need For The Binomial Array? The need for a binomial array is In uniform linear array as the array length is increased to increase the directivity, the secondary lobes also occurs. For certain applications, it is highly desirable that secondary lobes should be eliminated completely or reduced to minimum desirable level compared to main lobes. 40. Define Power Pattern? Graphical representation of the radial component of the poynting vector Sr at a constant radius as a function of angle is called power density pattern or power pattern. 41. What is Meant By Similar Point Sources? Whenever the variation of the amplitude and the phase of the field with respect to the absolute angle for any two sources are same then they are called similar point sources. The maximum amplitudes of the individual sources may be unequal. 42. What is Meant By Identical Point Sources? Similar point sources with equal maximum amplitudes are called identical point sources. 43. What is The Principle Of The Pattern Multiplication? The total field pattern of an array of non isotropic but similar sources is the product of the Individual source pattern and The array pattern of isotropic point sources each located at the phase center of the individual source having the same amplitude and phase. While the total phase pattern is the sum of the phase patterns of the individual source pattern and array pattern. 44. What is The Advantage Of Pattern Multiplication? Useful tool in designing antenna. It approximates the pattern of a complicated array without making lengthy computations. 45. What is Tapering Of Arrays? Tapering of array is a technique used for reduction of unwanted side lobes. The amplitude of currents in the linear array source is non-uniform; hence the central source radiates more energy than the ends. Tapering is done from center to end. 46. What is A Binomial Array? It is an array in which the amplitudes of the antenna elements in the array are arranged according to the coefficients of the binomial series. 47. What are The Advantages Of Binomial Array? Advantages: No minor lobes. Disadvantages: Increased beam width. Maintaining the large ratio of current amplitude in large arrays is difficult. 48. What is The Difference Between Isotropic And Non-isotropic Source? Isotropic source radiates energy in all directions but non-isotropic source radiates energy only in some desired directions. Isotropic source is not physically realizable but non-isotropic source is physically realizable. 49. Define Side Lobe Ratio? Side Lobe Ratio is defined as the ratio of power density in the principal or main lobe to the power density of the longest minor lobe. 50. List The Arrays Used For Array Tapering? Binomial Array:Tapering follows the coefficient of binomial series. Dolph Tchebycheff Array: Tapering follows the coefficient of Tchebycheff polynomial. 51. What Do You Understand By Retarded Current? Since,the short electric dipole is so short, the current which is flowing through the dipole is assumed to be constant throughout its length. The effect of this current is not felt instantaneous at a distance point only after an interval equal to the time required for the wave to propagate over the distance r is called the retardation time. The retarded current =Io exp( jw' ( t - r / c ) ) Where w'r / c is the phase retardation. 52. Define Induction Field? The induction field will predominate at points close to the current element, where the distance from the center of the dipole to the particular point is less. This field is more effective in the vicinity of the current element only. It represents the energy stored in the magnetic field surrounding the current element or conductor. This field is also known as near field. 53. Explain Radiation Field? The radiation field will be produced at a larger distance from the the current element, where the distance from the centre of the dipole to the particular point is very large. It is also called as distant field or far field. 54. At What Distance From The Dipole Is The Induction Field Equal To The Radiation Field? As the distance from the current element or the short dipole increases, both induction and radiation fields emerge and start decreasing. However, a distance reaches from the conductor at which both the induction and radiation field becomes equal and the particular distance depends upon the wavelength. The two fields will thus have equal amplitude at that particular distance. This distance is given by r = 0.159 λ. 55. Define Radiation Resistance? It is defined as the fictitious resistance which when inserted in series with the antenna will consume the same amount of power as it is actually radiated. The antenna appears to the transmission line as a resistive component and this is known as the radiation resistance. 56. Give The Expression For The Effective Aperture Of A Short Dipole? The effective aperture of a short dipole is given by Ae = 0.119 λ2. 57. What is A Dipole Antenna? A dipole antenna may be defined as a symmetrical antenna in which the two ends are at equal potential relative to the midpoint. 58. What is A Half Wave Dipole? A half wave antenna is the fundamental radio antenna of metal rod or tubing or thin wire which has a physical length of half wavelength in free space at the frequency of operation. 59. Give The Expression For The Effective Aperture Of A Half Wave Dipole? The effective aperture of a half wave dipole is given by Ae = 0.13 λ2. 60. What is The Radiation Resistance Of A Half Wave Dipole? The radiation resistance of a half wave dipole is given by Rr = 73 ohm. 61. What is A Loop Antenna? A loop antenna is a radiating coil of any convenient cross-section of one or more turns carrying radio frequency current. It may assume any shape (e.g. rectangular, square, triangular and hexagonal). 62. Give An Expression Of Radiation Resistance Of A Small Loop? Radiation resistance of a small loop is given by Rr = 31,200 ( A / λ2 )2 63. How To Increase The Radiation Resistance Of A Loop Antenna? The radiation resistance of a loop antenna can be increased by: Increasing the number of turns. Inserting a ferrite core of very high permeability with loop antenna’ s circumference which will rise the magnetic field intensity called ferrite loop. 64. What are The Types Of Loop Antennas? Loop antennas are classified into: Electrically Small (Circumference Electrically Small (Dimension comparable to λ ) 65. What are Electrically Small Loop Antennas? Electrically Small loop antennas is one in which the overall length of the loop is less than one-tenth of the wavelength. Electrically Small loop antennas have small radiation resistances that are usually smaller than their loop resistances. They are very poor radiators and seldom employed for transmission in radio communication. 66. List The Applications Of Helical Antenna? The applications of helical antenna are: It became the workhouse of space communications for telephone, television and data, being employed both on satellites and at ground stations. Many satellites including weather satellites, data relay satellites all have helical antennas. It is on many other probes of planets and comets, including moon and mars, being used alone, in arrays or as feeds for parabolic reflectors, its circular polarization and high gain and simplicity making it effective for space application. 67. Define Sky Wave? Waves that arrive at the receiver after reflection in the ionosphere is called sky wave. 68. Define Tropospheric Wave? Waves that arrive at the receiver after reflection from the troposphere region is called Tropospheric wave (i.e. 10 Km from Earth surface). 69. Explain Ground Wave? Waves propagated over other paths near the earth surface is called ground wave propagation. 70. What are The Type Of Ground Wave? Ground wave classified into two types. Space wave. Surface wave. 71. What is Meant By Space Wave? It is made up of direct wave and ground reflected wave. Also includes the portion of energy received as a result of diffraction around the earth surface and the reflection from the upper atmosphere. 72. What is Meant By Surface Wave? Wave that is guided along the earth’ s surface like an EM wave is guided by a transmission is called surface wave. Attenuation of this wave is directly affected by the constant of earth along which it travels. 73. What is Meant By Fading? Fading is variation of signal strength occur on line of sight paths as a result of the atmospheric conditions. It can not be predicted properly. 74. What are The Type Of Fading? Two types: Inverse fading. Multi path fading. 75. What is Inverse And Multi Path Fading? Inverse bending may transform line of sight path into an obstructed one. Multi path fading is caused by interference between the direct and ground reflected waves as well as interference between two are more paths in the atmosphere. 76. What is Meant By Diversity Reception? To minimize the fading and to avoid the multi path interference the technique used are diversity reception. It is obtained by three ways: Space diversity reception. Frequency diversity reception. Polarization diversity. 77. Define Space Diversity Reception? This method exploits the fact that signals received at different locations do not fade together. It requires antennas spaced at least 100λ apart are preferred and the antenna which high signal strength at the moment dominates. 78. Define Frequency Diversity Reception? This method takes advantage of the fact that signals of slightly different frequencies do not fade synchronously. This fact is utilized to minimize fading in radio telegraph circuits. 79. Define Polarization Diversity Reception? It is used in normally in microwave links, and it is found that signal transmitted over the same path in two polarization have independent fading patterns. In broadband dish antenna system, Polarization diversity combined with frequency diversity reception achieve excellent results. 80. What is Meant By Faraday's Rotation? Due to the earth’ s magnetic fields, the ionosheric medium becomes anisotropic and the incident plane wave entering the ionosphere will split into ordinary and extra ordinary waves/modes. When these modes re-emerge from the ionosphere they recombine into a single plane wave again. Finally the plane of polarization will usually have changed, this phenomenon is known as Faraday's rotation. 81. What are The Factors That Affect The Propagation Of Radio Waves? Curvature of earth. Earth’ s magnetic field. Frequency of the signal. Plane earth reflection. 82. Define Gyro Frequency? Frequency whose period is equal to the period of an electron in its orbit under the influence of the earths magnetic flux density B. 83. Define Critical Frequency? For any layer, the highest frequency that will be reflected back for vertical incidence is fcr = 9 √Nmax 84. Define Magneto-ions Splitting? The phenomenon of splitting the wave into two different components (ordinary and extra-ordinary) by the earths magnetic field is called Magneto-Ions Splitting. 85. What is Luhf? The lowest useful HF for a given distance and transmitter power is defined as the lowest frequency that will give satisfactory reception for that distance and power. It depends on: The effective radiated power Absorption character of ionosphere for the paths between transmitter and receiver. The required field strength which in turn depends upon the radio noise at the receiving location and type of service involved. 86. Define Refractive Index? It is defined as n = c / Vp where n = √εr 87. Define Maximum Usable Frequency? The maximum Frequency that can be reflected back for a given distance of transmission is called the maximum usable frequency (MUF) for that distance. MUF = fcr sec φi 88. Define Skip Distance? The distance with in which a signal of given frequency fails to be reflected back is the skip distance for that frequency. The higher the frequency the greater the skip distance. 89. Define Optimum Frequency? Optimum frequency for transmitting between any two points is therefore selected as some frequency lying between about 50 and 85 percent of the predictedmaximum usable frequency between those points. 90. What is Antenna Matching? When the antenna is receiving with a load resistance matched to the antenna radiation resistance, maximum power is transferred to the load and the power is also re-radiated from the dipole. This is called antenna matching. 91. What is A Short Dipole? A short dipole is one in which the field is oscillating because of the oscillating voltage and current. It is called so, because the length of the dipole is short and the current is almost constant throughtout the entire length of the dipole. 92. How Are Fields Created From Short Dipole / Oscillating Dipole? The dipole has two equal charges of opposite sign oscillating up and down in a harmonic motion. The charges will move towards each other and electric filed lines were created. When the charges meet at the midpoint, the field lines cut each other and new field are created.This process is spontaneous and so more filed are created around the antenna. This is how radiations are obtained from a short dipole. 93. What are Antenna Field Zones? The regions containing the radiations that are present around the antenna are called field zones. The fields around an antenna ay be divided into two principal regions. Near field zone (Fresnel zone). Far field zone (Fraunhofer zone). 94. What is Self Impedance And Mutual Impedance? Self impedance of an antenna is defined as its input impedance with all other antennas are completely removed i.e away from it. The presence of near by antenna no.2 induces a current in the antenna no.1 indicates that presence of antenna no.2 changes the impedance of the antenna no.1. This effect is called mutual coupling and results in mutual impedance. ANTENNA Questions and Answers Pdf Download Read the full article

[mamtajuyal1986]

IIT JAM 2020 Physics (PH) Syllabus | IIT JAM 2020 Physics (PH) Exam Pattern

IIT JAM 2020 Physics (PH) Syllabus | IIT JAM 2020 Physics (PH) Exam Pattern Physics (PH): The syllabus is a very important aspect while preparing for the examination. Therefore it is advised to all the appearing candidates that they should go through the Physics (PH) syllabus properly before preparing for the examination. Mathematical Methods: Calculus of single and multiple variables, partial derivatives, Jacobian, imperfect and perfect differentials, Taylor expansion, Fourier series. Vector algebra, Vector Calculus, Multiple integrals, Divergence theorem, Green's theorem, Stokes' theorem. First order equations and linear second order differential equations with constant coefficients. Matrices and determinants, Algebra of complex numbers. Mechanics and General Properties of Matter: Newton's laws of motion and applications, Velocity and acceleration in Cartesian, polar and cylindrical coordinate systems, uniformly rotating frame, centrifugal and Coriolis forces, Motion under a central force, Kepler's laws, Gravitational Law and field, Conservative and non-conservative forces. System of particles, Center of mass, equation of motion of the CM, conservation of linear and angular momentum, conservation of energy, variable mass systems. Elastic and inelastic collisions. Rigid body motion, fixed axis rotations, rotation and translation, moments of Inertia and products of Inertia, parallel and perpendicular axes theorem. Principal moments and axes. Kinematics of moving fluids, equation of continuity, Euler's equation, Bernoulli's theorem. Oscillations, Waves and Optics: Differential equation for simple harmonic oscillator and its general solution. Superposition of two or more simple harmonic oscillators. Lissajous figures. Damped and forced oscillators, resonance. Wave equation, traveling and standing waves in one-dimension. Energy density and energy transmission in waves. Group velocity and phase velocity. Sound waves in media. Doppler Effect. Fermat's Principle. General theory of image formation. Thick lens, thin lens and lens combinations. Interference of light, optical path retardation. Fraunhofer diffraction. Rayleigh criterion and resolving power. Diffraction gratings. Polarization: linear, circular and elliptic polarization. Double refraction and optical rotation. Electricity and Magnetism: Coulomb's law, Gauss's law. Electric field and potential. Electrostatic boundary conditions, Solution of Laplace's equation for simple cases. Conductors, capacitors, dielectrics, dielectric polarization, volume and surface charges, electrostatic energy. Biot-Savart law, Ampere's law, Faraday's law of electromagnetic induction, Self and mutual inductance. Alternating currents. Simple DC and AC circuits with R, L and C components. Displacement current, Maxwelll's equations and plane electromagnetic waves, Poynting's theorem, reflection and refraction at a dielectric interface, transmission and reflection coefficients (normal incidence only). Lorentz Force and motion of charged particles in electric and magnetic fields. Kinetic theory, Thermodynamics: Elements of Kinetic theory of gases. Velocity distribution and Equipartition of energy. Specific heat of Mono-, di- and tri-atomic gases. Ideal gas, van-der-Waals gas and equation of state. Mean free path. Laws of thermodynamics. Zeroth law and concept of thermal equilibrium. First law and its consequences. Isothermal and adiabatic processes. Reversible, irreversible and quasi-static processes. Second law and entropy. Carnot cycle. Maxwell's thermodynamic relations and simple applications. Thermodynamic potentials and their applications. Phase transitions and Clausius-Clapeyron equation. Ideas of ensembles, Maxwell-Boltzmann, Fermi-Dirac and Bose-Einstein distributions. Modern Physics: Inertial frames and Galilean invariance. Postulates of special relativity. Lorentz transformations. Length contraction, time dilation. Relativistic velocity addition theorem, mass energy equivalence. Blackbody radiation, photoelectric effect, Compton effect, Bohr's atomic model, X-rays. Wave-particle duality, Uncertainty principle, the superposition principle, calculation of expectation values, Schrodinger equation and its solution for one, two and three dimensional boxes. Solution of Schrodinger equation for the one dimensional harmonic oscillator. Reflection and transmission at a step potential, Pauli exclusion principle. Structure of atomic nucleus, mass and binding energy. Radioactivity and its applications. Laws of radioactive decay. Solid State Physics, Devices and Electronics: Crystal structure, Bravais lattices and basis. Miller indices. X-ray diffraction and Bragg's law; Intrinsic and extrinsic semiconductors, variation of resistivity with temperature. Fermi level. p-n junction diode, I-V characteristics, Zener diode and its applications, BJT: characteristics in CB, CE, CC modes. Single stage amplifier, two stage R-C coupled amplifiers. Simple Oscillators: Barkhausen condition, sinusoidal oscillators. OPAMP and applications: Inverting and non-inverting amplifier. Boolean algebra: Binary number systems; conversion from one system to another system; binary addition and subtraction. Logic Gates AND, OR, NOT, NAND, NOR exclusive OR; Truth tables; combination of gates; de Morgan's theorem. Related Articles: IIT JAM 2020 Syllabus Biotechnology (BT) Syllabus Biological Sciences (BL) Syllabus Chemistry (CY) Syllabus Geology (GG) Syllabus Mathematics (MA) Syllabus Mathematical Statistics (MS) Syllabus Physics (PH) Syllabus Read the full article

[universallyhumanspyfriend]

Contents Introduction Moments of Inertia of an Area Moment of Inertia of an Area by Integration Polar Moment of Inertia Radius of Gyration of an Area Sample Problem 9.1 Sample Problem 9.2 Parallel Axis Theorem Moments of Inertia of Composite Areas Sample Problem 9.4 Sample Problem 9.5 Product of Inertia Principal Axes and Principal Moments of Inertia Sample Problem 9.6 Sample Problem 9.7 Mohr’s Circle for Moments and Products of Inertia Sample Problem 9.8 Moment of Inertia of a Mass Parallel Axis Theorem Moment of Inertia of Thin Plates Moment of Inertia of a 3D Body by Integration Moment of Inertia of Common Geometric Shapes Sample Problem 9.12 Moment of Inertia With Respect to an Arbitrary Axis Ellipsoid of Inertia. Principle Axes of Axes of Inertia of a Mass

[omc-juniperpublishers]

Polarizability Study of Fullerene Nano- g Structures C20 to C300 by Using Monopole-Dipole s Interactions Theorem-JuniperPublishers

Journal of Chemistry-JuniperPublishers

Abstract

Since the discovery of fullerenes (Cn), one of the main classes of carbon compounds, the unusual structures and physiochemical properties of these molecules have been discovered, and many potential applications and physicochemical properties have been introduced. Up to now, various empty carbon fullerenes with different numbers "n,” such as C20 through C300 (like C60, C70, C76, C82,..., C300) have been obtained. The linear uniform field electric dipole polarizability tensors of 46 fullerenes in the range C20 through C240 were calculated by the Atom MonopoleDipole Interaction (AMDI) theory, using the monopole and dipole polarizabilities of the carbon atom found previously to fit polarizability tensors of aromatic hydrocarbons. The structures are taken to be those predicted by molecular dynamics energy optimization. The isotropic mean polarizabilities calculated for C60 and C70 are comparable to experimental data from solid film studies and to quantum mechanical calculations. Topological indices are digital values that are assigned based on chemical composition. These values are purported to correlate chemical structures with various chemical and physical properties. They have been successfully used to construct effective and useful mathematical methods to establish clear relationships between structural data and the physical properties of these materials. In this study were extended the calculation of the parameters concern to atom monopole-dipole moment such as Ellipsoid (αl to α3 and α), AMDI (Atom monopole-dipole interaction theory; αl to α3 and ā) and semi-axes a,b,c of a thin ellipsoidal shell of uniform thickness (in Å, ABC al to α3) by QSAR for C20 through C300 .

Keywords: Fullerenes; Polarizability; Amdi Theory; Ellipsoid; Semi-Axes Thin Ellipsoidal Shell

Abbreviations: AMDI: Atom Monopole Dipole Interaction; FC: Ferrocene; TI: Topological Indices; Atom Monopole Dipole Interaction (AMDI); TI: Topological Indices; MLR: Modeling; MLR: Modeling Both Linear

Introduction

The electrochemical properties of the fullerene C60 have been studied since the early 1990s, when these materials became available in macroscopic quantities (for a review see [1]). [1-3] in 1990, have shown that C60 is electrochemically reducible in the CH2Cl2 medium to C60- and C602-. In 1992, have cathodically reduced both C60 in six reversible one-electron steps for -0.97 vs. Fc/Fc+ (FC=Ferrocene). This fact, along with the absence of anodic electrochemistry of fullerenes, matches the electronic structure of fullerenes: the LUMO of C60 can accept up to six electrons to form C606-, but the position of the HOMO does not allow for hole-doping under the usual electrochemical conditions. In 1991, Bard et al. [4-8] first reported on irreversible electrochemical and structural reorganization of solid fullerenes in acetonitrile medium. Dunsch et al. [5] have upgraded the experimental conditions by investigating highly organized C60 films on HOPG in aqueous medium. The reduction of such films manifested itself by re-structuring into conductive nanoclusters of ~102 nm in diameter [5-9].

The linear uniform field electric dipole polarizability tensors of 46 fullerenes in the range C20 through C240 are calculated by the Olson Sundberg Atom Monopole-Dipole Interaction (AMDI) theory, using the monopole and dipole polarizabilities of the carbon atom found previously to fit polarizability tensors of aromatic hydrocarbons. The structures are taken to be those predicted by Zhang and co-workers by molecular dynamics energy optimization. The isotropic mean polarizabilities calculated for C60 and C70 are comparable to experimental data from solid film studies and to quantum mechanical calculations. Polarizability tensors are also calculated for conducting ellipsoidal shells which have the same moment of inertia tensor as the corresponding fullerenes. These are substantially smaller than the AMDI polarizabilities for the smaller fullerenes, but the two calculations tend to converge for the larger molecules. [7-15]

Graph theory has been found to be a useful tool in assessing the QSAR (Quantitative Structure Activity Relationship) and QSPR (Quantitative Structure Property Relationship). Numerous studies in the above areas have also used what are called Topological Indices (TI). It is important to use effective mathematical methods to make good correlations between several data properties of chemicals. Numerous studies have been performed related to the above mentioned fields by using the so-called Topological Indices (TI). The numbers of carbon atoms at the structures of the fullerenes were utilized here [7-15].

In this study were extended the calculation of the parameters concern to atom monopole-dipole moment such as Ellipsoid (α1 to α3 and ā), AMDI (Atom monopole-dipole interaction theory; al to α3 and ā) and semi-axes a,b,c of a thin ellipsoidal shell of uniform thickness (in Å, ABC α1 to α3) by QSAR for C20 through C300 .

Graphs And Mathematical Method

All graphing operations were performed using the Microsoft Office Excel 2003 program. The numbers of carbon atoms at the structures of the fullerenes Cn were utilized to make the relationship and calculate the Ellipsoid, AMDI and thin ellipsoidal shell of uniform thickness. For Modeling, Both Linear (MLR) and nonlinear (ANN) models were used in this study.

Discussion

The polarizabilities of the ellipoids are simply correlated with their geometry, as can be seen from the fact that the principal polarizabilities are approximately proportional to the lengths of the corresponding axes. To some extent this holds for the AMDI model as well, but for the smaller members of the series there are cases where the principal polarizabilities are not in the same ratio as the axes. His is apparently because the atom dipole contribution, which is not simply related to the axis lengths, is relatively larger for the smaller members. A further measure of the correspondence between the molecules and the ellipsoids is found in the comparison of the principal polarizability axes found by the AMDI theory with the principal geometric axes of the ellipsoids. Where the three semi-axes are distinct, the axes directions are the same to within a few tenths of a degree. The numbers of carbon atoms at the structures of the fullerenes Cn were utilized and extended the calculation of the parameters concern to atom monopole-dipole moment such as Ellipsoid (α1to α3 and ā), AMDI (Atom monopole-dipole interaction theory;α1 to α3 and ā) and semi-axes a,b,c of a thin ellipsoidal shell ofuniform thickness (in Å, ABC al to α3) by QSAR for C20 through C300.

To know more about Journal of chemistry,

Click here: https://juniperpublishers.com/omcij/index.php

To know more abour juniper Publishers,

click here: https://juniperpublishers.com/index.php

[physical-theories-en-blog]

Tennis racket theorem

The tennis racket theorem or intermediate axis theorem is a result in classical mechanics describing the movement of a rigid body with three distinct principal moments of inertia. It is also dubbed the Dzhanibekov effect, after Russian cosmonaut Vladimir Dzhanibekov who discovered the theorem's consequences while in space in 1985. An article explaining the effect was published in 1991. Play media Dzhanibekov effect in weightlessness The theorem describes the following effect: rotation of an object about its first and third principal axes is stable, while rotation about its second principal axis (or intermediate axis) is not. This can be demonstrated with the following experiment: hold a tennis racket at its handle, with face horizontal, and try to throw it in the air so that it will perform a full rotation about the horizontal axis perpendicular to the handle, and try to catch the handle. In almost all cases, during that rotation the face will also have completed a half rotation, so that the other face is now up. By contrast, it is easy to throw the racket so that it will rotate about the handle axis (the third principal axis) without accompanying half-rotation about another axis; it is also possible to make it rotate about the vertical axis perpendicular to the handle (the first principal axis) without any accompanying half-rotation. The experiment can be performed with any object that has three different moments of inertia, for instance with a book or a remote control. The effect occurs whenever the axis of rotation differs slightly from the object's second principal axis; air resistance or gravity are not necessary. More details Android, Windows

[andystechgarage]

Geekiest thing imaginable!!! The #tennisrackettheorem is a result in classical mechanics describing the movement of a rigid body with three distinct principal moments of inertia. Also known as #dzhanibekoveffect, after Russian astronaut #Vladimir #Dzhanibekov who discovered the theorem's consequences while in space in 1985. An article explaining the effect was published in 1991. The theorem describes the following effect: rotation of an object about its first and third principal axes is stable, while rotation about its second principal axis is not. This can be demonstrated with the following experiment: hold a tennis racket at its handle, with face horizontal, and try to throw it in the air so that it will perform a full rotation about the horizontal axis perpendicular to the handle, and try to catch the handle. In almost all cases, during that rotation the face will also have completed a half rotation, so Read more at https://m.liveleak.com/view?i=ba1_1440392668#Sz1VsDh7JpJVe11y.99 Had to share this one. For the full clip google search Tennis Racket Theorem . @andystechgarage #andystechgarage #atg #physics #stem #stemeducation #learningeveryday #learningisfun #stematg #stemandy #stemeva #atgstem #evastem #andystem

[dnsiaody]

CSIR UGC NET Application 2017

COMMON SYLLABUS FOR PART ‘B’ PLUS ‘C’ MATHEMATICAL SCIENCES DEVICE - 1 Analysis: Primary set theory, finite, countable and uncountable sets, True number system as the complete ordered field, Archimedean property, supremum, infimum. admission.scholarshipbag.com Sequences and series, convergence, limsup, liminf. Bolzano Weierstrass theorem, Heine Borel theorem. Continuity, uniform continuity, differentiability, indicate value theorem. Sequences plus a number of functions, homogeneous convergence. Riemann sums plus Riemann integral, Improper Integrals. Monotonic functions, types associated with discontinuity, functions of bounded variation, Lebesgue measure, Lebesgue integral. Functions of various variables, directional derivative, partially derivative, derivative as being a geradlinig transformation, inverse and implied function theorems. Metric areas, compactness, connectedness. Normed geradlinig Spaces. Spaces of constant functions as examples. Geradlinig Algebra: Vector spaces, subspaces, linear dependence, basis, aspect, algebra of linear changes. Algebra of matrices, position and determinant of matrices, linear equations. Eigenvalues plus eigenvectors, Cayley-Hamilton theorem. Matrix representation of linear changes. Change of basis, canonical forms, diagonal forms, triangular forms, Jordan forms. Internal product spaces, orthonormal base. Quadratic forms, reduction plus classification of quadratic types UNIT - two Complicated Analysis: Algebra of complicated numbers, the complex aircraft, polynomials, power series, transcendental functions such as rapid, trigonometric and hyperbolic features. Analytic functions, Cauchy-Riemann equations. Contour integral, Cauchy’s theorem, Cauchy’s integral formula, Liouville’s theorem, Maximum modulus rule, Schwarz lemma, Open umschlüsselung theorem. Taylor series, Laurent series, calculus of residues. Conformal mappings, Mobius changes. Algebra: Permutations, combinations, pigeon-hole principle, inclusion-exclusion principle, derangements. Fundamental theorem of math, divisibility in Z, congruences, Chinese Remainder Theorem, Euler’s Ø- function, primitive origins. Groups, subgroups, normal subgroups, quotient groups, homomorphisms, cyclic groups, permutation groups, Cayley’s theorem, class equations, Sylow theorems. Rings, ideals, excellent and maximal ideals, quotient rings, unique factorization site, principal ideal domain, Euclidean domain. Polynomial rings plus irreducibility criteria. Fields, limited fields, field extensions, Galois Theory. Topology: basis, thick sets, subspace and item topology, separation axioms, connectedness and compactness. UNIT -- 3 Ordinary Differential Equations (ODEs): Existence and originality of solutions of preliminary value problems for initial order ordinary differential equations, singular solutions of initial order ODEs, a system associated with first order ODEs. The common theory of homogenous plus nonhomogeneous linear ODEs, deviation of parameters, Sturm-Liouville border value problem, Green’s functionality. Partial Differential Equations (PDEs): Lagrange and Charpit strategies for solving first purchase PDEs, Cauchy problem intended for first order PDEs. Category of second order PDEs, General solution of increased order PDEs with continuous coefficients, Method of splitting up of variables for Laplace, Heat and Wave equations. Numerical Analysis: Numerical options of algebraic equations, Technique of iteration and Newton-Raphson method, Rate of convergence, Solution of systems associated with linear algebraic equations making use of Gauss elimination and Gauss-Seidel methods, Finite differences, Lagrange, Hermite and spline interpolation, Numerical differentiation and incorporation, Numerical solutions of ODEs using Picard, Euler, customised Euler andRunge-Kutta methods. Calculus of Variations: A variety associated with a functional, Euler-Lagrange formula, Necessary and sufficient situations for extreme. Variational strategies for boundary value troubles in ordinary and partially differential equations. Linear Essential Equations: The Linear integral formula of the first plus second kind of Fredholm and Volterra type, Options with separable kernels. Feature numbers and eigenfunctions, resolvent kernel. Classical Mechanics: General coordinates, Lagrange’s equations, Hamilton’s canonical equations, Hamilton’s rule and the principle of minimum action, Two-dimensional motion associated with rigid bodies, Euler’s dynamical equations for the movement of the rigid entire body about an axis, the concept of small oscillations. DEVICE - four Descriptive figures, exploratory data analysis Example space, discrete probability, 3rd party events, Bayes theorem. Unique variables and distribution features (univariate and multivariate); requirement and moments. Independent unique variables, marginal and conditional distributions. Characteristic functions. Possibility inequalities (Tchebyshef, Markov, Jensen). Modes of convergence weakened and strong laws associated with large numbers, Central Restrict theorems (i. i. g. case). Markov chains along with finite and countable condition space, classification of claims, limiting behaviour of n-step transition probabilities, stationary submission, Poisson and birth-and-death procedures. Standard discrete and constant univariate distributions. sampling distributions, standard errors and asymptotic distributions, distribution of purchase statistics and range. Strategies of estimation, properties associated with estimators, confidence intervals. Testing of hypotheses: most effective and uniformly most effective tests, likelihood ratio testing. Analysis of discrete information and chi-square test associated with goodness of fit. Big sample tests. Simple non-parametric tests for just one particular and two sample troubles, rank correlation and check for independence. Elementary Bayesian inference. Gauss-Markov models, estimability of parameters, best geradlinig unbiased estimators, confidence times, tests for linear ideas. Analysis of variance plus covariance. Fixed, random plus mixed effects models. Assured multiple linear regression. Primary regression diagnostics. Logistic regression. Multivariate normal distribution, Wishart distribution and their qualities. Distribution of quadratic types. Inference for parameters, partially and multiple correlation coefficients and related tests. Information reduction techniques: Principle element analysis, Discriminant analysis, Bunch analysis, Canonical correlation. Easy random sampling, stratified sample and systematic sampling. Possibility proportional to size sample. Ratio and regression strategies. Completely randomised designs, randomised block designs and Latin-square designs. Connectedness and orthogonality of block designs, BIBD. 2K factorial experiments: confounding and construction. Hazard functionality and failure rates, censoring and life testing, collection and parallel systems. Geradlinig programming problem, simple strategies, duality. Elementary queuing plus inventory models. Steady-state options of Markovian queuing versions: M/M/1, M/M/1 with restricted waiting space, M/M/C, M/M/C with the limited waiting area, M/G/1. All students are usually required to answer queries from Unit I. College students in mathematics are anticipated to answer an additional query from Unit II plus III. Students with within statistics are required in order to answer the additional question through Unit IV.