#SYM: Diagonal
Explore tagged Tumblr posts
Text
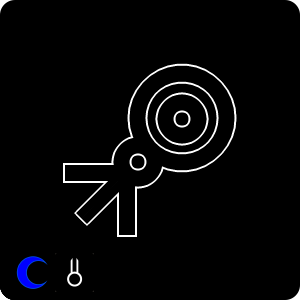
CORBUS Sign of the Curator
COR(V)* = Onyx Sign • *BUS = Prospit + Lust
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
#823: A sign for seekers of madness. They search for the universe's strangest oddities (regardless of the damage it leaves) for the benefit of anyone that needs guidance towards or away from them.
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
Onyx Signs • Lustbound Signs • Prospit Signs
#TTSEZ#Onyx Caste Signs#Signs of Lust#Prospit Signs#SYM: Diagonal#SMPL: Three#Style: Right Angle#Style: Circle
0 notes
Text
Then we all headed out to the beach. Sym shed her cloak and revealed a flowy yellow swimsuit that complemented her skin. She strode ahead of us over the rocky path in her boots. A diagonal stretch of her back showed between strips of yellow fabric—it was strong and smooth and golden, her shoulders back, ready to embrace the world or fight it, her hair swishing in the strong morning wind, teasing her shoulders.... Admiration poured through me, along with a strange magnetic feeling, as if she were pulling me toward her.... pulling me closer, yet never close enough to touch—
Sol walked beside me. Her glow cast over his face, spilling a gold overlay across his coppery hue. His gaze tangled in her hair—then swept back out to the heaving sea.
- Revolution Chapter 22
#writing#scifi#wip#justice march#sol#sym#beach#mirage#hint#of what to come?#or.... we dont go anywhere with any of ths
2 notes
·
View notes
Text
Rutina De Ejercicios Sencillos Y Saludables
Mejorar la ejecución deportiva (lanzamientos, fintas, golpeos, etc.), los ejercicios.
Si bien cualquier tipo de actividad física resulta buena para el organismo, desde hace ya algún tiempo se estudia la diferencia de entrenar en lugares cerrados con respecto a la ejercitación al aire libre, pues esta última alternativa ha demostrado ser más saludable. Tanto el trabajo aeróbico como el anaeróbico aumentan la eficiencia mecánica del corazón mediante el aumento del volumen cardíaco (entrenamiento aeróbico) el espesor del miocardio (entrenamiento de fuerza). Estos cambios son en general beneficiosos y saludables si se producen en respuesta al ejercicio. El ejercicio también es bueno para la mente. Las personas que introducen alguna actividad física regular en su rutina están de mejor humor, duermen mejor, tienen niveles más bajos de estrés y ansiedad y perciben cambios positivos en su propio concepto. Para algunas personas con depresión, la actividad física puede resultar tan efectiva como seguir un tratamiento tomar medicación. Con tan solo 20 30 minutos de ejercicio diario se podrá activar todo el cuerpo. Con el fin de mejorar la circulación, fortalecer los músculos y proteger el corazón. 2. Más frutas y verduras. Siguiendo la idea anterior, las frutas y verduras tienen un alto contenido en agua y ayudan a hidratar. Además, su aporte vitamínico proporcionan al cuerpo lo necesario para no desfallecer ante el calor. Tal como exponen Sapsford y Kelley, (2006), cuando los sujetos reciben de sus entrenadores explicaciones referidas a los músculos de la zona abdominal, sería aconsejable obtener información sobre posibles alteraciones del suelo pélvico (incontinencia, prolapsos, etc.). Si se admite la presencia de éstos, se puede sugerir la derivación para recibir un tratamiento adicional (que en la mayoría de casos puede exigir la intervención el asesoramiento de otros especialistas). No obstante, y considerando estas cuestiones podríamos atender a la necesidad de considerar la necesidad de integrar ciertas propuestas que pudieran considerar tales requerimientos, integrando de esta manera, algunos ejercicios y tareas que atiendan al acondicionamiento de la musculatura del suelo pélvico. El decúbito lateral horizontal es un ejercicio efectivo por su capacidad para activar la musculatura oblicua y cuadrado lumbar (un músculo que posee una gran actividad estabilizadora (McGill, 1997; 2001; Nadler y cols., 2002; Fritz y cols., 1998) alrededor del 50% de la máxima contracción voluntaria (McGill, 2001). Genera una actividad mioeléctrica muy baja en el psoas y resto de flexores coxofemorales (Juker cols., 1998; McGill y cols., 1999). Tener un estilo de vida sano, cuidando tu cuerpo, es más fácil de lo que imaginas. Hacer ejercicio y consumir alimentos saludables, son claves para aumentar tu calidad de vida. Realizar actividad física 3 veces a la semana evita el riesgo de enfermedad cardiovascular, osteoporosis, diabetes; ayuda a bajar el colesterol y te hará sentirte llena de vitalidad. Para mejorar el sistema cardio-respiratorio se recomienda el ejercicio aeróbico. Para el refuerzo de articulaciones y musculatura, está prescrita la calistenia y, de modo más avanzado, para el incremento de la fuerza, los ejercicios con aparatos y pesas. https://amesmen.es/xtrasize-opiniones/ Para un buen ejercicio no se recomienda realizar más de 20 minutos las primeras semanas. A medida de que el cuerpo tome como hábito el ejercicio físico, podrá irse agregando más tiempo de ejercicio. 9. Hacer deporte. El hacer deporte es fundamental para un correcto crecimiento del cuerpo de los niños. Hacer estiramiento ayuda a su cuerpo a evitar lesiones dolores. También es importante cuidar la salud bucal, ya que la boca, incluyendo dientes y lengua es la puerta de entrada del aparato digestivo. Dormir es entonces fundamental para no padecer el cambio horario. La profesora de la Facultad de Ciencias Biomédicas de la Universidad Austral puntualiza que la falta de sueño produce muchas consecuencias sobre la salud (depresión, hipertensión arterial, diabetes tipo II, obesidad, aumento de la mortalidad, depresión del sistema inmune, disminución del rendimiento cognitivo), muchas de las que impactan directamente en la performance, como la velocidad de reacción, de la capacidad de concentración y de la toma de decisiones, entre otras. https://mejorconsalud.com/como-tener-tendones-y-ligamentos-mas-fuertes/

Come frutas y verduras: tener una nutrición balanceada, en la que incluyas este tipo de alimentos ricos en vitaminas y minerales, te ayudará a mantener tu peso controlado y a sentirte más enérgica.
Al iniciar una actividad de ejercicio físico se debe ser consciente de las propias limitaciones físicas y elegir una práctica deportiva que no suponga una sobre carga para nuestro cuerpo. Recomiendo leer El ejercicio físico es un elemento básico para la formación de niños y jóvenes y el mejoramiento y mantenimiento de nuestra salud. La hidratación es fundamental para que el cuerpo de la mujer funcione mejor, sobre todo durante el embarazo. Beber aproximadamente dos litros de agua favorece la circulación sanguínea, ayuda a eliminar toxinas innecesarias del organismo y a reducir la retención de líquidos. Para conseguir un estilo de vida saludable, es necesario tener en cuenta la salud de modo integral, ya que así se gozará de una existencia más plena. A continuación se presentan algunas pautas de conducta y consejos de salud que ayudarán a proporcionar una mejor calidad a nuestro existir. Danneels LA, Vanderstraeten GG, Cambier DC, Witurouw EE, Bourgois J, Dankaerts W, Cuyper HJ. Effects of Three Different Training Modalities on the Cross Sectional Area of the Lumbar Multifidus Muscle in Patients with Chronic Low Back Pain. Br J Sports Med 2001; 35:186-191. El usuario autoriza a Grupo Nutresa S.A., sus filiales Value SYM S.A.S y Netbangers S.A.S, (cualquier otra compañía que sea contratada para las mismas finalidades) (en adelante Responsables y Encargados) a tratar los datos personales que en desarrollo de Comunidad Doria” (en adelante La Actividad) se obtengan, con la finalidad de contactar a los ganadores, hacer entrega del premio y en general, todo lo necesario para el desarrollo de la actividad, además enviar información de las compañías filiales del Grupo Nutresa S.A. 2. Las dietas yoyo”: Se ha demostrado que las personas que realizan una dieta pero al poco tiempo recuperan su peso anterior, ganan más, son propensas a padecer de diabetes tipo 2. Esto sucede porque la insulina que genera el cuerpo comienza a fallar lo que genera que el cuerpo la utilice de manera incorrecta. Actualmente el mejor remedio contra la sarcopenia es el ejercicio. Existe evidencia científica de que tiene un efecto mucho mayor que cualquier tratamiento farmacológico. Cuando hay tratamiento farmacológico unido al ejercicio los efectos producidos de forma conjunta son mayores que cuando se hacen por separado.

Prisma Publicaciones 2002 S.L.U., con CIF B62048038, será la responsable de los datos personales facilitados a través de la presente página web, así como de los facilitados telefónicamente, a través de cualquiera de nuestros formularios en formato papel, de los obtenidos como consecuencia de la relación que Usted mantenga con nosotros y de los derivados de sus hábitos de navegación y consumo. Dicha compañía se encuentra ubicada en Av. Diagonal, 662-664, 4º B, 08034 Barcelona, pudiendo ponerse en contacto con la misma a través de la dirección electrónica lpd@. Las antiguas baterías de Níquel había que descargarlas y cargarlas por completo, no sólo por alargar la vida sino por evitar el efecto memoria. Las actuales baterías de Litio, que no tienen efecto memoria, no conviene descargarlas nunca al máximo ya que se dañan. Igualmente la carga máxima es perjudicial, aunque la mayoría de las baterías vienen capadas de serie y nunca pasan el 90% de carga (aunque nosotros vemos 100%).
Rutina práctica y rápida de 10 pasos para realizar todos los días y mantener la firmeza de tu piel en todo el cuerpo, combatiendo los signos de la edad.
1 note
·
View note
Video
EIGENVALUES AND EIGENVECTORS; DIAGONALIZATION; EIGENVALUES OF A REAL SYM...
0 notes
Text
Strong conceptual completeness for \(\aleph_0\)-categorical theories, 3:
This series of posts is a serialization of (what started as) notes for a talk I gave at the Harvard logic seminar on 6 February 2018. You can view them in order here.
Of course, the point of all this is that when the theory is nice enough, we can ignore the more general ultramorphisms and still obtain a statement of strong conceptual completeness. In this section, we show that when the theory \(T\) is additionally assumed to be \(\aleph_0\)-categorical, we can replace “ultrafunctor” with \(\Delta\)-functor in the statement of strong conceptual completeness, so that only the simplest ultramorphisms suffice to state strong conceptual completeness for \(\aleph_0\)-categorical theories.
Preliminaries on \(\aleph_0\)-categorical theories
Definition. A theory \(T\) is \(\aleph_0\)-categorical if \(T\) is countable and has, up to isomorphism, a single countable model.
The definable sets of \(\aleph_0\)-categorical theories are exceptionally easy to understand: they are precisely the finite disjoint unions of orbits of the automorphism group; furthermore, \(\aleph_0\)-categorical theories are determined up to bi-interpretability by the automorphism group of the unique countable model topologized by pointwise convergence.
Theorem. (Ryll-Nardzewski) \(T\) is \(\aleph_0\)-categorical if and only if it has only finitely many types in each sort (this implies that all the types are isolated.)
Corollary. If \(M \models T\) is the unique countable model of the \(\aleph_0\)-categorical theory \(T\), then \(M\) has only finitely many \(\operatorname{Aut}(M)\)-orbits in each sort (each corresponding to the points of an isolated type.)
Theorem. (Coquand-Ahlbrandt-Ziegler) Let \(T\) and \(T'\) be \(\aleph_0\)-categorical with countable models \(M\) and \(M'\). Then \(T\) and \(T'\) are bi-interpretable if and only if there is an isomorphism of topological groups \(\operatorname{Aut}(M) \simeq \operatorname{Aut}(M')\), where \(\operatorname{Aut}(M)\) and \(\operatorname{Aut}(M')\) are topologized by pointwise convergence.
It follows that in the unique countable model \(M \models T\) of an \(\aleph_0\)-categorical theory, a subset of a sort in \(M\) is definable if and only if it is invariant under the action of \(\operatorname{Aut}(M)\). In fact, any \(\operatorname{Aut}(M)\)-invariant quotient of a definable subset of \(M\) is definable in \(T^{\operatorname{eq}}\), since the kernel relation of the quotient will be a definable set.
Diagonal embeddings and the finite support property
As a warm-up to the theorem , we will show in general that if \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) is a \(\Delta\)-functor, \(X\) must map \(\operatorname{Aut}(M)\) continuously to \(\operatorname{Sym}(X(M))\).
Proposition. Let \(T\) be any theory, and let \((X, \Phi) : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) be a \(\Delta\)-functor. Then for any model \(M \models T\), the restriction of \(X\) to a map \(\operatorname{Aut}(M) \to \operatorname{Sym}(X(M))\) is a continuous group homomorphism (where both groups are topologized by pointwise convergence).
Since \(X\) is a functor, its restriction to \(\operatorname{Aut}(M)\) is a group homomorphism. To check continuity, let \(\mathcal{D}\) be a directed partial order indexing a net of automorphisms \([\sigma_{\alpha}]_{\alpha \in \mathcal{D}}\). It suffices to check that if \([\sigma_{\alpha}]_{\alpha \in \mathcal{D}} \to \sigma\) in \(\operatorname{Aut}(M)\), then \([X \sigma_{\alpha}]_{\alpha \in \mathcal{D}} \to X \sigma\) in \(\operatorname{Sym}(X(M))\).
We will suppose not and take an ultraproduct of counterexamples. So suppose that \([X \sigma_{\alpha}]_{\alpha \in \mathcal{D}}\) does not converge to \(X \sigma\). The basic open neighborhoods \(B_{c \hspace{0.5mm} \mapsto \hspace{0.5mm} d}\) of \(X \sigma\) are parametrized by tuples \(c,d\) of the same sort, and they look like this: \[B_{c \hspace{0.5mm} \mapsto \hspace{0.5mm} d} \overset{\operatorname{df}}{=} \{\rho : X(M) \to X(M) \operatorname{\big{|}} \rho( c ) = d\}.\] Since \([X \sigma_{\alpha}]_{\alpha \in \mathcal{D}}\) does not converge to \(X \sigma\), then there exists some neighborhood \(B_{c \hspace{0.5mm} \mapsto \hspace{0.5mm} d}\) such that for every \(\alpha \in \mathcal{D}\), there exists an \(\alpha' \geq \alpha \in \mathcal{D}\) such that \(X \sigma_{\alpha'} \not \in B_{c \hspace{0.5mm} \mapsto \hspace{0.5mm} d}\).
Now, let \(I\) be the underlying set of \(\mathcal{D}\), and consider the collection of subsets \(\{P_{\alpha} \subseteq I\}_{\alpha \in \mathcal{D}}\), where each \(P_{\alpha}\) is the set of all \(\beta \in \mathcal{D}\) such that \(\beta \geq \alpha\). Since \(\mathcal{D}\) was a directed partial order, \(\{P_{\alpha}\}_{\alpha \in \mathcal{D}}\) has the finite intersection property, and can therefore be completed to an ultrafilter \(\mathcal{U}\).
Then consider the ultraproduct of automorphisms \[\left[X \sigma_{\alpha'}\right]_{\alpha \to \mathcal{U}} : X(M)^{\mathcal{U}} \to X(M)^{\mathcal{U}}.\] Let \(\Delta_{X(M)}\) be the diagonal embedding of \(X(M)\) into \(X(M)^{\mathcal{U}}\). Since every \(X \sigma_{\alpha'}\) sends \(c\) to \(d' \neq d\), \(\left[X \sigma_{\alpha'} \right]_{\alpha \to \mathcal{U}}\) sends \(\Delta_{X(M)}( c )\) to \(\Delta_{X(M)}(d') \neq \Delta_{X(M)}(d)\). Therefore, \[\left[X \sigma_{\alpha'}\right]_{\alpha \to \mathcal{U}} \circ \Delta_{X(M)} \neq \left[X \sigma \right]_{\alpha \to \mathcal{U}} \circ \Delta_{X(M)}.\] By the definition of a \(\Delta\)-functor, we can replace \(\Delta_{X(M)}\) with \(\Phi_{(M)} \circ X \left(\Delta_M\right)\). By the definition of a pre-ultrafunctor, we can replace \(\left[X \sigma_{\alpha'} \right]_{\alpha \to \mathcal{U}}\) and \(\left[X \sigma \right]_{\alpha \to \mathcal{U}}\) with \[\Phi_{(M)} \circ X\left([\sigma_{\alpha'}]_{\alpha \to \mathcal{U}}\right) \circ \Phi_{(M)}^{-1} \text{ and } \Phi_{(M)} \circ X\left([\sigma]_{\alpha \to \mathcal{U}}\right) \circ \Phi_{(M)}^{-1}.\] Substituting into the displayed inequality above and letting inverse transition isomorphisms cancel out, we obtain \[\Phi_{(M)} \circ X\left([\sigma_{\alpha'}]_{\alpha \to \mathcal{U}}\right) \circ X \left(\Delta_M\right) \neq \Phi_{(M)} \circ X\left([\sigma]_{\alpha \to \mathcal{U}}\right) \circ X \left(\Delta_M\right)\] and since \(\Phi_{(M)}\) is a bijection, we may omit it: \[X\left([\sigma_{\alpha'}]_{\alpha \to \mathcal{U}}\right) \circ X \left(\Delta_M\right) \neq X\left([\sigma]_{\alpha \to \mathcal{U}}\right) \circ X \left(\Delta_M\right).\] Since \(X\) is a functor, we conclude that \[X\left([\sigma_{\alpha'}]_{\alpha \to \mathcal{U}} \circ \Delta_M\right) \neq X\left([\sigma]_{\alpha \to \mathcal{U}} \circ\Delta_M\right)\] and since \(X\) is certainly a function from \(\operatorname{\mathbf{Mod}}(T)(M, M^{\mathcal{U}}) \to \mathbf{Set}\left(X(M), X\left(M^{\mathcal{U}}\right)\right)\), this means that \[[\sigma_{\alpha'}]_{\alpha \to \mathcal{U}} \circ \Delta_M \neq [\sigma]_{\alpha \to \mathcal{U}} \circ\Delta_M.\] But this inequality says that there is some \(a \in M\) such that for every \(\alpha\), there is an \(\alpha'\) such that \(\{\sigma_{\alpha'}(a)\}_{\alpha}\) disagrees with \(\{\sigma(a)\}_{\alpha}\) on some \(\mathcal{U}\)-large set of indices \(P\). Letting \(c = a\) and \(d = \sigma( c )\), we have that a \(\mathcal{U}\)-large subset of \(\{\sigma_{\alpha'}(a)\}_{\alpha}\) lies outside of the basic open \(B_{c \hspace{0.5mm} \mapsto \hspace{0.5mm} d} \ni \sigma\). Since \(\mathcal{U}\) contains all the principal filters in \(\mathcal{D}\), we have that for every \(\alpha \in \mathcal{D}\), the intersection \(P \cap P_{\alpha}\) is nonempty. So, for the basic open \(B_{c \hspace{0.5mm} \mapsto \hspace{0.5mm} d} \ni \sigma\), we have that for every \(\alpha\) we can find some \(\alpha'' \in P \cap P_{\alpha}\) such that \(\sigma_{\alpha''} \not \in B_{c \hspace{0.5mm} \mapsto \hspace{0.5mm} d}\). Therefore, \([\sigma_{\alpha}]_{\alpha \in \mathcal{D}}\) does not converge to \(\sigma\), which is the contrapositive.
Definition. Fix \(X\) a functor \(\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) which restricts to continuous maps on automorphism groups. Fix \(M \models T\). From the continuity we can associate to every tuple \(x \in X(M)\) a tuple \(a_x \in M\) as follows: the preimage \(X^* \operatorname{Stab}(x)\) of the basic open subgroup \(\operatorname{Stab}(x) \subseteq \operatorname{Sym}(X(M))\) must be open, and must therefore be covered by the cosets of a basic open subgroup of \(\operatorname{Aut}(M)\), which is of the form \(\operatorname{Stab}(a_x)\) for some tuple \(a_x\).
We call the tuple \(a_x\) the support of \(x\). It satisfies the following property: whenever \(\sigma_1, \sigma_2 \in \operatorname{Aut}(M)\) agree on \(a_x\), then \(X \sigma_1, X \sigma_2\) agree on \(x\). By sending \(a_x \mapsto x\) and letting \(\operatorname{Aut}(M)\) act, this induces an \(\operatorname{Aut}(M)\)-equivariant surjection from the orbit of \(a_x\) to the orbit of \(x\).
Lemma. Let \(T\) be any theory, and let \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) be a \(\Delta\)-functor. Then \(X\) preserves filtered colimits of models: for any model \(N\), if \(N\) can be written as the filtered colimit \(N \simeq \operatorname{\underset{\longrightarrow}{\lim}} M_i\), then \(X(N) \simeq \operatorname{\underset{\longrightarrow}{\lim}} X(M_i)\).
First, we’ll show that being a \(\Delta\)-functor implies that elementary embeddings are sent to injective functions:
Claim. Let \(f : M \to N\) be an elementary embedding. Then \(X(f) : X(M) \to X(N)\) is injective.
[Proof of claim.] By Scott’s lemma (see e.g. Bell and Slomson’s Model Theory for a proof), there is an ultrapower \(M^{\mathcal{U}}\) of \(M\) and an elementary map \(g : N \to M^{\mathcal{U}}\) such that the diagram

commutes. Since \(X\) was assumed to be a \(\Delta\)-functor, the diagram

commutes. Since \(\Delta_{X(M)} : X(M) \hookrightarrow X(M)^{\mathcal{U}}\) is injective and \(\Phi_{(M)}\) is a transition isomorphism, \(X(\Delta_M)\) is injective, and therefore the composite \(X(g) \circ X(f)\) is injective. Therefore, \(X(f)\) was injective.
Claim. For any \(N \models T\), the collection of maps \(\{X(f) \operatorname{\big{|}} f : M \to N, M \text{ countable}\}\) jointly surject onto \(X(N)\).
[Proof of claim.] Since \(N\) is covered by copies of countable models, we do know that \(\{f \operatorname{\big{|}} f : M \to N, M \text{ countable}\}\) jointly covers \(N\).
Let \(I\) index the elementary embeddings from (representatives of isomorphism classes of) all countable models to \(N\). Let \(\mathcal{U}\) be a non-principal ultrafilter on \(I\) which contains the sets \(P_{\vec{n}} \overset{\operatorname{df}}{=} \{i \in I \operatorname{\big{|}} \operatorname{im}(f_i) \ni \vec{n}\}\), which has the finite intersection property by the downward Lowenheim-Skolem theorem.
Consider the map \[\prod_{i \to \mathcal{U}} M_i \overset{[f_i]_{i \to \mathcal{U}}}{\to} N^{\mathcal{U}}.\] The diagonal copy of \(N\) in \(N^{\mathcal{U}}\) is in the image of this map: if \([n]_{i \to \mathcal{U}} \in N^{\mathcal{U}}\), then \(\{i \in I \operatorname{\big{|}} \exists m_i \text{ s.t. } f_i(m_i) = n\}\) is in \(\mathcal{U}\), so \([f_i]_{i \to \mathcal{U}} [m_i]_{i \to \mathcal{U}} = [n]_{i \to \mathcal{U}}\). Pulling back \(\Delta_N(N)\) along \([f_i]_{i \to \mathcal{U}}\), we obtain a map \(\eta\) from \(N\) into \(\prod_{i \to \mathcal{U}} M_i\) such that the diagram

commutes.
Now apply \(X\), obtaining the commutative diagram (it is easy to check that the extra subdiagrams involving \(X(\eta)\) commute by \(\Phi_{(N)}\) and \(\Phi_{(M_i)}\) being isomorphisms):

In particular, \[\Delta_{X(N)} = [X(f_i)]_{i \to \mathcal{U}} \circ \Phi_{(M_i)} \circ X(\eta).\] This implies that \(\Delta_{X(N)}\) is contained inside the image of \([X(f_i)]_{i \to \mathcal{U}}\).
Now, suppose that the \(X(f_i)\) did not cover \(X(N)\). That is, suppose that there exists an \(x \in X(N)\) such that \(x\) lies outside of the image of \(X(f_i)\) for every \(i \in I\). Then for any \([m_i]_{i \to \mathcal{U}} \in \prod_{i \to \mathcal{U}} M_i\), \(f_i(m_i) \neq x\) for all \(i \in I\). Therefore, \(\Delta_{X(N)}(x)\) is not contained in the image of \([X(f_i)]_{i \to \mathcal{U}}\), a contradiction.
We conclude that \(\{X(f) \operatorname{\big{|}} f : M \to N\}\) jointly surjects onto \(X(N)\). This concludes the proof of the claim.
Claim. Present \(N\) as a filtered colimit of its countable submodels \(M_i\). Then \(X(N) \simeq \operatorname{\underset{\longrightarrow}{\lim}} X(M_i)\).
[Proof of claim.] Our two previous claims show that we may view \(X(N)\) as the union of the \(X(M_i)\)’s. \(\operatorname{\underset{\longrightarrow}{\lim}} X(M_i)\) can be canonically written as \(\) /. \(\) where \((x \in X(M_i)) \sim_E (y \in X(M_j))\) if and only if \(x\) and \(y\) become the same element in some \(X(M_k)\) for \(M_k\) amalgamating \(M_i\) and \(M_j\). It is easy to check that sending an \(x \in X(N)\) to the \(E\)-class of an arbitrary lift \(x' \in X(M_i)\) (for a choice of some \(X(M_i)\) containing \(x'\)) gives a bijection \[X(N) \simeq \operatorname{\underset{\longrightarrow}{\lim}} X(M_i) \text{ by } x \mapsto [x']_E,\] compatible over the \(X(M_i)\)’s. This concludes the proof of the claim.
So far, we have shown that \(X\) preserves filtered colimits of countable models. But every model is a filtered colimit of countable models. Explicitly, if we have \(N = \operatorname{\underset{\longrightarrow}{\lim}}_i N_i\) where the \(N_i\) are possible uncountable, we have that each \(N_i = \operatorname{\underset{\longrightarrow}{\lim}}_j N^i_j\), so that we have written \(N\) as a filtered colimit of countable models \(N^i_j\): \[N = \operatorname{\underset{\longrightarrow}{\lim}}_i \operatorname{\underset{\longrightarrow}{\lim}}_j N^u_j = \operatorname{\underset{\longrightarrow}{\lim}}_{(i,j)} N^i_j\] Then \[X(N) \simeq \operatorname{\underset{\longrightarrow}{\lim}}_{(i,j)} X(N^i_j) \simeq \operatorname{\underset{\longrightarrow}{\lim}}_i \operatorname{\underset{\longrightarrow}{\lim}}_j X(N^i_j) \simeq \operatorname{\underset{\longrightarrow}{\lim}}_i X(N_i).\]
Theorem. Let \(T\) be \(\aleph_0\)-categorical. A functor \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) is definable if and only if there is a transition isomorphism \(\Phi\) such that \((X, \Phi)\) is a \(\Delta\)-functor.
If \(X\) is definable, then its isomorphism to an evaluation functor \(\varphi\) pulls back \(\varphi\)’s transition isomorphism \(\Phi'\) to a transition isomorphism \(\Phi\) for \(X\), and since \((\varphi, \Phi')\) was an ultrafunctor \((X, \Phi)\) is also (these are diagrammatic conditions on \(\Phi'\) and so are invariant under conjugation by isomorphisms).
On the other hand, suppose that \((X, \Phi)\) is a \(\Delta\)-functor. \(\operatorname{Aut}(M)\) acts via \(X\) on \(X(M)\), and so \(X(M)\) splits up into \(\operatorname{Aut}(M)\)-orbits. For each representative \(x\) of these orbits, we know from the remarks following that there is a tuple \(a_x \in M\) which supports \(x\), and the map \(a_x \mapsto x\) induces an \(\operatorname{Aut}(M)\)-equivariant map from the orbit (type) of \(a_x\) to the orbit of \(x\).
Therefore, each \(\operatorname{Aut}(M)\)-orbit of \(X(M)\) is a quotient of an \(\operatorname{Aut}(M)\)-orbit of \(M\) by some \(\operatorname{Aut}(M)\)-invariant equivalence relation. Since \(M\) is \(\aleph_0\)-categorical, these equivalence relations are definable and all types are isolated by formulas, so we can write:
\[X(M) \simeq \bigvee_{i \in I} M(\varphi_i(x_i)) \simeq \bigsqcup_{i \in I} M(\varphi_i(x_i)).\]
By the previous lemma and the fact that colimits always commute with colimits and definable functors always commute with filtered colimits of models, we conclude (writing \(N = \operatorname{\underset{\longrightarrow}{\lim}}_j M_j\)): \[\begin{aligned} X(N) &\simeq \underset{j}{\operatorname{\underset{\longrightarrow}{\lim}}} \left(\bigsqcup_{i \in I} \varphi_i(M_j) \right)\\ &\simeq \bigsqcup_{i \in I} \left(\underset{j}{\operatorname{\underset{\longrightarrow}{\lim}}} \varphi_i(M_j)\right) \\ &\simeq \bigsqcup_{i \in I} \left( \varphi_i( \underset{j}{\operatorname{\underset{\longrightarrow}{\lim}}} M_j) \right)\\ &\simeq \bigsqcup_{i \in I} \varphi_i(N). \end{aligned}\]
Now we will show that the \(I\) indexing the \(\varphi_i\) must be finite.
In the pre-ultrafunctor condition

restricting our attention to just ultraproducts of automorphisms tells us that \(\Phi_{(M_i)} : X\left(\prod_{i \to \mathcal{U}}\right) M_i \to \prod_{i \to \mathcal{U}} X(M_i)\) is a \(\prod_{i \to \mathcal{U}} \operatorname{Aut}(M_i)\)-equivariant bijection, and therefore induces a bijection on the orbits of the action on either side.
Let \(\mathcal{U}\) be some ultrafilter such that \(|I^{\mathcal{U}}| > |I|\). Then, at the countable model \(M\), we have the bijection: \[X \left( M^{\mathcal{U}} \right) \overset{\Phi_{(M)}}{\simeq} \left(X(M)\right)^{\mathcal{U}}.\]
Now, the left hand side is \(\bigsqcup_{i \in I} \varphi_i\left(M^{\mathcal{U}}\right)\). Each \(\varphi_i \left(M^{\mathcal{U}}\right)\) is actually an \(\operatorname{Aut}(M)^{\mathcal{U}}\)-orbit, since \(\varphi_i(M)\) was an \(\operatorname{Aut}(M)\)-orbit. Therefore, the number of \(\operatorname{Aut}(M)^{\mathcal{U}}\)-orbits on the left hand side is \(|I|\).
On the right hand side, we have \(\left(\bigsqcup_{i \in I} \varphi_i(M)\right)^{\mathcal{U}}\). Two points \([x_i]_{i \to \mathcal{U}}\) and \([y_i]_{i \to \mathcal{U}}\) are \(\operatorname{Aut}(M)^{\mathcal{U}}\)-conjugate if and only if there exists a \(P \in \mathcal{U}\) such that for all \(j \in P\), \(\varphi_{x_j} = \varphi_{y_j}\) (where \(\varphi_{x_i}\) means which \(\varphi_k\) \(x_i\) came from.) But, this is the same as saying \([\varphi_{x_j}]_{j \to \mathcal{U}} = [\varphi_{y_j}]_{j \to \mathcal{U}}\). So the number of orbits on the right hand side is \(|I|^{\mathcal{U}}\).
Therefore, \(|I^{\mathcal{U}}| = |I|\), so \(I\) must be finite. Hence there is a formula \(\varphi(x)\) such that \(X(N) \simeq \varphi(N)\) for all \(N \models T\). Since for each \(N\), this isomorphism \(X(N) \simeq \varphi(N)\) is induced via filtered colimits by \(X(M) \simeq \varphi(M)\), this is a natural isomorphism, so \(X\) is definable.
43 notes
·
View notes
Note
So for Sym's new let, me and my friends have a problem with how you can just... walk pastie and thats a perfectly valid solution. like, it's felt very underwhelming in gameplay to us so far with just some very specific situations as outliers. So, since we see sim's role as kind of area/choke denial and that seems to be the case with this ult, what do you think if when interacting with an enemy sim's wall it damaged and slowed you down like her turrets?
Hmmmm I think slowing the enemy would be kind of OP, but knocking an enemy down by 5 HP every time they phase through it would be interesting. Personally I really like watching the scramble that happens when you place the wall diagonally through the point while the enemy’s contesting it, so I don’t really mind that it has the same physics as a Reinhardt shield.
4 notes
·
View notes
Text
So after playing the new sym a bit more:

Her damage potential is pretty obscene; however I think it's less consistent than before. Most of that was with the charge ball, not her laser (although if you have the opportunity to charge up her laser in a teamfight do it because it ramps up to insane levels of damage) and turrets.
That said in general she’s a lot better at either poking from afar or fighting with a full team only; the loss of the lock on laser and her shield projector mean she’s pretty weak 1v1 now. Particularly I’ve noticed it’s now impossible to fight D.Va with her, and hard to fight Genji without flawless accuracy - two heroes she was pretty effective against before (solo).
Her turrets do a lot more damage now it seems, and because they can be launched are fairly nice for "chasing down" low health retreating enemies. That said, they can be shot down in midair, and particularly syms charge ball will destroy a turret in flight instantly, and travels faster; I managed to shoot down all three of an enemy syms turrets in flight that game.
Teleporter is kinda whatever; the delay in it being able to teleport, the fact you need to be exactly on top of it to do so, and the slightly unintuitive mechanism of control stick click all make it more gimmicky than I was hoping for - although I didn’t have anyone on my team who could really effectively use it for ults etc, and I was just in QP so...however I managed to not save myself from a genji ult because I fell off the step the teleporter was on to the one below on ilos, which meant I couldn't activate it (and thus died since I was just standing next to the ulting genji)...
Her ult is better than I thought, although how they showed it being used in videos seems pretty ineffective. I find it most effective to just throw it down diagonally across the point while both teams are contesting it; your team can weave in and out and any major damage ults have to pick one half to activate on only (so pharah, dva, rein, etc ults are a lot less powerful). It's still weak against moving ults like soldier, genji, and maybe roadhog/reaper; I've not seen it against hanzo but I assume it does nothing to that either, but far from the useless thing we were fearing.
#symmetra#fyi i'm p sure i've never gotten 10k damage in a game before lol#i tried to put a read more but i dont think it worked lol#also tbh i probably have had that muh damage on moira or something before but never after 3 rounds only
2 notes
·
View notes
Text
Hackaday Superconference Badge Hacking

At the Hackaday Superconference this year Blaine and I finally decided to try our hand at a conference badge puzzle. The cambadge was introduced a month before the conference with the source code following shortly after so you you could prepare hack ideas and even start prototyping shields and addons. In their words:
It’s a camera. It has games, and it’s designed by [Mike Harrison] of Mike’s Electric Stuff. He designed and prototyped this badge in a single weekend. On board is a PIC32 microcontroller, an OV9650 camera module, and a bright, crisp 128×128 resolution color OLED display.
There would be prizes for best hardware hack, best app hack and even a film fest prize. But most importantly, there was also a puzzle prize. The puzzle firmware was implemented by Mike Szczys with the ciphers being developed by Jeff Rosowski (Krux).
Navigating to the puzzle menu revealed three options in binary, 00, 01, 10.

00 was some graphical 'game', 01 appeared to be a reciting of the hacker's manifesto, and 10 was a ouija board. That's all the information we were given.
PUZZLE 00

We halfheartedly played with the 00 puzzle while trying to be social during the pre party and started to put together a ruleset. A green cursor could be moved around an 8x8 grid by tilting the accelerometer. One button seemed to ‘place’ a red circle under the cursor. Further placements that shared a row (vertically, horizontally or diagonally) would light up the row in orange.

This was presumably a failure scenario but it was puzzling that we still had control of the cursor. A very jetlagged Scotty from StrangeParts got six placements before giving it up and handing it back, suggesting to google it or write a script to solve it. We finally figured out the failure screen allows you to remove a failed placement and continue the game. This allowed us to put down a random six placements and continue taking back movements until we had all eight which went surprisingly quickly. In just a few minutes and roughly five take backs we had "Winner Winner!" printed on screen.

Suspiciously, the menu screen also now has a set of hieroglyphic symbols under the 00 menu item. In googling later, we’d find out later this is a Queens Puzzle and we got a bit lucky. Theres 92 possible solutions but our methodology is called iterative repair and does not guarantee a solution.
PUZZLE 10

We talked to John Dahan who won last year by using the strings command on the binary to find the success email to skip all puzzles. Strings is a common utility that prints all ascii characters it can find in a binary. We talked to Mike who said that wasn't going to work this year, but were were undeterred. Before even bothering to understand the puzzle ruleset we just started looking at the scrubbed source and production hex file. The source was definitely missing the puzzles, though we did get a dist folder with intact elf files. That could come in very handy and also means we don’t have to install MPLAB-X IDE ide to generate it myself. The .hex file was strange though. Generally .hex are intel hex format, ie ascii hex code representation with checksumming, but this was a binary. We wasted a bunch of time here remembering obj-copy stuff, only to realize we weren’t gaining anything and this was indeed a binary we could utilize as is. Running “strings Badge103.hex” output the results in this gist.
After entering eight letters into ouija board the screen reads “What was that?” and appears to tell you which letters you had right by “X”ing out incorrect letters.

This would be super easy in retrospect, but hacking was way more fun. We searched the strings list for “What was that” hoping to find any suspicious text around it.
$ strings Badge103.hex | grep -A 5 "What was that"
What was that?
HACKADAY
MARKUSHESS
None
Not found
Read Err
HACKADAY is indeed eight characters which when entered was answered with “The planchette moves by itself:” and the code “PNIRHJZYL GSIXDF WFDNXJF JH CZDRI.”

Too lazy to bother cracking the cipher we entered “MARKUSHESS.” Though we still have no idea how to crack this code, Markus was the hacker from Clifford Stoll’s The Cuckoo's Egg so we weren’t surprised to receive an egg image.

We were subsequently kicked back out to the puzzle menu now with more symbols.

PUZZLE 01

The puzzle consists of twenty-seven lines of the Hacker’s Manifesto where you must scroll each line left or right to read it on the tiny screen. For some reason the cursor always starts at the fourth line which seems odd. At the bottom there is a list of twenty-seven negative and positive numbers with a four alpha character input to presumably complete the puzzle.

It seems obvious that the list of numbers maps to the lines of the manifesto. We looked to see if aligning the rows might spell a question in far right or left column that we could answer with four characters, but couldn't see anything obvious.

It was a huge pain to click buttons and invariably the badge would turn off or we’d get distracted and lose our place. We glanced through the strings dump for anything that might make sense for puzzle 10, but didn't see anything this time. As the party was ending we spent time running down mysterious QR codes that showed up around the venue thinking they could be related somehow, but were thrown out before we could get more than a few.

Later we woudl find there was a (seperate) prize that unlocked on the badge if you scanned all ten of the mysterious QR codes sprinkled throughout the venues.
The next day we were bored looking at puzzles and wanted to do more reverse engineering. I've been looking for a reason to get better with Radare forever. Radare lets you snoop through binaries, disassemble them, rebuild the function graph, and even edit the code in place! So not unlike a crackme, we could presumably find the code that prints Winner, backtrace to find the branching instruction that decides success, and hardcode it to so that when we enter the game it gives us the winner screen. TLDR feel free to skip this section as we didn’t get anywhere, but we would love guidance to be better at this for the next conference.
HUGE DIVERSION AHEAD
Radare has a bit of a learning curve, as described by a slide from a recent talk from the founding developer, pancake.

We can open our binary file in Radare and analyze it for functions, printing the results.
$ r2 -a mips -e asm.bits=32 Badge103.hex
WARNING: bin_strings buffer is too big (0x02bf8a80). Use -zzz or set bin.maxstrbuf (RABIN2_MAXSTRBUF) in r2 (rabin2)
-- It's not a bug, it's a work in progress
[0x00000000]> aaa
[x] Analyze all flags starting with sym. and entry0 (aa)
[ ]
[aav: Cannot find section at this address
aav: Cannot find section at this address
[x] Analyze len bytes of instructions for references (aar)
[x] Analyze function calls (aac)
[ ] [*] Use -AA or aaaa to perform additional experimental analysis.
[x] Constructing a function name for fcn.* and sym.func.* functions (aan))
[0x00000000]> afl
0x00000000 1 16 fcn.00000000
[0x00000000]>
We should see a huge list of functions, but sadly we don’t. Earlier we found someone saved us having to install MPLAB-X IDE and we also have an unmangled elf to mess with.
$ r2 -a mips ~/Downloads/cambadge.X/dist/Normal/production/cambadge.X.production.elf
Warning: Cannot initialize dynamic strings
-- The unix-like reverse engineering framework.
[0x9d009000]> aaa
[x] Analyze all flags starting with sym. and entry0 (aa)
[ ]
[aav: using from to 0x9d000000 0x9d08b3f3
Using vmin 0x9d000000 and vmax 0xbfc00c00
aav: using from to 0x9d000000 0x9d08b3f3
Using vmin 0x9d000000 and vmax 0xbfc00c00
[x] Analyze len bytes of instructions for references (aar)
[x] Analyze function calls (aac)
[ ] [*] Use -AA or aaaa to perform additional experimental analysis.
[x] Constructing a function name for fcn.* and sym.func.* functions (aan))
0x9d008180 1 16 sym._gen_exception
0x9d008200 44 1384 sym.__vector_dispatch_0
0x9d008220 43 1352 sym.__vector_dispatch_1
….
0x9d023cd8 1 8 sym._on_bootstrap
0x9d023ce0 1 8 sym._libc_private_storage
0xbfc00480 3 1908 sym.__DbgExecReturn
[0x9d009000]>
That’s what we’re supposed to see! We can even visualize a complete call graph.

But remember, we know this has all our puzzles stripped so there won’t be much to see here. What we want is this view in our puzzle inclusive binary. Why doesn't our binary ‘hex’ file load cleanly into Radare? Presumably the elf file has a bunch of debug info like sections and entry point (reset vector) to help set up Radare automatically which we don’t understand how to do manually. So how do we help it? In our production dist files we also have a .map file that has the function names and addresses in it. There we find the reset address
.reset 0x9d009000 0x1e4 484 Reset handler
And from cambadge.X.production.elf we can get the entry point(reset vector) to confirm
[0x9d009000]> ie
[Entrypoints]
vaddr=0x9d009000 paddr=0x00009000 baddr=0x9d000000 laddr=0x00000000 haddr=0x00000018 type=program
1 entrypoints
[0x9d009000]>
And we can print the hexdump of the binary code at that location
[0x9d009000]> px @ 0x9d009000
- offset - 0 1 2 3 4 5 6 7 8 9 A B C D E F 0123456789ABCDEF
0x9d009000 0224 400f 0000 0000 0060 1a40 c004 5a7f .$@......`[email protected].
0x9d009010 0500 4013 0000 0000 029d 1a3c a43c 5a27 ..@........<.<Z'
0x9d009020 0800 4003 0000 0000 01a0 1d3c f0ff bd27 ..@........<...'
0x9d009030 00a0 1c3c f07f 9c27 029d 083c d03c 0825 ...<...'...<.<.%
0x9d009040 09f8 0001 0000 0000 00a0 083c 1c00 0825 ...........<...%
0x9d009050 01a0 093c 5cea 2925 0600 0010 0000 0000 ...<\.)%........
0x9d009060 0000 00ad 0400 00ad 0800 00ad 0c00 00ad ................
0x9d009070 1000 0825 2b08 0901 f9ff 2014 0000 0000 ...%+..... .....
0x9d009080 029d 083c f8fb 0825 0000 098d 1800 2011 ...<...%...... .
0x9d009090 0400 0825 0000 0a8d 0400 0825 0000 0b8d ...%.......%....
0x9d0090a0 0900 6011 0400 0825 0000 0c91 ffff 4a25 ..`....%......J%
0x9d0090b0 0100 0825 0000 2ca1 fbff 4015 0100 2925 ...%..,...@...)%
0x9d0090c0 0500 0010 0000 0000 0000 20a1 ffff 4a25 .......... ...J%
0x9d0090d0 fdff 4015 0100 2925 0300 0825 fcff 0a24 ..@...)%...%...$
0x9d0090e0 2440 4801 0000 098d e7ff 2015 0000 0000 $@H....... .....
0x9d0090f0 0000 093c 0000 2925 1000 2011 0000 0000 ...<..)%.. .....
[0x9d009000]>
Back to our puzzle inclusive binary code, Let’s search for that reset vector bytecode “0224 400f” as that shouldn't have changed even with puzzles stripped out:
$ r2 -a mips -e asm.bits=32 Badge103.hex
[0x00000000]> /x 0224 400f
Searching 3 bytes in [0x0-0x2bf8a80]
hits: 5
0x00000e80 hit0_0 022440
0x00006d66 hit0_1 022440
0x000102ce hit0_2 022440
0x000191fe hit0_3 022440
0x00025466 hit0_4 022440
[0x00000000]> px @ hit0_0
- offset - 0 1 2 3 4 5 6 7 8 9 A B C D E F 0123456789ABCDEF
0x00000e80 0224 400f 0000 0000 0060 1a40 c004 5a7f .$@......`[email protected].
0x00000e90 0500 4013 0000 0000 039d 1a3c 9cd6 5a27 ..@........<..Z'
0x00000ea0 0800 4003 0000 0000 01a0 1d3c f0ff bd27 ..@........<...'
0x00000eb0 00a0 1c3c f07f 9c27 039d 083c c8d6 0825 ...<...'...<...%
0x00000ec0 09f8 0001 0000 0000 00a0 083c 3c00 0825 ...........<<..%
0x00000ed0 01a0 093c b0ea 2925 0600 0010 0000 0000 ...<..)%........
0x00000ee0 0000 00ad 0400 00ad 0800 00ad 0c00 00ad ................
0x00000ef0 1000 0825 2b08 0901 f9ff 2014 0000 0000 ...%+..... .....
0x00000f00 029d 083c d478 0825 0000 098d 1800 2011 ...<.x.%...... .
0x00000f10 0400 0825 0000 0a8d 0400 0825 0000 0b8d ...%.......%....
0x00000f20 0900 6011 0400 0825 0000 0c91 ffff 4a25 ..`....%......J%
0x00000f30 0100 0825 0000 2ca1 fbff 4015 0100 2925 ...%..,...@...)%
0x00000f40 0500 0010 0000 0000 0000 20a1 ffff 4a25 .......... ...J%
0x00000f50 fdff 4015 0100 2925 0300 0825 fcff 0a24 ..@...)%...%...$
0x00000f60 2440 4801 0000 098d e7ff 2015 0000 0000 $@H....... .....
0x00000f70 0000 093c 0000 2925 1000 2011 0000 0000 ...<..)%.. .....
[0x00000000]>
Found it! Maybe we can shift our 0x00000e80 address by 0x9D008180 so it becomes 0x9d009000 and Radare has more success analyzing functions? This is where we gave up though. Anyone reading this please reach out if you can help us understand Radare better for the next conference.
Back on track
A day lost, we went back to solving it the honest way -- sort of. Blaine wasn’t even an official attendee so we were having to share a badge. Since we were armed with the strings dump of the manifesto text and list of integes we turned to node to script something to print the columns so we could maybe see what we couldn’t see with our own eyes.
Still, nothing looked right and we went down a hundred other rabbit holes that didn't work out, all the while begging Krux and Mike for any guidance. Finally when the conference ceremony was just hours away Krux helped us find our script had an off by one error. With that fixed it turns out all this time a middle column read “realbunniehuanghardwarehack” Bunnie was perhaps first known for hacking the xbox. “Winner Winner!”
A Fourth Puzzle

Now we had a third set of hieroglyphs and “[email protected]”. To be fair we saw this email in the strings earlier, so we're pretty sure we'd be seeing it again. But what were these glyphs?
Several, especially the last one sure looks like unicode but we couldn’t find many of the rest. We spent a lot of time on that before asking Krux who didn't seem interested in that line of reasoning. We decided to do a transposition arbitrarily to the english alphabet just to play with the characters. Transposing the first character to a, and so one, we got “abcde fgahidjkclefg gmgce ccgcm nkeopfi” There were only 16 distinct 'letters', with c, g, and e being highest in frequency. However this tiny subset of text just doesn't lend to any kind of frequency analysis. We spent a lot of time thinking the spaces were useful and that “ccgcm” would be an odd word with double repeated starting letter. Llama didn’t seem likely, but you never know. We looked at brute forcing rot, morse and other symbol alphabets but didn’t come up with anything that worked before we finally ran out of time.
During the badge ceremony one other team had apparently also got this far and was awarded some cash for their efforts. Mike and Krux spoiled the last puzzle on stage, it's apparently the Commander Keen, Standard Galactic Alphabet. When translated it reads: “PRESTONPLUSWHEATONNINETEENEIGHTYFOUR” which is a Last Starfighter reference. Presumably emailing “Last Starfighter” to [email protected] would have won us the that sweet $256 prize.
Next time
Huge thanks to everyone involved at Superconference. It was a crazy lineup of amazing speakers. It was also awesome to see so much money given away to the Hackaday prize entrants I had been bumping into all weekend. Huge thanks to Mike and Krux for getting us to commit to a badge puzzle for the first time and for helping us through to the (very) end.

0 notes
Text

CETID Sign of the Spiralling
CE(T)* = Lavender Sign • *ID = Prospit + Land
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
#806: A sign for those always growing and always changing, but never learning and endlessly repeating the same mistakes every step of the way. Two steps forward, one step backward...
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
Lavender Signs • Landbound Signs • Prospit Signs
#TTSEZ#Lavender Caste Signs#Signs of Land#Prospit Signs#SYM: Diagonal#SMPL: One#Style: Right Angle#Style: Drops
0 notes
Photo

FORCER Sign of the Riveting
FOR* = Steel Sign • *C = Prospit + Blood
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
#499: A sign for masters of the bolts, nuts, screws, pivots, and nails that keep a community held together. Columns of the community that are very particular about how it operates - one bad turn and they start crumbling.
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
Steel Signs • Bloodbound Signs • Prospit Signs
1 note
·
View note
Photo

LYRIA Sign of the Accepting
LY(R)* = Azure Sign • *RIA = Prospit + Rot
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
#366: A sign for those with unassuming exteriors, so much so that their peers take them as complacent or naive. A sign for those whose interior is bombs, burns, barbed wire, and the gnashing of teeth, all waiting for their time of need. Production fun facts: This sign started life as a banjo (in line with the instruments/music theme of azure caste signs) and eventually mutated into this fish skeleton.
◈≫༻──◇──◇──༺≪◈≫༻──◇──◇──༺≪◈
Azure Signs • Rotbound Signs • Derse Signs
#TTSEZ#Azure Caste Signs#Signs of Rot#Derse Signs#SYM: Diagonal#SMPL: Four#Style: Circle#Style: Trident#Style: Right Angle
1 note
·
View note
Photo

TRUE VOLANS Sign of the Dreamer
VOL* = Garnet Sign • *ANS = Derse + Sleep
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈

The sign of one who shapes the world around them without ever truly living in it, and without whom that world would fall apart. Patron sign of the garnet caste, associated with nightly visions and the recuperation inherent with rest.
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈
Garnet Signs • Sleepbound Signs • Derse Signs
#TTSEZ#Garnet Caste Signs#Signs of Sleep#Derse Signs#SYM: Diagonal#SMPL: Two#Style: Cord#Style: Curvy Sign
5 notes
·
View notes
Photo

ORMURY Sign of the Quizmaster
OR* = Sapphire Sign • *MURY = Derse + Chains
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈

The sign of one who is full of questions, inside and out. They weren't always this way but they're taking full advantage of the opportunity now. This sign's design was inspired by multiple-choice tests, and features a crossed-out "correct" bubble and a null-sign "incorrect" bubble.
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈
Sapphire Signs • Chainsbound Signs • Derse Signs
#TTSEZ#Sapphire Caste Signs#Signs of Chains#Derse Signs#SYM: Diagonal#SMPL: Three#Style: Circle#Style: Half-Circle#Style: Quarter-Circle#Style: Right Angle
2 notes
·
View notes
Photo

HOROLIA Sign of the Wasting
HOR(O)* = Stone Sign • *LIA = Prospit + Rot
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈

A sign for the slow; either slow to change or slow to stay, the blame can be laid at the overabundance of people in their schedule. A quirk of the stone caste is that nearly every sign represents 1 or 2 specific times of day. This sign represents 2:40.
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈
Stone Signs • Rotbound Signs • Prospit Signs
#TTSEZ#Stone Caste Signs#Signs of Rot#Prospit Signs#SYM: Diagonal#Style: Quarter-Circle#Style: Right Angle#Style: Arrow#SMPL: Three
2 notes
·
View notes
Photo

VEXULA Sign of the Rejuvenative
V(E)* = Chocolate Sign • *EXULA = Prospit + Tricks
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈

#155: A sign for those who find new and inventive ways to make their way through the world. Gadgeteers. Urban explorers. Speedrunners. Chocolate signs like this are designed to be paired with a moss and verdigris sign to create a larger image. This sign's partners are Puppvi and Carpio, which it combines with to form the image of a rowboat with rower. This post was edited on 4-26-2020 to bring it up to speed with the current post format.
◈≫༻───◇───◇───༺≪◈≫༻───◇───◇───༺≪◈
Chocolate Signs • Tricksbound Signs • Prospit Signs
#TTSEZ#Chocolate Caste Signs#Signs of Tricks#Prospit Signs#SYM: Diagonal#SMPL: Two#Style: Right Angle
2 notes
·
View notes
Photo

FORECULA Sign of the Level
FOR* = Steel Sign • *ECULA = Derse + Tricks
This sign is the symbol created by Denis Moskowitz for the constellation Norma. Norma is a constellation that was not chosen to be a patron sign of the TTS hemospectrum and was inserted into the steel caste.

2 notes
·
View notes