#bivectors
Explore tagged Tumblr posts
Note
Bivectors

24 notes
·
View notes
Text
More on time derivatives of integrals.
[Click here for a PDF version of this post] Motivation. I was asked about geometric algebra equivalents for a couple identities found in [1], one for line integrals \begin{equation}\label{eqn:more_feynmans_trick:20} \ddt{} \int_{C(t)} \Bf \cdot d\Bx = \int_{C(t)} \lr{ \PD{t}{\Bf} + \spacegrad \lr{ \Bv \cdot \Bf } – \Bv \cross \lr{ \spacegrad \cross \Bf } } \cdot d\Bx, \end{equation} and one for…
View On WordPress
#bivector#boundary#convective derivative#curl#divergence#dot product#Feynman&039;s trick#gradient#Hestenes overdot notation#Leibniz integral theorem#multivector#parameterization#vector#wedge product
0 notes
Text
Mathematical Etymology (cont.)
more excerpts from the Veriloquace Glossary o'Mathematics, a reference quire in the Merch language compiled by Rotcham [Rochdale] University Primers.
æther /ˈiː.θə/ [field] the assignment of a quantity (e.g. a dart [vector]) to each point in space. In the modern sense from the late 19C, formerly used to refer to the supposed medium within which phenomena like light, heat or astraphor [electricity] propagate. Early Merch ether (later re-classicised) < Old French < Latin æthēr "the heavens" < Greek αἰθήρ • aithḗr "heavens, open sky".
hedre /ˈhɛ.də/ [face; bivector] one of the mozate [2D] components of the surface of a solid figure; a physical quantity of mozate kind, such as rotation. 16C, extracted from compounds like octahedre < Scholastic Latin -hedrum "-faced" < Greek ἕδρᾱ • hédrā "seat, chair; face".
matching /ˈma.tʃɪŋg/ [bijection] a reversible correspondence between the elements of two collections W and X, both severing [injective] and covering [surjective], so that each element of X is associated to a unique element of W and vice versa. 1831 < translation of Saxon jochung "yoking" in Dümmeyer, 1827. The verb match comes from the identical noun < Old English mæċċa "consort" < Classical German macciō "partner".
oversamn /ˈoː.sa.mn̩/ [superset] a collection X which contains all of the elements of another collection W, and usually more besides. 1831 < calque of Saxon övrsammel in Dümmeyer, 1827. Noun samn "set" < Old English verb samnian "collect, gather" < Classical German samnō "I gather".
stepth /ˈstɛpθ/ [gradient] the ratio of a change in vertical displacement to the corresponding change in horizontal displacement, a measure of how sloped an incline is. 1690 in mathematics < early Merch steapth < adjective steap "steep, sheer" < Old English stēap "high, lofty" < Classical German staupas "high, lofty".
vater /ˈvɛː.tə/ [sine] the ratio of the lengths of the side of a triangle opposite a given angle to the length of the hypotenuse. 17C < Scholastic Latin vatrus (cf. earlier alvatrō etc) < Arabic وَتَر • watar < Sanscrit ज्या • jyā́ "bowstring" for vater.
12 notes
·
View notes
Text
Possible Reason for the 3+1 Dimensional Structure of Spacetime using Geometric Algebra
Outermorphisms are a generalisation of matrices to work with geometric algebra: they distribute over addition and the outer product. Scalars are left unchanged, and vectors are modified in a similar way to how matrices work for vectors in R^{n}, however this also works on bivectors and any multivectors in general. It turns out that if we have a geometric algebra that is equivalent to the outermorphisms over it, we require n^{2}=2^{n} (n^{2} for the number of degrees of freedom of outermorphisms, and 2^{n} for the number of degrees of freedom for geometric algebras) where n is the number of basis vectors. This is only satisfied by n=2 and n=4. By brute forcing the possible combinations of quadratic forms, we end up with the only geometric algebras that are isomorphic to the algebra of outermorphisms over it are G(1,1) and G(3,1)
G(3,1) has the exact metric of spacetime, meaning that a theory that only works with the geometric algebra associated with the base space being isomorphic to the outermorphisms forces the -+++ metric on the theory.
0 notes
Text

Coasters (Set of 4) - Bivector Overlaunch, Artsy blur, wavy, gradient and pixelate black and white background
Abstract designs challenge traditional notions of representation, inviting viewers to appreciate art in a more imaginative and non-literal manner. Abstract designs are artistic compositions that prioritize the use of shapes, lines, colors, and forms divorced from their representational or real-world references. Abstract art is a diverse and innovative artistic movement that prioritizes non-representational and non-figurative forms. Art allows you to explore and express their creativity beyond the constraints of depicting recognizable objects or scenes.
Bivector Overlaunch, Coasters (Set of 4).
Order available in @Redbubble
#like4like#product#style#random#graphic#decoration#wall#latest#ecommercestore#shopping#item#background#cool#pattern#wallpaper#art#gradient#splash#items#design
0 notes
Text
how am i of all people just finding out that on the inside of my body there are three semicircles of motion-detecting fluids laying in perpendicular planes to each other in each ear for my body to determine my spatial orientation
two things being orthogonal to each other is rare enough in nature as is and THREE orthogonal things is unheard of, so seeing it happen in EXACTLY the type of situation you’d expect if you’ve ever had to deal with the inefficient grotesqueness of non-orthogonal vector bases (or in this case, technically bivector bases) is CRAZY
there's an STL file of an MRI scan of one over on Wikipedia - https://en.wikipedia.org/wiki/File:3DPX-002432_Cochlea_and_semicircular_canals_Nevit_Dilmen.stl - and look at this shit oh my god it looks like you could put a cube in that corner
and so i nested the blender default cube in the nook right there ☺️ i should get someone to do this to my body when i die

WHY does the inner ear have a direct line to your stomach? What evolutionary advantage is there to throwing up when you're dizzy?
#only took me forever to remember how to use blender enough to reposition the damn object correctly lmao#be warned - blender thinks the center of the object is ridiculously far away from what it actually is#that made this far harder to actually position to the blender default cube's location
38K notes
·
View notes
Text
Triangle area problem
[Click here for a PDF version of this post] On LinkedIn, James asked for ideas about how to solve What is the total area of ABC? You should be able to solve this! using geometric algebra. I found one way, but suspect it’s not the easiest way to solve the problem. To start with I’ve re-sketched the triangle with the areas slightly more to scale in fig. 1, where areas $A_1, A_2, A_3, A_5$ are…
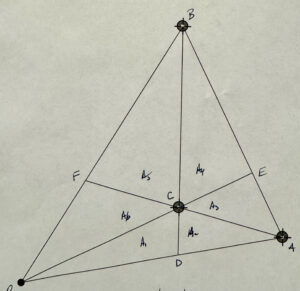
View On WordPress
0 notes
Text
Flat Bead Crochet Tests
Flat Bead Crochet Tests of Threads, Beads, Stitches - I tested several things for my upcoming jewelry class, "Bivector Bangle". Flat bead crochet is rarely slip stitched, even though it's great how the beads are fully visible on both sides!

These four swatches test beads, threads, and stitches for my upcoming jewelry class, “Bivector Bangle, The Class”. I’ve specified flat bead crochet in this blog post for two reasons.
First, I photographed them flat before seaming into a stretchy tube. Slip stitch crochet makes it easy to slip it on the wrist with a good fit; that’s the “bangle” part.
Not the Rope Kind
Second and maybe…
View On WordPress
0 notes
Text
Yeah it's gauge invariance. You can find a section on it on the charge conservation wiki page.
Also, another fun Noether's theorem fact: Conservarion of probability, you know the whole Born probability thing (specifically bivector magnitude, the square magnitude of field amplitude), is derived from symmetry of duals in the bivector notation of Clifford algebra electromagnetism.
Noether’s theorem implies any conservation law arises from a symmetry, e.g., angular momentum from rotational symmetry or energy due to time symmetry. Is the conservation of charge in electromagnetism due to gauge symmetry, or some other symmetry? I feel like I saw something like this mentioned somewhere once but Google is being unhelpful as usual.
53 notes
·
View notes
Text
BiVector: Community for Geometric Algebra for CGI, Vision and Engineering
https://bivector.net/ Comments
0 notes
Photo

Teaser lagi #art #artmonkey #bin #binart #bivector #vectorart #bestvector #digitalillustration #illustrator #adobeillustrator #ai #clickclickclick #binsketch #bindesign #designer #artist #artwork #sketch #sketching #drawing #draw #design #conceptart #traveller #jackpurcel #bagpackers #backpacker #TakHabisHabis #ZenFone3MaxMy (at Mahkota Cheras)
#traveller#conceptart#bivector#digitalillustration#sketching#jackpurcel#backpacker#illustrator#adobeillustrator#vectorart#bindesign#bagpackers#draw#binsketch#clickclickclick#ai#bestvector#bin#zenfone3maxmy#sketch#designer#artwork#takhabishabis#binart#drawing#artmonkey#artist#art#design
0 notes
Link
Article URL: https://bivector.net/
Comments URL: https://news.ycombinator.com/item?id=20597101
Points: 5
# Comments: 1
0 notes
Link
Since the group SO(n) is not simply connected, the representation theory of the orthogonal Lie algebras includes both representations corresponding to ordinary representations of the orthogonal groups, and representations corresponding to projective representations of the orthogonal groups. (The projective representations of SO(n) are just linear representations of the universal cover, the spin groupSpin(n).) The latter are the so-called spin representation, which are important in physics.
More intrinsically, given a vector space with an inner product[clarification needed], the special orthogonal Lie algebra is given by the bivectorson the space, which are sums of simple bivectors (2-blades) v ∧ w. The correspondence is given by the map {\displaystyle \mathbf {v} \wedge \mathbf {w} \mapsto \mathbf {v} ^{*}\otimes \mathbf {w} -\mathbf {w} ^{*}\otimes \mathbf {v} ,} where v∗ is the covector dual to the vector v;[clarification needed] in coordinates these are exactly the elementary skew-symmetric[clarification needed] matrices.
0 notes
Photo
If the length of AB is standardized to be 1, then the directed length of BA is -1. So I guess the length of a segment of the same absolute length but in a perpendicular direction could be i.
So if e and f are standard basis vectors, we have the labeled sides of this square as if on top and ie on the left, which amounts to -e on top and f on the left.
So the directed area is represented by the bivector (ie)^(if), if we assume a conjugation in the second component like the inner product, should give (ie)^(if)=-(iie)^f=e ^f=f ^(-e)=(-1)f ^e.
In short: yup, that checks out.

168 notes
·
View notes
Text
Bivector transformation, and reciprocal frame for column vectors of a transformation
[Click here for a PDF version of this and previous two posts] The author of a book draft I am reading pointed out if a vector transforms as \begin{equation}\label{eqn:adjoint:760} \Bv \rightarrow M \Bv, \end{equation} then cross products must transform as \begin{equation}\label{eqn:adjoint:780} \Ba \cross \Bb \rightarrow \lr{ \textrm{adj}\, M }^\T \lr{ \Ba \cross \Bb }. \end{equation} Bivectors…
View On WordPress
0 notes
Note
So first off, you're right to point out that there are other theories out there. This was mostly to describe what Schrodinger was doing and then also rag on collapsed postulate for being really stupid, but my post definitely didn't exclude any of the other alternatives.
With that said: The assumption that the Born rule's ultimate source is some kind of mystery or in dispute is given as almost axiomatic in most undergrad or pop science physics explanations of quantum mechanics but it's just not true. I think it's fairly understandable at lower levels though because it's impossible to derive with only complex numbers and most physicists never go beyond that point.
But the moment you're working with Clifford algebras and bivectors of quaternions, it falls right out of the math. It's part of conservation law of bivector duals I mentioned briefly. Essentially the thing that's conserved in the conservation of probability law is the object with which quantum fields are defined, multiplied by its conjugate, and it's no more mysterious than any other derivation of a conservation law. (I think it is kind of embarrassing for our field that a lot of quantum physicists and teachers don't know this one, but not nearly as much as the devotion to the collapse postulate. Like, you don't have to be able to derive it for yourself, but it's a little weird that so many people who work with quantum physics think this is a mystery when it's extremely settled physics at the core of the standard model.)
Pilot wave theory is a continual source of bemusement to me. Because like, it's a really good way to visualize quantum mechanics. I really appreciate it as a teaching tool. But ummmm. It's unnecessary? If you take pilot wave theory and just remove the wave packets from it, you get many worlds. The wave packets part of it does nothing. It is totally superfluous to any experiment that you could devise, but it adds the violation of causality, CPT symmetry, and the conservation law of bivector duals.
Now, there's no experimental disproof of it in a direct sense, not like how very thoroughly collapsed postulate has been trashed. But I would consider the ability of the standard model to predict new particles, which again is rooted in that bivector dual conservation, to be very strong indirect counterevidence though, and Occam's razor is swinging pretty hard against it. It seems like a lot of extra work and burden of evidence to explain something that doesn't need to be explained.
And I'm aware that there are famous physicists who believe in collapse postulate, but it's still baffles me. Just a couple years ago there was a new thought experiment about nested and enangled Schrödinger cats that purported to demonstrate a paradox in quantum mechanics. And my very first thought was "paradox in quantum mechanics or just everything but many worlds?"
Wouldn't you know it, it's not a paradox in many worlds! It was in fact, quite baffling to me! This paper went over seven different models of quantum mechanics and how each and every single one of them either struggled with paradox or lacks the mathematical formalism to describe the scenario unambiguously. They talked about the need to add structure to certain theories or to refine them and talked in wonder about whether this might mean there's some aspect of quantum mechanics we haven't seen yet.
And then you get to the many worlds section. And it is a single paragraph noting that this isn't a problem for many worlds, without even bothering to lay out the math for it, but with phrasing that implies they're not going to talk about it more because that's absurd. And then they get to the conclusion and they talk about basically every formalism except for many worlds. You know, the thing I would argue their paper showed handle their thought experiment better than any other formalism out there!
The absolute desperation of some quantum physicists to believe in a single unified worldline baffles me, and at this point it's just embarrassing. Like, we all recognize the existence of multiple worldlines, it is fundamental to our math. Anyone doing work on quantum computing can tell you, the experimental results we see are just not possible without the superposition of indescribably many states across macroscopic regions between hundreds of particles, and that these particles slowly fall out of coherence and become unable to interact with one another even when we erase their distinguishing entangled particles under the action of noise from the rest of the world. You know. What many worlds describes.
But for some reason so many physicists are obsessed with trying to find a way where this describes how the world works for everything but us. And just ... no. Since when has trying to define a theory of physics which places a unique emphasis on humans in the absence of direct evidence ever worked out for us?
Anyway, sorry if this was a bit acerbic. I have just dealt with a lot of very dumb stuff around collapse postulate in my time. I have lost track of the number of professors with phds I have spoken to who were not aware of the experimental tests disproving the wave function size limit aspect of collapse postulate who just ... did not bother reevaluating anything and who later kept teaching it. And I don't mean they looked at the evidence and found it wanting, I mean they looked at it, acknowledged it, acknowledged that it wasn't compatible with their lessons, acknowledged that quantum physics keeps working even without a specific threshold at which collapse occurs, and then just ... internalized nothing.
It's really weird. I don't know why there is so much resistance to letting go of collapse postulate, or for permitting many worlds as one of the alternative explanations. I have never heard any complaint about many worlds other that doesn't book down to "that's too many worlds" and like. This is quantum physics y'all. Since when have we ever shied away from counterintuitive results that fell out of the math?
Why is this the line?
Hey I just wanted to say that despite formally studying and doing research in physics my entire adult life, with a particular interest in standard model field theory, I never felt like I really understood the weak force until your angels / god / physics post. You've got a real talent for this stuff, and the understanding of these topics you have without a formal education on the topic is genuinely astounding. The other knowledge I've seen you display too, heck even just the questions you know to ask.
So thanks for the insight and, if it matters, you have this random physics researcher's seal of approval to be ridiculously proud of your understanding of physics.
Thanks! I had a thing a little while ago where I was absolutely determined to try to finally understand the weak force/electroweak symmetry breaking even though I had literally none of the mathematical background necessary to do so, and thanks to a ton of really good explainers online and some very patient mutuals on Tumblr I think I finally got to a point where it made some kind of sense.
I do think this area of physics is one that sometimes suffers from suboptimal analogies when trying to communicate these concepts qualitatively--there's a problem where formally correct analogies are sometimes difficult to use to build intuition and where intuitive analogies deviate from formal correctness in important ways. There are a ton of stock analogies in physics that I think get repeated because they are seen as canonical somehow, but which are actually kind of misleading if you're not very careful about how you explain them. Most explainers of electroweak symmetry breaking definitely suffer from this a little bit!
81 notes
·
View notes