#category theory

[algebraic-dumbass]

[math-memes]

[janmisali]

now if you thought "group" is an unhelpful and nondescriptive name for a mathematical concept. just remember that the broader category of mathematical concepts that groups belong to is called, a "category". so it could always be worse

[proof-by-intimidation]

A lot of diagrams were chased today.

[algebraic-dualist]

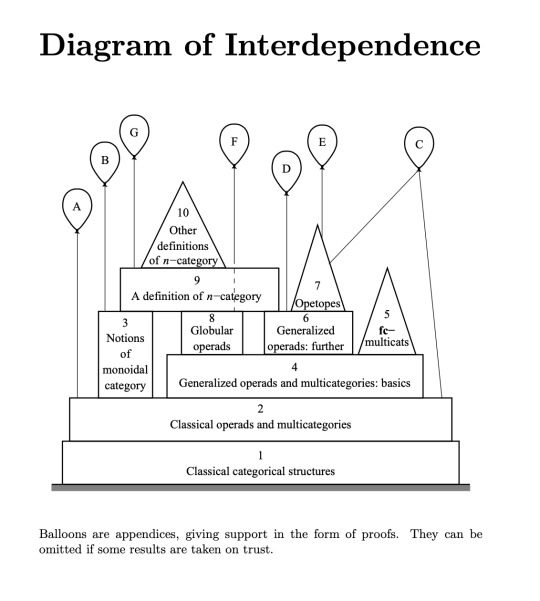
Every book should have a diagram of interdependence like this (taken from Higher Operads, Higher Categories).

[zemathememequeen]

"The mathematicians delved too greedily and too deep. You know what they awoke in the darkness."

[positively-knotted]

The polycule category

So obviously a polycule is just an undirected graph with no double edges or self-loops. Properly we should probably only consider connected polycules, but for technical convenience we'll say that an object of Polycule isn't necessarily connected.

The big question is what is a morphism of polycules. The natural idea is that a morphism should roughly be a cobordism, reflecting the evolution of a polycule.

Inspired by this, we define the following elementary morphisms:

A(v): Addition/deletion of a disconnected vertex v;

E(v,w): Addition/deletion of an edge between v and w.

We probably want to define a morphism to just be sequence of elementary morphisms (that is, a word). But to make things slightly interesting, we add two equivalences:

(Independence). If W, X are words involving disjoint sets of vertices, then WX = XW.

(Antibubbling). A(v)A(v) = E(v,w)E(v,w) = id.

Informally, changes in separated parts of the polycule commute, and if you form a relationship and break up (or vice versa) too fast it doesn't count.

So a morphism in Polycule(G,H) is an equivalence class of words taking G to H.

Interesting properties?

Idk but it probably has some. I wanted the empty polycule to be initial but there are two maps from the empty set to u—v—w depending on the order that you add the edges.

So yeah. I assume it has properties but I'll leave that as an exercise to the category theorists.

[mildlyramified]

Love math textbooks so much <333

[homotexas]

proof by stirring it then blowing a bubble

[lipshits-continuous]

A Short Intro to Category Theory

A common theme in mathematics is to study certain objects and the maps between that preserve the specific structure of said objects. For example, linear algebra is the study of vector spaces and linear maps. Often we have that the identity maps are structure preserving and the composition of maps is also structure preserving. In the case of vector spaces, the identity map is a linear map and the composition of linear maps is again a linear map. Category theory generalises and axiomatises this common way of studying mathematical objects.

I'll introduce the notion of a category as well as the notion of a functor, which is another very important and ubiquitous notion in category theory. And I will finish with a very powerful result involving functors and isomorphisms!

Definition 1:

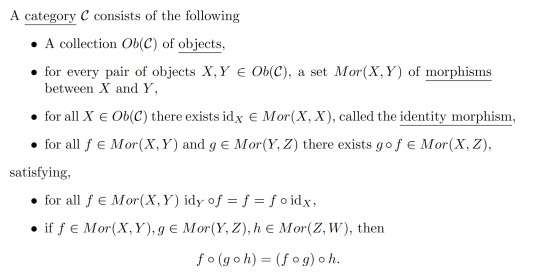
We call the last property the associative property.

Here are some examples:

Examples 2:

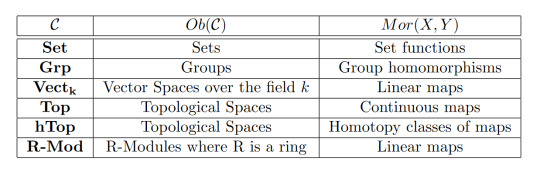
Note that whilst all of these examples are built from sets and set functions, we can have other kinds of objects and morphisms. However the most common categories are those built from Set.

Functors:

In the spirit of category theory being the study of objects and their morphisms, we want to define some kind of map between categories. It turns out that these are very powerful and show up everywhere in pure maths. Naturally, we want a functor to map objects to objects and morphisms to morphisms in a way that respects identity morphisms and our associative property.

Definition 3:

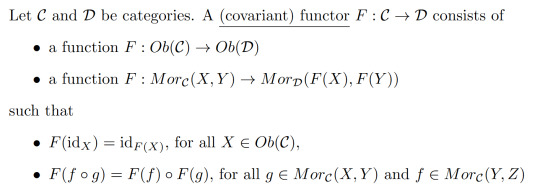
Example 4:

For those familiar with a some topology, the fundamental group is another exmaple of a covariant functor from the category of based spaces and based maps to Grp.

We also have another kind of functor:

Defintion 5:

It may seem a bit odd to introduce at first since all we've done is swap the directions of the morphisms, but it turns out that contravariant functors show up a lot!

This example requires a little bit of knowledge of linear algebra.

Example 6:

In fact, this is somewhat related to example 5! We can produce a contravariant functor Mor(-,X) is a similar way. For V and W vector spaces over k, we have that Mor(V,W) is a vector space over k. In particular, V*=Mor(V,k). So really this -* functor is just Mor(-,k)!

Isomorphisms

Here we generalise the familiar notion of isomorphisms of any algebraic structure!

Definition 7:

For a category of algebraic objects like Vectₖ, isomorphism are exactly the same as isomorphisms defined the typical way. In Top the isomorphisms are homeomorphisms. In Set the isomorphisms are bijective maps.

Remark:

So if f is invertible, we call it's right (or left) inverse, g, the inverse of f.

Isomorphisms give us a way to say when two objects of a category are "the same". More formally, being isomorphic defines an equivalence relation.

Lemma 8:

A natural question one might as is how do functors interact with isomorphisms? The answer is the very important result I hinted at in the intro!

Theorem 9:

Remark: In general, the converse is not true. That is F(X) isomorphic to F(Y) does not imply X is isomorphic to Y. An example of this is the fundamental groups of both S² and ℝ² are isomorphic to the trivial group but these spaces are not homeomorphic.

Taking the negation of Theorem 9 gives us a very powerful result:

Corollary 10:

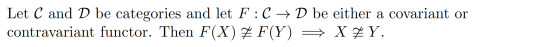
This means that if we can find a functor such that F(X) and F(Y) aren't isomorphic, we know that X and Y are not isomorphic. This is of particular importance in algebraic topology where we construct functors from Top or hTop to a category of a given algebraic structure. This gives us some very powerful topological invariants for telling when two spaces aren't homeomorphic or homotopy equivalent. (In fact, this is where category theory originated from!)

[abalidoth]

If a homophobe is someone who can't cooperate with homosexuals, then a cohomophobe is someone who cohomosexuals can't operate with

[algebraic-dumbass]

babe, are you ok? you've barely drawn any commutative diagrams today :/

[pv1isalsoimportant]

Babe, you've left your infinity-category lecture notes at my house-

[m---a---x]

So you people like convoluted diagrams, too?

Here ya go, filthy

[proof-by-intimidation]