#group theory

[knotty-et-al]

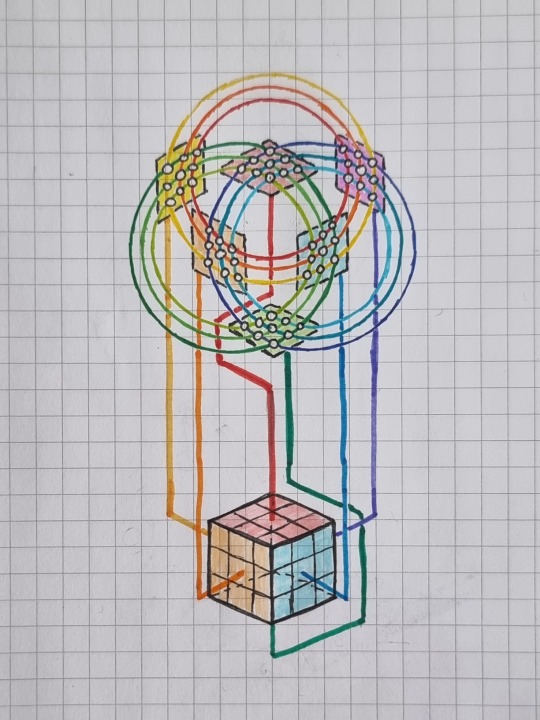
Visualization of the Rubik's cube

[janmisali]

now if you thought "group" is an unhelpful and nondescriptive name for a mathematical concept. just remember that the broader category of mathematical concepts that groups belong to is called, a "category". so it could always be worse

[algebraic-dumbass]

(talking about a group homomorphism from G to the circle group) yeah χ is quite a complex character in this story

[groupoids]

"I was told that generators in the braid group were their own inverse," I said, double-crossed.

[xyymath]

Symmetry: The beauty of Mathematics

Listen, symmetry isn’t just aesthetic. It’s the backbone of mathematics, the reason your equations behave, and honestly, the only thing keeping some functions from spiraling into utter chaos. And here’s the truth: symmetry isn’t just about looking pretty; it’s about mathematical harmony, balance, and the deeply satisfying moment when everything aligns perfectly, just as it should.

The Y-Axis Mirror Selfie (a.k.a Even Functions)

2. The Rotational Drama Queens (a.k.a Symmetry about the Origin; odd functions)

3. Group Theory Symmetry : the reason your Rubik's Cube works and why physicists don’t spiral into existential despair when studying quantum particles.

Cyclic groups, Dihedral groups and Lie groups

4. Polar Coordinates—aka the Art Students of Math

Polar graphs SCREAM symmetry. Roses? Circles? LEMNISCATES?

the bottom line : Symmetry is how we recognize order in chaos. And symmetry isn’t just confined to math. You see it in biology (DNA), art (da Vinci’s Vitruvian Man), and even in the way we naturally find faces with symmetry more attractive. It's everywhere, from the humble parabola to the complex eigenfunctions of quantum systems. So next time you plot a graph, take a second to appreciate the sheer elegance of its symmetry. Or lack of symmetry—because asymmetry can be just as hot.

[changing-notation]

I've got this idea for a very short introduction/presentation of group theory titled "Groups from ℤ to A" where you introduce basic notions of groups in the context of the integers (and how they generalize), move onto more general non-cyclic and non-abelian groups and for the final section you hit the simplicity of A_5 and such

[lipshits-continuous]

Only in mathematics will someone say something like "the empty word"

[spectrallysequenced]

Cute Group Theory Problem

I've been TAing for this math summer program at Penn, and we were doing some group theory on a Rubik's Cube. I gave them the problem of finding the center of the Rubik's Cube group, which is a really cute problem! (I actually got this problem from emily riehl by proxy, and by which I mean I learned it from someone who heard it from emily riehl).

So yea, try and determine Z(G) for G the Rubik's Cube Group.

RB for hints.

[more-mathematics-mor-lam]

Finally understanding group actions and all it took was looking at this picture (from Michael Artin’s Algebra)

[eka-mark]

One of students jokingly said something, when we were just talking about getting started learning math, about learning "the arcane secrets of the universe". There's only one piece of math I know that actually feels like an arcane secret of the universe to me, and it's the existence of the exceptional outer automorphism of S_6.

[mathman0k]

The phrase "give a single fuck" implies fucks form part of a group with a multiplicative identity. However, they are not commutative because giving a fuck before an event has a different effect than giving a fuck afterwards. This also implies that there is a multiplicative inverse to giving a fuck, which in general can be shown to be true.

Thus, fucks can form a non-commutative multiplicative group.

[janmisali]

idea I had for notation for the symmetric group S4 (the rotational symmetries of a cube, the rotations and reflections of a tetrahedron, the permutations of a list of four objects, etc). this is the multiplication table for the "numbers" in this group, for example dr = z.

[algebraic-dumbass]

hey! I'm a 4th year math undergrad in the States and I am astounded by your knowledge of algebra. it's my favorite branch of math and I know a lot more than my peers but not nearly as much as you. where did you learn? any textbook recommendations?

keep up the great mathematics and posts!

haha, well, I don't know that much algebra to be honest (me using a fancy word in a joke means i have heard of it before, not that I actually know how to work with it!)

But yknow I could give out some resources, so here they are (so far I have mostly learned from classes but yknow i'm at that point where i'm starting to need to transition from listening to someone ramble to reading someone's ramblings and then rambling myself)

For basic linear algebra I didn't learn through a textbook, but I have heard good things about Sheldon Axler's Linear Algebra Done Right and it seems similar to what the classes I had did (besides the whole hating on determinants part, though I kinda get it).

For some introductory group theory, I also had a class on it, but the lecture notes are wonderful. I would happily give the link to them here but since they're specifically the lecture notes of the class from my uni I would be kinda doxxing myself. Also they're in French. I will give out some of the references my prof gave in the bibliography of the lecture notes (I have not read them, pardon me if they're actually terrible and shot your dog): FInite Groups, an Introduction by Serre (pdf link), Linear Representations of Finite Groups also by Serre (pdf link), Algebra by Serge Lang (pdf link). Since our prof is a number theorist he sometimes went on number theory tangents and for that there's Serre's A Course in Arithmetic (pdf link). I'm starting to think our prof likes how Serre writes.

For pure category theory and homological algebra I have read part of these lecture notes. I think a good book for category theory is Emily Riehl's Category Theory in Context (pdf link). For homological algebra, a famous book that I have read some parts of is Weibel's An Introduction to Homological Algebra (pdf link). Warning: all pdfs I found of it on the internet all have some typographygore going on. If anyone knows of a good pdf please tell me.

For commutative algebra, A Term of Commutative Algebra by Altman and Kleinman (pdf link). I haven't read all of it (I intend to read more as I need more CA) but the parts of it I read are good. It also has solutions to the exercises which is neat.

For algebraic geometry (admittedly not fully algebra), I am currently reading Ravi Vakil's The Rising Sea, and I intend on getting a physical copy when it gets published because I like it. It tries to have few prerequisites, so for instance it has chapters on category theory and sheaf theory (though I don't claim it is the best place to learn category theory).

For algebraic topology (even less fully algebra, but yknow), I have learned singular cohomology and some other stuff using Hatcher. I know some people despise the book (and I get where they're coming from). For "basic" algebraic topology i.e. the fundamental group and singular homology I have learned through a class and by reading Topologie Algébrique by Félix and Tanré (pdf link). The book is very good but only in French AFAIK.

For (basic) homotopy theory (does it count as algebra? not fully but what you gonna do this is my post) I have read the first part of Bruno Vallette's lecture notes. I don't know if they're that good. Now I'm reading a bit of obstruction theory from Davis and Kirk's Lecture Notes in Algebraic Topology (pdf link) and I like it a lot! The only frustrating part is when you want to learn one specific thing and find they left it as a "Project", but apart from that I like how they write. It also has exercises within the text which I appreciate.

For pure sheaf theory, a friend recommended me Torsten Wedhorn's Manifolds, Sheaves and Cohomology, specifically chapter 3 (which is, you guessed it, the chapter on sheaves). I only read chapter 3, and I think it was alright (maybe a bit dry). I also gave up at the inverse image sheaf because I can only tolerate so much pure sheaf theory. I will come back to it when I need it. The whole book itself actually does differential geometry, but using the language of modern geometry i.e. locally ringed spaces. I have no idea how good it is at that or how good this POV is in general, read at your own risk.

Also please note I have not fully read through any of these references, but I don't think you're supposed to read every math book you ever touch cover to cover.

thanks for the kind comments, and I hope at least one of the things above may be helpful to you!

[michaelrotonal]

group theoryers: share some groups you think should be more known. I'll start with two of my favorites:

The free Burnside group B(2, 3) (27 elements)

The automorphism group of S6 (1440 elements)

The free Burnside group B(2, 3) is a group it's really hard to type the name of the free group on two generators but any element repeated 3 times becomes the neutral element

The automorphism group of S6 is the group of automorphisms of S6.

[xyymath]

The Mathematical Beauty of Snowflakes

Snowflakes form when water vapor in clouds freezes directly into ice, bypassing the liquid phase in a process called deposition. This typically occurs around a microscopic particle, like dust or pollen, which acts as a nucleus for the ice crystals.

Six-Fold Rotational Symmetry:

Snowflakes typically exhibit six-fold rotational symmetry, meaning that you can rotate a snowflake by 60 degrees around its center, and it will look the same.

This symmetry arises from the hexagonal lattice structure of ice molecules. At a molecular level, hydrogen bonds arrange water molecules in a repeating hexagonal pattern.

Reflectional Symmetry:

Snowflakes also display reflectional symmetry along six axes. If you place a mirror along one arm of the snowflake, the reflection perfectly aligns with the adjacent arm.

Their shape & structure (hint: it has to do with temperature and humidity)

High humidity near 0°C leads to dendritic, branching shapes—those classic, intricate snowflakes we see in illustrations.

Lower humidity or colder temperatures result in simpler shapes, like hexagonal plates or needles.

Group Theory:

The six-fold symmetry of snowflakes makes them a practical example of cyclic and dihedral groups, concepts that are foundational in modern mathematics.

Fractals:

The dendritic arms of snowflakes are often fractal-like, meaning they show self-similarity—smaller branches resemble larger ones.

While not perfect fractals, snowflakes illustrate how recursive growth in nature often creates complex, beautiful patterns.

Why Every Snowflake is Unique

Tiny variations in temperature, wind, and humidity during its fall create differences at a microscopic level, ensuring that no two snowflakes are ever the same.

Why Snowflakes are a Symbol of Nature’s Precision

The hexagonal shape of snowflakes isn't arbitrary—it’s the most efficient way for water molecules to pack together as ice. It mirrors nature’s tendency to optimize, from the spirals of sunflowers to the hexagonal cells of a beehive.

Snowflakes are a testament to how universal rules (like symmetry and molecular bonding) can lead to endless variety. This duality—order creating uniqueness—is a recurring theme in nature and mathematics.

References (& further reading material):

ref 1

ref 2

ref 3

ref 4

ref 5

ref 6

ref 7