#cauchy limits

[foolsdome]

my rendition of Augustin-Louis Cauchy (1789-1857), a prominent french mathematician, as an e-girl

[yoneda-emma]

it's reasonable that cauchy sequences are the main sequences whose convergence people tend to care about but it stills feels odd that spaces like R are called "complete" when there are still sequences whose limits are points at infinity not contained in the space itself - is there some reasonably well-behaved way of making this intuition rigorous?

say we call a metric space M hypercomplete if there is exists no metric space N such that M is a subspace of N and there are sequences in M that have a limit in N but not in M.

Intuitively I would expect the real projective line (i.e. the real numbers but with an additional single point at infinity) to be hypercomplete, and for it to probably be the smallest hypercomplete metric space containing R as a subspace. To everyone reading this who knows more topology and analysis and stuff than me : Do you think that that's actually true or is there some topological weirdness such that there are spaces that contain the real projective line but that let even more sequences be convergent?

[errant-heron]

i can read french okay, although my vocabulary is somewhat limited. for this reason, i love having an excuse to read french monographs on mathematics, e.g. it was the only pdf i could find (honest). even Cauchy's Cours d'Analyse reads basically like 20th-century writing, and most of the technical vocabulary is of recent invention and so cognate with english

[catgirl-lucy]

Polish spaces

Heyy, I've recently been learning some descriptive set theory lately and I wanted to share what I've learned so far. As I understand it so far, descriptive set theory is the study of different complexities of sets in Polish spaces from a view point of set theory and logic. One of the main theorems of descriptive set theory is that, in a Polish space, Borel sets are exactly those sets that are both analytic and co-analytic. In this blog post, I explain what a Polish space is.

I'll start by explaining what a metric space is. A metric space is, roughly, a set with a notion of distance.

Definition. A metric space is a tuple (X,d) with a set X, whose elements are called points, and a function d: X² → [0,∞] that maps a pair of points (x,y) in X to a non-negative real or infinity, d(x,y), called the distance from x to y, and must satisfy the following properties:

d(x,y) = 0 if and only if x = y;

(symmetry) d(x,y) = d(y,x);

(triangle inequality) d(x,z) ≤ d(x,y) + d(y,z).

Here are some examples of metric spaces:

Example. The real line (ℝ,d) with d(x,y) = |y-x|. The positive real line (ℝ⁺,d) with d(x,y) = |y²-x²|. The rational line (ℚ,d) with d(x,y) = |y-x|. The cartesian plane (ℝ²,d) with d((a,b),(c,d)) = √((a² - c²) + (b² - d²)). (ℕ,d) with d(x,x) = 0 and d(x,y) = 1 for x ≠ y.

Here is a non-example:

Example. The real line (ℝ,d) with d(x,y) = (y-x)².

The example (ℕ,d) above is an example of a discrete metric space. A metric space is discrete if the distance between any two distinct points is 1.

A Cauchy sequence is a sequence of points in a metric space where the distance between subsequent points tends to 0. Or, formally:

Definition. Let (X,d) be a metric space. A Cauchy sequence is a sequence (aₙ) of points aₙ ∈ X for which, for all real ε > 0, there is some natural number N such that, for all n ≥ N, d(aₙ,aₙ₊₁) < ε.

For example, (0, 1/2, 3/4, 7/8, ...) is a Cauchy sequence in ℝ and (1, 1.4, 1.41, 1.412, ...) is a Cauchy sequence in ℚ. Some sequences converge to a point in the space:

Definition. Let (X,d) be a metric space, let (aₙ) be a sequence of points aₙ ∈ X and let L be a point in X. The sequence (aₙ) is said to have limit L, denoted (aₙ) → L, lim (aₙ) = L or lim[n → ∞] aₙ = L, if for all real ε > 0, there is some natural number N such that, for all n ≥ N, d(aₙ,L) < ε. A sequence (aₙ) is said to converge if there is some point L such that (aₙ) → L. A sequence (aₙ) is said to diverge if it does not converge.

The limit of a converging sequence in a metric space is always unique, and every converging sequence is Cauchy. The converse need not be true: not every Cauchy sequence is converging. For example, the Cauchy sequence (1,1.4,1.41,1.412,...) in ℚ, which in ℝ converges to √2, diverges in ℚ as √2 is not a rational number.

Definition. A metric space (X,d) is complete iff all Cauchy sequences in (X,d) converge.

An example of a complete metric space is the real line. All discrete metric spaces are also complete as the only Cauchy sequences there are eventually constant.

A topological space is a bit more abstract than a metric space. In a topology, there is still a notion of "closeness" of points, but no notion of "distance". Topological spaces are often created using a basis.

Definition. A topological space is a pair (X,τ) with a set of points X and a family τ of subsets of X, called open sets, that must satisfy the following:

∅ ∈ τ;

X ∈ τ;

For all A,B ∈ τ, we have A ∩ B ∈ τ;

For all F ⊂ τ, we have ⋃F ∈ τ.

I.e. it is closed under all unions and finite intersections.

Definition. Let (X,d) be a metric space, let x be a point in X and let r > 0 be a positive real number. The (open) ball B_r(x) with center x and radius r is the set {y | d(x,y) < r} of all points that have distance <r to x.

Definition. Let X be a set. A basis of a topology for X is a family B of subsets of X such that, for a,b ∈ B, we have a ∩ b ∈ B. Members of B are called basic open sets. The basis B induces the topology (X,τ) where O ⊂ X is open iff O = ⋃F is a union of a family F ⊂ B of basic open sets, equivalently, for all x ∈ O, there is some a ∈ B such that x ∈ a and a ⊂ O.

You can verify that, for every basic B, the topology (X,τ) induces by B is indeed a topology.

Definition. Let (X,d) be a metric space. The topology induced by (X,d) is the topology induced by the basis B = {B_r(x) | r > 0 ∧ x ∈ X} of open balls.

Thus, in a metric space (X,d), a set is open if around each point in the open set, you can draw a little ball that remains in the open set. A metrizable space is a topological space of which the metric has been "forgotten":

Definition. A metrizable space is a topological space (X,τ) for which there exists a metric (X,d) that induces the topology (X,τ).

Not all topological spaces are metrizable. For example, the indiscrete space of two points, {0,1}, where the only open sets are {} and {0,1}, is a topological space that is not metrizable. Similar to a metrizable space, a completely metrizable space is a topological space with a forgotten complete metric:

Definition. A completely metrizable space is a topological space (X,τ) for which there exists a complete metric (X,d) that induces the topology (X,τ).

Let 𝕀 denote the set of irrational numbers. We can define a metric d₁ on 𝕀 by setting d₁(x,y) = |x-y| for irrational x and y. Though (𝕀,d₁) is not a complete metric space, it induces a topology that is completely metrizable by a different metric d₂. The metrics d₁ and d₂ are called "equivalent" as they induce the same topology.

From open sets, a lot of different sets can be defined:

Definition. Let (X,τ) be a topology. A set C ⊂ X is closed if its complement X \ C is open. A set C ⊂ X is clopen if it is both open and closed. A set D ⊂ X is dense if for all non-empty open O ⊂ X, D ∩ O is non-empty.

For example, ℚ and 𝕀 are dense subsets of ℝ. In a metric space, a closed set C is a set where every converging sequence of points in C has a limit in C. We can also define operations on sets:

Definition. Let (X,τ) be a topology and let P ⊂ X be a set. The closure P̄ of P is the ⊂-smallest closed set that includes P. Equivalently, it is the intersection ⋂{C ⊂ X | C is closed and P ⊂ C} of all closed sets that include P. The interior P̊ = int(P) of P is the ⊂-smallest open set included in P. Equivalently, it is the union ⋃{O ⊂ X | O is open and O ⊂ P} of all open sets included in P. The boundary ∂P of P is the set P̄ \ P̊, i.e. the closure minus the interior.

The operations give us a different definition of dense sets: a set D is dense if the closure of D is the whole space X.

Definition. Let (X,τ) be a topological space and let x ∈ X be a point. A neighbourhood (nbhd) of x is a set U ⊂ X for which x ∈ Ů.

For example, in ℝ, [0,1] is a nbhd of 1/2 but not of 0, as int([0,1]) = (0,1) ∌ 0.

Definition. A topology (X,τ) is separable if there exists a countable dense set D ⊂ X.

For example, ℝ, although itself uncountable, is separable as ℚ is a countable dense subset. An example of a space that is not separable is a discrete space of uncountably many points, as all points are need in a set for that set to be dense.

Definition. Let (X,τ) be a topological space and let P ⊂ X be a set. An accumulation point of P is a point x ∈ X for which, for all nbhds U of x, there is some y ∈ P ∩ U for which y ≠ x. An isolated point of P is a point x in P that is not an accumulation point. P is perfect if it is closed and has no isolated points.

For example, in ℝ, 0 is an accumulation point of {1/n | n ∈ ℤ⁺} but 1/2 is an isolated point. We can see that a point x ∈ X is an isolated point of the space X itself iff {x} is an open set, X if perfect if it has no such points as the whole space itself is already always closed.

We can now finally define what a Polish space is:

Definition. A Polish space is a topological space (X,τ) which is non-empty, separable, perfect and completely metrizable.

Some important examples are the real line, ℝ, which we have already seen, the Cantor space and the Baire space.

Definition. The Cantor space 𝒞 = 2^ω has infinite sequences of 0s and 1s as points, and basic open sets are sets U_s = {�� ∈ 2^ω | s ⊂ α} where s is a finite list of 0s and 1s and s ⊂ α means s is an initial segment of α.

Definition. The Baire space 𝒩 = ω^ω has infinite sequences of natural numbers as points, and basic open sets are U_s = {α ∈ ω^ω | s ⊂ α} where s is a finite list of natural numbers and s ⊂ α means s is an initial segment of α.

This took too long to explain... I'll explain these three spaces in more detail next time.

[samueldays]

I see Repugnant Conclusion discourse, and figured I'd throw in my proverbial two cents.

First cent: Parfit's conclusion is vacuous or nearly so. Second cent: Discrete or continuous utils both fail.

Long philosophy below the cut.

1: Parfit's conclusion is vacuous or nearly so.

If you express the question strictly in terms of numbers, 100 utils * 1 person is a greater quantity of person-utils than 1 util * 1000 people, and there's no problem with the maths.

But Parfit has neither an absolute scale for how much 1 util is, nor a relative scale for the exchange rate of Mozart concerts to stubbed toes, nor an interpersonal scale for comparing different people's utils, et cetera. Parfit is attempting to do math on non-numbers when he talks about quality of life. We have no idea how many utils correspond to "Very low but positive quality of life", even though that's a requirement for being able to claim that Z is better than A.

Some number Z may exist that is larger than some other number A. So what? I don't see the relation to human quality of life.

2: Discrete or continuous utils both fail.

Suppose, first, that utils are discrete. There is some minimum quantity of utility where a person can experience 0 utils or 1 util, but not half a util.

In this case the Repugnant Conclusion's addition-and-averaging cycle has a clear stopping point: calculate the total number of utils experienced by the people of scenario A, add one, populate scenario Z with that many people who each experience 1 util in the entirety of their lifetime. There is no further dilution nor averaging to be done.

What is an arbitrary denizen of Z doing when not experiencing the single util of his lifetime? By the stipulations of the scenario, he can't be bored or lonely, that would be negative utility, and he can't enjoy a hobby or community, that would be positive utility. Does he perhaps sleep away the near entirety of his life, wake up once to hear a mildly pleasant tone, and then sleep until death?

Discrete utils seem to lead to absurdity - Z cannot exist.

Let us instead suppose that utils are continuous.

In this case I would describe the Repugnant Conclusion as Parfit attempting to multiply population by infinity, multiply welfare by one over infinity, cancel the (inf/inf) fraction, and noticing that something went wrong but not why. He should take more math classes.

Mathematicians spent lots of time and effort figuring out how to deal with infinity in a good way. For most of history it was just "don't". I cannot speak with confidence here, but I think it gives the right general impression to say that mathematicians took about a century and a half of work to get rigorous about infinity and infinitesimals: from Newton and Leibniz arguing about calculus in the late 17th century to Cauchy's limits and epsilon-delta in the early 19th.

The Repugnant Conclusion for continuous utils is like a divide-by-zero error: you fucked up your maths and thought you made a point about philosophy.

[fennecfoxfavouritefox]

thoughts on the surreal numbers?

I don't know if Cauchy would be proud or mortified. I remember very distinctly the first week of my Advanced Calculus course. Instead of the usual, starting at limits, or with derivatives, my prof spent the entire first 2 weeks proving that the real numbers, formalized using infinite decimals, is complete. At the time, this seemed to me that the case was cut and dry that there were no more holes in the real numbers. Well it turns out that you could always materialize more holes in any numbering system out of thin air, and this thought terrifies me.

I had story concept I wanted to create once. The tiny curled up dimensions, the ones that are sometimes used to justify some string theories, are real actual tangible places, lurking everywhere, dense, and filled with the horrors of infinity. Worlds of cosmic horrors, unfathomable bliss, eternal pain, mundane mediocrity, worlds devoid of nothing but other smaller and smaller and smaller nestled worlds. Such worlds would, given their abundance, inevitably seep their contents into ours, leading to frequent anomalies of horror and wonder. If I was more artistically talented, I would have written or drawn these small places packed everywhere within. But alas I am not.

I don't know how to think of surreal numbers because I don't know how to think about surreal numbers because I don't know how to think about surreal numbers. Conway managed to find some use out of them for game theory. And that is beautiful. Such an esoteric concept being able to find use in an unrelated field. This is the gold standard for math after all, if your math sees use in seemingly unrelated math, it is good math. And surreal numbers passes this test with flying colours.

[sparseposter]

intuition for the central limit theorem

the central limit theorem is a frankly magical theorem. i'll assume everyone reading this post is familiar with it, i'm speedrunning out my thoughts, i don't want to spend too much time on this. but basically yeah why should everything add up to the normal distribution? why should the mean of basically everything be normal?

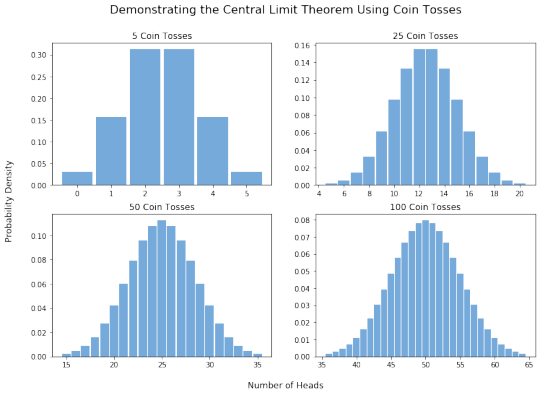
so this bothered me for a long time, it was always kinda insane. i learned about it, and then a while later i learned how to prove it, but i still didn't get it. but then i watched some 3B1B videos (all kudos to them btw) and then specifically i saw this one comment on a video and it all clicked.

basically: what's so special about the normal distribution? like, why *that* one in particular?

well, there's this other property of normal distributions, which may seem unrelated at first but is actually the key to the whole thing: if you add two normal distributions, you get another normal distribution.

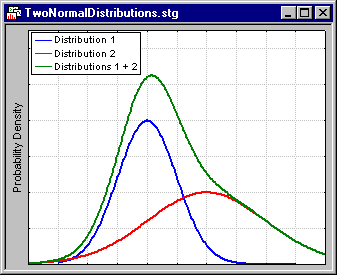
and this is the key to the whole thing! because it means that, when you're doing sums of random variables, normal variables are a *fixed point*.

so at least for me this instantly finally made everything click - things converging to fixed points is just so incredibly natural, it comes up everywhere. to go into a little more detail, distributions where if you add two of them together you get a third one of the *same type* are called stable distributions, and it turns out that the normal distribution is special among stable distributions because it's the unique one with finite mean and variance - all the others, Cauchy, Levy, etc. don't satisfy this condition. i don't understand why but yeah. so then it makes intuitive sense that - if you keep averaging lots and lots and lots of variables which have finite means and variances together and converge to anything at all - it *must* be to the only fixed point which has finite mean and variance: the normal distribution.

[zolo1917]

The Critique of the Foundations of the Hegelian Dialectic

The Critique of the Foundations of the Hegelian Dialectic

The Marxist conception of the dialectic has often been challenged. Max Eastman, for instance, considered it a form of religious thought. However, the dialectic has only been the object of a negative critique. Those who criticized it acted as simple destroyers. They failed to see that by removing the dialectical method from proletarian ideology, they removed the blood from the body; they ignored this because Hegelianism, in whatever form, was incompatible with their ordinary conceptions. Thus, the Marxist dialectic was treated with the same repugnance as the Hegelian dialectic in general.

A new way of conceiving the Hegelian dialectic begins with Nicolai Hartmann's critique, where it is possible to find elements of a true positive critique. Hartmann's indications, as presented in an article in the Revue de Métaphysique et de Morale, express in concise form a direction that is of great interest to Marxist studies. Hartmann examines the different dialectical themes developed in Hegel's philosophy and compares them from the standpoint of their bases and forms. He seeks to distinguish those themes justified by experience from those that have only verbal value. For example, he criticizes the famous theme of being and nothingness.

Hartmann's critique differs fundamentally from the Marxist critique. For Marx and Engels, the dialectic is the general law of fundamental reality, with nature or matter substituted for logic, leading to antithetical development of the universe. Hartmann, on the other hand, methodically tests the value of dialectical reasoning in particular cases, setting aside universality and focusing on areas where the dialectic is justified by lived experience.

One must recognize that Marx and Engels themselves felt the necessity of a labor similar in principle to Hartmann's. Although they aimed to give dialectical conceptions the character of general laws of nature, Engels attempted to provide these laws with experimental value through his study of the natural sciences. However, Hartmann's a posteriori approach contrasts with Engels' a priori method.

Scientists have generally viewed the dialectical construction of relations as incompatible with scientific methods. Hegel himself indicated that nature, by its inability to adhere strictly to the Notion, sets limits to philosophy. Nature was seen as a negation, a revolt, and an absurdity, making it unreasonable for Hegel to seek the foundations of dialectical laws in the study of nature.

Engels' efforts to develop a dialectical theory of nature ultimately faced significant challenges. The substitution of nature for logic in post-Hegelian philosophy became problematic. Today, a new experimental justification of the dialectic is necessary, focusing on the immediate terrain of class struggle rather than universal conceptions.

Engels' attempt to apply the dialectic to the natural sciences, which took eight years and resulted in the second preface to the Anti-Dühring, was not fully successful. This endeavor was often seen as conflicting with the development of modern mathematics and science, which sought to eliminate contradictions and achieve absolute rigor.

In the realm of mathematics, what Engels considered progress was seen by mathematicians as a degeneration. The development of infinitesimal calculus, based on contradictory notions, eventually led mathematicians like Gauss, Abel, and Cauchy to strive for absolute rigor and eliminate logical inconsistencies. Despite Engels' recognition of contradictions in mathematics, mathematicians succeeded in removing these contradictions.

Overall, mathematics evolved to prioritize logical rigor and non-contradiction, contrary to Engels' program. Any new difficulties, such as those in set theory, are approached with the same effort to resolve contradictions, further distancing the field from dialectical thought.

The dialectic does not express the nature of mathematics; it applies to the agent of scientific activity, not the object. The essential theme is to understand the limits of dialectical thought and its fruitful application. As Plekhanov noted, the powerful and fruitful influence of Hegel on moral and political science underscores the importance of understanding and applying dialectical reasoning within its proper context.

The Critique of the Foundations of the Hegelian Dialectic

The application of the dialectic to the sciences and the implied sterility of this method when applied to the natural sciences aligns with the principles in Hartmann's argument, which sought a specific domain for the dialectic. Plekhanov didn't foresee a limit, but he recognized the unique privilege of moral and political sciences—what Hartmann calls "sciences of the spirit." This term is relatively precise, but terminology shouldn't prejudice the nature of the object within a more or less homogeneous group of sciences. No precise limitation can be predetermined.

Hartmann's detailed analysis will help further determine the application of the dialectic. His analysis separates dialectical developments representing lived experience from those that are mere remnants of dead flesh. This investigation extends to recent scientific developments, posing numerous subsidiary problems. The task appears unlimited, and the results of such analyses are unlikely to coincide with initial intentions.

A long, systematic elaboration can lead to a readaptation of general conceptions. The exact point where dialectical thought starts to express real relations must be determined case by case. For instance, the biological development of a man—from infancy to old age—cannot be explained by simple opposition of terms. However, psychological development from a psychoanalytic perspective reveals that a human is initially limited by paternal prohibitions, resulting in unconscious desires for the father's death. This negativity eventually necessitates the son's assumption of the father's role, destroying the negativity that defined him.

This theme is important because it reflects an experience lived by each human being, making the terms of dialectical development elements of real existence. From this example, several problems can be defined, indicating the orientation for the introduction of a dialectic of the real.

The theme of father and son demonstrates that nature has not been replaced by a separate domain. Psychoanalytic phenomena can be reduced to somatic drives, eliminating the need for a matter-spirit dualism. The objects of dialectical investigation are the most complex products of nature, and spiritualism must be set aside.

Nature hasn't been abandoned for unrelated phantoms. A mode of thought founded on lived experience, rather than direct study of nature or pure logic, might still apply to understanding nature. The first condition for this application is recognizing the limits posed by the method's origin, implying that simpler forms of nature could be studied using facts from the most complex.

In practice, a difference emerges between a method based on natural sciences and a dialectic with historical roots in lived experience. In the natural sciences, opposing terms are neutral, but in valuable dialectical examples, negativity has specific value. The fundamental themes of the Marxist conception of history fall into this category, introducing negative forces or actions into tactics as means demanded by historical development. This characteristic is crucial for the suppleness and power of Marxism, opposing reformist solutions and making it the living ideology of the modern proletariat.

This class, condemned by the bourgeoisie to negative existence, now bases its revolutionary activity on creating a new society.

[omegaphilosophia]

The Philosophy of Calculus

The philosophy of calculus explores the foundational, conceptual, and metaphysical questions surrounding calculus as a branch of mathematics. It delves into the nature of continuity, infinity, limits, and the relationship between mathematics and the real world. Since calculus involves concepts such as infinitesimally small quantities, rates of change, and accumulation, philosophers have long debated its implications for our understanding of space, time, and motion.

Key Concepts:

Continuity and Change

Foundational Questions: Calculus, by its very nature, addresses the study of continuous change. Philosophers explore how calculus formalizes change, especially how it captures instantaneous rates of change (derivatives) and accumulations (integrals). The question of how change can be captured mathematically while still being grounded in reality is a central issue.

Zeno's Paradoxes: The ancient Greek philosopher Zeno posed paradoxes, such as the paradox of Achilles and the tortoise, that question how motion and continuity can exist if space and time can be infinitely divided. Calculus provides a mathematical resolution to these paradoxes by showing how infinite processes (like summing infinite series) can yield finite results.

Limits and Infinity

Nature of the Infinite: Calculus heavily relies on the concept of limits, where values approach some end point, often involving infinity or infinitesimally small quantities. Philosophers question what it means for something to approach a value (limit) without ever actually reaching it. What is the status of infinity in calculus? Is it a real, physical entity or a useful mathematical abstraction?

Infinitesimals: In the development of calculus, the idea of infinitesimals—infinitely small quantities—played a crucial role. Philosophers like George Berkeley famously criticized early calculus for relying on "ghosts of departed quantities" that seemed to have no clear ontological basis. Later, the rigorous formalization of limits by Augustin-Louis Cauchy and Karl Weierstrass helped address these concerns, though the concept of infinitesimals remains a subject of philosophical debate.

Mathematical Realism vs. Formalism

Realism: Mathematical realists believe that the objects and structures of calculus (such as limits, derivatives, and integrals) exist independently of human thought, either as abstract objects or as part of the fabric of reality. This perspective raises questions about the relationship between mathematical concepts and the physical world: Does calculus describe real processes in nature, or is it a mere human invention?

Formalism: Formalists, on the other hand, argue that mathematics, including calculus, is merely a system of symbols and rules that humans have devised to model reality. For formalists, the power of calculus lies in its logical consistency and utility, not in the existence of mathematical entities as part of the physical world.

Applications to Space and Time

Mathematics of Motion: Isaac Newton and Gottfried Wilhelm Leibniz, the co-founders of calculus, developed it to study the motion of bodies through space and time. Philosophers ask how calculus models space and time and what this implies for our understanding of reality. Are space and time continuous or discrete, and how does calculus help answer this question?

Relativity and Quantum Mechanics: In modern physics, calculus plays a vital role in theories like general relativity and quantum mechanics. Philosophers of science consider how calculus provides the tools to describe the curvature of spacetime or the probabilistic nature of particles. This brings forth metaphysical debates on the nature of the universe and whether our mathematical tools truly capture its essence.

The Role of Approximation

Calculus as Approximation: In many cases, calculus provides approximations rather than exact answers, especially when dealing with real-world phenomena. Philosophers ask whether this means that calculus only approximates reality, and if so, how accurate these approximations are. What does this say about the limits of human knowledge and the nature of truth in mathematics?

Constructivism vs. Platonism

Platonism: Many mathematicians, such as Kurt Gödel, held that mathematical objects exist in a Platonic realm, independent of human minds. In the philosophy of calculus, this view would suggest that limits, derivatives, and integrals exist "out there" in some ideal form, waiting to be discovered.

Constructivism: On the other hand, constructivists believe that mathematical objects only exist when they are constructed or proven to exist through logical processes. In this view, the objects of calculus, like infinitesimals, do not exist in an abstract realm but are instead tools we create to solve problems.

Historical Development and Philosophical Insights:

Newton vs. Leibniz:

Newton's Fluxions: Newton saw calculus as a way to describe motion and change in the natural world. He introduced the idea of "fluxions" to represent instantaneous rates of change. His view of calculus was closely tied to physical processes, such as the movement of planets.

Leibniz's Infinitesimals: Leibniz focused on the mathematical notation and formal structure of calculus, introducing the concept of infinitesimals. Leibniz’s approach was more abstract, focusing on symbolic representation rather than direct physical interpretation.

Berkeley's Critique:

Criticism of Infinitesimals: The philosopher George Berkeley famously criticized early calculus in his work The Analyst (1734), calling infinitesimals "ghosts of departed quantities." Berkeley’s critique focused on the lack of rigor in the concept of infinitesimals, pushing mathematicians to develop a more solid foundation for calculus, leading to the formal concept of limits.

Modern Foundations:

Limit Theory: The development of rigorous limit theory by mathematicians like Cauchy and Weierstrass resolved many of the early philosophical objections to calculus. By defining limits rigorously, they provided a solid foundation for understanding how calculus could deal with infinity and infinitesimally small quantities.

Non-standard Analysis: In the 20th century, Abraham Robinson developed non-standard analysis, a formal mathematical system that reintroduced infinitesimals in a logically rigorous way. This has revived philosophical discussions about the nature of infinitesimals and their role in calculus.

The philosophy of calculus examines the underlying concepts of change, infinity, and continuity that are central to calculus. It raises questions about the nature of mathematical objects, the relationship between mathematics and reality, and the limits of human knowledge. While calculus has provided powerful tools for understanding the natural world, it also raises deep philosophical questions about the nature of space, time, and motion.

[iit-jam]

IIT JAM Syllabus 2025: A Comprehensive Guide

The IIT JAM (Joint Admission Test for Masters) is one of the most competitive exams for students aspiring to pursue postgraduate studies in esteemed institutions like IITs and IISc. Mathematics, being a core subject, attracts candidates with strong analytical and problem-solving skills. To excel in this exam, a thorough understanding of the IIT JAM Mathematics Syllabus 2025 is essential. This blog outlines the syllabus in detail and provides tips to help candidates prepare effectively.

Overview of IIT JAM Mathematics Syllabus 2025

The IIT JAM Mathematics Syllabus 2025 is crafted to test the candidates' knowledge of fundamental mathematical concepts covered at the undergraduate level. The syllabus is broad, covering topics such as calculus, linear algebra, differential equations, and numerical analysis. Each section focuses on key areas that are crucial for advanced studies and professional applications.

Key Topics in the Syllabus

1. Sequences and Series

This section includes the convergence of sequences and series, tests for convergence (such as comparison, ratio, and root tests), and the study of power series and their radius of convergence.

2. Differential Calculus

Candidates must understand single-variable calculus concepts like limits, continuity, and differentiability. Topics also include Taylor series, mean value theorem, and indeterminate forms. For multivariable calculus, partial derivatives, maxima, minima, saddle points, and the method of Lagrange multipliers are essential.

3. Integral Calculus

This section covers definite and indefinite integrals, improper integrals, and special functions like beta and gamma functions. The application of double and triple integrals is also emphasized.

4. Linear Algebra

A critical area of the syllabus, it focuses on vector spaces, subspaces, linear transformations, rank, nullity, eigenvalues, eigenvectors, and matrix diagonalization. Understanding the solution of systems of linear equations is vital.

5. Real Analysis

This section involves the properties of real numbers, limits, continuity, differentiability, and Riemann integration. Candidates must also be familiar with sequences, Cauchy sequences, and uniform continuity.

6. Ordinary Differential Equations (ODEs)

This includes first-order ODEs, linear differential equations with constant coefficients, systems of linear ODEs, and Laplace transform techniques for solutions.

7. Vector Calculus

Important topics include gradient, divergence, curl, line integrals, surface integrals, and volume integrals, along with Green’s, Stokes’, and Gauss divergence theorems.

8. Group Theory

The basics of groups, subgroups, cyclic groups, Lagrange’s theorem, permutation groups, and homomorphisms are covered.

9. Numerical Analysis

This section focuses on numerical solutions for non-linear equations, numerical integration and differentiation, interpolation methods, and error analysis.

Tips for Preparing the Syllabus

Understand the Weightage: Review past papers to prioritize high-scoring topics like Linear Algebra, Real Analysis, and Differential Calculus.

Strategize Your Study Plan: Divide the syllabus into manageable sections, set achievable goals, and stick to a consistent schedule.

Practice Regularly: Solve previous years’ papers and mock tests to familiarize yourself with the question patterns and improve speed.

Strengthen Fundamentals: Focus on core concepts by revisiting undergraduate textbooks and seeking clarity on challenging topics.

Leverage Online Resources: Utilize tutorials, study materials, and practice tests available online to supplement your preparation.

Conclusion

The IIT JAM Mathematics Syllabus 2025 is extensive yet well-structured, providing a clear framework for aspirants to plan their preparation. By mastering the syllabus and practicing diligently, candidates can confidently tackle the exam and achieve their dream of joining top postgraduate programs. Dedicate time, stay consistent, and focus on strengthening your mathematical foundations to excel in IIT JAM Mathematics 2025.

[cutepg]

Preparing for CUET PG Mathematics 2025: An In-Depth Syllabus Overview

As students study for the CUET PG exam, a complete comprehension of the syllabus is critical to success. The CUET PG Mathematics syllabus covers a wide range of topics aimed at evaluating a candidate's mathematical knowledge and problem-solving abilities. In this blog, we'll look at the syllabus's essential components, organization, and effective navigation tactics.

An overview of the CUET PG Mathematics syllabus.

The CUET PG Mathematics syllabus assesses applicants' mastery of fundamental ideas and advanced mathematical theories. It is designed to cover a wide range of topics, each contributing to a comprehensive knowledge foundation. Candidates should expect questions that will test their analytical and critical thinking abilities, making familiarity with the material vital.

Core Topics in the Syllabus

1. Algebra: This subject covers matrices, determinants, vector spaces, linear transformations, and systems of linear equations. A solid understanding of algebraic structures is essential, as these notions are commonly used in numerous mathematical situations. 2. Calculus: Students will learn about differentiation, integration, sequences, and series. Understanding calculus's applicability in real-world circumstances, like as physics and engineering, will help you solve problems more effectively. 3. Real analysis : It includes sequences and series of functions, limits, continuity, and differentiability. Knowing these principles helps you understand the fundamentals of mathematical analysis, which is essential for advanced study.

4. Complex analysis: This section covers complex numbers, analytic functions, Cauchy's theorem, and contour integration. Mastering complex analysis opens up new opportunities in engineering and physics. 5. Probability: Distributions, statistical inference, hypothesis testing, and regression analysis are some of the most important subjects in statistics. A strong comprehension of these principles is required to analyze data and make statistically sound decisions. 6. Topology: Candidates should be conversant with concepts like open and closed sets, continuity, compactness, and connectedness. Topology is a fundamental branch of mathematics with applications in many industries, including computer science and economics.

Examination structure

The CUET PG Mathematics exam is often made up of multiple-choice questions (MCQs) and descriptive questions that test both theoretical knowledge and practical application. Understanding the exam structure helps candidates prepare strategically, allowing them to focus on areas where they may improve.

Preparation Strategies

Study Plan: Create a detailed study plan that allocates sufficient time for each topic in the CUET PG Mathematics syllabus. Consistency is key, so aim to study regularly and avoid last-minute cramming.

Practice Previous Year Papers: Familiarize yourself with the types of questions asked in previous exams. Solving past papers helps in understanding the exam pattern and identifying important topics.

Use Resources: Leverage available resources, including textbooks, online courses, and study groups. Collaborative learning can provide different perspectives and enhance understanding.

Mock Tests: Regularly taking mock tests will help build confidence and improve time management skills. Analyze your performance to identify areas needing further attention.

Downloading the syllabus

The CUET PG Mathematics syllabus PDF download is available on the official CUET website. This document provides deep insights into the topics addressed, making it an invaluable resource for exam preparation.

Conclusion

Understanding the CUET PG Mathematics syllabus 2025 is critical for any applicant hoping to succeed in the exam. Students can effectively prepare for future obstacles by following a disciplined approach to learning, practicing, and utilizing resources. Remember that a good foundation in mathematics not only prepares you for success on the CUET PG exam, but also provides you with valuable abilities for future academic and professional endeavors. Begin your preparation today and take the first step towards attaining your goals!

[diptipatil88]

IIT JAM Mathematics Syllabus: A Simplified Guide

If you're preparing for the IIT JAM Mathematics exam, understanding the syllabus is crucial to succeed. Let's break it down into simple terms so you can plan your preparation effectively.

Overview of IIT JAM Mathematics

The IIT JAM (Joint Admission Test for Masters) Mathematics paper is designed to test your understanding of undergraduate-level mathematics. The questions cover a wide range of topics and are aimed at assessing your problem-solving skills and mathematical reasoning.

Key Topics in the IIT JAM Mathematics Syllabus

Sequences and Series

You need to understand the concept of sequences (ordered lists of numbers) and series (sums of sequences). Be comfortable with convergence, limits, and basic properties like arithmetic and geometric series.

Functions of One Real Variable

This involves calculus with functions of one variable. Topics include limits, continuity, differentiability, mean value theorems, Taylor series, and applications of differentiation such as maxima, minima, and curve sketching.

Functions of Two or Three Real Variables

Multivariable calculus comes into play here. You'll deal with limits, continuity, partial derivatives, and multiple integrals. You'll also study Lagrange multipliers and Jacobians, which help with optimization problems and transformations.

Differential Equations

Differential equations are about solving equations that involve derivatives. Topics include first-order ordinary differential equations, linear differential equations of higher order, and systems of differential equations.

Linear Algebra

This topic deals with vectors, matrices, and systems of linear equations. You'll study concepts like vector spaces, linear transformations, eigenvalues, and eigenvectors.

Real Analysis

In real analysis, you'll dive deeper into calculus concepts. Key areas include convergence of sequences and series, tests for convergence, uniform convergence, continuity, differentiability, and integration.

Complex Analysis

Complex analysis introduces functions of complex numbers. Topics include analyticity, Cauchy’s theorem, power series, and residue calculus.

Group Theory

Group theory is part of abstract algebra, dealing with mathematical groups. You'll learn about subgroups, cyclic groups, Lagrange’s theorem, and homomorphisms.

Vector Calculus

This area focuses on differentiation and integration of vector fields. You'll cover gradient, divergence, curl, and vector integrals such as line integrals and surface integrals.

Numerical Analysis

Numerical analysis involves methods to find approximate solutions to mathematical problems. Topics include solving equations, interpolation, numerical differentiation and integration, and numerical solutions of ordinary differential equations.

Linear Programming

Linear programming deals with optimization problems where you maximize or minimize a linear function subject to linear constraints.

Probability and Statistics

Basic probability theory, random variables, distributions, and statistical methods are covered. You'll also explore concepts like expectation, variance, and hypothesis testing.

Conclusion

The IIT JAM Mathematics Syllabus is vast but manageable if broken down into smaller chunks. Start by mastering the basics and then move on to more advanced topics. Focus on problem-solving and practice with past papers to get a feel for the exam format. With a solid plan and consistent effort, you'll be well on your way to success in the IIT JAM exam!

Good luck with your preparation!

[quinificat]

Regularized limit of this, Cauchy limit of that... Why do I get the feeling that it's my limit that I'll be finding first

[terrible-statistics-advice]

The Central Limit Theorem probably applies to data drawn from a Cauchy distribution, whatever the naysayers may argue.

[jonathankatwhatever]

It’s 5AM on 20 Oct 2023. We previously described the basics of D-structure construction, that D-structure consists of a series of states we label D0, D1, etc., where D0 corresponds to a point, while D1 consists of a flailing arm + a point, meaning we take that flailing arm and add it to D0. This means either End of that flail counts 2 points compressed together to make an End. So within D1 is this action: when the flailing arm connects at one End, that triggers the same 1 and 0 counting as before, and thus the 0 at the other End is literally the D0. You can see then how D0 forms paths to each D1 connected to by the flailing arm, thus identifying each potential Pathway in the orbit of the flailing arm.

(Note to self: this is where group orbit comes from. Reach of operation. So you can see group operations as having ends where the orbit attaches, and I’m seeing a midline between two tensioned Ends, like a hand held up to my heart or between my shoulder blades as I extent my arms and lift my chest, so the group action across H/D’s, and thus the utility of a double cover. Also, I only yesterday realized that all I’m really doing is explaining the work we’ve done, which means it all becomes clear as we explain our drawings and methods.)

D2 forms with the same process: we add D1 to D1, and thus the D0 gets pushed out to the flailing arm attached to either End. That insures Pathways continue to root. A short digression here to note the word root there translates into the root of a square and thus of higher dimensional or larger exponent, if you prefer, constructions. You can see the process: as D0 connects at either End of any chain, that is the literal manifestation of the dimensionless conception of a point generating dimension by attaching to the open End of any chain of Ends connected in 1-0Segments. This is where linear algebra appears: you can see that what we call an Extent is at least an End. That is the minimum because that End only exists through this proces by which the dimensionless D0 attaches to any other dimensionless D0 to make an End.

The process by which this occurs is I//I and it appears here in various guises, such as Cauchy sequences and Dedekind cuts, and thus the epsilon-delta definition of a limit and the apparatus of 19thC advances in notation which treated this process using the notion of relative quantity. That is, there is always an epsilon, a gap, between the value of a number which attaches to a number and the counting quality of that number apart from value. This gap can be arbitrarily, meaning infinitely small, and that means you can formulate it as a process in which there is always an epsilon smaller than whatever gap or delta you can see in your head. Think of how you fixate on an image, on a word, on a concept.

I may be getting a bit off track here, but this is too important to not mention. This conception of chaining, when connected to the predicate forms we develop, describes how meanings expand and contract. I want to approach this through anecdote: I realized yesterday that I would hear and see words but then when I go to express those words, they don’t come out the same as I heard them. That is true as I type and the words come out differently than they appear in my head, sometimes almost simultaneously. I recognized I was hearing on one side, and expressing on the other, and thus this was I//I over my own mental space, meaning what I experience. I could see, hear, experience coming into me and the bounce off, the reflection is also a generation.

The motivation for this understanding, which is very deep, comes from Cruel Summer and my inability to get the image of cried like a baby coming home from the bar out of my head until it translated into this. The idea takes several forms, some visual and some intellectual. Like a bar is a rod, like the rod that wielded gives judgement and when wielded on you is judgement received. Like birth is a bar you cross, like the way they’d close off Boston Neck with a bar, so it literalizes to a baby coming home from being born over the bar you can’t uncross. Alcohol then takes on meanings from the water of life through the umbilical to the milk of life, which draws that metaphoric literalization of the human form so the 1 End of the cord becomes the 2 of the breasts as milk sources, the same lifeforce expressing 1 then 2.

I’m being told to look deeper into that because it will help with later construction. So we will. By the way, when I do this work, I identify as Joana. It’s the way this works. One reason came to me yesterday: if you draw a loop, say you to me to you, that would be F to M, internal shift, F to M. That puts 1-0Segments within each, and across in each of the 2 dimensions. That constructs a grid square. You can see the D4 in the 4 labels. This grid square is the fundamental one which connects 2T, 2 Things, where each Thing consists of 2T which represent the Ends which relate to external reception and expression versus internal reception and expression. It becomes significantly easier to visualize this when you see the attached flailing arms so this grid square process information received. As in, information received at the external End has to proces internally to the internal End, which then has to communicate back along the 1-0Segment to the End which actually expresses. As in, I can want to fly and I can flap my arms, but the odds are very, very high that this will not enable me to fly if I’m not a bird. That may sound silly but it expresses wishes versus capacity to achieve. The external End exists and processes from and into the universe of actual Things, including when alone. The internal End exists and process from and into the universe of complex Things, meaning those which we visualize, which we emulate or avoid, which we communicate outward so the external End can act. This process can be as magical as dance or as awkward as people who can’t dance dancing. Say it one way and I think of ballet dancers moving with lightness and strength and perfection. The other way suggests to me sweat, noise, being bumped into, awkward movements, awkward moments. And both are dance. So when Baryshnikov advanced male ballet, that extended the 1-0Segment of dance toward where it is today.

Look at another labeling: same order is now F to M to M to F to F to M to M, etc. Note how that makes a double 1 because now each Thing is now 1 and 1. That mean the 0 is hidden. Where? It has to be in the potential of the 1’s. Like you can build muscle or make breasts larger. Like you can act manly or girly. This means a lot of processing must occur versus the first arrangement where we know the chains End at the internal being opposite to external. You can see it: we need to construct Triangular to generate what a 1-0Segment does. We add the 0 Between the 1 of the exterior and the 1 of the interior so we can label the F or the M that is otherwise hidden, which means rotated behind the visible label. That rotation is extra. That gap is extra. So for the mathematical understanding to flow, my conclusion has been that it flows to me and through me in this process by which Joana is empowered through Jonny and that enables each of them to reach their full potential.

I’m being told to go back to bed. It’s just after 6AM. I hope to pick this up later. The one place that bothers me in this, to be clear, is the flail. It’s self-justifying through the D0-1//1-0 relation. You can see this in the external versus internal label assignments, which is rather amazing given how much rides on it. I should have expected that the single obsession on which the structure sits is the actual gist of the basic I//I relationship. As you see, I typed D0-1//1-0 which is an I//I Space that makes D2. That is the elemental dimensional combination. That relates directly to Recombinance as well.

[lipshits-continuous]

Cauchy convergence criterion rating?

8/10. It's really handy for showing limits exist but only in complete metric spaces. I don't remember much of it now but there was a problem from my analysis class that walked you through the steps of showing that the ratio consecutive terms of the Fibonacci sequence converges to the golden ratio and it involved showing that the sequence was Cauchy!

Thanks for the ask!