#cauchy’s residue theorem

[lipshits-continuous]

I had a revelation earlier whilst talking to a friend about some maths. The big integral theorems from Complex Analysis, i.e. Cauchy's Theorem, Cauchy's Integral Formula, and Cauchy's Residue Theorem, all don't really depend on what curve we're integrating over but is more about the structure of the set that the function is defined on. Since the former two theorems can be recovered from CRT I'll only talk about that one. The residue is non-zero cause of the holes in the domain so the integral is really measuring something more fundamental than anything to do with the particular curve other than the fact they're a whole in the interior of the set the curve bounds.

Maybe there's something more general about how we can use integrals "measure" the holes in a space that I don't know about but this seems really interesting

[mathematical-cheese]

Woahh you like math :0?

What's your favorite.. number...

It is i. As in i²=-1. Maybe it's cliché but literally everything cool from complex analysis hinges on the fact that i²=-1.

(Jargon warning) Basically, complex differentiable functions must satisfy these things called the Cauchy-Riemann equations. These equations rely on the algebraic properties of the complex numbers. We technically deal with a stronger notion of functions, i.e. holomorphic functions, which are complex differentiable in an open neighbourhood of each people in their domain, but the Cauchy-Riemann equations must still be satisfied. Then we get all sorts of wonderful theorems like Cauchy's Residue Theorem, Liouville's Theorem (which lets you prove the fundamental theorem of algebra), and much more!

[lipshits-continuous]

Yes! Cauchy's Residue Theorem!

I've talked about it before but it's just so good! The fact that you can get information about the topology of the codomain of a meromorphic purely by taking an integral is really cool! Conversely, the fact that complex integrals only depend on the homotopy type of the contour is also really cool!

For example, 7x3=21, 5x9=45, etc. If you do, what is it?

–

We ask your questions so you don’t have to! Submit your questions to have them posted anonymously as polls.

[diptipatil88]

IIT JAM Mathematics Syllabus: A Simplified Guide

If you're preparing for the IIT JAM Mathematics exam, understanding the syllabus is crucial to succeed. Let's break it down into simple terms so you can plan your preparation effectively.

Overview of IIT JAM Mathematics

The IIT JAM (Joint Admission Test for Masters) Mathematics paper is designed to test your understanding of undergraduate-level mathematics. The questions cover a wide range of topics and are aimed at assessing your problem-solving skills and mathematical reasoning.

Key Topics in the IIT JAM Mathematics Syllabus

Sequences and Series

You need to understand the concept of sequences (ordered lists of numbers) and series (sums of sequences). Be comfortable with convergence, limits, and basic properties like arithmetic and geometric series.

Functions of One Real Variable

This involves calculus with functions of one variable. Topics include limits, continuity, differentiability, mean value theorems, Taylor series, and applications of differentiation such as maxima, minima, and curve sketching.

Functions of Two or Three Real Variables

Multivariable calculus comes into play here. You'll deal with limits, continuity, partial derivatives, and multiple integrals. You'll also study Lagrange multipliers and Jacobians, which help with optimization problems and transformations.

Differential Equations

Differential equations are about solving equations that involve derivatives. Topics include first-order ordinary differential equations, linear differential equations of higher order, and systems of differential equations.

Linear Algebra

This topic deals with vectors, matrices, and systems of linear equations. You'll study concepts like vector spaces, linear transformations, eigenvalues, and eigenvectors.

Real Analysis

In real analysis, you'll dive deeper into calculus concepts. Key areas include convergence of sequences and series, tests for convergence, uniform convergence, continuity, differentiability, and integration.

Complex Analysis

Complex analysis introduces functions of complex numbers. Topics include analyticity, Cauchy’s theorem, power series, and residue calculus.

Group Theory

Group theory is part of abstract algebra, dealing with mathematical groups. You'll learn about subgroups, cyclic groups, Lagrange’s theorem, and homomorphisms.

Vector Calculus

This area focuses on differentiation and integration of vector fields. You'll cover gradient, divergence, curl, and vector integrals such as line integrals and surface integrals.

Numerical Analysis

Numerical analysis involves methods to find approximate solutions to mathematical problems. Topics include solving equations, interpolation, numerical differentiation and integration, and numerical solutions of ordinary differential equations.

Linear Programming

Linear programming deals with optimization problems where you maximize or minimize a linear function subject to linear constraints.

Probability and Statistics

Basic probability theory, random variables, distributions, and statistical methods are covered. You'll also explore concepts like expectation, variance, and hypothesis testing.

Conclusion

The IIT JAM Mathematics Syllabus is vast but manageable if broken down into smaller chunks. Start by mastering the basics and then move on to more advanced topics. Focus on problem-solving and practice with past papers to get a feel for the exam format. With a solid plan and consistent effort, you'll be well on your way to success in the IIT JAM exam!

Good luck with your preparation!

[shoehorseconstant]

omg i just sat in on my second classical mechanics lecture and i asked the prof a bunch of questions afterwards and he literally guided me all the way from solving a basic second order ODE to the analyticity of holomorphic functions and the cauchy residue theorem and he was literally so nice and patient and i was like "im trying to leave chemmmm what should i do" and he was like "AH if you're afraid of chemicals i understand . . . well it seems to me like you might be more interested in math than even physics or chemistry !!!" and i was liek AH!!! POSSIBLY!!!

and i asked him if i could sit in on his lectures where he has quizzes and he was like "ahhhh i can give you a fake quiz but i wish you had asked earlier so you could have audited the entire course!!! you can even show up to the final if you want, i'll just see that you're not enrolled and just not grade your test :)" like omg......i'm feeling loved

[diogo-beloto]

Complex integration, Cauchy and residue theorems | Essence of Complex An...

[lipshits-continuous]

Currently I have two favourites!

First is Cauchy's Residue Theorem. I've talked a decent amount about it on here already but it's so cool that we can get information about the holes in the codomain of a meromorphic function purely by doing an integral!

My other favourite is the Gauss-Bonnet Theorem. It's so cool that you can get information about the topology of a surface (the Euler characteristic) purely by considering notions of curvature of a surface. Like there is no reason to expect that we should get information about the topology from studying properties that arise from doing calculus on a surface but we do!

Math people, reblog with your fav theorem and why.

I'll start, the Wedderburn-Artin theorem is a beautiful structure theorem on semisimple rings which says they decompose uniquely as a product of matrix rings over division rings. This is a beautiful result but it also underlies a lot of very cool theory like Brauer Theory, Galois Cohomology and the theory of Galois and Étale Algebras.

What's yours?

[tilde-he]

an attempt towards yet another notion of “a derivative for finite fields”

I meant to do this as a full write-up thing, with pretty pictures and such, but I decided that I’m just going to start saying what I’ve already got, and re-blog this post with additions to this later, so that I actually ever get any of it posted. So, let’s get this post started.

If you have any feedback on the way I have written this (ideally, how to improve my writing for things like this), I would appreciate it!

Part 1 : Preliminaries, the definition, and some basic parts of the results

Part 1, Section 1: Preliminaries

At least two notions of derivatives for functions over finite fields have already been proposed, the Hasse derivative, and the Negacyclic derivative (citation : “Introducing an Analysis in Finite Fields” by de Oliveira and deSouza )

Somewhat like the linked paper, I am partially motivated by the idea of a “unit circle” using finite fields. However, in this case, I am motivated by analogy with complex analysis.

Where q is a prime power (or just a prime) congruent to 3 (mod 4), there is no element x of Fq such that x2=-1 (see ...elsewhere... for a proof of this, or if you just want a citation, not a proof, here or here), and therefore, we can adjoin an element i to the field, such that i2=-1, to produce a field Fq[i] .

Now, for any finite field with characteristic not equal to 2, half of the non-zero elements are the square of some non-zero element, and half are not . The elements which are, are called “quadratic residues” (for example, in Fq where q is 3 mod 4, -1 is not a quadratic residue. However, in Fq[i], it is a quadratic residue, as i2=-1.). (the reason that exactly half of the (non-zero) elements are quadratic residues is because (-x)2=x2, so 2 non-zero elements get mapped to each (non-zero) quadratic residue, so, there are half as many quadratic residues as there are non-zero elements. This doesn’t work in the fields of characteristic 2, because in those fields, -x=x.)

[for the remainder of this post, and probably any other posts in sequence with this one, q will always be assumed to be congruent to 3, mod 4 (unless possibly if stated otherwise, in a later post)]

In this analogy with the complex numbers, we are treating the field Fq as being analogous to the real numbers, and treating the quadratic residues of Fq as being analogous to the positive numbers. This works nicely, as the non-zero non-quadratic residues are exactly the additive inverses (”negatives”) of the quadratic residues. However, the analogy doesn’t extend too far, as the “positive numbers” in this analogy, are not closed under addition (though they are under multiplication and division).

All of what I’ve said in this post so far is definitely things I’ve seen elsewhere, and are well known. In the following I don’t remember exactly which of the things I’ve read elsewhere.

Now, I want a notion of the unit circle in Fq[i] . So, this should be those points z such that |z|2=1 , yeah? So, what is |z|2?

Well, of course, when z=x+y*i for x and y “real numbers”, (by which, in this context, I actually mean elements of Fq, rather than the actual real numbers), then |z|2=|x+iy|2 is of course x2+y2.

So, for how many elements z of Fq[i] is |z|2=1 ?

for any c in Fq , |cz|2=|-cz|2=c2 * (x2 + y2) = c2 * |z|2. This scales |z|2 by a quadratic residue. So, for any element z of Fq[i], there are 2 elements c, -c of Fq that z can be scaled by, such that, if |z|2 is a quadratic residue of Fq (so, if it is “positive”), then |cz|2=1 , and otherwise, such that |cz|2=-1 .

Well, that’s kind of a weird idea, isn’t it. Something having a negative absolute value squared. Nevertheless, we continue.

Oh, one side note : you may be concerned about “how do we know that the ‘absolute value squared’ of one of these elements won’t be zero?”. If this were the case, it would be because x2+y2=0, and so x2=-y2, and that therefore 1=-y2/x2=(x/y)2 and that therefore -1 would be a quadratic residue of Fq , which we know never happens when q is congruent to 3 mod 4. Moving on.

So, each “line through the origin” (i.e. for each fixed nonzero z in Fq[i], the set {c*z : c in Fq}) contains either 2 points with “squared magnitude 1″ or 2 points with “squared magnitude” -1. Because there are q2-1 nonzero elements of Fq[i] , and each of these “lines” has q-1 non-zero points on it, 2 of which with “squared magnitude” 1, or “squared magnitude” -1, there are therefore 2*(q2-1)/(q-1)=2*(q+1) points in Fq[i] with “squared magnitude” either 1 or -1 .

As might or might not be expected, |z1*z2|2=|z1|2 * |z2|2 . (try proving this yourself if you are not convinced.)

Therefore, these 2*(q+1) points are closed under multiplication.

As the non-zero elements of a finite field form a cyclic group under multiplication, these 2*(q+1) elements also form a group under multiplication.

Exactly half of them have “squared magnitude” -1 , and the half that has “squared magnitude” 1, is a subgroup of it.

Therefore, what we are calling our “unit circle” is the q+1 elements of Fq[i] with “squared magnitude” 1. We will call this set S, and the larger set with 2*(q+1) elements , S+/- . We might occasionally call S “S+“ in order to emphasize that we mean the smaller set, but probably not all that often, because using the superscripts is slightly inconvenient.

Part 1, Section 2 : The motivation for the definitions, and the definitions

Now! Now we have the preliminaries out of the way, let’s get on to the actual idea!

The idea is inspired by Cauchy’s Differentiation Formula , in particular, applied when integrating around the unit circle.

Cauchy’s Differentiation Formula states that when f(z) is a complex differentiable function on some simply connected open region of the complex plane, and c is a point in that region, then a contour integral in the counterclockwise direction around c of f(z)/((z-c)(n+1)) , times n!/(2*pi*i), is equal to the n-th derivative of f evaluated at c.

 Or, to steal a picture from Wikipedia

(except they called the variable “a” instead of “c”).

My idea was to, unlike in the complex analysis case where this result is a theorem that comes after defining what complex differentiation means, to instead use this formula as a basis for defining a type of derivative for functions over certain finite fields (specifically, those finite fields for which the notion of the unit circle described above, works).

So, to use something analogous to

to define the derivative of f at c, where the contour integral is the unit circle, except translated to be centered at c,.

That is,

when

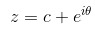
. Which is,

(Not sure why tumblr scaled up this image more than the other ones. Oh well.)

now, because we are trying to do this in our finite field thing, we of course do not actually have an actual integral, so we just treat it as a sum. Similarly, instead of eiθ for different theta in order to produce the different points on the unit circle, we just make the sum be over the points in the unit circle directly, as we haven’t defined a notion of ez in our finite field.

So, remembering that S is the set we are treating as analogous to the unit circle, we get

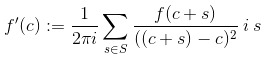
And, because the number of elements in our “unit circle” is q+1, and this seems the most natural analogy to the value of 2*pi , and, in addition, q+1 is congruent to 1 mod p (where p is the characteristic of the field), it seems reasonable, in the analogy, to replace the 2*pi term in the denominator there, with 1.

Also, the i term inside the sum cancels with the 1/i as the coeffecient of the entire sum,

and the ((c+s)-c) is of course just s, and (f(c+s)/s2)*s is, of course, just (f(c+s)/s) , this all simplifies down to:

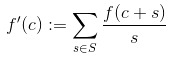
Which is nice and simple.

But, what does this operation actually act like? Is there any good reason that it should deserve the name “differentiation”?

You may want to try computing it out for some simple functions, like 3z , or z2 - 1 or the like, to check that it indeed does produce the values that one would expect for the derivative of such functions.

One can also plainly see that this operation is linear on the vector space over Fq[i] which is the set of functions from Fq[i] to Fq[i] ( so, deriv(a*f + b*g)=a*deriv(f)+b*deriv(g) ) , and also that it is translation invariant, which are both appropriate properties for differentiation.

Now, this operation can be applied to any of these functions from the field to itself, but there are many functions from the complex plane to the complex plane that are not differentiable. As such, I thought to look for a definition of “differentiable” which would be appropriate.

So, for this, I thought to base it on the Cauchy’s Integral Formula

and, by going through the same sort of analogy, we arrive at

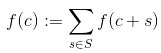
as a proposed equation which should hold whenever the function is “differentiable”. I suggest taking this equation as the definition of a function f from Fq[i] to Fq[i] being “differentiable”.

Part 1, Section 3 : Some results

Note that, for the same linearity reasons as with the “differentiation” definition above, the “differentiable” functions form a linear subspace of the full space of functions (as they should).

I have also shown (but don’t include the proof here right now, because I’d like to get this post out tonight, and it is almost midnight) that if a function is “differentiable” in this sense, then the “derivative” of that function is also differentiable in this sense. So, any function which is once differentiable is infinitely differentiable, just like in the actual complex numbers! I think that’s pretty cool.

I have also shown that any polynomial of degree up to q is “differentiable” in this sense, and also that the “derivative” is what one would expect for polynomials for when the degree is at most q. (zq+1 is not “differentiable” in this sense, and zq+2 , if you go through with the definition of the “differentiation” despite it not being “differentiable” results in like, 1 + [the derivative you would expect] , iirc. I might be remembering with an off by one error. Anyway, it has to do with the binomial expansion of stuff having a power of s which is divisible by q+1 . I intend to explain why later. )

I suspect that the “differentiable” functions turn out to be exactly the polynomials of degree at most q, but I have not proven this to be the case. (yes, unfortunately this means that there are no sine and cosine functions here which have sine’(x)=cos(x), cos’(x)=-sine(x) . However, I think this can maybe be recovered in a slightly different context. More on this later when I figure it out maybe?)

I think I’ve shown that, if that is the case, then a “differentiable” function is uniquely determined by its value on the unit circle (or any translate of it), which matches with actual complex analysis quite nicely!

Generally, these definitions appears to give results that mirror complex analysis results quite nicely!

Part 1, Section 4 : etc.

Thank you very much for reading.

Please let me know if you would like clarification on any part of this post, or if you have any advice for how I could improve it, or how I could improve future math things I write.

Thank you!

[physicsmadeeasykota]

CAUCHY`S RESIDUES THEOREM; LAURENT`S SERIES; LAURENT`S THEOREM; CAUCHY`S...

[spring-of-mathematics]

A Riemann surface

is a “universe” locally modelled on open sets in the complex plane, and equipped with extra structure so that complex analysis can be done. Simple examples include

the complex plane,

the graph of the complex square root (rotating the second coordinate),

the graph of the complex logarithm,

the Riemann sphere.

Polynomial equations in two variables define special Riemann surfaces, called plane curves, such as

the “circle” z2 + w2 = 1, (rotating the w-plane),

the “cubic” z3 + w2 = 1,

the “nodal cubic” z3 + z2 = w2, and

the “Fermat quartic” z4 + w4 = 1.

In the seminar, we'll review tools from complex analysis, including differential forms, contour integration, the Cauchy integral formula, and residues. We'll learn how to “build” Riemann surfaces by (i) “gluing” together pieces of the complex plane, (ii) analytic continuation, and (iii) “dividing” an existing Riemann surface by the action of a group. We'll study the local and global behavior of holomorphic maps between Riemann surfaces. Topological covering maps and mappings between plane curves defined by projection will furnish particularly interesting examples.

If time and student interest permit, we'll study the interrelationship between complex analytic structure, topology, and differential geometry embodied by the Gauss-Bonnet and Uniformization theorems. All necessary background material from differential geometry will be covered in the seminar.

[lipshits-continuous]

#17, #20, #49

MATH ask

17. Are there any great female Mathematicians (living or dead) you would give a shout-out to?

Emmy Noether is the obvious go to but she's one of my favourite mathematicians because she was the one who first formulated simplicial homology!

There are a few living women I'd like to shout-out but that would end up doxxing me /lh

20. Can you share any problem solving tips?

The thing I do when I start trying to write a proof is write out the hypotheses and their definitions. Then I might write some results that come to mind that might be helpful and play about with these things to see if something sticks. Sometimes it'll work and I'll have at least some part of the proof figured out.

If that doesn't work and you've been trying for ages to solve it the best advice I can give is do something else. If it's a homework problem, do something completely different, e.g. watch a YouTube video or go for a short walk. If it's an exam, do a different question. But it should be different enough so it gives your brain time to digest the information and often I've found that a new idea will pop into my head. And even if it doesn't, taking a break so that you don't get to overwhelmed is always a good idea.

49. What’s your favorite number system? Integers? Reals? Rationals? Hyper-reals? Surreals? Complex? Natural numbers?

Easily the complex numbers. Complex analysis is one of my favourite areas of maths and is probably the starting point of my adoration of topology. The theorems involving holomorphic functions are so nice and Cauchy's Residue Theorem is so so powerful

Thanks for the ask!

[kpoints]

Cauchy's Residue Theorem

[thetwomeatmeal]

bernoulli would’ve won

Today I learned that Bernoulli numbers are p-adic integrals. TeX-heavy so click to read on.

First of all, Bernoulli numbers are traditionally defined as coefficients of the Taylor series $$ \frac{s}{e^s - 1} = \sum_{k=0}^\infty B_k\frac{s^k}{k!}. $$ We have $$B_0 = 1, B_1 = -\frac{1}{2}, B_2 = \frac{1}{6}, B_3 = 0, B_4 = \frac{1}{30}, $$ and $B_{2n+1} = 0$ for $n \ge 1$. I don’t have a cute slogan for what they mean, because they’re one of these sequences that shows up all throughout math: in calculating sums of powers of natural numbers, in the Euler-Maclaurin summation formula, and in Kummer’s half-proof of Fermat’s Last Theorem, for starters. One of my favorite theorems, Frank Adams’ computation of the image of the J homomorphism in the homotopy groups of spheres, uses the denominators of the Bernoulli numbers in its statement, apparently because they satisfy a certain divisibility criterion, though topologists to this day are looking for deeper reasons. The numerators, meanwhile, are more of a mystery, and it’s an open problem whether infinitely many primes $p$ divide the numerator of $B_{2p}$.

On the other hand, there’s a $p$-adic integral called the Volkenborn integral, which I learned about from Robert’s A Course in p-Adic Analysis. If $f$ is a continuous function on $\mathbb{Z}_p$, the Volkenborn integral is defined as a limit of Riemann sums where you sample at integer points: $$\int_{\mathbb{Z}_p} f(x)\,dx = \lim_{n \to \infty} \sum_{i=0}^{p^n - 1} \frac{f(i)}{p^n}. $$ Note that the factor of $1/p^n$ is the measure of the disk around $i$ of radius $|p^n|$, so that $\mathbb{Z}_p$ itself has measure 1; it’s a weird feature of $p$-adic analysis that these measures get larger as the disks get smaller.

There’s an “indefinite sum” operator $S$, defined on the natural numbers by $$Sf(n) = \sum_{i=0}^{n-1} f(i),$$ and extended to $\mathbb{Z}_p$ by continuity. We see that $$\int_{\mathbb{Z}_p} f(x)\,dx = \lim_{n \to \infty} \frac{Sf(p^n)}{p^n} = (Sf)’(0),$$ i.e., the integral is also a derivative.

Now the trick is to take the function $f(x) = (1 + t)^x$, where $t$ is some sufficiently small $p$-adic number, and write it two different ways. On the one hand, this function has an expansion in terms of binomial coefficients, $$(1 + t)^x = \sum_{k=0}^\infty t^k\binom{x}{k}.$$ This is obviously true if $x$ is a natural number, if we take $\binom{x}{k} = 0$ for $x < k$, and it’s true in general because the binomial coefficient functions are $p$-adically continuous. They’re also well-behaved for indefinite sum: $$S\binom{x}{k} = \binom{x}{k+1}.$$ It follows that $$\int (1 + t)^x\,dx = \frac{d}{dx}\left(\sum_{k=0}^\infty t^k\binom{x}{k+1}\right)\big\vert_{x=0}.$$ But $\binom{x}{k+1} = \frac{x}{k+1}\binom{x-1}{k}$, so its derivative at 0 is $$\frac{1}{k+1}\binom{-1}{k} = \frac{1}{k+1}\cdot\frac{(-1)(-2)\dotsm(-k)}{(k)(k-1)\dotsm (1)} = \frac{(-1)^k}{k+1}.$$ Therefore, $$\int (1+t)^x\,dx = \sum_{k=0}^\infty t^k \frac{(-1)^k}{k+1} = \frac{1}{t}\log(1+t).$$ You can take my word for it (I can talk about it separately, if people care) that this logarithm makes $p$-adic sense for small $t$.

Let’s put $s = \log(1+t)$. We’ve just proved that $$\int e^{sx}\,dx = \frac{s}{e^s - 1},$$ and the right-hand side is the function whose Taylor series gave us the Bernoulli numbers! Now, again taking my word for it, we can write $$e^{sx} = \sum_{k=0}^\infty \frac{s^k x^k}{k!},$$ and the convergence is nice enough that we can swap the sum and integral sign. We get $$\sum_{k=0}^\infty \frac{s^k}{k!} \int_{\mathbb{Z}_p} x^k\,dx = \sum_{k=0}^\infty B_k \frac{s^k}{k!},$$ or $$ \int_{\mathbb{Z}_p} x^k\,dx = B_k.$$

A number of nice properties of the Bernoulli numbers follow from this theorem plus some mild $p$-adic integration theory. For instance, the odd Bernoulli numbers vanish because for these $k$, $x^k$ is an odd function with zero first derivative. (The problem with $B_1$ is that the integral is really symmetric under the involution $x \mapsto -1-x$, and it’s not quite translation-invariant, so reflecting about 0 ends up introducing an error term of $-f’(0)/2$.) There’s also a nice bound on the size of the integral, $|(Sf)’(0)|$, in terms of the coefficients of the polynomial $Sf$, which says in this case that $pB_k \in \mathbb{Z}_p$. This means that the denominators of the Bernoulli numbers are squarefree -- probably not obvious from the definition! The full Clausen-von Staudt theorem -- that the primes dividing the denominator of $B_k$ (for $k$ even) are just those $p$ such that $p-1$ divides $k$ -- isn’t much harder.

Of course, the most amazing part of this theorem is that we can define these rational numbers with a $p$-adic integral that just happens to not depend on $p$. The first thing I did when I read this was to look for an analogous description in terms of an archimedean integral. Using Cauchy’s residue theorem, you can calculate Bernoulli numbers as contour integrals: $$ \frac{2\pi i B_k}{k!} = \oint_{|z| = 1} \frac{z}{e^z - 1} \frac{1}{z^{k+1}}\,dz.$$ I don’t think this is a great parallel to the $p$-adic formula, and it’s not quite as shocking, either, seeing as you could do the same thing for any function that’s analytic in a neighborhood of 0. However, I’m tempted by the fact that both the residue theorem and the Volkenborn integral show a certain unity between differentiation and integration...

[mathematicianadda]

Residue Theorem if Pole is on Contour

This is a question on contour integration. The particular problem has a (simple) pole on the contour which prohibits a direct application of Cauchy's Residue Theorem.

Daniel Fischer commented as follows

Not really. [...] if the contour is smooth at the pole, it's as if half of the pole lies inside the contour and half outside. If the contour has a corner at the pole, with (inner) angle $\alpha$, the fraction is $\alpha2\pi$, so you get $\alpha i$ times the residue of the pole instead of $2\pi i$ times as for singularities properly enclosed by the contour.

The same result is mentioned in this question.

Unfortunately, Daniel didn't know a reference for this (generalised) result. Can anyone point me to a book/paper/recourse which covers this result? I'd like to see a proof and some maths underlying this intuition.

Thank you very much!

from Hot Weekly Questions - Mathematics Stack Exchange from Blogger https://ift.tt/2tzPsQN

[diogo-beloto]

Complex integration, Cauchy and residue theorems | Essence of Complex An...

[markyishanthonymartinez]

4/24/17

i just wanna cuddle and eat grapes.

my body is tired, but my face isn’t sleppy yet.

i mark anthony martinez the third (minus 2) hereby place my word on it, that i will have two videos out within the next week. promise promise.

what do i talk about in these again? i actually thought of something earlier but i always forget before i actually sit down to write..

my systems exam was today. the only midterm cause we switched professors the week before spring break and stuff. the midterm worth 30%. Well I mean, my heat transfer exams are also worth 30%. wait no, well yes, the first was 25%, then 30%, then the final is 30% as well and HW is 15 i thinks. but yeah honestly, i was not in a good spot 30 minutes into the exam. i couldn't get the long problem to work out and i was low key freaking. like i was frustrated and i just could not get the numbers to make sense and the stupid cauchy residue theorem wasn't cancelling out with anything and i literally had no idea wha the other two questions were asking. it legitimately flashed through my head that i might fail the course and have to end my life. KIDDING (okay it’s probably not appropriate to say that, but yes if i couldn't graduate next year i’d be incredibly upset forever). But yeah i was in a bad spot, both on the exam and mentally i was shook. but i paused, drank water, chillaxed, looked around the room for a bit, thought about people who’s smiles are too big for their faces and got down to business. i went ham the final 20 minutes, got the first problem to work out nicely (although i still had no clue on how to do the final part of it) i did the majority of that problem and should get most of those points. the third problem, that i initially had no clue how to even approach, actually ended up not being that bad and i completely worked through it and got the same answer as all my friends so pretty sure thats a gimme gimme 25 puntos. the second problem, i still really dont get what the legit way to do it was, but i kinda jerry-rigged an answer with some logic and a formula on my equation sheet and i actually think i did it right somehow. probs didn't get all the points there, but if i copped half of those, I'm happy. if i’m being honest, i think I'm looking at somewhere around a 70, which will probably be easily above the average. yay go me.

i think am tired now.

i just wanna remember the thingy i thought of to talk about earlier ))))):

sad merk

we won our game today. yay go us. nathan went on an absolute mission, i think he ended up netting like 8 goals??? i missed a penalty. lmaoooooo. but luckily i got an absolute banger of a volley just before the game ended which kinda made up for it. (hint hint: you’ll get to see that volley in one of my videos this week)

i dont have grapes

or cuddles

this is lame

more sad merk

jk pretty much always haps tbh

i have classssss in 8 hourssss why i do dis to myself. blogs are high maintenance. and by high maintenance i mean i’m bad with anything requiring any maintenance. so what. crucify me. wow i haven't said that in a while. that still makes the list of memorable ridiculously funny things i’ve said on the fly that just caused everyone to cry and became an instant meme. we were hot tubbing at Uly’s apartments, back when we used to hot tub like every other night cause it was chill and no one could kick us out because it was late and it didn't cost money and we could just chill. so yeah squad was hot tubbing and then we’re like, fuck it fam, let’s get some slurpees. wait i’m not gonna tell this story rn i’m gon’ slep. will tell mañana. gn.

it’s not nothing

dft//sb

- mark anthony martinez