#examples of countable and uncountable sets. Real line | Explore Tumblr posts and blogs

jonathankatwhatever · 2 years ago

Text

It’s sort of my day because it’s 4 August 2023, which is 4/8 and I’m 4/4, so it’s a doubling of me in months! I’m modular.

Turning over how to present D-structure. There’s a lot to say, including the reduction of Incomprehensible to Comprehensibile, which mirrors the shift from uncountable to countable in some senses. That is, Incomprehensible is a much larger concept, and thus reaches sets. I remain amazed at how good the notation fits, though it often was developed decades ago in the dark.

————-

I know the problem. It’s the same thing every time: that you can’t cross from 0Space into 1Space, whether you equate that idea with religion, with this life and eternity, or with math. And the reason is the Attachment over the 1-0Segment which connects the pieces. That Attachment may be next to invisible in the flow of events, but it represents all the work, all the grisp that happens to make that Attachment appear invisible so much of the time.

The metaphor of a slot machine. Of a rotating mirror. These are representations of the CR which occurs when we overlay 1 and 0, and 0 and 1. I mean that when you count to an edge in gs, that takes you to the CR of the Attached End. Like it’s a slot machine and you get the cherries, as if those were presented in pairs, like on an actual wheel as opposed to being computer generated to appear like wheels.

I see why a gs can form anywhere: it constructs at the 1Space level, meaning where D4 sparks evenly, meaning the D3-4 existence is fully encased in D4, without any of those annoying gaps we may imagine in science fiction. So we can have any 4 Ends make a grid square. And those 4 Ends take various forms. One is a single person holding ideals about what to be, what to want, etc. That sets up with the comparison of any other, including those not met or not even real, which is non-specific. Another form is 2 specified Ends, which is implicit in the first in both perspectives. That is how we generated IC and LC.

What’s missing above is the other 2 Ends, the Betweens. And those identify as the intangible Irreducible of the tangible Irreducible, meaning the representation in each sphere. But wait, dere’s moah! The perceived End is actually 2 Ends, so there’s the intangible Irreducible is actually the intangile external to the tObject’s Boundary (and thus internal to the Thing’s Boundary), and the intangible internal to the tObject’s Boundary. In other words, that which pulls and pushes inside to outside and outside to inside with the physical, tangible body Between. That Between is then the 1 in the 0-1-0.

And again, that is the overlap of 1 and 0, 0 and 1 so the line of events reads 1-1-1-1- at some appropriate scale. That is the solution to the old ant problem of they go about their business with no awareness of a foot about to crash down on them. Their existence is narrowly focused. This connects to Navier-Stokes because this is another example of how Things add together: they need to add together in the ashes to ashes, all things must pass sense. But what is the phrase for the intermediary space? Well, it’s because grid squares construct. I see lots of kinds, like polynomial space is a grisp form.

That again is why p≠np: the grisp levels are different. It takes work to shift from one level to the other, and that work is over CR. I can say this better, with more abstract rigor. Just give me a moment. It’s on the tip of my mind. I see the gs form, boxes, squares, and a ball or sphere or circle, and the issue is that you can’t know what you pair to until you pair to it. This method thus creates levels or kinds of spaces, which means I finally can say that the ‘calculation’ space is the Attachment space. And that is why the notation Attachment Theory made sense when it first came up, though I really was wondering what they fuck made it a ‘theory’. Now I see: it’s the theory of Attachment defining the grisp spaces. Now that is loverly.

To be clear: the Betweens are the other 2 Ends. That allows the flickering of states, even to a choreographed fight scene or dance number, where you see the tangibles pair and the intangibles pair, both as Irreducibles.

I heard Come Together on the radio this morning.

0 notes

matekon · 6 years ago

Text

The shortest proof that there are countably many algebraic numbers

This article explores a technique for proving that certain sets are countable that I find so easy, fast and clever that I am surprised it isn’t used more often in casual mathematics. I will present it and then apply it to prove there are countably many algebraic numbers.

I use the following personal conventions:

● - Definitions - Propositions I assume are true

○ - Theorems – Propositions I deduce from the definitions

___________________

Section 0 - Cantor Set Theory (Prerequisites)

I will assume the readers of this article are already a bit familiar with Cantor Set Theory. (If you are not, this video by TED-Ed is a nice accessible introduction: https://www.youtube.com/watch?v=UPA3bwVVzGI)

The point of this section is to fix the definitions really clearly.

$\bullet\:\aleph_0=\vert\mathbb{N}\vert$, meaning Aleph-0 ($\aleph_0$) is defined as the cardinal of the set of the natural numbers ($\mathbb{N}$) $\bullet$ The set A is infinite if $\vert A \vert \ge \aleph_0$ ($\aleph_0$ being the smallest infinity) $\bullet$ The set A is countable if $\vert A \vert \le \aleph_0$

● Given 2 sets $A$ and $B$, $|A| = |B|$(or they have the same cardinality) if I can find a “bijective” function from $A$ to $B$.

From experience, the next 2 definitions are less known from casual mathematicians, but are they crucial for this article.

● Given 2 sets $A$ and $B$ , $|A| \le |B|$ if I can find an “injective” function from $A$ to $B$ .

● Given 2 sets $A$ and $B$ , $|A| \ge |B|$ if I can find a “surjective” function from $A$ to $B$ .

I do realize that these definitions aren’t that trivial. Why they describe our intuitive understanding of “ $|A| \le |B|$ ” and “ $|A| \ge |B|$ ” needs to be thought out a little bit.

Just to illustrate it, let’s take $A= \{a,b,c\}$ and $B = \{d,e,f,g\}$, and then define 2 functions $f$ and $g$ in the following manner:

Because $f$ is injective, that implies that $|A| \le |B|$ or that $3 \le 4$, which is true. Because $g$ is not injective (the “elements” $f$ and g have the same output), its existence does not imply that $|B| \le |A|$ or $4 \le 3$, which would be false.

On the other hand, because $g$ is surjective (all the elements of A are the outputs of some elements of $B$ ), that implies that $|B| \ge |A|$. Similaily, $f$ not being surjective means we can’t deduce that $|A| \ge |B|$.

Finally, we just have to note that we can apply the 3 definitions above ( $|A| = |B|$, $|A| \le |B|$ and $|A| \ge |B|$ ) to infinite sets as well.

___________________

Section 1 - The Technique

We will now present the technique this article is mainly concerned with. Here is its statement:

○ Any set for which all its elements can be expressed in a “finite” sequence using a “finite” alphabet is countable.

To illustrate and clarify this, let’s look at an example:

Let $\mathbb{N}^3$ be the set of all triplets of natural numbers, $(1,3,9)$ being one for example. We easily see that $\mathbb{N}^3$ is infinite. But we would like to show that it is countable. Here’s our plan:

We will conceive a “language” that will allow us to express any triplet possible. For this, we first need the symbols from 0 to 9 to write the natural numbers. Then, we introduce the “:” that will be used to separate the numbers in the triplets. For example, $(1,3,9)$ will be written as “1:3:9″ in this language. So, our alphabet has 11 symbols total!

Now, with this alphabet, I will create the set W, which consists of every finite word that can be written using our alphabet of 11 symbols. “1:3:9″ would be a member of this set, but also words like “2::4::::” which aren’t “grammatical” and don’t represent any triplet.

Here are now the majors lines for our proof:

1) We show that $| \mathbb{N}^3 | \le|W|$. For that, we can create a “surjective” function $ f: W \to \mathbb{N}^3 $ whose existence would imply that $|W|\ge| \mathbb{N}^3|$

2) We show that $|W|\le|\mathbb{N}|$. Again, we just have to construct an “injective” function $g:W\to\mathbb{N}$ and that will imply that $|W|\le|\mathbb{N}|$

And from these 2 inequalities, we deduce that $| \mathbb{N}^3|\le|\mathbb{N}|$

Let’s do the details!

1) I will define a function $ f: W\to \mathbb{N}^3 $ that associates each word of $W$ with its associated triplet if the word is of the form “a:b:c”, where a,b and c are natural numbers. Otherwise, the word would be grammatically incorrect and I will associate the word with the triplet $(0,0,0)$.

For example,

$ f($1:3:9$) = (1,3,9)\in\:\mathbb{N}^3 $

$f($01:03:009$)=(1,3,9)\in \:\mathbb{N}^3 $ (technically a different word from the previous)

$f($2::4::::$) = (0,0,0)\in \: \mathbb{N}^3$ (because it is grammatically incorrect)

We can see that $f$ is surjective because every triplet of $ \mathbb{N}^3 $ is an output of this function. We are done with this part and have shown that $ | \mathbb{N}^3 | \le |W|$.

2) I can define a function $g:W\to\mathbb{N}$ that associates each word of $W$ with a unique natural number by reinterpreting it as a number expressed in base 12. I associate “1″ with $1$, “2″ with $2$, .... “9″ with $9$, “0″ with $10$ and “:” with $11$. I will explain later why I don’t associate “0″ with $0$.

For example,

$g$(1:3:9) $= 1*12^4+11*12^3+3*12^2+11*12^1+9*12^0 \in \mathbb{N}$

$g$(33:0:101)$= 3*12^7+3*12^6+11*12^5+10*12^4+11*12^3+$

$1*12^2+10*12^1+1*12^0 \in \:\mathbb{N}$

You can see that $g$ would never associate 2 different words with the same number, meaning $g$ is injective. That’s because, if we exclude the zeros on the right of the comma and on the left, there is a unique way to write a natural in base 12 (in any natural base bigger than or equal to 2 in general).

So, earlier, I didn’t associate “0″ with $0$ because, otherwise, “3″ and “03″, 2 technically different words, would have the same output by the function $g$, so it wouldn’t be injective.

So, with that, we’ve just proven that $|W| \le | \mathbb{N} | $.

With 1) and 2) together, we deduce:

$\vert \mathbb{N}^3\vert\le\vert\mathbb{N}\vert\Rightarrow | \mathbb{N}^3 |\le\aleph_0\\ $ This really means that $ \mathbb{N}^3$ is “countable”. But we know that $\mathbb{N}^3$ is “infinite”, that is $ | \mathbb{N}^3 |\ge\aleph_0\\ $ So, together, we get that $ \mathbb{N}^3 $ is “countably infinite” or that $ | \mathbb{N}^3 |=\aleph_0\\ $

$QED$

All the great principles behind the technique are there.

The existence of the functions $f$ and $g$ is guaranteed once the condition “every element of our infinite set can be expressed by a finite sequence using a finite alphabet” is verified. So, for now on, when applying this technique, we really don’t have to construct $f$ and $g$ anymore. We can immediately deduce that the set is countable. Thus, the technique gains on speed!

And now…

___________________

Section 2 - The proof that there are countably many algebraic numbers

Let’s make the definition clear:

● All the zeros of polynomials with integer coefficients make up the set of the algebraic numbers.

So, for example, $4/3$ is an algebraic number because it is a (the only) zero of the polynomial $3x-4$. In the same way, $\sqrt[3]{2}$ is algebraic because it’s a zero of $ x^3-2$.

We first note that they are infinitely many algebraic numbers, simply because every natural number is algebraic.

We know:

○ Any set for which all its elements can be expressed in a “finite” sequence using a “finite” alphabet is countable.

So, to prove there are countably many algebraic numbers, we just have to find a finite alphabet that can allow us to express each one of them in a finite sequence.

Expressing every polynomial doesn’t seem like much of a problem. We could just use the numbers from 0 to 9, +, - , ^ and x (14 symbols). For example, the polynomial $ 7x^{12}-10x^5+4 $ is expressed as “7x^12-10x^5+4″.

But, how do we express the zeros of a polynomial?

Trying to express all of them with “rooty expressions” (like $5+\sqrt{3}$) really is too complicated for what we are trying to do. Anyway, we know from Galois Theory that this is impossible in general. There is another, more elegant, way to do it:

It is not hard to show that every polynomial have finitely many zeros. So, I could create a system that can enumerate all of them in a given order. I will decide not to count multiplicity of zeros, so $x^2$ would have just 1 zero.

Let’s take the following zeros of a polynomial in the complex plane:

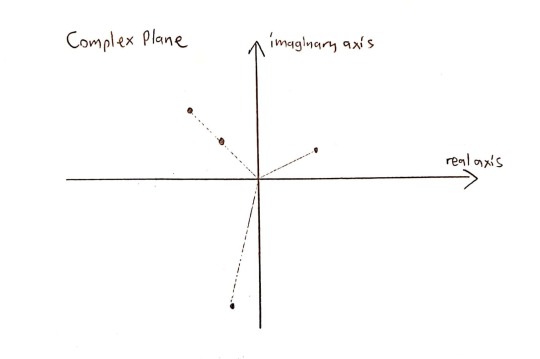
(Yes, this polynomial can’t have real coefficients (why?), but the argument still holds.)

Let’s order them using the following conventions: 1) Zeros are ordered by their arguments (angles) 2) But if 2 zeros have the same argument, then they are ordered by their norms

So, we can order the zeros above like that:

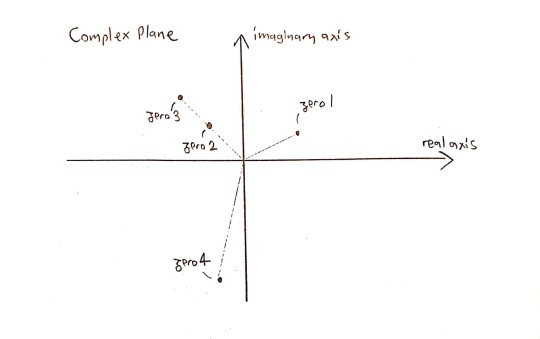
Now, I will introduce “$” in my alphabet. It will work this way:

“ 2$x^5+4x^3-6 ” expresses the 2nd zero of the polynomial $x^5+4x^3-6$.

And … we are done!

We can express every algebraic number with a finite sequence using a finite alphabet of 15 symbols (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, -, ^, x and $). It follows from this that there are countably many algebraic numbers.

Also, knowing that there are uncountably many complex numbers, we’ve just proven that transcendental numbers exist (why?).

From experience, I am sure a “pure mathematician” would have written this entire proof in a single paragraph. So, it really is the shortest proof that I know

#mathematics #set theory #numbers

1 note · View note

tokinanpa · 2 years ago

Text

concepts like the long line are founded on multiple layers of mathematical machinery, and if you aren't familiar with those foundations then trying to understand definitions like these is just going to give you a headache.

as a high-level overview of the concepts at play here:

mathematics primarily works with sets, which are unordered collections of unique objects. if you have some number of sets, you can merge all their elements into one set. (this is typically called the "union")

a topological space is a set of values (the points of the space) with extra information called the topology. to avoid getting into details, a topology essentially specifies what points are "close together", as opposed to ones that are separated. this is a fundamental concept in modern geometry and lets us define a notion of continuous functions, as opposed to functions that "jump."

all sets, finite or infinite, have a number of elements within them, called the cardinality. for example, the set {1,4,5} has cardinality 3.

there are obviously multiple finite cardinalities that a set can have (like 1 vs 2), but a foundational result of set theory is that there are multiple infinite cardinalities, or in order words, some infinite sets are strictly larger than other infinite sets. ω and ω₁ are two sets that can be proven to exist; ω has the same number of elements as the infinite set of all integers (a countably infinite set), while ω₁ is a larger still than that (an uncountably infinite set).

with all that in mind, the real number line is a topological space (set of points with a notion of "closeness") that can be shown to be equivalent to a countably infinite number of real intervals attached to each other; in other words, if for every integer you take an interval of length 1 and glue them all together (to use the technical term), you get the real number line.

the long line is constructed by doing the same gluing but for an ω₁ number of real intervals. since ω₁ is strictly larger than the set of all integers, this line must be longer than the real number line, even though that is extremely counterintuitive and doesn't make sense to our brains.

Hope This Helps!

#mathematics #topology #long line #long line posting #kikis explanations #tokinanpa

7K notes · View notes

coursesforallacademynoida · 5 years ago

Text

BSc Mathematics Online Tutor For Real Analysis

Join Online Live Tuition Class For BSc Mathematics. Online Live BSc Mathematics Tuition Class Available Across All Location Of India. Courses For All Academy Offer All University BSc Mathematics Online Tuition Class.

Finite and infinite sets, examples of countable and uncountable sets. Real line, bounded sets, suprema and infima, completeness…

View On WordPress

#Abstract Algebra #Abstract Algebra II #Abstract Algebra II Online Tuition #Abstract Algebra Online Tuition #alternating series #Archimedean property of R #Bounded sequence #bounded sets #BSc Math Online Tuition For Agra University #BSc Math Online Tuition For Amity University #BSc Math Online Tuition For Ignou University #BSc Math Online Tuition For Jamia University #BSc Math Online Tuition For Lalit Narayan Mithila University and Many More State and Central Universities. B.Sc Others Subjects For Which Tu #BSc Math Online Tuition For Sharda University #BSc Mathematics Online Tutor For Real Analysis #BSc Mathematics Online Tutor For Real Analysis Join Online Live Tuition Class For BSc Mathematics. Online Live BSc Mathematics Tuition Class #Cauchy convergence criterion for sequences. Cauchy’s theorem on limits #comparison test #completeness property of R #convergence of p-series #Differential Equations I #Differential Equations I Online Tuition #Differential Equations II #Differential Equations II Online Tuition #examples of countable and uncountable sets. Real line #geometric series #intervals. Concept of cluster points and statement of Bolzano-Weierstrass theorem. Real Sequence #Introduction to MATLAB Programming #Introduction to MATLAB Programming Online Tuition #Leibnitz’s test (Tests of Convergence without proof). Definition and examples of absolute and conditional convergence. Sequences and series

0 notes

mathematicianadda · 5 years ago

Text

More Great Ways to Annoy a Mathematician

Which Ratio is Truly Golden?

I find it troubling that the golden ratio has so little in common with the golden rule.

Like, if you did unto others 1.618 times what you’d have them do unto you, then we’d all wind up exhausted.

And if you’re only doing 1/1.618 times unto them, then isn’t that a bit lazy?

A Puzzle About Rates

I’ve always enjoyed those puzzles like, “If 3 chickens can lay 3 eggs in 3 days, then how long will it take 100 chickens to lay 100 eggs?” They’re counter-intuitive (e.g., in my example, each chicken lays 1 egg per 3 days, so the answer is also 3 days), yet deal only with simple constant rates.

So what if the rates weren’t constant? Like in, say, a bureaucracy, where 20 times more people will accomplish only 1/20th as much?

(Sorry for putting the answer upside down. It reads: “Please complete the attached form (Z302: Aggregate Task Completion Rate Information Request) and we’ll process your inquiry in 4-6 weeks.”)

In this case, “a mathematician” refers specifically to Matt Parker, whose excellent book Humble Pi discusses the first two of these mistakes.

The Asymptote of Happiness

Lots of poets have found asymptotes a convenient literary symbol – the idea of eternal striving is a resonant one (even beyond the eternal striving of the struggling algebra student).

I love me some Raymond Smullyan.

Sorry again for putting the answer upside down. I dunno why I thought that was a clever idea. Mostly just forces you to turn off the auto-rotate setting on your phone.

Anyway, it reads: “Ask anything. You should already know not to buy lowfat yogurt.”)

Proving a New Theorem

Not that I’ve ever felt this myself. I’m just speculating.

P-R-E-N-A-T-A-L

What is parenting, if not a neat LARP?

(LARP = Live-Action Role-Playing Game, for those of you with less geeky acumen than I anticipate my audience to have.)

By the way, my friend Rayleen once described to me a brilliant comic, where one person asks, “When’s the baby due?” and the other person is drawn with a small horizontal stick figure emerging from their stick torso. (See? It’s such a good comic, I can just describe it.)

The Sales Pitch for Math

I think a lot about the different arguments for math, and the ways that they support or contradict each other. Is it a beautiful art? An urgent set of universal civic skills? Key preparation for technical professions?

The answer is yes to all three. But not for all math, and not all at once – and attempting to blend the purposes can lead to a muddle.

The Meaning of “Let”

It’s always tickled me that the mathematician’s verb ��let,” which sounds so chill and laissez-faire, is actually a binding command.

“All Happy Families Are Alike; Every Unhappy Family is Unhappy In Its Own Way”

I wrote a bunch of these a few years ago. This one has the benefit of being true: all circles are geometrically similar, but not all ellipses are.

(The same is true, by the way, of parabolas and hyperbolas. The former are all the same basic shape, just zoomed in or zoomed out, whereas the latter constitute a whole family of different shapes.)

(Chew on that, Tolstoy.)

The Court-Appointed Translator

I wrote this little dialogue after listening to a great episode of The Allusionist, before it turned out that Game of Thrones would suffer the worst collapse in storytelling that I have ever experienced.

Oh well!

As my wife said, “At least this way we’ll never have to bargain with our daughter about when she’s old enough to watch Game of Thrones. The ending is so bad, in 10 or 15 years no one will be watching it anymore.”

Identity Politics

This is a really dumb pun.

Also one of the more popular cartoons in this list.

Go figure.

Another Dumb Pun

This one is inspired by that time Malcolm Gladwell referred to eigenvectors as “igon vectors,” and Steven Pinker blasted him for it, at which point Gladwell blasted Pinker for something else, and eventually we all lost the thread and just went about our days.

And if you want more godawful matrix puns, I’ve got ’em.

I don’t know what day you’re reading this, but guess what? It’s also a bad approximation of pi! So go ahead and celebrate!

(Though if you want some very clever alternative pi days, check out Evelyn Lamb’s page-a-day calendar, which includes a Pi Day each month, and not where you’d expect!)

Uncountably Many Wishes

After I posted this, there was a bunch of discussion on Twitter about whether I’d mischaracterized the Axiom of Choice, which is totally possible, in which case, oops.

Also, some folks pointed out that it’s pretty greedy to wish for uncountably many wishes, when you could just as easily wish for countably many.

To which I say: What’s the point of a magic lamp, if not to have greed be your undoing?

Maximization vs. Minimization

For lots of optimization problems, maximizing makes sense, but minimizing doesn’t. (Or vice versa.) An example: What’s the largest rectangle you can make from 4 feet of wire?

It’s the 1-by-1 square, with an area of 1 square foot.

But what’s the smallest rectangle you can make (in terms of area)? Well, you could make the 1.9999 by 0.0001 rectangle, which has a very tiny area…

Or you could make the 1.999999 by 0.000001 rectangle, which has an even smaller area…

Or the 1.99999999999999 by 0.000000000000001 rectangle, whose area is microscopic…

…and so on.

I hope that was worth it! And I suspect it wasn’t! Anyway, moving on.

More thoughts here.

The Villainous Mathematician Explains His Plan

Clearly this villain should be assigning more group work.

Anyway, I for one am curious to know how a complex-valued currency might work. I’d pay a hefty fee for an accountant or tax attorney who can turn imaginary assets into real ones, or real debts into imaginary ones.

The Cat on the Bed

I found it very hard to draw a decent space-filling curve.

Also, to draw a decent cat.

Only Slept Four Hours

This is how I feel about anyone who sleeps less than 7 hours in a given night.

Axioms of Life

This is my version of that xkcd about kitties.

Also pretty well summarizes parenthood. I still enjoy a cerebral geek-out, as I always have; but I also really enjoy holding my daughter in my arms and calling her the world’s best monkey over and over.

How Many Stars?

I would totally read a graphic novel about the dating life of Georg Cantor.

The problem is that no one is going to write this graphic novel except for me.

Oh well. I’m under contract for two more books at the moment, but after that will come TRANSFINITE LOVE: THE ROMANTIC ESCAPADES OF A SET THEORIST.

Quick-Draw Answers

Drawn from an actual experience, in my first week teaching 7th grade. I hadn’t really figured out how to tee up a problem-solving experience yet.

Twenty Questions

Drew this one for a Jim Propp essay. Recommended as always!

A New Proof

A teaching friend of mine had a whole list of proofs that 1 = 0, which he busted out at various developmentally appropriate points in grades 6 through 12.

I love that. Curious how far you could get writing a book of proofs that 1 = 0, each introducing a key idea in mathematics…

Maybe that’ll be my next project after the George Cantor romance novel.

E = mc

Philosophical question: Is this a pun?

The case against: “A pun is a joke that plays on words that sound similar but mean different things. This isn’t doing that.”

The case for: “A pun is a joke that plays on linguistic expressions with similar surface features, but different deep meanings. This is doing exactly that: the premise of the joke is that an exponent and a footnote are both denoted with a superscript, yet mean very different things.”

So I guess this has a deep resemblance to puns, but lacks a surface resemblance… which is itself, not very pun-like.

Ruling: Not a pun!

“The Exception Proves the Rule”

I guess you hear this inane phrase less often these days. But there was a time, kiddos, when people could hear a devastating counterexample to what they were arguing, and then blithely say “the exception proves the rule” with a straight face.

The Math Sequence

I’m pretty agnostic on the math sequence. But I have strong intuitions that Star Wars should be screened in the order: IV, V, I, II, III, VI, and so on. (I view the sequels as pretty optional. Prequels too, for that matter, but if you limit yourself to the original trilogy, it’s a boring problem.)

The “Same” Age

A lot of people on Facebook seemed to read this as though the right-hand character was creeping on Ariana Grande. Not my intention at all! I just wanted to pick a mid-20s celebrity. Could’ve just as easily been Bieber.

(My primary association with Ariana Grande, by the way, is her performance in the short-lived bar mitzvah-themed Broadway musical Thirteen.)

Lemniskate

I’m not sure there’s a joke here.

I’m fond of this drawing anyway.

Linear Child

Michael Pershan, the internet’s most relentlessly analytical math educator, inexplicably loved this joke, so I call it a win.

Someone on social media speculated about the position by which this linear combination had been “conceived,” which I found quite vulgar and upsetting (but which I also sort of invited by drawing a comic about procreating vectors).

If P, then Q

Where do we draw the line between logical succession, and outright stalking? I leave that to the courts.

Loons and Lunes

Sometimes I just want to do a cute drawing that has no joke in it, okay?

The Vertical Line Test

I’m actually skeptical that the phrase “vertical line test” has any value. To me it feels like a fancy name for a fact that doesn’t need a fancy name. And, as in the two-column-proof version of geometry, giving fancy names to facts that students should be reasoning out for themselves can become obfuscatory rather than clarifying.

Whose Fractal is Whose?

Please join me in making “Patricia gasket” a thing! E.g., “Did you know Copley Square in Boston is the approximate shape of the mathematical figure known as a Patricia Gasket?”

from Math with Bad Drawings https://ift.tt/2RlT021 from Blogger https://ift.tt/2wnolKj

#Blogger

0 notes

brianmcnett-blog · 2 years ago

Text

While this is brilliant and awesome something very like it is a concept at the heart of mathematics: Normal Numbers.

Imagine if you will a number line. It contains the positive integers. 0, 1, 2, 3, 4… there’s an infinity of them. Now add to this negative numbers -1, -2, -3, -4… another infinity. Add fractions. 1/2, 1/4, 1/3, 1/8… yet another infinity. These are all what are known as “countable” infinities. Conceivably, you could make a list containing all of them.

Georg Cantor called this smallest infinity “ℵ-null.” He continued on, however and quite controversially for his day, EXTENDED the very concept of infinity by demonstrating uncountable infinity.

For this, instead of considering the entire number line, we’ll just look at the numbers between 0 and 1, but in addition to the counting numbers and the rational numbers we’ll include “real” numbers. Cantor showed, quite eloquently, that any attempted list of these numbers would ALWAYS be incomplete. You can never count them all. And this is just between 0, and 1.

Now within the set of the real numbers lie the normal numbers, and since the real numbers are uncountable, the normal numbers are ALSO uncountable. A real number is said to be normal in the integer base b if it’s infinite sequence of digits is uniformly distributed in the sense that each of the b values has the same natural density 1/b. So in base 10, every digit would occur 1/10th of the time.

This has some implications. Pairs of digits appear in a base 10 normal number exactly 1/100th of the time, triplets 1/1000th, etc.

Normal numbers should therefore contain every possible sequence of digits no matter how long

As numbers can be used to represent any symbols, it is not inconceivable that within any randomly selected normal number there is a perfect copy of the entirety of Jorge Luis Borge’s “Library of Babel.”

Unfortunately, one of the unresolved problems of mathematics is how to determine whether a number is normal.

So, outside of a few specially constructed examples, such as the Copeland-Erdös constant, obtained by concatenation of consecutive primes, or Champernowne’s constant, created by concatenation of consecutive positive integers, we know exactly zero normal numbers.

It’s believed, however, that most of the irrational real numbers are normal numbers. Most of the uncountable infinity of numbers are normal numbers and we basically have no way of identifying them. Every normal number contains every possible sequence of digits up to and including sequences of infinite lengths. There is a complete copy of the “Library of Babel” within each and every normal number, AND WE HAVE NO WAY OF FINDING THEM. But this goes beyond that. Because normal numbers can represent any sequence of symbols and aren’t limited by the rules Borges set for his library. Any randomly selected normal number contains within it every mathematical formula ever created or that ever will be. All the laws of physics are encoded within normal numbers.

These are most of the numbers. Every last one a complete Library of Babel and more. We know only a few specially constructed examples.

The perplexing nexus exists within nature. It’s a fundamental part of the universe. We know it exists. We are unable to detect it.

The fact that there’s an actually functional website for the library of Babel is one of those things that fucks me up more and more the more I think about the implications.

112K notes · View notes

richard1lauritsen-blog · 7 years ago

Text

Test Bank Languages and Machines An Introduction to the Theory 3rd Edition Solution

For Order This And Any Other Test

Banks And Solutions Manuals, Course,

Assignments, Discussions, Quizzes, Exams,

Chapter 1

Mathematical Preliminaries

5. To prove that X ∩ Y = (X ∪ Y) requires establishing both of the inclusions X ∩ Y ⊆ (X ∪ Y) and (X ∪ Y) ⊆ X ∩ Y.

i) Let a ∈ X ∩ Y. By the definition of intersection, a ∈ X and a ∈Y.Thus a ∈ X and a ∈ Y or, in terms of union, a ∈ (X ∪ Y). It follows that a ∈ (X ∪ Y).

ii) Now assume that a ∈ (X ∪ Y). Then a ∈ X ∪ Y. This implies that a ∈ X and a ∈ Y. Consequently, a ∈ X ∩ Y.

Part (i) shows that X ∩ Y is a subset of (X ∪ Y), while (ii) establishes the inclusion (X ∪ Y) ⊆ X ∩ Y.

A completely analogous argument can be used to establish the equality of the sets (X ∩ Y) and X ∪ Y.

6. a) The function f (n) = 2n is total and one-to-one. However, it is not onto since the range

is the set of even numbers.

b) The function {

0 if n = 0

f (n) =

n−1 otherwise

is total and onto. It is not one-to-one since f (0) = f (1) = 0.

c) The function 

 1 if n = 0

f (n) = 0 if n = 1



n otherwise

is total, one-to-one, and onto but not the identity.

d) The function f (n) =

{

n/2 if n is even

↑ otherwise

maps the even natural numbers onto the entire set of natural numbers. It is not a total function from N to N, since it is not defined for odd natural numbers.

13. To prove that ≡p is an equivalence relation, we must show that it is reflexive, symmetric, and transitive. This is shown using the same argument given in Example 1.3.1, which explicitly considers the case when p = 2.

i) Reflexivity: For every natural number n, n mod p = n mod p. 1

2 CHAPTER 1. MATHEMATICAL PRELIMINARIES

ii) Symmetry: If n mod p = m mod p, then m mod p = n mod p.

iii) Transitivity: If n mod p = m mod p and m mod p = k mod p, then n mod p = k mod p. The equivalence classes of ≡p are the sets consisting of natural numbers that are equal mod p: [0]≡p = {0, p, 2p, 3p, . . .}

[1]≡p = {1, p + 1, 2p + 1, 3p + 1, . . .} [2]≡p = {2, p + 2, 2p + 2, 3p + 2, . . .}

[p − 1]≡p = {p − 1, 2p − 1, 3p − 1, 4p − 1, . . .}.

15. i) Reflexivity: To demonstrate reflexivity, we must show that every ordered pair [m, n] is

related to itself. The requirement for [m, n] to be related to [m, n] by ≡ is m + n = n + m, which follows from the commutativity of addition.

ii) Symmetry: If [m, n] ≡ [j, k], then m + k = n + j. Again, by commutativity, j + n = k + m and [j, k] ≡ [m, n].

iii) Transitivity: [m, n] ≡ [j, k] and [j, k] ≡ [s, t] imply m + k = n + j and j + t = k + s.

Adding the second equality to the first, we obtain

m + k + j + t = n + j + k + s.

Subtracting j + k from each side yields m + t = n + s, showing that [m, n] ≡ [s, t] as desired.

18. The set of non-negative rational numbers is defined by

{n/m | n ∈ N, m ∈ N − {0}}

A rational number n/m can be represented by the ordered pair [n, m]. This representation defines a one-to-one correspondence between the rational numbers and the set N × (N − {0}). The latter set is known to be countable by Theorem 1.4.4.

22. Diagonalization is used to prove that there are an uncountable number of monotone increasing functions. Assume that the set of monotone increasing functions is countable. Then these functions can be listed in a sequence f0, f1, f2, . . . ,fn,......

Now we will show that there is at least one (in fact there are infinitely many) monotone increasing function that is not in the listing. Define a function f as follows:

f (0) = f0(0) + 1

f (i) = fi(i) + f (i − 1)

for i > 0. Since fi(i) > 0, it follows that f (i) > f (i − 1) for all i and f is monotone increasing.

Clearly f (i) = fi(i) for any i, contradicting the assumption that f0, f1, . . ., fn, . . . exhaus- tively enumerates the monotone increasing functions. Thus the assumption that the monotone increasing functions comprise a countable set leads to a contradiction and we conclude that the set is uncountable.

25. To show that the set of real numbers in the interval [0, a] is uncountable, we first observe that

every real number in (0, 1] can be expressed by an infinite decimal .x0x1x2. . .xn.... With such

a representation, the number12 isrepresentedbyboth.50000...and.49999.............. To obtain a

SOLUTIONS TO EXERCISES 3

unique representation, we consider only decimal expansions that do not end with an infinite sequence of zeros.

Assume the set of real numbers in (0, 1] is countable. This implies that there is a sequence r0, r1, r2, ... ,rn, ...

that contains all of the real numbers in the interval (0, 1]. Let the decimal expansion of rn

be denoted .xn0xn1xn2........... The enumeration given above is used to construct an infinite

two-dimensional array, the ith row of which consists of the expansion of ri.

r0= x00 x01 x02

r1= x10 x11 x12

r2= x20 x21 x22

With the unique decimal representation, two numbers are distinct if they differ at any position in the decimal expansion. A real number r = x0x1 . . . is defined using the diagonal elements in the array formed by the xii’s as follows:

{

xi =

2 if xii = 1

1 otherwise.

Clearly r = ri for any i since the ith position of r, xi, is not identical to the ith position of ri. Therefore the assumption that the enumeration contains all real numbers in (0, 1] fails, and we conclude that the set is uncountable.

28. Before proving the Schröder-Bernstein Theorem, we consider the special case where card(B) ≤ card(A), card(A) ≤ card(B), and B ⊆ A.

The relationship card(B) ≤ card(A) follows immediately from the inclusion B ⊆ A since the identity function id : B → A is a one-to-one function from B into A.

By definition, card(A) ≤ card(B) means there is a one-to-one function f from A into B. We will use f to construct a one-to-one function h : A → B from A onto B. The function h demonstrates that A and B have the same cardinality.

The diagram

f A

4 CHAPTER 1. MATHEMATICAL PRELIMINARIES

illustrates the mapping f . The function f is defined for all elements in A (which includes all elements of B) and the values of f , indicated by the heads of the arrows, must all be in B.

For each x ∈ A − B, we define the set

ch(x) = {x, f (x), f (f (x))), . . . , fi(x), . . .}.

Every element in ch(x) is in B, except for x itself which is in A −B. Let ⋃

C= ch(x).

x∈ A−B

Now define the function h : A → B as follows:

{

f (z), if z ∈ C;

h(z) =

z, otherwise.

To show that h is a one-to-one, we must prove that h(x) = h(y) implies that x = y. There are four cases to consider.

Case 1: x, y ∈ C. Then x = h(x) = h(y) = y.

Case 2: x ∈ C and y ∈ C. Since x ∈ C, h(x) = f (x) is in C. But h(x) = h(y) = y. This implies that y ∈ C, which is a contradiction. Thus h(x) cannot equal h(y) in this case.

Case 3: x ∈ C and y ∈ C. Same argument as case 2.

Case 4: x, y ∈ C. Let fi denote the composition of f with itself i times, and f0 denote the identity function. The proof uses the fact that the composition of one-to-one functions is one- to-one. Although you will be familiar with functional composition from previous mathematical studies, a description and formal definition are given in Section 9.4 of the text if you need a reminder.

Since x and y are both in C, x = fm(s) and y = fn(t) for some s, t ∈ A − B. Then h(x) = f (fm(s)) = h(y) = f (fn(t)).

If m = n, then s = t and x = y and we are done. Assume that m > n. Then fm−n(s) = t. Applying the function fn to both sides we get fm(s) = fn(t), or equivalently, x = y. A similar argument shows x = y when m < n.

We now show that h maps A onto B. For each x ∈ B but not in C, h(x) = x and x is covered by the mapping. If x ∈ B and x ∈ C, then x = f (t) for some t ∈ C because each element in C is either in A − B or obtained by the result of applying f to an element in C. Consequently, each element of B is ‘hit’ by the mapping h. Because h is a one-to-one function from A to B, we conclude that card(A) = card(B).

To prove the Schröder-Bernstein Theorem in its generality, we must show that card(X) ≤card(Y) and card(Y) ≤ card(X) implies card(X) = card(Y) for arbitrary sets X and Y. By the assumption, there are one-to-one functions f : X → Y and g : Y → X. Let

Im(Y) = {x ∈ X | x = g(y) for some y in Y}

be the image of Y in X under g. Now

- Im(Y) is a subset of X,

- Im(Y) has the same cardinality as Y (g is one-to-one and onto), and

- the composition f ◦ g is a one-to-one mapping from X into Im(Y).

SOLUTIONS TO EXERCISES 5

By the preceding result, card(X) = card(Im(Y)). It follows that card(X) = card(Y) by Exercise 27.

31. Let L be the set of the points in N × N on the line defined by n = 3 · m. L can be defined recursively by

Basis: [0, 0] ∈ L.

Recursive step: If [m, n] ∈ L, then [s(m), s(s(s(n)))] ∈ L.

Closure: [m, n] ∈ L only if it can be obtained from [0, 0] using finitely many applications of the recursive step.

33. The product of two natural numbers can be defined recursively using addition and the successor operator s.

Basis: if n = 0 then m · n = 0

Recursive step: m · s(n) = m + (m · n)

Closure: m · n = k only if this equality can be obtained from m · 0 = 0 using finitely many applications of the recursive step.

37. The set F of finite subsets of the natural numbers can be defined recursively as follows: Basis: ∅, {0} ∈ F

Recursive step: If {n} ∈F , then {s(n)} ∈ F . If X, Y ∈F , then X ∪ Y ∈ F .

Closure: A set X is in F only if it can be obtained from the basis elements by a finite number of applications of the recursive step.

The first rule in the recursive step generates all sets containing a single natural number. The second rule combines previously generated sets to obtain sets of larger cardinality.

39. We prove, by induction on n, that

∑

2i = 2n+1−1

i=0

Basis: The basis is n = 0. We explicitly show that the equality holds for this case. ∑

2i = 20 = 1 = 21−1

i=0

Inductive hypothesis: Assume, for all values k = 1, 2, . . . , n, that ∑

2i = 2k+1− 1

i=0

Inductive step: We need to show that

∑

2i = 2(n+1)+1−1

i=0

To utilize the inductive hypothesis, the summation is decomposed into the sum of the first n powers of 2 and 2n+1.

n+1

6 CHAPTER 1. MATHEMATICAL PRELIMINARIES

∑ n∑

2i = 2i + 2n+1

i=0 i=0

= 2n+1−1+2n+1 (inductive hypothesis)

= 2·2n+1−1 = 2(n+1)+1−1

43. The set R of nodes reachable from a given node x in a directed graph is defined recursively using the adjacency relation A.

Basis: x ∈ R.

Recursive step: If y ∈ R and [y, z] ∈ A, then z ∈ R.

Closure: y ∈ R only if y can be obtained from x by finitely many applications of the recursive step.

46. a) The depth of the tree is 4.

b) The set of ancestors of x11 is {x11, x7, x2, x1}. Recall that by our definition is node is an ancestor of itself, which is certainly not the case in family trees.

c) The minimal common ancestor of x14 and x11 is x2; of x15 and x11 is x1.

d) The subtree generated by x2 is comprised of the arcs [x2, x5], [x2, x6], [x2, x7], [x5, x10], [x7, x11], and [x10, x14].

e) The frontier is the set {x14, x6, x11, x3, x8, x12, x15, x16}.

48. Induction on the depth of the tree is used to prove that a complete binary tree T of depth n has 2n+1− 1 nodes. Let nodes(T) and leaves(T) denote the number of nodes and leaves in a tree T.

Basis: The basis consists of trees of depth zero; that is, trees consisting solely of the root. For any such tree T, nodes(T) = 1 = 21− 1.

Inductive hypothesis: Assume that every complete binary tree T of depth k, k = 0, . . . , n, satisfies nodes(T) = 2k+1− 1.

Inductive step: Let T be a complete binary tree of depth n + 1, where n ≥ 0. We need to show that nodes(T) = 2(n+1)+1− 1. T is obtained by adding two children to each leaf of a complete binary tree T′ of depth n. Since T′ is complete binary, it is also strictly binary and

leaves(T′) = (nodes(T′) + 1)/2

by Exercise 47. Thus

nodes(T) = nodes(T′) + 2 · leaves(T′)

= nodes(T′) + 2 · [(nodes(T′) + 1)/2] (Exercise 47) = 2 · nodes(T′) + 1

= 2 · (2n+1− 1) + 1 (inductive hypothesis)

=2(n+1)+1−1

n+1

#Test Bank Languages and Machines An Introduction to the Theory 3rd Edition Solution

0 notes