#googology

[lunaxio]

hehe really big number with 69s and 420s and such

the number in brackets is the hyperoperation. (1=add, 2=multiply, 3=exponent) 3[3]3=27 4[4]4 is made with tetration, which makes the number so big, that you can't even write it with with exponents, as 3[4]4 is some number with trillions of digits. F1=360[69420[420[1337]420]69420]360 F2=F1^F1[F1^F1[F1^F1[F1^F1[F1^F1[F1^F1]F1^F1]F1^F1]F1^F1]F1^F1]F1^F1 F3 is the same equation as F2, but replace F1 with F2. continue until F694203601337.

i like making up really big numbers

[a-googology-acount]

Derived Sets

Hey everyone. Cantor defined the ordinal numbers in 1883 for a theorem about derived sets. I want to explain this theorem to you today. This isn't very related to googology, but it shows an interesting use of ordinal numbers, which are prominent in googology.

Given a set of real numbers P, an accumulation point of P is some real number x for which all neighbourhoods of x contain a point in P other than x itself. Equivalently, for all ε > 0, there is some y ∈ P such that x-ε < y < x+ε. For example, if P = {1/n | n a positive integer} then 0 is an accumulation point of P, as every neighbourhood of 0 contains all 1/n for large enough n. 1 is not an accumulation point of P as the neighbourhood (3/4,5/4) of 1 contains no points in P other than 1 (!remember: neighbourhoods of x are required to have points in P that are distinct from x itself for x to be an accumulation point). Accumulation points are also called limit points and their definition applies to all topologies, not just the real number line.

Given a set P, its derivative, denoted P', is the set of all accumulation points of P. Some basic properties of derivatives are: P' is always a closed set, and conversely, every closed set (of reals) is a derivative of some other set. P'' (that is, the derivative of the derivative of P, i.e. the second derivative of P) is always included in P', but P' needn't be included in P. A set P is called a perfect set if P' = P. For example, if P = {1/n | n a positive integer}, then P' = {0} and P'' = {}.

You can iterate the derivative of a set P. The n+1'th derivative of P is the derivative of the n'th derivative of P, where the 0th derivative is P itself. The n'th derivative of P is denoted P^(n). You can also take the infiniteth derivative of P: P^(∞) = ⋂[n a natural number] P^(n). And you can continue from there, with P^(∞+1) being the derivative of P^(∞), P^(∞+2) is the derivative of P^(∞+1), etc.

The α in P^(α) is called an ordinal number. Usually, the smallest infinite ordinal number is denoted with the Greek letter ω. So the P^(∞) described in the above paragraph is normally written as P^(ω). The definition of iterated derivatives is extended to ordinal numbers by adding a limit case: P^(λ) = ⋂[α < λ] P^(α) for limit ordinal λ, where a limit ordinal is an infinite ordinal with no direct predecessor (e.g. ω, ω2, ω², etc).

Cantor's theorem is as follows:

Theorem (Cantor, 1883). Let P ⊆ ℝ be a set of real numbers. Its derivative P' is countable if and only if P^(α) is empty for some ordinal α.

I won't give a proof in this blog post, but I will prove a simpler theorem concerning perfect sets. This theorem is used in the proof of the above theorem. The proof is my own and might not be the best proof of this theorem, but I still like it.

Theorem. Let P ⊆ ℝ. If P is a non-empty perfect set (i.e. P' = P), then P is uncountable.

Proof. Suppose P is a non-empty perfect set. Since P is non-empty, let x ∈ P. P is perfect, thus x ∈ P'. Define a sequence (x₀,x₁,x₂,...) as follows: x₀ is some point in P in the neighbourhood (-∞,+∞) of x other than x itself, which exists by x ∈ P'. To define xₙ₊₁, let ε = |x - xₙ| be the distance from x to xₙ, and let xₙ₊₁ be some point in P in the neighbourhood (x-ε,x+ε) of x other than x itself, which (again) exists by x ∈ P'. All elements of (x₀,x₁,x₂,...) are distinct, thus P is infinite. Assume, aiming for a contradiction, P is countably infinite and let a = (a₀,a₁,a₂,...) be an enumeration of P (when proving something about a countable set, picking an enumeration is often a good first step). If P is unbounded, then let x ∈ P, we have that [x-1,x+1] ∩ P is a bounded countable perfect set, thus, WLOG, assume P is bounded. We will define a subsequence (a_i₀,a_i₁,a_i₂,...) of (a₀,a₁,a₂,...) using a game played by Alice. The rules of this game are as follows: at the kth turn, Alice first chooses some εₖ > 0 and promises that, from now on, she won't choose a_iₘ in the neighbourhood (aₖ-εₖ,aₖ+εₖ) of aₖ, then she chooses some index iₖ > i₀..iₖ₋₁ such that a_iₖ abides by her previous promises. She loses if she cannot choose such an iₖ I will now show that Alice has a winning strategy. At turn k, A denotes the union of neighbourhoods of points a₀..aₖ that Alice promised no a_iₘ for m ≥ k would be in, and A̅ denotes the closure of A. In the strategy I'll describe, there are always infinitely many aₘ outside of A̅, which can be proven by induction. At turn k, Alice first picks some x in P outside of A̅ that is not equal to aₖ (e.g. the first such x in the enumeration (a₀,a₁,a₂,...)), which exists as P \ A̅ is infinite. Then, she chooses some δ such that (x-δ,x+δ) does not intersect A̅ ∪ {aₖ} (e.g. the largest such δ), which exists as A̅ ∪ {aₖ} is closed. P is perfect, thus (x-δ,x+δ) ∩ P is infinite. She then chooses δ/2 as εₖ. (x-δ/2,x+δ/2) ∩ P is infinite and disjoint from A̅, and in the next turn its still disjoint from A̅ (in the next turn, A̅ also includes [aₖ-δ/2,aₖ+δ/2], which is disjoint from (x-δ/2,x+δ/2) as x and aₖ have distance ≤δ), meaning that the property of A̅ that infinitely many points outside it are in P is preserved (those points being in (x-δ/2,x+δ/2) ∩ P). Now, Alice chooses some iₖ so that a_iₖ ∈ P \ A (e.g. the least such iₖ), which exists as P \ A̅ ⊆ P \ A is infinite. We now have a sequence (a_i₀,a_i₁,a_i₂,...) of points in P. P is bounded thus the sequence (a_i₀,a_i₁,a_i₂,...) is bounded and thus has a converging subsequences, which converges to some point l. We thus have l ∈ P', and by the assumption that P is perfect, we have l ∈ P. By construction of the sequence (a_i₀,a_i₁,a_i₂,...), l is distinct from a₀, a₁, a₂, ..., contradicting a = (a₀,a₁,a₂,...) being an enumeration of P, meaning that P is uncountable. ∎

Notes: The use of a game in the above proof was unneeded, I could've just defined (a_iₖ) by simple induction but I thought using a game for it is funny. The proof works without the axiom of choice.

[orbthaija]

Eiper He notation (FIXED VERSION)

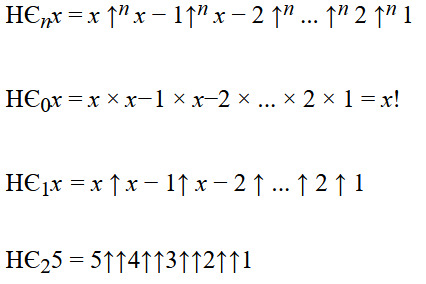
MY BEAUTIFUL REDESIGN OF FACTORIAL WHICH ALLOWS ONE TO ITERATE THE MULTIPLICATION TO THE DEPTHS OF HELL

HЄnx

HЄ(n, x) is the acceptable format for platforms without certain formatting capabilities.

In my original post I had the idea of improved factorial in mind, but failed to notice that I wrote every example backwards. (HЄ(1, 5) = 1↑2↑3↑4↑5 instead of HЄ(1, 5) = 5↑4↑3↑2↑1 etc..)

Thank you @specialkindofidiot for pointing this out LOL

[hyperoperationfractallisation]

How far does this notation get (I think at least dimensional beaf?) and how can I continue it to nesting the last expression? I don't know...

(no, there is no difference between ()s and []s)

$$\let\up\uparrow\let\und\underbrace\begin{matrix}a\up^\up b=\und{a\up^{a\up^{a\up^\cdots a}a}a}_b\\a\up^\up\up b=a\up^{\up+1}b=\und{a\up^\up a\up^\up a\up^\up\cdots}_b\\a\up^\up\up\up b=a\up^{\up+2}b=\und{a\up^\up\up a\up^\up\up a\cdots}_b\\a\up^\up\up^\up b=a\up^{\up\times2}b=\und{a\up^\up\up^{a\up^\up\up^\cdots a}a}_b\\a\up^{\up\up}b=a\up^{\up^2}b=\und{a\up^{\up\times a\up^\cdots a}a}_b\\a\up^{\up^3}b=\und{a\up^{\up^2\times a\up^{\up^2\times\cdots}a}a}_b\\a\up^{\up^\up}b=a((\up)\up^23)b=\und{a\up^{\up^{a\up^{\up^\cdots}a}}a}_b\\a\up^{\up^{\up\up}}b=\und{a\up^{\up^{\up\times a\up^{\up^{\up\times\cdots}}a}}a}_b\\a([\up]\up^2[\up])b=\und{a([\up]\up^2[a([\up]\up^2[\cdots])])a}_b\\a([\up]\up^\up[\up])b=\und{a([\up]\up^{a([\up]\up^\cdots[\up])a}[\up])a}_b\\a([\up]([\up]\up^2[\up])[\up])b=\und{a([\up]([\up]\up[a([\up]([\up]\up\cdots)[\up])a])[\up])a}_b\end{matrix}$$

[globalintellectualbeverage]

What makes a number big?

What makes a number big is how dense it is compared to the information required to describe it.

What is the biggest math? Lambda calculus seems pretty big. You might need to include the definitions of the operators there to get full coverage. So if you want to use a symbol, you have to define it. Lambda calculus still looks to win here.

[madeofkaons]

here's a fun concept:

imagine a function f(x) where f(x) = x↑[x↑[x↑[x...]x]x]x. where the number of nested ↑[x↑x] structures (number of up arrows = x↑x) equals x.

f(1) = 1↑[1↑1]1 (1↑...↑1, number of up arrows = 1↑1) = 1↑1 = 1

f(2) = 2↑[2↑[2↑2]2]2 = 2↑[2↑[4]2]2 = 2↑[2↑↑↑↑2]2 = 2↑...↑2, number of up arrows = 2↑↑↑↑2)

etc.

[placeholdername-1]

you’re not wrong

googology is the study of numbers too big to count to or even comprehend, such as 100

[a-googology-acount]

derivative of a normal function

My drafts get too long too quickly so I'll try to explain something small. I assume you have a basic understanding of ordinal numbers before reading this.

An ordinal function is a function f: Ord → Ord that accepts ordinals α as arguments and gives back ordinals f(α) as values. Examples of ordinal functions are:

α ↦ 6

α ↦ α+1

α ↦ ω^α

α ↦ #α, where #α is the cardinality of α identified by the smallest ordinal with that cardinality

α ↦ n where α is of the form ωβ+n

An ordinal function can be increasing. This means that, for α < β, we have f(α) < f(β). Try figuring out which of the above five functions are increasing and which are not. Here are the answers:

The constant α ↦ 6 is not increasing. For example, 0 < 1 but f(0) = 6 is not less than f(1) = 6.

α ↦ α+1 is increasing.

α ↦ ω^α is increasing.

α ↦ #α is not increasing. For example, ω < ω+1 but f(ω) = ω is not less than f(ω+1) = ω.

ωβ+n ↦ n is not increasing. For example, 0 < ω but f(0) = f(ω0+0) = 0 is not less than f(ω) = f(ω1+0) = 0.

There is a weaker statement called non-decreasing. A function f is non-decreasing if for α < β, we have f(α) ≤ f(β), where f(α) and f(β) are allowed to be equal. The first four examples are all non-decreasing, while the last one is not.

An ordinal function f: Ord → Ord is continuous if for limit ordinals λ, we have that the limit lim[α → λ] f(α) exists and is equal to f(λ). The limit lim[α → λ] f(α) is defined as: lim[α → λ] f(α) = β iff for all γ < β, we have some α₀ < λ so that, for all α with α₀ < α < λ, we have γ < f(α₀), and β is minimal with this property. We can also define continuous functions in terms of topology, where an ordinal function is continuous if preimages of open classes (unions of open intervals of ordinals) are also open.

Of the five examples, try figuring out which ones are continuous. Here are the answers:

The constant α ↦ 6 is continuous.

α ↦ α+1 is not continuous. For example, lim[n → ω] f(n) = lim[n → ω] n+1 = ω, but f(ω) = ω+1 ≠ ω.

α ↦ ω^α is continuous.

α ↦ #α is continuous. α ↦ #α is not continuous. For example, lim[α → ω₁] f(n) = ω but f(ω₁) = ω₁ ≠ ω.

ωβ+n ↦ n is not continuous. For example, lim[n → ω] f(n) = lim[n → ω] n = ω, but f(ω) = 0 ≠ ω.

A function that is both continuous and increasing is called a normal function. For an increasing function f, limits are supremums, so we can simplify the definition of continuity: an increasing function f is continuous (hence, normal) if for all limit ordinals λ, we have that sup{f(α) | α < λ} = λ.

Normal functions are exactly the ordinal functions that enumerate clubs. Given a set or class A of ordinals, the enumeration function enum[A] of A is defined using induction: enum[A](α) = min{β ∈ A | ∀α' < α. enum[A](α') < β}. In other words, enum[A](α) is the 1+α'th element of A. The "1+" is because normal people start counting at 1 and not at 0, but ordinal people start counting at 0. For example, given A = {4,5,ω²+6}, we have that enum[A](0) = 4, enum[A](1) = 5 and enum[A](2) = ω²+6, and enum[A](α) for α > 2 is undefined. A club is a closed unbounded set or class. "Closed" means that, for every set S ⊂ A, we have that sup(S) ∈ A (equivalently, it is the complement of an open class, it might be a fun exercise to prove that but idk since I haven't tried). "Unbounded" is that for every ordinal α, there is some ordinal β in A that is larger than α. Given a normal function f, we have that im(f), the image of f, is club (closed as f is normal, unbounded as f is increasing), and that f = enum[im(f)], i.e. f enumerates its image. And given a club A, we have that enum[A] is normal and A = im(enum[A]).

For an ordinal function f, we have a class {x | f(x) = x} of fixed points of f. A fixed point of f is a point x for which f(x) = x. For example, ε₀ is a fixed-point of α ↦ ω^α. If f is a normal function, the class {x | f(x) = x} is club, and thus the enumeration enum[{x | f(x) = x}] is continuous as well. This enumeration, enum[{x | f(x) = x}], is called the derivative of f, denoted f'. For example, the derivative of α ↦ 1+α is α ↦ ω+α.

Here is your homework: prove that the derivative of a normal function is itself an ordinal function (it is defined on all ordinals) and is also normal.

That's all. Bye.

[orbthaija]

Eiper He notation (WRITTEN COMPLETELY WRONG, REGARD THE NEW VERSION)

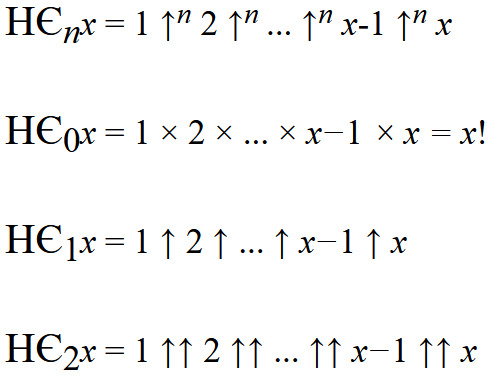
Eiper He notation will be used in multiple equations involving the sphere/hypersphere of influence of Orb Thaija.

The notation can alternatively be written like this:

HЄ(n, x)

for platforms that do not allow super/subscript.

(OUTDATED)

[glutko]

Real Page Titles (And Their Corresponding Large Numbers) From The Googology Wiki

[madeofkaons]

i think big number-naming competitions should be more widespread. like spelling bees, except if you had to make up the words by continuously inventing more compact representations of larger words based on repeating individual rules applied to the previous word created by your opponent, all within a time limit. the prize for first place would be getting to see the audience go oh no. Oh No. as they try to comprehend your number

[michaelrotonal]

nobody tell him about googology

just took a math class. the numbers get pretty big, folks

[crispyparsnips]

Ever since I fell head-first into the world of Googology, I thought it high time (heh) to wander into some other ludicrously-named areas of maths and develop my 100% serious science fiction universe using them. So everyone give it up (or keep it, it's not mine) for the wibbly wobbly world of Polytopes!

[gelidponies]

just learned about googology, twilight sparkle ass field of study

[dogwasp]

I was recently reading the list of googleisms on the googology wiki and felt compelled to draw some of them as eldrich monsters. Starting with: https://googology.fandom.com/wiki/Quadrolapulus

[a-googology-acount]

Veblen's φ

Hi everyone. I assume you are familiar with ordinal numbers, derivatives of normal functions and club sets before reading this post. I aim to explain Veblen's φ.

In a previous blog post, we saw that every normal function has a normal derivative, which enumerates the set of fixed points. Veblen's φ is obtained from iterating this derivative. φ₀ is an ordinal function that sends α to ω^α. φ₀ is a normal function, and thus has a derivative φ₀', which sends α to the 1+α'th fixed point of φ₀. An ordinal α for which α = ω^α is called an epsilon number. Thus, φ₀' enumerates epsilon numbers. The function φ₀' (the derivative of φ₀) is called φ₁. The αth epsilon number is also written ε_α, thus φ₁(α) = ε_α. φ₁ is itself normal (derivatives of normal functions are normal) and thus also has a derivative, φ₂, which enumerates what are called zeta numbers. We can keep going with this, with φ₃ the derivative of φ₂, φ₄ the derivative of φ₃, etc.

The nth derivative of f I'll write f^(n). The parentheses are to distinguish it from the nth iteration of f, which I write f^n or sometimes f^{n}. We have φ_n = φ₀^(n). To give another example, the second derivative f⁽²⁾ of f(α) = 1+α is f⁽²⁾(α) = ω²+α.

We can define F₀ = {x | φ₀(x) = x} to be the set of fixed points of φ₀, F₁ = {x | φ₁(x) = x} to be the set of fixed points of φ₁ and, generally, F_n = {x | φ_n(x) = x} to be the set of fixed points of φ_n. We can see that {F_n | n < ω} is a size ω family of closed and unbounded classes. From another previous blog post, we know that their intersection, ⋂[n < ω] F_n, which is the set of ordinals which are fixed points of all functions φ_n, must be closed and unbounded as well. The enumeration function of this intersection is φ_ω. φ_ω(0) is the limit of the sequence φ₀(0), φ₁(0), φ₂(0), ..., and φ_ω(1) is the limit of φ₀(φ_ω(0)+1), φ₁(φ_ω(0)+1), φ₂(φ_ω(0)+1), .... We can keep going like this, with φ_{ω+1} being the derivative of φ_ω, and generally, φ_α enumerates the class of ordinals that are a common fixed point of φ_β for β < α.

For each α, φ_α is continuous, and the function x ↦ φ_x(0) is also continuous. The 2-variable Veblen's φ itself, however, is not continuous. For example, lim[n → ω] φ_n(1) = φ_ω(0) ≠ φ_ω(1). For y > 0, φ_x(y) is always strictly greater than x, thus x ↦ φ_x(y) cannot be a continuous function. x ↦ φ_x(0) is continuous and does have fixed points, the least of which is called the Feferman-Schütte ordinal, denoted Γ₀.