#gamma-phi formulation | Explore Tumblr posts and blogs

jayflrt · 3 years ago

Note

I'm spamming you with these I hope that's okay, only pick the ones you actually like aha

"gorgeous gorgeous girls love soup"

hihi anon !! I SEE UR SPAM MUCH LOVE <33 i appreciate ur dedication to the ask game HAHAH so im gonna respond all of yours in this one ask :’’) 🥰 ALSO GORGEOUS GORGEOUS GIRLS LOVE SOUP IS SENDING MEE

....... anon............ im ngl........... im feeling a series for this one :o UR MIND 🤩 okay some of these titles are funny but the last title you sent ties a lot up rlly nicely??? and um. since i am in love with jay (loml) i think i will make these for jay <33 im seeing a lighthearted college au bc everyone knows im a slut for college aus :/ sorry

also sorry idk why most of these got so angsty LMFAO :’D

gorgeous gorgeous girls love soup

you don’t take the whole sorority girl thing that seriously. you don’t even care about the feud that delta sigma theta has against omega phi gamma; your gripe with jay park lies solely in the fact that he’s an insufferable asshole who nearly got you suspended for starting an argument at your charity ball. now, though, you both have to volunteer at the soup kitchen together for the next two months.

you thought your issues with this arrangement would be the fact that you couldn’t stand jay, but now things are different when you get to know jay better. and maybe it’s a little hot that he’s part of a band. for once, you think you can tolerate the guy, and maybe—just maybe—you might be catching feelings.

never have i ever

to no one’s surprise, you and jay are a thing, and everyone’s relieved that your only gripe with each other is being deemed as spongebob and patrick by your organizations. now, you and jay don’t really do things, but nevertheless, you test out being exclusive.

however, a game of never have i ever has you both questioning whether you two will truly work out. more specifically, the prompt “never have i ever been in love” kicks you in the ass (and jay in the heart).

strawberries and cigarettes

getting close to jay makes you vulnerable, you realize. thus, you both formulate a set of rules to keep your affairs strictly “no strings attached.” said strings start to fall apart at the seams, and you find yourself growing more and more attached to jay. you think this might actually be love.

there’s a problem, though. you don’t want to be in love, and you certainly don’t want to open your heart to jay park. you have to break his heart before he writes more songs about you.

back to square one

at the ripe age of sixteen, you learned that people will always disappoint you. you realized this when you discovered your ex-boyfriend cheating on you. so, to protect your own heart, you decided to break others instead.

you think you’ve shattered jay’s heart to pieces, but he can’t get you out of his head.

code word: pineapple

okay, so maybe you’ve made a lot of mistakes along the way (jisung confirms this a lot), but you have never been so sure of wanting jay back. the only way to do that, however, is be completely honest about your feelings. you have to tell jay that you love him. that he lights you on fire. that the burns that followed are worthwhile.

one problem: you have no idea how to confess.

luckily for you, code word: pineapple was created by your social organizations as a warning for whenever you and jay—fire and gasoline—were in close proximity. it was now time for you to reinvent that meaning.

or, the one where code word: pineapple is how you try to tell jay he’s your home.

baby blue

jay thinks you’re the color red—bold, vibrant, and blunt. but now you’re navigating a full-fledged relationship and have never felt so wary of every little thing. you’re baby blue, but maybe you’re okay with that.

or, the one where you try your hardest to be the best girlfriend you can be.

hope i never lose you, hope it never ends

college is coming to an end and everyone’s thinking about the future—about internships, about jobs, about marriage. when jay reveals that he wants to go to graduate school across the country while you’re entering the work force, you wonder if your relationship is hanging on by a string.

for once, thankfully, you both want to make it work.

#💌 : jayflrt love notes #anon #ask games

11 notes · View notes

ellinapark · 2 years ago

Text

Relaxation BeveragesMarket Is Likely to Experience a Tremendous Growth in Near Future

Latest edition released by AMA on Global Relaxation Beverages Market to regulate the balance of demand and supply. This intelligence report on Relaxation Beverages includes Investigation of past progress, ongoing market scenarios, and future prospects. Data True to market on the products, strategies and market share of leading companies of this particular market are mentioned. It’s a 360-degree overview of the global market’s competitive landscape. The report further predicts the size and valuation of the global market during the forecast period. Some of the key players profiled in the study are:

Funktional Beverage Company (United States)

iChill Beverages, Inc.

Bimble Beverages

New Age Beverages Corporation

Neurobrands LLC

Tranquini GmbH (Germany)

Life On Earth, Inc.

Harvest Beverage (United States)

Boisson Slow Cow, Inc. (Canada)

Som Friends, Inc.

Phi Drinks, Inc.

Seek Physis, LLC

Hanyi Biotechnology (Beijing) Co., Ltd. (China)

Kalm with Kava (United States)

Relaxation Beverages are formulated to help in reducing stress, and anxiety, improve focus and promote better sleep. These beverages are consumed as non-alcoholic drinks containing natural plant extracts such as herbs. People with Attention Deficit Hyperactivity Disorder (ADHD) are the major consumers of relaxation beverages. Relaxation drinks decrease stress levels which are the main cause of insomnia. Relaxation drinks usually contain gamma-aminobutyric acid (GABA) that affects the consumer's nervous system by helping to relax and reduce the level of stress. The rising stressed lifestyle of people has increased the demand for easy-to-consume relaxation beverages. Market Trends: Trend for Marijuana-infused Relaxation Beverages

Opportunities: Rising Occurrence of Chronic Stress Globally

Demand for Herbal And Green Tea Infused Relaxation Drinks

Market Drivers: Increasing Preference For Healthier Beverages

Growing Demand for Relaxation Beverages to Reduce Stress and Anxiety

Challenges: Adoption of Pharmaceutical Sleeping Aid to Deal with Stress

Presented By

AMA Research & Media LLP

0 notes

eatsleepmath · 7 years ago

Text

Strong conceptual completeness for \(\aleph_0\)-categorical theories, 2:

This series of posts is a serialization of (what started as) notes for a talk I gave at the Harvard logic seminar on 6 February 2018. You can view them in order here.

Pre-ultrafunctors

When \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) is \(\operatorname{ev}_{\varphi(x)}\) and one proves the Łos theorem \[X\left(\prod_{i \to \mathcal{U}} M_i \right) = \prod_{i \to \mathcal{U}} X(M_i),\] one has the luxury of being able to test the displayed equation above between two subsets of (the interpretation in \(\prod_{i \to \mathcal{U}} M_i\) of) the ambient sort of the formula \(\varphi(x)\). If \(X\) is merely isomorphic to \(\operatorname{ev}_{\varphi(x)}\), then \(X\left(\prod_{i \to \mathcal{U}} M_i\right)\) and \(\prod_{i \to \mathcal{U}} X(M_i)\) might be entirely different sets, with only the isomorphism to \(\operatorname{ev}_{\varphi(x)}\) to compare them, so that testing equality as above is not a well-formulated question; rather, one asks for an isomorphism.

Remark. Given a natural isomorphism \(\eta : X \simeq \operatorname{ev}_{\varphi(x)}\) with components \(\{\eta_{M} : X(M) \simeq \varphi(M)\}_{M \in \operatorname{\mathbf{Mod}}(T)}\), we have for every ultraproduct \(\prod_{i \to \mathcal{U}} M_i\) a commutative square

where the dashed map \(\Phi_{(M_i)}\) is the composition of isomorphisms \(\left(\prod_{i \to \mathcal{U}} \eta_{M_i} \right)^{-1} \circ \eta_{\prod_{i \to \mathcal{U}} M_i}\).

It is easy to see that the statement of Łos’ theorem is functorial on elementary embeddings. That is, for every \(I\), every ultrafilter \(\mathcal{U}\) on \(I\), and every sequence of elementary embeddings \(f_i : M_i \to N_i\), the diagram

commutes.

Definition. For an arbitrary functor \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\), if we additionally specify for every \(I, \mathcal{U}, (M_i)_{i \in I}\) the data of a transition isomorphism \(\Phi_{(M_i)} : X\left(\prod_{i \to \mathcal{U}} M_i\right) \to \prod_{i \to \mathcal{U}} X(M_i)\), then we say that \((X, \Phi)\) “commutes with ultraproducts” if all diagrams

commute. We let \(\Phi\) abbreviate all the transition isomorphisms, and we call a pair \((X,\Phi)\) a pre-ultrafunctor. We will abuse terminology by referring to \(\Phi\) as “the” transition isomorphism of the pre-ultrafunctor \((X, \Phi)\).

Given two pre-ultrafunctors \((X, \Phi)\) and \((X', \Phi')\), we define a map between them, called an ultratransformation, to be a natural transformation \(\eta : X \to X'\) which satisfies the following additional property: all diagrams

must commute.

With this terminology, the theorem says that if \(X\) is a sub-pre-ultrafunctor of an evaluation functor \(\operatorname{ev}_{\varphi(x)}\), then \(X\) is definable.

In light of the above definition, we can reformulate our observation about a definable functor \(X \overset{\eta}{\simeq} \operatorname{ev}_{\varphi(x)}\) above as saying that the natural isomorphism \(\eta\) canonically equips \(X\) with a transition isomorphism such that \(\eta\) is an ultratransformation.

Remark. Every functor of points \(\operatorname{ev}_{\varphi(x)}\) can be canonically viewed as a pre-ultrafunctor with the transition isomorphisms \(\Phi\) just the identity maps (corresponding to the equality signs in the above diagrams).

One checks that if \(X\) and \(Y\) are definable sets, and \(f : X \to Y\) is a definable function, then the induced natural transformation between evaluation functors \(\operatorname{ev}_f : ev_X \to \operatorname{ev}_Y\) is in fact an ultratransformation. (This contains Los’ theorem: in the proof, one is really showing that if \(S\) is the sort containing a formula \(\varphi(x)\), then the canonical definable injection \(i : \varphi(x) \hookrightarrow S\) induces an ultratransformation; the fact that the transition isomorphisms are all identities means that one ends up with the usual equality.)

Definition. The category of pre-ultrafunctors \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) comprises objects preultrafunctors \((X, \Phi)\) and morphisms the ultratransformations.

Remark. By the remark, the evaluation functor \(\operatorname{ev} : \operatorname{\mathbf{Def}}(T) \to [\operatorname{\mathbf{Mod}}(T), \mathbf{Set}]\) further factors through \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\):

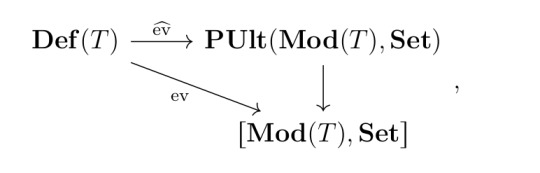
where the arrow \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) is just the forgetful functor \((X, \Phi) \mapsto X\).

Note that whenever there is an isomorphism \(\eta : X \simeq Y\) as functors \(\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\), and \((X, \Phi)\) is a pre-ultrafunctor, then by conjugating \(\Phi\) by the isomorphism \(X \simeq Y\) (as in the diagram), one canonically equips \(Y\) with a transition isomorphism \(\Phi'\) such that \(\eta : (X, \Phi) \to (Y, \Phi')\) is an ultratransformation.

Remark. That is, \(X\) is definable if and only if there is a transition isomorphism \(\Phi\) such that \((X,\Phi)\) is isomorphic to \((\operatorname{ev}_{\varphi(x)}, \operatorname{id})\) for some formula \(\varphi(x) \in T\). We will suppress the canonical transition isomorphism \(\operatorname{id}\) and just say that \((X,\Phi)\) is isomorphic to \(\operatorname{ev}_{\varphi(x)}\), understanding that this isomorphism is happening in \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\).

The pre-ultrafunctor condition only stipulates compatibility with respect to ultraproducts of elementary embeddings. However, there are other elementary embeddings which arise purely formally between different ultraproducts with respect to different indexing sets and ultrafilters, and should be viewed as part of the formal structure on \(\operatorname{\mathbf{Mod}}(T)\) which is induced by being able to take ultraproducts. The canonical example is the diagonal embedding of a model into its ultrapower (which compares an ultrapower \(M\) with respect to the trivial indexing set and trivial ultrafilter to an ultrapower \(M^{\mathcal{U}}\) with respect to a nontrivial indexing set and a nontrivial ultrafilter).

Definition. Fix \(I\), \(\mathcal{U}\), and a model \(M \models T\).

The diagonal embedding \(\Delta_M : M \to M^{\mathcal{U}}\) is given by sending each \(a \in M\) to the equivalence class of the constant sequence \([a]_{i \to \mathcal{U}}\).

We can stipulate that a pre-ultrafunctor furthermore preserves the diagonal embeddings.

Definition. We say that a pre-ultrafunctor \((X,\Phi)\) is a \(\Delta\)-functor if for every \(I\), for every \(\mathcal{U}\), and for every \(M\) and the diagonal embedding \(M \overset{\Delta_M}{\longrightarrow} M^{\mathcal{U}}\), the diagram

commutes.

Remark. It is not true in general that the embedding \(\widehat{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) is an equivalence of categories. If \((X, \Phi)\) is isomorphic to \(\operatorname{ev}_{\varphi(x)}\), then \((X, \Phi)\) preserves the diagonal embeddings of models into their ultrapowers (in the sense of the definition). However, later, we will exhibit an example of a pre-ultrafunctor which does not preserve diagonal embeddings.

It is not true either that in general being a \(\Delta\)-functor characterizes the image of \(\widehat{\operatorname{ev}}\); we later construct a counterexample.

Strong conceptual completeness says that if we sufficiently generalize the diagonal embeddings to a large-enough class of formal comparison maps between ultraproducts (with respect to possibly different indexing sets and ultrafilters), then we can characterize the image of \(\widehat{\operatorname{ev}}\) as precisely those pre-ultrafunctors which additionally preserve all these formal comparison maps. The notion we want is that of an ultramorphism.

Ultramorphisms

Definition. An ultragraph \(\Gamma\) comprises:

Two disjoint sets \(\Gamma^f\) and \(\Gamma^b\), called the sets of free nodes and bound nodes, respectively.

For any pair \(\gamma, \gamma' \in \Gamma\), there exists a set \(E(\gamma, \gamma')\) of edges. This gives the data of a directed graph.

For any bound node \(\beta \in \Gamma^b\), we assign a triple \(\langle I, \mathcal{U}, g \rangle \overset{\operatorname{df}}{=} \langle I_{\beta}, \mathcal{U}_{\beta}, g_{\beta} \rangle\) where \(\mathcal{U}\) is an ultrafilter on \(I\) and \(g\) is a function \(g : I \to \Gamma^f\).

Definition. An ultradiagram of type \(\Gamma\) in a pre-ultracategory \(\underline{\mathbf{S}}\) is a diagram \(A : \Gamma \to \mathbf{S}\) assigning an object \(A\) to each node \(\gamma \in X\), and assigning a morphism in \(\mathbf{S}\) to each edge \(e \in E(\gamma, \gamma')\), such that \[\label{eqn-ultradiagram-condition} A(\beta) = \prod_{i \in I_{\beta}} A(g_{\beta}(i))/\mathcal{U}_{\beta}\] for all bound nodes \(\beta \in \Gamma^b\).

Given this notion of a diagram with extra structure, there is an obvious notion of natural transformations between such diagrams which preserve the extra given structure.

Definition. Let \(A, B : \Gamma \to \mathbf{S}\). A morphism of ultradiagrams \(\Phi : A \to B\) is a natural transformation \(\Phi\) satisfying \[\label{eqn-ultradiagram-morphism-condition} \Phi_{\beta} = \prod_{i \to \mathcal{U}_{\beta}} \Phi_{g_{\beta}(i)}\] for all bound nodes \(\beta \in \Gamma^b\).

Now we define ultramorphisms.

Definition. Let \(\operatorname{Hom}(\Gamma, \underline{\mathbf{S}})\) be the category of all ultradiagrams of type \(\Gamma\) inside \(\underline{\mathbf{S}}\) with morphisms the ultradiagram morphisms defined above. Any two nodes \(k, \ell \in \Gamma\) define evaluation functors \((k), (\ell) : \operatorname{Hom}(\Gamma, \underline{\mathbf{S}}) \rightrightarrows \mathbf{S},\) by \[(k) \left(A \overset{\Phi}{\to} B \right) = A(k) \overset{\Phi_k}{\to} B(k)\] (resp. \(\ell\)).

An ultramorphism of type \(\langle \Gamma, k, \ell \rangle\) in \(\underline{\mathbf{S}}\) is a natural transformation \(\delta : (k) \to (\ell)\).

Let us unravel the definition for the prototypical example \(\Delta : M \hookrightarrow M^{\mathcal{U}}\) of an ultramorphism.

Example. Given an ultrafilter \(\mathcal{U}\) on \(I\), put:

\(\Gamma^f = \{k\}\),

\(\Gamma^b = \{\ell\}\),

\(E(\gamma, \gamma') = \emptyset\) for all \(\gamma, \gamma' \in \Gamma\),

\(\langle I_{\ell}, \mathcal{U}_{\ell}, g_{\ell} \rangle = \langle I, \mathcal{U}, g \rangle\) where \(g\) is the constant map to \(k\) from \(I\).

By the ultradiagram condition, an ultradiagram \(A\) of type \(\Gamma\) in \(\underline{\mathbf{S}}\) is determined by \(A(k)\), with \(A(\ell) = A(k)^{\mathcal{U}}\).

By the ultradiagram morphism condition, an ultramorphism of type \(\langle \Gamma, k, \ell \rangle\) must be a collection of maps \(\left(\delta_M : M \to M^{\mathcal{U}} \right)_{M \in \operatorname{\mathbf{Mod}}(T)}\) which make all squares of the form

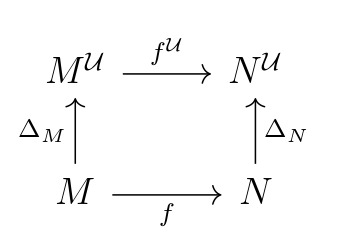
commute. It is easy to check that setting \(\delta_M = \Delta_M\) the diagonal embedding gives an ultramorphism.

Definition. The next least complicated example of an ultramorphism are the generalized diagonal embeddings. Here is how they arise: let \(g : I \to J\) be a function between two indexing sets \(I\) and \(J\). \(g\) induces a pushforward map \(g_* : \beta I \to \beta J\) between the spaces of ultrafilters on \(I\) and \(J\), by \(g_* \mathcal{U} \overset{\operatorname{df}}{=} \{P \subseteq J \operatorname{\big{|}} g^{-1}(P) \in \mathcal{U}\). Fix \(\mathcal{U} \in \beta I\) and put \(\mathcal{V} \overset{\operatorname{df}}{=} g_* \mathcal{U}\). Let \((M_j)_{j \in J}\) be a \(J\)-indexed family of models.

Then there is a canonical “fiberwise diagonal embedding” \[\Delta_g : \prod_{j \to \mathcal{V}} M_j \to \prod_{i \to \mathcal{U}} M_{g(i)}\] given on \([a_j]_{j \to \mathcal{V}}\) by replacing each entry \(a_j\) with \(g^{-1}(\{a_j\})\)-many copies of itself.

In terms of the definition of an ultramorphism, the free nodes are \(J\), and there are two bound nodes \(k\) and \(\ell\). To \(k\) we assign the triple \(\langle J, \mathcal{V}, \operatorname{id}_J \rangle\) and to \(\ell\) we assign the triple \(\langle I, \mathcal{U}, g \rangle\). Then \(\Delta_g\) induces an ultramorphism \((k) \to (\ell)\).

Now we state what it means for ultramorphisms to be preserved. One should keep in mind the special case of the diagonal ultramorphism.

Definition. Let \((X,\Phi) : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) be a pre-ultrafunctor, and let \(\delta\) be an ultramorphism in \(\operatorname{\mathbf{Mod}}(T)\) and \(\delta'\) an ultramorphism in \(\mathbf{Set}\), both of ultramorphism type \(\langle \Gamma, k, \ell \rangle\)

Recall that in the terminology of the definition, \(\delta\) is a natural transformation \((k) \overset{\delta}{\to} (\ell)\) of the evaluation functors \[(k), (\ell) : \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T)) \to \operatorname{\mathbf{Mod}}(T).\] (Resp. \(\delta'\), \(\mathbf{Set}\).)

Note that for any ultradiagram \(\mathscr{M} \in \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T))\), \(X \circ \mathscr{M}\) is an ultradiagram in \(\operatorname{Hom}(\Gamma, \mathbf{Set})\). We say that \(X\) carries \(\delta\) into \(\delta'\) (prototypically, \(\delta\) and \(\delta'\) will both be canonically defined in the same way in both \(\operatorname{\mathbf{Mod}}(T)\) and \(\mathbf{Set}\) and in this case we say that \(\delta\) has been preserved) if for every ultradiagram \(\mathscr{M} \in \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T))\), the diagram

commutes. (We are abusing notation and understand that in the above if \(k\) is not a bound node, then the ultraproduct on the bottom left becomes trivial and \(\Phi_{\mathscr{M}(k)}\) is actually the identity map \(\operatorname{id}_{X(\mathscr{M}(k))}\) (resp. \(\ell\), ultraproduct on the bottom right).)

Note that what is really happening is that we are applying the covariant Hom-functor \(\operatorname{Hom}(X,-)\) to push forward each ultradiagram \(\mathscr{M}\) to an ultradiagram \(X \circ \mathscr{M}\), and then asking that the pushed-forward ultramorphism \(X(\delta)\) is isomorphic to \(\delta'_{X \mathscr{M}}\) via \(X\)’s transition isomorphism \(\Phi\).

Stating strong conceptual completeness

Just as \(\Delta\)-functors are pre-ultrafunctors which additionally preserve the diagonal embedding ultramorphisms, we define ultrafunctors to be pre-ultrafunctors which preserve all ultramorphisms.

Definition. An ultrafunctor \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) is a pre-ultrafunctor which respects the fibering over \(\mathbf{Set}\): for every \(\delta \in \Delta(\mathbf{Set})\), \(X\) carries \(\delta_{\operatorname{\mathbf{Mod}}(T)}\) into \(\delta_{\mathbf{Set}}\) (in the sense of the definition above) for all \(\delta \in \Delta(\mathbf{Set})\).

Definition. A map between ultrafunctors is just an ultratransformation of the underlying pre-ultrafunctors. Write \(\mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) for the category of ultrafunctors \(\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\).

There is a canonical evaluation functor \[\widetilde{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\] sending each definable set \(A \in T\) to its corresponding ultrafunctor \(\widetilde{\operatorname{ev}}_A\), and we now have the following picture of factorizations of the original evaluation map \(\operatorname{ev} : \operatorname{\mathbf{Def}}(T) \to [\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}]\):

Now, we can state strong conceptual completeness.

Theorem. The functor \(\widetilde{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) is an equivalence of categories.

#math #model theory #strong conceptual completeness

22 notes · View notes

unpeudephysique · 6 years ago

Text

Image d’un disque d’accrétion autour d’un trou noir de Schwarzschild

La déflexion des rayons lumineux à proximité d’un corps massif est l’une des prédictions les plus spectaculaires de la relativité générale. Sa vérification en 1919 par Sir Arthur Eddington à l’occasion d’une éclipse du Soleil a d’ailleurs grandement contribué à asseoir la crédibilité de cette théorie auprès des scientifiques du monde entier. Cette déviation est imperceptible sans faire des mesures précises et n’a aucun impact dans la vie courante. Il est cependant un domaine dans lequel la déflexion des rayons peut jouer un rôle important, c’est celui de l’astrophysique.

En 1978, Jean-Pierre Luminet, un scientifique travaillant au laboratoire d’astrophysique de Marseille, a calculé la déflexion induite par le passage d’un rayon lumineux à proximité d’un trou noir. Il a ainsi pu déterminer « l’image » qu’un astronaute pourrait voir en approchant d’un trou noir. Ce même type de calcul a été utilisé par Kip Thorne (un astrophysicien américain qui a reçu le prix Nobel en 2017) pour réaliser les effets spéciaux du film Interstellar. Naturellement, aucun télescope n’a jamais pu capter ce genre d’image… Plus sérieusement, la modélisation du comportement des rayons lumineux autour d’une forte concentration de masse permet de comprendre le fonctionnement des lentilles gravitationnelles. La présence d’une lentille gravitationnelle entre une galaxie et un observateur permet de focaliser et d’amplifier les rayons lumineux en provenance de cette galaxie. Le phénomène de lentille gravitationnelle a été prédit par Albert Einstein et Fritz Zwicky au cours des années 1930. La première lentille gravitationnelle a été identifiée en 1979. On en a observé de nombreuses autres depuis.

Trajectoire d’un photon dans la métrique de Schwarzschild

Rappelons l’équation de la trajectoire d’un photon dans la métrique de Schwarzschild (voir le post à ce sujet) :

Pour pousser plus loin l’analyse, on fait un changement de variable qui simplifie la résolution des équations. Soit u = 1/r. L’équation de la trajectoire peut s’écrire :

ou encore :

… ce qui permet de calculer phi en fonction de u :

Jean-Pierre Luminet montre que cette intégrale peut se mettre sous la forme d’une intégrale elliptique (tous les calculs qui suivent sont issus de son article) :

avec :

A étant le périastre de la trajectoire et F(xi, k) l’intégrale elliptique de première espèce. On trouvera dans un post en annexe les conditions de validité de ces équations en fonction de A. On peut voir qu’il suffit que A soit supérieur à 3rs/2. Cette condition n’est pas très restrictive puisque c’est aussi la condition d’existence d’une orbite stable pour un photon autour d’un trou noir. On démontre également que k et xi sont des fonctions monotones de A. Jean-Pierre Luminet montre en outre que dès lors que A est inférieur à r la trajectoire angulaire Phi et le paramètre A sont reliés par une équation qui fait intervenir la fonction sinus elliptique de Jacobi :

K(k) étant l’intégrale elliptique complète de première espèce (intégrale de première espèce pour xi = pi/2). La fonction sinus elliptique de Jacobi est définie comme suit :

On remarquera que la condition A < r est remplie automatiquement puisque A est, par définition, le périastre de la trajectoire.

Image lointaine d’un disque d’accrétion autour d’un trou noir de Schwarzschild

Revenons au problème qui nous occupe : l’image d’un disque d’accrétion en rotation autour d’un trou noir.

Considérons tout d’abord une particule appartenant au disque d’accrétion. Nous allons chercher à caractériser la trajectoire d’un photon émis par cette particule dans la direction d’un observateur lointain. Il nous faut pour cela calculer le paramètre d’impact b d’un photon émis par cette particule en fonction du rayon r de son orbite autour du trou noir et de sa position angulaire alpha. Dans ce qui suit nous ferons les hypothèses suivantes :

Le disque d’accrétion se trouve dans le plan XOY. L’axe OZ est l’axe polaire du système constitué par le trou noir et le disque d’accrétion.

Les coordonnées de l’observateur lointain O’ sont (rinfini, theta0, 0).

Les coordonnées de la particule émettrice M sont (r, pi/2, phi).

b est le paramètre d’impact du photon qui parvient à l’observateur lointain.

On procède tout d’abord à un changement de référentiel en faisant pivoter le repère OXYZ d’un angle pi/2-theta0 autour de l’axe OX de façon à pointer OY’ en direction de l’observateur lointain. La trajectoire du photon émis par la particule M et qui parvient à l’observateur lointain appartient au plan OO’X’=OO’M qui fait un angle pi/2 - alpha avec le plan OXY’.

Soit soit gamma l’angle MOY’. Un peu de trigonométrie en coordonnées sphériques conduit à écrire les relations suivantes :

Il y a donc une relation directe entre alpha et le couple (phi, theta0) tout comme il y a une relation directe entre gamma et le couple de valeurs (alpha, theta0). Analysons l’évolution de alpha et gamma avec phi.

Lorsque phi est nul (sur la figure, cela correspond à l’intersection de la sphère avec l’axe OY) l’angle alpha est également nul. Le plan équatorial qui comprend la trajectoire est le plan OY’Z’. Comme il apparaît clairement sur la figure, l’angle gamma est égal à pi/2 – theta0.

Lorsque phi croît pour atteindre pi/2, le plan équatorial pivote autour de l’axe OY’’ et alpha tend également vers pi/2. Lorsque phi = pi/2, le point M est à l’intersection de OX avec la sphère et l’angle gamma est égal à l’angle XOY’ qui vaut pi/2.

Au-delà de pi/2, le plan équatorial continue de basculer autour de l’axe OY’’ et alpha vaut pi lorsque = pi. Dans ce cas, il est facile de voir sur la figure que gamma = pi/2 + theta0.

Comment calculer les points d’impact ?

Ce qui précède nous conduit à la méthode de calcul exposée ci-dessous.

Première étape : On part d’un couple (r, theta0) déterminé. L’équation suivante :

permet de définir la fonction xi = xi(u,A) = xi(r,A) . Or :

En tenant compte de la formule ci-dessus et de la relation k = k(A) on peut écrire :

Deuxième étape : Comme par ailleurs on peut calculer gamma puisque (voir plus haut) :

il est possible de déterminer la valeur de A = A(r, theta0, phi) par interpolation. On en déduit aisément le paramètre d’impact :

Ceci permet de construire la courbe b = b(alpha) pour un rayon r donné.

Exemples

Les exemples qui suivent ont été obtenus au moyen d’un programme simple écrit en langage C++. La figure représente l’image perçue par un observateur lointain situé dans un plan qui fait 10 degrés avec le plan d’accrétion. Seules 3 isoradiales ont été calculées. Elles correspondent à trois valeurs de r : 3rs, 5rs et 10rs.

Il apparaît très clairement sur cette figure que l’image de la partie du disque d’accrétion qui se trouve devant le trou noir est peu déformée alors que l’image de la partie arrière, qui devrait être cachée, est clairement visible au-dessus du trou noir ! Cette forme d’illusion d’optique dépend bien sûr de l’angle sous lequel l’observateur voit le plan d’accrétion. La figure qui suit représente l’isoradiale 3rs vue sous trois angles (10, 20 et 30 degrés).

La série de figures qui suivent nous montre la trajectoire suivie par un photon émis depuis l’isoradiale 3rs et en se plaçant à différents endroits de cette isoradiale. On se place à chaque fois dans le plan de la trajectoire (le plan OO’M dans notre repère de coordonnées). Dans ces figures, le cercle noir est le cercle de rayon rs et le cercle en pointillés vert le cercle de rayon 3/2rs. L’ellipse bleue représente la projection de l’isoradiale 3rs sur le plan OO’M.

Décalage Doppler du photon capté par l’observateur lointain

Dans le référentiel au repos de la particule M l’énergie d’un photon est fonction de la quadri-vitesse de la particule et du quadri-moment de ce photon. On considère que l’observateur est suffisamment éloigné pour que le calcul à l’infini soit valable… mais suffisamment proche pour que le redshift cosmologique soit négligeable.

(Les deux seules composantes non nulles de la quadri-vitesse sont ut et uphi.) On peut réécrire cette équation comme suit :

Dans le cas d’une orbite circulaire, le terme uphi/ut vaut :

La métrique de Schwarzschild ne dépendant ni de t ni de phi les composantes pt et pphi du quadri-moment du photon restent invariantes tout au long de sa géodésique (voir le post sur la mécanique relativiste). L’énergie observée par l’observateur fixe est donc égale à pt. Le décalage de fréquence entre l’émission et la réception peut s’exprimer comme suit :

Revenons à la définition du paramètre d’impact : L = E.b, L étant le moment du photon et E son énergie. La composante pphi du quadri-moment est la projection de ce moment sur l’axe OZ. On peut donc écrire :

Ceci conduit à la relation suivante :

or :

Il vient :

Le facteur 1 + z intervient à la puissance 4 dans le calcul de l’intensité des rayons émis par M et perçu par l’observateur lointain :

l’énergie individuelle des photons est affectée du facteur 1 + z,

la fréquence d’émission des photons est affectée du même facteur en raison du décalage des horloges,

le rapport entre les angles solides tels qu’ils sont mesurés dans le référentiel de la particule et ceux qui sont perçus par l’observateur lointain est égal à (1+z)2. C’est une conséquence de la transformation relativiste des distances.

On peut se convaincre rapidement du 3ème point en faisant un raisonnement basé sur la relativité restreinte. Considérons un cône de lumière émis par une source se déplaçant avec une vitesse v par rapport à un observateur fixe. Dans le référentiel de la source, le décalage maximum d’un photon par rapport à l’axe reliant la source et l’observateur est tel que tan(alpha) = dx/x. Si dx est petit devant x, alpha est donc très proche de dx/x.

Dans le référentiel de l’observateur, le décalage n’est pas affecté par la transformation des longueurs. Ce n’est pas le cas pour la distance x :

d’où il vient :

Comme (voir le post sur l’effet Doppler relativiste) :

On aboutit bien au résultat annoncé. Comme le montre les simulations de Jean-Pierre Luminet, il y a un très fort décalage entre la partie gauche et la partie droite de l’image perçue par l’observateur. L’une est très brillante, l’autre fortement décalée vers le rouge et peu lumineuse.

Pour en savoir plus :

post sur la mécanique relativiste

post sur la métrique de Schwarzschild

post sur les trajectoires dans la métrique de Schwarzschild

post sur la trajectoire d’un photon dans la métrique de Schwarzschild

post sur les particules en orbite circulaire dans la métrique de Schwarzschild

post sur l’effet Doppler relativiste

annexe sur les intégrales de Legendre

index

0 notes