#online encyclopedia of integer sequences

[oeistournament]

Announcement: OEIS Tournament

This is @pc36thorn. Recently, I had the idea to do a poll bracket tournament on Tumblr with sequences from the OEIS (On-Line Encyclopedia of Integer Sequences). To determine the competitors, I will be accepting submissions. I have not yet decided how many competitors there will be, or when to cut off submissions. The rules for submissions are in the Google Form linked above. Seeding will be determined by how many submission a sequence gets, so don't be afraid to submit all your favorites even if they might have already been submitted.

[imperfect-autodidact]

377 days to application season

I am too tired to live right now.

Haven’t done any math since Friday, too much 9-to-5 bullshit to deal with, it exhausts me.

Decided to read for fun and went for Math Girls. HIGLY RECOMMENDED. If you know it, tell me, how long did it take you to crack the sequence 6,2,8,2,10,18. For me it was two days and I gave up and used the Online Encyclopedia of Integer Sequences (oeis.org).

Met again a fox this morning, that folk likes to hang out on campus of Humboldt University (this one was catching rats near Faculty of Chemistry). Gods, I adore these animals!

[numbersareimaginary]

I used to go on the Online Encyclopedia of Integer Sequences and download the MIDI file of a random sequence and use that as my alarm.

Hey kids here's a piece of actual for real experienced adult advice: don't make songs you like your alarm. Ever. You're gonna Pavlov yourself into hating it or sleep through it and have weird dreams. Don't do that to yourself. Seriously.

[albobonobo]

The Online Encyclopedia for Integer Sequences is my best friend thank you R. J. A. Sloane

[hackernewsrobot]

Online Encyclopedia of Integer Sequences

https://oeis.org/

[amphitheresarewingednoodles]

Ya girl got a sequence on the OEIS :3

(If you like arbitrary patterns or number sequences and haven't heard of the Online Encyclopedia of Integer Sequences, you're in for a treat)

[apprendere]

see also online encyclopedia of integer sequences A037276

https://oeis.org/A037276

system of mathematical notation where concatenation always means multiplication and each prime number has a unique one digit symbol. so counting to ten looks like "2, 3, 22, 5, 23, 7, 222, 33, 25". the advantages of this system would be making multiplication and division trivial, as well as accurately representing the true form and identity of every positive integer according to the fundamental theorem of arithmetic. the disadvantages to this system would be everything

[backslashdelta]

I was thinking about the Fibonacci sequence and how cool it is, but did you know that there are lots of other integer sequences as well?

With the On-Line Encyclopedia of Integer Sequences, you can search any finite sequence of integers and the OEIS will give you any known integer sequences containing that subsequence, complete with formulas, related references, and more!

[somethingusefulfromflorida]

On-line Encyclopedia of Integer Sequences

A006880 Number of primes < 10^n

0, 4, 25, 168, 1229, 9592, 78498, 664579, 5761455, 50847534, 455052511, 4118054813, 37607912018, 346065536839, 3204941750802, 29844570422669, 279238341033925, 2623557157654233, 24739954287740860, 234057667276344607, 2220819602560918840, 21127269486018731928, 201467286689315906290 

There are 0 primes below 10^0 (1)

There are 4 primes below 10^1 (10)

There are 25 primes below 10^2 (100)

etc.

This shows that primes become less frequent as you go on

40% of numbers under 10 are prime

25% of numbers under 100 are prime

16.8% under 1,000

12.29% under 10,000

9.592% under 100,000

7.8498% under 1,000,000

etc.

3, 5, and 7 are the only numbers below which a majority are prime, though 2, 4, 6, and 8 come close.

not prime (0/1, 0%)

prime (1/2, 50%)

prime (2/3, 66.6...%, highest percentage of primes)

not prime (2/4, 50%, most common percentage of primes)

prime (3/5, 60%)

not prime (3/6, 50%)

prime (4/7, 57.142857...%)

not prime (4/8, 50%)

not prime (4/9, 44.4...%)

not prime (4/10, 40%)

prime (5/11, 45.45...%)

not prime (5/12, 41.6...%)

prime (6/13, 46.153846...%)

not prime (6/14,  42.857142...%)

not prime (6/15,  40%)

not prime (6/15, 37.5%)

prime (7/17, 41.17647059...%)

not prime (7/18, 38.8...%)

prime (8/19, 42.10526316...%)

not prime (8/20, 40%)

not prime (8/21, 38.0952381...%)

not prime (8/22, 36.36...%)

prime (9/23, 39.13043478...%)

not prime (9/24, 37.5%)

not prime (9/25, 36%)

not prime (9/26, 34.61538462...%)

not prime (9/27, 33.3...%)

not prime (9/28, 32.142857...%)

prime (10/29, 34.4827586207%)

not prime (10/30, 33.3...%)

This post has no larger point, I just wanted to show this off

[mergist]

I've realized that you can do contemporary recreational numerology by taking whatever numbers you encounter close together and plugging them into the Online Encyclopedia of Integer Sequences.

I was going to demonstrate this with the numbers on the bots following me but Tumblr removed them already. Sometimes I do it with the little factoids Duolingo gives me about how many users are active at the same time as me.

[beardedmrbean]

I got approved as a contributor on the Online Encyclopedia of Integer Sequences, or OEIS for short. Now I can fulfill my dream of rickrolling the mathematical community !!

Oh man, just looking at that gives me a headache.

I wish you luck and great fun.

Be sure and slip the Spanish inquisition in there from time to time, they'll never expect it

[noneedtofearorhope]

thought i’d found an integer sequence not listed on the online encyclopedia of integer sequences, buuuuut it turns out i just made a simple mistake at the start which threw it off

[10oclockdot]

10oclockdot 2020 year in review

As I seem to drift farther and farther from tumblr (though the #Peace posts and my side project on On Kawara keep a thin tether attached), 2020 actually saw me stepping more solidly into my stated vocation as an academic, even if I also lost my job as a university professor this year. Trying to look on the bright sides.

Here we go:

10. I got my first properly peer-reviewed article accepted for publication in 2020. After 2 years of submitting to journals and a protracted review process, “Why is Reverse Motion Funny?: Happy End and the Comic Potential of the Cinematographic Mechanism” was accepted by Journal of Film and Video for publication... TBA. Based on some gossip I read online later, I might be waiting upwards of two years for the article to ever come out. But hopefully not. Either way, it was accepted, and that’s at least something for the CV.

9. Will DiGravio’s excellent The Video Essay Podcast (here) was a great companion this summer while I was working on a big project (see #1), and just for fun I decided to complete some “homework” he assigned on the podcast. My submission is here. Everyone else’s submissions are here.

8. Early in the year, I updated a compilation of all the times John Ford used the hymn “Shall We Gather at the River” in one of his films. An eagle-eyed YouTuber found one more. Here’s the new version.

7. When some prominent Math YouTubers put out a call for videos on favorite numbers greater than a million -- aka #MegaFavNumbers -- I couldn’t see a reason not to join in, and made this video, based on one of my old tumblr posts. In it I also mention that as of late 2019 I’m also published on the Online Encyclopedia of Integer Sequences. Not sure if I ever mentioned that here. Anyway, contributing a #MegaFavNumber seems like a fitting project for a year in which I also became a math tutor. (Here’s the full playlist.)

6. I didn’t make much art this year of note, but this bit of constrained poetry executed as a 10-part conceptual painting is easily one of the best and most important artworks I’ve ever made (if any could be assigned importance).

5. I finally watched Twin Peaks: The Return. Here’s a post I made about that, which somehow became the most popular new thing on the blog this year. Aphelis also liked this gif I made for him. Nobody seemed to understand this post (or maybe I just think it’s better than it is), but that’s okay, I guess.

4. I started a new video essay series called “Video Postcards.” There are only two so far (”About Time,” and “Drone Swarms”), but the idea is to keep making them on a regular basis (monthly, maybe?). The concept is that each video is addressed to a friend of mine, and I weigh in on some topic that we’re both interested in and have talked about before. I actually SEND the addressee the postcard you see me writing in the video, with the link written out on it. After they view this private video correspondence, they get to decide whether the rest of the world will get to see it too. So far 2 for 2.

3. It was hard to write much that was meaningful this year politically (at least, it was hard for me). But I still wrote a short story that I’m proud of called Somewhere in the middle of an angry mob in Jerusalem, ca. 2000 years ago (here). I wish every Evangelical Christian in the country (my heritage) would read it. Oh, I also drew this cartoon about who establishment democrats really are. Oh, and this diagram over on Facebook about the inscrutable slowness of the apocalypse.

2. My first professional publication came in the form of a long data-driven article for Bright Lights Film Journal that dropped back in January: “Tracking Mass Ideology on IMDb’s Top 250: How Shifts in Societal Values Appear in the Popular Film Canon” (here). The Bright Lights people were so easy to work with that I’m looking forward to writing another article for them in the new year, if they’ll take it. This article even drew the attention of the great film reviewer Darren Mooney (of the m0vie blog), who invited me to record an episode of his podcast The 250 (here) on Sherlock, Jr. (Buster Keaton, 1924). We taped it a couple months ago, but it should land in the new year. I’ll share it here when it does. 

1. And, of course, after three years of work and a rejection from [in]Transition, my first feature-length project, a video essay called A Supercut of Supercuts: Aesthetics, Histories, Databases, was accepted for publication at Open Screens Journal. It should be live in January. I’ve also sent it out to some film festivals with what little money I could scrape together for that purpose. Hopefully at least one of them wants to play it, so I can add some laurels to that poster!

See you next year!

[mathandnumberystuff]

LCM of binomial coefficients

A few months ago, when I was doodling in math class, I stumbled across a surprising formula for the least common multiple (LCM) of all terms in a row of Pascal's triangle.

I wasn't even looking for such a formula. I was just experimenting with numbers of the form LCM(1, 2, ..., n). The formula for the LCM of all terms on the nth row of Pascal's triangle (i.e. the one that starts 1, n...) is: LCM(1, 2, ..., n + 1)/(n + 1).

Researching online, I found that this identity was proven in 2009 by Bakir Fahri (see [1]). The OEIS entry (A002944) links the proof, which is based on finding the p-adic valuations (exponent on the prime p in the prime factorization) of the left and right side of the identity for all primes p. However, the proof I found was quite different and I am not sure whether it has been found before.

First consider the harmonic triangle. The harmonic triangle, developed by Gottfried Leibniz, is like the reciprocal of Pascal's triangle, except each term on the nth row is divided by n + 1:

Because the formula for the rth term on the nth row of Pascal's triangle is nCr = n!/(r!(n - r)!), the rth term on the nth row of the harmonic triangle has the formula 1/((n + 1)(nCr)) = r!(n - r)!/(n + 1)!. Let us denote this value by F(n, r).

We know that each term in Pascal's triangle is the sum of the two terms above it: nCr + nC(r + 1) = (n + 1)C(r + 1). Similarly, the following relation holds for the terms in the harmonic triangle: F(n, r) + F(n, r + 1) = (r!(n - r)! + (r + 1)!(n - r - 1)!)/(n + 1)! = r!(n - r - 1)!(n + 1)/(n + 1)! = r!(n - r - 1)!/n! = F(n - 1, r).

In other words, each term in the harmonic triangle is the sum of the two terms below it.

Now, consider the nth row for a particular value of n. To make the reasoning easier to understand, I will choose n = 7, but the logic is the same for all rows.

1/8, 1/56, 1/168, 1/280, 1/280, 1/168, 1/56, 1/8

What is the smallest value that we can multiply by all these terms to produce integers? Note that the reciprocals of the terms are just (n + 1) nCr. Thus, the question is the same as asking for the least common multiple of (n + 1) nCr for r from 0 to n. By factoring out n + 1, we see that this value is equal to m = (n + 1) LCM(nC0, nC1, ..., nCn). In our example, m = 840. Let's try multiplying every term by m:

105, 15, 5, 3, 3, 5, 15, 105

Because each term is the sum of the two below it, we can build 840 times the entire first eight rows of the triangle by adding from below and all the terms will be integers:

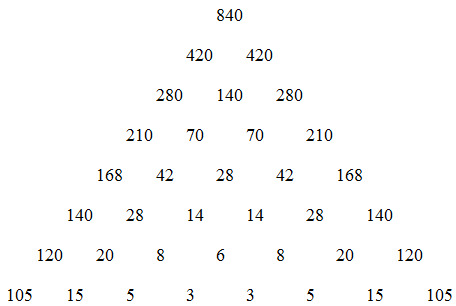
In general, if all the terms in a row are integers, all terms in the rows above will also be integers. Furthermore, because we multiplied by the least common multiple of the denominators, the numbers in the bottom row have 1 as their greatest common factor.

In fact, because the third of any three numbers in an upward pointing triangle can be determined from the other two, the left and right diagonal of the triangle also have 1 as their greatest common factor. If they didn't and had some common factor of f > 1, all numbers in the first n + 1 rows of the triangle would have the same factor f. This is because the entire triangle can be constructed by subtracting adjacent terms in the left diagonal to form the next diagonal over, and then repeating for each subsequent diagonal. Then a smaller common multiple of all the numbers in the triangle would be m/f. But m is the least common multiple by definition, which is a contradiction.

In fact, the numbers down either outer diagonal are m, m/2, m/3, ..., m/(n + 1). In our example, these are 840, 420, 280, 210, 168, 140, 120, 105. In trying to identify m, we see that it must be divisible by 1, 2, ..., n + 1. Furthermore, if m were not the least common multiple of 1 through n + 1, then some factor m/k would be. Then m, m/2, ..., m/(n + 1) would all be divisible by k, but we have just established that their greatest common divisor is 1. In conclusion, we must have m = (n + 1) LCM(nC0, nC1, ..., nCn) = LCM(1, 2, ..., n + 1). Therefore, LCM(nC0, nC1, ..., nCn) = LCM(1, 2, ..., n + 1)/(n + 1). QED.

An interesting consequence of this theorem is that the LCM of one row of Pascal's triangle is usually less than the LCM of the previous row. This is because LCM(1, 2, ..., k) = LCM(1, 2, ..., k - 1) whenever k is not a prime power. However, the increases in the value of LCM(1, 2, ..., k)/k that occur with increasing rarity, whenever k is a prime power, make up for the slight decreases caused by increasing k whenever k is not a prime power, and the sequence increases overall.

Here are the first few terms of the sequence, from n = 0 to n = 21:

1, 1, 2, 3, 12, 10, 60, 105, 280, 252, 2520, 2310, 27720, 25740, 24024, 45045, 720720, 680680, 12252240, 11639628, 11085360, 10581480

And here are the quotients when the terms in each row of Pascal's triangle are divided into the corresponding multiple:

1

1, 1

2, 1, 2

3, 1, 1, 3

12, 3, 2, 3, 12

10, 2, 1, 1, 2, 10

60, 10, 4, 3, 4, 10, 60

105, 15, 5, 3, 3, 5, 15, 105

280, 35, 10, 5, 4, 5, 10, 35, 280

252, 28, 7, 3, 2, 2, 3, 7, 28, 252

2520, 252, 56, 21, 12, 10, 12, 21, 56, 252, 2520

2310, 210, 42, 14, 7, 5, 5, 7, 14, 42, 210, 2310

27720, 2310, 420, 126, 56, 35, 30, 35, 56, 126, 420, 2310, 27720

25740, 1980, 330, 90, 36, 20, 15, 15, 20, 36, 90, 330, 1980, 25740

24024, 1716, 264, 66, 24, 12, 8, 7, 8, 12, 24, 66, 264, 1716, 24024

45045, 3003, 429, 99, 33, 15, 9, 7, 7, 9, 15, 33, 99, 429, 3003, 45045

720720, 45045, 6006, 1287, 396, 165, 90, 63, 56, 63, 90, 165, 396, 1287, 6006, 45045, 720720

680680, 40040, 5005, 1001, 286, 110, 55, 35, 28, 28, 35, 55, 110, 286, 1001, 5005, 40040, 680680

12252240, 680680, 80080, 15015, 4004, 1430, 660, 385, 280, 252, 280, 385, 660, 1430, 4004, 15015, 80080, 680680, 12252240

11639628, 612612, 68068, 12012, 3003, 1001, 429, 231, 154, 126, 126, 154, 231, 429, 1001, 3003, 12012, 68068, 612612, 11639628

11085360, 554268, 58344, 9724, 2288, 715, 286, 143, 88, 66, 60, 66, 88, 143, 286, 715, 2288, 9724, 58344, 554268, 11085360

10581480, 503880, 50388, 7956, 1768, 520, 195, 91, 52, 36, 30, 30, 36, 52, 91, 195, 520, 1768, 7956, 50388, 503880, 10581480

References

Bakir Farhi, An identity involving the least common multiple of binomial coefficients and its application, arXiv:0906.2295

A002944 - Online Encyclopedia of Integer Sequences

[ohaithe-re]

I don't have gills

This is a PSA that I, Timeroot, am a gill-free human. I cannot survive underwater for more than a few minutes.

There's plenty of discussion of GPT already online, and I don't want to crowd that discussion. But there's one viewpoint that I am frustrated by seeing. Today I read the following, from someone whom I generally think of as respected and intelligent:

Which shows that "ChatGPT knows" means that it just reproduces what it has "read" without understanding anything, or even being able to "use" this "knowledge" otherwise than by making new phrases from it.

This is in reference to ChatGPT not having an encyclopedic knowledge of the OEIS. The OEIS is, for those unfamiliar, the Online Encyclopedia of Integer Sequences. It contains all manner of lists of integers, from the simple to the very specific. There are over 350,000 sequences at the time of writing. When someone asked ChatGPT for information on which sequence contained a certain pair of numbers, ChatGPT gave a best guess; it was very wrong.

What does this tell us? ChatGPT currently does not have the OEIS memorized. Does that imply that ChatGPT doesn't understand anything it reads? Certainly not.

Humans are also trained on a series of visual stimuli, without ever "understanding" what they're seeing. It wasn't until a few hundred years ago that people realized that the mold they saw was alive; it wasn't until a hundred years ago that people realized that the light see is actually electromagnetism. People are regularly fooled by optical illusions -- there are pictures you can print out on a piece of flat paper, and many humans will happily point out which are "higher" or "lower" than others! If you paint the illusion on the ground, people will express hormonal fear responses of falling "off the edge" of the illusion!

An animal like a bat, with echolocation, would not be fooled. They might look at humans and conclude that we just look and respond based on what we have "seen", without ever "understanding" what we see.

I consider myself to have understanding of what I see. For the same reason, I consider GPT to have understanding what it reads. Does it make embarrassing or silly mistakes? Yes, because GPT is trained in a very different environment than my brain is. We both make silly mistakes. They are very different mistakes.

Someone said that if you judge a fish by its ability to climb a tree, it will live its whole life believing it is stupid. (This is commonly attributed to Einstein; this is inaccurate.) Claiming that GPT cannot understand the world based on these tests is really asking it to climb a tree. I think that if we kept in mind the common human fumbles we make, we might be humbled into giving GPT a bit more credit. If GPT is the fish, then I'm a monkey who certainly cannot match it many regards. I can't even survive underwater: I ain't go no gills.

[mantacid-art]

I’m both an artist and a math major, and let me tell you, math can be beautiful. You are completely right.

If you go to the online encyclopedia for integer sequences (OEIS), and pick any sequence, you can listen to it. Someone’s out there transcribing a sequence into music, just because they wanted to, or because it might help someone understand something.

People see math as practical, something used, not experienced. Those people are wrong.

Math is a game we’ve been playing and building for most if not all of history. It can surprise us, inspire us, and cause us to question. The same can’t be said of much of what people are willing to call “art”

/sad robot rant/

The bad thing about being an artist who illustrates scientific/ mathematical concepts in a surreal way is the rejection in the art community... I get told constantly that my art doesn't convey any feelings and is therefore not enjoyable to look at... But that is not the actual point of art; It is a form of expression: And why should art be limited to express emotions? I literally feel like an alien.... well then, I take my shitty art in my grave if they despise it so much.

Engaging with the art community gave me nothing positive, it just made me realize even more that no one cares what I do...