#on-line encyclopedia on integer sequences

[oeistournament]

Announcement: OEIS Tournament

This is @pc36thorn. Recently, I had the idea to do a poll bracket tournament on Tumblr with sequences from the OEIS (On-Line Encyclopedia of Integer Sequences). To determine the competitors, I will be accepting submissions. I have not yet decided how many competitors there will be, or when to cut off submissions. The rules for submissions are in the Google Form linked above. Seeding will be determined by how many submission a sequence gets, so don't be afraid to submit all your favorites even if they might have already been submitted.

[relevant-wikipedia-articles]

trick or treat!!

[mybeanalgebra]

hey this is sort of a random question but how many and which notable integer sequences can you list. i don't know the formal name for them i just need sequences of integers with attached meaning

I don't really know how many. I've probably seen a lot of them. But anyway, I usually refer to the OEIS

[noneedtofearorhope]

so i looked up the sequence this is part of on the oeis (on-line encyclopedia of integer sequences) and there was this helpful comment

Comment from Trevor Green: The fourth term in this sequence has about as many digits - 8.07 * 10^153 - as the square of the number of protons in the universe.

additionally

The last 60 decimal digits of a(4) are ...67586985427238232605843019607448189676936860456095261392896. - Daniel Forgues, Jun 25 2016

and

The fractional part of 4^4^4*log[10](4) starts .373100157363599870..., so the first few digits of a(4) are 23610226714597313.... - Robert Israel, Jul 06 2016

you know a number is pretty big when a calculator that goes at least up to 10^123 says the number is too big. i just want to know how ridiculous 4^4^4^4 is :'(

[somethingusefulfromflorida]

On-line Encyclopedia of Integer Sequences

A006880 Number of primes < 10^n

0, 4, 25, 168, 1229, 9592, 78498, 664579, 5761455, 50847534, 455052511, 4118054813, 37607912018, 346065536839, 3204941750802, 29844570422669, 279238341033925, 2623557157654233, 24739954287740860, 234057667276344607, 2220819602560918840, 21127269486018731928, 201467286689315906290 

There are 0 primes below 10^0 (1)

There are 4 primes below 10^1 (10)

There are 25 primes below 10^2 (100)

etc.

This shows that primes become less frequent as you go on

40% of numbers under 10 are prime

25% of numbers under 100 are prime

16.8% under 1,000

12.29% under 10,000

9.592% under 100,000

7.8498% under 1,000,000

etc.

3, 5, and 7 are the only numbers below which a majority are prime, though 2, 4, 6, and 8 come close.

not prime (0/1, 0%)

prime (1/2, 50%)

prime (2/3, 66.6...%, highest percentage of primes)

not prime (2/4, 50%, most common percentage of primes)

prime (3/5, 60%)

not prime (3/6, 50%)

prime (4/7, 57.142857...%)

not prime (4/8, 50%)

not prime (4/9, 44.4...%)

not prime (4/10, 40%)

prime (5/11, 45.45...%)

not prime (5/12, 41.6...%)

prime (6/13, 46.153846...%)

not prime (6/14,  42.857142...%)

not prime (6/15,  40%)

not prime (6/15, 37.5%)

prime (7/17, 41.17647059...%)

not prime (7/18, 38.8...%)

prime (8/19, 42.10526316...%)

not prime (8/20, 40%)

not prime (8/21, 38.0952381...%)

not prime (8/22, 36.36...%)

prime (9/23, 39.13043478...%)

not prime (9/24, 37.5%)

not prime (9/25, 36%)

not prime (9/26, 34.61538462...%)

not prime (9/27, 33.3...%)

not prime (9/28, 32.142857...%)

prime (10/29, 34.4827586207%)

not prime (10/30, 33.3...%)

This post has no larger point, I just wanted to show this off

[argumate]

I was assuming the On-line (sic) Encyclopedia of Integer Sequences would have something amusing for "a one, a two, a one, two, three, four" but apparently not.

[backslashdelta]

I was thinking about the Fibonacci sequence and how cool it is, but did you know that there are lots of other integer sequences as well?

With the On-Line Encyclopedia of Integer Sequences, you can search any finite sequence of integers and the OEIS will give you any known integer sequences containing that subsequence, complete with formulas, related references, and more!

[kaiasky]

have fun!

ok fine i'll read the sequences

[triciansmithdesign]

What Number Comes Next? The On-Line Encyclopedia of Integer Sequences Knows.

http://dlvr.it/SpNbpF

[qifeng618618]

Qi's papers and preprints cited by The On-Line Encyclopedia of Integer Sequences

Qi’s papers and preprints cited by The On-Line Encyclopedia of Integer Sequences

Qi’s papers and preprints cited by The On-Line Encyclopedia of Integer Sequences The following papers and preprints by Dr. Professor Feng Qi are cited at the web sites https://oeis.org/A000110,       https://oeis.org/A000262, https://oeis.org/A001003,       https://oeis.org/A001497, https://oeis.org/A006318,       https://oeis.org/A008277, https://oeis.org/A014307. Feng Qi, An explicit formula…

[yonoise]

A000861​: On-line Encyclopedia of Integer Sequences (Sloane/AT&T) | March 19, 2005

[hackernewsrobot]

The On-Line Encyclopedia of Integer Sequences

https://oeis.org/ Comments

[mathematicianadda]

What is the next number on the constructibility sequence? And what is the asymptotic growth?

Let us systematically generate all constructible points in the plane. We begin with just two points, which specify the unit distance.

With the straightedge, we may construct the line joining them. And with the compass, we may construct the two circles centered at each of them, having that unit segment as radius. These circles intersect each other and the line, creating four additional points of intersection. Thus, we have now six points in all.

Using these six points, we proceed to the next stage, constructing all possible lines and circles using those six points, and finding the resulting points of intersection.

I believe that we now have 203 points. Let us proceed in this way to systematically construct all constructible points in the plane, in a hierarchy of finite stages. At each stage, we form all possible lines and circles that may be formed from our current points using straightedge and compass, and then we find all points of intersection from the resulting figures.

This produces what I call the constructibility sequence:

$$2\qquad\qquad 6\qquad\qquad 203\qquad\qquad ?$$

Each entry is the number of points constructed at that stage. I have a number of questions about the constructibility sequence:

Question 1. What is the next constructibility number?

There is no entry in the online encyclopedia of integer sequences beginning 2, 6, 203, and so I would like to create an entry for the constructibility sequence. But they request at least four numbers, and so we seem to need to know the next number. I'm not sure exactly how to proceed with this, since if one proceeds computationally, then one will inevitably have to decide if two very-close points count as identical are not, and I don't see any principled way to ensure that this is done correctly. So it seems that one will need to proceed with some kind of idealized geometric calculus, which gets the right answer about coincidence of intersection points.

Question 2. What kind of asymptotic upper bounds can you prove on the growth of the constructibility sequence?

At each stage, every pair of points determine a line and two circles. And every intersection point is realized as the intersection of two lines, two circles or a line and circle, which have two intersection points in each case. So a rough upper bound is that from $k$ points, we produce $3k^2$ many lines and circles, and so up to $(3k^2)^2$ many pairs of line and circles, and so $2(3k^2)^2$ many points of intersection. This leads to an upper bound of growth something like $2^{4^n}$ after $n$ stages. Can anyone give a more precise bound?

Question 3. And what of lower bounds?

I suspect that the sequence grows very quickly, probably doubly exponentially. But to prove this, we would seem to need to identify a realm of construction patterns where there is little interference of intersection coincidence, so that one can be sure of a certain known growth in new points.

from Hot Weekly Questions - Mathematics Stack Exchange from Blogger https://ift.tt/2oz4gMJ

[wiskwa-en]

A `mathematical’ problem

The following `mathematical’ problem is doing the rounds on the internet.

Personally I am not a big fan of this kind of `problem’ because the purpose is not to determine the system behind the data, because there is no unique law that governs it, but whatever it was that was in the head of the poser of the problem.

My standard reply to such a question is: 0 (or sometimes 42, the universal answer from The Hitch-hikers Guide to the Galaxy). Can we say something sensible about a problem like this?

Let us see. For starters: the function of + is clearly not that of addition (if = is supposed to mean equality); this suggested to many people to replace it by some other symbol, @ say. The question then is: is there an operation @ that produces for every pair of natural numbers m and n a natural number m@n and in such a way that 1@4=5, 2@5=12 and 3@6=21? And if yes then what is 5@8?

For a mathematician the answer is clear: apart from the three demands we are free to do as we please, so the answer is “yes” and 5@8 is not determined it can be what we want it to be. For eaxample: define m@n=0, except in the three prescribed cases; that justifies my standard answer. If we separately define 5@8=42 then Deep Thought’s universal answer becomes correct.

Most people do not expect an answer like the two given above but rather a `formula’; some expression with m and n in it that `predicts’ what 5@8 should be. Formulas like that are plentiful. If you look at the data then the three equations are of the form m@(m+3)=x, so it could very well be that the operation simply works with the first coordinate only.

We have three values and these can be fitted by a quadratic polynomial in m alone. You can check that m@n=m2+4m meets our three requirements (plug in m=1, 2, 3). That will produce the answer given by most of the internet: 5@8=45.

With a little twist you can make infinitely many formulas that give the three desired outcomes all produce different results for 5@8. The trick is to find something that produces the value 0 when you substitute 1, 2, or 3 for m and only then. You can take (m-1)(m-2)(m-3). Using that we can produce infinitely many formulas: for every natural number k define m@kn=m2+4m+k(m-1)(m-2)(m-3).

With some tinkering it should be possible to make formulas that have 5@8 take on any value you like; I’d say: get to work. Here’s an example.

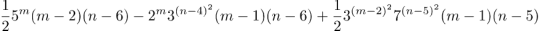
It produces 5@8=4754660328285.

To those who want to know if the sequence 5, 12 21 has any `natural’ extensions I recommend the On-line Encyclopedia of Integer Sequences; put the sequence in the search box to see what’s available.

[merrikstryfe]

Oh god, it’s a literal encyclopedia of integer sequences and I am going to lose my life to it D: