#polyhedra in perspective

[knotty-et-al]

Dodecahedron and stellated dodecahedron WIP - perspective drawing on isometric dot paper

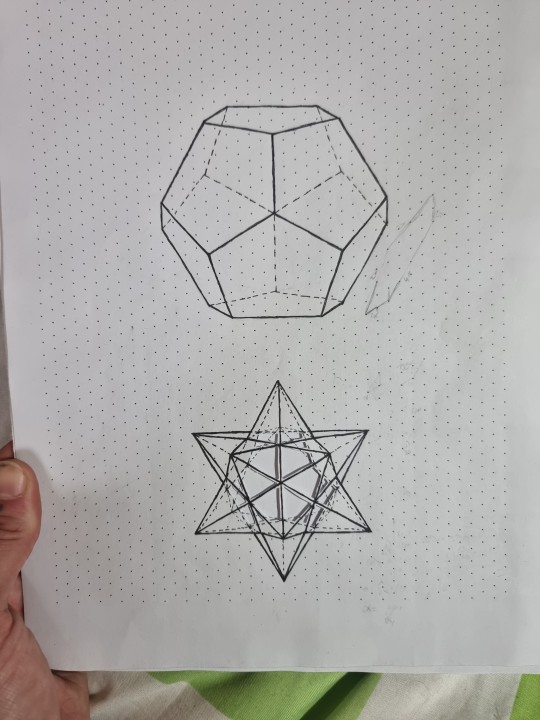
So I drew this dodecahedron and then the stellated dodecahedron below.

And when I drew that stellated dodecahedron I made some very annoying mistakes (in the last steps!)...

As I could not erase those ink lines, I improved and cut out the parts with mistakes...

Sadly, the cut outs are irritating for the perspective drawing. (I will show you why shading the faces will help make sense of this shape once I have made a second drawing of it.)

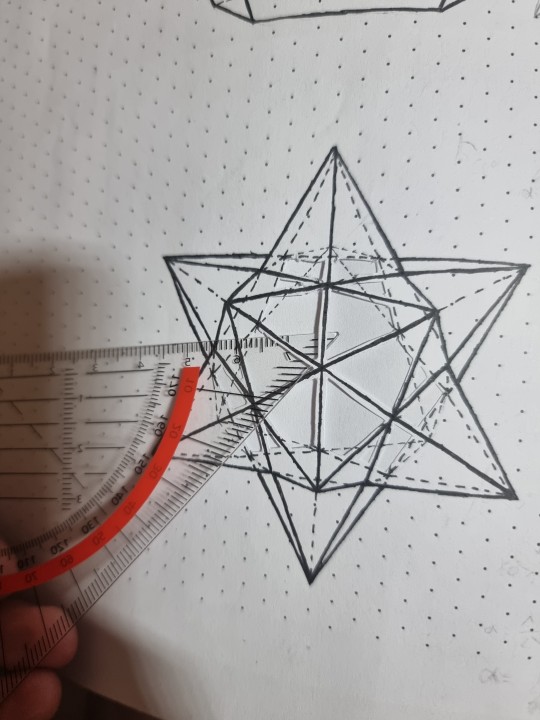
Now I cannot shade the stellated dodecehedron as it would look very messy with the cuts.

So I just use the stellated octahedron part as an interesting collage item.

I could even insert neon-colored paper, which would make it look fancy.

But for making a shaded drawing I might draw a second one - but without those mistakes...

[thelegolink]

mARTch Day 7: Object Study.

For Day 7, I drew one of the sets of dice I keep on my desk. It was pretty fun to consider the perspective of these simple polyhedra!

[art-of-mathematics]

In this perspective the icosahedron drawing fits neatly into this hexagon shape.

[amyasgothique]

|Beautiful 3D representations that were made by Leonardo da Vinci| ___________________________________ Leonardo di ser Piero da Vinci, more commonly Leonardo da Vinci, was an Italian Renaissance polymath, whose areas of interest is a vast list of creative activities, including invention, painting, sculpting, architecture, science, anatomy, geology, astronomy and mach more. That his work in engineering, architecture and astronomy might have triggered his interest in mathematics, but not to what extent he actually studied it. It is well known that one of his many friends included the mathematician Luca Pacioli. Luca Pacioli was a Franciscan friar and mathematician, who is best known for his collection of fifteenth century mathematics (Summa de arithmetica, geometrica, proportioni et proportionalita – 1494). He was extremely interested in studying polyhedra (or polyhedrons), are solids in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. At the time quite a significant number of people were studying polyhedra, especially the regular ones, sometimes called Platonic Solids (tetrahedron,  cube,  octahedron,  dodecahedron and icosahedron). It turns up that Luca Pacioli collaborated with Leonardo da Vinci on the book De divina proportione (1509). In this book he discussed the concept of “golden proportion” and the properties of different polyhedra. Actually, in the 1490s da Vinci studied mathematics under Pacioli and it feels just normal that they also collaborated on this book. It seems that da Vinci was more interested in descriptive features of objects (shape, size, perspective) rather then theoretical foundations. Therefore, he illustrated the book, creating around 60 plates for the book. Bellow some examples from his work. Shapes’ names from top left: #icosahedron #octahedron #sphere #dodecahedron #tetrahedron #cube #leonardodavinci #illustrated #platonicsolids #polyhedra #threedimension #perspective #fifteenthcentury #1509 #davinci #dedivinaproportione #goldenproportion #polygonal #mathematician #mathematics #creativeactivities #invention #painting #sculpting #architecture #science #anatomy #geology #astronomy #🎩 @be_amyas https://www.instagram.com/p/CB7PS9zHqcZ/?igshid=6aolmx09rx1z

[etoastie]

As an intuition for how this gets tricky, imagine a series of polyhedra whose limit is a sphere. We know from Euler and later Gauss that you can't map a sphere's surface onto a plane without distortion. Yet we require that every possible polyhedra in the series must be able to do exactly that.

To make things more interesting: we heuristically know that as the polyhedra gain vertices, the probability that any individual unfolding will work without overlaps approaches zero. It also turns out that testing whether any individual shape has an unfolding is NP-complete. So as we step through this series, it's going to become increasingly harder to unfold the shapes.

From that perspective, I think it becomes a lot less obvious that this is always possible.

Exercise for the reader: take your favorite proof that a sphere can't be mapped onto a plane. Where does the proof break down when you try to apply it to the series of increasingly-fine tilings of a sphere?

ok so. thinking about polyhedral nets. seemingly you can always fold the same polyhedral net either direction, right. like if you cut this net out you could fold it such that the yellow side formed the interior or the exterior, depending on your first choice of fold. is there some way to prove that?? or some counterexample where the direction you have to fold is embedded in the net itself?

[crossconnectmag]

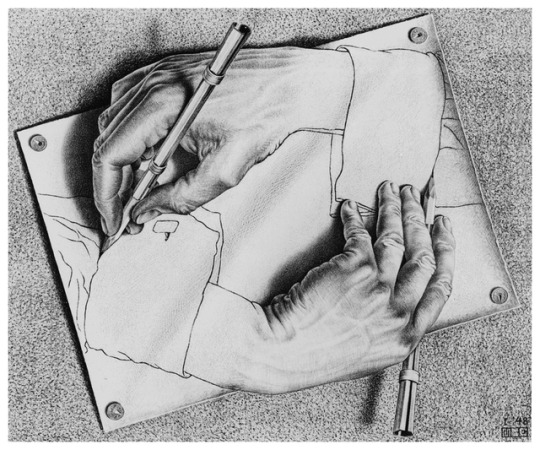
Graphic Work by M.C. Escher

Maurits Cornelis Escher (1898 - 1972) was a Dutch graphic artist who made mathematically-inspired woodcuts, lithographs, and mezzotints. Despite the wide popular interest, Escher was for long somewhat neglected in the art world, even in his native Netherlands. He was 70 before a retrospective exhibition was held. In the twenty-first century, he became more widely appreciated, with exhibitions across the world. His work features mathematical objects and operations including impossible objects, explorations of infinity, reflection, symmetry, perspective, truncated and stellated polyhedra, hyperbolic geometry, and tessellations.

Art not only for connoisseurs. Posted by Margaret from tu recepcja via

[lthmath]

Celebrating Escher’s birthday!

Maurits Cornelis Escher (17 June 1898 – 27 March 1972) was a Dutch graphic artist who made mathematically-inspired woodcuts, lithographs, and mezzotints. He was 70 before a retrospective exhibition was held. His work features mathematical objects and operations including impossible objects, explorations of infinity, reflection, symmetry, perspective, truncated and stellated polyhedra, hyperbolic geometry, and tessellations. 

Although Escher believed he had no mathematical ability, he interacted with the mathematicians George Pólya, Roger Penrose, Harold Coxeter and crystallographer Friedrich Haag, and conducted his own research into tessellation.

[bm2ab]

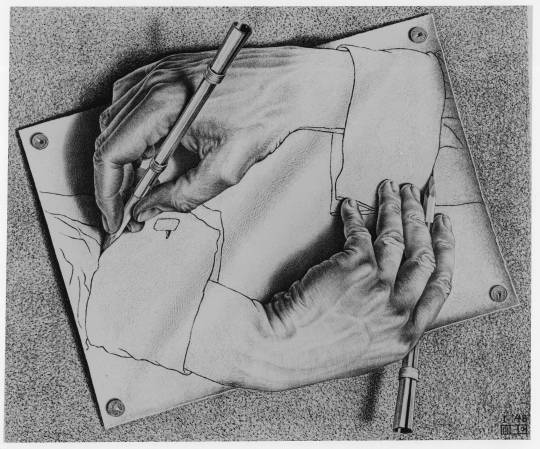
Arrivals & Departures 17 June 1898 – 27 March 1972 Celebrate Maurits Cornelis Escher Day!

Maurits Cornelis Escher (Dutch pronunciation: [ˈmʌurɪt͡s kɔrˈneːlɪs ˈɛʃər]; 17 June 1898 – 27 March 1972) was a Dutch graphic artist who made mathematically inspired woodcuts, lithographs, and mezzotints. Despite wide popular interest, Escher was for long somewhat neglected in the art world, even in his native Netherlands. He was 70 before a retrospective exhibition was held. In the twenty-first century, he became more widely appreciated, with exhibitions across the world.

His work features mathematical objects and operations including impossible objects, explorations of infinity, reflection, symmetry, perspective, truncated and stellated polyhedra, hyperbolic geometry, and tessellations. Although Escher believed he had no mathematical ability, he interacted with the mathematicians George Pólya, Roger Penrose, Harold Coxeter and crystallographer Friedrich Haag, and conducted his own research into tessellation.

Early in his career, he drew inspiration from nature, making studies of insects, landscapes, and plants such as lichens, all of which he used as details in his artworks. He traveled in Italy and Spain, sketching buildings, townscapes, architecture and the tilings of the Alhambra and the Mezquita of Cordoba, and became steadily more interested in their mathematical structure.

Escher's art became well known among scientists and mathematicians, and in popular culture, especially after it was featured by Martin Gardner in his April 1966 Mathematical Games column in Scientific American. Apart from being used in a variety of technical papers, his work has appeared on the covers of many books and albums. He was one of the major inspirations of Douglas Hofstadter's Pulitzer Prize-winning 1979 book Gödel, Escher, Bach.

[kiragecko]

I just realized that the original post no longer has the image it was supposed to! Don’t know when during the posting process that happened.

Cards are 9 x 6.5cm (3.5 x 2.5 inches). They don’t really have the space for little polyhedra around the main image.

And I think my use of “3D” when I meant “axonometric projection” or “perspective projection” may have caused confusion. I am not planning on making a 3D model. I was trying to communicate that coxeter plane diagrams aren’t my preferred form of projection.

Hi, Math Tumblr!

Question first, than I will allow myself to ramble.

Are there names for the families of polytopes¹? Triangle based polytopes are simplexes, square based are hypercubes and orthoplexes, the demicubes are, I guess, demicubes. (I do not yet understand demicubes.) But do 24, 120, and 600-cells have matching group names with their higher and lower dimensional counterparts?

-

Me and my weird little kids love shapes. My youngest also loves collecting and my eldest loves trading (but mostly cubes. Trading is a way to get more cubes). For the last 2 years, I've been making my kids collectible trading cards of convex polyhedra.

If they get a full set (like the 5 platonic solids, the 3 pyramids, or the 8 antiprisms [we don't use any regular polygons above the decagon]) they can trade them in for a special card. In an effort to provide more cubes (there's only one. So it's been a challenge) the special cards are the fundamental complex and regular polytopes in dimensions 3 to 10.

But I don't know much about extra dimensions. My math skills mostly stopped developing when schools brought in the math that requires calculators and ~shiver~ evil decimals. (With a brief glowing resurgence for some aspects of linear algebra in university. Beautiful matrices!) While I COULD just make a set of hypercubes, my completionist tendencies do not accept this. Can anyone tell me if there are names I could use for sets for each of the uniform polychorons?

Additional appreciated information:

Do any of the higher dimensions have a specific term for their polytopes? (Including old terms that aren't often used but sound cool.)

Are there any fun visualization for higher dimensional polytopes? I can use orthographic representations, but anything with pseudo-3D would be more appealing to the kids. Also, do you know somewhere I could find such things online? Currently, I am using wikipedia. I like sets to have consistent visuals with each other, but they don't always need to be consistent with the rest of the cards.

-

¹for the non-math weirdos: 'polytopes' are objects with flat sides (faces). A 2D object is a 'polygon', a 3D object is a 'polyhedron', and 4D things like the tesseract from the Marvel movies are 'polychorons'. You can keep adding dimensions forever.

[lesliegrover]

Maurits Cornelis Escher 17 June 1898 - 27 March 1972 ‘Operations including impossible objects, explorations of infinity, reflection, symmetry, perspective, truncated and stellated polyhedra, hyperbolic geometry, and tessellations.’ Combining the world of math and art, Escher created calculated art poetically expressing his souls essence. Not sure why his work speaks to me as much as it does. Perhaps it’s the symbolic reflection of the many dimensions he ties together. Perhaps it’s the simplicity of his expression delicately and methodically articulated. In any case, his work is amazing. Felt from the heart and soul, just how I like it ❤️ #mcescher #art #artists #amazing #appreciation #connected #reflection #reflections (at National Gallery of Victoria) https://www.instagram.com/p/BsPk9rVl9RA/?utm_source=ig_tumblr_share&igshid=dgz7rz3pf1xi

[joyfuldelusionchaosvaliant]

Science and Chemistry Classes

Roadmap for finding new functional porous materials

Ulsan National Institute of Science and Technology

"The emergence of new structures would provide a new opportunity to control their properties," said Professor Wonyoung Choe. "Taking a different perspective on cage-based frameworks can lead to a new stage of functional porous materials."

The discovery of new structures holds tremendous promise for accessing advanced functional materials in energy and environmental applications. Although cage-based porous materials, metal-organic polyhedra (MOPs), are attracting attention as an emerging functional platform for numerous applications, hardly predictable and seemingly uncontrollable packing structures remain an open question. There is a high demand for a roadmap for discovering and rationally designing new MOP structures.

A research team, led by Professor Wonyoung Choe in the Department of Chemistry at Ulsan National Institute of Science and Technology (UNIST), South Korea, has made a major leap forward in revealing how future structures of MOPs can be predicted and designed at the molecular level. Their findings are expected to create a new paradigm for accelerating materials development and application of MOPs.

Prior to MOPs, metal-organic frameworks (MOFs), another well-known class of porous material, have developed rapidly. MOFs share compositional similarities (i.e., metal clusters and organic ligands) to MOPs. However, the molecular building blocks of MOFs are connected in an extended manner, while discrete cages consisting of metal clusters and organic ligands are packed by weak interactions in MOPs. Unlike MOPs, thousands of MOFs have been synthesized since their first discovery and now they are becoming increasingly important materials in academia and industries alike. A major driving force behind the phenomenal success of MOFs is their predictable and designable structures with a rich choice of molecular building blocks. By considering the molecular geometry of building blocks, the possible structures can be predicted and designed.

So far, it was believed that strong bonds to connect building blocks are necessary to construct structures in a predictable way. Since weak or non-directional interactions have often resulted in unpredictable structures, the rational design of MOPs has been less illuminated. In this study, the research team discovered a special type of MOPs where the design principle can be applied to molecular packing systems, despite the absence of strong bonds. The zirconium (Zr)-based MOPs are notable examples. The authors unveiled multiple weaker bonds can do a similar role to strong bonds.

Zr-based MOPs are an emerging class of MOPs with their excellent chemical stability. While the Zr-MOPs are essentially cage-based compounds, features mainly found in MOFs, such as robust framework and permanent porosity, also appear in Zr-MOPs. The authors say that such extraordinary dual features motivated them to further investigate the solid-state packing of Zr-MOPs. In this study, the authors not only provided a comprehensive study of the existing structures but also discovered future structures that have not been observed but are potentially accessible. A fundamental understanding of the nanoscale self-assembly of cages provides opportunities to control the packing structure, porosity, and properties. The authors expected that these unique dual features of Zr-MOPs can lead to many intriguing applications that are not accessible by typical MOPs or MOFs. They also encouraged to find other interesting classes of cage-based frameworks.

The findings of this research have been published as a Perspective in Chem, a sister journal to Cell, on March 10, 2022.

[blod-stream]

M. C. Escher

Maurits Cornelis Escher (17 June 1898 – 27 March 1972) was a Dutch graphic artist who made mathematically-inspired woodcuts, lithographs, and mezzotints.

His work features mathematical objects and operations including impossible objects, explorations of infinity, reflection, symmetry, perspective, truncated and stellated polyhedra, hyperbolic geometry, and tessellations.

via Wikipedia

[1962dude420-blog]

Today we remember the passing of Maurits Cornelis(MC) Escher who Died: March 27, 1972 in Laren, Netherlands

Maurits Cornelis Escher (17 June 1898 – 27 March 1972) was a Dutch graphic artist who made mathematically inspired woodcuts, lithographs, and mezzotints. Despite wide popular interest, Escher was for long somewhat neglected in the art world, even in his native Netherlands. He was 70 before a retrospective exhibition was held. In the late twentieth century, he became more widely appreciated, and in the twenty-first century he has been celebrated in exhibitions across the world.

His work features mathematical objects and operations including impossible objects, explorations of infinity, reflection, symmetry, perspective, truncated and stellated polyhedra, hyperbolic geometry, and tessellations. Although Escher believed he had no mathematical ability, he interacted with the mathematicians George Pólya, Roger Penrose, Harold Coxeter and crystallographer Friedrich Haag, and conducted his own research into tessellation.

Early in his career, he drew inspiration from nature, making studies of insects, landscapes, and plants such as lichens, all of which he used as details in his artworks. He traveled in Italy and Spain, sketching buildings, townscapes, architecture and the tilings of the Alhambra and the Mezquita of Cordoba, and became steadily more interested in their mathematical structure.

Escher's art became well known among scientists and mathematicians, and in popular culture, especially after it was featured by Martin Gardner in his April 1966 Mathematical Games column in Scientific American. Apart from being used in a variety of technical papers, his work has appeared on the covers of many books and albums. He was one of the major inspirations of Douglas Hofstadter's Pulitzer Prize-winning 1979 book Gödel, Escher, Bach.

Maurits Cornelis Escher was born on 17 June 1898 in Leeuwarden, Friesland, the Netherlands, in a house that forms part of the Princessehof Ceramics Museum today. He was the youngest son of the civil engineer George Arnold Escher and his second wife, Sara Gleichman. In 1903, the family moved to Arnhem, where he attended primary and secondary school until 1918. Known to his friends and family as "Mauk", he was a sickly child and was placed in a special school at the age of seven; he failed the second grade. Although he excelled at drawing, his grades were generally poor. He took carpentry and piano lessons until he was thirteen years old.

In 1918, he went to the Technical College of Delft. From 1919 to 1922, Escher attended the Haarlem School of Architecture and Decorative Arts, learning drawing and the art of making woodcuts. He briefly studied architecture, but he failed a number of subjects (due partly to a persistent skin infection) and switched to decorative arts, studying under the graphic artist Samuel Jessurun de Mesquita.

Despite wide popular interest, Escher was for a long time somewhat neglected in the art world; even in his native Netherlands, he was 70 before a retrospective exhibition was held. In the twenty-first century, major exhibitions have been held in cities across the world. An exhibition of his work in Rio de Janeiro attracted more than 573,000 visitors in 2011; its daily visitor count of 9,677 made it the most visited museum exhibition of the year, anywhere in the world. No major exhibition of Escher's work was held in Britain until 2015, when the Scottish National Gallery of Modern Art ran one in Edinburgh from June to September 2015, moving in October 2015 to the Dulwich Picture Gallery, London. The exhibition poster is based on Hand with Reflecting Sphere, 1935, which shows Escher in his house reflected in a handheld sphere, thus illustrating the artist, his interest in levels of reality in art (e.g., is the hand in the foreground more real than the reflected one?), perspective, and spherical geometry. The exhibition moved to Italy in 2015–2016, attracting over 500,000 visitors in Rome and Bologna, and then Milan.

In 1935, the political climate in Italy under Mussolini became unacceptable to Escher. He had no interest in politics, finding it impossible to involve himself with any ideals other than the expressions of his own concepts through his own particular medium, but he was averse to fanaticism and hypocrisy. When his eldest son, George, was forced at the age of nine to wear a Ballila uniform in school, the family left Italy and moved to Château-d'Œx, Switzerland, where they remained for two years.

The Netherlands post office had Escher design a semi-postal stamp for the "Air Fund" (Dutch: Het Nationaal Luchtvaartfonds) in 1935, and again in 1949 he designed Dutch stamps. These were for the 75th anniversary of the Universal Postal Union; a different design was used by Surinam and the Netherlands Antilles for the same commemoration.

Escher, who had been very fond of and inspired by the landscapes in Italy, was decidedly unhappy in Switzerland. In 1937, the family moved again, to Uccle (Ukkel), a suburb of Brussels, Belgium. World War II forced them to move in January 1941, this time to Baarn, Netherlands, where Escher lived until 1970. Most of Escher's best-known works date from this period. The sometimes cloudy, cold, and wet weather of the Netherlands allowed him to focus intently on his work. After 1953, Escher lectured widely. A planned series of lectures in North America in 1962 was cancelled after an illness, and he stopped creating artworks for a time, but the illustrations and text for the lectures were later published as part of the book Escher on Escher. He was awarded the Knighthood of the Order of Orange-Nassau in 1955; he was later made an Officer in 1967.

In July 1969 he finished his last work, a large woodcut with threefold rotational symmetry called Snakes, in which snakes wind through a pattern of linked rings. These shrink to infinity toward both the center and the edge of a circle. It was exceptionally elaborate, being printed using three blocks, each rotated three times about the center of the image and precisely aligned to avoid gaps and overlaps, for a total of nine print operations for each finished print. The image encapsulates Escher's love of symmetry; of interlocking patterns; and, at the end of his life, of his approach to infinity. The care that Escher took in creating and printing this woodcut can be seen in a video recording.

Escher moved to the Rosa Spier Huis in Laren in 1970, an artists' retirement home in which he had his own studio. He died in a hospital in Hilversum on 27 March 1972, aged 73. He is buried at the New Cemetery in Baarn.

[slanting-walls]

Mathematics and art have a long historical relationship. Artists have used mathematics since the 4th century BC when the Greek sculptor Polykleitos wrote his Canon, prescribing proportions conjectured to have been based on the ratio 1:√2 for the ideal male nude. Persistent popular claims have been made for the use of the golden ratio in ancient art and architecture, without reliable evidence. In the Italian Renaissance, Luca Pacioli wrote the influential treatise De divina proportione (1509), illustrated with woodcuts by Leonardo da Vinci, on the use of the golden ratio in art. Another Italian painter, Piero della Francesca, developed Euclid's ideas on perspective in treatises such as De Prospectiva Pingendi, and in his paintings. The engraver Albrecht Dürer made many references to mathematics in his work Melencolia I. In modern times, the graphic artist M. C. Escher made intensive use of tessellation and hyperbolic geometry, with the help of the mathematician H. S. M. Coxeter, while the De Stijl movement led by Theo van Doesburg and Piet Mondrian explicitly embraced geometrical forms. Mathematics has inspired textile arts such as quilting, knitting, cross-stitch, crochet, embroidery, weaving, Turkish and other carpet-making, as well as kilim. In Islamic art, symmetries are evident in forms as varied as Persian girih and Moroccan zellige tilework, Mughal jali pierced stone screens, and widespread muqarnas vaulting.

Mathematics has directly influenced art with conceptual tools such as linear perspective, the analysis of symmetry, and mathematical objects such as polyhedra and the Möbius strip. Magnus Wenninger creates colourful stellated polyhedra, originally as models for teaching. Mathematical concepts such as recursion and logical paradox can be seen in paintings by René Magritte and in engravings by M. C. Escher. Computer art often makes use of fractals including the Mandelbrot set, and sometimes explores other mathematical objects such as cellular automata. Controversially, the artist David Hockney has argued that artists from the Renaissance onwards made use of the camera lucida to draw precise representations of scenes; the architect Philip Steadman similarly argued that Vermeer used the camera obscura in his distinctively observed paintings.

Other relationships include the algorithmic analysis of artworks by X-ray fluorescence spectroscopy, the finding that traditional batiks from different regions of Java have distinct fractal dimensions, and stimuli to mathematics research, especially Filippo Brunelleschi's theory of perspective, which eventually led to Girard Desargues's projective geometry. A persistent view, based ultimately on the Pythagorean notion of harmony in music, holds that everything was arranged by Number, that God is the geometer of the world, and that therefore the world's geometry is sacred.

All that to say, I'm not separating the two! Mathematics is simply the only logical art, and therefore the only one I care for.

CODE YELLOW IF U SEE TOMAS DO NOT ENGAGE

What does this even mean.

[isomorphismes]

There are no theorems in category theory.

Emily Riehl, Category Theory In Context

Mathematicians often tell her this; hence the book.

If I had to summarise her views in one sentence, it would be:

Everything is an adjunction.

I also like the division these mathematicians are making to her: essentially, a theorem is anything that solves Feynman’s challenge: by a series of clear, unsurprising steps, one arrives at an unexpected conclusion.

Examples for me include:

17 possible tessellations

6 ways to foliate a surface

27 lines on a cubic

1, 1, 1, 1, 1, 1, 28, 2, 8, 6, 992, 1, 3, 2, 16256, 2, 16, 16, 523264, 24, 8, 4 ways to link any-dimensional spheres.

the existence of sporadic groups

surprising rep-theory consequences of Young diagrams, Ferrers sequences, and so on (you could say the strangeness of integer partitions is really to blame here…)

59 icosahedra

8 geometric layouts

Books which are bristling with mathematical ideas of this kind include Montesinos on tessellations, Geometry and the Imagination (the original one), and Coxeter’s book on polyhedra (start with Baez on A-D-E if you want to follow my path). Moonshine and anything by Thurston or his students, I’ve found similarly flush with shockng content—quite different to what I thought mathematics would be like. (I had pictured something more like a formal logic book: row by row of symbols. But instead, the deeper I got into mathematics, the fewer the symbols and the more the surnames thanking the person who came up with some good idea.)

Note that a theorem is different here to some geometry — as in The Geometry of Schemes. The word geometry used in that sense, I feel, is to have a comprehensive enough vision of a subject to say how it “looks” — but the word theorem means the result is surprising or unintuitive.

This definition of a theorem, to me, presents a useful challenge to annoying pop-psychology that today lurks under the headings of Bayesianism, cognitive _______, behavioural econ/finance, and so on.

Following Buliga and Thurston to understand the nature of mathematical progress, within mathematics at least (where it’s clearer than elsewhere whether you understand something or not—compare to economic theory for example), there is a clear delination of what’s obvious and what’s not.

What is definitely not the case in mathematics, is that every logical or computable consequence of a set of definitions is computed and known immediately when the definitions are stated! You can look at a (particularly a good) mathematical exposition as walking you through the steps of which shifts in perspective you need to take to understand a conclusion. For example start with some group, then consider it as a topological object with a cohomology to get the centraliser. Or in Fourier analysis: re-present line-elements on a series of widening circles. Use hyperbolic geometry to learn about integers. Use stable commutator length (geometry) to learn about groups. Or read about Teichmüller stuff and mapping class groups because it’s the confluence of three rivers.

Sometimes mathematical explanations require fortitude (Gromov’s "energy") and sometimes a shift in perspective (Gromov’s (neg)"entropy").

This view of theorems should be contrasted to the disease of generalisation in mathematical culture. Citing two real-life grad students and a tenured professor in logic (one philosophical, one mathematical, the professor in computer science):

I like your distinction between hemi-toposes, demi-toposes, and semi-toposes

I care about hyper-reals, sur-reals, para-consistency, and so on

Abstract thought — like mathematicians do — is the best kind of thought.

(twitter.com/replicakill, the author of twitter.com/logicians, ragged on David Lewis by saying “What do mathematicians like?” “What do mathematicians think?” —— And Corey Mohler has done a wonderful job of mocking Platonism, which is how I guess the thirst for over-generalisation reaches non-mathematicians.)

Paul Halmos knew that cool examples beat generalisations for generalisation’s sake, as did V. I. Arnol’d. And it seems that the people a Harvard mathematician spends her time with make reasonable demands of a mathematical idea as well. It shouldn’t just contain previous theories; it should surprise. In Buliga’s Blake/Reynolds dispute, Blake wins hands down.

[sciencebulletin]

Why viruses like Herpes and Zika will need to be reclassified, and its biotech impact

New research reveals that the way viruses were perceived in terms of their architecture will need to be retooled, because they are actually structured in many more patterns than previously understood. The findings could have significant impact on how they are classified, our understanding of how they form, evolve and infect hosts, and strategies to identify ways to design vaccines to target them. In the 1950s and '60s as scientists began to obtain high resolution images of viruses, they discovered the detailed structure of the capsid—an outer protective layer composed of multiple copies of the same protein—which protects the virus' genetic material. The majority of viruses have capsids that are typically quasi-spherical and display icosahedral symmetry—like a 20-sided dice for instance. The capsid shell is what protects them, and as scientists discovered their structure, they proposed that capsids could have different sizes and hold different amounts of genome, and therefore could infect hosts differently. Why this matters When designing drugs to target viruses, scientists can now take their varying structural shapes into account to improve efficacy. Two researchers who study the structures of viruses, Antoni Luque, a theoretical biophysicist at San Diego State University and a member of its Viral Information Institute, and Reidun Twarock, a mathematical biologist from the University of York, UK, and a member of York's Cross-disciplinary Centre for Systems Analysis, show that many viruses have essentially been misclassified for 60 years, including common viruses such as Herpes simplex and Zika. This was because despite having the structural images from cryo-electron microscopy, we did not have the mathematical description of many of the architectures of different viruses. "We discovered six new ways in which proteins can organize to form icosahedral capsid shells," Luque said. "So, many viruses don't adopt only the two broadly understood capsid architectures. There are now at least eight ways in which their icosahedral capsids could be designed." They used a generalization of the quasiequivalence principle to see how proteins can wrap around an icosahedral capsid. Their study, which will be published in Nature Communications on Friday, September 27, also shows that viruses that are part of the same structural lineage, based on the protein that they're composed of, adopt consistent icosahedral capsid layouts, providing a new approach to study virus evolution. Biotech applications Structural biologists can now take this information and reclassify the structure of the viruses, which will help unveil molecular and evolutionary relationships between different viruses. It will also provide a guide to engineer new molecular containers for nanotech and biotech applications, and it will help scientists to identify specific strategies to target the assembly of proteins in the capsid. This can eventually lead to a more systematic approach to developing antiviral vaccines. "We can use this discovery to target both the assembly and stability of the capsid, to either prevent the formation of the virus when it infects the host cell, or break it apart after it's formed," Luque said. "This could facilitate the characterization and identification of antiviral targets for viruses sharing the same icosahedral layout." This new framework accommodates viruses that were previously outliers, provides new predictions of viral capsid architectures, and has identified common geometrical patterns among distant evolutionary related viruses that infect everyone from humans to bacteria. Twarock said the new blueprints also provide "a new perspective on viral evolution, suggesting novel routes in which larger and more complex viruses may have evolved from simple ones at evolutionary timescales." Architectural applications The geometries could be also used in new architectural designs in buildings and construction. Since the 1960s, these viral capsids have been classified using the geometrical framework introduced by structural biologist Donald Caspar and biophysicist Aaron Klug, which were inspired by the geodesic domes designed by the renowned architect R. Buckminster Fuller. However, as molecular imaging techniques have advanced, an increasing number of 3-D viral capsid reconstructions that included viruses like Herpes or Zika have fallen out from this classical geometrical framework. "This study introduces a more general framework than the classic Caspar-Klug construction. It is based on the conservation of the local vertices formed by the proteins that interact in the capsid," Luque explained. "This approach led to the discovery of six new types of icosahedral capsid layouts, while recovering the two classical layouts from Caspar-Klug based on Goldberg and geodesic polyhedra." "Structural puzzles in virology solved with an overarching icosahedral design principle" is published in Nature Communications. Provided by: San Diego State University More information: Reidun Twarock et al. Structural puzzles in virology solved with an overarching icosahedral design principle. Nature Communications (2019). doi.org/10.1038/s41467-019-12367-3 Image: Evolutionary related viruses infecting bacteria and humans adopting one of the newly established protein layouts of icosahedral capsids. Bacillus phage Basilisk (a), herpes simplex virus 1 (b), and bacteriophage lambda (c). Credit: Antoni Luque, San Diego State University and Reidun Twarock, University of York. Read the full article