#adjoint functor

[carmilla-the-dog]

What is the dual of the forgetful functor?

Ooooh my, this is going to be fun.

Ok, so first things first, what do we mean here by dual? Well, duality in category theory is a very loose concept, and one must examine the particular use case before deciding what dual means.

In this post, duality will be given by adjunction. And what is adjunction, you ask? Adjunction is when

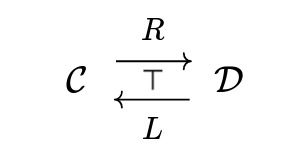
are related by

$$\mathcal{D}(x,Ry)\cong\mathcal{C}(Lx,y),$$

(the isomorphism being natural). And in this case we say that \(R\) is a right adjoint to \(L\) and \(L\) is a left adjoint to \(R\). By Yoneda bullshit, all right adjoints of a functor have to be isomorphic. (dually, the same is true for left adjoints).

THE SECOND THING is that forgetful functor is also a loosely defined concept (https://ncatlab.org/nlab/show/stuff%2C+structure%2C+property). But here I'll be talking about the family of functors of the form

$$U:\mathcal{E}\to\mathbf{Set},$$

in which \(\mathcal{E}\) is a concrete algebraic category like modules, vector spaces, groups or abelian groups. This functor takes an algebraic structure and send it to its underlying set.

Remark. More generally you can take the category of monoids, or the category of algebraic theory, over a category \(\mathcal{C}\) and you have a natural forgetful functor into \(\mathcal{C}\) itself.

OK. So if we want a left adjoint to \(U\), we require that, given a set \(x\) and a algebraic structure \(y\) (which has underlying set \(y\) because fuck you), we have

$$\mathbf{Set}(x,y)\cong\mathcal{E}(Lx,y).$$

That is, algebraic maps

$$\phi:Lx\to y,$$

are completely determined by the map in \(x\):

$$f:x\to y.$$

If you feel like this is familiar, you are not wrong! If you have any formal training in mathematics (and if you don't, I'm so sorry for using jargon and stuff… I can answer any questions after ^^( but I know for a fact that anon has formal training)) then you maybe recognize this from linear algebra.

Indeeeeeeeeed, given any vector spaces \(V\text{ and } W\), a linear map

$$T:V\to W$$

is completely determined by what it does to the basis of \(V\). Even more, if the set \(v\) is as basis for \(V\) (I am completely aware that my notation can cause psychic damage), then every function of sets

$$f:v\to W,$$

determine a linear transformation

$$T:V\to W.$$

AND EVEN FURTHER every linear transformation is obtained in this way. Abstracting again, the left functor \(L\) represents taking a set \(x\) and using it as a basis for a algebraic structure \(Lx\).

As algebraic structures with a basis are called free, the left adjoint of a forgetful functor is called the free functor. :)

If someone guess the name of the right adjoint of the forgetful functor, I'll give them a kiss

[real-real-numbers]

right adjoints are basically the most classic functors to preserve limits 😂😂😂

[bubbloquacious]

Do you have any recommendations for texts for a first reading of category theory? :))

So this is a super common question and I think it's a little hard to give a good answer to! I'll tell you what I did.

Back in the summer of the beautiful year 2019 I had just finished my first year of university mathematics education. I don't remember where I had even heard of the subject, but the first math book I ever self-studied out of was Mac Lane's Categories for the Working Mathematician (the second edition, specifically). It's a good book, I think! But I only really appreciated it on my reread (i.e. my more-than-the-first-three-chapters read) last year. For one, I had not done a lick of topology by this point, and I really do recommend knowing basic topology and basic abstract algebra before getting into categories; it gives you a nice two-pronged approach to view every construction.

So I washed out of that one pretty quickly. I learned the basic definitions of categories, functors, and natural transformations. I could work out what it meant for a product to be the limit of a discrete diagram (super neat when you just learned what a group was five months ago!), but if you asked me to give an example of a pair of adjoint functors that wasn't in the text I would've been stumped (natural transformations between hom-functors? what?).

Over the course of the next semester I got familiar with the basics of topology (and I made this blog!). Now I could see why a lot of Mac Lane's examples were so nice. Compositions of homotopic maps are homotopic, so you can take a quotient category the same way you take a quotient group. The fundamental group is so useful exactly because it is functorial. A map into a product space is continuous precisely when its composition with the projections is continuous. And so on. I sampled some more books. I read the first few chapters of Awodey's Category Theory and of Adámek, Herrlich, and Strecker's Abstract and Concrete Categories. Each offers a slightly different perspective, but every time I would wash out after the first several chapters.

But it was exactly rereading all of these different perspectives that made me grok what it was all about. How to work with these structures. I had limits and colimits pretty much down by this point. Ah, it's not a coincidence that the least upper bound and greatest lower bound are categorical limits, they're expressing the same idea. I realized on my own that not only is the discrete space functor to topological spaces left adjoint to the forgetful functor to sets, the indiscrete (or chaotic, or trivial) space functor is right adjoint. The abelianization of a group or the completion of a metric space are left adjoint to the inclusion functors of abelian groups and complete metric spaces, because a map from a group/metric space into an abelian group/complete metric space determines a unique map (in fact it factors through this map) out of the abelianization/completion. Even though the abelianization makes the group smaller, and the completion makes the space bigger, they're expressing the same relationship.

This went on for a while. I read Bartosz Milewski's blog on Category Theory for Programmers, but I didn't know Haskell so that didn't get me very far. I read a lot of nLab pages (I still do). I read a small bit of Borceux's Handbook of Categorical Algebra, which is very nicely written if you can get your hands on it. I spent a summer in a reading group for Tai-Danae Bradley's Topology: A Categorical Approach (this one's probably a good pick for you in particular!). Like two years ago I played the Natural Number Game (which they changed recently apparently!), which got me really into Lean and proof assistants in general. Playing around with Lean gave me a great appreciation for what category theory brings to the table for logic and computational mathematics. Reading Dan Marsden's blog on monads got me really into monad theory, which is just super cool and I love it very much. I had a brief fling with bicategories, mostly because of the monads. Around this time I made a bunch of explanatory posts on the things I was learning about, and that was just terrifically helpful for my understanding. I read Mac Lane and Eilenberg's original paper introducing categories, General Theory of Natural Equivalences, and it's fascinating to see the perspective that it takes. Last year I got really into sheaf theory by reading Mac Lane and Moerdijk's Sheaves in Geometry and Logic, which finally made me understand the Yoneda Lemma.

These last few examples are what I would call pretty intermediate, as far as categories go. Somehow by reading all these different sources (and progressing in my studies in other mathematical subjects!) I had gathered up enough experience to understand the higher-level structures built on top of the basics. I still don't understand Kan extensions (though I tried reading Riehl's Category Theory in Context to understand it) or fibrations, or model categories, or co/end calculus, but I'm sure I will once the need arises.

So that's my advice! Read as many different introductions to the subject as you can, in as many different contexts as you have the experience for! The power and beauty of category lies in the bridging over the gaps between these contexts. Any of the books I mentioned I would recommend, but really the most important rule of category theory is to have fun and be yourself :-)

[proof-by-intimidation]

Product of topological spaces categorically.

Let's say we want to define the product of two topological spaces X and Y. First of all, what's the underlying set? Well, the forgetful functor from Top to Set has a right (as well as a left) adjoint. So it preserves limits (and colimits).

So, if the product of the topological spaces exists, then the underlying set should be X \times Y !

Ok, now the topology. Well, we have an obvious candidate for the projection maps, namely the usual projection maps from X\times Y to each of its component. So, we impose a topology on X\times Y such that these maps are continuous. We also need to make it the coarsest such topology, so that it satisfies the universal property!

And that is precisely the product topology.

I know this is not very profound but this perspective really helped me move on to CGWH category. The bizarre topology of the categorical product of CGWH spaces is not always homeomorphic to the product topology. But it is the more natural choice (look at product of CW complexes and prod-hom adjunctino) just like how the projection maps were the natural choice for categorical projection maps in Top.

So, yeah i thought this was cool.

[measurementcat]

I am attempting to learn “real algebraic geometry” (schemes) and it is the most brutal. The density of new concepts is like, 5 times as high as any previous math class I’ve been in. It took us about a month to define what a scheme even is (using locally ringed spaces). I’m somewhat hoping the difficulty / density of new concepts thins out from here, but I’m not sure if it will or not. 

I do have this wondering about, learning about sheafs and categories and so on so far doesn’t feel super directly related to what schemes actually are (this is a bit silly, I suppose, since a scheme is “mostly” “just a sheaf” (plus the Zariski topology)). But I can’t help but wonder whether I’m feeling this overwhelmed because I’ve done the equivalent of learning assembly before learning C, instead of learning C or better Python and then opening it up under the hood. I do expect we’ll be using a lot of category theory and some sheaf theory though. The first big proof we’ve done so far was the proof that the global sections functor is adjoint to the Spec functor, which both is a theorem of category theory as well as using a lot of category theory in the proof. 

It is definitely the first time a math class has made me wonder if I should make flashcards to memorize things though. 

[endofunktor]

So you can forget that a unital ring is unital.

Denote Ring the category of unital rings and Rng the category of (general) rings. Then this should constitute a forgetful functor

S : Ring → Rng.

Can this functor be adjoint? What does it yield?

[mathsuggestions]

Try to understand adjoint functors one more time.

[jonathankatwhatever]

It’s 26 April 2025, and more is falling into place. Example: we can relate Ends to ‘comma category’, being a construction in which a morphism, meaning a process, is an object, which we treat as identity, local and in other senses. Example: ‘universal property’ in category theory. We generate the universality of the universal property, including how it relates to instances of identity, how it identifies shared and separate objects, etc.

I am hoping this is the connecting idea. They have concepts like adjoint and adjunct functors. We fit to that as an enclosure, meaning an associative next count. Which is the n-1 again because it is to that count out of higher n-1 as those always have observable limits. Those are shockingly close, especially for tObjects. Is it clear why that is associative? It is projected (szK//zsK) so all the orderings occur along the branching counts of the cardinal. Which is now clearly cardinal for the first time.

Going to gym.

[theohonohan]

Cocktails and Adjunctions

Loosely inspired by Hans Peter Luhn's Cocktail Oracle, this is a brief, and relatively concrete, exploration of adjunctions (the category theory concept) in the setting of relations.

It is straightforward to consider a mapping from cocktail recipes to ingredients as a relation. A given recipe contains zero or more ingredients. (Let's assume that some conceptual cocktails exist which have no physical ingredients). This relation can be thought of as taking the name of a cocktail and mapping it to a set of ingredients. Because it's a relation (not a function) it is unlikely to have an inverse: the same set of ingredients could map to multiple cocktails.

Category theory puts forward the concept of an adjunction, which is a kind of best-effort analogue of an inverse. A left adjunction is analogous to a left inverse, and a right adjunction is analogous to a right inverse.

Concretely, if we use our recipe relation to map a cocktail name to a set of ingredients, we can then use the left adjoint of the recipe relation to map that set of ingredients back to a set of recipes. This new set of recipes will include any cocktail that includes any one of the ingredients. This is an example of the "exists" functor—it is expansive (or inclusive) in its attempt to figure out, from a set of ingredients, what cocktail was originally asked for. Of course, the set of ingredients that we pass to the left adjoint might not come directly from a cocktail recipe. It could just reflect the contents of a drinks cabinet. The "exists" functor performs best in this case when the set only includes ingredients that are unique to a particular cocktail, and worst when an ingredient that is used in many cocktails is present.

On the other side, we can use the right adjoint, the "forall" functor, to map a set of ingredients to a set of cocktail names. Very simply, this set of cocktail names will include only the cocktails that can be made using those ingredients. The right adjoint is restrictive (or strict).

Every adjunction gives rise to a monad. So what monads can we derive from this situation? Well, the first one arises from composing our recipe map with its left adjoint. It maps a set of ingredients to a set of recipes, and that set of recipes is then mapped back to a set of ingredients. The effect of this is to complete the set of ingredients so that any cocktail that might be "suggested" by the initial set of ingredients can now be mixed. The fact that a monad is a kind of generation of a closure operator is clear here: what we've calculated is a kind of closure of the set of ingredients, pulling in extra ingredients where needed so that any cocktail which uses any one of the initial set of ingredients can now be made.

The second monad we can derive comes from our recipe mapping and its right adjoint. We compose the right adjoint with the recipe map. The result of this is to take a set of cocktail names, find all of the ingredients necessary, and then find all of the cocktails that can be made using only ingredients from that set. So this monad is a kind of closure of the cocktail "menu": if, given a menu listing cocktails A, B and C, we must have the ingredients to also make D and E, then this monad maps our menu "A, B, C" to "A, B, C, D, E": it is a completion of the menu based on all of the ingredients we have to hand.

In a sense, the adjoints attempt to reconstruct a set of cocktail names based on set of ingredients. I think of this as a detective problem: in a room, you come across a drinks cabinet with some half-full bottles in it, and you want to know what cocktails the inhabitant was making. It isn't possible to give a definitive correct answer, in general. If you think some bottles might be missing, you'll need to use the left adjoint (the "exists" functor) to get a best guess. If you suspect that there are some extraneous bottles, the right adjoint (the "forall" functor) might help in ignoring them.

Trying to draw inferences in this way is logical but maybe not that impressive. Like category theory in general, though, it's an absolutely principled and mechanical method.

I learned some of this by asking a StackExchange question.

[bubbloquacious]

So the fact that the underlying sets of products and coproducts of topological spaces are themselves the products and coproducts of the underlying sets is a consequence of the fact that the forgetful functor from the category of topological spaces and continuous maps to the category of sets and functions has both a left and right adjoint (namely the discrete space functor and the indiscrete space functor), so it preserves both limits and colimits (compare this with the fact that the underlying set of a direct sum of abelian groups is not generally the disjoint union of their underlying sets).

But it also goes the other way! The discrete space functor has a right adjoint (namely the forgetful functor), so any disjoint union of discrete spaces is discrete. Products of discrete spaces can be non-discrete, so it does not have a left adjoint. The indiscrete space functor has a left adjoint, so products of indiscrete spaces are indiscrete. Disjoint unions of indiscrete spaces are almost never indiscrete, so it does not have a right adjoint.

[isomorphismes]

There are no theorems in category theory.

Emily Riehl, Category Theory In Context

Mathematicians often tell her this; hence the book.

If I had to summarise her views in one sentence, it would be:

Everything is an adjunction.

I also like the division these mathematicians are making to her: essentially, a theorem is anything that solves Feynman’s challenge: by a series of clear, unsurprising steps, one arrives at an unexpected conclusion.

Examples for me include:

17 possible tessellations

6 ways to foliate a surface

27 lines on a cubic

1, 1, 1, 1, 1, 1, 28, 2, 8, 6, 992, 1, 3, 2, 16256, 2, 16, 16, 523264, 24, 8, 4 ways to link any-dimensional spheres.

the existence of sporadic groups

surprising rep-theory consequences of Young diagrams, Ferrers sequences, and so on (you could say the strangeness of integer partitions is really to blame here…)

59 icosahedra

8 geometric layouts

Books which are bristling with mathematical ideas of this kind include Montesinos on tessellations, Geometry and the Imagination (the original one), and Coxeter’s book on polyhedra (start with Baez on A-D-E if you want to follow my path). Moonshine and anything by Thurston or his students, I’ve found similarly flush with shockng content—quite different to what I thought mathematics would be like. (I had pictured something more like a formal logic book: row by row of symbols. But instead, the deeper I got into mathematics, the fewer the symbols and the more the surnames thanking the person who came up with some good idea.)

Note that a theorem is different here to some geometry — as in The Geometry of Schemes. The word geometry used in that sense, I feel, is to have a comprehensive enough vision of a subject to say how it “looks” — but the word theorem means the result is surprising or unintuitive.

This definition of a theorem, to me, presents a useful challenge to annoying pop-psychology that today lurks under the headings of Bayesianism, cognitive _______, behavioural econ/finance, and so on.

Following Buliga and Thurston to understand the nature of mathematical progress, within mathematics at least (where it’s clearer than elsewhere whether you understand something or not—compare to economic theory for example), there is a clear delination of what’s obvious and what’s not.

What is definitely not the case in mathematics, is that every logical or computable consequence of a set of definitions is computed and known immediately when the definitions are stated! You can look at a (particularly a good) mathematical exposition as walking you through the steps of which shifts in perspective you need to take to understand a conclusion. For example start with some group, then consider it as a topological object with a cohomology to get the centraliser. Or in Fourier analysis: re-present line-elements on a series of widening circles. Use hyperbolic geometry to learn about integers. Use stable commutator length (geometry) to learn about groups. Or read about Teichmüller stuff and mapping class groups because it’s the confluence of three rivers.

Sometimes mathematical explanations require fortitude (Gromov’s "energy") and sometimes a shift in perspective (Gromov’s (neg)"entropy").

This view of theorems should be contrasted to the disease of generalisation in mathematical culture. Citing two real-life grad students and a tenured professor in logic (one philosophical, one mathematical, the professor in computer science):

I like your distinction between hemi-toposes, demi-toposes, and semi-toposes

I care about hyper-reals, sur-reals, para-consistency, and so on

Abstract thought — like mathematicians do — is the best kind of thought.

(twitter.com/replicakill, the author of twitter.com/logicians, ragged on David Lewis by saying “What do mathematicians like?” “What do mathematicians think?” —— And Corey Mohler has done a wonderful job of mocking Platonism, which is how I guess the thirst for over-generalisation reaches non-mathematicians.)

Paul Halmos knew that cool examples beat generalisations for generalisation’s sake, as did V. I. Arnol’d. And it seems that the people a Harvard mathematician spends her time with make reasonable demands of a mathematical idea as well. It shouldn’t just contain previous theories; it should surprise. In Buliga’s Blake/Reynolds dispute, Blake wins hands down.

[twocubes]

the span thing is getting more and more complicated

like. I have now a bit of evidence that my notion of generalized polycategory is "correct" (it has extremely weak requirements and very classical examples that don't work within the paradigm of... the paper I corrected i guess...) but to get it to work i had to use a notion of "unbiased lax bicategory" which iirc was implicit in a different paper on multicategories but not spelled out

and, a lot of the theory of internal profunctors seems to generalize... somewhat.

like, ok, an arrow f : A → B can be made into a span B ← A = A and a span A = A → B which are left and right adjoint in the bicategory of spans, right, and every span X ← F → Y factors as a left followed by a right adjoint. Similarly, a functor F: C → D can be made into a profunctor F*: C ⊸ D and a profunctor F°: D ⊸ C which are adjoint and if you have a profunctor C ← P → D (C and D are categories this time) then there is a category P' and functors F : P' → C and G : P' → D such that P factors as like, G*F°, or w/e

Ok, skipping over how, given arbitrary monads S and T (and some other data), i can make an (unbiased lax) bicategory of spans SX ← F → TY, which stands in relation to generalized polycategories as the category of spans stands in relation to internal categories, right

Now, given a Kleisli arrow A → TB, you can make that into a span SA ← A → TB by using the unit for S, right; in fact for... reasons... arbitrary spans SX ← F → TY will "laxly factor" as a composite of SX ← F → TF and SF ← F → TY. But arrows of those types... aren't usually adjoints. Which is unfortunate.

Now, some... incomplete work... seems to suggest that something like this should extend to factoring poly-profunctors between polycategories. Or at least I... think I can get the polycategory P' to exist; the trouble is that it factors as a pair of "kinda functors" that like, send the objects of P' to S- and T-collections of objects of C and D (respectively). (I call these "kinda" functors, because there are also "proper" functors (which incidentally can themselves be lifted to both those kinds of "kinda" functors.))

Or at least that's how it looks right now... the coherences for these things are, complicated to work through, so i haven't nailed everything down yet.

Anyways this is unfortunate because the limit-preservation properties of adjoints are like, an important part of how you characterize geometric morphisms among profunctors so... either i have to find some other trick to characterize right-torsors or "right torsors are such that tensoring with them on the right is cartesian" is the wrong definition...

And the only way to tell if that last one is the case is to keep reading the Elephant.

So maybe I'll get back on that tomorrow...

Anyways. The point is: the theory seems to... "work", like I've gotten partial results, stuff seems to lead to other stuff, but also i keep having to develop new notions and the definitions for a lot of these things are kind of complicated...

[algebraic-dumbass]

I think you can ask for stuff to commute if you make the arrows go the other way. Basically an arrow here means that what it points to is where it starts + some added hypothesis. This means that reversing the arrows gives us a bunch of forgetful functors (e.g. a group is a particular case of monoid so you have a forgetful functor from groups to monoids). And the diagram of functors we obtain probably commutes (i'm not an expert on morphisms in between niche alg structures such as quasigroups but i still expect everything to work out fine) (but don't quote me on that) (yes i'm supposed to know algebra but i'm an algebraic dumbass so that checks out)

However we have reversed the arrows. What if we don't want to? Well idk maybe consider adjoint functors to the ones i described. Provided they exist. which maybe they don't idk i haven't checked

does this diagram commute? does it even make sense to ask that question? this is basically a cube right, do cubes commute? do i know what commuting means? im having so much fun

[eatsleepmath]

So I realized that part of a post I wrote this time last year

about non-adjoint equivalences between categories was wrong, because I didn’t make myself check that an “obvious-looking” unit map was actually a natural transformation.

Anyways, I spent last night re-convincing myself that non-adjoint equivalences still exist.

I ended up checking the following (identifying a group with its delooping, i.e. the one-object category carrying that group as the automorphism group of the unique object):

Any equivalence \(F : H \leftrightarrows H : G\) of a group with itself comprises two automorphisms \(F, G\), such that \(F G\) and \(G F\) are inner. The unit and counit are the group elements \(g_{\rho}\) such that \(GF(k) = g_{\rho} k g_{\rho}^{-1}\) and  \(g_{\sigma}\) such that \(FG(k) = g_{\sigma}^{-1} k g_{\sigma}\) for any \(k \in H\).

Any equivalence of \(H\) with itself where \(F\) and \(G\) are themselves also inner is an adjoint equivalence.

If \(H\) has trivial center, then any equivalence of \(H\) with itself is an adjoint equivalence.

To obtain a non-adjoint equivalence, we therefore need a group \(H\) with nontrivial center and nontrivial outer automorphisms, such that we can pick two whose products are inner.

So take \(H = K\) the Klein 4-group. This is a product of abelian groups, so abelian, so is its own center. In fact, it’s \(\mathbb{Z}/2 \mathbb{Z} \times \mathbb{Z} / 2 \mathbb{Z}\), so let \(F = G\) the automorphism which interchanges coordinates. \(FG = GF = \operatorname{id}_{K}\), which is given by conjugation by any element.

One of the triangle equalities stipulates that \(F(g_{\rho}) = g_{\sigma}^{-1}\). We can pick \(g_{\rho}\) and \(g_{\sigma}\) to break this. For example, let \(g_{\rho}\) be \((1,1)\) and let \(g_{\sigma}\) be \((0,1)\).

This is an illuminating special case of the fact that, given a non-adjoint equivalence, you can always replace its unit with another unit that makes the equivalence adjoint, without any real loss.

[notarealwelder]

...i'm guessing that three exercises ten pages of exercises and a couple pages of handwaving is only a surface scratch of adjoint functors

But finally I can at least see how some of them work

...is it that no-one can be told about adjoints, one can only do enough exercises to see for themself, is that why no explanation I read before made sense

(beside the formal definition, which was definitive and useful for computations, but not enlightening)

[locally-normal]

(I copied my own tags for context) @tilde-he

Not sure what level of detail to explain in.. there's an operation called the smash product of (pointed) spaces. It acts like a tensor product, in that it's adjoint to the hom functor. With spaces though, there's no good "ground space" for this tensor product, even if you ask for your spaces to have a multiplication operation.

The smash product with a circle is an important enough operation to have its own name, suspension. You can imagine it as taking your space to be the base of a cone, ie drawing in the cone over it, and then drawing a second cone under it.

For lots of reasons, in homotopy theory we work with things called spectra rather than with spaces. These are spaces that are stable under suspension, that is, if you suspend them again you get the same thing out. These also correspond to (co)homology theories, and because suspension is adjoint to loops (tensor/smash is adjoint to hom, so smashing with the circle is adjoint to taking maps out of a circle, ie loops), they also correspond to infinite loop spaces (take loops of loops of loops of....).

Higher homotopy groups eventually stabilize under the suspension operation, which is another motivation for all of this. That is, if you take the j+kth homotopy group of the kth suspension of your space (suspend k times), that's the same as the jth homotopy group of the original space, for sufficiently high k. The group that you get for sufficiently high k is called the jth stable homotopy group, and people are interested in these.

If you take a circle, and its suspension (the 2 sphere), and its suspension (the 3 sphere), and so on, all together that's the sphere spectrum. It's homotopy groups are the stable homotopy groups of spheres, and people are *very* interested in these. Finding all of these would be probably the next best thing after like solving the Riemann hypothesis. No one poses the question because it's wildly out of reach though. The sphere spectrum is what I meant by "spheres".

Ok. So. Back to the smash product - if you take everything up to homotopy (or play other tricks), then the smash product is also like a tensor product for spectra! But, the situation in spectra is better. Spectra are more like abelian groups: there's natural ways to add and subtract maps of spectra, up to homotopy. You can kind of see the beginnings of this behavior in homotopy groups of spaces, which makes sense - if you forget the "up to homotopy" part of the definition of a homotopy group, you get a loop space. A homotopy group uses that homotopy classes of maps have a group operation, if you change perspectives, a loop space has an up-to-homotopy group structure. Spectra are all like infinite loop spaces, so they're all like abelian groups with the operations defined up to homotopy. Sorta.

Rings are abelian groups with a multiplication operation, and in rings, the integers Z are the initial ring - every ring has a unique (up to unique iso) map from Z by simply mapping 1 to the multiplicative unit in the ring. So by default if you tensor two abelian groups (Z modules) your tensor is over Z.

If A is an R algebra, we simply have a map from R to A, and we can base change R modules M to A modules by taking M tensor_R A. Every ring is a Z algebra.

In spectra with an associative multiplication operation, called ring spectra, the sphere spectrum S is initial. So every ring spectrum is an S algebra, and you can define modules just like in algebra and define base change the same way. For a ring spectrum R and an S module M, M tensor_S R is an R module.

There's something called the eilenberg maclane spectrum of a ring, it takes a normal ring R and makes it into a ring spectrum, HR, whose 0th homotopy group is R and the other homotopy groups are 0.

However, in spectra everything is up to homotopy. So doing algebra over HZ is like doing derived algebra over Z - "up to homotopy" is the same in this case as, "up to homology with Z coefficients" which is to say, derived algebra over Z.

You can take any old homological algebra thing and play with it and make it topological this way.

For example, Hochschild homology is a classic algebraic invariant of rings. I won't define it, but, you take some ring and you use tensor products and cook up a differential take homology.

If you take that process, and think of it as something that happens to HZ modules (which is to say, you do nothing but shift perspectives), then suddenly you can base change this whole process and do it over the sphere spectrum instead. Your ring was an HZ module, tensor over HZ with the sphere spectrum and there you go. This defines "topological Hochschild homology" and it's interesting for a variety of reasons.

If you're more algebraically minded, I think this whole thing is interesting because there's more "prime" fields and the eilenberg maclane spectra of finite fields, HFp, behave less like you're used to, and there's interesting information in the map from the sphere spectrum to HFp. People are interested in doing algebraic geometry over the sphere spectrum as opposed to over Fp or the integers or the complex numbers, so called spectral algebraic geometry. I'm less informed about this, but, for an example of how bizarre this algebra is, there's a way to define a multiplication by 2 map on the sphere spectrum. You can take the cofiber of this map, that is, more or less, you can consider S / 2S the same way you construct the group Z / 2Z. However. The multiplication by 2 map descends to S / 2S and is nonzero!!! Very unlike Z/2Z, the image of the *2 map is nontrivial! This is because the sphere spectrum is very weird and algebra over it is very strange.

Another oddity is that there's levels of how commutative a ring spectrum can be, and commutativity is data not a property. An E_1 ring spectrum is associative, by specifying homotopies you can find it's commutative up to homotopy, E_2, but perhaps not up to higher homotopy. There's infinitely many higher homotopies to specify, so infinitely many degrees of commutativity. The free E_1 spectrum over HFp on one variable is not the same as the free E_2 spectrum over HFp on one variable is not the same as the free E_infinity (commutative) spectrum yadda yadda.

So the algebra here is pretty crazy.

To formalize all of this properly, you need* to work in infinity categories, these let you track all the infinitely many homotopies which are hiding in the background every time I said "up to homotopy". This has been done though, quite successfully, and people are studying this "brave new"/homotopical algebra more and more. About 5 years ago a fields medalist connected this sort of stuff to p-adic hodge theory, whatever that is, which has made quite some buzz.

*This was done before infinity categories, but, the concept of base change from HZ to S was only fully formalized in infinity categories, I think. The vision has been around since the 70s or 80s though. Saying "need" may be controversial.

Maybe I should stop telling people I'm an algebraic topologist and just say I do homotopical algebra. It's truer I think. But less well known. Which is weird because everyone knows about homotopy theory.

I guess the brave new algebra program was only fully realized fairly recently.