#functors

[algebraic-dualist]

Me when someone asks me for an example of functor.

It acts on morphisms by direct images….. (you need the axiom of foundation to know this is well-defined).

[nb-swordk9]

Shit man, this math war is fucked. I just saw a guy draw a commutative diagram and say "one point compactification" or some similar shit, and everyone around him got folded into a 3-sphere and vanished into 4d-space. The camera didn't even go onto him, that's how common shit like this is. My ass is casting ε-δ and quotient spaces. I think I just heard "infinity-groupoid coskeleton tower" two groups over. I gotta get the fuck outta here.

[as-if-and-only-if]

Consider now the Cainian functor C : Grp → Grp given by G ↦ [G, G], which annihilates all abelian groups,

[carmilla-the-dog]

What is the dual of the forgetful functor?

Ooooh my, this is going to be fun.

Ok, so first things first, what do we mean here by dual? Well, duality in category theory is a very loose concept, and one must examine the particular use case before deciding what dual means.

In this post, duality will be given by adjunction. And what is adjunction, you ask? Adjunction is when

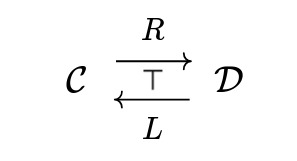
are related by

$$\mathcal{D}(x,Ry)\cong\mathcal{C}(Lx,y),$$

(the isomorphism being natural). And in this case we say that \(R\) is a right adjoint to \(L\) and \(L\) is a left adjoint to \(R\). By Yoneda bullshit, all right adjoints of a functor have to be isomorphic. (dually, the same is true for left adjoints).

THE SECOND THING is that forgetful functor is also a loosely defined concept (https://ncatlab.org/nlab/show/stuff%2C+structure%2C+property). But here I'll be talking about the family of functors of the form

$$U:\mathcal{E}\to\mathbf{Set},$$

in which \(\mathcal{E}\) is a concrete algebraic category like modules, vector spaces, groups or abelian groups. This functor takes an algebraic structure and send it to its underlying set.

Remark. More generally you can take the category of monoids, or the category of algebraic theory, over a category \(\mathcal{C}\) and you have a natural forgetful functor into \(\mathcal{C}\) itself.

OK. So if we want a left adjoint to \(U\), we require that, given a set \(x\) and a algebraic structure \(y\) (which has underlying set \(y\) because fuck you), we have

$$\mathbf{Set}(x,y)\cong\mathcal{E}(Lx,y).$$

That is, algebraic maps

$$\phi:Lx\to y,$$

are completely determined by the map in \(x\):

$$f:x\to y.$$

If you feel like this is familiar, you are not wrong! If you have any formal training in mathematics (and if you don't, I'm so sorry for using jargon and stuff… I can answer any questions after ^^( but I know for a fact that anon has formal training)) then you maybe recognize this from linear algebra.

Indeeeeeeeeed, given any vector spaces \(V\text{ and } W\), a linear map

$$T:V\to W$$

is completely determined by what it does to the basis of \(V\). Even more, if the set \(v\) is as basis for \(V\) (I am completely aware that my notation can cause psychic damage), then every function of sets

$$f:v\to W,$$

determine a linear transformation

$$T:V\to W.$$

AND EVEN FURTHER every linear transformation is obtained in this way. Abstracting again, the left functor \(L\) represents taking a set \(x\) and using it as a basis for a algebraic structure \(Lx\).

As algebraic structures with a basis are called free, the left adjoint of a forgetful functor is called the free functor. :)

If someone guess the name of the right adjoint of the forgetful functor, I'll give them a kiss

[proof-by-intimidation]

I never really understood this business of classes and sets. I get that certain collections cannot be called a set (for instance, the Russell's Paradox). Ok then what exactly are classes? Do they behave like sets? Why should I care if a category is small !!

[adjoint-law]

Varies week by week, but the functor from Sets^op to CLat-∧ taking functions to weakest precondition transformers (conjunctive maps between powersets) is pretty great

Hey what is y'all's favorite functor?

Mine's the fundamental group functor going from Top* to Grp.

[max1461]

there['s a functor from males to females and its called transgenderization and its invertible but im mainly using it on my male mutuals except one of them cause hes the exception to this but my other man mutuals are becoming transgenderized to girls

[futchmoding]

got kitty cat high and stayed up too late playing with numbers on the computer 😵‍💫😵‍💫

[bubbloquacious]

Why yes I am still thinking about graphs as presheaves. Another thing you can do with functors from small categories is think about their limits and colimits. We usually think of limits and colimits as objects of the codomain category, so in this case the limit of a graph-as-functor would be a set. However, we can turn it back into a graph by then applying the diagonal functor Δ from the category of sets to the category of graphs.

Let's think about what this functor does. It maps a set X onto the constant functor from Q^op at X. Such a functor maps every object of Q onto X and every morphism of Q onto the identity function of X. So, the vertex set and the arrow set of Δ(X) are equal, and the source and target functions are the identity. The graph we get consists of one vertex for every element of X and each vertex has a single loop.

A cone under or cocone over a functor F: C -> D is exactly a natural transformation from a constant functor to F or from F to a constant functor, respectively. The limit of F is the terminal object in the category of cones under F, so in addition to the limit object we have a natural transformation from the constant functor at that object to F. Dually for colimits. Natural transformations in Q^hat are graph homomorphisms, so we can do some fun interpretation here.

The limit of a functor with domain Q^op (or Q, as they are isomorphic) is an equalizer. In Set, the equalizer of functions f,g: X -> Y is the set { x ∈ X : f(x) = g(x) } (up to a canonical bijection). It follows that the limit of a graph is exactly the set of arrows of G whose source vertex coincides with their target vertex. The set of all loops of G. Applying Δ to this we get the graph that has a vertex for every loop, and a loop on each of these vertices. The universal cone from this graph to G is the graph homomorphism that maps each loop in this graph onto the corresponding loop in G.

The colimit of a functor from Q^op is a coequalizer (surprise surprise), and in Set the coequalizer of f and g is the quotient set of Y by the smallest equivalence relation ~ such that f(x) ~ g(x) for all x ∈ X. In a graph G we have that Y is the vertex set, X is the arrow set, and f and g are the source and target functions. This means that if two vertices v and w are connected by some arrow, then they will be equivalent under ~. Applying transitivity and symmetry, we find that the equivalence classes of ~ are exactly the connected components of G. The universal cocone over G is the graph homomorphism that maps all vertices in a connected component of G onto the corresponding vertex of the graph-that-has-a-vertex-for-every-connected-component, and all arrows in that connected component onto the unique loop on that vertex.

[didsomeonesaysoup]

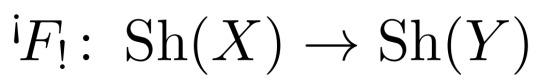
is this how spanish mathematicians notate the direct image w compact support

[trivalentlinks]

their horrible incantations vs our beautiful spells

Once you get to a certain level of advanced maths, you basically become a wizard.

[scalpel-mom-mori]

Ouch

[emeritusterzo]

it's so annoying to be at the point in which no media that is unrelated to my work interests me

not that it's necessarily bad that my brain is wired on the thing I do but. you know. it's a sunday evening why can't my brain let me see anything that doesn't involve functors or long algorithms

[algebraic-dumbass]

Shit man, this algebra war is fucked. I just saw a guy clap his hands together and say "the six functors" or some similar shit, and every chain complex around him got put into a short exact sequence, had their long exact sequence taken out and then got their homology calculated. The camera didn't even go onto him, that's how common shit like this is. My ass is casting lagrange's theorem and degree 2 equations. I think I just heard "power word: operad" two groups over. I gotta get the fuck outta here.

[locally-normal]

Aww come on surely it's not any contravariant functor, surely you need a topos involved. A contravariant functor into sets, now we're talking.

love that "number theory" and "linear algebra" sound like idiot math for babies

[mourning-again-in-america]

I've said this before but now I'm even more certain that I would really like Rust if it actually had a specification