#regular polyhedron

[art-of-mathematics]

In this perspective the icosahedron drawing fits neatly into this hexagon shape.

[muckmagister]

my cuubes:)

[some-teeth-in-a-trench-coat]

One edge is on the x axis and offset from the origin on the y axis by the apothem. The side length allows us to know the exact coordinates of its vertices. We know the interior angle of the vertex figure as well.

We can rotate around the x axis with a vertex as the center in order to find the edge's second face, but how do we find the axis of the next edge to rotate around? Perhaps we can use the interior angle of the face to find the second edge of the vertex and rotate that vector as we do the face in order to follow its movement and define the next axis.

Carry through the loop a "previous axis" (axis a) socket along with the "current axis" (axis b). Initialize axis a as (1,0,0) rotated about the z axis by the interior angle to align with the adjacent edge and initialize axis b as simply (1,0,0). Rotate the face about axis b and let b plug into a. Rotate a about axis b and let the result plug into b. Repeat n-1 times where n is the number of vertices in the vertex figure.

Sure yeah I'll solve my geometry nodes issues lying in bed half awake instead of while actually having the thing in front of me.

[louis-hypo]

Johnson Solids & Unsightly Definitions

Something I am fascinated by, beguiled by, is the Johnson Solid, a special class of 3D polyhedron. If I give you the definition of a Johnson Solid, I will have to mention a number of caveats, and I don’t think that’s a nice way to start this article, so let’s do what mathematicians do best and start with something simpler. Quadrilaterals: 4 walls and a rule A quadrilateral is a shape in two…

[some-teeth-in-a-trench-coat]

Small fire-hydrant-stellated dodecahedron

[dailypolyhedra]

Polyhedron of the Day #126: Mucube

The mucube is a regular skew apeirohedron. Its Bowers-style acronym is muc. It can be constructed from the cubic honeycomb by removing certain square faces. Its Schläfli symbol is {4,6|4}. It does not have an interior or exterior; rather, it divides 3D space into two indistinguishable sections (according to its symmetry group), hence its regularity. Its dual is the muoctahedron.

GIF created by TED-43, CC BY-SA 3.0, https://upload.wikimedia.org/wikipedia/commons/8/8c/Petrie-1.gif.

Image created by Sycamore916, CC BY-SA 4.0, https://upload.wikimedia.org/wikipedia/commons/6/6b/Mucube_external.png.

Suggested by @infinite-planes.

[absolxguardian]

summoned to talk about Daniil's skill cabinet

As PermianTropos said, I wrote a Disco Elysium/Patho crossover fic. When writing it, I went with the conceit that everyone has skills, just part of Harry's brain being messed up is that he's the most aware of his skills and they have the most distinct personalities. A majority of Harry's skills are common in all people, but they can have different personalities. Harry's exclusive skills are Inland Empire, Espirit De Corps, and Shivers. However the drug addiction aspect of electrochemistry is only present in addicts. The short term sort of drug addictions the healers would develop in their extreme circumstances would fall under a different skill, probably Physical Instrument. Which would be the skill telling you about all your stats dropping into danger levels (since the fic relies on Classic's metaphysics specifically, both Healers were in a survival horror game).

Daniil and Atermy both have low emotional intelligence (as I phrased it when writing the fic. Since I've figured out what my empathy autism situation is since then, I'd say that they are just low empathy in the sense that figuring out what people feel just by looking at them doesn't come naturally to them, but their ability to conceptualize what others are thinking is fine), they don't have an Empathy skill and instead rely on Perception to figure out other people's emotions. The exception is with the skill The Binding, which is basically Espirit De Corps crossed with Empathy specifically for the Healers and the Bound (all of them, not there's specifically). Now this doesn't really hold with Quarantine, but when playing Classic it really feels a lot like the bound are more really than generic civilians. So when the Sand Plague was happening and the Healers were part of a Game (the metaphysics of the fic is that both worlds exist beyond the boundaries of their respective games, but that the worlds were created and given structure by those games. People lived entire real for the purpose of making sure an item was in the right place), the regular civilians of the town were subsumed by their roles/classes, except for the Bound. And now all the Healers and Bound have light telepathy with each other.

The other skill I had for Daniil was (Un)Natural Sciences. Which is both scientific reasoning and scientific knowledge. It has the gimmick of preceding its input with either "conclusion", "hypothesis", "inference", or "observation".

If I was writing it these days, I would totally replace Volition with Mania and Apathy. And obviously, one would wax while the other wanes.

Daniil's version of Conceputalization would be less about art and more about his ability to imagine what the world could be and appreciate its wonderousness. This would be the skill that falls in love with the Polyhedron. Since they both chose the Classic Termite ending in my fic, the skill isn't as strong as his ethical values. Although I'm not sure what skill that would be. Seems more like the kind of thing that would be captured in a choice using DE framing.

[homestuckreplay]

hauntingly relaxing basslines to grow/disappearify pumpkins to

(page 818-825)

Jade irradiates a tasty dinner for Bec, leaving it full of ‘nice depleted steak isotopes’ (p.819). I was wondering about the science behind this, and learned that while radioactive decay naturally gives off heat, it’s probably not enough to cook a steak. Radioisotope thermal generators convert the heat of radiation into electricity, and there’s a lot of theory about radioisotopic batteries that could operate similarly to solar cells, but their efficiency is below 2% in laboratory tests.

This got me thinking about Skaia as a perfect conserver of energy – on page 193, Rose expends six units of build grist to construct three Perfectly Generic Objects. On p.261, she deletes them and regains six build grist. Next page, she uses the recovered grist to build a platform extending from John’s house, and finally on p.485 turns that platform back into six grist to build more stairs. In the real world, there is always a loss of energy and raw materials when changing something’s form, and many games model this (for example, an in game item costing 100 gold but only sold back for 50) to discourage players changing their minds. But Sburb explicitly allows for this experimentation, and a similar principle could explain why Jade’s uranium powered devices are so efficient.

Speaking of Jade’s technology, we see her ECLECTIC BASS, which is a kind of triple keytar. It definitely does not need to exist but it is so cool that it does. Jade (via the narrator) is frustratingly vague again with ‘obviously it's too complicated to play it in person like this’, refusing to clarify what ‘in person’ means, but I’d guess it’s a remote controlled hand or several that can play bass remotely without the limitations of human fingers. Possibly controlled through her other invention: the computer.

Instead of a regular desktop, Jade’s LUNCHTOP works through beams of light emitting from small floating polyhedrons, positioning her literally within the digital space. Amidst floating clouds, extra pixels and jpeg debris, and spinning chromosomes of light is a cool dragon as a wallpaper, icons for Pesterchum, Echidna (probably a browser) and Fresh Jamz!, which has an icon of a musical note over a jar of fruit jam. Is Jade a composer too? Did she write her own hauntingly relaxing bassline that caused the plants to grow? Is this a hobby she and Dave have in common?

Jade’s hauntingly relaxing bassline (p.822) is a great companion piece to WV: Ascend, showing Jade’s island in its current state as opposed to in extended timelapse. The house, with its orbs atop spires, is clearly modeled on a now broken part of the frog statue, and was designed to fit in with the existing architecture and shape of the island (it forms a peak to the small second mountain). The house was built for aesthetics, not function, and is primarily vertical especially towards the top. No wonder Jade ‘almost never use[s] the stairs’.

Putting the timeline together, we know that Jade is about to message John at 16:34 his time (p.110), but they don’t actually talk until 17:25 (p.169), almost an hour later, at which point there’s an explosion outside Jade’s house. In page 822’s animation, an aeroplane flies low over Jade’s island and drops off a delivery (a blue package – something from John, perhaps?). This must be an uncommonly loud sound in a remote area. Depending on how this flash syncs with the timeline, this may or may not be the ‘explosion’. Either way, Jade will be on the computer during the explosion, and as her likely homemade computer involves complete immersion in the digital surroundings, I can believe that she would interpret a noise from her computer as something that’s happening outside her house.

We’ve explored Jade’s room, interests, musical talents, fetch modus, and now computer. In all of these she’s been set up differently to her friends. We have yet to explore the rest of her house and its surroundings (featuring, presumably, strange themed decor, a large humanoid doll and a piece of visual art Jade has created) and to meet Jade’s grandfather, witnessing her attempts to evade and eventually strife with him.

> Jade: Open Echidna and watch your favorite Squiddles episode.

[zkylearnstherope]

AvGeometry [An Analysis]

Disclaimer: This is a very short Analysis for Animation vs. Geometry by Alan Becker. I am not a geometer, (according to Merriam-Webster, a person who specializes in geometry) this purely for fun.

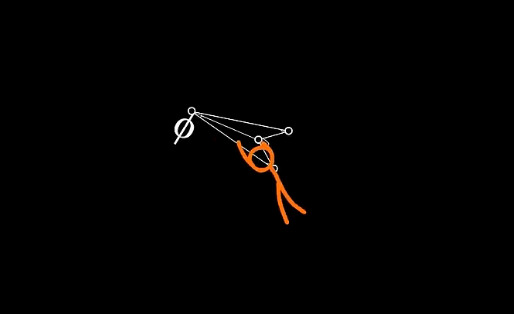
First of all, I will NOT explain everything in the video. I will just focus on answering a few questions to which I found the answer for. I also have some conclusions at the end.

I will leave the in-depth explanations of everything to those YouTubers. Also, I have linked my sources using hyperlinks.

So, let's get into it- shall we?

Let's start with-

Which version of TSC is the main character for this one?

If you read my AvPhysics Analysis, you would realize that I named the TSC with the cowboy hat TSC_0 of Universe D.

Since the start of the AvGeometry video, I immediately realized that this is NOT the same guy from AvMath, since he didn't show signs of aggressiveness with phi Φ.

He's more curious versus the guy in AvMath who attacked Euler's Identity immediately. This is also the same guy who spawned in AvPhysics, TSC_0.

I think this MC is a TSC from a different Universe. I will call him TSC_0 of the AvG Universe.

Now you might ask yourself, why did I gave him the 0 designation?

Because the video ended with another TSC knocking at the point.

Now, you might argue, that this is not a perfect loop because there is a line below the point. While the start of the video, doesn't have that line.

You are right. Again, if you read my AvPhysics Analysis, I said that the TSCs in there are not stuck in a time loop.

It's just an infinite cycle that happens to different versions of them. Everyone spends only a short amount of time inside the singularity.

So the next TSC to arrive will not be TSC_0 but TSC_1.

How did TSC and phi Φ beat that Boss?

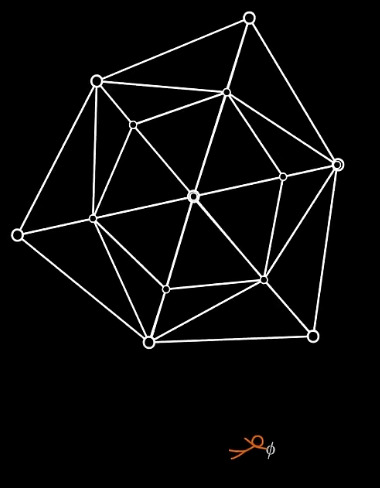
To start, let's define a few things. Click the hyperlinks to view my source.

Polyhedron - is any three-dimensional figure with flat faces that are polygons. They intersect at straight, linear edges. The edges themselves intersect at points called vertices.

Tetrakis Hexahedron - It is a Catalan Solid with 24 isosceles triangle faces and 14 vertices. It is the d24 die. It is also a 3-dimensional polyhedron, not 4D.

Now, first of all, the Boss is not 4D. It is two Tetrakis Hexahedrons overlapping each other and rotates at different speeds.

Platonic Solids - a convex polyhedron that is regular, in the sense of a regular polygon. These are also 3D shapes. There are Five Platonic Solids

Note that this not the original image from the website, but I rearranged the rows to highlight my points. I also added the dice names, incase you're more familiar with DnD.

In fighting the Boss, TSC and phi Φ started with lines that has 2 vertices or points. Then they slowly moved to the Platonic Solids, eventually defeating the Boss using a dodecahedron.

The Boss had 14 vertices vs the dodecahedron that had 20.

Now, I can't really say why more vertices is superior. It could be structural integrity, or the idea that the universe's topology and shape, references the shape of dodecahedron.

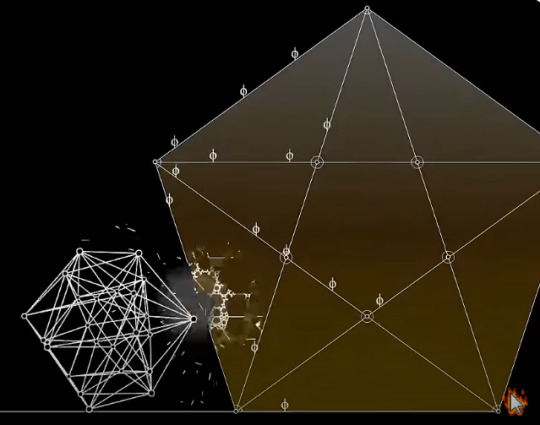
Or, that the golden ratio is the length from the vertex to the center of the dodecahedron, and is also the ratio of the diagonal of the pentagonal face as demonstrated in the video.

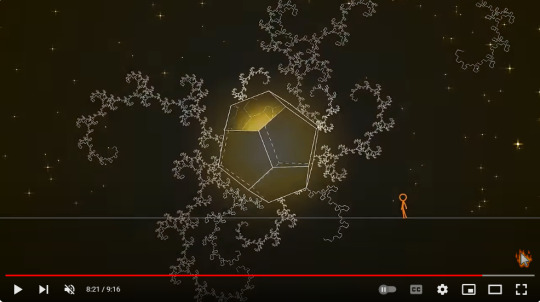
The Hyperdodecahedron and Singularity

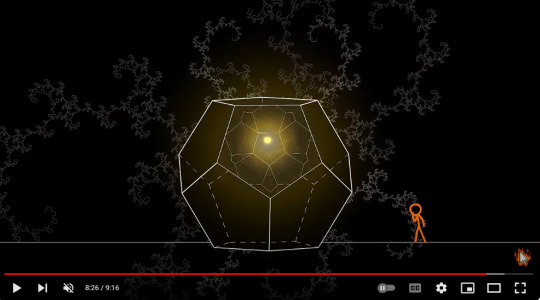
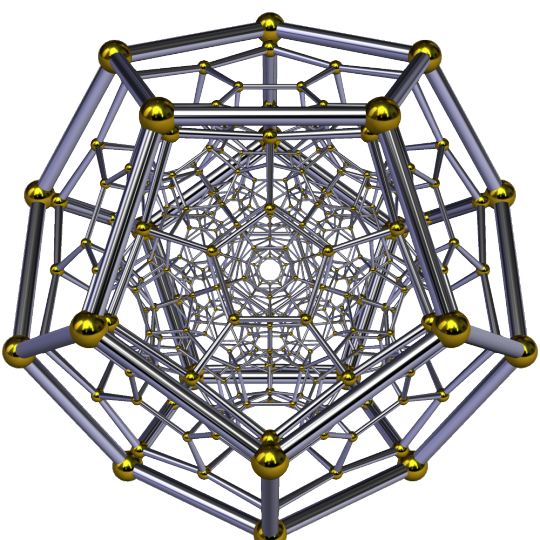
Hyperdodecahedron aka 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid.) It is the 4-dimensional analogue of the regular dodecahedron. It has 720 pentagonal faces and 600 vertices.

It's basically 4D dodecahedron.

According to ChatGPT, in higher-dimensional geometry and theoretical physics, singularities often refer to points or regions where certain physical quantities become infinite or undefined.

Here's how I see it. If that yellow dot is indeed a singularity, the only explanation I could come up with, is at some point, the hyperdodecahedron's infinite insides would shrink to a single point in its 4-dimensional space.

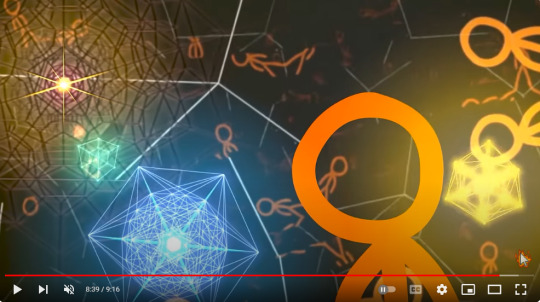
Fractals

Now I think these are fractals by I cannot be sure. Also, I couldn't get a definite answer as to how fractals would be relevant to singularities.

What I got from ChatGPT were related to the event horizon instead.

That irregularities of the event horizon might have fractal patterns or exhibit fractal characteristics in its shape when examined at a different (smaller) scale.

The visual and structural complexity of the event horizon evoke fractal-like qualities.

Now, this Analysis is a lot shorter, and also inconclusive. I did try my best. My brain is now mush.

[art-of-mathematics]

Icosahedron

Today I improved the thread connections.

[xyymath]

Fun with Geometry: Shapes You Didn’t Know You Needed

Geometry is far more than the basic shapes we learn in high school; it’s a world brimming with bizarre and captivating figures that push the boundaries of our imagination.

1. The Hypercube (Tesseract)

The hypercube, or tesseract, is the 4-dimensional analog of the cube. While we live in a 3-dimensional world, the concept of a fourth dimension has fascinated mathematicians and artists alike. A hypercube consists of 16 vertices, 32 edges, and 24 square faces, each one being a 3D cube in a higher-dimensional space.

In the real world, hypercubes don’t physically exist, but they serve as key tools in higher-dimensional geometry and theoretical physics. Think of them as a "spatial metaphor" for the kinds of higher-dimensional spaces used in string theory or machine learning. Mathematicians use them to explore the complex relationships between different dimensions. The tesseract also shows up in pop culture, notably in the movie Interstellar, where it represents the connection between time and space.

2. The Pentagon (Not Just in Architecture)

The regular pentagon (five sides of equal length and five equal angles) has a fascinating relationship with the golden ratio. If you draw diagonals within a regular pentagon, they intersect in such a way that the ratio of the longer segment to the shorter segment is the golden ratio (ϕ ≈ 1.618). This means that pentagons are not just aesthetically pleasing in architecture, they have deep connections to mathematical beauty.

In nature, sunflowers and pine cones exhibit pentagonal symmetry. The arrangement of seeds in the flower follows a Fibonacci spiral, and the spirals are governed by golden angle, which closely ties to the pentagon’s unique proportions.

3. The Dodecahedron

A dodecahedron is a regular polyhedron made up of 12 pentagonal faces, 30 edges, and 20 vertices. It is one of Platonic solids, which means each face is identical, and the same number of faces meet at each vertex. This geometric shape is not just abstract; it appears in various 3D modeling applications and is used in architecture, like in the London 2012 Olympic torch design.

What’s particularly fascinating is its appearance in pop culture. The dodecahedron serves as a crucial symbol in the book and movie adaptation of The Hitchhiker's Guide to the Galaxy (the "Meaning of Life" puzzle) and is part of a well-loved mathematical riddle known as the "dodecahedron paradox."

4. The Möbius Strip

The Möbius strip is a non-orientable surface with only one side and one edge, and it is a staple of topological geometry. The twist in a Möbius strip turns the concept of inside and outside on its head. Take a strip of paper, give it a half twist, and then join the ends. The result is a surface where you can trace your finger along its edge endlessly, without ever lifting it or reaching a boundary.

Mathematically, the Möbius strip is a symbol of non-orientability and plays a crucial role in knot theory and the study of 3-manifolds. The Möbius strip also sneaks its way into art and architecture, often used as a visual symbol of infinity or paradox in both visual and sculptural art forms.

5. The Klein Bottle

Another topological marvel is the Klein bottle, a non-orientable surface with no boundary. Unlike the Möbius strip, which has only one side, the Klein bottle essentially has a single continuous surface where both sides are connected in a higher-dimensional space. If you attempted to build one in 3D, it would have to intersect itself. However, it can be imagined in 4-dimensional space.

The Klein bottle's properties make it a critical concept in topology, with applications in advanced physics and geometry, particularly when studying the shape of the universe and space-time curvature.

6. The Truncated Icosahedron (Football Shape)

Have you ever wondered about the shape of a soccer ball? It’s a truncated icosahedron. This polyhedron has 12 black pentagonal faces and 20 white hexagonal faces, a geometric structure that makes it easy to create spherical objects with flat faces. The truncated icosahedron is a close-packed shape and appears in carbon molecule structures such as buckyballs (or fullerenes) used in nanotechnology.

7. The Archimedean Solids

The Archimedean solids are a set of 13 convex polyhedra, where each face is a regular polygon and the same number of faces meet at each vertex. These shapes, such as the icosahedron (20 faces) and octahedron (8 faces), pop up in all kinds of real-world applications, like in architecture and crystallography. In fact, many molecular structures (like the shape of viruses) reflect these highly symmetrical solids.

Next time you look at a soccer ball, admire a piece of modern art, or even browse through a movie with some mind-bending geometry, remember: the world is built on shapes you never knew you needed, and math is at the heart of them all.

[ninvic-rbs]

2, 10 & 17 for the ask game <3

2. Wildest theory you’d defend?

Already answered!

10. What do you think the Changeling’s story was really about?

OUGH this is a tough one😭 okay here's what I think. All of pathologic is, in a way, about sacrifice right? or about its inevitability? the way i see it, pathologic presents you with a question (though i still can't really say what it is) and lets you approach that question from two different angles (the bachelor and the haruspex) arriving at two different conclusions.

The changeling route feels a bit like a victory lap, in that you get a bunch of lore about characters that you didn't have access to as the other two healers. I think I'd say it's more about human sacrifice, like in a more personal way.

Daniil manages stuff in big numbers right? Like setting quarantines and the morgue and whatnot, and then just investigating. Artemy basically spends the whole game searching for a panacea, and in the second half deals more with the kin and his place in it. But Clara has to drag herself out of the dirt, she goes personally to interview people, she gets the worst of both worlds. The townfolk don't trust her and the kin want nothing to do with her. She learns by touch. To get her ending, you leave both the polyhedron and the town standing, but the sacrifice to do so is a lot bigger, in a different way. Not to mention that, to even play as Clara, you have to have beat the game once already, which we all know is not an easy feat.

I'd say the sacrifices you have to make in the utopian and termite endings are more impersonal, and then the changeling route comes at you out of nowhere on day 10 with having to sacrifice most of your bound, even though at this point you've been wih these characters for at least a couple dozen hours.

I guess right now I'd say the changeling route is about the sacrifices that regular, day to day people have to make in order for things to work properly, and how those often are forgotten when talking about societal issues in broad, abstract ways. I'm going with that [*answer might change at any point]

17. Which character do you see yourself befriending IRL?

Honestly as much as i love them, most of the cast seems like they'd be insufferable irl!🥰✨️ I'm gonna go with grace bc i'd love to offer her a warm meal and a bed

pathologic asks

[notreallyherehahaha]

A Polyhedron Featuring Twenty Regular Enneagons and Sixty Kites

I made this using Stella 4d, which you can try for free at this website.

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 3

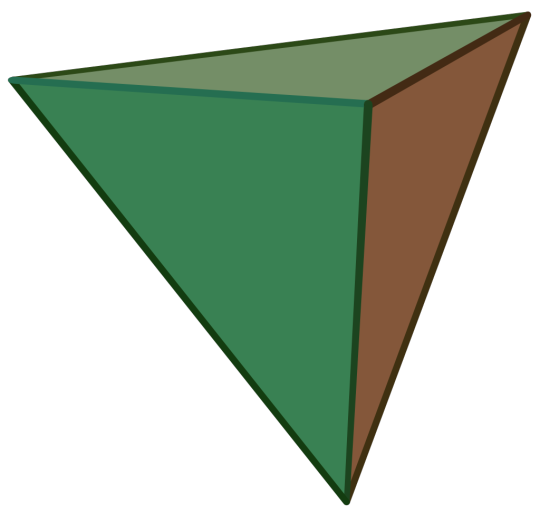
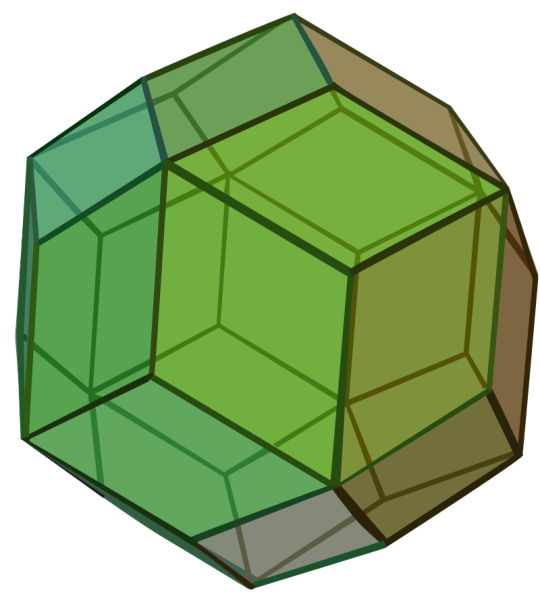
Propaganda

Regular Tetrahedron:

Also called the Triangular Pyramid

Platonic Solid

Regular

Dual of the Regular Tetrahedron

It has 4 regular triangular faces, 6 edges, and 4 vertices.

Self-Dual

Image Credit: Cyp

Rhombic Triacontahedron:

Also called the Triacontahedron

Catalan Solid

Dual of a quasiregular polyhedron

Dual of the Icosidodecahedron

It has 30 rhombic faces, 62 edges, and 32 vertices of two types.

One of the 9 edge-transitive convex polyhedra along with the 5 Platonic Solids, the 2 Quasiregular Convex Polyhedra, and the Rhombic Dodecahedron.

Image Credit: Maxim Razin based on Cyp

[veiledinviolet]

Spherical hex¹ grid based on a class II Goldberg polyhedron, generated using the inverse of Lee's conformal projection of the sphere upon a regular icosahedron [1, pp. 62–65]. When the camera is close to the surface, stereographic projection is applied to flatten the surface.

¹ All faces are hexagonal except for twelve pentagons required by the Euler characteristic of the 2-sphere.

[1] L.P. Lee, “Conformal Projections Based on Elliptic Function”, url: https://archive.org/details/conformalproject0000leel