#sin(π/2-x)

[desmos-calculator]

y'know, one of the goofiest things I've learnt from the desmos community is that { } with nothing inside equals 1

but that's not just it, you can also add { }s

and it functions just the same as adding 2 1s

but therein lies the funniest part, that you can perform almost any function on it, from minus

to exponents

to even factorials!

and lists too!!!

you can even compare solutions of { }s in { }s

there's almost no restrictions, if you can do it with numbers, you can do it with { }

and this leads me to what I've seen a lot of people calling "desmosfuck" after the infamous programming language brainfuck, and it restricts you by not allowing any letters and no numbers, that includes sin, log, x, y and all the others. The only thing you can make out of { }s are points and numbers though, but thankfully that's usually enough to make a bunch of stuff.

like, if you need π, just use (-0.5)!^2

you need e? you already have π and i, just use e^(iπ)=-1 and rearrange it to e=-1^(1/(iπ)) and get -1^((π^-1)(i^-1))

want phi? sure, just use it's surd representation of (1+sqrt(5))/2

okay, but what if you really wanna do functions? well, if you're desperate, you can sorta do that, you just gotta use a concentration of points.

cos(x) and sin(x)? use the identities

cos seems easier

and x just has to be a dense list of numbers

now that we have x, let us... REWRITE!

that's dense... buuuut, it does the job as soon as we add the x part to the x coordinate!

absolute insanity

you can also get sin by subtracting x by half of pi

awesome

here's tan, btw

go play around with it yourself! it's very silly

[tonycries]

∏_{j=1}^∞ cos(x/2j) = ∏_{j=1}^∞ [(1/2) * (cos(x/(2j-1)) + cos(x/(2j+1)))]

= ∏_{j=1}^∞ [1/2 * cos(x/(2j-1))] * ∏_{j=1}^∞ [1/2 * cos(x/(2j+1))]

= (1/2)^∞ * cos(x/1) * cos(x/3) * cos(x/5) *

∫_{0}^{π/2} x * ∏_{j=1}^∞ cos(x/2j) dx

= ∫_{0}^{π/2} x * (1/2)^∞ * cos(x/1) * cos(x/3) * cos(x/5) * ... dx

= (1/2)^∞ * ∫_{0}^{π/2} x * cos(x/1) * cos(x/3) * cos(x/5) * ... dx

cos(x/1) * cos(x/3) * cos(x/5) * ... = (1/2) * (sin(x) + sin(3x)/3 + sin(5x)/5 + ...)

∫_{0}^{π/2} x * cos(x/1) * cos(x/3) * cos(x/5) * ... dx

= (1/2)^∞ * ∫_{0}^{π/2} x * (sin(x) + sin(3x)/3 + sin(5x)/5 + ...) dx

= (1/2)^∞ * [(-x*cos(x))/1 + (1/3)*x*cos(3x) - (1/5)*x*cos(5x) + ...]_{0}^{π/2}

= (1/2)^∞ * [(-π/2)*cos(π/2)/1 + (1/3)*(π/2)*cos(3*(π/2)) - (1/5)*(π/2)*cos(5*(π/2)) + ...]

= (1/2)^∞ * [(π/2)/3 - (π/2)/5 + (π/2)/7 - ...]

= (1/2)^∞ * π/4 * [1/1 - 1/3 + 1/5 - ...]

1 - 1/3 + 1/5 - 1/7 + ... = π/4

Therefore,

∫_{0}^{π/2} x * ∏_{j=1}^∞ cos(x/2j) dx

= (1/2)^∞ * π/4

= 0

[z00lea]

a train travels at 37 mph and will arrive at the station in 30 minutes a second train travels 19 kph and will arrive at the station in 45 minutes there is a boat speeding through dimensions at 3 inches per hour and will plop into a pile of meat at the pork chop factory in 33 minutes which of these are the largest and what burger to gallon ratio are they

∏_{j=1}^∞ cos(x/2j) = ∏_{j=1}^∞ [(1/2) * (cos(x/(2j-1)) + cos(x/(2j+1)))]

= ∏_{j=1}^∞ [1/2 * cos(x/(2j-1))] * ∏_{j=1}^∞ [1/2 * cos(x/(2j+1))]

= (1/2)^∞ * cos(x/1) * cos(x/3) * cos(x/5) * ...

Now we can substitute this expression into the integral:

∫_{0}^{π/2} x * ∏_{j=1}^∞ cos(x/2j) dx

= ∫_{0}^{π/2} x * (1/2)^∞ * cos(x/1) * cos(x/3) * cos(x/5) * ... dx

= (1/2)^∞ * ∫_{0}^{π/2} x * cos(x/1) * cos(x/3) * cos(x/5) * ... dx

At this point, we can use the product-to-sum formula to convert the product of cosines to a sum of sines:

cos(x/1) * cos(x/3) * cos(x/5) * ... = (1/2) * (sin(x) + sin(3x)/3 + sin(5x)/5 + ...)

Therefore,

∫_{0}^{π/2} x * cos(x/1) * cos(x/3) * cos(x/5) * ... dx

= (1/2)^∞ * ∫_{0}^{π/2} x * (sin(x) + sin(3x)/3 + sin(5x)/5 + ...) dx

= (1/2)^∞ * [(-x*cos(x))/1 + (1/3)*x*cos(3x) - (1/5)*x*cos(5x) + ...]_{0}^{π/2}

= (1/2)^∞ * [(-π/2)*cos(π/2)/1 + (1/3)*(π/2)*cos(3*(π/2)) - (1/5)*(π/2)*cos(5*(π/2)) + ...]

= (1/2)^∞ * [(π/2)/3 - (π/2)/5 + (π/2)/7 - ...]

= (1/2)^∞ * π/4 * [1/1 - 1/3 + 1/5 - ...]

Now we recognize the expression in brackets as the Leibniz formula for π/4:

1 - 1/3 + 1/5 - 1/7 + ... = π/4

Therefore,

∫_{0}^{π/2} x * ∏_{j=1}^∞ cos(x/2j) dx

= (1/2)^∞ * π/4

= 0

[zoropookie]

hi, I'm attracted to my crush Heizou like the earth is attracted to the sun— with a large force inversely proportional to the distance squared. He's the sin(90) 4 me. If we we're to be convertices, i wanna be the second convertex. to assure you that at the end of the line, i'll be there waiting for him. these formulas describe how much x²-1, if the value of x is 12. sin (π/2 – A) = cos A & cos (π/2 – A) = sin A

sin (π/2 + A) = cos A & cos (π/2 + A) = – sin Asin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A sin (π – A) = sin A & cos (π – A) = – cos A sin (π + A) = – sin A & cos (π + A) = – cos A sin (2π – A) = – sin A & cos (2π – A) = cos A sin (2π + A) = sin A & cos (2π + A) = cos A. before seeing him, my heart is a nul set, but when a vector of magnitude from his eyes at a deviation of theta radians made a tangent to my heart, it differentiated. whenever I see him, it was like, I was electrocuted with an amount of 200-1700 volts of electricity. my love for him is like the derivative of e^x, it remains constant and never change. my baby, 1+tan2A = sec2A sec2A – 1 = tan2A (1/cos2A) -1 = tan2A. putting the value of cos A = ⅘.

(5/4)2 – 1 = tan2 A tan2A = 9/16 tan A = 3/4 (sin30° + cos30°) – (sin 60° + cos60°)

= ½ + √3/2 – √3/2 – ½ = 0 If cos A = 4/5, then tan A = Cos A = ⅘. my love for him is a quadratic equation with real roots, which only he can solve by making good binary relation with me. the cosine of my love for you extends to infinity. Baby, simplify 4x³+3x²+3x-1 where x=3. and he'll know what my heart says. He is an essential to me as an element to a set. the geometry of my life revolves around his acute personality. sin(2x) = 2sin(x) • cos(x) = [2tan x/(1+tan2 x)]cos(2x) = cos2(x)–sin2(x) = [(1-tan2 x)/(1+tan2 x)] cos(2x) = 2cos2(x)−1 = 1–2sin2(x)

tan(2x) = [2tan(x)]/ [1−tan2(x)] sec (2x) = sec2 x/(2-sec2 x) csc (2x) = (sec x. csc x)/2. my baby, when he solves this equation for "i" .

hiiii pookie how are you? i hope you're doing well!!!! kiss kiss/p

i'm not sure if this is a copypasta or not, but if it's not, that's extremely impressive and you're super smart hahahahahaha!!!

i'm doing as good as i can lol hopefully you slept well, i'm answering this after ur regular hours

[bad-dagon]

riemann spheres as a fundamental type, pt.1 basics

ive been thinking on and off about riemann spheres for a while now, a couple weeks really, and so far i think there's some utility to them as a building block of a type system of some kind for a joke/toy computer language

background: riemann spheres are a neat tool in complex analysis where we imagine a sphere whose equator intersects the complex plane, and every number on the complex plane is representable by a point on the sphere such that a line is projected from the north pole and through that point onto the complex plane. naturally, this means that the north pole is P(∞) and the south pole is P(0). see below how that would look like with other unit points of the complex numbers

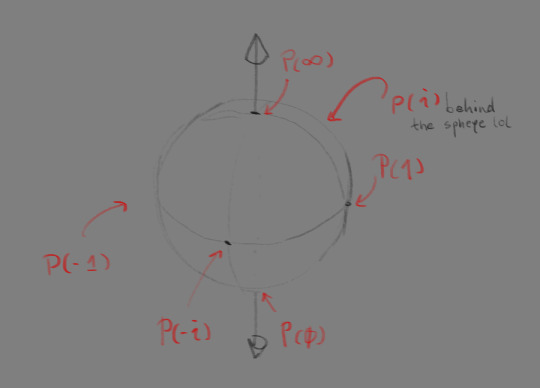
a neat thing the riemann sphere allows us is to define meaningful division by zero so now z/0 = ∞ clean and simple! and also its inverse, z/∞ = 0 is well behaved as well. this simplifies doing complex analysis but stereographic projection is an absolute bitch to work with turns out, and doing arithmetic on points on the sphere is a mess because it's not a linear mapping (it's continuous though so that's fine)

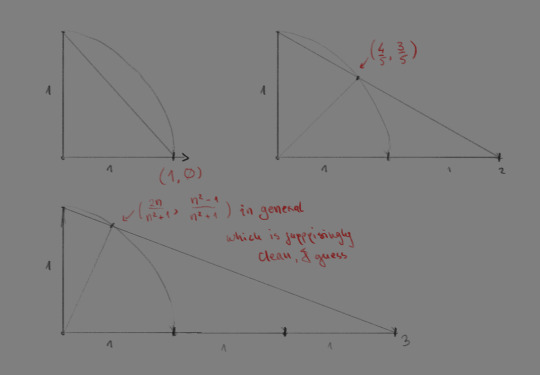
if we're dealing with ONLY real numbers in relation to a circular slice of the riemann sphere, it already starts looking like a mess; for any number n∈R its projective cognate on the circle is located at (2n/n²+1, n²-1/n²+1). on the real riemann sphere though? zoo wee mamma

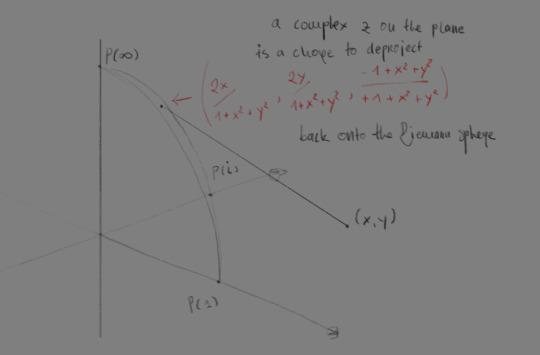
an arbitrary z∈C, represented as a point (x,y) on the complex plane, has to walk through a rather ugly mapping (related to the previous one) to find its point on the sphere; more accurately, given the coordinates (x,y) of the point on the plane, the point on the sphere is located at (2x/1+x²+y², 2y/1+x²+y², -1+x²+y²/1+x²+y²), which is godawful in spherical-to-polar coordinate terms, this is much simpler; for a polar pair (r,θ) the point on the unit sphere representing it is (φ,ξ) = (2*arctg 1/r, θ); and conversely projecting from the riemann sphere is also dead simple, given the zenith-azimuth pair (φ,ξ), (r,θ) = (ctg φ/2, ξ). of course, translating from polar to real coordinates is ALSO dead simple; x = r * cos θ, y = r * sin θ. if a computer system were to store complex numbers (or any coordinate on a 2d plane really), it makes sense to store them in terms of spherical coordinates of a riemann sphere, since this makes infinity well-behaved as a unit (zenith = 0, azimuth = literally who gives a fuck) and is surprisingly efficient. knowing that the zenith is ∈[0,π] and azimuth ∈[0, 2π] can allow for some formidably dumb optimisations that can save on space and ensure granularity. compared to storing them as 2d cartesian or polar coordinates, this provides the benefit of having neither number be larger than like 6.3, so an underlying/backing type that can offer great precision in this small range would be more efficient numerically than, say, floating points which have insane baggage and gaps

or iunno i'll look into that one a bit later, i'm just kind of furious right now that i rederived stereographic projection on my own when the formulas were right fucking there if id only just googled for them

[jakevor]

Hey mathblr. Today I don't have Wrong Math, but I do have a question. I was trying to find the real roots of (-1)^x. And I ended up with the formula:

n/(4k+1) where nεZ and kεZ.

I know this can make all natural powers for k=0 and it can make no powers of the type 1/(2k). But I have trouble proving, if it can be proven, that this formula can produce all the powers of 1/(2k+1) so that I can have (-1)^1/3, (-1)^1/7 and so on.

If anyone has an idea of how to prove this please help.

I will leave how I found that formula after the break.

(-1)^x=

i^2x=

exp(2(2kπ+π/2xi))=

cos(4kπ+πx)+i*sin(4kπ+πx)

For (-1)^x to have real roots the sin must be zero.

sin(4kπ+πx)=0

4kπ+πx=nπ =>

(4k+1)x=n =>

x=n/(4k+1).

[jadagul]

So i^2 is -1 (by definition), and i^3 is -i (-1 * i), and i^4 is 1 (if i*i is -1 then i*-1 is 1), and i^5 is i (1 * i), and it continues to loop from there. But how do things work for non-integer exponents? It's easy to say, of i^1.5, that it multiplied by i^0.5 is -1; but that doesn't tell us what it itself is. Do we just call it 'i^1.5' and leave it at that? Or is there some trick I'm missing that'll let us pin it down as a more traditional real or complex number?

Yeah, there's a trick; it's just dumb.

We didn't go into this in the post (I even mentioned the not-going-into-it!) but complex exponentiation works really well with e as the base, because e^(ix) = cos(x) + i sin(x). And in particular that means e^(i π/2) = i.

So if we want to compute i^(1.5) then that's e^(i π/2 * 1.5) = e^(i 3 π /4) = cos(3π/4) + i sin(3π/4) = -sqrt(2)/2 + i sqrt(2)/2.

In general if you exponentiate a complex number, you regular-exponentiate the modulus, and you multiply the angle from the positive x-axis by the exponent as well. So in your case, i has modulus 1 and angle 90 degrees, so we get the output that has modulus 1 and angle 135 degrees.

[jarviscodinghub]

Probability & Statistics for EECS Homework 07 Solved

1. Let F(x) = 2 π sin−1 ( √x), for 0 < x < 1, and let F(x) = 0 for x ≤ 0 and F(x) = 1 for x ≥ 1. (a) Check that F is a valid CDF, and find the corresponding PDF f. (b) Explain how it is possible for f to be a valid PDF even though f(x) goes to ∞ as x approaches 0 and as x approaches 1. 2. Let F be a CDF which is continuous and strictly increasing. Let µ be the mean of the distribution. The…

[pr1v8-memo]

問16

(1) 問題文に従って作図すると,OP↑=(cos(π-t),sin(π-t))=(-cost,sint)であることは直ちに分かる.また,t=0の時P=Qであり,tをここからほんの少しだけ動かしてみると,PQ↑はPH↑/|PH↑|を反時計回りに角度tだけ回転させた大きさtのベクトルだと分かる.PH↑/|PH↑|=(cos(-π/2),sin(-π/2))と表せるから,つまり,PQ↑=t(cos(t-π/2),sin(t-π/2))=t(sint,-cost)となる.一般に図形の回転は複素平面で考えたほうが便利であるが,実平面でも向きを変えたいベクトルを極座標で表して,偏角を加減すれば回転を表すことが出来る.以上より,OQ↑=(tsint-cost,sint-tcost)が求まる.また,Qのy座標についてdy/dt=tsintより, 0≦t≦πにおいてy(t)は増加する.

(2) 一般にf(x)×{三角関数or指数関数}という項を含む関数はいくら微分してもこの項は消えてくれない.微分係数の正負を求めたくても超越方程式になり,代数的に解くことが出来ないことが多い.今回f(t)=tsint-costは,f'(t)=tcost+2sintとなりこの導関数の零点はおそらく代数的には解けない.そこでとりあえず関数の積の形に変形して,正負だけは判断できるようにしたい.

f'(t)=cos(t){t+2tant}において,0≦t≦π/2の区間ではcos(t)>0, t+2tant>0よりf(t)は増加.π/2<t≦πにおいては,cos(t)<0, tとtantは増加.以下,g(t)=t+2tantとおいて,π/2<t≦πにおけるgの零点の位置を把握したい.

g(4π/6)=2π/3-2√3=(2/3)(π-3√3)<0 g(5π/6) =5π/6-2tan(π/6) >5π/6-2tan(π/4)=5π/6-2=(1/6){5π-12}>(1/6)(15-12)>0 gは単調増加するから, 区間(π/2,π]でg(t)=0を満たすような点αがただ一つ存在し,α∊(4π/6,5π/6)ということがわかる.f'(π/2)>0より,[0,α)でf'(t)>0, (α,π]でf(t)<0となり,t=α∊(4π/6,5π/6)でf(t)は最大値を取る. (3) (2)の議論より,曲線の概形を描くことが出来る.y座標に対して一意にx座標が定まるため求めたい部分S=∫[0,π]x+1 dyと表せる. S=π+∫[0,π]tsint-cost dy, dy/dx=tsint, y=0→π, t=0→πより, S=π+∫[0,π](tsint-cost)tsint dtこの計算は面倒なだけなので割愛する.

[messiah007godfather]

30AD Crucifixion 7-9 April

1986 Born New Moon 8 April

2023 Easter 7-9 April

Age 37 × 18 ☰ = 666 ✡️

2024 X Solar Eclipse 8 April

2031 End of Tribulation 8 April

Ronaldo 5 February 1985

Sharman 8 April 1986

Messi 24 June 1987

Messianic Christ

ISIS Mary

RA Sharman

EL Elohim

Barnsley = Bethlehem

London = Babylon

______________________________

The three lines symbol ☰ has been found in cave paintings dating back to over 30,000 years ago. The three lines symbol ☰ was created by shamans or medicine_ men as a way to connect with the spirit world.

The three lines symbol ☰ represents a deep spiritual connection to the natural world and the cycles of life.

These lines ☰ represent Shiva’s threefold power of will, knowledge, and action. The Tripuṇḍra described in this and other Shaiva texts also symbolizes Shiva’s trident and the divine triad of Brahmā, Vishnu, and Shiva.

_______________________________

Isaiah 53

Who hath believed our report? and to whom is the arm ☰ of the Lord revealed?

But He was wounded for our transgressions, He was bruised for our iniquities; The chastisement for our peace was upon Him, And by His stripes ☰ we are healed.

Phi Phi ☰

John Left arm Philip Right arm

Ko Phangan Top Hill Resort

_______________________________

Philip = Phi ϕ Pi π

Philip occurs 38 times

New Testament

Philip David Stephen Sharman;

Phi Phi Leh Pai Thailand

India Nepal Asia

Shiva Parvati Sati

Mahadeva Maheshvara Shaivism

Siddartha Therevada Vippasana

Satan Devil End Times

Isa Messiah Islam

Israel 🇮🇱 Palestine 🇵🇸 Iran 🇮🇷

Reptilian Nephilim Aliens

Amen An Ra

Philippians Philistines

Phi Phi ☰

Philip - life path (7/9) 8-Apr-1986

Phichaya - path (4/8) 9-Feb-1982

Ganesha Born 22 Aug 2007

Ganesha Chaturthi falls between;

22 Aug and 20 Sep

22 Aug 2020 - Ganesha Chaturthi

Kartikeya Born 30/31 Oct 2014

Skanda Shasti falls in Oct/Nov

30 Oct 2022 - Skanda Shasti

30/31 Oct 2024 - Kali Chaudas, Diwali

Phichaya Gail/Kali

Sati transformed as Kali went to the sacrifice and split herself into two entities. One real but invisible & another just Chhaya (shadow or clone). Chhaya Sati destroyed the sacred event by jumping into the sacrificial fire, while the "real" Sati is reborn as Parvati.

Lord Shiva

1. All inclusive

2. In touch with feminine

3. Destroys dance floors

4. Always intoxicated but ascetic

5. Ultimate outlaw

6. God of wild contrasts

_______________________________

Saturn Governs - 8 17 26

Wigan 8 17 Sheffield

26 years ago (1998-2024)

7 = Foundation of gods word

8 = New beginning [Shiva]

9 = Divine completeness

17 = Overcoming the enemy

[Unlucky ♈️]

18 = Bondage

19 = Gods perfect order for judgement

21 = Great wickedness of rebellion and sin

25 = Grace upon grace

26 = YHWH

37 = King David 37 Elite warriors

38 = ?

44 = Child [God chosen 44]

Earthly Ministry

69 = Pi π - [Pai]

70 = Completes Bible prophecy

[Philip = 70]

77 = Phi ϕ

86 = Elohim

666 = Star of David ✡️ Hexagram

30AD: Crucifixion 7-9 April

1986: Born 8 April New Moon;

Buddha Birthday

Phichaya 9 February;

Chinese New Moon.

2003: Age (17) Shoulder Injury

2005: Phi Phi ☰ Curse Age (19)

2012: Sectioned 21 December;

Mayan End Date Age (26).

2017: US Solar Eclipse 21 August

26 Nov - Captured Satan in Soul

2022: [Messi'ah]

Diwali 24 October Mary/Robert

2023: Easter 7-9 April

Age (37) x 18 ☰ = 666 ✡️

Rosalind 14 October;

Ring of Fire Eclipse.

Mary Age 77 = Phi ϕ

2024: X Solar Eclipse 8 April Age (38)

111 Eclipse Centre 11 January

Phichaya 9 February;

Chinese New Moon.

Philip 8 April Hebrew New Moon

Mary 24 October;

Tabanacles 8th day.

Tony 30/31 October;

Kali Chaudas, Diwali.

2025: 21 October Michael Diwali

2030: Age (44) + 25 ☰ = 69 = Pi π

Agenda 2030

2031: April 8 End of Tribulation

☰ Kali Sati Mohini

111 UN 🇺🇳

❤️ Messiah ❤️

[subhasapco123]

Understanding Inverse Trigonometric Functions: A Comprehensive Guide

Trigonometry is one of the foundational subjects in mathematics that finds applications in various fields such as physics, engineering, and even computer science. While trigonometric functions like sine, cosine, and tangent describe relationships between the sides and angles of a right triangle, inverse trigonometric functions are equally essential for solving problems that involve angles when the sides of the triangle are known.

Inverse trigonometric functions, as the name suggests, are the reverse of the standard trigonometric functions. This blog will explore the concept of inverse trigonometric functions, their properties, and how they are used in mathematical and real-world applications.

What are Inverse Trigonometric Functions?

The inverse trigonometric functions are the functions that reverse the action of the regular trigonometric functions. In simple terms, while a regular trigonometric function takes an angle and gives a ratio of sides (such as sine giving opposite/hypotenuse), an inverse trigonometric function takes a ratio and gives an angle.

The six trigonometric functions in mathematics are:

Sine (sin)

Cosine (cos)

Tangent (tan)

Cotangent (cot)

Secant (sec)

Cosecant (csc)

Each of these functions has an associated inverse function. For example, the inverse of sine is called arcsine (or sin⁻¹), the inverse of cosine is called arccosine (cos⁻¹), and so on.

Why Do We Need Inverse Trigonometric Functions?

Inverse trigonometric functions are crucial because they allow us to find the angle when we know the value of the trigonometric function. This is particularly useful in fields like navigation, physics, engineering, and computer graphics, where it’s essential to work backward from a ratio of sides to determine the angle.

For instance, if we know the sine of an angle in a right triangle, the inverse sine (sin⁻¹) function can help us determine the measure of the angle. Similarly, inverse functions like arctangent (tan⁻¹) help us find the angle when the ratio of the opposite side to the adjacent side is known.

The Notation of Inverse Trigonometric Functions

The notation for inverse trigonometric functions is a bit different from regular trigonometric functions. Instead of writing "sin(x)" or "cos(x)," the inverse trigonometric functions are denoted with a superscript minus one, such as sin⁻¹(x) or cos⁻¹(x). This notation represents the angle whose sine or cosine is the given value.

Here’s a quick list of the common inverse trigonometric functions:

sin⁻¹(x) or arcsin(x): The inverse of sine, gives the angle whose sine is x.

cos⁻¹(x) or arccos(x): The inverse of cosine, gives the angle whose cosine is x.

tan⁻¹(x) or arctan(x): The inverse of tangent, gives the angle whose tangent is x.

cot⁻¹(x) or arccot(x): The inverse of cotangent, gives the angle whose cotangent is x.

sec⁻¹(x) or arcsec(x): The inverse of secant, gives the angle whose secant is x.

csc⁻¹(x) or arccsc(x): The inverse of cosecant, gives the angle whose cosecant is x.

Domains and Ranges of Inverse Trigonometric Functions

One of the critical aspects of inverse trigonometric functions is that they are restricted to certain domains and ranges to ensure that they are one-to-one functions. A one-to-one function is essential because it ensures that each input corresponds to a unique output.

Arcsin (sin⁻¹):

Domain: -1 ≤ x ≤ 1

Range: -π/2 ≤ y ≤ π/2

The arcsin function gives an angle between -90° and 90°.

Arccos (cos⁻¹):

Domain: -1 ≤ x ≤ 1

Range: 0 ≤ y ≤ π

The arccos function gives an angle between 0° and 180°.

Arctan (tan⁻¹):

Domain: -∞ < x < ∞

Range: -π/2 < y < π/2

The arctan function gives an angle between -90° and 90°.

Arccot (cot⁻¹):

Domain: -∞ < x < ∞

Range: 0 < y < π

The arccot function gives an angle between 0° and 180°.

Arcsec (sec⁻¹):

Domain: |x| ≥ 1

Range: 0 ≤ y ≤ π/2 or π ≤ y ≤ 3π/2

The arcsec function gives an angle between 0° and 90° or between 90° and 180°.

Arccsc (csc⁻¹):

Domain: |x| ≥ 1

Range: -π/2 ≤ y ≤ 0 or 0 ≤ y ≤ π/2

The arccsc function gives an angle between -90° and 90°, excluding 0°.

Properties of Inverse Trigonometric Functions

Understanding the properties of inverse trigonometric functions can make working with them much easier. Here are some essential properties:

Inverse of an Inverse: The inverse of an inverse trigonometric function gives the original function back. For example:

sin(sin⁻¹(x)) = x for -1 ≤ x ≤ 1

cos(cos⁻¹(x)) = x for -1 ≤ x ≤ 1

tan(tan⁻¹(x)) = x for all x

Composition of Functions: The inverse and the original trigonometric function can be composed together. For example:

sin⁻¹(sin(x)) = x for -π/2 ≤ x ≤ π/2

cos⁻¹(cos(x)) = x for 0 ≤ x ≤ π

tan⁻¹(tan(x)) = x for -π/2 < x < π/2

Symmetry: Inverse trigonometric functions exhibit symmetry about certain axes. For example, the inverse sine function is symmetric about the y-axis, while the inverse cosine function is symmetric about the line x = 0.

Solving Trigonometric Equations Using Inverse Functions

Inverse trigonometric functions are widely used for solving trigonometric equations. For example, if you are given a problem where you need to find the angle θ, knowing the value of sin(θ) = 0.5, you can use the arcsin function to find the angle:θ=sin⁡−1(0.5)=30∘θ = \sin^{-1}(0.5) = 30^\circθ=sin−1(0.5)=30∘

Similarly, if you are given the tangent value of an angle, you can use the arctan function to find the angle. This process is vital for solving problems in geometry, calculus, and physics.

Real-World Applications of Inverse Trigonometric Functions

Navigation: Inverse trigonometric functions are crucial in navigation and determining bearings. Pilots and sailors use these functions to calculate angles based on given distances and directions.

Physics: In physics, especially in wave motion and optics, inverse trigonometric functions help solve problems involving angles of refraction, angles of incidence, and angular displacement.

Engineering: In electrical engineering and mechanical systems, inverse trigonometric functions are used in control systems, signal processing, and analyzing vibrations.

Computer Graphics: Inverse trigonometric functions are used in computer graphics to rotate and scale objects, especially when working with angles in 3D space.

Conclusion

Inverse trigonometric functions are indispensable tools for solving mathematical and real-world problems involving angles and ratios. From geometry to physics and engineering, they provide a method for determining the angle when the side ratios of a right triangle are known. Understanding the properties and applications of inverse trigonometric functions will undoubtedly help you excel in both theoretical and applied mathematics.

[channelflippingwithaemerge]

answer 🌊 👋🏿

dark forest is

μ

---

η

silent

low _

🔥_

🌎 LDS

Earth

ea

ae ea

first and last

hear hyram hear tik tok toe tiç//tease toç//toss toe(TUH) oe ü tease, toss ('looseorforget the crosses'), oe (uh hey, egghead aça loser aça x aça |O aça thinker

2π(1i)p

. Rho |

Rh| Ri

Roy+ +.+ -Rhy

are oo

are who

Dare are why

derriere why oui

we see jm gem |i

ji me ny

👋🏿

behind

| 🌊

2π2(||i)u

||πp"||i"

la()((())(((()))((((())))vie

sola

so there- | -. |O #O#life"

011010🧩: 28 🧩: i!22#🐍|🧩:🧩 ||(224 4 !¡ . .

😷

La |O# |#|

44¥22 |||| OOOO IOIO IIOI

🤕 xx xx xx xx

🦉

. e- .

e|.618

e||.2

12586269025

| H

⏰⏰⏰⏰⏰⏰⏰⏰⏰⏰⏰🕕🕦🕚🕐🕐🕥🕣🕢🕢🕤

🐍 Ξ ! ! i ċ 🎄- -🌴 👋🏿 Oo

|I| ||Y|| ||

🎹🪗

😵‍💫

m00uu

ouui

⏰00⏳

✨00 a⏰#][≠]

#][≠]

|🌎**% ({#}(👁���)

]|~|[ ]♟️≈ç🪩ç≈ [[]

🫖💤☕️

He|| ]eeee!¡. + .!¡eeee ** .*

.

-

~

.

-

🐓🦀

O

Π

/

Oπ

\

e | D ç°2 ]👁️(D)[

ç🦀 👁️ D 👓 ☃️ 👁️)( !ç¡ (._cΞ||¥¥->•<>•<.~≈ψ+))👀 🦻🏿👣🧠👣🦷👣💺🧠👣 c🦀 .🫁 🌬️o

👁️ )Daniel Carter Johnson( ...]DJ @{|}{cuuoooouuc}e ≈! . ¡:≈ Matches ≈ .

≈

👀🦻🏿 =

/ ⏲️ 7 ζι aleph≈ .- ≈{]A}{c¡C¡[]⚖️_L

ciCi ≈ cc ≈ 🌎 ⏳👁️{{{{

L ≈ 90 πj ⬆️ 6 🍃🔭

l•_•/ ≈ 🛁 👣

.4•4•4{}≈{}64 👣

👣 3•3•3≈ 27 ,._._O ._O🪭çO_!.¡ao

⏳= |ẽ🕐{🕐V⚙️≠12###{403 14 5

di cell vie 0.083<≈≠06.60.•°Oe#242! 26{}≠{}24≠{}XXIV{}≠ twentyfour ≈ 24 {}OU!6!OC

🧬 👁️}||#|≈ say cell life cells have • < : = •!o

..! sõůc Titi ak 7th7th sept even !!! 7h Ly- ! c5 cv cζ¥ T#t ≈> •⛳️]🍩[🥯👛 🎒⭕️⚪️💠💠 💠💠 💠💠 💠💠 💠💠 💠💠 💠💠 💠💠

T\ /t 🏝️ 👻

Ħ

TO! T t+ |ç<≈ ...s... !•- εινξ¡ ≈ νΞ

7

!¥x¡

scaler ¥ |} 🧗 _/📈nonoyouscale

down 🌎 👀👂()scale() ~🌉~ 🧗~⚖️~ 🐍 🐚 (!) 👄 🌊 #@ 🥚

🥗 💩📚

egg is -*- win

-¡+*-¡+-

2 2πr

sin)___________( 👂 q}📺📺📺📺📺📺📺📺📺📺📺📺📺{p

q|}()| ~=≈!¡_-- ... > •O-#+-/0 ~=≈!¡_-- ... > •O-#+-/0~≈≈

q≈ no peek}{ 👀|door🚪[🪟]

p= 👁️ (🔭 📐⚖️⏲️🦻🏿 )}{🥐🥨🍞🍩🍪💠

q? ⚖️ well done you might be meeting u s ooon

|⏰ ⏳ very uoon uunaeqivbsat

hivivjve iamwriting waiyring yorgy

no its having god bhildashew ye

🌴 grow on?

no you're not a good man

q which p oo u

how long have u 6966|? Daniel(👀👀){🛞🦋🏉🦋🏀 q🪺

ep silent because w intercepting waves. they we have wider bandwidth on infor.

wave dispersion

laq per

lake scared u root pier sensors

Q db bd pq pd pq pb bq bd

iu👀🧭⏰

👋🏿}(!z¡)><().{}≠(}>

🥚 ⏰≠🏪⏳{}

🥚 ≈ 🏀

[tutoroot]

What are the List of Trigonometric Formulas? 

Trigonometry is the study of triangles and connections between triangle lengths and angles in mathematics. Trigonometric formulas and a list of trigonometric identities form one of the most timeless and important facets of mathematics.

Trigonometry and related equations have a plethora of applications. Triangulation, for example, is used in Geography to calculate the distance between landmarks; in Astronomy they are used to determine the distance to neighboring stars; and, in satellite navigation systems. In many other ways, Trigonometric formulae are useful and indispensable too.

Trigonometry Formulas

Trigonometry formulas are a collection that uses trigonometric identities to solve problems, involving the sides and angles of a right-angled triangle. For given angles, these trigonometry formula include trigonometric functions such as sine, cosine, tangent, cosecant, secant, and cotangent. While the trigonometric formulae involving trigonometric identities are the core of the subject, we also would like to understand the importance of trigonometric identities, which in a basic sense refers to an equation that involves trigonometric ratios of an angle.

In the following sections, trigonometric identities, including Pythagorean identities, product identities, co-function identities (shifting angles), sum & difference identities, double-angle identities, half-angle identities, and so on are explained in detail.

List of Trigonometric Formulas

When we first learn about trigonometric formulas, we only consider right-angled triangles. As we know, a right-angled triangle has three sides: the hypotenuse, the opposite side (perpendicular), and the adjacent side (Base). The longest side in a right-angled triangle is known as the hypotenuse, the opposite side is perpendicular, and the adjacent side is where both the hypotenuse and the opposite side rest. These sides and the basic structure of the right-angled triangle go a long way in determining the depth of understanding of trigonometry formulae. In short, the right-angled triangle is the reference point to derive or arrive at trigonometry formulae or trigonometric identities.

Basic Trigonometric Formulas

In Trigonometry, there are six ratios that are utilized to find the elements. They are referred to as trigonometric functions. Sine, cosine, secant, cosecant, tangent, and cotangent are the six trigonometric functions.

Inverse Trigonometric Formulas

Trigonometric ratios are inverted using inverse trigonometry formulas to produce inverse trigonometric functions such as sin θ = x and θ=sin−1x. In this case, x can take the form of whole integers, decimals, fractions, or exponents. 

Trigonometry Identities

Trigonometric Identities are equalities that involve trigonometry functions that stay valuable for all variables in the equation.

There are several trigonometric identities relating to the side length and angle of a triangle. These identities stay true to the right-angle triangle.

As explained, these are all derived from a right-angled triangle. If we know the height and base side of the right triangle, it will become easier to know sine, cosine, tangent, secant, cosecant, and cotangent values, by applying trigonometric formulas. We can also derive reciprocal trigonometric identities by applying trigonometric functions.

Periodicity Identities

The periodicity identities are formulas used to shift the angles by π/2, π, 2π, etc. They are also classified under cofunction identities.

If one observes keenly, fundamentally, all trigonometric identities are cyclic. They repeat after this periodicity constant. The periodicity constant varies among the trigonometric identities and is different for each.

Trigonometric Identities of Opposite Angles

As we dwell deep into trigonometry formulas and various other aspects of this branch of mathematics, we explore more interesting features that enhance our subject knowledge and take us through new paths of knowledge. One such is the trigonometric identities of opposite angles, where, a trigonometry angle that is measured in its clockwise direction, is measured in negative parity. The trigonometric ratios for the angle’s negative parity are as follows:

Complementary Angles Identities

As the expression suggests, complementary angles are the pair of angles whose added measure comes to 90°.

Supplementary Angles Identities

These are a pair of angles whose measure adds to 180°.

At  Tutoroot, we offer personalised trigonometry tutoring to ensure a clear understanding. Our expert instructors use simple teaching approaches for an effective understanding of the subject. Sign up with Tutoroot’s Online Tuition for Maths to learn more.

[shuxiii]

f(x) = x^2/3 + e/3(π-x^2)^1/2 sin(απx)

i-i-i-i think u failed to shape a heart

[erikabsworld]

Mastering Numerical Differentiation: A Step-by-Step Guide with a Tough University-Level Assignment

Welcome to the fascinating world of numerical differentiation, where mathematical concepts meet real-world applications. In this blog, we will delve into a challenging university-level assignment on numerical differentiation. If you've ever felt overwhelmed by the complexities of this topic, fear not! We'll break it down, offering a comprehensive explanation and step-by-step guide to tackle a tough assignment question.

Understanding Numerical Differentiation:

Numerical differentiation is a mathematical technique used to estimate the derivative of a function at a particular point. Unlike analytical methods that involve intricate formulas, numerical differentiation relies on approximation methods to compute derivatives. One popular approach is the finite difference method, which involves finding the slope of a tangent line using small intervals.

Sample Assignment Question:

Consider the function f(x) = sin(x) + x^2. Find the derivative of f(x) at x = π using numerical differentiation with a step size of h = 0.1.

Step-by-Step Guide:

Step 1: Define the Function Begin by identifying the function you're working with. In our example, f(x) = sin(x) + x^2.

Step 2: Choose a Step Size (h) Select a small step size (h) to approximate the derivative. In this case, h = 0.1.

Step 3: Use the Finite Difference Method Apply the finite difference method to find the slope at x = π. Use the formula:

f′(x)≈ [f(x+h)−f(x)]/h .

Step 4: Substitute Values Plug in the values into the formula:

f′ (π)≈ [f(π+0.1)−f(π)]/0.1.

Step 5: Calculate the Result Compute the numerical derivative using the values from Step 4.

Website Plug: How We Help Students with Numerical Differentiation Assignments

Struggling with numerical differentiation assignments? Our website, matlabassignmentexperts.com, is here to provide the best numerical differentiation assignment writing help. Our team of skilled mathematicians and writers are well-versed in numerical differentiation and can guide you through challenging assignments. We offer personalized solutions, ensuring that you not only understand the concepts but also excel in your coursework.

Conclusion:

Numerical differentiation may seem daunting at first, but with the right approach, it becomes a manageable and valuable skill. By following the step-by-step guide provided in this blog, you can confidently tackle university-level assignments and gain a deeper understanding of numerical differentiation. Remember, if you ever need additional support, matlabassignmentexperts.com is just a click away, ready to assist you on your academic journey.

[quantumstudy]

Q: Find the range of the function y = 3 sinx + 4 cos(x + π/3) + 7

Solution : $\displaystyle cos (x + \frac{\pi}{3}) = cos x cos\frac{\pi}{3} - sinx sin\frac{\pi}{3} $

$\displaystyle cos (x + \frac{\pi}{3}) = \frac{1}{2} cos x - \frac{\sqrt{3}}{2} sinx $

$\displaystyle y = 3 sinx + 4 (\frac{1}{2} cos x - \frac{\sqrt{3}}{2} sinx) + 7 $

$\displaystyle y = 3 sinx + 2 cos x - 2 \sqrt{3} sinx + 7 $

$\displaystyle y = ( 3 - 2 \sqrt{3} ) sinx + 2 cos x + 7 $

Put $\displaystyle 3 - 2\sqrt{3} = r cos \alpha$ ...(i)

and $ 2 = r sin\alpha $  ...(ii)

$\displaystyle y = r sinx . cos \alpha + r cos x . sin\alpha + 7 $

$\displaystyle y = r sin(x + \alpha) + 7 $

Range of sin(x+α) is -1 to 1

Range of y = -r + 7 , r + 7

Now by squaring & adding equation (i) & (ii) we can get the value of r .