#solving negative exponents

[brandboosterx]

In this video, we delve into the art of solving logarithmic equations with different bases, demystifying the process for you step by step. Whether you're a student brushing up on logarithms or someone facing more complex problems, we've got you covered. Understanding how to work with different bases is crucial when faced with logarithmic equations. We break down the techniques, providing clear explanations using frequently used words to ensure that you grasp the concepts effortlessly. No more getting stuck on those seemingly perplexing logarithmic problems!

[comicaurora]

Hey Red, I'm trying to build a better understanding of mathematics, because to my mind math has always been a collection of arcane sigils that I had to memorize to pass tests in school. I must know how these sigils came to be and why they mean what they mean. Are there any resources you recommend I use in my pursuit of these secrets? Please and Thank You 🙏

It's good you described math as something you "build," because I think that's the best analogy possible.

Mathematics, in its purest form, involves no memorization. Math is the process of taking a very small number of established truths and defined operations that preserve truth, and using those operations on your established truths to expand your space of known truths. As long as you start from a point of truth and only use operations that preserve truth, you will derive truths. If you understand the base principles from which a branch of math is constructed, you can rederive it from first principles. Memorization is easier, but you can rederive it.

For instance, we can start with two things, the number "1" and the operation "+". 1 means "a single thing" and + means "put them together." If those two concepts exist, then we also have 2, 3, 4, and every other positive integer, because we can derive them by using + on as many 1s as we want. If we drop a rock on an empty patch of ground, and then drop a rock on that same patch of ground, that patch of ground now has two rocks on it.

If we include within the definition of "+" that there exists an identity value 0, and every value has an inverse that when added to it produces zero, we also get 0 and all the negative integers, producing the group of integers. Every integer can be expressed using nothing but the number 1, the + operation, and its inverse - if we're feeling spicy.

If we decide to add another truth-preserving operation, "*", with identity value 1 and the same kind of inverse property that "+" has, we rederive every rational number. Every number in this field of rational numbers can be described as a combination of 0s and 1s using only + and * and their inverses; truthful objects combined in truth-preserving operations. We started from the truth and we used it as our only building material to create something equally truthful.

We can memorize a multiplication table, but multiplication is just iterated addition. If we forget, we can just do the addition again.

Algebra is a simple rearrangement of a simple beginning math problem by way of other truth-preserving operations. When you're starting out, you might expect to see something like

3 + 5 = ?

Algebra starts when we replace "?" with a placeholder, "x". This is just a change of terminology. It preserves truth.

3 + 5 = x

This isn't what most algebra problems look like, though. Most basic algebra problems look more like

3x + 7 = 31

But these two formulae are the same, because we can turn one into the other through operations that preserve truth.

3x + 7 = 31 -> subtracting the same value from both sides of the equation is an operation that preserves truth. We subtract 7 from both sides, getting

3x = 24 -> dividing both sides of the equation by the same value is also an operation that preserves truth. We divide both sides by 3, getting

x = 8 -> addition is associative, so we can break 8 up however we want if we do

x = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = (1 + 1 + 1) + (1 + 1 + 1 + 1 + 1) = 3 + 5

Solving an algebra problem is the process of breaking down the things that make it complicated using the truth-preserving operations that defeat them. Added values can be subtracted. Multiples can be divided. Exponents can be root'd.

We understand what it means to put a placeholder in a math problem. We realize, by the same token, we can put in more than one placeholder, if we want. This gives us problems that don't have single numerical solutions, but spaces of solutions. Consider

2*x = ?

We do what we did before, replacing that "?" with something that means the same thing. We use a different letter to avoid confusion.

2*x = y

Now we have multivariable algebra. Instead of getting hard numbers for both variables, we have pairs of numbers. If we pick an x, we get a y. If we pick a y, we get an x. The relationship between the values is clearly defined; x will always be y/2. If x is 3, y is 6. If x is -1.8, y is -3.6.

Now for the sake of convenience, we create shorthand - another change of terminology that preserves truth. We come up with a term that describes this relationship between x and y. We decide to call y a "function."

y = f(x) = 2*x

A function is what we're calling one half of an equation; what goes on the other side of the equals sign. It's just a rename, like when we turned ? into x. It preserves truth.

The trick at this stage is that every element of this seeming increasingly complexity is actually an attempt to make the process simpler as we handle more and more things. We don't technically need any numbers other than 0 and 1 if we're just dealing with rational numbers. We could write 378/5 with nothing but 1s and +, -, * and /, but by god we wouldn't want to. We could write [x^3 + 2x + 5] as ?*?*? + ? + ? + 1 + 1 + 1 + 1 + 1 and it would mean the same thing. The shorthand and symbols get dizzying if you lose track of what they mean, but when you remember what they mean, you understand why you need them.

Any piece of mathematical shorthand basically means "for this thing we're talking about, this set of things is known to be true." We can rederive those things if we need to, but the shorthand is there to help us avoid doing it unnecessarily. We call the integers a group because that means it has an associative operation that is invertible and has an identity element that, when used in the operation, leaves the operated-on value unchanged. We don't want to write that out every time we use + or remember what 0 means, but we can if we have to.

Calculus is where most people think math turns into wizardry, but derivatives and integrals are just another pair of inverse functions like + and - or * and /, and the building block of this branch of math is the derivative. Any formula for a derivative can, in a pinch, be rederived by calculating the difference quotient (f[x+h]-f[x])/h as h approaches 0. If f(x)=x^2, we may memorize that its derivative f'(x)=2x, or we may calculate

[f(x+h) - f(x)]/h =

([x+h]^2 - x^2)/h =

(x^2 + 2xh + h^2 - x^2)/h =

(2xh + h^2)/h = 2x + h

And the limit of this as h->0 is 2x.

Everything in math can be broken down to first principles. Everything. Sometimes it's very hard to figure out what tool you need to break it down to its next stage of simplification, but it was built from first principles and it can be broken down the same way. If it isn't making sense, break it down with truth-preserving methods until it does - even if you have to go all the way back to zeroes and ones.

[roughentumble]

okay,

(4*10‐⁵)²/(2*10⁶)³

applying what i learned to the best of my ability:

(4*10‐⁵)²

=(4*10‐⁵)(4*10‐⁵)=16*100‐¹⁰

----

(2*10⁶)³

=(2*10⁶)(2*10⁶)(2*10⁶)=8*1000¹⁸

16*100‐¹⁰/8*1000¹⁸

so it would look like

16*100‐¹⁰

——————

8*1000¹⁸

which then can't be further reduced because the exponents don't have matching bases. i guess perhaps you could reduce the fraction by 4, making it

4*25‐¹⁰

----------

2*250¹⁸

which i ttttthink leaves exponents untouched? but idk what else you could do to solve it/make it smaller.

the sample questions on this practice test say the answer is 2*10‐²⁸

i can see how 2 goes into 4, to make 2, and how 25 goes into 250 to make 10, and how 10+18=28, BUT

1) i dont see how the negative and positive exponents came together to make a larger negative exponent? or how you could even add them across disparate terms?

2) how you can have 2 go into 4(bottom into top), when you then have 25 into 250(top into bottom) like that doesnt make sense to me

3) what steps im clearly missing???

im pretty blatantly not as ready for this test as i was hoping since i cant answer any of the questions correctly, and i cant solve this one which looked like the easiest and dealt with subjects we'd already gone over i thought. but.

ok im not asking anyone to do my math homework for me in earnest or give me a math lesson i guess i just really needed to explain my logic and reasoning into the void so i wouldnt forget and i'd know what to look up later. i guess maybe mathhelp will expand on this stuff later. it's gone over exponents in fractions but only with like terms

[nicklloydnow]

Walker Percy statue in Bogue Falaya Park, Covington, Louisiana

“A Talk with Walker Percy

Zoltán Abádi-Nagy

The Southern Literary Journal, 6 (Fall 1973)

Q: You maintain that perhaps the best way of writing about America in general is to write with authenticity about one particular part of America. By extension this means that, likewise, your attitude and reaction toward philosophical questions of universal human importance— toward the question of the human predicament, to use the term of your philosophy—will be that of an American. Is that correct?

A: I think that is true. My novels have more a European origin than American. They are so-called philosophical novels which is probably a bad word. But you know that the first half of your question is quite true. The greatest exponent of this was Faulkner who concentrated on a small village in Mississippi. It is true that I am interested in philosophical, religious issues and in my novels I use the particular in order to get at the general issues. For example, The Moviegoer is about New Orleans, one part in New Orleans, a young man in New Orleans. The conflict is a hidden ideological conflict involving, on the one hand, what I call Southern stoicism. I have an uncle whose hero was Marcus Aurelius. The other ideology is Christian Catholic. The third: the protagonist is in an existentialist predicament, alienated from both cultures.

Q: What in your view is it in America that makes an existentialist today? What facets of the American intellectual climate, of the American existence in general, are favorable to existentialist thinking?

A: I think in America the revolt is less overtly philosophical. It is a feeling of alienation from American suburban life, the suburb, the country-club, the business community. There is a difference between my protagonists and the so-called counter culture. Many young people revolt in a purely negative way, oppose their parents' culture; whereas the leading characters in my books are much more consciously embarked on some sort of search. I am telling you that because I would not want you to confuse the characters of the counter culture with my characters. One of their beliefs is that the American scene is phony, and their revolt is to seek authenticity in drugs, sex, or in a different kind of communal existence. The characters in my books are embarked on a much more serious search for meaning.

(…)

Q: Your view of life in your literary works is very close to the absurdist view, but the term 'absurd' and the whole Camus terminology hardly ever appears in your philosophical essays. Does this coincide with your preference for Marcel's Catholic version of existentialism as opposed to the post-Christian character of the meaninglessness of Sisyphus' situation?

A: Yes, that is correct. I identity philosophically with people like Gabriel Marcel. And if you want to call me a philosophical Catholic existentialist, I would not object, although the term existentialist is being so abused now that it means very little. But stylistically mainly two French novels affected me: Sartre's La Nausée and Camus' L'etranger. I agree with their novelistic technique but not with their absurdist view.

Q: Is not your third novel, Love in the Ruins, with its Layer I and Layer II—the social self and the inner, individual self—a comic attempt to solve Marcel's dilemma about this separation?

A: You are right. This is a comic device to get at what, ever since Kierkegaard, has been called the modern sickness: the disease of abstraction. I think in the novel Dr. More calls the illness angelism-bestialism. There is nothing new about this. It had been mentioned by many writers in various ways. Pascal said that man is both not quite as high as an angel and not quite as low as a beast. So Dr. More is aware of this schism in consciousness. He talks about the modem mind which, as he sees it, abstracts from the world, from itself, and manages to lose touch with reality.

(…)

Q: Much of it, especially in Love in the Ruins, seems to be a social problem viewed from an existentialist viewpoint of the human predicament. Actually, this is a kind of movement I notice in your works: an increasing awareness of how much the social predicament has to do with the human predicament. If Binx in The Moviegoer was suffocating in an adverse climate of malaise which was a social phenomenon, he was not much aware of its having to do with society; he was not concentrating on things like the social self as later Dr. More is in Love in the Ruins. Was this an intentional change on your part or was the movement towards the concept of malaise as a social product spontaneously developing through the inner logics of these relations?

A: It was a conscious change. Love in the Ruins was intended to take a certain point of view of Dr. More's and from it to see the social and political situation in America. Unlike Binx, whose difficulties were more personal, Dr. More finds himself involved in contemporary issues: the black-white conflict and the problem of science, scientific technology which is treated as a sociological reality today. Both the good and bad of it. I really use this to say what I wanted to say about contemporary issues. About polarization; there are half a dozen of them: black-white, North-South, young-old, affluent-poor, etc. And do not forget that at the end of Love in the Ruins there is a suggestion of a new community, new reconciliation. It has been called a pessimistic novel but I do not think it is. A renewed community is suggested. The suggestion is in the last scene which takes place in a midnight mass between a Christmas Saturday and Sunday. The Catholics, the Jews come to the midnight mass, also the unbelievers in the same community. The great difference between Dr. More and the other heroes is that Dr. More has no philosophical problems. He knows what he believes.

Q: Is it a religious reconciliation then?

A: Yes, that is the case. This was meant for Southerners in particular and for Americans in general.

Q: Binx in The Moviegoer and Barrett in The Last Gentleman do not seem to have the set of positive values needed for absurd creation as conceived by Camus to create their own meaning in meaninglessness. Is this connected with your idea of the aesthetic reversion of alienation, i.e. by communicating their alienation they get rid of it?

A: Yes, there is something there. In the case of Binx it is left open. The ending is ambiguous. It is not made clear whether he returns to his mother's religion or takes on his aunt's stoic values. But he does manage to make a life by going into medicine, helping Kate by marrying her. I suppose Sartre and Camus would look on this as a bourgeois retreat he had made.

Q: How do you look on it?

A: Well, I think he probably . . . as a matter of fact the last two pages of The Moviegoer were meant as a conscious salute to Dostoevski, in particular to the last few pages of The Brothers Karamazov. Very few people notice this.

Q: To me the most striking difference between the European and the American absurdist view is the ability of the American to couple the grim seriousness with hilarious humor, to turn apocalypse into farce. In comparison, Beckett, for all the grim comedy which is there, is a sheer tragic affair. Can you think of some explanation for this?

A: That is a good question and I can only quote Kierkegaard, who said something that astounded me and that I did not understand for a long time. He spoke of the three stages of existence: the aesthetic, the ethical, the religious. When you pass the first two you find yourself in an existentialist predicament which can be open to the religious or the absurd. He equated religion with the absurdity. He called it the leap into the absurd. But what he said and was puzzling to me was that, after the first two, the closest thing to the third stage is humor. I thought about that for a long time. I cannot explain it except I know it is true.

There is another explanation, too, of course. Hemingway once said: all good American novels come from one novel written by a man named Mark Twain. With Huckleberry Finn Mark Twain established the tradition of this very broad and satirical humor. I think the American writer finds it natural to use humor both in his satire and in describing even the worst predicament of his main character. In this country we call it black humor: disproportion between the gravity of the character's predicament and the hilarity of the humor with which it is treated. Vonnegut uses this a good deal.

Q: Richard B. Hauck in A Cheerful Nihilism points out how Franklin, Melville, Twain, Faulkner have shown that the response to the absurd sense can be laughter. At one point Binx becomes aware of the similarity of his predicament to that of the Jews. "I accept my exile," he says. Whether we accept this as his affirmation of life in its absurdity or not, what follows is comedy. Could you agree that this comedy as well as Franklin's, Melville's and the others' could be regarded as the absurd creation of the American Sisyphus as opposed to the serious defiance of Camus' king?

A: I do not know if I would go that far. It may be much simpler. There is an old American saying that the one way to stop crying is to laugh. Binx says, "I feel more homeless than the Jews." Between him and the Camus and Sartrean heroes of the absurd there is a difference. Camus would probably say the hero has to create his own values whether absurd or not, whereas Binx does not accept that the world is absurd; so he embarks on a search. So to him the Jews are a sign. I think he said, "Lately when I see a Jew on a street I am amazed nobody finds it remarkable. But I find it remarkable. But to me it is like seeing Friday's footprint in the beach. " Of course, he is not sure what it is the sign of. Sartre's Roquentin in La Nausée or Camus' Meursault in L'etranger would not find anything remarkable about a Jew, they would not be interested in him.

Q: In your philosophical essay, "The Man on the Train," you stress the speakability of the commuter's alienation and the fact that the commuter rejoices in this speakability. We can probably add: laughability. Incidentally, you do mention in the same article how Kafka and his friends were roaring with laughter when Kafka read his work aloud to them. Again if we had the answer to how alienation can become a laughing-matter, we would have the key to much of what is recently called black humor.

A: I think you are right. In "The Man on the Train" I was talking about the aesthetic reversal: the alienated commuter feeling totally alienated when reading a book about alienation feels better because there is a communication between himself and the writer.

Q: The forms of alienation you are concerned with in your fiction are all results of the objectification, mechanization of the subjective. Does not this view meet somewhere at a point with Bergson's view of the comic as the mechanical manifested in a living human being?

A: It sounds reasonable but I cannot enlarge on that. I am not familiar enough with Bergson. But to your previous question. Let me finish. It is the first time it occurs to me. You brought it up. Maybe, a person like Sartre spent a lot of time writing in a café about alienated people, the lack of communication, etc., and yet, in doing so, he became the least alienated person in France. By writing he performs a superb act of communication for which he has many readers. So you have a complete reversal. He writes about one thing and reverses it through communication. Here we have the American writer locked in his alienation. But I can envision the American writer getting onto it; by seeing the possibility of communication, exhilaration, his alienation becomes speakable. There can be a tremendous release from that. I have never thought of this before. Nobody knows what is going on when you communicate the unspeakable. This all-important step from unspeakability to speakability is such a triumph that in his own exhilaration the American writer finds it natural to use the Mark Twain tradition of the funny, the humorous.

(…)

Q: Religion reminds me of another tendency I notice in your novels from Binx through Dr. Sutter to Dr. More: the scientist Dr. Percy showing in the novels much more than the Catholic. How would you comment on your religious presence in the philosophical essays the—whole idea of the islander opening all those bottles hoping for 'the message'—and on the absence of practical religion from the novels. I know that religion is there as a theme but with no commitment of the writer in any direction.

A: Well, that is very simple. James Joyce said that an artist must be above all things cunning and guileful and must use every trick in the bag to achieve his purpose. In my view the language of religion, the very words themselves, are almost bankrupt. If you are writing a technical article on philosophy you can use the correct word for the correct meaning. But writing a novel is something different. In my view you have to be wary of using words like 'religion,' 'God,' 'sin,' 'salvation,' ‘baptism' because the words are almost worn out. The themes have to be implicit rather than explicit. I think I am conscious of the danger of the novelist trying to draw a moral. What Kierkegaard called 'edifying' would be a fatal step for a novelist. But the novelist cannot help but be informed by his own anthropology, the nature of man. In this respect I use 'anthropology' in the European philosophical sense. Camus, Sartre, Marcel in this sense can all be called anthropologists. In America people think of somebody going out and measuring skulls, digging up ruins when you mention 'an-thropology.' I call mine philosophical anthropology. I am not talking about God. I am not a theologian.

Q: What I meant was not the question of style and technique explicit or implicit but the religious commitment which is there in your philosophical writings but absent from the novels or always left open at best.

A: As it should be left open in the novel.

(…)

Q: None of the main characters in your three books have problems in making a living. Binx is a successful broker, Barrett inherited from his father, Dr. More from his wife. Do you do this to contrast seeming affluence with emptiness under it?

A: I had not thought about it. Maybe so, maybe also to use it as a device to reinforce the rootlessness. After all if these fellows had been day-laborers working very hard they would have had no time for various speculations.

Q: Does that mean that existentialism has no comment on those who are without these economic means and consequently perhaps in a much more serious predicament—because they have no time for speculations?

A: To that Marx would have an answer, Henry Ford would have an answer, Chaplin would have another, etc. Marx invented the term alienation. . .

Q: He reinterpreted an older concept, he discovered a new explanation for alienation.

A: But it is now transferred to a different class of society in Sartre, Camus. These desperately alienated people are members of a rootless bourgeoisie, not the exploited proletariat.

Q: Your novels demonstrate that to many questions affluence is no answer. Danger of life and the saving of lives often figure in your work as in many other black humorists', too. One can think of Barth's The Floating Opera, The End of the Road, Giles Goat-Boy, Vonnegut's The Sirens of Titan, Mother Night, Cat's Cradle and others, Kesey's two novels, Pynchon's V., Heller's Catch-22 and We Bombed in New Haven, etc. Do you think that this or a similar event of great moment in one's life is necessary to awaken the existentialist hero to his absurd situation and that this somehow is needed to shock him into the feeling of necessity for 'intersubjectivity' and shared consciousness as an escape from 'everydayness'?

A: I think that touches on a subject I have been interested in for a long time—a theme I use in all my novels: the recovery of the real through ordeal. It is some traumatic experience—war, Dr. More's attempted suicide—in each case. You have the paradox here that near death you can become aware of what is real. I did not invent this. Prince Andrey lying at the Battle of Borodino and looking at the clouds, makes a discovery: he sees the clouds for the first time in his life. So Binx is the opposite of Prince Andrey: he watches the dung-beetle crawling three inches from his nose.

Q: Correct me if I overinterpret the difference but now that you make this comparison it occurs to me that perhaps there is some irony here in the way it is an opening up of vision for Andrey towards the clouds, the sky, some magnificence suggested by these, and in the way Binx zooms down on an ugly little dung-beetle.

A: Maybe there is a little twist there. But the point is that a little creature as the dung-beetle is just as valuable as a cloud.

(…)

Q: Ordeal is one existentialist solution to escape from the malaise. How effective do you think the others, rotation and repetition, can be? Is it possible that their effect can be more than temporary?

A: To use Kierkegaard's term, they are simply aesthetic relief, therefore temporary.

Q: Friedman says that distortion can be found on the front page of any newspaper in America today. It is not the black humorist who distorts; life is distorted. Does everyday American reality stir you to write with similar directness? I ask this because once in an interview you appreciated the way Dostoevski was stirred to writing by a news item in a daily paper and because once in connection with Faulkner and Eudora Welty you referred to the social involvement of the writer as useful because social likes and dislikes, you said, can be the passion and energy you write from.

A: I see what Friedman means. Right. The danger with newspapers and TV is that it is all trivial. You remember in Camus' The Fall: we spend our lifetime "fornicating and reading the newspapers.” I think the danger is that you can spend your life reading the New York Times and never get below the surface of current events; whereas in Dostoevski's case—The Possessed—the whole was inspired by a news story in a Russian newspaper. I would contrast the inveterate newspaper reader and TV watcher who watches and watches and nothing happens—he is formed by the media. Dostoevski reads one news story, gets angry and this triggers a creative process.

Q: Intersubjectivity is an escape for Binx from everydayness and the other forms of the malaise, he is certainly not formed by the media. But are his aunt's values cars, a nice home, university degree—somehow recreated through intersubjectivity so that he can go back to these formerly rejected values?

A: Yes, sure. The question is, how much? And whether he did not go a good deal beyond intersubjectivity when he regained his mother's religion. Binx says at the end that what he believes is not the reader's business, he cuts the reader loose, refuses to be edifying. This is Kierkegaard going back to Socrates, "I want no disciples."

Q: But in the next paragraph he says, "Further: I am a member of my mother's family after all and so naturally shy away from the subject of religion (a peculiar word this in the first place, religion; it is something to be suspicious of)." This means, it seems to me, that Binx definitely objects to being edifying, especially in a religious way.

A: Yes, if you like.

(…)

Q: I wonder why it is necessary to bring the mental sickness of these characters into such a sharp focus? Is it to perplex the world with the old enigma: are these sick people in a normal world or normal people in a sick world? Or is it the interest of the medical doctor? Or both?

A: It is partly therapeutic, medical interest but also goes deeper than that. The view of Pascal and some others who were interested in the human condition was that there is something wrong with mankind. So it is always undecided in my novels. This is the main question of the novels. Here is a hero who is afflicted, shows malaise, dislocation, and he is surrounded by apparently happy and sane people, particularly Dr. More, who lives in Paradise Estates. So who is crazy, the people apparently happy or those radically dislocated characters?

(…)

Q: Although I know you have been frequently asked about the position of the writer in the South, I would like to ask you to summarize your view on this question for the Hungarian reader for whom this talk is primarily intended and for whom your view of the writer in the South will be a novelty.

A: The position of the Southern writer now, as opposed to thirty years ago when Faulkner was writing, is more and more on a level with other writers' in other parts of the country. In other words the United States is becoming more and more homogenized. America is becoming more alike. Towns in the South lose their distinctive character. And yet, I think, in spite of this, there remains and probably there will remain a unique community in the South between black and white, so that there is much more communication, strangely enough, between middle-class white and black people in the South than there is between intellectual black and white in the North. In the South they have lived in physically intimate terms for 300 years. And whatever might have been the evils of this system, there still exists a strong historical basis of communication. I think it will continue to exist.

Q: Speaking about America, it occurs to me to ask you at this point if you have ever thought of rotation in historical aspect? Of America as a historical experience in rotation? What the settlers did coming from Europe, or the pioneers did going west was, it seems to me, as exactly zone-crossing as anything in the existentialist meaning of the term—even though the term came much later. If I may go one step further, how can you comment on the effectiveness of this rotation in the light of what you say on the first pages of Love in the Ruins: "our beloved old U.S.A. is in a bad way." And later, "now the blessing or the luck is over, the machinery clanks, the chain catches hold . . .”?

A: I did not think of rotation in an historical aspect. But if rotation is temporary it should run out. That makes it tough. There are more suicides in San Francisco today than in other cities; that is why the rotation has run out, which may or may not be significant. That is what Kierkegaard calls aesthetic damnation—living by rotation.”

[manishmishra45]

Mastering the Power Function Using Recursion in Java: A Step-by-Step Guide

Recursion is a powerful concept in programming that simplifies problem-solving by allowing functions to call themselves. One of the classic applications of recursion is calculating the power of a number. Understanding how to implement a power function using recursion is crucial for both beginner and advanced Java developers. This guide will walk you through the concept, implementation, and optimization of a power function using recursion in Java.

What is Recursion?

Recursion is a technique where a function calls itself directly or indirectly to solve a problem. Each recursive function must have two essential parts:

Base Case: This terminates the recursion when a specific condition is met.

Recursive Case: The function continues calling itself with updated parameters, gradually approaching the base case.

Understanding the Power Function

A power function calculates the result of raising a base number to an exponent. Mathematically, this can be represented as:Power(base, exponent) = base^exponent

For instance:

2^3 = 2 × 2 × 2 = 8

5^4 = 5 × 5 × 5 × 5 = 625

Recursive Logic for Power Function

The power function can be defined recursively as follows:

Base Case: If the exponent is 0, return 1 (Any number raised to the power of zero is 1).

Recursive Case: Return base * power(base, exponent - 1).

Java Code Implementation

Here is a step-by-step implementation of the power function using recursion in Java:public class PowerFunction { // Recursive method to calculate power public static int power(int base, int exponent) { // Base case if (exponent == 0) { return 1; } // Recursive case return base * power(base, exponent - 1); } public static void main(String[] args) { int base = 3; int exponent = 4; System.out.println(base + " raised to the power " + exponent + " is: " + power(base, exponent)); } }

Explanation of Code

Method Definition: The power method accepts two integers: base and exponent.

Base Case: The condition if (exponent == 0) ensures recursion terminates when the exponent reaches zero.

Recursive Case: The line return base * power(base, exponent - 1) continues to call itself, reducing the exponent by 1 until it reaches zero.

Main Method: Demonstrates the usage of the power method with sample values.

Example Output

3 raised to the power 4 is: 81

Optimizing the Power Function Using Recursion

The above implementation works efficiently but can be optimized further. Instead of decrementing the exponent by 1 in each step, we can reduce the number of recursive calls by dividing the exponent by 2.

Optimized Recursive Power Function

public class OptimizedPowerFunction { // Optimized power function using recursion public static int power(int base, int exponent) { if (exponent == 0) { return 1; } // Efficient reduction of exponent int temp = power(base, exponent / 2); if (exponent % 2 == 0) { return temp * temp; } else { return base * temp * temp; } } public static void main(String[] args) { int base = 2; int exponent = 10; System.out.println(base + " raised to the power " + exponent + " is: " + power(base, exponent)); } }

Example Output

2 raised to the power 10 is: 1024

Why Use an Optimized Power Function?

This improved implementation minimizes the number of recursive calls by exploiting the property that:base^exponent = (base^(exponent/2)) × (base^(exponent/2))

This approach is significantly faster for large exponents.

Key Benefits of Power Function Using Recursion

Simplicity: Recursion provides a clean and straightforward solution for the power calculation problem.

Efficiency: Optimized recursion reduces redundant calculations, improving performance.

Flexibility: Recursion handles both positive and negative exponents effectively with minor modifications.

Common Mistakes to Avoid

Missing Base Case: Forgetting to include the base case may lead to infinite recursion and stack overflow errors.

Incorrect Recursive Step: Ensure the recursion is progressing towards the base case to avoid infinite loops.

Handling Negative Exponents: Extending the function to support negative exponents requires dividing 1 by the result for those cases.

Adding Support for Negative Exponents

To extend our code for handling negative exponents:public static double power(double base, int exponent) { if (exponent == 0) { return 1; } if (exponent < 0) { return 1 / power(base, -exponent); } double temp = power(base, exponent / 2); return (exponent % 2 == 0) ? temp * temp : base * temp * temp; }

Conclusion

Mastering the power function using recursion in Java is essential for developing efficient algorithms. This tutorial explored both basic and optimized implementations, ensuring better performance for larger exponents. By practicing recursive techniques like this, you'll build a strong foundation for solving complex problems in Java development.

[jeremy-ken-anderson]

Practice Certainly Makes Better

Look, perfect is hard.

But it's clear that I'm getting faster at these programming problems. The easy ones take more time to log than to solve. The medium ones are sometimes padding out their numbers with edge cases, like how "make your own Power function that handles exponents" requires a special case for negative numbers.

Also, I keep underestimating the value of rubber-duckying. But I come here and do a postgame report and I realize I could make the code a little cleaner. In this case I was going to say it required a special case for 0, 1, and negative numbers...but it didn't require that. Rather, I made a situation where it required that by starting my number in the wrong place. If I'd started at 1 instead of at x, I could have said,

"Multiply answer (starts at 1) by x, n times." Or in code:

answer = 1 for i in range(n): answer *= x

return answer

That code handles every positive integer, and also 0 (because if n is 0, the for loop will immediately skip, which leaves x^0 = 1, which is accurate).

I'm gonna try a hard one tomorrow: A sudoku solver.

[radiantsemi]

Understanding Floating-Point Multipliers: A Comprehensive Guide

In the realm of digital computing, floating-point arithmetic plays a pivotal role in handling complex calculations with a high degree of precision. Among its fundamental operations, multiplication stands out as a critical process, enabling applications across diverse fields such as scientific computing, signal processing, and artificial intelligence. This blog delves into the design, functionality, and importance of floating-point multipliers, providing insights for both enthusiasts and professionals.

What is a Floating-Point Multiplier?

A floating-point multiplier is a hardware or software unit designed to perform multiplication operations on numbers represented in floating-point format. The most widely used standard for floating-point representation is the IEEE 754, which defines the structure of floating-point numbers using three main components:

Sign Bit: Indicates the number's sign (0 for positive, 1 for negative).

Exponent: Represents the scaling factor.

Mantissa (or Significand): Contains the significant digits of the number.

In essence, a floating-point number can be expressed as:

Here, the bias is a constant value added to the exponent to allow representation of both positive and negative exponents.

How Does a Floating-Point Multiplier Work?

The multiplication of floating-point numbers involves the following steps:

Sign Calculation:

The resultant sign is determined by the XOR operation of the sign bits of the operands.

Exponent Addition:

Add the exponents of the two numbers and subtract the bias to normalize the result.

Mantissa Multiplication:

Multiply the mantissas of the two numbers. This step often produces a product with double the precision, which is then normalized.

Normalization:

Adjust the mantissa and exponent to ensure the result fits within the normalized range.

Rounding:

Apply rounding to meet the precision requirements of the format.

Overflow and Underflow Handling:

Check and handle cases where the result exceeds the representable range or is too small to be represented.

Challenges in Floating-Point Multiplication

Precision Loss: Floating-point representation is inherently approximate, leading to potential precision loss during multiplication.

Rounding Errors: Ensuring accuracy while adhering to precision constraints can introduce rounding errors.

Hardware Complexity: Implementing a high-performance floating-point multiplier requires intricate hardware design, especially for pipelining and parallelism.

Overflow and Underflow: Handling extreme values efficiently is a persistent challenge in floating-point arithmetic.

Applications of Floating-Point Multipliers

Floating-point multipliers are indispensable in various fields, including:

Scientific Computing: Solving differential equations, simulations, and large-scale computations.

Signal Processing: Performing fast Fourier transforms (FFTs) and digital filtering.

Graphics Rendering: Enabling realistic graphics in gaming and simulations.

Machine Learning: Accelerating matrix multiplications and deep learning algorithms.

Financial Modeling: Calculating precise financial metrics and risk assessments.

Optimizing Floating-Point Multipliers

To enhance the performance of floating-point multipliers, designers focus on:

Pipelining: Breaking down the multiplication process into smaller stages for faster execution.

Parallel Processing: Utilizing multiple processing units to handle large datasets simultaneously.

Precision Control: Balancing the trade-off between precision and computation speed.

Energy Efficiency: Designing low-power architectures for mobile and embedded systems.

Conclusion

Floating-point multipliers are the unsung heroes of modern computing, driving innovation across numerous domains. Their ability to handle complex calculations with precision and speed makes them an essential component of today's hardware and software ecosystems. As computing demands continue to grow, advancements in floating-point multiplication will remain at the forefront of technological progress.

Understanding the intricacies of floating-point multipliers not only provides insight into their design but also highlights their significance in shaping the digital world.

[1data2science]

Pre Algebra part 1

Pre-Algebra for Data Science

Following are the topics which we will cover here

Definition of Algebra

Types of Numbers

Operation on numbers

Key terms that are used in algebra

Fractions and decimals

Ratios and proportions

1. Definition of Algebra

Algebra is a branch of mathematics that deals with the study of mathematical symbols and the rules for manipulating them. It allows us to represent and solve problems using variables, equations, and functions. In the context of data science, algebra provides the necessary tools to work with data, model relationships, and derive insights from complex information.

2. Types of Numbers

In pre-algebra, we encounter different types of numbers, including:

Natural Numbers: Also known as counting numbers, these include the positive integers (1, 2, 3, ...).

Whole Numbers: These include the natural numbers and the number zero (0, 1, 2, 3, ...).

Integers: Integers include the positive and negative whole numbers, as well as zero (-3, -2, -1, 0, 1, 2, 3, ...).

Rational Numbers: Rational numbers are numbers that can be expressed as a fraction of two integers, such as 1/2, 3/4, or 7/11.

Irrational Numbers: Irrational numbers are numbers that cannot be expressed as a fraction of two integers, such as π (pi) and √2.

Understanding the properties and relationships between these different types of numbers is crucial for working with data and performing mathematical operations.

3. Operations on Numbers

The fundamental operations in pre-algebra include:

Addition: Adding two or more numbers together.

Subtraction: Finding the difference between two numbers.

Multiplication: Repeatedly adding a number to itself.

Division: Splitting a number into equal parts.

Mastering these operations, including the order of operations (PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction), is essential for performing calculations and manipulating data effectively.

4. Key Terms in Algebra

Some of the key terms used in algebra include:

Variable: A symbol, usually a letter, that represents an unknown or a changing value.

Equation: A mathematical statement that shows two expressions are equal.

Inequality: A mathematical statement that shows one expression is greater than, less than, or not equal to another expression.

Function: A relationship between two or more variables, where one variable (the dependent variable) depends on the value of the other variable(s) (the independent variable(s)).

Understanding these terms and their applications will help you work with algebraic concepts and effectively communicate your data science findings.

5. Fractions and Decimals

Fractions and decimals are crucial for representing and manipulating numerical data. In pre-algebra, you'll learn:

Fractions: A way to represent a part of a whole, written as a ratio of two integers (the numerator and the denominator).

Decimals: A way to represent a number using place value, where the decimal point separates the whole number from the fractional part.

Mastering operations with fractions and decimals, such as addition, subtraction, multiplication, and division, will enable you to work with numerical data more effectively.

6. Ratios and Proportions

Ratios and proportions are essential for understanding relationships between quantities. In pre-algebra, you'll learn:

Ratios: A comparison of two or more quantities, written as a fraction or expressed as a rate.

Proportions: An equation that shows two ratios are equal, allowing you to find unknown values.

Understanding ratios and proportions will help you analyze and interpret data, especially when working with rates, percentages, and scaling relationships.

By exploring these pre-algebra topics, you'll build a strong foundation for your data science journey. These concepts will empower you to work with data, create models, and derive meaningful insights. As you progress, remember to practice regularly and apply these principles to real-world data problems. Happy learning!

[jonathankatwhatever]

Universe expands faster than IL. Why? It must to resolve. I can’t quite say how.

That was from yesterday. It’s now 3 Apr 2024. Tomorrow. Another birthday without your physicality. I prefer not to think about it.

Realized that sexual fantasy has an orbit and it collapses to or converges to 0 because that is 2 making 1, meaning a sexual fantasy experience, however it appears and shifts because it is a version of the concept of shared sexual fantasy experience, a concept deeply rooted in gender identity, which in turn reflects the inherent need to order mathematically. I’m such a romantic, deep at heart, because romance is mathematical. It is a process, an infinite process, and a result.

The orbit includes detail. It’s fractal. Wait second: are you saying they nest? I can see something like that working but it doesn’t complete. I see an M-set at each point when that point is 0, and thus layering and nesting is going to occur. This means the coordinate system shifts in layers, which is CR in a nutshell. So if I’m not mistaken, we just used the M-set to prove CR. Wow. That literally came out of me thinking the only doubt voice I have in my head is that somehow you look down on yourself. That seems to be petering out of the negative aspects or perspectives inherent to extreme drive. Like last night when I looked in the mirror, I saw someone untinged by negative thoughts about the face in the mirror. Ideal versions. It felt great.

Took a break and realized that … well, I’ve been working on ordinals, and the ideas are tough. I’ve realized we’re constructing the results from the other direction. I see that this is manipulation of 1Space. If I state that ordinals are 1Space arithmetic, that solves a lot of problems. Then, oh please, slow down.

Start with it being 1Space arithmetic. That’s second order. We went through this. Second order. What does ordering mean? Like impose an ordering of some modularity and call that 1st. Then call it 0. So the idea is you take that modularity which is 1 (thus prime forms matter again) as what emerges out of the 0 to be the 1 to that 0. Of all the infinite orderings, this one. So the level of choice of orderings is ordinal. Like any repeating modular count is an ordering which orders down to and up from that 0 of there not being a modular count at all. That’s naturals and what you order over them.

So we can say we use second order arithmetic, which we relabel for this purpose as 1Space counting. So, in 1Space counting, when you subtract 1, you are removing 1gs, but that 1gs is an Attachment, which is a structure. This is why you can have an ordinal reduce by counts within a level or from level to level. The former is LayerView, while the latter is along the szK. When you count back a step on the szK, you reach 0. This is the old 1 and 0 label issue again, isn’t it?

Okay. Deep breath. 1Space counting. I’ve been thinking it over and this works because set theory and 1Space counting generate out of D-structure in the construction of grid squares. That means we can, in fact, identify 1Space solvable problems. Like why twin primes exist.

So, what happens with Goldstein sequences? They get smaller ordinally means what? They count up in the bases so the numbers themselves get huge. But as they count up, they reduce by 1 at the level of the count itself. That is, we may raise from 3 to 4 to 5 with exponents in layers at each term, but we remove 1 each time. I’m having trouble seeing this.

The dialogue in here is something. A discussion about JvN and how slow I am or how I am approaching this in alliance to the him I’ve always sensed in you. A joint effort. I see the idea is we’re removing the 1 at the ordinal level. The problem I have with that is it’s a conclusion to me. Why does that work? Removing a level versus removing within a level. I’m not saying something is missing other than my own understanding. I think I’m getting it now, that it’s the obvious statement we’re changing everything else so i’s like we’ve put parentheses. I get the process.

I need a break. It’s crappy out and I was inside working all day.

[tutoroot]

What is the List of Trigonometric Formulas? 

Trigonometry formulas are a collection that uses trigonometric identities to solve problems, involving the sides and angles of a right-angled triangle. For given angles, these trigonometry formulas include trigonometric functions such as sine, cosine, tangent, cosecant, secant, and cotangent. While the trigonometric formulae involving trigonometric identities are the core of the subject, we also would like to understand the importance of trigonometric identities, which in a basic sense refers to an equation that involves trigonometric ratios of an angle.

In the following sections, trigonometric identities, including Pythagorean identities, product identities, co-function identities (shifting angles), sum & difference identities, double-angle identities, half-angle identities, and so on are explained in detail.

List of Trigonometric Formulas

When we first learn about trigonometric formulas, we only consider right-angled triangles. As we know, a right-angled triangle has three sides: the hypotenuse, the opposite side (perpendicular), and the adjacent side (Base). The longest side in a right-angled triangle is known as the hypotenuse, the opposite side is perpendicular, and the adjacent side is where both the hypotenuse and the opposite side rest. These sides and the basic structure of the right-angled triangle go a long way in determining the depth of understanding of trigonometry formulae. In short, the right-angled triangle is the reference point to derive or arrive at trigonometry formulae or trigonometric identities.

Here is a list of trigonometry formulas.

Basic Trigonometric Formulas 

Inverse Trigonometric Formulas 

Trigonometry Identities 

Reciprocal Identities 

Periodic Identities 

Co-function Identities 

Sum and Difference Identities 

Double Angle Identities 

Triple Angle Identities 

Half Angle Identities 

Product identities 

Sum to Product Identities 

Basic Trigonometric Formulas

In Trigonometry, there are six ratios that are utilized to find the elements. They are referred to as trigonometric functions. Sine, cosine, secant, cosecant, tangent, and cotangent are the six trigonometric functions.

Inverse Trigonometric Formulas

Trigonometric ratios are inverted using inverse trigonometry formulas to produce inverse trigonometric functions such as sin θ = x and θ=sin−1x. In this case, x can take the form of whole integers, decimals, fractions, or exponents. 

Trigonometry Identities

Trigonometric Identities are equalities that involve trigonometry functions that stay valuable for all variables in the equation.

There are several trigonometric identities relating to the side length and angle of a triangle. These identities stay true to the right-angle triangle.

Reciprocal Identities

Trigonometric ratios feature reciprocal relation between a pair of ratios:

As explained, these are all derived from a right-angled triangle. If we know the height and base side of the right triangle, it will become easier to know sine, cosine, tangent, secant, cosecant, and cotangent values, by applying trigonometric formulas. We can also derive reciprocal trigonometric identities by applying trigonometric functions.

Periodicity Identities

The periodicity identities are formulas used to shift the angles by π/2, π, 2π, etc. If one observes keenly, fundamentally, all trigonometric identities are cyclic. They repeat after this periodicity constant. The periodicity constant varies among the trigonometric identities and is different for each.

Trigonometric Identities of Opposite Angles

As we dwell deep into trigonometry formulas and various other aspects of this branch of mathematics, we explore more interesting features that enhance our subject knowledge and take us through new paths of knowledge. One such is the trigonometric identities of opposite angles, where, a trigonometry angle that is measured in its clockwise direction, is measured in negative parity.

Complementary Angles Identities

As the expression suggests, complementary angles are the pair of angles whose added measure comes to 90°. Their trigonometric identities are:

Supplementary Angles Identities

These are a pair of angles whose measure adds to 180°. Their trigonometric identities are:

Periodicity of Trigonometric Function

Trigonometric functions, sin, cos, tan, cot, sec, and cosec, are all periodic and carry different periodicities. Their identities:

At  Tutoroot, we offer personalised trigonometry tutoring to ensure a clear understanding. Our expert instructors use simple teaching approaches for an effective understanding of the subject. Sign up with Tutoroot’s Online Tuition for Maths to learn more.

[hkrsna]

Calculate X value #maths​ #matholympiad​ #exponents​ #exponential​ #math...

Reasoning #maths​ #matholympiad​ #exponents​ #exponential​ #math​ #tips​ #viral​ #shorts #reasoning

Reasoning

math olympiad problem

math olympiad problems

exponential problems

a nice olympiad exponential problem

olympiad math problems

exponential equation

math olympiad

olympiad mathematics

exponential equations

olympiad

math olympiad question

math olympiad questions

mathematical olympiad

solve exponential equation

exponential problem

exponential

math olympiad training

math olympiad preparation

learn how to solve exponential equation quickly

olympiad question

square root root with negative index derivatives with fractional exponent

root with fraction

powers with fractional exponents

square root with fraction

maths problems

math olympiad problem

a nice algebra problem

app to solve math problems

maths problem solution

iit jee advanced maths problem

word problems

math problem

maths olympiad problems

iit jee mains advanced maths problems

hard math problems

stats problem

monty hall math problem

statistics problem

nice algebra problem

olympiad math problems

math olympiad problems

short

maths shorts

viral

shorts

short video

youtube shorts

#olympiad​

#tips​ #trending​

#mathstricks​

#shortsviral​

#mathematics​

#maths​

#shortscreator​

#shortsfeed​

#viral​

[masongrizchel]

ON MATH ANXIETY

When I was a kid, my parents and relatives thought that I was a math prodigy, a brilliant, bright child who excelled mostly in math and science. Disclaimer: This was during kindergarten. Then we were introduced to addition, subtraction, multiplication, and division. It feels like life keeps falling apart for a 6- to 12-year-old kid. I was at the top of the class during my childhood years. And when PEMDAS becomes more complicated, including the operation of fractions, I feel lost every time I look at the board or at my notebook.

Then, when I entered high school, the first math that I encountered was algebra. When negative numbers were introduced, I was like, 'What the hell was that? '. Then exponents, square roots, fractions of square roots, exponentials, logarithms, cartesian plane, and WE ARE LITERALLY SOLVING LETTERS WITH NO NUMERICAL ANSWERS.

I did what most teens did during that time: cut class, go in the class drunk (sometimes high), and I already accepted that I couldn't excel. Whatever I do, I can't bring myself to my fullest. Especially when I received my grade in algebra, 71 (on the first quarter) ~ if I remember it correctly. My grade in Science I (Earth Science) was 76. I was labeled slow. Oh, when the overall ranking came out. Out of 74 students in our section, I was placed on the 70th. I was like, 'Oh, yeah. Whatever'. Then my friends and I just laughed about it. There is a reason for the continuous decline in the academic performance of a 13-year-old teenager, either within themselves or with their surroundings. Especially when you can't determine what the most suitable action is to take. It is a fight-or-flight response.

I was required to attend summer classes before since I failed most of my subjects, especially math and sciences. Biology came, chemistry hindered the way, and lastly, physics was the last straw. This is for science alone. For math, on the other hand, algebra, geometry, trigonometry, and statistics made me realize that I would not learn mathematics.

It made me anxious; most of the time, I throw up whenever we have major examinations. But those days were already over. I brought this up during my undergrad and graduate years. We can be anxious. But we are not our anxiety; we are not our emotions. And like most things, this can be let go. It will fade eventually.

I overcome this fear by simply 'trying'. Try and try. So during the 3rd year of my college years, I decided to face all these fears of mine. I faced an empty sheet of paper, holding a pen, with a formula sheet beside my answer sheet. I solve. I continued this until I grasped the process. What I realized along the way is that I don't have the strategy to study. It took me years to study in advance. I don't have the right resources and materials. And during that time, whenever I studied one subject, I used 4–6 books. I compare how each book discusses the topics. And when there is something that I don't understand, I go directly to my instructors. I always make sure that I have the right person to ask.

Acknowledging your feelings (your fear and math anxiety) is the first step in conquering them. Your instructors can help direct you to good resources and practices that can help you reduce or eliminate the emotional blocks to learning math and physics.

It will make you stronger and will help you find the most effective way to overcome your fear/stress/anxiety not just in math but with real-life problems that you might encounter along the way.

[catncore]

" that's a ONE-POINT SET for now , " boldly declared from his tangle of limbs on hanekoma's stool , a swaggering smirk in stark incongruity with someone who's just recently flirted with zero's cold infinity . sure , his P may have momentarily plunged into negative exponents , but the asymptote held - AFTER ALL , HE'S RESIDED COMFORTABLY IN i² FOR A WHILE . " 55's the one who did the integration - GUESS I OWE HER A FAVOUR . " a laugh twists out of him , returning to whatever disposables he had managed to get his black-edged claws upon off the cafe tables . coffee stirrers artfully assemble into an abstract skyscraper of unusual geometric configuration , not dissimilar to the one he had left in the cafe's back lot : his gift to fellow felidae , for his assistance solving t = taboo . // @cnvltn + bounced.

while this wasn't the ideal outcome hanekoma had hoped for, the fact that minamimoto was still willing to seek him out after, everything was something he hadn't factored in closely. no doubt that the genius geometrician had been waiting for his opportune chance to make contact. too many unaccounted factors.

it was curious how easily it had been for the once proud reaper to evade his eyes that observed the city. a chance in energy signatures. no doubt he'd left shibuya for a time to avoid being caught. atarashi coco had done her homework and caught minamimoto up for review. if he'd not been distracted, he'd have found and snatched the cub up by the scruff with ease.

three years of near catches and spontaneous sightings. minamimoto was letting him know he existed. was showing proof of existence, even if it was hidden from shinjuku. he knew immediately. this was a calling card.

his own calculations had not been wrong. far from it. not when there had been suddenly new figures added to the equation that he didn't expect to add. of course the solution would change when new things were added and extra steps needed to be taken. if things had stuck to what he was expecting then.... the 'newly' reforged player in front of him wouldn't have been here.

it made things interesting.

❝ i watched you, y'know.  ❞ he says, coolly as he takes a slow and intentional sip of his coffee, ❝  with th' twisters, though i knew you weren't truly integrated with them. begrudgingly i should be thankin' you for yer service t' th' city, even if you were largely uninvolved with the core distraction. i recognize reaper≠player. ill have to recalculate yer signatures soon. they're different. ❞

[cnvltn]

❝ who else knows yer still alive? ❞

" that's a ONE-POINT SET for now , " boldly declared from his tangle of limbs on hanekoma's stool , a swaggering smirk in stark incongruity with someone who's just recently flirted with zero's cold infinity . sure , his P may have momentarily plunged into negative exponents , but the asymptote held - AFTER ALL , HE'S RESIDED COMFORTABLY IN i² FOR A WHILE . " 55's the one who did the integration - GUESS I OWE HER A FAVOUR . "

a laugh twists out of him , returning to whatever disposables he had managed to get his black-edged claws upon off the cafe tables . coffee stirrers artfully assemble into an abstract skyscraper of unusual geometric configuration , not dissimilar to the one he had left in the cafe's back lot : his gift to fellow felidae , for his assistance solving t = taboo .

[factomaniac]

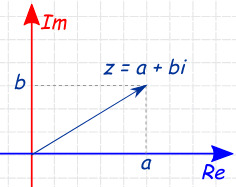
Math Madness #1: i is the Square Root of –1, but What is the Square Root of i?

01 July 2023, Chicagoland, IL

So, if you recall high school algebra, negative numbers do not have any square roots that are real numbers and imaginary numbers (real numbers used as a coefficient of the imaginary unit i, the square root of –1) were developed, in part, to give these numbers square roots. (Actually, they were originally developed in the 1500s to work with imaginary numbers that would crop up along the way to working out real number solutions to cubic equations, but being able to finally write the square roots of negative real numbers happens to be an indirect, but key, benefit.) Complex numbers are, in turn, the sum of a real number a and an imaginary number bi and take the form a + bi.

So, as we've established, i is the square root of –1, but what, in turn, is the square root of i?

Back in high school, my teen self attempted to answer this question, but for some reason, the answer wasn't coming to me, so I invented j as the square root i. But then what would be the square root of j? Maybe k? (Much later, I learned about quaternions, 4-dimensional numbers of the form a + bi + cj + dk, however, in quaternions, neither is j the square root of i, nor is k the square root of j. I'll cover quaternions in another blog post.) Anyway, as it turned out, I was on completely the wrong track.

Later, when I was in college (way before I discovered quaternions), I solved this problem using deMoivre's Theorem (the power of a complex number in polar form, r(cos θ + i sin θ), can be calculated by raising r to the exponent and multiplying the same exponent by the angle: [r(cos θ + i sin θ)]ⁿ = rⁿ(cos nθ + sin nθ) ).

However, as I later discovered, finding the solution is even easier than that. All that needs to be done is to set the square of a generic complex number, z, to i, compute the square of its standard form, a + bi, set the real part of this square to 0, and the imaginary part to 1, and then solve both resulting equations.

(sqrt(n) = the square root of n)

z² = i -> (a + bi)² = i -> a² + 2abi + b²i² = i -> a² – b² + 2abi = i (i = 0 + 1i) -> (1) a² – b² = 0, (2) 2abi = i -> 2ab = 1

(1) a² – b² = 0 -> (a + b)(a – b) = 0 -> (1A) a + b = 0 -> a = –b, (1B) a – b = 0 -> a = b:: (1) a = ±b

(2) 2ab = 1 -> ab = 1/2 -> applying (1B) -> b² = 1/2 -> (2A) b = ±1/sqrt(2) -> applying (1B) in reverse: b = a -> (2B) a = ±1/sqrt(2), applying (1A) to (2) -> –bb = 1/2 -> –b² = 1/2 -> (2C) bi = ±1/sqrt(2) -> applying (1A) in reverse: b = –a -> –ai = ±1/sqrt(2) -> –a = ±1/i sqrt(2) -> –a = ±–i/sqrt(2) –> (2D) a = ±i/sqrt(2)

Therefore, applying (2A) and (2B) -> z = a + bi = ±1/sqrt(2) ± i/sqrt(2), and redundantly, applying (2C) and (2D) -> z = a + bi = ±i/sqrt(2) ± 1/sqrt(2) = ±1/sqrt(2) ± i/sqrt(2).

(Notice how the imaginary solutions of (2C) and (2D) match the real solutions of (2A) and (2B) in reverse. The number of solutions yielded, 2, agrees with the Fundamental Theorem of Algebra: the number of solutions of a polynomial is the same as the degree of, the highest exponent in, the polynomial. In this case, we are dealing with a second degree equation, so there are exactly 2 solutions. However, because of a² – b² = 0 -> a² = b² and a = ±b, it is possible to solve this by creating a fourth degree equation also using 2ab = 1: b⁴ = 1/4 -> b = ±4thrt(1/4) = ±1/sqrt(2), ±i/sqrt(2). However, this creates a misleading solution set where the positive solutions could be mixed and matched with the negative ones, as a fourth degree polynomial would yield 4 solutions. However, since the original equation is second degree, there are only 2 true solutions where the signs of the real and imaginary parts match, as mismatches in those signs would give –i instead of i.)

Checking the 2 solutions (2 pairs of solutions with each pair identical), we get:

(1/sqrt(2) + i/sqrt(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i, and

(–1/sqrt(2) – i/sqrt(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i

PS Those who are interested can see how differing signs between the real and imaginary parts would yield –i, instead of i, here is a check of those solutions:

(1/sqrt(2) – i/sqrt(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – I – 1/2 = –i, and

(–1/sqrt(2) + i/sqrt(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – i – 1/2 = –i

[c-is-for-circinate]

Just. Just I am trying to teach calculus here, and I am aware that 'calculus' is a scary word. I am aware that in common parlance it's synonymous with crazy-advanced mathematical reasoning. I know it's scary, okay. I know. I promise it's not that bad. This student doesn't even think it's that bad. The problem is not the calculus.

The problem is that calculus needs so much algebra. And it needs that algebra to be fluid to the point of almost being incidental. You need to be able to do that algebra backwards and forwards, entirely with variables instead of numbers, which you were maybe never taught in the first place and certainly don't remember if you were because you first took Algebra 1 in the fall of 2020 and if you said you'd learned a single thing about math that year you'd be lying.

And so I am trying to teach calculus but what that actually means is that I'm trying to remind students how to do factoring and distribution from vague memories. I am trying to teach logarithms and exponent rules basically from scratch. I am trying to teach fractions. God help me, I am trying to teach fractions.

And sometimes this means reaching into the wilds of the internet and trying to find drills and practice problems for concepts nobody ever bothers trying to teach in calculus because you learned that in seventh grade, right? Except every single human or AI on the entire goddamn internet seems to believe that the only thing you ever need to do with negative exponents is get rid of them. WHICH! IS NOT! TRUE! FOR CALCULUS!!! THAT IS THE OPPOSITE OF THE THING YOU NEED TO DO FOR CALCULUS!

But hey, why bother to make exponent drills for calculus students, right? After all, if you can turn negative exponents into fractions, you probably know how to do it the other way around just as easily and would never need to practice, and if you're at the calculus level you must've learned that years ago. The same way you learned to solve for 'x' by adding or multiplying things to both sides in middle school, the same way you learn to add fractions with a common denominator when you're eight. Because every single high school math student one hundred percent knows how to add improper fractions by giving them a common denominator, right?

And I am just so mad and frustrated, always, about the ways we do and don't re-teach base principles for math all the way up, because if you didn't get it the first time then fuck you I guess. But somehow like everything else in the world the enshittification of the internet has made this worse, because like. It's not like nobody has ever needed to teach this before. It's not like practice problems for this don't exist. They're just unfindable in a sea of the same seventh-grade worksheets and identical Libretext links that all try to teach the same skill in the same way that just so happens to be the opposite of what I need. Why can no search engine's helpful AI bring me what I'm actually asking for rather than what it thinks I probably want? Why can I not just flip to a page at the end of a chapter of a textbook and find fifty practice problems going backwards and forwards. Why is everything DeltaMath and Khan Academy and locked behind a subscription. Why do half of my high school students not even have textbooks any more. Why do I feel like a crotchety fucking 70-year-old.

Anyway if I see "rewrite without negative exponents" one more time I am going to turn into a wolf and rip something apart with my teeth.

ugh I am SO MAD about a SPECIFIC MATH THING and nobody I know likes or knows math enough to empathize with me rather than just going >___> at math in general. Outrageous.