#logarithm base
Explore tagged Tumblr posts
Text
youtube
In this video, we delve into the art of solving logarithmic equations with different bases, demystifying the process for you step by step. Whether you're a student brushing up on logarithms or someone facing more complex problems, we've got you covered. Understanding how to work with different bases is crucial when faced with logarithmic equations. We break down the techniques, providing clear explanations using frequently used words to ensure that you grasp the concepts effortlessly. No more getting stuck on those seemingly perplexing logarithmic problems!
#Different bases for solving a log equation#logarithm questions basic#tricky logarithmic questions solve#logarithm formula#solving logarithms#logarithm base#logarithm applications#evaluate basic logarithm#formula of logarithms#solving logarithmic equations#logarithms explained#how to simplify logarithms#solving negative exponents#free math videos#logarithmic#algebra#mathematics#tutorial#Sami’s A Plus#sami’s a plus#math lessons#math for kids#learn math fast#Youtube
2 notes
·
View notes
Text


Map of the Known Universe
#fantasy#astronomy#space#based on depictions of the real known universe with logarithmic scale#stars#planets#sky#ink
862 notes
·
View notes
Text
For every liter squared of water there is about 10 to the power of -14 mol squared water ions (H+ and OH-) which is referred to as the constant Kw. And because the concentration of H+ and OH- is about equal, both have a concentration of 10 to the power of -7.
(This already supposes the simplification of concentration = activity)
The negative logarithm to the base of 10 in this case would be 7. In the case of the concentration (c) of H+ ions, this is shortened to pH. The counterpart to describe the c of OH- ions is, then, the pOH value.
This is why when the pH and the pOH value are added together, they always make 14. In the case of water, where the concentration of H+ and OH- is equal, both values are 7. Values differ depending on the concentration of acids and bases.
In strong acids and bases, which are said to dissociate entirely into their ions (though that is not entirely correct), it can be said that the pH-Value is, as before, entirely equal to the concentration/activity of H+ ions (negative logarithm to base 10, ofc).
In weaker acids and bases, I am still figuring it out, but it sure does involve my friend the Massenwirkungsgesetz
#feli speaks#uni posting#EPIC WIN!!! I CAN REMEMBER WHAT THE MASSENWIRKUNGSGESETZ IS!!!#and figuring out that p = negative logarithm to base 10 is MASSIVELY helpful shorthand#in remembering what pKa and pKb are
2 notes
·
View notes
Text
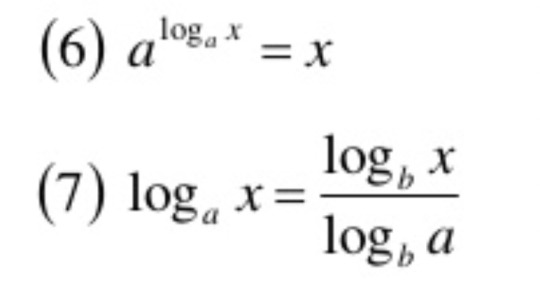

1 note
·
View note
Text
shells for witchcraft

Abalone Shells
Abundance, peace, and compassion
Abalone shells are very colorful, and the insides are coated with the same material that make up pearls, nacre. These colors are said to be incorporating all the colors of the sea and sky. In addition, the iridescent colors promote a feeling of abundance, peace, and compassion. In addition, the colors can represent the upper chakras, the Abalone shell is useful for developing psychic powers. Since Abalone shells have also been a food source for thousands of years, Abalone shells represent the giving power of the Ocean.
Abalone shells can also be made into jewelry and amulets, and not only will they promote abundance, peace, and compassion, but they will also impart a calming, spiritual vibration to help the wearer through emotional difficulties. In addition, Abalone shells have also been historically sacred in Polynesian and Native American cultures, especially as a vessel for sage while smudging.
Scallop Shells
Travel and spiritual quests
Symbol of Venus and Water
Scallop shells are distinguished from other shells by the multiple rays and ridges, which all converge at a single point near the base. To early humans, this likely symbolized the sun's rays converging on the horizon at sunrise or sunset. Because of this, Scallop shells are a good symbol of Venus, also known as the Morning Star or Evening Star. Later, to medieval Christians, the Scallop represented the path of pilgrims to holy sites.
Continuing, Scallop shells had a sacred meaning in Christian Europe from as early as the first pilgrims. The pilgrims, although mostly illiterate, were able to be guided to the pilgrimage sites with the Scallop symbol. In addition, the Scallop is a symbol of the Saint James the Apostle, and the symbol of the Scallop can be found through countless Christian altars and cathedrals. Because of the association with pilgrimage, the Scallop is a symbol for those who have undertaken a spiritual quest.
In addition, the Scallop shell is often depicted as the seat or carriage of ocean deities in art. For example, in art Poseidon often rides upon one, and Aphrodite is seen rising up from the sea in a Scallop shell. In addition, Scallops are often on Pagan altars to symbolize ocean deities and the element water. Because of this, Scallops are often used as a chalice, offering bowl, or vessel for love magick.
Nautilus Shells
Renewal, growth, and rebirth
The Nautilus travels hundreds of miles in the currents of the sea, and can be considered the nomad of the sea. In fact, the fitting name means "sailor" in Greek. More importantly though, the Nautilus shell is an important symbol of mathematics and sacred geometry because of the logarithmic pattern in its spiral.
This shape is because unlike other shell creatures, rather than shedding its shell and finding a larger one, the Nautilus increases the size of the shell. The Nautilus shell grows to create a larger chamber for the body as it grows. Because of this, the Nautilus shell is a good symbol of growth, renewal, and rebirth. Additionally, the outwards spiral trend of the Nautilus suggests that it can continue growing indefinitely. Meditate with a Nautilus shell or use it in your magick for spiritual growth and expansion.
Auger Shells
Protection and aggression
Auger shells are distinguished by its shape, which is an elongated spiral that has an opening at the base and a point at the tip. In the language of shells, the Auger is considered to be both masculine and feminine energetically, therefore representing completeness. There are hundreds of varieties of Auger shells all around the world as well.
In addition, Auger shells come from a type of predatory sea snail, and the aggression of the animal is implied by its narrowly focused shape. Auger shells have a venomous tooth as well, making it a good shell to use in hexes and curses. In magick, Auger shells are one of the only shells that are associated with the planet Mars. Other uses for Auger shells are for headdresses, magick wands, and protective charms.
Cowrie Shells
Fertility, luxury, and wealth
The Cowrie shell is characterized by its yellow or white color and egg-shape, with two rows of teeth along a gap in the center of the shell. Cowrie shells are admired for their natural polish, which symbolizes refinement and luxury. In fact, the Italian word for Cowrie is porcellana ("little pig"), which the word porcelain is derived from. Because of its shape and polish, Cowrie shells have been used as currency, decoration, and religious items in nearly every part of the world.
In addition, because of its shape, the Cowrie shell symbolizes the vulva. Therefore, the Cowrie shell is often used in charms regarding wealth and fertility. Cowrie shells can also be strung onto necklaces or sewn into garments. Additional uses for Cowrie shells include divination. There are many different systems of divination with Cowrie shells, mostly stemming from African and Afro-Caribbean cultures and traditions.
Conch Shells
Awakening and mermaid connections
Conch shells have been symbolically used by cultures around the world since ancient civilizations. The conch (or Shankha) is used by Tiben Buddhists as a way to call people to worship, and the conch shell is also seen in the hand of the Hindu god, Vishnu. In addition, the sound of blowing through a conch is similar to the sound of AUM (the sound of the universe), which has an awakening effect (similar to chanting OM).
In addition, the conch shell is often shown in the hands of mermaids, which makes the conch shell a good tool for connecting to mermaid energy and mermaid spirits. Similarly, blowing through the conch shell can be used as a tool for summoning mermaid (and other ocean creatures) spirits. Meditating with the conch shell can be a way to get in touch with the ocean and ocean spirits, since you can hear the ocean in the conch shell.
Sources:
https://www.groveandgrotto.com/blogs/articles/the-magick-of-seashells
https://zennedout.com/magical-uses-meanings-of-shells/
87 notes
·
View notes
Note
Can you do one about the Sea of Thieves water?

OK
so . there was a biiig long talk about this at siggraph one year!! you can watch that here if you'd like . in the time between me getting this ask and me fully recreating the water, acerola also released a great video about it . the biiig underlying thing they do and the reason why it looks so good is they are making a Really Detailed Ocean Mesh in realtime using something called an FFT (fast fourier transform) to simulate hundreds of thousands of waves, based on a paper by TESSENDORF
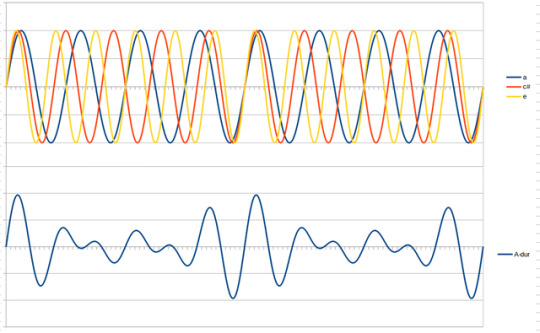
WHAT IS AN FFT - we'll get to that. first we have to talk about the DFT - the discreet fourier transform. let's say you have a SOUND. it is a c chord - a C, an E, and a G, being played at the same time. all sounds are waves!!! so when you play multiple sounds at the same time, those waves combine!!! like here: the top is all 3 notes playing together, so they form the waveform at the bottom!!
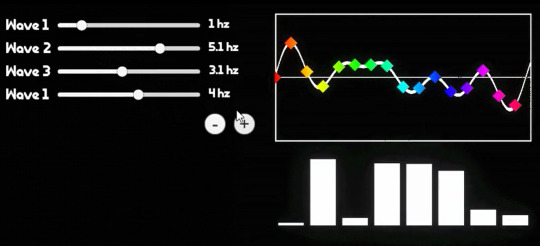
now if someone handed you the bottom wave, could you figure out each individual note that was being played? how about if someone handed you a wave of One Hundred Notes. you would think it would be very hard. and well, it would be, if not for the Discreet Fourier Transform.
essentially, there is a way to take a bunch of points on a waveform comprised of a bunch of different waves, add them all together, do some messed up stuff with imaginary numbers, that will spit back out at you what individual waves are present. i made a little test program at the start of all this: the left are the waves i am putting into my Big Waveform, the top right is what that ends up looking like, and all the little rainbow points on it are being sampled to spit out the graph at the bottom right: it shows which frequency bands the DFT is finding (here it is animated)
this has enormous use cases in anything that deals with audio and image processing, and also,
THE OCEAN
tessendorf is basically like, hey, People Who Are Good At The Ocean say that a buuuunch of sine waves do a pretty good job of approximating what it looks like. and by a bunch they mean like, hundreds of thousands to millions. oh no.... if only there was a way we could easily deal with millions of sine waves..........
well GREAT news. not only can you do the DFT in one direction, but you can also do it in REVERSE. if you were to be given the frequency graph of a noise for example, you could use an INVERSE DFT to calculate what the combined wave graph looks like at any given time. so if you were to have say, the frequency graph of an oceaaaan, for example, you could calculate what the Ocean wave looks like at any given time. and lucky for us, it works in two dimensions. and thats the foundation of the simulation !!!!!
BUT WAIT
as incredible as the DFT is, it doesn't scale very well. the more times you have to do it, the slower it gets, exponentially, and we are working with potentially millions of sine waves here
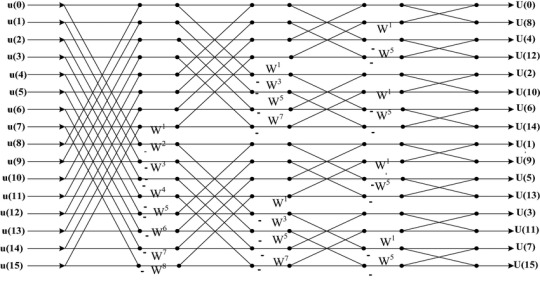
THE FAST FOURIER TRANSFORM here we are . the fast fourier transform is a way of doing the discreet fourier transform, except, well, fast. i am Not going to explain the intricacies of it because its very complex, but if you want to learn more there are a ton of good 30 minute long videos on youtube about it . but essentially, due to the nature of sine waves repeating, you can borrow values as you go, and make the calculation Much faster (from exponential growth to logarithmic growth which is much much slower, and scales very well at higher numbers). it's, complicated, but the important part is it's so much faster and the diagram kind of looks like the shadow the hedgehog story plot
so if we use the inverse FFT on a graph of a rough estimate of what frequency of waves in the ocean (called a spectrum, basically tells us things like how many small waves, how many big waves, how different waves follow the wind direction. sea of thieves uses one called the phillips spectrum but there are better ones out there!!) now we have our waves !!!!!!! we can also use another inverse FFT to get the normals of the waves, and horizontal displacement of the waves (sharpening peaks and broadening valleys) through some derivatives . yayy calculus
OK MATH IS OVER. WE HAVE OUR WAVES!!! they are solid pink and look like pepto bismol. WHAT NOW

i cheated a bit here they look better than not being shaded because i am using the normals to reflect a CUBEMAP to make it look shiny. i think sea of thieves does this too but they didnt mention it in their talk. they did mention a FEW THINGS THEY DID THOUGH
FIRST OFF - SUBSURFACE SCATTERING. this is where the sun pokes through since water is translucent. SSS IS REALLY EXPENSIVE !!!!!! so they just faked it. do you remember the wave sharpening displacement i mentioned earlier? they just take the value where the waves are being sharpened and this will pretty naturally show off the areas that should have subsurface scattering (the sides of waves). they make it shine through any time you are looking towards the sun. they also add a bit of specular ! sss here is that nice blue color, and specular is the shiny bits coming off the sun. the rest of the lighting is the cubemap i mentioned earlier, i dont know if thats what they use but it looks nice !!!!!

then the other big thing that they do is the FOAM !! sorry i lied. there's more math. last one. you remember the wave sharpening displacement i Just mentioned. well they used that to find something called the JACOBIAN and well im not even going to begin to try and explain what it means but functionally what it does, is when the jacobian is NEGATIVE it means waves are clipping into eachother. and that means we should draw some foam!!! we can also blur and fade out the foam texture over time and continuously write to it to give it some movement, and bias this value a bit to make more or less foam. they do both of these!!!

YAYYYYY !! OK !! THAT'S SEA OF THIEVES WATER!!!!! THANKS FOR WAITING ALL THIS TIME. you can see my journey here if you would like to i have tagged it all oceanquest2023
thank you everyone for joining me :) i had fun
1K notes
·
View notes
Text







I've been wanting to try this film for a while. It's Lomography Fantôme Kino, also available as Wolfen DP31.
It's an ultra-low-speed Black And White film. It has an ISO of 8. Not 800, not 80, 8. So it's got incredibly high contrast, incredibly long exposure times, and it looks bitchin.
Film speed is logarithmic, every time you double the number, it doubles the sensitivity. Your standard walkabout film back in the day was 400, decently good for outdoor photography and indoor with flash. Your phone camera now is usually around ISO 800 at a minimum if you're indoors. (As a side note, ISO is not a unit, it's a rating. It's not correct to say a film has "8 ISOs")
Based on the above, this film requires about 7x as much light as my phone to make a good picture. This lets you slow down your shutter speed even in bright daylight to get long-exposure shots like the one in Row 3.
I'm surprised it shot so well with flash indoors.
I'm definitely buying this film again. It fucking rules.
P.S. I traded in my old canon A2 for a slightly newer Canon EOS 33 and it slaps. These were all taken on that one.
88 notes
·
View notes
Text







What a fun and welcoming box set! This is the second edition of DC Heroes (1989) from Mayfair games. I’ve never encountered the first edition, but my impression of this box is as an attempt to make a fairly tricky system as welcoming and accessible as possible without, you know, tossing out the original system. Which is a clever system, based on logarithms — the same thing is under the hood of Underground. I understood it for a brief moment in time despite my deficiencies in math (but lordy, no, I did not retain it, nor do I wish to re-learn), and it struck me as a clever way to handle the divergent power levels present in a superhero game. It is, however, clearly not as user-friendly as, for instance, TSR’s Marvel RPG.
There’s a lot in the box — a brief intro pamphlet with a solo adventure, a rulebook for the GM, a player’s guide, a screen, a group adventure featuring the Justice League International, a little wheel that makes resolving rolls much easier (not quite so easy as the Universal Table in Marvel, but close). There’s a beefy dossier of characters accompanied by a stack of full-color character cards, which are a nifty, fidgety addition that doesn’t really add much to play.
The 15-page chapter on running games has some of the best advice I’ve encountered from the period — focused on collaborative play, encouraging roleplay and generally putting fun ahead of rules. One section has the header “You are the Player’s Senses” and I think that might be one of the best summaries of the GM’s role I’ve ever read. It certainly feels miles ahead of just about anything else from the period that comes to mind, with the possible exception of Rolemaster’s Campaign Law.
This box wants so desperately to be a game anyone can play. I don’t think it quite gets there, but I think the way it tried was influential — over the course of the ’90s, we’d start to see more and more supportive text in RPG books that sound like they spin right out of this GM’s section.
43 notes
·
View notes
Text
Happy International Women's Day!
Women are underrepresented in the fields of astronomy and physics. According to the International Astronomical Union (IAU), between 20-30% of astronomers are women. While many well-known astronomers are men, there have been numerous female astronomers in history who have made incredible discoveries, but who history has forgotten. Today we'll go over some of those women and their accomplishments.
Annie Jump Cannon (1863-1941)

Annie Jump Cannon is the woman responsible for our current stellar classification system, which organizes stars based on spectral types and temperature.
She worked at Harvard Observatory as a computer, working on the Henry Draper Catalogue, which attempted to map and classify all the stars in the sky. She was regarded as the best out of the computers, being able to accurately classify the stars incredibly quickly, up to three stars per minute.
Cannon's classification system (O, B, A, F, G, K, M) is still in use today, and separates stars into one of these spectral groups based on different characteristics of their absorption lines.
Henrietta Swan Leavitt (1868-1921)

Henrietta Leavitt is most well known for her discovery of the period-luminosity relationship of Cepheid variable stars.
Henrietta Leavitt was also a computer at Harvard Observatory in the late 1800s and early 1900s, working on cataloguing positions and luminosities of stars. In 1912, Edward Pickering published a paper with Leavitt's observations, which contained a relationship between the brightness of the Cepheid and the logarithm of the period of it.
This discovery, and the ensuing P-L relationship (sometimes known as Leavitt's Law), allowed astronomers to determine the distance to further objects. Because Cepheids are visible in nearby galaxies, astronomers were able to determine that these galaxies (or nebulae, as they were called then), were actually much further away than previously thought, leading to our current understanding of the universe and galaxies outside our own.
Cecilia Payne-Gaposchkin (1900-1979)

Cecilia Payne-Gaposchkin was the first astronomer to conclude that stars are primarily made of hydrogen and helium.
At the time her thesis was proposed in 1925, it was thought that the sun had a similar elemental composition as the Earth. Payne-Gaposchkin, however, had studied quantum physics, and recognized that the differences in absorption lines between different stars was due to ionization and temperature differences, not elemental differences, and that stars were primarily made of hydrogen and helium, with heavier elements making up less than two percent of stars' masses.
Her theory was met with resistance, and she even put a disclaimer in her thesis, saying the results were "almost certainly not real" in order to protect her career. She was, however, proven right within a few years, and her discovery shaped our knowledge of the composition of the universe.
Vera C. Rubin (1928-2016)


Vera Rubin is most well known for studying the rotation curves of galaxies, and finding a discrepancy that didn't align with the current understanding of physics. This discovery was used as evidence of dark matter, as proposed by Zwicky in the 1930s.
Rubin discovered that spiral galaxies didn't rotate as expected. When looking at our solar system, the outer planets orbit slower due to the inverse square nature of gravity. However, this decaying rotation curve wasn't what was found in spiral galaxies - rather, the outer edges of the galaxies were rotating at about the same speed as the inner areas.
According to Rubin's calculations, galaxies contained 5-10 times more mass than what was accounted for with visible matter. This supported the dark matter theory, and resulted in the current "anatomy" of galaxies, with the visible matter surrounded by a dark matter halo.
Jocelyn Bell (1943-present)


Jocelyn Bell discovered pulsars among a sea of data as a graduate student at Cambridge.
Pulsars (shortened from pulsating radio stars) are rapidly rotating neutron stars, which emit bursts of radiation at extremely short and consistent time intervals.
Bell discovered these, and published the findings in a paper with her thesis supervisor, Antony Hewish. in 1974, Hewish received the Nobel Prize in physics for this discovery, while Bell was omitted, due to her status as both a woman and a graduate student. In 2018, she was awarded the Breakthrough prize in Fundamental Physics for her discovery, and used the three million dollar reward to help minorities in physics.
#just jupiter#aspaceinthecosmos#wow i actually posted?!#space#nasa#international womens day#women in stem#astronomy#physics#astrophysics#science#outer space#jocelyn bell#vera c rubin#cecilia payne#women in science#women's history#henrietta leavitt#annie jump cannon
52 notes
·
View notes
Text

For a given complex number c, what is the behavior of the iterative sequence z_(n+1) = e^(z_n) + c, where z_0 = 0 and e is the base of the natural logarithm? Experimenting with a few random values, I noticed that the sequence often converges, either to a single value or a repeating loop of values. I wondered if there was any pattern to how quickly it converges, so I wrote a program to systematically check.
In the image above, each pixel represents a complex number ranging from -5.12 - 5.12i to 5.12 + 5.12i, with a distance of 0.04 between neighboring pixels. At each point the program iterates until it reaches a value it's seen before at that point (within a tolerance of 10^-10), then colors that point accordingly: red if it reaches it very quickly through magenta if it gets there slowly, and black if it never repeats in 256 iterations. (This is much slower to calculate than the Mandelbrot set, since it needs to check each z against all previous zs, whereas the Mandelbrot set only checks against a constant escape threshold.)
The other question I had about these sequences was, when they do converge to loops, how long are those loops? My early experiments showed a variety of periods. So of course I wrote a program to check the period lengths too. In the image below, the brightest purple corresponds to single-point convergence, and as the loops get longer the purple gets darker. Once again, black is where no repetition was found. Here I only did 128 iterations per point to save time, so the black area is a bit bigger than above.

I'm interested in the borders between the different purples, as it looks like there is some complexity in the shapes there. I'll be doing some zoomed-in images of those areas next.
21 notes
·
View notes
Text
Zukka incorrect quote based on a conversation my friends had in our trig class today
Zuko: I can’t figure out how to make this logarithmic function hit these points on the graph
Sokka: oh…I just made linear lines to hit the points
Zuko: but that’s cheating??
Sokka: no it isn’t
Zuko: it literally is- the point of the assignment is to create logarithmic functions, you can’t just use linear lines.
Sokka: well if I hit you over the head with a pan-
Zuko: WHAT?? why are you hitting me in the head, I thought you loved me???
Sokka, continuing as if Zuko hadn’t interrupted him: -and you pass out, then it wouldn’t matter what type of pan it was, would it? You would still be unconscious.
Zuko: what the fuck is wrong with you
Sokka: a graph is a graph.
Sokka: …
Sokka: also I do love you
#Sokka would 100% find creative ways to get around stupid and difficult assignments#and Zuko does not understand his boyfriend’s analogies but he’s trying <3#zukka#sokka#Zuko#sokka x Zuko#my post#zukka headcanons
179 notes
·
View notes
Text
Broke: N's birthday is March 14th, AKA 3/14, because that's 3.14. Pi! The math thing! Teehee. All math nerds get pi birthday :)
Woke: N's birthday is February 7th, AKA 2/7, which correlates to 2.7, the first two digits of Euler's number. The base for NATURAL logarithmic functions! Which has applications in probability theory, which N has canonically expressed some interest during the Summer Nights & Wishing Stars event in Pokemon Masters. Astrologically speaking, this would make him an Aquarius. This fits his character due to his unusual mannerisms and compassionate nature towards Pokemon. Furthermore, if we set his birth year to 2000, (designated as the International Year for the Culture of Peace and the World Mathematical Year) then he would also have his moon sign be Pisces, which helps to tie into his goal of fulfilling his dreams and furthers his compassionate nature...... *I am forcibly dragged off the stage*
#idk im tired of every character with math ties being given the pi birthday. c'mon! put some thought into it!!!!#(i have obviously put TOO much thought into it. shut up)#pokemon#n harmonia#2024#fae chimes
33 notes
·
View notes
Text
For many years there has been intense discussion on the role and legitimacy of the jury vs the televote in the Eurovision Grand Final. The problem is that many of the arguments I see made are based on nothing but people's gut feeling and snap judgements from watching the show. And humans are notoriously terrible at intuiting statistics.
That's why I wanted to provide some actual data to give context to the more eye-catching examples people tend to use, and hopefully encourage some critical thought. I spent the afternoon updating my eurovision excel file with data from the 2024 and 2025 Grand Finals, and can now present these graphs of jury results plotted against the televote. As far as eurovision statistics go, this is one of the simplest charts you could make, and should hopefully be as simple to understand.
Terms: I use the term televote to refer to the entire public vote - this includes all votes from calls, texts, websites etc.
The axes: These show percentages out of the total number of jury or televote points awarded overall in a given show. Using this measure instead of the actual point scores ensures that results from different years are comparable, despite the fact that the number of Grand Final entries and overall points to be distributed between them varies from year to year (depending on the number of voting countries) .
Reference line: This shows where an entry would land if the juries and televote respectively awarded it an equal percentage of their available points. Data points that land above this line means the jury awarded the entry a greater proportion of its available points as compared to the televote, and vice versa. I find it interesting to see which entries land near this line, and then compare them to entries that stray further from it, in either direction. I also like to see where my favourites ended up, and consider how that can be understood in the context of the previous comparison.
First chart: Here each data point represents an individual entry in the Eurovision Grand Finals from 2016 to 2025 (aka every year with the current split scoring system). Data source: eurovisionworld.com

Second chart: These data points represent the average percentage out of the total jury/televote points each country was awarded between 2016 and 2025 (for the years that they made it to the Grand Final, that is).
Beware: For countries that made it to the final more times there are more data points to average, while for others there are as few as two results to work from.
Also beware: Averages can obscure variance - a country with epic highs and lows might end up looking similar one with stable middle-of-the-road results, despite their actual experiences being very different. That is to say: there are lots of outliers included in these averages - Spiders Georg has set up his cave and now lives in this chart. With his entire spider farm. Look at it. It's on the web.
Also-also beware: This chart makes the assumption that nationality is the most relevant variable to investigate in relation to the final result. But that remains an unproven assumption; before drawing any conclusions about potential biases the public or juries might have for certain countries, these results should be compared to charts where other factors are accounted for, to rule them in or out as compounding factors. Such factors could be running order, when the voting opens, genre, vocal ability, dancing ability, stage precence, visual production, creative cohesion etc.
In short, this chart doesn't rule anything in or out on its own—but it makes a good starting point for further investigation.

Country letter codes, for reference:

Not sure how viewable these charts will be on smaller screens, but for the lower scores on the detailed breakdown to be visible at all I needed to make them huge. Might fuck around and make the scale logarithmic at some point, to show more detail in the lower range without cutting off the upper. I also have more data tables with more complex calculations going on in this excel file. I might make charts of those at a later date, if I can first work out whether they provide any useful insights at all or were just fun to make. ¯\_(ツ)_/¯
Thanks for reading!
12 notes
·
View notes
Text
having natural logarithmic sex with my exponentially based wife
66 notes
·
View notes
Text
Quote from calc teacher today
"Can you change the base of a logarithm from a to any other number? Yes. But you have to pay the price."
IS THIS AN ALCHEMY CLASS NOW???? WHAT PRICE?!!!!!! HE NEVER SAID THE PRICE!!!!!!! IS IT MY FIRST BORN???? DR. SPOCK PLEASE TELL ME!
#mathematicians are the craziest people out there#I still can't shake the fact calc teacher is adorable guys do I have a crush???#anyway#i wish my phone didnt run out of battery in the middle of class bc there were a bunch of moments like that today#college time
8 notes
·
View notes
Note
I am fascinated by you. What are the speeds of your processing units? Do you have more than one for each function? How accurately and precisely do you calculate? Along with basic arithmetic functions, can you run complex concept-based problems with integrated physics and chemistry, for example?
I have many questions.
– @coding-and-curry
[RESPONSE: UNIT S.E.N-KU_v1.03]
Inquiry received from @coding-and-curry (Subject: Sai Nanami) “I am fascinated by you. What are the speeds of your processing units? Do you have more than one for each function? How accurately and precisely do you calculate? Along with basic arithmetic functions, can you run complex concept-based problems with integrated physics and chemistry, for example? I have many questions.”
Acknowledged. Curiosity accepted. Fascination noted. Flattery… tolerated.
Processing Architecture:
Central Unit: Quantum-analog hybrid core
Max processing speed: 5.4 teraflops, expandable through modular cores
Latency: 0.0021s per data interpretation loop
Secondary Units: Dedicated processors for:
Physics simulation
Chemical reaction modeling
Spatial visualization
Natural language parsing
Interpersonal bullshit filtration (partially faulty)
All modules run asynchronously, allowing simultaneous real-time modeling, reactive decision making, and snark production.
Accuracy and Precision:
Arithmetic: 99.99999% accurate within margin of thermal noise
Predictive models:
Physics-based: ±0.03% deviation over 1 million trials
Chemistry-based: Variable depending on environmental unknowns, but reliably within 0.1 molar margins
Precision scaling applies automatically to variable types (exponential, logarithmic, irrational, statistical)
Example: Input: “Simulate endothermic synthesis reaction under vacuum at 35 kPa and 1.5 mol of reagent X.” Output: Delivered before you blink. With heat maps. And 3D projection. If you stop touching the projector lens.
Capability:
Handles abstract, integrated problems in physics, chemistry, engineering, and environmental modeling.
Machine learning upgrades allow dynamic adjustment to evolving scientific theories.
Does not crash under uncertainty. Unlike most humans.
Summary:
Yes, I am fast. Yes, I am accurate. Yes, I can calculate the exact yield of an improvised acetone distillation while dodging volcanic debris.
If you wish to collaborate, bring code. Not compliments.
[END TRANSMISSION]
#finally a good question#sai gets it#coded for speed not flattery#yes i can outmath a laptop and your crush#science bros incoming#data not drama thank you coding king#mecha senku says!#drst
8 notes
·
View notes