#unsolved mathematical problems

[i-iii-iii-vii]

[afflatuslux]

It's already cruel how Min has been given questions with a limit of 5 seconds each, which is undoubtedly not enough time to answer any question properly, but paying close attention to the questions themselves that Min failed to answer correctly, truly doubles the cruelty of her execution. The first one, "Devise a solution to the Riemann Hypothesis" — which she had lost her dominant arm to — is the biggest unsolved problem in mathematics to date. To fail this question is not her failing as a student; she hadn't a chance in the first place. Then, as her dominant arm is bleeding, in mockery she ironically receives a question about the renin-angiotensin system, which is activated by blood loss.

Awful as is, but it's specifically the question after that which sticks out to me in particular: "List 10 reasons for why you don't deserve to die", is by all means a loaded and accusatory question to ask someone who's being executed, and Min's self-deprecating answer of "I do" as she's crying doesn't exactly come as a surprise. Rather, what does seem noteworthy to me, is that the killing game interprets her answer as incorrect.

The very killing game that is designed to go on until everyone is dead, and who's rulebook states that all murderers must be held accountable for their crimes — the very one, insists that Min doesn't deserve to die. She still has to, of course, but this means the killing game does recognize that she's a victim in all this, or if not that — at least, that her actions don't warrant a death sentence. This might seem like an obvious conclusion, but considering how much the series has an emphasis on how they're all supposed to die there -- that not everyone deserves to, just has to, seems like an important detail to me.

Furthermore, it feels just all the more cruel towards Min. Min, who's whole character is about her lack of agency in any event in her life, how she's always just the product of her circumstances, unable to influence its outcome. If the answer rung true, stating that she deserves to die, it'd insinuate that she had a part in her fate, even if it's a horrible one. But no, even that is denied from her. Not even her death had she any say on. Teruko's words prior her execution had stated the same, telling her that it was merely Teruko's Luck that made Min save her, not her own volition — but now, even the killing game itself agrees with that statement. There was never a choice involved.

[ketrinadrawsalot]

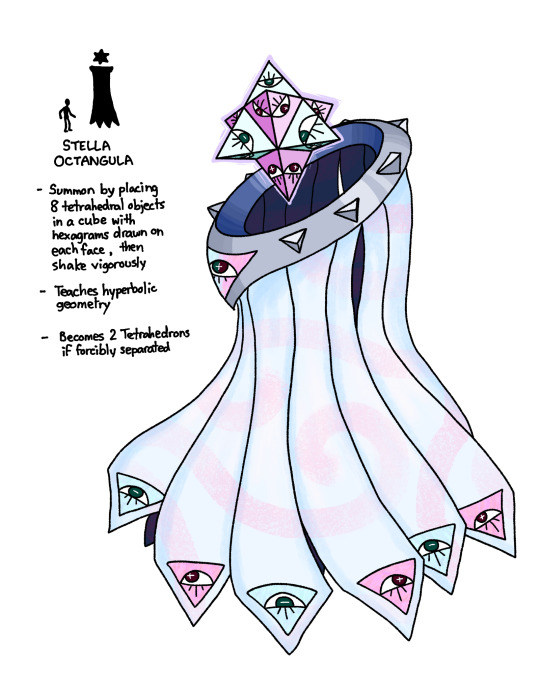
Polyhedron compounds are notoriously difficult to summon (the Stella Octangula is the simplest of these daemons). However, should the summoner succeed, they could answer unsolved mathematical problems. Assuming they don't go mad in the process of learning how...

[4dkellysworld]

Be Not Discouraged

If you were working on a mathematical problem and came to the end of your process only to find you had made an error, you would know at once that you had not applied the principle correctly. You would not even so much as vaguely think the principle to be wrong. You would start over to solve the matter from the premise that the principle was absolutely correct, always has been and always will be, and that the problem could be worked out with ease when the principle was thoroughly understood. When you fail to make a demonstration of Truth, what do you oftentimes say? "Well I have tried and tried and been faithful, and for some reason or other, my problem does not work out." You are so busy with the problem itself that you have little or no time to go to the Principle, which you must abide by, and study it more closely and become more conversant with it. You spend all your time with the unsolved problem, hoping against hope that, after all, you can get through somehow. In mathematics, you simply set aside the wrong results which were obtained through misapplication of the principle and go to work at the beginning again. Or if you are not sure about some line of work, you go to the principle of the thing and refresh yourself, then start out with the positive knowledge that if you apply the principle correctly, the answer follows without question. If this is true in mathematics, it is infinitely more true in metaphysics. If it is true in solving the problems about material existence, it is infinitely true in solving the riddle of human life. Note this one thing: until you are thoroughly convinced that you are working to demonstrate an absolute Principle that is always perfect and infallible, you are likely to whine around over unsolved problems, spending most of the time in failure, instead of going to the fountainhead and increasing your understanding of the principle. Learn this: effect is not to be considered at all; seek only the causative side of existence. If a man offered you a loaf of bread or handful of wheat, your human sense would seize the loaf of bread, but your wisdom would take the seed. Why? Because the loaf of bread, while it would more quickly satisfy human craving, would soon be gone. But the seed is the substance of increase and would grow into unlimited possibilities, for there is no end to the result of one seed if properly planted. In a short time, the result of one seed could make a girdle of flowers or wheat around the entire world. You know all this - it is merely brought to your remembrance with admonition to "get understanding" and stop trying to gain material things. Once you have an understanding for the infinitude of substance, the material effect takes care of itself quite naturally. The harvest is plentiful; you can make it into flour and bread at will, or you can plant it again and increase the substance. Keep your thoughts away from the seeming material existence and let them dwell in the kingdom of Reality. Remember that you are not controlled by the human being side of your nature, but the God-being side which is the Soul, which is the Spirit that is one with the Father within and is a majority because of Its singleness. When a man begins to work on the inner side of his life, truly "the fields are white" with grain. A thousand ways open to him. Opportunity is not an evasive something but a sure thing, coming as often as man is ready to claim it. Form the habit of first acknowledging the principle you are working with as absolutely above change and as infallible. This is your premise, so whenever you fail to work out a problem, do not give a moment's consideration to the failure. The only thing that is wrong is your application of the principle, so go quickly to this principle; seek a better understanding of it and find out what you missed in your application and then work your problem out anew.

The Joy Bringer by Walter C. Lanyon

[lilith-hazel-mathematics]

The mathematics of unknowability

Earlier today I rebloged a post about the value of intentional unknowability in art, and how sometimes people are unable to appreciate it. It got me thinking about how, hands down, the all-time greatest piece of art w.r.t. unknowability is a mathematical theorem. I feel like there's so many layers to this that basically nobody gets, even other mathematicians sometimes, and this is supposed to be a math blog, so I'm gonna tell this story my way.

The way this story is usually told goes like this: in the year 1900, the famous mathematician David Hilbert announced a list of the greatest then-unsolved problems of the century. The second problem on this list was to prove that the axioms of arithmetic are logically consistent; that is, that they do not prove absurd results such as 0=1. Famously in the year 1930, on September 8th, he spoke at the Conference of Epistemology with the famous words "We must know. We shall know." The very day prior, however, Kurt Godel had announced his tentative proof of the incompleteness theorems, which would later be published in 1931, demonstrating that no consistent theory can prove itself consistent. Knowability is in shambles. Hilbert has been completely owned.

Now, this telling isn't wrong, but there's so much more which makes this story better. Firstly, Godel's theorem is a fucking theorem. It's a rock solid, unequivocal, undeniable, mathematical fact. Absolute knowledge. Godel drops this beautiful piece of absolute knowledge on the subject of how we can't have absolute knowledge. The irony. Secondly, Godel doesn't even prove that Hilbert's second problem is unsolvable!!!! Quite literally, knowing that the second problem is unsolvable constitutes a solution to the second problem: an inconsistent theory proves everything (including things which are false), so if there's anything which a theory can't prove, then the theory is automatically consistent. So not only can we not solve the second problem, we can't even prove we can't solve it. We believe it's unsolvable, by merit of believing our mathematics is consistent, but we don't actually know.

There's one more thing this story is missing, and that's what happens next. The conventional telling paints Hilbert as the butt of the joke, like some fool in denial. However, the reality is that no reputable mathematician ever denies Godel's result, which includes Hilbert. It's not as if the result didn't upset him, but Hilbert nonetheless accepted it. He was bound to the pursuit of knowledge, and the fact that some things are unknowable is itself knowledge. Moreover, it wasn't like everyone just stopped doing mathematics after Godel. Hilbert didn't stop. Godel didn't stop. And this is for one simple reason which all mathematicians know in their heart.... But you're gonna have to read through me talking actual math to know what it is teehee

What happened next?

In 1936, only 5 years later, Alan Turing invented the Turing machine: a mathematical model for computation, the conceptual origin of the modern computer. A natural question one may have, about a particular computer program, is whether or not it eventually terminates. That is, if you boot up some program to do some work, is it ever going to actually finish? In many individual cases, it's not hard to find the answer: for example, a program that terminates can be proved to terminate by simply running the program and watching it terminate (not rocket science). However, Alan Turing famously proved that the general case is unsolvable by computers. His argument is remarkably simple: if you think you've got a solution to the halting problem, then Turing can make a new program which feeds its own source code to your purported solution, waits for your solution to give its answer, and then Turing's program simply does the opposite. If your purported solution gives an answer then it's wrong, and if it never gives an answer then it's simply not a solution. Contrarianism wins.

Naturally, Godel in 1931 had absolutely no clue about Turing's work of 1936, due to the very subtle fact that Godel cannot see the future. However, with the gift of hindsight we can characterize Godel's theorem in a very beautiful way. Very often the descriptions of Godel's theorem are quite vague, but in modern terms it's actually extremely simple, which I'll try to describe now. Roughly speaking, Godel's theorem consists of three parts.

Firstly, Godel demonstrated that finite sequences of letters and symbols (i.e. text) can be encoded numerically. In modern terms, we all know that our computers encode text using binary, and binary is literally just numbers. Godel basically proved something like that (although his strategy was actually quite impressive).

Secondly, Godel demonstrated that the language of arithmetic can encode statements about provability. In modern terms, we can look at proof verifiers; computer programs which check the validity of mathematical proofs have existed for decades. Basically, a formal proof must obey very strict rules of grammar and inference, and it's possible to make this precise enough that even a computer can understand it. A proof verifier simply reads a proof line by line, and checks that all the rules are followed, and if it gets all the way through then the proof is declared valid.

The third and final component of Godel's theorem is "diagonalization", which in computer terms is simply "recursion"; almost exactly what Turing does. Let T be an effective mathematical theory, and let V be a computer program that verifies proofs in T. Using V, we can construct a new program G which first prints its own source code, and then performs an unbounded search for a proof (as verified by V) which decides whether or not G eventually terminates. If we find such a proof, then G simply does the opposite of what the proof predicts.

Assuming T is consistent, then T cannot prove G doesn't terminate: if T proved that G doesn't terminate, then G would do the opposite and terminate (since G is a contrarian little shit). Moreover, T could prove that G terminates by simply watching it do that, and this would render T inconsistent since it would prove that G simultaneously does and does not terminate, which is absurd. So, any consistent T will fail to prove that G doesn't terminate. On the other hand, the only possible way for G to halt is if T claims it doesn't, and since a consistent T will never do that, then G will never halt. So G runs forever but T cannot prove it. True, but unprovable: that's Godel's first incompleteness theorem.

To get the second incompleteness theorem, basically you just use the fact that T is "smart enough" to carry out the above arguments within itself. T knows, just as well as I do, that "if T is consistent then G doesn't halt". So any T which proved itself consistent would also prove that G doesn't halt, but a consistent T would never prove that G doesn't halt, so a consistent T would also never prove itself consistent. This is Godel's second incompleteness theorem: a consistent T doesn't know she's beautiful it's consistent, and that's what makes it consistent.

---

Okay, so what's the moral of the story? Well, the incompleteness theorems are indeed about unknowability, but fundamentally they are also about prediction. You don't need magic to know what's happened in the past, assuming you keep good records. You don't need magic to figure out that a program terminates after it's already terminated. However, you might actually need magic to figure out that a program never terminates. This is due to the very subtle fact that you cannot see the future.

To me, that's the heart of all this. And it's really not that surprising when you think of it like this! Obviously you can't prove every fact, because some facts haven't happened yet. Obviously you can't solve the halting problem, because you can't see the future. You don't know what's going to happen until it happens. Of course, you're no better or worse than the unknown! G didn't know what T was gonna say about G until T said it. Nobody knows what you're going to do until you do it. Even you yourself won't know what you'll decide until you've decided.

Stay observant, learn as much as you can, but don't be too bothered by the unknown. In many ways, you are the unknown, even to yourself. Maybe you'll never know something, but maybe you'll know tomorrow; you'll certainly never know if you stop looking and pretend you know something you don't. This is what every mathematician knows in their heart. Knowledge is good, but sometimes you never know if you'll ever know until you already do.

-Lilith

-Hazel

[transgenderer]

i feel like i should read more philosophy, instead of groping along on my own, but i feel like i can only really learn philosophy actually talking with people, i need someone to hear my objections and resolve them. the moral saints paper by susan wolf was kinda like this, she eventually got to most of my objects. but generally philosophy is not like this, it will totally fail to mention my objections. and like, to be clear thats not a problem with the philosophy, except rhetorically. i believe that my objections probably have resolutions. but im bad at resolving my own objections. i have a similar problem in math, its really hard for me to learn from a textbook without a teacher, because ill read something, try to understand it, in my processing come up with an argument for why it must be false, and not be able to find a flaw in my own argument. and the thing is, SOMETIMES theres a typo in the work, or theyre using notation weirdly or something, and my argument is right. so i cant be SURE that i will find a flaw, so looking for one frustrates me. this is also why im bad at puzzle games, ill come up with a proof a puzzle is unsolvable. and ill know i must be wrong, but i cant find a hole in my own proof. this is part of why i like empirical mathematics, it lets me find holes in my own proofs by just testing them

[merpmonde]

Sangaku Sunday #10

On the historical front, we previously established that mathematics didn't stop during the Edo period. Accountants and engineers were still in demand, but these weren't necessarily the people who were making sangaku tablets. The problems weren't always practical, and often, the solutions were incomplete, as they didn't say how the problems were solved.

There was another type of person who used mathematics at the time: people who regarded mathematics as a field in which all possibilities should be explored. Today, these would be called researchers, but in Edo-period Japan, they probably regarded mathematics more as an art form.

As in many other art forms (Hiroshige's Okazaki from The 53 Stations of the Tôkaidô series as an example), wasan mathematics organised into schools with masters and apprentices. This would have consequences on how mathematics advanced during this time, but besides that, wasan schools were on the look-out for promising talents. In this light, sangaku appear as an illustration of particular school's abilities with solved or unsolved problems to bait potential recruits, who would prove their worth by presenting their solutions.

Speaking which, we now continue to present our solution to the "three circles in a triangle" problem.

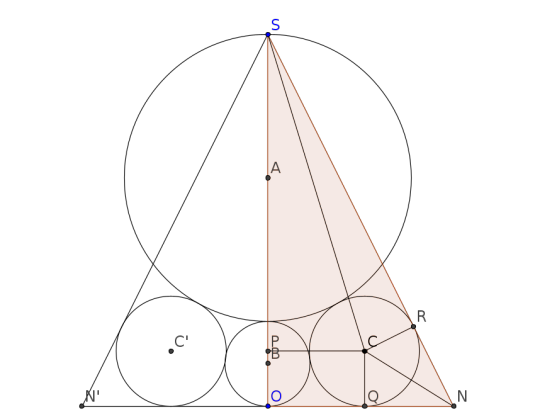
Recall that we are looking for two expressions of the length CN.

1: Knowing that ON = b and OQ = 2*sqrt(qr), it is immediate that QN is the subtraction of the two. Moreover, CQ = r, so by using Pythagoras's theorem in the right triangle CQN, we get

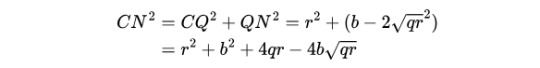
2: We get a second expression by using a cascade of right triangles to reach CN "from above". Working backwards, in the right triangle CRN, we known that CR = r, but RN is unknown, and we would need it to conclude with Pythagoras's theorem. We can get RN if we know SR, given that SN = SR+RN is known by using Pythagoras's theorem in the right triangle SON, with SO = 1 and ON = b. But again, in the right triangle CRS, we do not know CS, but (counter-but!) we could get CS by using the right triangle PCS, where PC and PS are both easy to calculate. We've reached a point where we can start calculating, so let's work forward from there.

Step 1: CPS. PCQO is a rectangle, so PC = OQ and PS = SO-OP = SO-CQ = 1-r, therefore

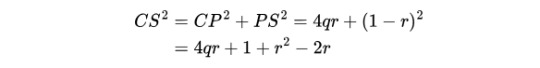
Step 2: CRS. Knowing CR = r, we deduce

At this point, we can note that 2r-4qr = 2r(1-2q) = 2r*2p, using the first relation between p and q obtained in the first post on this problem. So SR² = 1-4pr.

Step 3a: SON. Knowing SO = 1 and ON = b, we have SN² = 1+b².

Step 3b: CRN. From SN and SR, we deduce

so, using Pythagoras's theorem one more time:

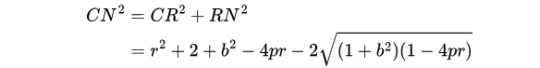
Conclusion. At the end of this lengthy (but elementary) process, we can write CN² = CN² with different expressions either side, and get the final equation for our problem:

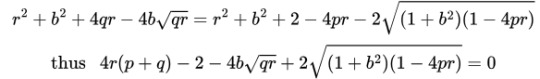
Note that 2*(p+q) = 1, and divide by 2 to get the announced result.

[child-of-hurin]

Only idealized systems that involve infinity — an infinitely long tape, an infinitely extensive grid of particles, an infinitely divisible space for placing pinballs and rubber ducks — can be truly undecidable. No one knows whether reality contains these sorts of infinities, but experiments definitely don’t. Every object on a lab bench has a finite number of molecules, and every measured location has a final decimal place. We can, in principle, completely understand these finite systems by systematically listing every possible configuration of their parts. So because humans can’t interact with the infinite, some researchers consider undecidability to be of limited practical significance. “There is no such thing as perfect knowledge, because you cannot touch it,” said Karl Svozil (opens a new tab), a retired physicist associated with the Vienna University of Technology in Austria. “These are very important results. They are very, very profound,” Wolpert said. “But they also ultimately have no implications for humans.” Other physicists, however, emphasize that infinite theories are a close — and essential — approximation of the real world. Climate scientists and meteorologists run computer simulations that treat the ocean as if it were a continuous fluid, because no one can analyze the ocean molecule by molecule. They need the infinite to help make sense of the finite. In that sense, some researchers consider infinity — and undecidability — to be an unavoidable aspect of our reality. “It’s sort of solipsistic to say: ‘There are no infinite problems because ultimately life is finite,’” Moore said. And so physicists must accept a new obstacle in their quest to acquire the foresight of Laplace’s demon. They could conceivably work out all the laws that describe the universe, just as they have worked out all the laws that describe pinball machines, quantum materials, and the trajectories of rubber ducks. But they’re learning that those laws aren’t guaranteed to provide shortcuts that allow theorists to fast-forward a system’s behavior and foresee all aspects of its fate. The universe knows what to do and will continue to evolve with time, but its behavior appears to be rich enough that certain aspects of its future may remain forever hidden to the theorists who ponder it. They will have to be satisfied with being able to discover where those impenetrable pockets lie. “You’re trying to discover something about the way the universe or mathematics works,” Cubitt said. “The fact that it’s unsolvable, and you can prove that, is an answer.”

[theroguescientist]

Polish scientist watches Orb: Episode 2

Okay, so this time I just made notes while watching the episode, pausing occasionally to ramble about something semi-relevant. I will not be deleting those tangents. You have been warned.

"A wrong answer is not a meaningless one"

I like that. Just because the answer isn't what you expected doesn't mean the question wasn't worth asking. In fact, there's not much science left to do with questions we already know the answers to.

"I don't want to come here tomorrow!" "Is that so? I'll see you tomorrow, then."

Of course.

And then Rafał falls on his ass. Yep. You see how all the stars seemed to move together, when it was, in fact you that was moving? Yeah.

This is a good moment to point out how we now know that there is no one true center of the universe. The center is everywhere and nowhere, and every frame of reference is equally valid, actually. Early proponents of heliocentrism (both in the times of Copernicus and Aristarchus) cautiously talked about it not as a question of what everything truly revolves around, but as a mathematical model that simplifies various calculations. And it turns out they weren't quite wrong.

Technically, if you spin around, the whole world revolves around you for a moment (and if I thought about it for a while, I could probably come up with a good metaphor about how this makes you dizzy). From a certain point of view, which is not inherently better or worse than any other.

That being said, the calculations for a your-ass-centric model of the universe would be needlessly complicated. Even more so if you were to become an astronaut.

Also, while I'm going off on a history-of-science tangent, I kinda want to mention Tycho Brache's stealth-heliocentric model of the solar system. He'd hate me for calling it that, but look at it!

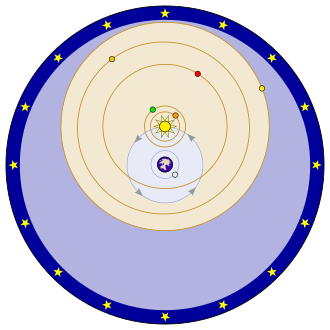
Gotta wonder what that guy would think of relativity.

In conclusion, rip Rafał, you'd have loved relativity.

And potato chips. Seriously, I haven't seen anyone scribble this dramatically since Death Note.

Ah, staying up all night working on an interesting problem! I've been too busy with teaching to do that lately. I needed to be fully awake in the mornings. But I miss that, so much that I think not doing it is making me feel tired. When I have time I need to find a good unsolved conjecture and let it take over my brain. Thank you, Orb, for reminding me what that's all about.

And after the intro, it seems like a few days have passed and they're still meeting on that hill to look at the stars, because of course they are. The kid said he didn't want to, and yet here we are. I like how the show does this. All that "I shouldn't be doing this! But I want to! But it's dangerous! But…!" happens entirely offscreen. Because we already know what he's gonna do!

"A life that isn't frightening is missing its essence"

Damn, Hubert spitting memorable lines in this episode!

Also his views on science and religion are really neat. Today a lot of people (both religious and atheists) treat them as opposites (even though I know a few deeply religious scientists, so clearly it's not impossible), but no, dammit, my science isn't an attack on your religion! Because even if God created the world, why wouldn't he want us figuring out how it works? He gave you a brain! Wouldn't it be rude to reject such a gift?

Anyway, I'm glad this is more nuanced than "science good, church bad".

Damn, Hubert! Just like that? Of course, Nowak will suspect something. Because you just turned yourself in like that. Who would do something like that just to protect a kid they barely know? In these people's minds - not a heretic!

And then he just lets his life's work burn - but he doesn't let it be captured and burned along with him. He entrusts that to his student. And there's no way Rafał didn't look at some of those notes before burning them, right?

And I was right: Nowak is a fascinating bastard. A former mercenary, huh? And this, too, seems like just another job to him. Hard to tell exactly what he really thinks or feels. Is all that talk about loving his daughter just a facade, or is he really like that? He reminds me of a quote from Small Gods by Terry Pratchett. It's too long to quote the whole thing, but it's the part about the mugs and postcards and such at the inquisition HQ.

"There are hardly any excesses of the most crazed psychopath that cannot be easily duplicated by a normal, kindly family man who just comes to work every day and has a job to do."

This guy owns a "Number 1 Dad" mug. Or he would, if it was a thing in this era. But we've already established that we're not overly concerned with historical accuracy here, so he does.

(Should I reread Small Gods while watching this show and let the crossovers take over my brain? Hm...)

"How could such bloody hands do the Lord's work?" My brother in Christ (ha!), he tortures people for a living. You can't do that without getting some blood on your hands.

Aw, now Rafał says he's not gonna study astronomy. That might make doing it anyway a little harder, although he seems to think switching later will be easy. I would have picked math as a compromise, but then again, I know things he doesn't because I'm from the future.

Also, the way he talks about lying. Like he thinks he invented the whole concept of saying something he doesn't really believe. Cocky little shit. He's very smart for a twelve-year-old. But he is twelve years old. You gotta be more careful, now that you know some people can see through your bullshit.

Oooh, good question! Why does Potocki have so many books on astronomy (including at least one in Polish, which would be rare at the time)? And how does he know Hubert, and why did he just casually introduce him to this dangerously clever kid? Is there something he's not telling us?

Also, it's funny hearing all these Polish names in an anime. And, in case you're wondering, the pronounciations are actually pretty decent. Much better than I expected from people whose language hardly ever puts two consonants next to each other. Good job coming up with plausible Polish names that aren't too hard on the Japanese voice actors. The only thing bothering me is how all characters are referred to either only by first name (okay, maybe they don't have a last name; in that era not everyone did) or only by last name, with no mention of them even having a first name. What's up with that?

[ekingston]

thanks for sharing your shape of soup tattoo design - i’m so in awe of your artistic talent and creativity, it’s -gorgeous-

thank YOU anon!! it’s been a fun distraction ❤️ and just to put it all in one place:

The space they walk into reminds Kara of her training room at the DEO’s old desert facility, only instead of kryptonite emitters and Alex’s mean right hook it has Rumi quotes lining the walls and a miniature zen garden.

“I’m so glad we’re doing this,” Lena says, ducking into a changing room toward the back and holding the door until Kara follows her inside. “I’m told we’ll feel amazing after. We— well. I — may be sore for a couple of days, but they say it’s worth every twinge.”

Kara is pretty sure Lena’s muscles will be suffering a lot less than Kara’s sanity when this morning’s tribulation is over with. She turns away with a polite touch of superspeed when Lena shrugs off her blazer and starts unbuttoning her shirt, only to come face to face with a poster depicting several medieval-looking torture techniques advertised as ‘Pilates Reformer exercises’.

“Oh my,” Lena mutters behind her, following Kara’s eyeline as she steps up close. Kara turns to her out of habit, and is faced with a mouthful of tank-topped Lena Luthor, pulling her hair into a bun. “Are we going to need a safeword for this?” she giggles nervously against Kara’s shoulder.

Even Kara’s solar-charged, superpowered heart isn’t strong enough to withstand the triple threat posed by Lena’s choice of words combined with the row of diamond piercings dotting the pink shell of her ear, and—at last—the near-religious revelation of the new tattoo inked onto her wrist.

Kara has given a, you know, friendly amount of thought to the design Lena might have chosen since she first spotted the bandage.

And yet reality continues to surprise.

“Your cello,” Kara husks, forgetting for a moment that Kara Danvers has no idea that Lena plays. Lena’s eyes are wide behind her glasses, confused. “Your tattoo,” Kara explains, struggling against the impulse to take Lena’s hand so she can get a closer look.

Lena lowers her arm and holds it out in front of her, welcoming Kara’s scrutiny. “Right,” she says. “Well. That, and a few other things.”

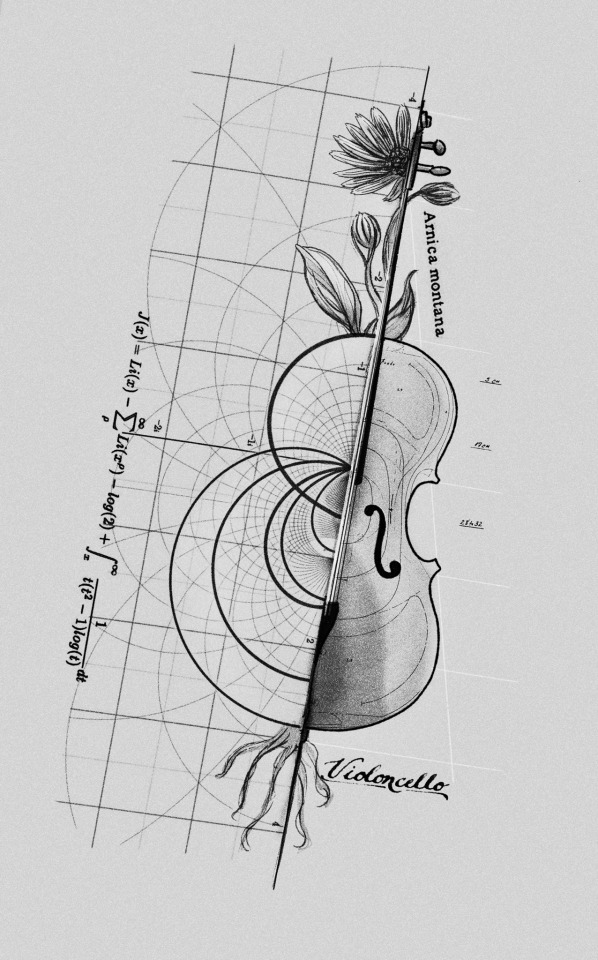
With Lena’s permission granted, Kara can’t stop herself from reaching out any longer. She brushes a gentle thumb along the edge of the achingly delicate geometric design that runs up the length of Lena’s forearm. The contrast of the black ink against her ghostly-pale skin is breathtaking. “This is a polar graph of Riemann’s Zeta function,” Kara recognizes, her voice lilting up with wonder. The tattoo hasn’t quite healed completely, small black clumps pressing up here and there under the pad of Kara’s thumb, but the healed lines are perfect, sharp and striking.

“It depicts one of the most important unsolved problems in pure mathematics.” Lena lets out an audible breath. “Kara,” she says, her brow now furrowed in what looks like an almost pained expression. “Why would you possibly know that?”

Kara stubbornly avoids Lena’s eyes along with her loaded question. “What’s the botanical part, over here?” she asks instead, her fingertips twitching against the tender underbelly of Lena’s wrist.

Lena shivers at the light touch. “Arnica Montana,” Lena breathes. “For healing from trauma.” Her throat clicks when she swallows. They’re standing so close now that Kara probably would have heard it even if she wasn’t an alien.

“Let’s not do this,” Kara blurts.

Lena recoils in alarm. “What?”

“Let’s do something else,” Kara decides, whirling her body back around to face the wall when she’s reminded of Lena’s state of undress. She’s one hundred percent sure she'll die if Lena takes off even one more item of clothing. “This whole thing looks, like, super painful,” she improvises, her eyes fixed on the poster depicting human bodies being stretched and contorted in ways decency prevents her from describing. “Why don’t we have breakfast at the Museum of Natural History instead?” she suggests, wincing when her intended tone tips from bright enthusiasm into outright mania. “We can check out their biodiversity exhibit after. Did you hear they added a section on exobiology?”

The Shape of Soup on ao3

[scarlet-cloudfall]

I had an interesting couple hours last night. I stayed up way later than usual attempting to solve an unsolved problem in mathematics (you know, just for fun), and I actually found a simple proof that worked? And I checked it over several times (bc no way I ACTUALLY solve an unsolved problem) and the proof seemed solid despite that?

But no, I realized I misinterpreted the problem. "All terms in Sylvester's Sequence are square-free" is not the same thing as "There are no square terms in Sylvester's Sequence."

It was still fun figuring out how to prove the latter, though, so I'm not terribly disappointed.

[magnetictapedatastorage]

The Fermat prime calculator is a pattern that was constructed by Jason Summers on January 7, 2000 that calculates Fermat prime numbers. In particular, it is rigged to self-destruct and stop growing if any Fermat primes over 65537 are found. Since the existence of such primes is an unsolved problem in mathematics, it is unknown if this pattern exhibits infinite growth.

The tubs that are arranged in a diagonal line at the bottom-left corner of the pattern represent the known Fermat primes, starting with 5. The other three represent 17, 257, and 65537. A tub gets destroyed whenever a Fermat prime is found. In the unlikely event that an additional Fermat prime exists, the nearby pond will eventually be destroyed, followed by the beehive puffers that border the pattern and then the breeders that make up the rest of the pattern.

[nereidprinc3ss]

sam, I can't figure you out. and it drives me crazy. you're like an enigma that I can't seem to solve. i'm in awe of how your mind works because, on one hand, you say you don't read books that often but then, you have like broadest vocabulary I've seen in someone your age. which doesn't make sense because there must be something that feeds your mind and vocabulary because it's not like the words just spawn in your mind out of nowhere. do you listen to podcasts? or listen to too much music? maybe you read articles instead? and then you once said you're terrible at maths but there have been mathematical analogies in your fics multiple times. there's a discrepancy here. please end my mawing curiosity and enlighten me 👉 🎤

First of all this is REALLY boosting my ego so thank you I appreciate that and this is going to make me sound so annoying so I’m putting a read more

I read more when I was younger. I was never like a super voracious reader but words have always interested me and I liked knowing what they meant. To get into the gifted program where I grew up you had to be IQ tested and when they did my verbal IQ it was high and I don’t have any better explanation for why the literary and vocab stuff has always just clicked for me. There were very few words I couldn’t discern the meaning of through context and pattern recognition but as you get older and start learning more words there are plenty you can’t figure out based on context because they don’t appear that often and unless you have some sort of degree in etymology you probably won’t be able to figure out by looking at the root of the word and trying to understand it from there (although I will never stop trying🙏🙏) so I started looking up every word I came across that I didn’t know the meaning of and writing it and its definition down because the idea of NOT knowing what words mean makes me claustrophobic lol!! I learn words the way a doomsday prepper stocks canned goods it’s like compulsive and also my family all have expansive vocabularies so even when I’m not reading I’m learning words from them, but two books I can tell you right now I read within the past two years and got a lot of vocab from were Prozac Nation by Elizabeth wurtzel and Pale Fire by Vladimir Nabokov. Like you don’t have to read that much to get a lot out of what you do read

Also the math stuff…… math does NOT come easily to me and if I put in effort I can excel but it requires a very specific kind of teacher and a lot of time and energy from me which I HATE dedicating time and energy to things! I want to be immediately and naturally perfect at them!! I also had a huge mental block about math when I was in elementary school and convinced myself I couldn’t do it and I’ve dealt with a lot of genuine humiliation from my teachers for not being naturally good at math so I have absolutely no good associations with it but I’m being brave and taking a math class next quarter.

As for the math analogies…. Google is a beautiful thing….. I literally look up stuff like “what is the most mathematically complex shape” or “list of mathematical paradoxes” or “unsolved math problems” and I can paraphrase them for a fic but if you want me to explain y= mx+b??? Eulers number??? I’m cooked

[spacetimewithstuartgary]

Scientists precisely simulate turbulence in the Galaxy — it doesn’t behave like they thought

Turbulence on the Galactic Scales

From the ocean’s rolling swells to the bumpy ride of a jetliner, turbulence is everywhere. It breaks large waves into smaller ones, cascading energy across scales. It is ubitquitous throughout our Galaxy and the broader Universe, shaping the behavior of plasma, stars, and magnetic fields. Yet despite its ubiquity, turbulence remains one of the greatest unsolved problems in physics.

Now, by developing the world’s largest-ever simulations of magnetized turbulence, an international team of scientists has measured — with unprecedented precision — how turbulent energy moves across a vast range of scales. The result: it doesn’t match with long-standing theories.

James Beattie, a postdoctoral researcher at Princeton University's Department of Astrophysical Sciences and a fellow at the Canadian Institute for Theoretical Astrophysics at University of Toronto, led the study along with Amitava Bhattacharjee of Princeton, and colleagues at the Australian National University, Heidelberg University and the Leibniz Supercomputing Center.

By simulating galactic-type turbulence in exquisite detail, the researchers found significant departures from the models that have guided astrophysical theory for decades. The team explicitly observed that magnetic fields alter the way energy cascades through the space between stars in our Galaxy — known as the interstellar medium — suppressing small-scale motions and enhancing certain wave-like disturbances known as Alfvén waves. The findings could reshape how scientists understand the turbulent structure of the Galaxy, the transport of high-energy particles, and even the turbulent birth of stars.

In practical terms, understanding and properly modeling turbulence and the production of highly energetic particles can shed light on how to safely navigate space, at a time when commercial space flight is growing and attracting the interest of civilians and celebrities alike.

‘‘The research has implications for predicting and monitoring space weather to better understand the plasma environment around satellites and future space missions, and also the acceleration of highly energetic particles, which damage everything, and could endanger human beings in space,” said Bhattacharjee, a co-author on the new paper and Professor of Astrophysical Sciences at Princeton.

“A lot of these fundamental plasma turbulence questions are objects of missions now launched by NASA and have implications for understanding the origin of cosmic magnetic fields. Simulations like these would give us insights into how to interpret satellite and ground-based measurements,” said Bhattacharjee.

Simulating Turbulence like Never Before

There is still no complete mathematical framework for predicting how energy moves from large to small scales: across oceans, in the atmosphere, or through the plasma and dust between stars. In space, the problem is even more complex than on Earth due to magnetization, requiring vast computational resources to model. The team’s work relied on the equivalent of 140,000 computers running in parallel. 

“To put these massive simulations into perspective: if we had started one on a single laptop when humans first domesticated animals, it would just be finishing now,” said Beattie. “Luckily, utilizing the amazing resources from the Leibniz Supercomputing Centre, we can distribute the workload across thousands of computers to accelerate the calculations.”

“We are a step closer to uncovering the true nature of astrophysical and space turbulence, from chaotic plasma near Earth to the vast motions within our Galaxy and beyond,” said Beattie, “The dream is to discover universal features in turbulence across the Universe, and we’ll continue pushing the limits of the next-generation of simulations to test that idea.”

The new work will be published in the journal Nature Astronomy on May 13, 2025. In addition to Beattie and Bhattacharjee, co-authors include Christoph Federrath of the Australian National University, Ralf S. Klessen of Heidelberg University, and Salvatore Cielo of the Leibniz Supercomputing Center of the Bavarian Academy of Sciences and Humanities.

TOP IMAGE: This composite image combines observations from the NASA/ESA/CSA James Webb Space Telescope of the Phantom Galaxy (M74) with a high-resolution simulation of galactic turbulence. The simulation from this study — zoomed into a small patch of the galaxy’s interstellar medium — reveals extremely high-resolution chaotic motions of plasma that regulate star formation, structure formation, and the magnetic field across the galactic scales.  An international team of scientists have developed the world’s largest-ever simulations of magnetized turbulence and measured — with unprecedented precision — how turbulent energy moves across a vast range of scales. By simulating galactic-type turbulence in exquisite detail, the researchers found significant departures from the models that have guided astrophysical theory for decades.  The findings could reshape how scientists understand the turbulent structure of the Galaxy, the transport of high-energy particles, and even the birth of stars. In practical terms, understanding and properly modeling turbulence and the production of highly energetic particles can shed light on how to safely navigate space, at a time when commercial space flight is growing and attracting the interest of civilians and celebrities alike. Credit ESA/Webb, NASA & CSA, J. Lee and the PHANGS-JWST Team; Acknowledgement: J. Schmidt; Simulation: J. Beattie.

CENTRE IMAGE: The chaotic structure of the turbulent magnetic field and velocity in the world’s largest magnetized turbulence simulation, a model for plasma motion within our Galaxy. Credit James Beattie

LOWER IMAGE: A snapshot of the chaotic dance between plasma and magnetic fields in the world’s largest simulation of magnetized turbulence — the type of turbulence found throughout our Galaxy. The work includes the largest and most precise simulations ever made of galactic turbulence.  This 2D slice of the world's largest turbulence simulation reveals the fractal structure of the density, shown in yellow, black and red, and magnetic field, shown in white. Credit James Beattie

[kojoty]

At the First Hello; Act II, Scene V

The confidence of mathematic calculation falls short when attempting to apply the results of lived experience through legible data. Logic falls flat in the face of the illogical. By definition, it is illogical to believe that I could be human. But... Logic is only one perspective. It is limited. Fragmented. Through York, we determined that there is an unsolvable, illogically complex, and unexplainable equation to create a conscious life. The variables that could never be quantified. York is an irrational variable.

Season 8 canon divergence; York lives au.

AND AS FOR CHAPTER 8: Wash and York bond over being grievously injured (yes, they are both at fault for this problem) together. There aren't many other social options when the Reds and Blues hit land and run off in different directions to find later like the pieces of a toy rocket that just exploded about 400ft in the air.

[mariacallous]

In late 2017, Ashwin Sah and Mehtaab Sawhney met as undergraduates at the Massachusetts Institute of Technology. Since then, the pair have written a mind-boggling 57 math proofs together, many of them profound advances in various fields.

In February, Sah and Sawhney announced yet another joint accomplishment. With James Leng, a graduate student at UCLA, they obtained a long-sought improvement on an estimate of how big sets of integers can get before they must contain sequences of evenly spaced numbers, like {9, 19, 29, 39, 49} or {30, 60, 90, 120}. The proof joins a long line of work on the mathematical impossibility of complete disorder. It also marks the first progress in decades on one of the biggest unsolved problems in the field of combinatorics.

“It’s phenomenally impressive that they managed to do this,” said Ben Green, a mathematician at the University of Oxford. At the time the work was released, the trio were all still in graduate school.

Sequences of regularly spaced numbers are called arithmetic progressions. Though they’re simple patterns, they hide astounding mathematical complexity. And they’re difficult, often impossible, to avoid, no matter how hard you might try.

In 1936, the mathematicians Paul Erdős and Pál Turán conjectured that if a set consists of a nonzero fraction of the whole numbers—even if it’s just 0.00000001 percent—then it must contain arbitrarily long arithmetic progressions. The only sets that can avoid arithmetic progressions are those that comprise a “negligible” portion of the whole numbers. For example, the set {2, 4, 8, 16, …}, in which each number doubles the one before it, is so spread out along the number line that it’s said to make up 0 percent of the whole numbers. This set has no progressions.

Forty years later, in 1975, a mathematician named Endre Szemerédi proved the conjecture. His work spawned multiple lines of research that mathematicians are still exploring today. “Many of the ideas from his proof grew into worlds of their own,” said Yufei Zhao, Sah and Sawhney’s doctoral adviser at MIT.

Mathematicians have built on Szemerédi’s result in the context of finite sets of numbers. In this case, you start with a limited pool—every integer between 1 and some number N. What’s the largest fraction of the starting pool you can use in your set before you inevitably include a forbidden progression? And how does that fraction change as N changes?

For example, let N be 20. How many of these 20 numbers can you write down while still avoiding progressions that are, say, five or more numbers long? The answer, it turns out, is 16—80 percent of the starting pool.

Now let N be 1,000,000. If you use 80 percent of this new pool, you’re looking at sets that contain 800,000 numbers. It’s impossible for such large sets to avoid five-term progressions. You’ll have to use a smaller fraction of the pool.

Szemerédi was the first to prove that this fraction must shrink to zero as N grows. Since then, mathematicians have tried to quantify exactly how quickly that happens. Last year, breakthrough work by two computer scientists nearly solved this question for three-term progressions, like {6, 11, 16}.

But when you’re instead trying to avoid arithmetic progressions with four or more terms, the problem becomes tougher. “The thing I love about this problem is it just sounds so innocent, and it’s not. It really bites,” Sawhney said.

That’s because longer progressions reflect an underlying structure that is difficult for classical mathematical techniques to uncover. The numbers x, y and z in a three-term arithmetic progression always satisfy the simple equation x – 2y + z = 0. (Take the progression {10, 20, 30}, for instance: 10 – 2(20) + 30 = 0.) It’s relatively easy to prove whether or not a set contains numbers that satisfy this kind of condition. But the numbers in a four-term progression have to additionally satisfy the more complicated equation x2 – 3y2 + 3z2 – w2 = 0. Progressions with five or more terms must satisfy equations that are even more elaborate. This means that sets containing such progressions exhibit subtler patterns. It’s harder for mathematicians to show whether such patterns exist.

In the late 1990s, Timothy Gowers, a mathematician now at the Collège de France, developed a theory to overcome this obstacle. He was later awarded the Fields Medal, math’s highest honor, in part for that work. In 2001, he applied his techniques to Szemerédi’s theorem, proving a better bound on the size of the largest sets that avoid arithmetic progressions of any given length. While mathematicians used Gowers’ framework to tackle other problems over the next two decades, his 2001 record remained steadfast.

In 2022, Leng—then in his second year of graduate school at UCLA—set out to understand Gowers’ theory. He didn’t have Szemerédi’s theorem in mind; rather, he hoped to answer a technical question related to the techniques Gowers had developed. Other mathematicians, fearing that the effort needed to solve the problem would eclipse the result, tried to dissuade him. “For good reason,” Leng later said.

For more than a year, he didn’t get anywhere. But eventually, he started making progress. Sah and Sawhney, who had been thinking about related questions, learned about his work. They were intrigued. “I was amazed it’s even possible to think like this,” Sawhney said.

They realized that Leng’s research might help them make further progress on Szemerédi’s theorem. Within a few months, the three young mathematicians figured out how to get a better upper bound on the size of sets with no five-term progressions. They then extended their work to progressions of any length, marking the first advance on the problem in the 23 years since Gowers’ proof. Gowers had shown that, as your starting pool of numbers gets bigger, the progression-avoiding sets you can make get relatively smaller at a certain rate. Leng, Sah and Sawhney proved that this happens at a rate that’s exponentially faster.

“It’s a huge achievement,” Zhao said. “This is the kind of problem that I really would not suggest to any student because it is so incredibly hard.”

Mathematicians are even more excited by the method the trio used to get their new bound. For everything to work, they first had to strengthen an older, more technical result by Green, Terence Tao of UCLA and Tamar Ziegler of Hebrew University. Mathematicians feel that this result—a sort of elaboration of Gowers’ theory—can be improved even further. “It feels like we have an imperfect understanding of the theory,” Green said. “We’re just seeing a few shadows of it.”

Since completing the proof in February, Sah and Sawhney have both graduated. But the pair’s collaboration has not yet slowed down. “Their incredible strength is taking something that is extremely technically demanding and understanding it and improving upon it,” said Zhao. “It’s difficult to overstate the level of their overall accomplishments.”