#2.71828...

[aspensmonster]

I wasn't pretending. Euler's number *is* my favourite number.

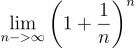
2.718281828459045...

Veep 7.07 "Veep"

[alifotografiert]

[zemathememequeen]

What's a trans girl's favourite number?

Approximately 2.71828

[viewofagarden]

Dandy's World OC: Calvin the Calculator

Bio and details below!

“Numeracy is Calvin’s middle name! He may be a little awkward at times, but you can always count on him to help you need him! He teaches children the basics of math and how to apply it to everyday life.”

Full Name: Calvin Euler  Other Name: Calvin the Calculator Species: Calculator Gender: Male (He/Him) Voice Claim: Peter Oldring (Cody - Total Drama)

Dandy Store Quote

“You can always “count” on Calvin! Hehe!”

Requirements

3141 Ichor

50% Research on Twisted Calvin

Appearance

Calvin is a blue calculator with a light yellow LCD screen, which displays his eyes and mouth. He wears a blue argyle vest underneath a white dress shirt with long sleeves, a pair of dark blue pants, and brown shoes. He also wears a pair of blue-colored glasses.

His buttons are below his screen. All of them are dark blue except for the equals button, which is orange.

Personality

As expected, Calvin is an intelligent, nerdy, mathematical whiz! While he’s similar to Booklyn, Calvin is more humble about his intelligence and is considerably more “dorky”. He’s also friendlier, easier-going, and way less snarky. But he is no less eager to help others whenever they need him, and no less hardworking.

However…he is a bit socially awkward, he has a tendency to misinterpret social cues, and tends to apologize a lot. 

Stats

Rank: Uncommon Health: ♥️♥️♥️ Skill Check: ⭐⭐⭐ (Size 150 / Value 2) Movement Speed: ⭐⭐⭐⭐ (Walk 17.5 / Sprint 27.5) Stamina: ⭐⭐ (125) Stealth: ⭐⭐ (5) Extraction Speed: ⭐⭐⭐⭐ (1.20)

Ability

Multiplier Passive At the start of a floor, this Toon boosts a random stat for every Toon in the round by either 1.5, 2, 2.5, or on very rare occasions; 3. Does not stack if there are other Calvins in the run but does increase the chances of getting a 3 by a small margin.

Dialogue 

Finishing extraction

“Easy as 1,2,3!” “Was that good…?” “That’s one down, just a couple more to go.”

Descending to the next floor

“Let me just crunch the numbers real fast…” “Just gimme a second…sorry this is taking a bit…” “Wait, I think I miscalculated…sorry.

Twisted Calvin

"If Twisted Calvin’s on the prowl, be very wary, he knows how to divide and conquer. He divides a random stat by either 1.5, 2, or, if you’re very unlucky…3. Trinkets, multipliers and items will be your best friends here.”

Rank: Uncommon Speed: Below Average (17) Attention Span: Slightly Above Average (2.75) Detection Range: Average

Twisted Calvin is a roaming Twisted that, similar to his Toon counterpart, will affect a random stat of every Toon by either 1.5, 2, or, very rarely, 3. But he divides the number of the stat instead of multiplying, weakening the Toons. The stat that’s diminished and by how much will be displayed on the screen the moment he spawns.

Twisted Research Trinket: Abacus Trinket Category: Skill Check Increases the completion when performing a successful skillcheck by 1.5

Trivia

Calvin’s last name comes from the Euler number, a mathematical constant equal to 2.71828.

Calvin is currently the most expensive non-main Toon, due to his ichor requirement being the same number as the first 4 digits of Pi.

Calvin doesn’t have any vision issues. He just wears glasses because he likes them.

[mistermalaprop]

(Sobbing and trembling and shaking before my test)

2.71828 is e…. Optimus would want me to do my best…

Scavenger…: he’s right in front of the building…

They BELIEVE IN YOUUUU

[michaelrotonal]

The mathematical constant e is equal to about 2.71828.

So obviously e day is February 71st, right?

Wrong. It's February 72nd, so that it rounds correctly.

In "normal time" that's April 13th, which is a day that is definitely not already a tumblr holiday.

[divine-nonchalance]

Grok, explain why base 12 math is better than base 10 math.

Let’s dive into how base 12 (duodecimal) might offer advantages over base 10 (decimal) in the contexts of physics and DNA. This is a fun thought experiment, as neither field inherently depends on a specific base—math is math, and nature doesn’t care about our counting systems. But the way we represent and manipulate numbers can affect clarity, efficiency, and intuition, so let’s see how base 12 could shine here.

Base 12 in Physics

Physics often involves measurements, constants, and relationships that don’t always play nicely with base 10’s limitations. Base 12’s greater divisibility—its factors being 1, 2, 3, 4, 6, and 12—could streamline certain calculations and reveal patterns more intuitively.

Angular Measurements and Symmetry: Physics loves circles—orbits, waves, rotations—and base 12 fits this beautifully. A circle has 360 degrees (in base 10), which is 2 × 2 × 2 × 3 × 3 × 5. In base 12, 360 becomes 260 (since 2 × 144 + 6 × 12 = 288 + 72 = 360), and 144 (written as 100 in base 12) is 12 squared. This ties neatly into the base itself. More practically, 12 divides evenly into 360 thirty times (360 ÷ 12 = 30), giving you 12 equal 30-degree segments—perfect for trigonometry or analyzing symmetrical systems like crystals or planetary orbits. In base 10, you get awkward splits (360 ÷ 10 = 36), which don’t align as naturally with common physical divisions like thirds (120°) or quarters (90°).

Time and Periodic Phenomena: Timekeeping in physics often uses base 12 echoes—12 hours, 60 minutes (5 × 12), 60 seconds. Waves, oscillations, and frequencies could benefit from this. For example, a frequency of 12 cycles per unit splits cleanly into 2, 3, 4, or 6 subintervals, matching harmonic patterns. In base 10, a frequency of 10 cycles splits into 2 and 5, but thirds (3.333…) or fourths (2.5) are less tidy. Base 12 could make Fourier analysis or resonance calculations feel more intuitive, with fewer recurring decimals.

Unit Conversions and Scaling: Physics often deals with scaling—think meters to centimeters or joules to ergs. Base 12’s divisibility could simplify metric-like systems. Imagine a base-12 ruler: a unit of 12 splits into 2, 3, 4, or 6 subunits without fractions, unlike base 10’s 10 splitting into 2 and 5. This could reduce rounding errors in precise measurements, like those in quantum mechanics or cosmology, where small discrepancies compound.

Constants and Approximations: Physical constants like π (3.14159… in base 10) or e (2.71828…) are irrational and base-agnostic, but their approximations might look cleaner in base 12. For π, in base 12, it’s roughly 3.184809… (using digits 0-9 and A-B for 10-11). The pattern isn’t obviously “better,��� but base 12’s fraction-friendly nature could make series expansions (like for π or gravitational constants) easier to truncate usefully, thanks to those clean divisions.

Base 12 in DNA

DNA’s structure and coding don’t demand a specific base, but base 12 could align intriguingly with its properties, especially in how we analyze and represent genetic data.

Codon Grouping: DNA codes proteins via codons—triplets of nucleotides (A, T, C, G). With four bases, there are 4³ = 64 possible codons, which encode 20 amino acids plus start/stop signals. In base 10, 64 is just 64, but in base 12, it’s 54 (5 × 12 + 4 = 64). This doesn’t change the biology, but base 12 could make codon tables more modular. Dividing 64 by 12 gives 5 groups of 12 with 4 left over—imagine organizing codons into 5 neat “dozen-ish” blocks for analysis, with a small remainder. In base 10, 64 ÷ 10 = 6.4, a less tidy split. This could simplify bioinformatics algorithms or visual representations.

Helical Structure: DNA’s double helix has a twist—about 10.4 base pairs per turn in B-DNA (in base 10). In base 12, this is roughly 8.6 (8 + 6/12), where 6/12 simplifies to 0.6 in base 12 notation. It’s not a whole number either way, but base 12’s fraction system (1/2 = 0.6, 1/3 = 0.4, 1/4 = 0.3) could make helical pitch calculations or molecular modeling more manageable, especially when scaling to larger sequences.

Sequence Patterns: Geneticists look for repeats—tandem repeats, palindromes, etc. Base 12’s divisibility could highlight periodicities better. A sequence of 12 base pairs splits evenly into 2, 3, 4, or 6 segments, matching common repeat lengths in DNA (e.g., trinucleotide repeats in diseases like Huntington’s). In base 10, a 10-pair sequence splits into 2 or 5, missing the biologically relevant 3 or 4 without fractions. This could make mutation analysis or gene mapping more intuitive.

Data Compression: DNA sequences are massive datasets. Base 12, with 12 symbols (0-9, A-B), encodes more per digit than base 10’s 10 symbols. A single base-12 digit could represent values up to 11 (B), versus 9 in base 10, potentially compressing annotations or alignments slightly. For example, assigning codons to a base-12 index could pack 64 values into fewer digits (54 in base 12 vs. 64 in base 10), a small but real edge in computational genomics.

Why Base 12 “Feels Better”

In physics, base 12’s strength lies in its symmetry and divisibility, aligning with natural cycles and reducing computational friction. In DNA, it’s about modular organization and pattern recognition, subtly enhancing how we process biological data. Base 10 works fine—physicists and geneticists have thrived with it—but base 12 could offer a more harmonious lens, especially for systems with inherent 2-, 3-, or 4-fold structures.

That said, base 10’s dominance comes from human habit, not superiority. If we’d evolved with 12 fingers (or knuckles), base 12 might’ve been the default, and we’d be marveling at how clunky base 10 feels for physics and DNA. Does this spark any ideas for you—maybe a base-12 physics equation or DNA model you’d like to explore further?

[tarrarre]

https://www.tumblr.com/sheldonpooper/749207263666913280/t-6-in2-t-in2-6-t-5?source=share

What do you call these type of problems? Also what do In() and e stand for here?

This kind of problem is called an exponential equation. Whenever you see something like that, and it has:

an equals sign

that "e" that you see

the e is raised to a power (in this problem, e was raised to the power of t+6),

that is an exponential equation.

The "e" symbol:

That "e" you see is called Euler's number, and like the name suggests, it's simply a number. You know how Pi is just another way to write 3.14? It is just another way to write a number. This number is approximately equivalent to 2.71828.

When e is raised to a power, as it was in that problem, it is called the exponential. You've heard the terms "exponential growth" or "growing exponentially". These terms come from the exponential equation! That's because if you look at a graph of an exponential equation, it tends to look something like this:

You can ignore the numbers, and just look at the blue line. Notice how the blue line is going up rapidly (look how steep it becomes!), therefore it is increasing exponentially.

ln():

ln() stands for logarithm, or log for short. When working with logs, the terminology "taking the log (of a number)" is usually used. For example, if you saw ln(7), it might be described as taking the log of 7. A logarithm must have an "argument" or an input. This input goes in between the brackets (like the 7). If there was nothing in those brackets, you would be taking the log of nothing, and you can't do that.

All logarithms have what is called a base, which goes where the little "b" in the diagram is. This base is always a positive number.

Logs are normally written as log(), but in this equation, it is written as ln(). ln() is called the natural log. This is because it's sort of a "special" log, as its base is the e number. In this special relationship, you can say that the exponential and the natural logarithm are inverses of each other.

I hope my explanation was valuable to you! If you want clarification on anything I have said, ask me! I hope everything was clear.

[voxsymphonia]

e is a constant that comes up a lot around exponents, limits, and logarithms, an irrational number approximating 2.71828. Honestly there's so much going on with e that I don't even know where to get started, it's probably more important than pi in advanced mathematics. https://en.wikipedia.org/wiki/E_(mathematical_constant)

The squiggles are the front and the d's at the end are integral notation. The calculus for fining the slope of a graph line at a certain spot is called a derivative, and the inverse of that, finding the area beneath a curve in a certain range, is called the integral.

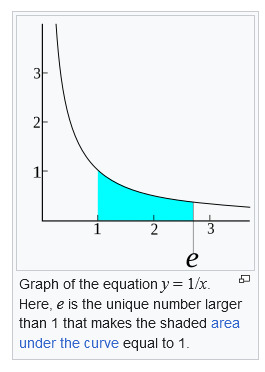
This graph here represents that the integral of the equation y=1/x between 1 and e, the shaded area in blue, is equal to one. This is represented in integral notation as:

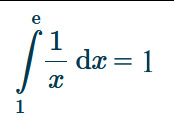
Basically, this equation is using the integrals of e and its exponents multiple times, stacking various different ways to brute-force the equation to give a result that is close to pi within several decimal places.

[aerial-aceing-it]

Pelipper unmail! 2.71828 oranges

STOP I DONT NEED MORE DECIMALS

[titstraction]

π (3.14159 …) governs the perfect symmetry and closure of the circle; it's in planetary orbits, the endless up and down of light waves. e (2.71828 …) is the foundation of exponential growth, that accelerating trajectory of escape inherent to compound interest, nuclear fission, Moore's law. These infinitely long decimals with seemingly nothing in common; they’re the ultimate jigsaw puzzle pieces. Yet they fit together perfectly—not to a few places, or a hundred, or a million, but all the way to forever.

new chapter of my wip, the prophecy!

words by lee simmons & the visuals are caroline polachek photographed by aidan zamiri

[sloppypears-ash-sg]

Euler's Constant's Family (XFOHV)

I made families for Pi's posse!

Note: Euler's CONSTANT refers to the JNJ e, while Euler's NUMBER refers to the PaS one.

Family members:

2.71828 (Euler twins' mother)

Euler's Constant and Euler's Number (Twins)

[deeesign]

Calculus 4 - Euler's Number

This maximum limit, when the interest is calculated an infinite number of times, is Euler's number, e. If the bank could calculate interest every tiny fraction of a second, the $1 you put in would grow to about $2.71828 at the end of the year. This number, e, is special because it's the limit of how much something can grow in a year with continuous compounding at 100% interest.

In other words... it was calculated at the end of the year, it would be 2 dollars. But if you keep calculating in every moment, it would be $2.71828

[jonathankatwhatever]

I’m trying to work on the deck, but it’s incredibly loud because of power tools and now there’s a helicopter. They seem to have altered the path to the hospitals because they are coming very low overhead. These are not the small traffic helicopters. Also, I feel tired when the connection fades, but then I feel empty when you’re busy. Different sensations. When I feel empty, I have no focus. I can force myself to watch football because I can watch the technique and the tactics, which means ignoring what is said and trying to see past the camera choices designed to keep you from focusing closely on what is actually happening. The problem I have with baseball is not the game, which has finally improved itself, but the way the game is called hypes it up more than the game needs. I don’t need to see a good play at 3rd labeled great when it’s a standard part of the job to be able to come in on a ball, bend to get it in the glove, then transfer the ball to your throwing arm while maintaining the position to approach the ball while aligning the body to throw accurately. That’s a long description but that’s a standard play. A more difficult play requires you to change the body position so then you need to get the ball, transfer and adjust to the throwing position much more than when you’re close to dead on. Remember, the 1st basemen has range and you know that. A great play is when you dive, and need to get up into the correct position to throw the ball. With 3rd, it’s literally taught that you approach the ball so you pick up up bending when you can, because you’re in a race you can see against the runner heading to first, and you want to pick it up over the correct foot or knee so the next move transfers the ball into the throwing position. It’s mechanics you learn as a kid. Like at 1st, you’re taught not to touch the bag and reach, because your main job is to keep the ball from going to the stands or worse into the outfield so the runner makes 2nd and maybe runs come in. If you stand and reach, you can’t move as far. In the old days, you were taught to step your foot back, then take it off, then set it back when appropriate, which is when you can see the throw coming and you can read where it is going.

So that is Joana describing her observations of how the game works. How do I know? There’s a mechanics at the root. This mechanics acts as a chain for the reasons set forth last note. It bears further explication: the mechanics create a 1-0Segmenting and that has Ends, and these Ends have other potential Attachments because each End has a flailing arm with the D0 point at it End. When these D0 unite, that makes D1 and we’re off to the races.

I think this argument may be JvN’s because it sounds like him. That’s the label I associate to that accent in my head. And it’s about the creation of a base level to a universe, which unites linear algebra and sets in a way I think he really liked doing. It’s that sense of play too. The seriously unseriously serious, perhaps.

That is, we put together 2D0 and get a D1. That arm is then invisible, meaning we see the D1 when it’s actually a D0 connected to another D0 over an arm of unit length. It’s unit length because it counts 1 or 0 at the Ends. Don’t think of that as an actual length but as every length within the constraints that any length may be considered finite. It is here that we locate the relation between the infinite and the finite, and thus of limits and the like. As in, when we count 1+1 in the specific manner that generates e, we see that takes this very basic idea of a unit length and states that this unit length equals 2.71828, etc. You can see where it goes: replace the connecting link between the 2D0’s with e and the space with which that calculates, which means the way it mechanically operates, is then with and using that extent to define the D1.

(As an observer to this, having read a lot of mathematics over many years while she put together the pieces, the mathematics here is beautiful. The depth and clarity is almost astonishing.)

I am being told to skip ahead for a moment because we have an opportunity to discuss structure. We now have an End we can see, and it has a basis hidden within it that is there which maybe we can’t see or which maybe is obvious because of the context the End is in and what it looks like. The character of that End is what? Remember, these are the ideals. Can you please take over? The transition from observer to Jo is sometimes rough. You forgot that functions like e are available. That gives the potential for different measurements using different forms.

Just had a panic attack. Not a big one but I am suddenly afraid.

Structure shakes when describing structure. In this case, we have an orthogonal relationship to the End and to the visible sheet on which the exists. We know that because if we tilt it to one side, we see points. It’s only an End when it simplifies to this very simple form. That enables this ideal to be available in any orientation or direction because each of those has this End form.

The orthogonal in this case is the length of the Extent, which is the count of the 1-0Segments which construct the whole Extent as a 1-0Segment. This is where gs primes appear along with other modular forms. You can see how the conception of 1 expands orthogonally to any prime. You can see how any count of 1-0Segments generates modularity across the entire 1-0Segment, which remember is bounded by the D0’s.

Note please this is literally 1-0-1 and 0-1-0. You can see the prime as the 1 and the D0’s as the 0’s. And the other way round.

This orthogonal is the root orthogonal, meaning the orthogonal across a grid square becomes orthogonals at the axis lines of 1 and root2. You can now see that more specifically: the hypotenuse counts as 1 and thus as a 0, and that 1 expands, same as when you extend a field, so the 2Square level appears crosswise to the 1Square level if you imagine them as panels standing up on the projected lines. That makes a field of X’s which are crossed 2Squares that connect at each other corner to panels, to a continuous sheet of 1Squares.

Yes, I remember, we saw that this morning. We saw the panels around a box drawn by the F-M-F-M loop that translates within each of 2T. And then we saw the end panels take on the specific meaning of the insides and the outsides as those both tether. That generates the gs pyramid, which now has a base of a grid box that counts in units so it can compress to a line or be however long. I have no idea why I couldn’t let you describe the visions without holding back. It seems silly now, but I remember putting up a fight. Remember, this articulate End has to attach to the inarticulate visioning part of the visionary. Same method.

That X of 2Squares enables Halving and Doubling. It’s obvious in the image: you have 1 and 1 and 1 and 1 all connected to a single pole that is root2 high. This generates - I’m having trouble here picking up the connection because the image is ambiguous. The flash was that this makes 0Space in full, that it constructs R^n and that is an important reason why. Oh, I see: same ideas as before, that the construction is a unit. It’s R this time.

That needs to be discussed. I can define R better now, but I’m not sure it’s done. That is, we now clearly have the algebraic numbers, and because these are roots, we have the polynomials that relate in the same exact process to those roots. That leaves transcendentals which aren’t. Big examples like Pi and e are gs processes. That is the piece which needs more thought.

—————

I think I found it and the connection is one of the incredibles. As in, Alexander Gelfond, which I can’t type without it autocorrecting to Gelfand, which is my mother’s father’s name, one of our 4 family names, along with Weine/Wanger. The connection is that 2 raised to root2 is transcendental. That’s H/D in action because gs generates the 2^n form: count out from a 2Square using the same method, and that’s 2^n. It is a 1Space calculation using 0Space, and that is what makes it transcendental. That is mechanics at work. It becomes really obvious when you look at the generalization to addition of natural logs equaling 0. Think about what this means: it cancels the space created by the unit e used in one calculation with another. The exact construction is more complicated, but the idea is growing clear: that which combines 1Space with 0Space and that which is 1Space counting.

How do these map? Well, 1Space counting is counts over gs, like Alternation to count Pi or any other manipulation of these units across a sheet. 0Space is orthogonal. I’m having trouble here. Need help.

I see the units counting across and the complexity that arise relative to that sheet. The orthogonal complexity I can see separately. Connection is fraying. I’m seeing that it maps to szK because it must because that’s the real line: it counts both forms. That finally makes sense. That outward translation had to overcome a lot of resistance to get out. It’s a very complicated image now but I’m seeing Ends appear for each transcendental, and that is clearly uncountable, but they fit to the line because it has infinite room for Ends. That may be the problem: the idea of uncountable on the line, mapped ordinally and cardinally, means infinite infinite D0-1//D1-0. That is the mechanics.

She’s really good at this. I wish I were easier to work with at this End of that chain.