#Complex Analysis
Explore tagged Tumblr posts
Text

#Rolf Nevanlinna#Nevanlinna#science#physics#math#mathematics#space time#complex analysis#book cover#cover design
126 notes
·
View notes
Text
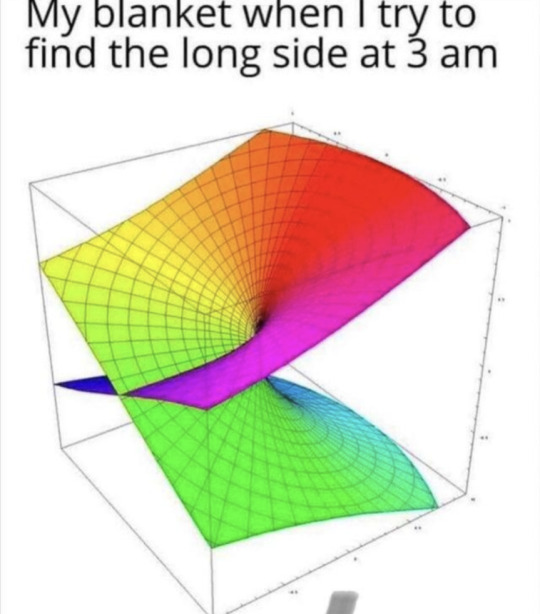
#riemann surface of sqrt#memes#meme#nerdy memes#nerdy meme#nerd humour#maths#calculus#complex analysis#riemann surface#maths memes
158 notes
·
View notes
Text

this one is for my 12 other homies out there who have been on both sides of this meme
#honestly im not even sure why you would ever use complex analysis in comp bio or theoretical bio for that matter#but it's also really not my field#so idk#maybe like some image processing stuff if you REALLY specialise in it? i don't know#if anyone actually has experience in both im curious what you do#i doubled in bio and physics in undergrad so my sitch is a little weird#i know some other ppl who do this but its not super common to my knowledge#also for anyone out there who wants to roast me for not using mmcif i don't care#everyone and their mom and their girlfriend and her girlfriend uses pdb#biology#mathblr#maths#math#math meme#biology meme#proteomics#dude theres NO way proteomics ppl r on tumblr following the tag#complex analysis#i need to stop making memes that are target audience almost exclusively me
12 notes
·
View notes
Text
To continue on the square discourse, here's a fun not-square:

This is the domain coloring of f(z)=z^{7}+bz^{3} (although any z^n + z^n-4 works)
I am not in any way claiming this fits the definition of a real square, but function's root has the appearance a square
#domain coloring method done by me but inspired by seeing u/TdubMorris's post on r/desmos.#the system I was using before partitioned the screen into arcs and was way less performant than this method and lacked saturation.#mathblr#mathmatics#complex analysis#complex numbers#math#desmos#desmos has complex numbers now check it out when you have the time it's fun
13 notes
·
View notes
Text
give me a harmonic function and i can find its conjugate no problem,,, but i can't help but wonder,,, when will i learn to make myself analytic :(
#personal#math#mathematics#complex analysis#it comes across that i'm being ironic#right?#harmonic functions#math joke#irony
11 notes
·
View notes
Text
why would someone study complex analysis?
(this isn't sarcasm, my professor is shit and we genuinely want to know the hype about it, because rn it seems really boring)
9 notes
·
View notes
Text
I had to explain a complex analysis meme to a friend which meant I took 11 days of my life cramming basic complex analysis into my brain

my head horts
edit: the contour Γ is the classic semicircle around 𝑖 and all
8 notes
·
View notes
Text
Mobius Transformations in Desmos
15 notes
·
View notes
Text
riemann spheres as a fundamental type, pt.1 basics
ive been thinking on and off about riemann spheres for a while now, a couple weeks really, and so far i think there's some utility to them as a building block of a type system of some kind for a joke/toy computer language
background: riemann spheres are a neat tool in complex analysis where we imagine a sphere whose equator intersects the complex plane, and every number on the complex plane is representable by a point on the sphere such that a line is projected from the north pole and through that point onto the complex plane. naturally, this means that the north pole is P(∞) and the south pole is P(0). see below how that would look like with other unit points of the complex numbers
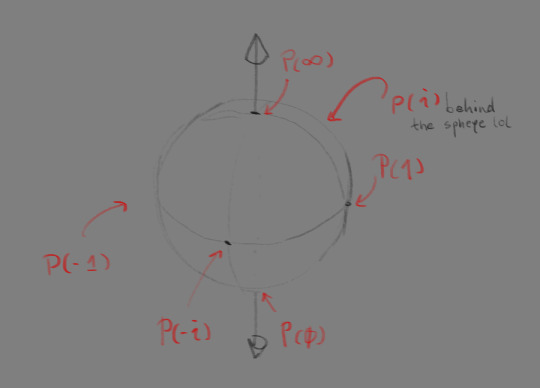
a neat thing the riemann sphere allows us is to define meaningful division by zero so now z/0 = ∞ clean and simple! and also its inverse, z/∞ = 0 is well behaved as well. this simplifies doing complex analysis but stereographic projection is an absolute bitch to work with turns out, and doing arithmetic on points on the sphere is a mess because it's not a linear mapping (it's continuous though so that's fine)
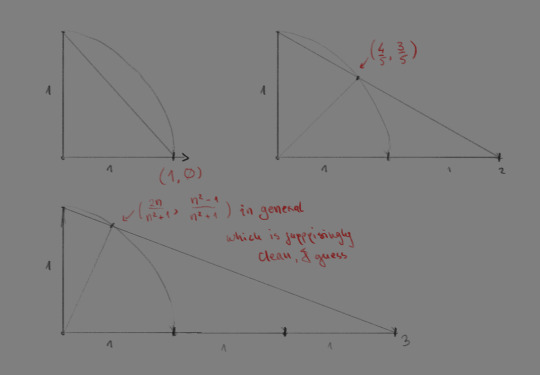
if we're dealing with ONLY real numbers in relation to a circular slice of the riemann sphere, it already starts looking like a mess; for any number n∈R its projective cognate on the circle is located at (2n/n²+1, n²-1/n²+1). on the real riemann sphere though? zoo wee mamma
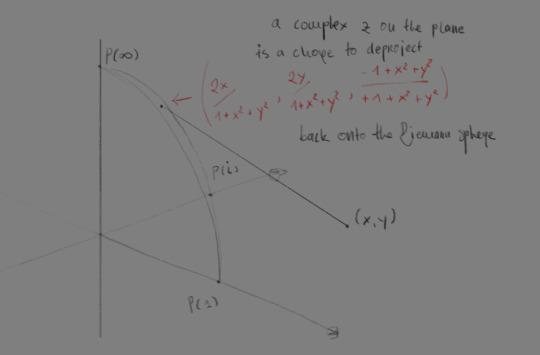
an arbitrary z∈C, represented as a point (x,y) on the complex plane, has to walk through a rather ugly mapping (related to the previous one) to find its point on the sphere; more accurately, given the coordinates (x,y) of the point on the plane, the point on the sphere is located at (2x/1+x²+y², 2y/1+x²+y², -1+x²+y²/1+x²+y²), which is godawful in spherical-to-polar coordinate terms, this is much simpler; for a polar pair (r,θ) the point on the unit sphere representing it is (φ,ξ) = (2*arctg 1/r, θ); and conversely projecting from the riemann sphere is also dead simple, given the zenith-azimuth pair (φ,ξ), (r,θ) = (ctg φ/2, ξ). of course, translating from polar to real coordinates is ALSO dead simple; x = r * cos θ, y = r * sin θ. if a computer system were to store complex numbers (or any coordinate on a 2d plane really), it makes sense to store them in terms of spherical coordinates of a riemann sphere, since this makes infinity well-behaved as a unit (zenith = 0, azimuth = literally who gives a fuck) and is surprisingly efficient. knowing that the zenith is ∈[0,π] and azimuth ∈[0, 2π] can allow for some formidably dumb optimisations that can save on space and ensure granularity. compared to storing them as 2d cartesian or polar coordinates, this provides the benefit of having neither number be larger than like 6.3, so an underlying/backing type that can offer great precision in this small range would be more efficient numerically than, say, floating points which have insane baggage and gaps
or iunno i'll look into that one a bit later, i'm just kind of furious right now that i rederived stereographic projection on my own when the formulas were right fucking there if id only just googled for them
#rambling#math#maths#mathematics#riemann sphere#stereographic projection#complex analysis#trigonometry#complex plane#complex numbers
5 notes
·
View notes
Text
I have a new post up on my blog, continuing the Fictional History of Numbers series. In part 1 we built on the natural numbers using algebraic operations, and got the algebraic numbers. In part 2 and part 3 we used geometric and analytic arguments to build up the real numbers.
These two sets of numbers overlap, but aren't the same; there are real numbers that aren't algebraic (as we saw in part 3) but also algebraic numbers that aren't real. So what happens if we combine the two? We get the complex numbers, which are complete and also algebraically closed. But proving this is a little tricky, and touches on the deep strangeness of complex analysis.
And in the process of adding algebraic closure to the real numbers, we lose the ability to order them, which has its own consequences.
28 notes
·
View notes
Text
Hey mathblr. Today I don't have Wrong Math, but I do have a question. I was trying to find the real roots of (-1)^x. And I ended up with the formula:
n/(4k+1) where nεZ and kεZ.
I know this can make all natural powers for k=0 and it can make no powers of the type 1/(2k). But I have trouble proving, if it can be proven, that this formula can produce all the powers of 1/(2k+1) so that I can have (-1)^1/3, (-1)^1/7 and so on.
If anyone has an idea of how to prove this please help.
I will leave how I found that formula after the break.
(-1)^x=
i^2x=
exp(2(2kπ+π/2xi))=
cos(4kπ+πx)+i*sin(4kπ+πx)
For (-1)^x to have real roots the sin must be zero.
sin(4kπ+πx)=0
4kπ+πx=nπ =>
(4k+1)x=n =>
x=n/(4k+1).
10 notes
·
View notes
Text
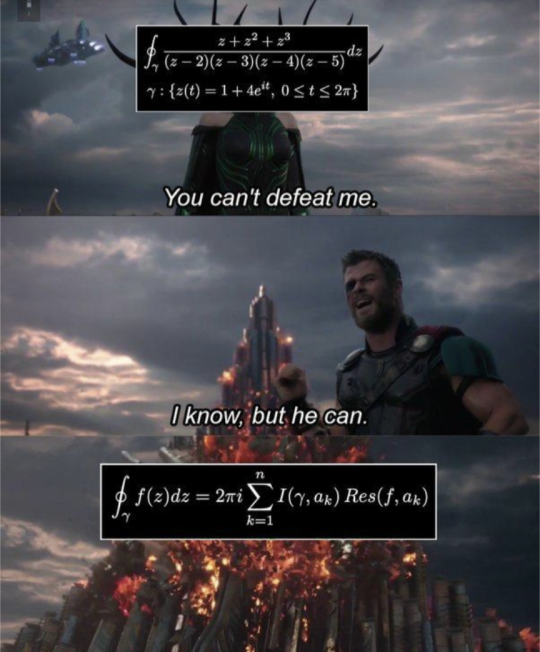
#to clarify#i have no idea what's going on#but oint oint#nerdy memes#memes#meme#nerd humour#nerdy meme#maths#calculus#complex analysis#maths meme
79 notes
·
View notes
Text
You know it’s real fucked up that you can raise a complex number to the 50th power and end up with like 0+i. I don’t like this on the surface, but I can feel my lust for chaos just below that
3 notes
·
View notes
Text
Domain coloring








2 notes
·
View notes
Text
I cannot express how much I love class getting cancelled
#math#we were supposed to have a test too#high school#I have no clue what we're doing anyways#complex analysis
4 notes
·
View notes
Text
complex analysis? i find it quite simple

#math#complex analysis#this is a low effort joke i apologize#(and i recognize that despite analysis on C being much better than R it does not trivialize the subject)
2 notes
·
View notes