#Pythagorean Theorem Calculator

[sesshy380]

Got an interview in about 3 hours (last job I interviewed for I thought it went well, but apparently it didn't go well enough 😞).

Honestly not looking forward to this one, because it's for shitty pay and probably equally shitty hours. And unfortunately with my current situation, if they decide to hire me I'll have to take it.

I've lost count of how many hours I've spent submitting applications and resumes, and out of the vast number I've submitted (including for fucking Walmart, which I swore I would never go back), so far only this place has called (and it was on a Saturday which really threw me, because who calls on a Saturday during a busy holiday weekend?)

[eldest-of-katts]

Me any other time: ohhh my gawd we will NEVER use half the math we learn it's literally just for brain strengthening and logic skill building urrrggghhh

Me doing papercrafts: OMG Pythagoras (⁠ ⁠ꈍ⁠ᴗ⁠ꈍ⁠) this theorem fucking slaps (⁠๑⁠♡⁠⌓⁠♡⁠๑⁠) just used it six times ♡⁠(⁠>⁠ ⁠ਊ⁠ ⁠<⁠)⁠♡ and sine and cosine my beloveds (⁠っ⁠˘⁠з⁠(⁠˘⁠⌣⁠˘⁠ ⁠) just helped me make this curve (⁠*⁠˘⁠︶⁠˘⁠*⁠)⁠.⁠｡⁠*⁠♡ (⁠◍⁠•⁠ᴗ⁠•⁠◍⁠)⁠✧⁠*⁠。peace and love on planet earth (⁠✿⁠^⁠‿⁠^⁠)

[hose270]

I remember the exact moment math clicked for me, not in a “I understand it” sense, but in an “I understand why this is meaningful” sense.

I was in calculus, and we were using integrals to calculate the area under a curve. The teacher showed us how to use that process to derive the formula for the volume of a cone—a formula I’d had to memorize five years before in geometry class. My mind was blown, not only because there was logic behind that seemingly arbitrary formula, but because I understood that logic.

It wasn’t the first time I’d understood something, but never before had something so incomprehensible been so quickly transformed into something so rational, and that moment of understanding still stands out in my memory six years later. It taught me that, with enough study and research, almost anything can be understood. Now, I haven’t used the formula for the volume of a cube in years, let alone to calculus necessary for deriving it, but I have used that principle of study and research, and that’s something that math taught me.

Are you willing to make a long personal post about how Math should be presented in an educational environment or in general conversation trying to convince the other participants about its daily usage. How it can advance a person’s problem-solving skills and approach in life.

I’m really good in Mathematics. I’ve given help for my classmates and friends about Math when they are having trouble or ask for it. But I have never been convinced of its importance outside of the classroom, outside of the test papers that gives me the variables to substitute in the given equation of that test of the day.

How can Math and it’s many properties relate back to everyday life in a casual manner?

Hm. Well, as someone who hasn't had to solve an antiderivative in years, my perspective on this is that the most important and widely-applicable skill math can teach you is the stuff behind the math - mostly the muscle-memory you get from proofs.

Math is, at its core, puzzles and logic and pattern-recognition. You learn a set of tools, you practice those tools on a set of simple problems until you get a feel for them, you are presented with a bigger problem, you recall which tools best applied to problems that are shaped like this, you break the problem down using your tools and eventually reduce it to something you know how to solve.

The fact of the matter is, the tools that are specific to branches of math don't really have much widespread use outside pure mathematics, and unless you go out of your way to keep using them you're likely to lose track of them. Studying math is not going to turn you into a super-calculator-wizard who can bounce stuff off the walls at perfect angles and do six-figure arithmetic in seconds, and I think some people feel overwhelmed at the assumption that that's what's expected of them if they learn math, and some other people feel cheated when they learn that that's absolutely not going to happen, because most writers don't know math and when they tell stories with math in them their best guess is it makes you a wizard.

I think the most advanced math I've used lately was trigonometry, and that was just because I was curious about how fast my plane was traveling relative to the sun's apparent movement at my latitude. We were flying back to the US from Iceland and we'd taken off at sunset, and we had been in that sunset for at least an hour by the time I got curious how the math worked out and started estimating our latitude, the circumference of the slice of the earth at that latitude, and correspondingly how fast we were flying vs how fast it was spinning to complete a full rotation in 24 hours. But even if the math involved didn't tap into any of the higher-level stuff I'd learned post-trig, those years doing proofs and figuring out which tools applied to which geometry meant that I could use the tools and my training applying those tools to calculate what I wanted to know, and confirm that our plane was actually outflying the sun when we were at iceland latitude, but as we curved south the sun's apparent relative movement (aka the rotational speed of that latitude of the earth) slowly accelerated until we were falling behind, landing right as the sun finally set. The math involved was high school level, but if I'd been given that problem in high school it would've taken more work and more stress to figure out how the tools I had needed to be applied to the problem I was facing. The years of practice I had tackling much more complicated proofs made the diagnostic process much faster.

I saw someone once analogize studying math to lifting weights. Where am I going to use this in real life? How often will I really be faced with two dumbbells that need to be lifted in three sets of twenty? Where am I going to apply the skill of holding a heavy thing straight out to one side of my body?

You don't lift weights because lifting weights is such a valuable and widely-applicable skillset, you do it because lifting weights makes you better at lifting everything.

You don't study math because math is going to fill your daily life with concepts that you need to prove true for 1 and for n+1 given true for n, or complex solids that you need to sum an approximate volume for, or a surplus of sunset plane flights that demand you calculate a bunch of cosines. You study math because it is the skillset of making things make sense. It trains you to break a huge, incomprehensible problem down into a series of small problems you already know how to solve. It lets you reach true and correct conclusions by starting from facts and transforming them through operations that preserve truth, and correspondingly that if you reach a false conclusion from these methods, then either the methods are flawed or the initial assumption is not as true as you believed. It teaches you to put two and two together and be confident, once you've double-checked your work, that you can say four.

This is stuff I use all the time in both my video research and my freeform writing. Building out a slow picture of how a story was told or changed over time involves finding the context it was created in, and reverse-engineering what parts of that context could have produced what standout portions of the story - what authorial or cultural bias results in this standout story element. Worldbuilding where I take two wildly disparate parts of the world, put them together and see what web of implications springs out of combining them, following the threads to new and interesting concepts that follow from what I've already established. Building a character arc by breaking down exactly what events are happening to them and what transformation each component will apply to the underlying character. If I want the story to go in a certain direction, what transformations do I need to apply to make that happen while still preserving truth? If I'm faced with a seemingly insurmountable problem, what methods can I use to break it down into bite-sized pieces?

This isn't something I think about most of the time. It's just how my brain works at this point, and I can't promise it'd work for anyone else. But thanks to all my years of hard work and training, my brain has been buff enough to solve every problem I've tangled with since graduation, and that feels pretty good.

[bignaz8]

Around 1770 BC, Babylonian scholars in ancient Mesopotamia inscribed a clay tablet (IM 67118), showcasing the Pythagorean theorem (a² + b² = c²) to calculate a rectangle’s diagonal, over 1,000 years before Greek mathematician Pythagoras. Discovered in modern-day Iraq, this tablet employs a base-60 numerical system, reflected today in our 60-minute hours, 60-second minutes, and 360° circles. The meticulous cuneiform inscriptions reveal step-by-step calculations, demonstrating sophisticated mathematical understanding. Even earlier, the Plimpton 322 tablet (c. 1800 BCE) records Pythagorean triples (e.g., 3-4-5), sets of three integers satisfying the theorem, written in elegant cuneiform. Likely used as a teaching tool for advanced students, it suggests a structured educational system for mathematical training. These artifacts, blending geometry and algebra, underscore Mesopotamia’s pioneering role in STEM, influencing modern mathematics and timekeeping systems millennia later.

[incorrect-moriarty-sherliam]

William sighs as he begins counting sheep. Instead of simply counting the fuzzy creatures, he starts to calculate permutations and combinations of numbers in his head, forming complex sequences.

William: "Five... Euler's number, pi. Six... Riemannian topology. Seven... Fourier series. Eight... differential equations. Nine... Pythagorean theorem..."

Sherlock: "Liam, aren't you supposed to be asleep?"

William, at the end, creates a new theorem... because he can XD

+++++++

@missshello contribution! Yeah!

[theriverbeyond]

what do theorems mean in tlt? that bit always confused me

a theorem is a (mathematical?) statement that has been proven as true (using a proof) and is often used to solve more complicated problems. i.e. the Pythagorean theorem being used to solve for various properties of a right triangle, and further than that, it can be used for useful IRL stuff like architecture and getting a plane off the ground.

the Locked Tomb treats necromancy like a science, with (unexplained) rules, methods, equations, theorems, etc. Harrowhark mentions the "theorem mathematics" of the creche massacre when she confesses to John in HtN, and later on in the same book Ianthe is mentioned as having a notebook filled with "substantial mathematics" related to her necromantic study.

THEREFORE when they say "theorem" in TLT I imagine how in order to get a plane off the ground you have to do a lot of math first to calculate stuff like interia and force and air resistance and friction, and then to keep it flying you have to do yet more math and think about things like how you will lose some amount of energy as heat.

following that, in order to get a skeleton to fold your laundry you have to do a lot of math first about the energy requierments of cell division (regarding building the skeletal frame up from a single bone chip), cell differentiation (building out ligaments as needed), etc necromantic verbage, and then to KEEP it folding that laundry you have to do yet more math about like, i dunno. Gravity and energy loss.

it seems like a lot of work, honestly. no wonder normal, non-Lyctoral necromancers are always bleeding and sweating all over the place

[apple-onigiri]

DISTANCE IN VAUGARGE (revamped edition)

IMPORTANT: this post was deleted and made again to make edits and not spread misinformation (because i made a stupid mistake and took earth's entire circumference and accidentally treated it like it was only half of it! it's really funny because i did think that this feels way too big of a distance... happens i guess! especially at 4am lmao but it did uh, increase all the numbers by a whole Two so. unfortunate! gotta fix it!!)

@cyten0 (sorry to tag you again just figured you'd like an update and an actual correct answer, and you're still the one who inquired about this) asked if i could provide more information about my calculations for traveling across vaguarde, and since it seems too long for a reblog and i want to categorize it properly on my blog, here it is in a whole separate post!

this honestly started out as a curiosity about what climate the northern island could've had given its distance from the equator compared to earth's countries and uh. spiraled into me thinking about this. don't ever think about anything guys

TL;DR (for people who don't want the super fun math part): it's 1111.4 km/690.59 miles from dormont to bambouche in a straight line and somewhere in the ballpark of 250 hours of constant travel by foot to cross the distance. with a bonnie-ordained preteen-friendly tempo of around 5 km/h (3.1 ish mph) and eight hours of travel per day from 8am until 1pm and then 3pm to 6pm to set up camp properly early, it'd take around a month or so to make the trip, not counting any and all longer stays to refill supplies and any irregularities caused by going to a town and not having to set up camp or pack it back up.

ok quick geography lesson: the lines on the globe running horizontally are the latitude. they go up to 90 in each direction from the equator, which is 0, so there's a 180 in total. obviously for specific locations you'd use decimals but who caressss

longitude is important too here - the vertical lines - but less so. they go up to 180 on each side of the latitude's version of the equator, the prime meridian, as well but it really doesn't matter where that meridian is placed here, the only thing that matters is that the lines are in a correct distance to each other.

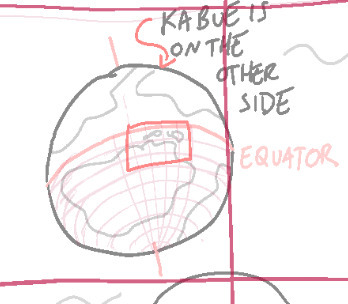
here's the globe id5, in her infinite wisdom, bestowed upon us (i'm completely normal about the existence of any and all maps. in the original post i said can be trusted with them but that is! clearly not the case!) that i added all the southern hemisphere latitude lines onto, as well as the longitude needed for my insane needs (math)

i obviously assumed the planet is the same size as the earth because i genuinely see no reason why it couldn't be other than to make my life sad and hell also. the general distance from one pole to another is 20,000 ish kilometers. (if you for some reason want the planet to be smaller or bigger, cool trick, literally just multiply the 20,000 by it. want it to be one third of its current size? multiply by 0.3. two-and-a-half times bigger? 2.5!) so what i did was draw out the lines onto the actual map and measure the estimated distance based on how big of a chunk it is out of this 20k.

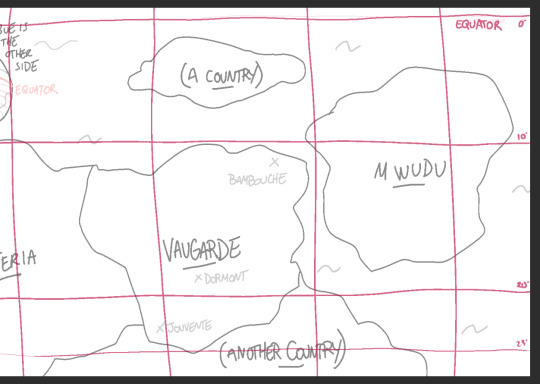
it seems dormont is at about 19 degrees, while bambouche is at 11. easy here!

just divide the whole distance by 180 and you get 111.(1) km (that 1 in a bracket telling you that that one goes on foreeeeever if you let it). since we're looking for the distance of 8 degrees, and we've got a distance of one, you can either multiply it by 8 or subtract the one degree times 2 to get 889. ish. any decimals are the enemy here at this point.

you do the same for the other direction - both bambouche and dormont seemed to be about 2 degrees from the longitude lines, so you do the process with just multiplying by 6 at the end or subtracting the one degree times 4 and get 1333. ish.

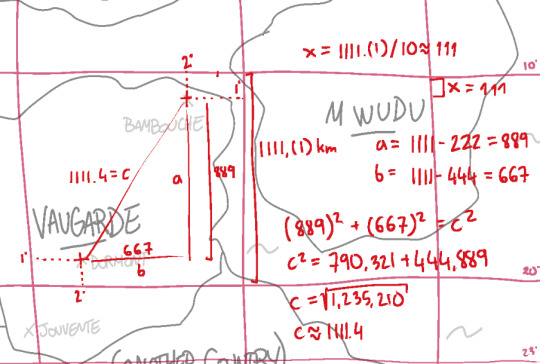
it's pythagorean theorem time!! it looks like a lot of big numbers but they do that only to get added nicely, it's okay, they're not that scary and they don't bite pretty promise with a cherry on top, and you get the resulting distance of 1111.4 kilometers like that!

here's how it measures up in reality for some scale:

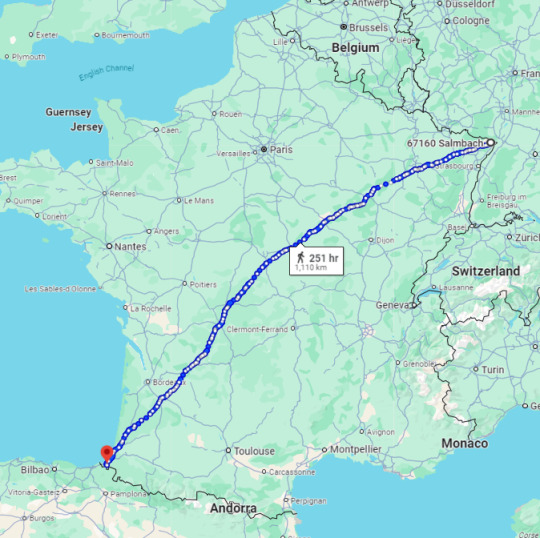
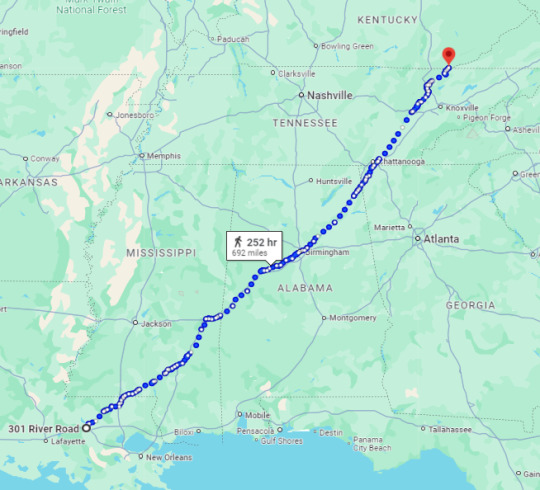
(hey it fits into all of france now!!)

the average recorded speed of a preteen - which the party logically must move at most of the time - is about 5 kilometers per hour (3.1 ish miles). with a travel plan of 4 hours of travel since 9am until 1pm, a two hour break, and another 3 hours until 6pm, because you need to set up camp and things like that need time, it's safe to assume they'd be crossing around 35 km/h a day. and this is still a really good pace!!! very endurance-heavy! divide the total distance by that and you get an estimated time of travel in days, which here is 31; just around a month.

this is, while less than my initial busted calculations, still a lot! lots of walking. so i uphold my statement that they better have sent a letter to nille ahead of them and that the vaugarde postal system is robust enough to deliver it in a timely manner right after the entire country defrosted, to keep her from worrying to death!

[ducktoonsfanart]

Scrooge McDuck as Julius Caesar and the March Ides and Donald Duck as an ancient Greek mathematician (Pythagoras and Archimedes) and Pi Day - Fearsome Four (Bushroot, Liquidator, Quackerjack and Megavolt) from Darkwing Duck and March and April holidays - Duck comics, Darkwing Duck and Duckverse - My style

Even though I'm late and don't arrive on time, I still decided to draw something related to the international days that are celebrated during March and early April. So I drew a few drawings related to that. The first drawing I drew shows Donald and Scrooge dressed from the classical period (the time of ancient Greece and ancient Rome) related to March 14th and 15th, or according to the ancient Romans, the days of the Ides of March. Ides, or in Latin Idus, means the middle of the month, and on that March 15th in 44 BC, before the birth of Christ, a terrible event occurred in the then Roman Republic when corrupt senators led by Brutus and Cassius killed the Roman dictator and leader Gaius Julius Caesar, which put the Roman state in danger and a new civil war. In the end, the senators who killed Caesar were punished and after more than 15 years, the civil war ended with the victory of Caesar's grandson-nephew Octavian Augustus, who declared himself emperor, and Rome became the capital of the Roman Empire. Scrooge McDuck is here as Gaius Julius Caesar and it's part of my Duckverse in History, luckily he wasn't killed, but he got a lot of knives in his salad like Caesar's salad. By the way, Caesar's salad was only created in 1924, named after the Italian chef Caesar Cardini who worked at Caesar's restaurant in Tijuana, Mexico, so it has nothing to do with Gaius Julius Caesar, but that's how a meme related to it was created. You can imagine Scrooge's reaction to that. "Beware of the Ides of March!" By the way, if you are more interested in Scrooge as Caesar, look here:

Donald Duck is here as an ancient Greek mathematician like Pythagoras who gave the Pythagorean theorem regarding a triangle and how it is calculated. "The sum of the areas of the two squares on the legs (a and b) equals the area of ​​the square on the hypotenuse (c)." You can see the given formula in the drawing. By the way, Pythagoras is one of the greatest mathematicians of all time and lived in the 6th century BC and came from the Greek island of Samos. He was an excellent geometer and was a lover of music, and he also founded a secret order related to that. More precisely, I was inspired by the cartoon "Donald in Mathmagic Land" from 1959 in which Donald goes to the land of mathematics and then goes back in time to Ancient Greece and meets Pythagoras and becomes a member of his society. March 14th is the International Day of Mathematics because of the infinite number Pi, which is a Greek letter in their alphabet and is often used in mathematics and physics. "It is defined as the ratio of the circumference to the diameter of a circle or as the ratio of the area of ​​a circle to the square over its radius." The number is actually 3.14159…It is also called Archimedes' constant by the ancient Greek mathematician Archimedes from the third century BC who lived in Syracuse, now Sicily. The number Pi was introduced there by William Jones and popularized by Leonard Euler in the 18th century. On that March 14th, 1879, physicist Albert Einstein was born, so that day is also celebrated as Einstein's Day. That's why I drew Donald wearing ancient Greek clothes with the letter Pi on his T-shirt, and wearing a green laurel wreath.

The other two drawings are related to Darkwing Duck, or rather the villainous team of the Fearsome Four consisting of Bushroot, Liquidator, Megavolt and Quackerjack, certainly a great team and I drew them also related to international days. Dr. Reginald Bushroot wears a Leprechaun hat and a four-leaf clover, which also marks St. Patrick's Day, which is celebrated on March 17. Bud Flud (Flood), or Liquidator, presents his product of bottled plastic water, which marks International Water Day, which is celebrated on March 22. Water is certainly important to us, and plants and water definitely go together. And finally, Quackerjack and Megavolt together while Quackerjack holds a toy tooth that winds up, and they mark International April Fool's Day, which is celebrated on April 1. I haven't drawn them in a long time, and they deserve it so I drew them, and they are also one of my favorite characters.

I hope you like these drawings and that you like these characters, especially from Darkwing Duck and that you like these ideas, and feel free to like and reblog this, just please don't copy this without mentioning me and without my permission. Thank you! And I apologize for the long post. Also happy holidays celebrating this that I tagged.

[tensorboi]

Why is the Pythagorean theorem true, really? (and a digression on p-adic vector spaces)

ok so if you've ever taken a math class in high school, you've probably seen the Pythagorean theorem at least a few times. It's a pretty useful formula, pretty much essential for calculating lengths of any kind. You may have even seen a proof of it, something to do with moving around triangles or something idk. If that's as far as you've gotten then you are probably unbothered by it.

Then, if you take a math class in university, you'll probably see the notion of an abstract vector space: it's a place where you can move things and scale them. We essentially use these spaces as models for the physical space we live in. A pretty important thing you can't do yet, though, is rotate things or say how long they are! We need to put more structure on our vector spaces to do that, called a norm.

Here's the problem, though: there are a *lot* of different choices of norm you can put on your vector space! You could use one which makes Pythagoras' theorem true; but you could also use one which makes a³ + b³ = c³ instead, or a whole host of other things! So all of a sudden, the legitimacy of the most well-known theorem is called into question: is it really true, or did we just choose for it to be true?

And if you were expecting me to say "then you learn the answer in grad school" or something, I am so sorry: almost nobody brings it up! So personally, I felt like I was going insane until very recently.

(Technical details: the few that do bring it up might say that the Pythagorean norm is induced from another thing called an inner product, so it's special in that way. But also, that doesn't really get us anywhere: you can get a norm where a⁴ + b⁴ = c⁴ if you are allowed to take products of 4 vectors instead!)

How is this resolved, then? It turns out the different norms are not created equal, and the Pythagorean norm has a very special property the others lack: it looks the same in every direction, and lengths don't change when you rotate them. (A mathematician would say that it is isotropic.) Now, all of a sudden, things start to make sense! We *could* choose any norm we like to model our own universe, but why are we going to choose one which has preferred directions? In the real world, there isn't anything special about up or down or left or right. So the Pythagorean norm isn't some cosmic law of the universe, nor is it some random decision we made at the beginning of time; it's just the most natural choice.

But! That's not even the best part! If you've gone even further in your mathematical education, you'll know about something called p-adic numbers. All of our vector spaces so far have been over the field of real numbers, but the p-adic numbers can make vector fields just as well. So... are the Pythagorean norms also isotropic in p-adic spaces? Perhaps surprisingly, the answer is no! It turns out that the isotropic norms in p-adic linear algebra are the ∞-norms, where you take the maximum coordinate (rather than summing squares)! So the Pythagorean theorem looks very different in p-adic spaces; instead of a² + b² = c², it looks more like a^∞ + b^∞ = c^∞.

If you're burning to know more details on this, like I am right now as I'm learning it, this link and pregunton's linked questions go into more details about this correspondence: https://math.stackexchange.com/questions/4935985/nature-of-the-euclidean-norm

The interesting thing is that these questions don't have well-known answers, so there is probably even more detail that we have yet to explore!

tl;dr: the pythagorean theorem is kind of a fact of the universe, but not really, but it kinda makes sense for it to be true anyway. also we change the squares to powers of infinity in p-adic numbers and nobody really knows why

[grenade-maid]

It's funny that the Pythagorean Theorem is frequently invoked as useless stuff we were taught in school when we could have been learning "how to do taxes" or whatever because basic trigonometry is honestly one of the most broadly useful forms of mathematics. Especially when it comes to posturing over "useless academics vs practical skills" they're really showing their ass cause the times I have had to have the strongest grasp of math was when i was doing forestry and construction. Even times tables, yeah, that shit sucked when we were eight years old I guess but actually when you're on the job it pays to be able to quickly pull up some numbers in your head without stopping to pull out the calculator every single time. We're not eight years old anymore bro you gotta let it go

[liquidcrystalsky]

lets talk about game files what a new an interesting concept

splatoon textures, along with all bfres textures, are stored using S3 compression, or "BCn" it's a series of formats from BC1 to BC7

this is only used in nintendo's ".bntx" format, and of course the industry standard for DirectX textures, ".dds"

(bntx can describe multiple images at once, like all the textures for an entire scene can be one bntx file, while dds only allows one image per file)

It's a bit similar to JPEG where things are stored in little chunks, jpeg is 8x8 and bcn is 4x4. JPEG uses combinations of cosine functions and fourier transforms to represent each block while bcn is fucking wizardry idk but it changes on each version.

Coloured textures in splatoon 3 use "BC1" It's a format which allows 3 colour channels and a single bit alpha channel. It kinda sucks, a normal image has 3 channels each with 8 bits of colour, but bc1 uses 5 bits red, 6 bits green, 5 bits blue. And somehow the alpha is stored in there through wizardry. It's 16 bits per pixel rather than 32 and compresses really well and u can barely notice it so whatever yay

Single colour textures, like roughness, alpha, metalness, anything black and white which represents data rather than colour is "BC4". It only supports one channel so it can be a pretty small file for the data it contains. 8 bits per pixel but again, only one channel, no alpha at all, but you wouldn't need it

That accounts for maybe 80% of the textures in game, and 19% goes to "BC5" which is nearly exclusively used on Normal Maps. Instead of a colour or some data, it represents a direction using 2 channels. It's really cool because, if you have an X and a Y channel, for a direction, you can calculate the Z channel with no loss of information!!

This is why some normal maps are yellow instead of blue!

Nerd Shit: the blue channel is just sqrt(1 - x^2 - y^2), so if you have a yellow normal map, you can use math nodes in blender to convert it to a 3 channel one. That equation is actually a rearranged version of the Pythagorean Theorem!

another interesting thing is that BC5 textures sometimes calculated in a weird format, "SNORM" (signed normalized) which allows for negative numbers! For a byte, it maps [0, 255] to [-1, 1]

Nerd shit: it's actually [0, 127] to [0, 1] and 128 turns to -1, and [129, 255] to [-1, 0), note the last one does not include 0, a value of 0xFF is just slightly less than 0. By having two negative ones, the interval of [-1, 1] is represented with evenly spaced values unlike a float, which gets more precise as it goes to 0

the final 1% is BC6 and unlike where the value of a pixel is gotten from signed or unsigned bits, it's stored as floats! floats can store basically any number but you lose precision at really large numbers, but hell even at low numbers. Splatoon 3 uses BC6 for the skyboxes! by having the numbers as floats, you can parts to be extremely different. The largest difference in a normal image is a pixel with brightness 1 to a pixel with brightness 255, which is 255x more. A float technically can be infinitely times more, but it allows you to also have a lot of detail in the dark parts, while having detail in the lighter parts too! if you're making a realistic scene, it would make sense that the sun would have to be more than 255x brighter than the rest of the sky. even if your monitor cant display things that bright, it allows for much more realistic lighting

switch toolbox doesnt allow you to export to an easily usable format which supports floats, i can export it as a dds but not many programs can use that, and even less use ASTC. I want to get it to export to EXR but thats gonna take a bit.

thats my explanation on why i haven't ripped skyboxes that was the whole point of this post. bye

[altblock-tm]

@goblinbugthing so. here’s how to solve for displacement in that werewolf post

Let’s take another look at the word problem again—

“Tumblr user wordfather is driving down a road on a sick-ass motorcycle. They drive 300 meters north, then turn right at an intersection. From there, they drive 400 meters east.

“What is the total distance they traveled? What is their final displacement?”

You were correct calculating the total distance— adding together the two distances got you the total.

However, displacement is different from distance. While distance is how far you’ve traveled total, displacement is how far away your start point is from your end point.

Let’s take a look at how the tumblr user on the sick-ass motorcycle travels.

They start by going north for 300 meters. Their start point is indicated by point A.

Then, they turn and head east for 400 m. Their end point is indicated by point B.

Now we need to know how far away Point A is from Point B. To visualize this, I connected the two points with a line.

What we have on our hands is a triangle. Specifically, a right triangle. A right triangle is a triangle containing a right angle— a 90 degree angle. We know that the 300 m and 400 m sides form a right angle because one goes North, and the other goes East— and those are perpendicular to each other.

Luckily, right triangles are very simple to solve! To find how far Point A is from Point B, we need to find the length of the unknown longest side of the triangle— aka the hypotenuse.

There’s a rule that can be used to easily find the length of the hypotenuse of a triangle using the other two sides— the Pythagorean Theorem.

This is the equation. The length of side a squared (squaring a number is when you multiply it by itself) PLUS the length of side b squared equals side c squared. And to find c, you just need to un-square it— aka taking the square root.

Using the numbers from the equation, I used a calculator to get it done—

I. Probably could’ve labeled it to be more clear but I am allergic to showing my work in a detailed way.

Side A (300 meters) squared turned out to be 90,000. Side B (400 meters) squared turned out to be 160,000. Then we add the two to find what c squared is— 250,000.

Then we take the square root, which gives us our answer of the length of the hypotenuse, the distance from Point A to Point B, and the final displacement.

The final displacement of tumblr user wordfather is 500 meters.

I have no idea how helpful this was. Sorry.

[be-co-me]

Anonymous

Miya Atsumu

1.9k Words

Summary: Homework help proves to be more useful with a cute tutor.

...

Some days college was hard, but the first week of the semester, you didn't think you would be struggling as much as you were. You sat at your desk, nearly at the sixth hour of trying to figure out physics. A lot of it was math. Your worst subject. You struggled with even some of the simplest parts of it.

You decided to take a small break, grabbing your phone and leaning back in your desk chair. You opened ChitChat, an app that many college students around you and the world used. It essentially allowed you to talk and post with people anonymously within a five mile radius of you. You scrolled the usual content that others posted before posting about your struggles with physics.

This physics class is going to be the death of me.

Once it was posted, you scrolled a bit longer, reading some of the threads about the drama going on around the school. There was always something with one of the fraternities or sororities going on, or more like a person in them.

Eventually, your focus returned to your homework, until you heard your phone ding.

New comment on your post, view now!

You sat back once more, picking up your phone and opening the app.

Anon: Which physics course are you in? 

You: The first one :'( I'm struggling hard. 

Anon: Wait till you take the second one. The end is rough.

You: Sounds like I'll be crying a lot next semester then lol

Anon: Well, let me help. Which part are you having trouble with?

You: We're going over trig right now.

Anon: The math is the hardest part. Give me an example problem and I'll see if I can help you understand how to solve it.

You eyed your homework for the problem that you least understood. Maybe if you could understand how to do the hardest problem you could understand the easiest parts, which most of the other problems seemed to be.

You: The hypotenuse is 6 and the adjacent is 5, find the cosine.

Anon: Remember SOHCAHTOA? Sin= Opposite over Hypotenuse and so on so forth?

You didn't know what he was talking about. What was this abbreviation? You remembered a lot of weird ones or songs you learned to remember things, like the quadratic formula and pythagorean theorem, but never one for trigonometry. 

You: I do not. Never learned it. Please elaborate.

Anon: Okay, so the CAH is Cosine= Adjacent over Hypotenuse and the TOA is Tangent= Opposite over Adjacent. Remember that, it's crucial.

You: Got it.

Anon: Now, you need to find the cosine, so you need the CAH part. Your cosine equals your adjacent over the hypotenuse, so 5 over 6. Which is 0.83 in decimal form. Take your calculator and press the cos-1 button and enter 0.83 in the parentheses and close it, then press enter. What'd you get?

You did as he said, eyeing the problem one more time to make sure you told him what it was correctly. 

You: 33.56 was my answer.

Anon: And it's the correct one. Congrats, now you know the basics of trigonometry. Those rules are so important to knowing what to do. If you need more help add me on Snap. My username is    tsumu_rice_&_volley.

You instantly changed to Snap and added him. You had an idea as to who it was and when he added you back and sent you a picture composed with a selfie of him holding his own homework reading "Miya Atsumu", you instantly knew you were correct.

The volleyball team captain. And one of the most well known fraternity members of the school. All the girls sought after him. You never imagined he'd be good at school, but then again how would he stay in it if he wasn't? And volleyball too.

You viewed yourself in the camera, making sure you looked decent, sending a selfie back with your own homework. He responded with one back, the caption reading,

Need help with anymore of those questions?

You could only laugh. At yourself and maybe at how kinda cute the setter was. Your brain wandered off to if there was a chance he would ever like you. There were so many other people he had the option of dating if he wanted to.

Is all of them an acceptable answer?

You sent back. You eyed the paper, none of the answers becoming any easier to you. You wished your professor would explain things a little better, and the online platform you did lessons and homework on wasn't helpful even one bit. He sent a picture back and you opened it.

Could you meet in the library? Maybe I can explain it better in person.

You pondered on if you wanted to go or not. It was very cold outside and you were holed away in warmth of your dorm room. On the other hand this homework was due the next day and you had 49 other problems to get through that you couldn't begin to understand on your own, therefore you opted to meet with him. You snapped a quick picture.

If it's not too much trouble then sure! But I'm buying you a coffee at the cafe. No questions asked.

You got up from the warmth of your desk and the heater pushed into the corner of the floor underneath it, turning it off and putting on a cozy outfit. You packed your backpack up and began your trek to the library/cafe.

You received a Snap from him as you walked, opening it.

I'm here in the corner. It's void of people in here, so I should be pretty easy to find.

His pictures were cute. You were glad he sent his Snap and not some other generic messaging app to talk on. You got to see him along with it. It made your heart leap a little bit when you saw the picture.

Almost there!

You responded, shoving your phone into your jacket pocket as you opened the door to go inside. You wiped the snow off of yourself and walked into the main study area. You looked around for him and met his eyes, him waving you down. You walked towards him.

"Well, I guess I should introduce myself properly. Hi Anon, I'm Atsumu." he said, sticking his hand out.

"And I'm (Y/N)." you responded, shaking his hand with your gloved one. You set your bag down and shrugged your winter attire off.

"So coffee? My treat for you helping me." you said. He nodded, standing up. You walked over to the cafe with him, pulling your wallet out. You eyed the menu for a little while before deciding on a brown sugar oat milk cold brew. He chose an iced matcha latte. You paid for the drinks and stood to the side, waiting for them to be made.

"It sure is dead in here. I didn't expect it to be with the first week of school and all." he said, breaking the ice and starting up a conversation.

"I know what you mean. Maybe everyone thinks it's too cold to go out. I don't have many friends here or I'd be in here studying with them all the time, I just don't wanna be alone in here. It would be kind of awkward." you responded, the barista handing the drinks to you. You handed him his own.

"I get that. I don't have wifi at my dorm yet. I'm in the new building so they haven't set it up. I've got no choice so I kinda got past the awkward part." he chuckled. You made your way back to the table and sat down.

"We even get this huge whiteboard all to ourselves to do as much trigonometry as we desire." he said, pointing out the whiteboard in the corner. Almost all study areas in the school had a whiteboard or, new as of that semester, a large tablet to do work on.

He began to explain the next homework problem you had, eyeing all of the erased pencil and light evidence of wrong answers on the paper. He stood and drew a problem on the whiteboard, prompting you to answer as he wrote down what you responded to his questions. You took your calculator and entered what you had come up with, the correct answer popping up. You smiled as you finally began to understand.

"Alright, I'm gonna take a problem for sine, cosine, and tangent each and put them up here. I want you to solve them on your own." he said, picking up your homework packet and rummaging through the pages to find one of each problem.

Once he was done, he sat back down, working on what seemed to be a literature essay. You took a while trying to make sure every detail was correct, typing into your calculator to get an answer occasionally. Once you were confident your answers and your work underneath each triangular model was correct, you turned around.

"Alright, finished." you said. He looked up from his laptop, setting down his latte and standing to review your work. You sat down, watching him as he carefully reviewed your writing. He leaned over the table and took your calculator, typing in what you hoped was your correct work on each problem. You sipped on your coffee as he reviewed.

"All correct! Good job! Do you think you're okay to finish them up on your own?" he asked. You nodded.

"Ask me if you have any questions." he said, sitting back down across from you. You nodded once more, beginning to work on the packet once more.

After thirty minutes of doing problems and typing into your calculator, you finally finished. You set the calculator down and stretched your arms, eyeing your now empty coffee cup.

"Finished?" he asked, looking up. You nodded, your eyes looking up to meet his own.

"Let me see it." he said, motioning with his hand for you to give it to him. He eyed the packet over, typing in a few problems from each page to make sure they were right.

"You did good! All the ones I put in are correct so I'm sure you did well on everything else." he said, handing the packet back to you. You packed it into it's respectful folder where it would sit until your class the following day.

"How about you? What have you been typing up over there?" you asked.

"Just reviewing this essay. Can you believe we had to do an essay the first week of school? Unbelievable." he said, shaking his head in disapointment. You chuckled in response. That was a little much of the teacher. You'd take note so you knew not to take that teacher's class in the future.

The two of you talked until the library hours were over. You packed your things and put your winter attire back on, ready to walk out. 

"I printed a paper off. Can you grab it for me please?" he asked you nodded, walking across the library to grab it. You stood in front of the printer, grabbing the slightly warm paper off of it. You turned around to wave it at him, but he was gone.

You frowned slightly, turning the paper over.

Let's make this a weekly thing so you don't have to study alone. Here's my number. You better text me! :P  XX-XXXX-XXXX. -Anonymous

[sakuraswordly]

Translate:

Sorry, Pythagoras! This 3,700-year-old Babylonian tablet(IM 67118) proves the ‘Pythagorean’ theorem was already old math by the time he was born. Ancient scribes were solving for *c²* while Greece was still in the Bronze Age! Babylonians’ 60-based system still rules our clocks (60 mins) and circles (360°)—talk about lasting influence!

In 1770 BCE, a Babylonian teacher pressed a reed into wet clay to demonstrate how to calculate a rectangle’s diagonal using what we now call the Pythagorean theorem(a² + b² = c²). The tablet, unearthed in Iraq, includes step-by-step base-60 math—proving Mesopotamians used the formula 1,000 years before Pythagoras drew his first triangle.

Even earlier, the Plimpton 322 tablet (c. 1800 BCE) lists Pythagorean triples (like 3-4-5) in neat cuneiform, suggesting it was a *textbook* for advanced students. How’s that for ancient STEM?

[canadianabroadvery]

Wonders of the Past - a Post by Silvia S.

"The Wonders of Ahmose's Papyrus 📜 Many are curious about how the ancient Egyptians managed to construct the pyramids using intricate mathematical calculations.

The Papyrus of Ahmose, also known as the Mathematical Rhind, is the oldest known manuscript featuring algebra and trigonometry. Its origins trace back 1500 years before the time of Christ, roughly 3500 years ago.

This manuscript reveals that the Egyptians were proficient in employing first-order equations and had various methods to solve them. They were also well-versed in quadratic equations, adept at solving them, and familiar with numerical and geometric sequences.

For instance, they were capable of handling equations like:

X2 + y2 = 100,

Y = 3/4 x, where x = 8, y = 6.

This equation serves as the foundation of the Pythagorean theorem, a2 = b2 + c2, and in Egyptian terms, the unknown number was referred to as "koom."

Also nwe should note that Pythagoras developed his mathematical theories after a visit to Egypt, where he learned from Egyptian priests. This historical fact has been substantiated by Greek historians and scholars like Farpharius of Sour, Herodotus, and Thales.

Remarkably, the Egyptians had mastered algebra, trigonometry, and geometry approximately 2,000 years before Pythagoras was born, and even around 3,000 years prior to the birth of al-Khwarizmi.

Today, this invaluable papyrus can be found in the British Museum in London."

[the-starry-lycan]

Okay, Lycan. Doing your vectors assignment for Calculus II. Let’s pick some variables for this problem.. easy ones to represent the boat and the water..

Lycan: Okay, we have to calculate the magnitude of the overall vector, which is easy-

Lycan’s Brain: W and B. It’s Wet B’st.

Lycan: -easy if we just use the Pythagorean theorem and find the third side of the right-angle triangle..

Lycan’s Brain: WET B’ST WEDNESDAY-

(Wet B’st Wednesday haunts this wolf’s mind now..)