#forgetful functor: set

[nb-swordk9]

Shit man, this math war is fucked. I just saw a guy draw a commutative diagram and say "one point compactification" or some similar shit, and everyone around him got folded into a 3-sphere and vanished into 4d-space. The camera didn't even go onto him, that's how common shit like this is. My ass is casting ε-δ and quotient spaces. I think I just heard "infinity-groupoid coskeleton tower" two groups over. I gotta get the fuck outta here.

[carmilla-the-dog]

What is the dual of the forgetful functor?

Ooooh my, this is going to be fun.

Ok, so first things first, what do we mean here by dual? Well, duality in category theory is a very loose concept, and one must examine the particular use case before deciding what dual means.

In this post, duality will be given by adjunction. And what is adjunction, you ask? Adjunction is when

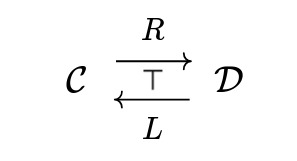
are related by

$$\mathcal{D}(x,Ry)\cong\mathcal{C}(Lx,y),$$

(the isomorphism being natural). And in this case we say that \(R\) is a right adjoint to \(L\) and \(L\) is a left adjoint to \(R\). By Yoneda bullshit, all right adjoints of a functor have to be isomorphic. (dually, the same is true for left adjoints).

THE SECOND THING is that forgetful functor is also a loosely defined concept (https://ncatlab.org/nlab/show/stuff%2C+structure%2C+property). But here I'll be talking about the family of functors of the form

$$U:\mathcal{E}\to\mathbf{Set},$$

in which \(\mathcal{E}\) is a concrete algebraic category like modules, vector spaces, groups or abelian groups. This functor takes an algebraic structure and send it to its underlying set.

Remark. More generally you can take the category of monoids, or the category of algebraic theory, over a category \(\mathcal{C}\) and you have a natural forgetful functor into \(\mathcal{C}\) itself.

OK. So if we want a left adjoint to \(U\), we require that, given a set \(x\) and a algebraic structure \(y\) (which has underlying set \(y\) because fuck you), we have

$$\mathbf{Set}(x,y)\cong\mathcal{E}(Lx,y).$$

That is, algebraic maps

$$\phi:Lx\to y,$$

are completely determined by the map in \(x\):

$$f:x\to y.$$

If you feel like this is familiar, you are not wrong! If you have any formal training in mathematics (and if you don't, I'm so sorry for using jargon and stuff… I can answer any questions after ^^( but I know for a fact that anon has formal training)) then you maybe recognize this from linear algebra.

Indeeeeeeeeed, given any vector spaces \(V\text{ and } W\), a linear map

$$T:V\to W$$

is completely determined by what it does to the basis of \(V\). Even more, if the set \(v\) is as basis for \(V\) (I am completely aware that my notation can cause psychic damage), then every function of sets

$$f:v\to W,$$

determine a linear transformation

$$T:V\to W.$$

AND EVEN FURTHER every linear transformation is obtained in this way. Abstracting again, the left functor \(L\) represents taking a set \(x\) and using it as a basis for a algebraic structure \(Lx\).

As algebraic structures with a basis are called free, the left adjoint of a forgetful functor is called the free functor. :)

If someone guess the name of the right adjoint of the forgetful functor, I'll give them a kiss

[bubbloquacious]

Do you have any recommendations for texts for a first reading of category theory? :))

So this is a super common question and I think it's a little hard to give a good answer to! I'll tell you what I did.

Back in the summer of the beautiful year 2019 I had just finished my first year of university mathematics education. I don't remember where I had even heard of the subject, but the first math book I ever self-studied out of was Mac Lane's Categories for the Working Mathematician (the second edition, specifically). It's a good book, I think! But I only really appreciated it on my reread (i.e. my more-than-the-first-three-chapters read) last year. For one, I had not done a lick of topology by this point, and I really do recommend knowing basic topology and basic abstract algebra before getting into categories; it gives you a nice two-pronged approach to view every construction.

So I washed out of that one pretty quickly. I learned the basic definitions of categories, functors, and natural transformations. I could work out what it meant for a product to be the limit of a discrete diagram (super neat when you just learned what a group was five months ago!), but if you asked me to give an example of a pair of adjoint functors that wasn't in the text I would've been stumped (natural transformations between hom-functors? what?).

Over the course of the next semester I got familiar with the basics of topology (and I made this blog!). Now I could see why a lot of Mac Lane's examples were so nice. Compositions of homotopic maps are homotopic, so you can take a quotient category the same way you take a quotient group. The fundamental group is so useful exactly because it is functorial. A map into a product space is continuous precisely when its composition with the projections is continuous. And so on. I sampled some more books. I read the first few chapters of Awodey's Category Theory and of Adámek, Herrlich, and Strecker's Abstract and Concrete Categories. Each offers a slightly different perspective, but every time I would wash out after the first several chapters.

But it was exactly rereading all of these different perspectives that made me grok what it was all about. How to work with these structures. I had limits and colimits pretty much down by this point. Ah, it's not a coincidence that the least upper bound and greatest lower bound are categorical limits, they're expressing the same idea. I realized on my own that not only is the discrete space functor to topological spaces left adjoint to the forgetful functor to sets, the indiscrete (or chaotic, or trivial) space functor is right adjoint. The abelianization of a group or the completion of a metric space are left adjoint to the inclusion functors of abelian groups and complete metric spaces, because a map from a group/metric space into an abelian group/complete metric space determines a unique map (in fact it factors through this map) out of the abelianization/completion. Even though the abelianization makes the group smaller, and the completion makes the space bigger, they're expressing the same relationship.

This went on for a while. I read Bartosz Milewski's blog on Category Theory for Programmers, but I didn't know Haskell so that didn't get me very far. I read a lot of nLab pages (I still do). I read a small bit of Borceux's Handbook of Categorical Algebra, which is very nicely written if you can get your hands on it. I spent a summer in a reading group for Tai-Danae Bradley's Topology: A Categorical Approach (this one's probably a good pick for you in particular!). Like two years ago I played the Natural Number Game (which they changed recently apparently!), which got me really into Lean and proof assistants in general. Playing around with Lean gave me a great appreciation for what category theory brings to the table for logic and computational mathematics. Reading Dan Marsden's blog on monads got me really into monad theory, which is just super cool and I love it very much. I had a brief fling with bicategories, mostly because of the monads. Around this time I made a bunch of explanatory posts on the things I was learning about, and that was just terrifically helpful for my understanding. I read Mac Lane and Eilenberg's original paper introducing categories, General Theory of Natural Equivalences, and it's fascinating to see the perspective that it takes. Last year I got really into sheaf theory by reading Mac Lane and Moerdijk's Sheaves in Geometry and Logic, which finally made me understand the Yoneda Lemma.

These last few examples are what I would call pretty intermediate, as far as categories go. Somehow by reading all these different sources (and progressing in my studies in other mathematical subjects!) I had gathered up enough experience to understand the higher-level structures built on top of the basics. I still don't understand Kan extensions (though I tried reading Riehl's Category Theory in Context to understand it) or fibrations, or model categories, or co/end calculus, but I'm sure I will once the need arises.

So that's my advice! Read as many different introductions to the subject as you can, in as many different contexts as you have the experience for! The power and beauty of category lies in the bridging over the gaps between these contexts. Any of the books I mentioned I would recommend, but really the most important rule of category theory is to have fun and be yourself :-)

[proof-by-intimidation]

Product of topological spaces categorically.

Let's say we want to define the product of two topological spaces X and Y. First of all, what's the underlying set? Well, the forgetful functor from Top to Set has a right (as well as a left) adjoint. So it preserves limits (and colimits).

So, if the product of the topological spaces exists, then the underlying set should be X \times Y !

Ok, now the topology. Well, we have an obvious candidate for the projection maps, namely the usual projection maps from X\times Y to each of its component. So, we impose a topology on X\times Y such that these maps are continuous. We also need to make it the coarsest such topology, so that it satisfies the universal property!

And that is precisely the product topology.

I know this is not very profound but this perspective really helped me move on to CGWH category. The bizarre topology of the categorical product of CGWH spaces is not always homeomorphic to the product topology. But it is the more natural choice (look at product of CW complexes and prod-hom adjunctino) just like how the projection maps were the natural choice for categorical projection maps in Top.

So, yeah i thought this was cool.

[algebraic-dualist]

Given a monad T on a cartesian category C recall the forgetful functor U : C^T -> C. It seems to me that we can recover the "operations" encoded by the monad by thinking of natural transformations: θ_A : U(A)^n -> U(A)

In the case that the monad T is encoding an algebraic theory on Set, it is clear that every term t(x_1, x_2, ..., x_n) induces, by evaluation, on each algebra a function t_A : A^n -> A which commutes with all T-homomorphisms. So, it would induce an element of Nat(U^n, U). Thus, we get sets Op_T(n) which we can use to assemble together an operad Op_T. Question: When are algebras of this operad encoding exactly the algebras of the monad?

[emmy-noethers-rings]

With all the talk about girl math, I think it’s worth understanding the concept. To that end, we have discovered the following results of note:

Proposition 1.1: there exists and isomorphism between girl math and math.

Proof:

Let t:girl math-> math be a set valued “forgetful” function, with t(x) = x.remove(Girl). t is clearly an embedding of girl math in math, thus we get for free that it is injective. Consider the codomain of t and consider Im(t) = { m : m ∈ math}.

We suppose Im(t) to be nonempty. Thus, consider m ∈ Im(t) ⇒ ∄ g ∈ girl math: t(g)=m. However, ∀ m ∈ Im(t), girl m ∈ girl math, a contradiction. Thus t is bijective.

Consider t(m*n)= m*n.remove(Girl)= m.remove(Girl)*n.remove(Girl)=t(m)*t(n). Thus t is structure preserving. Thus, it is an isomorphism. □

Proposition 1.2: the isomorphism between girl math and math is the “girl function” (really it’s better to formalize as the girl functor but that’s neither here nor there) e. As the astute reader may recall, e(x) = e.add(Girl)

Proof:

Left as an excercise to the reader □

[zesty-comrade]

A category is a collection of objects and morphisms (best to think of them as arrows) between them. For example you can think of a monoid (like the natural numbers(no zero) with multiplication) the class of objects being the set and the the collection of morphisms being the described by the binary operation by some element of the set(*,n for all n in the natural numbers). What happens when you want to move between categories? Well then you introduce functors, maps between categories. Full means for every pair of objects x,y in C the mapping f to F(f) defines a surjection Mor(x,y) to Mor(Fx, Fy); faithful means basically the same but injection not surjection, combined full and faithful is like injectivity, you need a third thing; essentially surjective. Essentially surjective means for every object d in D there is some c in C st Fc isom d. If you have fully faithful and essentially surjective you have an isomorphism on catagories.For example in the degenerate example of the category of the natural numbers with multiplication by a natural number, and the category of the integers, addition and multiplication by an integer, the identity from the natural numbers to the integers is a faithful functor trivially. For a less degenerate example think of k dimensional vector (obj) spaces and k linear maps (mor). This is not nessasarialy surjective on objects. What are some functors is a natural question. Now onto my favorite functor: the forgetful functor. The forgetful functor: U, from the catagory to the set maps objects to their underlying sets and morphisms to their underlying set-maps. it tosses out the structure of the catagory, hence forgetful. Its really fucking dope ngl. to define the next functor we need to define the C^{op}, the opposite category, it has the same object but with flipped arrows(swap the sources and targets of C's morphisms). There is a functor C to C^{op} that takes objects to themselves and arrows to their "flip". For the third example we will talk about based spaces. Let (X,x) be a based space, (X is a space, x in X). we call the fundemental group \pi_1(X,x) the set of based continous maps l:[0,1] to X st l(0)= l(1) = x, moding out homotopy equivilence. The group structure is loop conatenation: given l, l':[0,1] to X, define l'l:[0,1] to X to do one loop over [0.5] then one loop over [0.5, 1]. then given a based map f:(X,x) to (Y,y), there is aninduced map f_*:\pi_1 X to \pi_1 Y given by l to f \circ l. This defines a functor: \pi_1 (-): Top_* to Grp. for the forth and final example for this post for each n, singular homology defines a functor H_n(-): Top to Ab. Simularly, singular cohomology defines a functor H^n(-): Top^{op} to Ab. Next post we will talk about natural transormations. they are rather hype ngl.

[selormohene]

day 132 (sunday, november 12th 2023)

On what it means to be a Set-valued functor. This one is going to be pretty rough and not very coherent because I'm still thinking about this, it's very much in its initial inchoate stages. But it occurs to me that there are at least three ways to think of what it means to be a Set-valued functor. The first pertains to being a concrete category, consisting of sets with extra structure. So the idea here is (or seems to be) that a set is its own thing, and then a group (for instance) just is a set with extra structure relating its elements, and the imposition of that extra structure is what defines the category of groups. The existence of a forgetful functor is in a sense returning to the original starting point.

But you can also think of Set-valued functors as a generalisation of the notion of “sets with extra structure.” And here you could drop various constraints on the initial conception, such as the requirement of faithfulness. So forgetful functors from concrete categories to Set are faithful (i.e. injective on maps), because once you have the structure you're just concerned with certain set-maps between the structured sets, but (as far as I can tell) such functors need not be injective on objects, which morally corresponds to the idea that concrete categories can consist of the same set with different structures on it, but the functions are just, extensionally speaking, the appropriate set-functions between these sets with structure imposed (that is, those set maps which respect the given structure). On this second way of understanding Set-valued functors, you might (for instance) drop the condition that the functor should be faithful, so it no longer needs to be injective on maps. And a way of looking at things here is that you’re considering functions intensionally, so to speak, just as you were initially considering objects intensionally. So multiple maps in the given category may correspond to the same set-theoretic function. More generally, what you get is something like a mathematical structure that can be implemented by sets, but the structure is prior to its set-theoretic implication. For instance if we define a very general sort of structure over a category in C to be a functor in Set, we can think of that as a generalisation of a sort of structured set. Consider, for instance, the category of simplicial sets. Even the name attests to this. A simplicial set is a (contravariant) functor from the simplicial category to the category of sets, which you could think of as a diagram of sets shaped like the simplicial category. And if you think about the simplicial category as encoding the most abstract, most general algebraic relations that the various n-cells of a simplicial structure could have in relation to each other, then any diagram of that shape in Set can be thought of as consisting of the sets of n-cells of some real simplicial structure, together with the relations that in fact hold between the n-cells in question. (Note here that whereas in the first instance the image of each object under a functor was the set of interest, in this case it's the image of the entire functor that gives the entire structure of interest, so to speak.)

The third thing is that a Set-valued functor encodes mathematical structure that can be implemented in sets by a certain algebra of morphisms, or set maps. I suppose this is the viewpoint behind algebraic set theory. (And this viewpoint was implicit in the example given above.) Here the important thing is not which elements get sent to where, but how the maps compose. And it could be that there are general aspects of the category of sets which are convenient for encoding a certain kind of structure, but in fact you don’t even need to consider Set at all, any category which has those more global features will do. For instance, the fact that we can define a notion of simplicial set simply as a functor from the simplicial operator category to Set suggests that if we have an indexed category of sets for every natural number together with some subclass of maps between them subject to certain constraints, we can think of them as abstractly representing something like a set of n-simplices, or whatever. And to give another example, you can think of the category of topological spaces (and its realisation in Set) as a set-theoretic version of an abstract structure of morphisms which could in principle exist in any category which has enough maps that you can pick subsets of each hom-set which display the required combinatorial and universal properties. So then it would be as though all one really has is a set-theoretic instantiation of what is really the abstract theory of locales.

[anocana]

with the free/forgetful motivation in mind, and having looked up some details of free groups (the free group is the one with the morphism to anything compatible, i hadn't been sure if it was to or from) but forgetting which is left and which is right (i have already forgotten from the reply):

unit is basically, you didn't need to go through all these functors, you could have just gotten from there to here directly. which is a natural transformation from Id to FG. so it's the one that ends in the forgetful functor, you just added some structure and then deleted it?

counit is, don't worry, even though you went through all these functors you can get back to where you started. which is a natural transformation from GF to Id. so it ends in the free functor which has a morphism to the original object. you forgot the structure, did your best to reconstruct it, and the reconstruction is at least compatible with the original.

and then the isomorphism of homsets... in the group case, any function from one set to another gives us a homomorphism from the free group on the source to any group on the target, because there are no compatibilities to preserve in the free group? and any homomorphism that starts in a free group is basically just a set function for the same reason. so in Hom(F(x), y) ~= Hom(x, G(y)), the free functor is left and the forgetful functor is right?

okay i think that makes sense now. checking back at the reply i ended up at the right answer

as a poser, i can never remember the difference between left and right adjoints, or indeed what the motivation is for one over the other

[abalidoth]

hey um. I accidentally hit your boyfriend with a forgetful functor from Boyf to Set and he lost all his algebraic structure. he has the same cardinality but doesn't even have a distinguished element or anything. sorry.

[max1461]

If you don't mind (obviously feel free to ignore me if you do) can you give an explanation of what the point of universal properties is? My lecturer also mentions them all the time but they've never seemed really... useful for anything.

Well it's been a while, so this is sort of half-remembered, and if I make any mistakes hopefully someone can come along and correct me. I think I can pretty much give you the gist, though.

Universal properties are one way to characterize the behavior of objects in purely category-theoretic terms (that is, without reference to internal structure), which is something that you can always do in category theory because of, IIRC, the Yoneda Lemma. And the argument is that they're generally a lot "cleaner" than working directly with internal structure/a specific construction.

A good example of this in action is linear algebra, where we use universal properties (implicitly) all the time. We know that whenever we have two vector spaces V and W, we can define a linear map from V to W just by specifying how the map acts on the basis vectors. Any map (of sets) from a basis of V into W can be uniquely extended to linear map from V to W. This is like, the fact that all of linear algebra is based on, and it's essentially a restatement of the universal property of free objects for vector spaces (all vector spaces are free objects).

Basically the same thing is true of free groups: for any free group G and any other group H, and any map f from the generating set of G into H, the map f extends uniquely to a group homomorphism from G to H. In fact, all properties of free groups can be derived from this fact (once you've shown that free groups exist, that is). This is much nicer to work with than like, messing around with the actual construction of a free group, which is sort of awful. It also lets us see that something similar is going on with free groups and with vector spaces; that generating sets of a free group and bases of a vector space are in some sense "doing the same thing". In and of itself this is pretty cool.

What's going on here, in category-theoretic terms, is this: we've got some objects A and B in a category C (in the free groups example, C is the category of groups; in the vector space example, C is the category of vector spaces). In this category, there is a certain kind of morphism (group homomorphism; linear maps). However, we can also think of our objects as being in some category D, with a different kind of morphism (in both cases, we can think about our objects as living in the category of sets, with set maps between them). And so we have a functor F: C -> D (here, it's just the forgetful functor).

Now, say that S is the basis, or the generating set, of A. It's an object in D. Since it's a subset of A, there is an inclusion map i: S -> F(A) in D. If we have a morphism f: S -> F(B) in D, that represents an assignment of basis vectors to elements of B, or elements of the generating set to elements in B, respectively. And what the universal property of free objects says is that for any such f, there exists a unique map m: A -> B in the category C such that f = iF(m). In other words, f extends uniquely to a morphism from A to B in C.

A bunch of properties can be phrased in basically this same schema. D doesn't need to be Set, and F doesn't need to be the forgetful functor, and i doesn't need to be set inclusion. As long as the same diagrammatic structure is present, that's a universal property. Or you could also have the same thing with all the arrows reversed and it would still count, because of, uh, well category is just like that. But anyway. It turns out that a ton of things are characterized by universal properties: products, disjoint unions (sums), tensor algebras, categorical limits and colimits. So we have this framework for characterizing all these things purely in terms of the morphisms in and out of them, and that's really useful. And we implicitly reason with universal properties all the time anyway, so it's good to have a formalism for them.

At least, that's what I remember. Hopefully that's helpful!

[bubbloquacious]

So the fact that the underlying sets of products and coproducts of topological spaces are themselves the products and coproducts of the underlying sets is a consequence of the fact that the forgetful functor from the category of topological spaces and continuous maps to the category of sets and functions has both a left and right adjoint (namely the discrete space functor and the indiscrete space functor), so it preserves both limits and colimits (compare this with the fact that the underlying set of a direct sum of abelian groups is not generally the disjoint union of their underlying sets).

But it also goes the other way! The discrete space functor has a right adjoint (namely the forgetful functor), so any disjoint union of discrete spaces is discrete. Products of discrete spaces can be non-discrete, so it does not have a left adjoint. The indiscrete space functor has a left adjoint, so products of indiscrete spaces are indiscrete. Disjoint unions of indiscrete spaces are almost never indiscrete, so it does not have a right adjoint.

[weirdvic]

New ideas! Functoriality achieved :)

Have C again be a concrete category.

First new idea, I thought of a relatively obvious modification to your construction:

Have the objects be a an element of A for some A object of C, and morphisms from a in A to b in B be morphisms f from A to B such that f(a)=b.

Your construction from yesterday maps each object to a subcategory of this category.

Having shifted our focus away from endomorphisms, we are no longer looking to build f' such that F○f = f'○F (reusing notations from before), but simply F○f=f' (with f' from A to A').

This is obviously no longer an obstruction, but it is a much less interesting question! This modification is not neutral.

Second new idea, there is a cool projection functor from the associated category to C that I missed yesterday, mapping a in A to A and f from A to B such that f(a)=b to f from A to B.

This last part is really long. I'm so sorry.

You might notice I haven't adressed the functoriality of this new construction. This is still a problem, but now the struggle is with the objects, not the morphisms.

In short, if you have a functor F from C to D concrete categories and an element a in an object A, there is no natural way to associate to it an element of F(A) as is.

As is often the case in category theory, when something isn't functorial it's simply not abstract enough!

Third new idea, this can be generalized to a great extent. Take a category C and F a covariant functor from C to Sets.

You can use the forgetful functor if C is concrete, or hom(X, . ) for some X if C is locally small for example!

You can form a category whose objects are (A,a) where A is an object of C and a is an element of F(A), where the morphisms from (A,a) to (B,b) are morphisms f from A to B such that (F(f))(a) = b.

Notice that there is still a projection functor, which is neat :)

We are associating categories to functors, so in order to make this association functorial we need to associate a functor to a natural transformation!

To be precise, our objects are pairs (C, F) with C a category and F a covariant functor from C to Sets, so our morphisms from (C, F) to (D, G) should be pairs (E, eta) with E covariant functor from C to D and eta natural transformation from F to G○E.

Given an object A of C, eta gives a morphism from F(A) to G(E(A)). So we simply associate to (A,a) the pair (E(A), (eta(A))(a)).

Given a morphism f from (A,a) to (B,b), i.e a morphism from A to B such that (F(f))(a) = b, E(f) is a morphism of E(A) to E(B) such that, by definition of eta, (G(E(f))((eta(A))(a)) = (G(E(f))((eta(B))(b)).

At last, we have achieved functoriality!

So in order to make your previous association functorial, you have to

1. Associate only one category to a concrete category instead of one category for every object in a concrete category. Tragically, this takes the focus away from endomorphisms completely.

2. For morphisms between concrete categories, take functors that are compatible with the forgetful functors up to a natural transformation.

I need someone more knowledgeable than me to tell me if this is useful at all. Recently I’ve been thinking about endomorphisms in concrete categories (that is categories where we can speak of elements of objects) and I realized that for every object A in such a category can be associated with a category where objects are elements of A and for any two elements a and b hom(a,b) is the set of endomorphisms f such that f(a)=b. This association doesn’t seem to be functorial, or if it is I can’t figure out how it acts on morphisms. This construction seems interesting but I can’t figure out how. So my questions are:

1. Does what I’m describing already exist and if so where can I read about it?

2. Is this interesting at all or am I just being silly?

[vacuous-truth]

Learning about the forgetful functor and honestly it’s existentially kinda fucked, like you’ve transformed something in such a way that it’s an emptier version itself. Idk if it’s just my personal view of what maths is, but that feels really fundamentally wrong, would you strip someone of their soul to transform them into a husk? No. Well then why would you strip a group of its structure to transform it into a set? Imagine if your biology textbook said “Exhume the frog of its divine link to leave an automaton” to describe frog dissection

[thetwomeatmeal]

Just gave my partner this cute category theory problem:

Define four functors  Sets -> Spaces -> Sets -> Spaces -> Sets such that each one is left adjoint to the one before. The second one is the forgetful functor, and the others are all things you’ve seen before.

[eatsleepmath]

Strong conceptual completeness for \(\aleph_0\)-categorical theories, 2:

This series of posts is a serialization of (what started as) notes for a talk I gave at the Harvard logic seminar on 6 February 2018. You can view them in order here.

Pre-ultrafunctors

When \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) is \(\operatorname{ev}_{\varphi(x)}\) and one proves the Łos theorem \[X\left(\prod_{i \to \mathcal{U}} M_i \right) = \prod_{i \to \mathcal{U}} X(M_i),\] one has the luxury of being able to test the displayed equation above between two subsets of (the interpretation in \(\prod_{i \to \mathcal{U}} M_i\) of) the ambient sort of the formula \(\varphi(x)\). If \(X\) is merely isomorphic to \(\operatorname{ev}_{\varphi(x)}\), then \(X\left(\prod_{i \to \mathcal{U}} M_i\right)\) and \(\prod_{i \to \mathcal{U}} X(M_i)\) might be entirely different sets, with only the isomorphism to \(\operatorname{ev}_{\varphi(x)}\) to compare them, so that testing equality as above is not a well-formulated question; rather, one asks for an isomorphism.

Remark. Given a natural isomorphism \(\eta : X \simeq \operatorname{ev}_{\varphi(x)}\) with components \(\{\eta_{M} : X(M) \simeq \varphi(M)\}_{M \in \operatorname{\mathbf{Mod}}(T)}\), we have for every ultraproduct \(\prod_{i \to \mathcal{U}} M_i\) a commutative square

where the dashed map \(\Phi_{(M_i)}\) is the composition of isomorphisms \(\left(\prod_{i \to \mathcal{U}} \eta_{M_i} \right)^{-1} \circ \eta_{\prod_{i \to \mathcal{U}} M_i}\).

It is easy to see that the statement of Łos’ theorem is functorial on elementary embeddings. That is, for every \(I\), every ultrafilter \(\mathcal{U}\) on \(I\), and every sequence of elementary embeddings \(f_i : M_i \to N_i\), the diagram

commutes.

Definition. For an arbitrary functor \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\), if we additionally specify for every \(I, \mathcal{U}, (M_i)_{i \in I}\) the data of a transition isomorphism \(\Phi_{(M_i)} : X\left(\prod_{i \to \mathcal{U}} M_i\right) \to \prod_{i \to \mathcal{U}} X(M_i)\), then we say that \((X, \Phi)\) “commutes with ultraproducts” if all diagrams

commute. We let \(\Phi\) abbreviate all the transition isomorphisms, and we call a pair \((X,\Phi)\) a pre-ultrafunctor. We will abuse terminology by referring to \(\Phi\) as “the” transition isomorphism of the pre-ultrafunctor \((X, \Phi)\).

Given two pre-ultrafunctors \((X, \Phi)\) and \((X', \Phi')\), we define a map between them, called an ultratransformation, to be a natural transformation \(\eta : X \to X'\) which satisfies the following additional property: all diagrams

must commute.

With this terminology, the theorem says that if \(X\) is a sub-pre-ultrafunctor of an evaluation functor \(\operatorname{ev}_{\varphi(x)}\), then \(X\) is definable.

In light of the above definition, we can reformulate our observation about a definable functor \(X \overset{\eta}{\simeq} \operatorname{ev}_{\varphi(x)}\) above as saying that the natural isomorphism \(\eta\) canonically equips \(X\) with a transition isomorphism such that \(\eta\) is an ultratransformation.

Remark. Every functor of points \(\operatorname{ev}_{\varphi(x)}\) can be canonically viewed as a pre-ultrafunctor with the transition isomorphisms \(\Phi\) just the identity maps (corresponding to the equality signs in the above diagrams).

One checks that if \(X\) and \(Y\) are definable sets, and \(f : X \to Y\) is a definable function, then the induced natural transformation between evaluation functors \(\operatorname{ev}_f : ev_X \to \operatorname{ev}_Y\) is in fact an ultratransformation. (This contains Los’ theorem: in the proof, one is really showing that if \(S\) is the sort containing a formula \(\varphi(x)\), then the canonical definable injection \(i : \varphi(x) \hookrightarrow S\) induces an ultratransformation; the fact that the transition isomorphisms are all identities means that one ends up with the usual equality.)

Definition. The category of pre-ultrafunctors \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) comprises objects preultrafunctors \((X, \Phi)\) and morphisms the ultratransformations.

Remark. By the remark, the evaluation functor \(\operatorname{ev} : \operatorname{\mathbf{Def}}(T) \to [\operatorname{\mathbf{Mod}}(T), \mathbf{Set}]\) further factors through \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\):

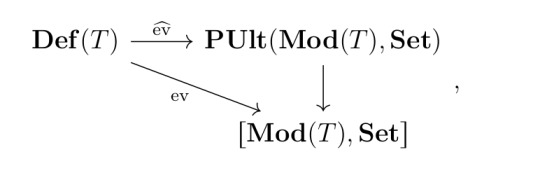
where the arrow \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) is just the forgetful functor \((X, \Phi) \mapsto X\).

Note that whenever there is an isomorphism \(\eta : X \simeq Y\) as functors \(\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\), and \((X, \Phi)\) is a pre-ultrafunctor, then by conjugating \(\Phi\) by the isomorphism \(X \simeq Y\) (as in the diagram), one canonically equips \(Y\) with a transition isomorphism \(\Phi'\) such that \(\eta : (X, \Phi) \to (Y, \Phi')\) is an ultratransformation.

Remark. That is, \(X\) is definable if and only if there is a transition isomorphism \(\Phi\) such that \((X,\Phi)\) is isomorphic to \((\operatorname{ev}_{\varphi(x)}, \operatorname{id})\) for some formula \(\varphi(x) \in T\). We will suppress the canonical transition isomorphism \(\operatorname{id}\) and just say that \((X,\Phi)\) is isomorphic to \(\operatorname{ev}_{\varphi(x)}\), understanding that this isomorphism is happening in \(\mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\).

The pre-ultrafunctor condition only stipulates compatibility with respect to ultraproducts of elementary embeddings. However, there are other elementary embeddings which arise purely formally between different ultraproducts with respect to different indexing sets and ultrafilters, and should be viewed as part of the formal structure on \(\operatorname{\mathbf{Mod}}(T)\) which is induced by being able to take ultraproducts. The canonical example is the diagonal embedding of a model into its ultrapower (which compares an ultrapower \(M\) with respect to the trivial indexing set and trivial ultrafilter to an ultrapower \(M^{\mathcal{U}}\) with respect to a nontrivial indexing set and a nontrivial ultrafilter).

Definition. Fix \(I\), \(\mathcal{U}\), and a model \(M \models T\).

The diagonal embedding \(\Delta_M : M \to M^{\mathcal{U}}\) is given by sending each \(a \in M\) to the equivalence class of the constant sequence \([a]_{i \to \mathcal{U}}\).

We can stipulate that a pre-ultrafunctor furthermore preserves the diagonal embeddings.

Definition. We say that a pre-ultrafunctor \((X,\Phi)\) is a \(\Delta\)-functor if for every \(I\), for every \(\mathcal{U}\), and for every \(M\) and the diagonal embedding \(M \overset{\Delta_M}{\longrightarrow} M^{\mathcal{U}}\), the diagram

commutes.

Remark. It is not true in general that the embedding \(\widehat{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{PUlt}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) is an equivalence of categories. If \((X, \Phi)\) is isomorphic to \(\operatorname{ev}_{\varphi(x)}\), then \((X, \Phi)\) preserves the diagonal embeddings of models into their ultrapowers (in the sense of the definition). However, later, we will exhibit an example of a pre-ultrafunctor which does not preserve diagonal embeddings.

It is not true either that in general being a \(\Delta\)-functor characterizes the image of \(\widehat{\operatorname{ev}}\); we later construct a counterexample.

Strong conceptual completeness says that if we sufficiently generalize the diagonal embeddings to a large-enough class of formal comparison maps between ultraproducts (with respect to possibly different indexing sets and ultrafilters), then we can characterize the image of \(\widehat{\operatorname{ev}}\) as precisely those pre-ultrafunctors which additionally preserve all these formal comparison maps. The notion we want is that of an ultramorphism.

Ultramorphisms

Definition. An ultragraph \(\Gamma\) comprises:

Two disjoint sets \(\Gamma^f\) and \(\Gamma^b\), called the sets of free nodes and bound nodes, respectively.

For any pair \(\gamma, \gamma' \in \Gamma\), there exists a set \(E(\gamma, \gamma')\) of edges. This gives the data of a directed graph.

For any bound node \(\beta \in \Gamma^b\), we assign a triple \(\langle I, \mathcal{U}, g \rangle \overset{\operatorname{df}}{=} \langle I_{\beta}, \mathcal{U}_{\beta}, g_{\beta} \rangle\) where \(\mathcal{U}\) is an ultrafilter on \(I\) and \(g\) is a function \(g : I \to \Gamma^f\).

Definition. An ultradiagram of type \(\Gamma\) in a pre-ultracategory \(\underline{\mathbf{S}}\) is a diagram \(A : \Gamma \to \mathbf{S}\) assigning an object \(A\) to each node \(\gamma \in X\), and assigning a morphism in \(\mathbf{S}\) to each edge \(e \in E(\gamma, \gamma')\), such that \[\label{eqn-ultradiagram-condition} A(\beta) = \prod_{i \in I_{\beta}} A(g_{\beta}(i))/\mathcal{U}_{\beta}\] for all bound nodes \(\beta \in \Gamma^b\).

Given this notion of a diagram with extra structure, there is an obvious notion of natural transformations between such diagrams which preserve the extra given structure.

Definition. Let \(A, B : \Gamma \to \mathbf{S}\). A morphism of ultradiagrams \(\Phi : A \to B\) is a natural transformation \(\Phi\) satisfying \[\label{eqn-ultradiagram-morphism-condition} \Phi_{\beta} = \prod_{i \to \mathcal{U}_{\beta}} \Phi_{g_{\beta}(i)}\] for all bound nodes \(\beta \in \Gamma^b\).

Now we define ultramorphisms.

Definition. Let \(\operatorname{Hom}(\Gamma, \underline{\mathbf{S}})\) be the category of all ultradiagrams of type \(\Gamma\) inside \(\underline{\mathbf{S}}\) with morphisms the ultradiagram morphisms defined above. Any two nodes \(k, \ell \in \Gamma\) define evaluation functors \((k), (\ell) : \operatorname{Hom}(\Gamma, \underline{\mathbf{S}}) \rightrightarrows \mathbf{S},\) by \[(k) \left(A \overset{\Phi}{\to} B \right) = A(k) \overset{\Phi_k}{\to} B(k)\] (resp. \(\ell\)).

An ultramorphism of type \(\langle \Gamma, k, \ell \rangle\) in \(\underline{\mathbf{S}}\) is a natural transformation \(\delta : (k) \to (\ell)\).

Let us unravel the definition for the prototypical example \(\Delta : M \hookrightarrow M^{\mathcal{U}}\) of an ultramorphism.

Example. Given an ultrafilter \(\mathcal{U}\) on \(I\), put:

\(\Gamma^f = \{k\}\),

\(\Gamma^b = \{\ell\}\),

\(E(\gamma, \gamma') = \emptyset\) for all \(\gamma, \gamma' \in \Gamma\),

\(\langle I_{\ell}, \mathcal{U}_{\ell}, g_{\ell} \rangle = \langle I, \mathcal{U}, g \rangle\) where \(g\) is the constant map to \(k\) from \(I\).

By the ultradiagram condition, an ultradiagram \(A\) of type \(\Gamma\) in \(\underline{\mathbf{S}}\) is determined by \(A(k)\), with \(A(\ell) = A(k)^{\mathcal{U}}\).

By the ultradiagram morphism condition, an ultramorphism of type \(\langle \Gamma, k, \ell \rangle\) must be a collection of maps \(\left(\delta_M : M \to M^{\mathcal{U}} \right)_{M \in \operatorname{\mathbf{Mod}}(T)}\) which make all squares of the form

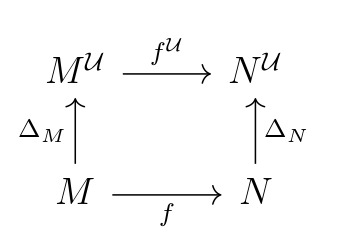
commute. It is easy to check that setting \(\delta_M = \Delta_M\) the diagonal embedding gives an ultramorphism.

Definition. The next least complicated example of an ultramorphism are the generalized diagonal embeddings. Here is how they arise: let \(g : I \to J\) be a function between two indexing sets \(I\) and \(J\). \(g\) induces a pushforward map \(g_* : \beta I \to \beta J\) between the spaces of ultrafilters on \(I\) and \(J\), by \(g_* \mathcal{U} \overset{\operatorname{df}}{=} \{P \subseteq J \operatorname{\big{|}} g^{-1}(P) \in \mathcal{U}\). Fix \(\mathcal{U} \in \beta I\) and put \(\mathcal{V} \overset{\operatorname{df}}{=} g_* \mathcal{U}\). Let \((M_j)_{j \in J}\) be a \(J\)-indexed family of models.

Then there is a canonical “fiberwise diagonal embedding” \[\Delta_g : \prod_{j \to \mathcal{V}} M_j \to \prod_{i \to \mathcal{U}} M_{g(i)}\] given on \([a_j]_{j \to \mathcal{V}}\) by replacing each entry \(a_j\) with \(g^{-1}(\{a_j\})\)-many copies of itself.

In terms of the definition of an ultramorphism, the free nodes are \(J\), and there are two bound nodes \(k\) and \(\ell\). To \(k\) we assign the triple \(\langle J, \mathcal{V}, \operatorname{id}_J \rangle\) and to \(\ell\) we assign the triple \(\langle I, \mathcal{U}, g \rangle\). Then \(\Delta_g\) induces an ultramorphism \((k) \to (\ell)\).

Now we state what it means for ultramorphisms to be preserved. One should keep in mind the special case of the diagonal ultramorphism.

Definition. Let \((X,\Phi) : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) be a pre-ultrafunctor, and let \(\delta\) be an ultramorphism in \(\operatorname{\mathbf{Mod}}(T)\) and \(\delta'\) an ultramorphism in \(\mathbf{Set}\), both of ultramorphism type \(\langle \Gamma, k, \ell \rangle\)

Recall that in the terminology of the definition, \(\delta\) is a natural transformation \((k) \overset{\delta}{\to} (\ell)\) of the evaluation functors \[(k), (\ell) : \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T)) \to \operatorname{\mathbf{Mod}}(T).\] (Resp. \(\delta'\), \(\mathbf{Set}\).)

Note that for any ultradiagram \(\mathscr{M} \in \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T))\), \(X \circ \mathscr{M}\) is an ultradiagram in \(\operatorname{Hom}(\Gamma, \mathbf{Set})\). We say that \(X\) carries \(\delta\) into \(\delta'\) (prototypically, \(\delta\) and \(\delta'\) will both be canonically defined in the same way in both \(\operatorname{\mathbf{Mod}}(T)\) and \(\mathbf{Set}\) and in this case we say that \(\delta\) has been preserved) if for every ultradiagram \(\mathscr{M} \in \operatorname{Hom}(\Gamma, \operatorname{\mathbf{Mod}}(T))\), the diagram

commutes. (We are abusing notation and understand that in the above if \(k\) is not a bound node, then the ultraproduct on the bottom left becomes trivial and \(\Phi_{\mathscr{M}(k)}\) is actually the identity map \(\operatorname{id}_{X(\mathscr{M}(k))}\) (resp. \(\ell\), ultraproduct on the bottom right).)

Note that what is really happening is that we are applying the covariant Hom-functor \(\operatorname{Hom}(X,-)\) to push forward each ultradiagram \(\mathscr{M}\) to an ultradiagram \(X \circ \mathscr{M}\), and then asking that the pushed-forward ultramorphism \(X(\delta)\) is isomorphic to \(\delta'_{X \mathscr{M}}\) via \(X\)’s transition isomorphism \(\Phi\).

Stating strong conceptual completeness

Just as \(\Delta\)-functors are pre-ultrafunctors which additionally preserve the diagonal embedding ultramorphisms, we define ultrafunctors to be pre-ultrafunctors which preserve all ultramorphisms.

Definition. An ultrafunctor \(X : \operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\) is a pre-ultrafunctor which respects the fibering over \(\mathbf{Set}\): for every \(\delta \in \Delta(\mathbf{Set})\), \(X\) carries \(\delta_{\operatorname{\mathbf{Mod}}(T)}\) into \(\delta_{\mathbf{Set}}\) (in the sense of the definition above) for all \(\delta \in \Delta(\mathbf{Set})\).

Definition. A map between ultrafunctors is just an ultratransformation of the underlying pre-ultrafunctors. Write \(\mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) for the category of ultrafunctors \(\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}\).

There is a canonical evaluation functor \[\widetilde{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\] sending each definable set \(A \in T\) to its corresponding ultrafunctor \(\widetilde{\operatorname{ev}}_A\), and we now have the following picture of factorizations of the original evaluation map \(\operatorname{ev} : \operatorname{\mathbf{Def}}(T) \to [\operatorname{\mathbf{Mod}}(T) \to \mathbf{Set}]\):

Now, we can state strong conceptual completeness.

Theorem. The functor \(\widetilde{\operatorname{ev}} : \operatorname{\mathbf{Def}}(T) \to \mathbf{Ult}(\operatorname{\mathbf{Mod}}(T), \mathbf{Set})\) is an equivalence of categories.