#full adder circuit

[wirewitchviolet]

How a Computer Works- Part 4 (Binary Math)

This is the 4th part in a series of posts explaining how computers work such that you can build your own from just wires and spare electronics (or hell, Minecraft redstone signals, a carefully balanced water fountain, anything you can build logic from really). The series starts in this post, the most recent entry before this was part 3, but the only REALLY required reading for this one should be part 2. Get that knowledge in your brain so this next bit can make sense to you.

Also, I'm basically teaching a pretty in-depth computer science class here for free out of the goodness of my heart, so if you have the cash to spare, maybe consider throwing a little money my way so I can keep surviving and doing stuff like this?

Our focus for today's lesson is going to be actually designing one of these modules we have hooked up to the bus to actually do stuff with any data we pass into it. As I've mentioned a few times, all of this stuff we're passing along can be thought of in a lot of different ways. Completing a circuit when one tracing wires out connects to a positive charge and another a negative means the same thing as a gate saying true, will turn a light tied in there on, we can call it a 1 in our abstract computery talk, or several other things, but we're dong math today so let's think about numbers.

Let's think in Binary

So I think I've referenced binary numbers a few times in a really hand-wavey sort of way, but it's good to stop and make sure we all get the concept thoroughly. Normally, when we think about numbers, we're using our good pals the Arabic numerals- 0 1 2 3 4 5 6 7 8 9. We just decided to make unique little squiggles to represent these first ten numbers if we include 0, and then if we add together 9+1, we're out of symbols, so we start a new column, put a 1 in it, and reset to 0 in the one we're in. So, 9+1=10. We call this "base ten math" because ten is where we have to start that new column... but really, we kinda just picked ten out of a hat for this? Presumably it's because most of us have ten fingers.

Maybe if we all had hands like typical American cartoon characters, we'd only have made eight unique symbols. 0 1 2 3 4 5 6 and 7. Add 1 to 7 and we start a new column there instead of after coming up with symbols for those fingers we don't have. In base eight math, 7+1=10. It's a smaller group we're dedicating that next numeral over to, but you can see how that works, right?

Or hey, what if the first person to start counting stuff on their fingers just thought about it differently. You can totally hold up 0 fingers. So really on just one hand you can easily go 0 1 2 3 4 5. Well, what if we just use our other hand past there? Every time we run out of fingers on our right hand, we reset it to zero and add one on our left. It's base six math in this example but hey with just our hands we can display any number from 0 to a base six 55! Which in base ten would be, let's see, 5x6+5, so, yeah, any number from 0 to 35, but that's still pretty good. Converting it into base six is kind of a pain since you've gotta stop and do the multiplication, but if we all just kinda thought in base six we wouldn't need to convert at all.

And hey, what if we really thought big here? Instead of using one hand for the next column of numbers, we could just treat every finger as a column on its own. Holding some of the required groupings of fingers up can kinda give you a hand cramp, but hey we've got ten columns that can hold a 0 or a 1, so we can count all the way up from 0 to 1111111111! Or uh, in base ten, 1023. Still a really impressive number though! Just explaining this to you I've upped how how you can count on your fingers by more than a hundred times. You're welcome! Sorry about the hand cramps. We're not looking into binary math for the sake of saving fingers though, we're doing it because we're designing logic circuits and doing math on the assumption that the only symbols we have to count with are 0 and 1. Anyway, just so we're on the same page, let's count up from 0 in binary for a while here:

0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1111, 10000.

You can follow along with the pattern right? And if you're curious what that'd be all standard base 10 style, let's count through that same number of... numbers that way.

0, 1, 2, 3, 4, 5, 6, 7 8, 9, 10, 11, 12, 13, 14, 15, 16. I made some of these bold to make it a little easier to count along. It's the ones where we're adding a new column in binary, and hey look, it's all the powers of 2. If you have to convert in your head, that makes it easier.

Binary Addition

So let's try thinking in JUST binary now and do some basic math. Before we get into the double-digits- Wait no, if we're pedantic, di- is the prefix for ten things so we shouldn't be saying "digits," we're in base two, so, bi- so... the double bits, I guess), we're just got:

0+0=0. 1+0=1. 0+1=1. 1+1=10

Hey, wait. does that pattern look familiar to you? Like we had to go to a second bit for 1+1, but just ignore that for a moment and look at the lowest one. Humor me. We saw this same pattern in part 2!

0 xor 0 outputs 0. 1 xor 0 outputs 1. 0 xor 1 outputs 1. 1 xor 1 outputs 0.

Oh damn. So if we want to add two bits of data, we just XOR them. All we have to worry about is the spill-over into the next column. Well.. hell, let's see what this looks like if we're looking at two columns here.

00+00=00. 01+00=01. 00+01=01. 01+01=10.

If we just look at the "1s column" digit, yeah, XOR works. And is there a pattern for the "10s column?" Well, it's a 0 for everything except when we go 1+1... we had a logic circuit for that too though, right? Yeah, good ol' AND. Only outputs 1 if both value A and value B it's looking at are both 1.

So OK. We rig up a circuit that has a XOR gate and an AND gate. We feed the first number we want to add into both of these gates, and we can display our answer as a two bit number, with what the AND spits out on the left, and the one the XOR spits out on the right. BAM. We are masters of addition... so long as the highest numbers we want to add together are 1+1. We uh... we should probably try to improve upon that. Also we've got this whole structure to the whole computer where we've got these registers feeding in and out of a bus with a fixed number of data bits on it, kinda would be nice if the number of bits going back out to our bus was the same as the number coming in to our addition circuit... and like, yeah, that's kind of an impossible goal since it's always possible when adding two numbers the same length that you need an extra column to display the answer, but you know, if the first bit of at least one of the numbers we're adding is a 0 it'll fit, so let's get to that point at least.

So OK. Let's expand things out. We're adding any 2 bit numbers now, and let's pretend we've got like a calculator with a 3 bit display.

000+000=000. 001+000=001. 000+001=001. 001+001=010.

010+000=010. 011+000=011. 010+001=011. 011+001=100.

000+010=010. 001+010=011. 000+011=011. 001+011=100.

010+010=100. 011+010=101. 010+011=101. 011+011=110.

I'm being kinda redundant with showing 0+1 and 1+0 and such. Let's narrow these down to just the ones we need a new bit of logic to make happen though. The 1s bit is groovy. We feed the 1s bits of ANY two numbers into a XOR gate, we get the correct 1s bit for our answer. And if the next bits over are 0s, we can pop what's coming out of our AND gate in there out to there and that's fine too. We're also good if we just look at the 10s column, everywhere we don't need to worry about the 1s column affecting it. The places where we need to do more with our logic are just where we're doing the whole "carry the 1 thing." I already set up the grid of all these so that's just the stuff in the far right column, but hey, let me bold those up too.

And let me just kinda blank out these other bits so we're really focused in on the part where there's a problem...

_0_+_0_=_1_. _1_+_0_=_0_. _0_+_1_=_0_. _1_+_1_=_1_.

Well huh. If we're just looking at a bit in the middle of our big long number, and we're carrying a 1 to that position, we sure seem to be getting the exact opposite of what we get when we aren't carrying anything in here. So OK, let's redesign our logic circuit here. We've got our bit A wire and our bit B wire coming in like we did before, going into that XOR for this output bit, but we need to add a wire for whether we're carrying a 1 in from the next circuit over, and if so, flip that result. Do we have a way to do that easily? Well OK, logic chart time. If we have a 0 and no carry, we want 0. I'm lazy, so, 0 bla 0=0, 1 bla 0=1, 0 bla 1= 1, 1 bla 1 = 0. Oh, that's another XOR gate. We XOR A and B like before, and then just XOR that result with our carry bit, and we are definitely displaying the right thing in this part of our answer. Now we just need to double check if our corner case of handling a carry messes with the next carry anywhere and... oh damn yeah.

011+001=100, and 001+011=100. These are the cases where the 1s column carrying a 1 to the 10s column means we have to do something different with that carry bit. So, we're still making our carry-the-1 result a 1 if A and B are 1... but we also need to make sure it's a 1 if we are both carrying something in, AND our original XOR gate is spitting a 1 out. Well we can throw that AND in there, and we can throw in an OR to check either of these two conditions, and there's our new and improved carry-the-1? result.

So let's put it all together now!

For a given bit, we have value A, value B, and Carry. We have a XOR gate that takes A and B in. We feed the result of that and Carry into another XOR gate. That spits out the sum for this bit. Then we AND the result of that first XOR and our Carry feed that result into one side of an OR gate. We feed A and B into a second AND gate, the result of that is the other input for our OR. That OR now spits out a fresh Carry bit. We can plug that into the next adder circuit down the line, for the next column to the left in our result. BAM, there we go. Just clone this whole weird set of 5 logic gates for as many bits as you want to deal with, daisy chain those carry values into each other, and congratulations. You have somehow rigged together something where electricity goes in, electricity goes out, and the weird path it has to take along the way has this weird side effect where you can work out what two binary numbers add up to. Please note again that we didn't at any point make some sort of magical computer person and teach it how to do math, we just found patterns in how electricity flows and where the pure math concept of logic gates and binary math happen to work the same way and exploited that for a result that's convenient to us. Shame that was such a pain wiring up, but hey, every time you add another copy of this onto the end, you double the range of numbers you're able to work with. Eventually that hits a point where it's worth the effort.

Well addition is all well and good, what about subtraction?

OK, so just to take stock, so far we have a big addressed block of memory somewhere we keep our numbers in. We have, for example, 8 bit lines on our bus, and when we want to do addition, we set stuff that turns on "hey, place with our first number, put it on the bus" then "hey register A, read the bus for a moment," then the same to get a number to slap in register B, and we've got this sum register sitting between registers A and B with a bunch of these adder circuits hooked in between all the bits. We might have some leftover carry line with a 1 on it and nowhere to plug it in, but ignoring that spill-over, every bit on our bus is to go good for addition. When we're setting up command codes, we can make more to do some other math with A and B and that's all well and good, but we have a real big problem when it comes to subtraction, because out of what's going into A, going into B, and coming out of sum, at least somewhere we're going to need to deal with the concept of negative numbers. So when we're doing subtraction, one line on our bus needs to be reserved for whether it's positive or negative. If you program, you're maybe familiar with the concept of unsigned integers vs. signed integers? This is that. With only positive numbers, if we've got say, 8 bits to work with, we've got a range of 00000000 to 11111111 to work with, or 0-255 in decimal, but if one of those is getting swiped for negative or positive, now we're talking like, -127-127.

But wait, that's not quite right, is it? Like if we arbitrarily say that leftmost digit is 1 if we're negative, we get things like, 1 being 00000001, 0 being 00000000, -2 being 10000010 etc. but... what's 10000000? -0? That's the same thing is 0. That's redundant and also gonna really screw the count up if we're like, adding 5 to -2! Or really, any other math we're doing.

Oh and we also need to remember when we're stuffing a negative number into a memory register, it's not like that register knows what concept the bits we're shoving into it represent, so like, you personally have to be responsible for remembering that that 1 on the leftmost line, for that particular value, is noting that it's negative, and not that the 10000000s place or whatever has a 1 for some number, or the first of 8 switch variables you're stashing in this address to save on space is on, or whatever else. We here at the memory address hotel are just trapping electron wiggles in a weird little latch or we aren't. No labels, no judgements.

So OK no matter how we're storing negative numbers we need to just actually remember or take notes some way on what the hell convention we're using to represent negative numbers, and where we're applying it. But we also need a convention where like, the math works, at all. Just having a bit be the is it negative bit works real bad because aside from having -0 in there, we're trying to count backwards from 0 and our math module has no conception of back. Or of counting for that matter. Or 0. It's just a circuit we made.

OK, so, let's maybe store our negative numbers in a different way. You know how a car has an odometer? Rolling numbers counting up how many miles you've gone? And there's a point where you run out of digits and it rolls back around to 0? Well funny thing about our addition thing is if you add a 1 to a display of all 1s, that also rolls back around to 0 (and has that carry value just hanging out in space unless we have a better idea of what to plug it into). So if we like, have all the numbers we can display printed out on paper, and we represent that rolling over by just rolling the paper up and taping it, so we have a bit where the count is going like: ..11111101, 11111110, 11111111, 00000000, 0000001... well we can just arbitrarily declare that all 0s is really 0, and the all 1s before it is -1, etc. Try to make that work maybe. And still remember that 10000000 or whatever is where we abruptly loop back between the highest positive/lowest negative numbers we're handling.

Here's a funny thing though. If we start counting backwards, we totally get this inverted version of what we get counting forwards. Just going to show this with 3 bits for convenience but going up from 000 you go:

000, 001, 010, 100, 101, 110... and going back from 111, you go

111, 110, 101, 100, 011, 010, 001... and yeah, look at that with a fixed with font, and it's all just flipped. And huh, you know what else is cool? If we go back to saying the first bit is 1 for negative numbers and a 0 for positive, you can just add these and it almost works. You want to subtract 1 from 1, that's the same as adding 1 and -1. Invert the negative, that's 001+110=111... 1 shy of the 000 we want. Huh.

What about 2-2? 010+101=111. 3-3? 011+100=111. Everything that should be 0 is 111, which is 1 less than 0 when we roll over. What about stuff that should be positive? 3-1? 011+110=(1)001. 2-1? 010+110=(1)000. 3-2? 011+101=000. Still all 1 off if we just ignore that carry going out of range.

-1-1? 110+110=(1)100, which translates back to -3... and that's kinda the only example I can give that's in range with this, but throw in more bits and follow this convention and it'll all keep working out that you get exactly 1 less than what you want, turns out. So, if we're in subtract mode, we just... invert something we're bringing in then add 1 to it and it should all work out?

So OK. We have a wire coming into math land from what mode are we in, it's a 1 if we're doing subtraction. We XOR that subtract line bit with every bit of what's coming into B, that does nothing if we're in addition mode, but if we're in subtraction mode, we're flipping every bit, and tada, the subtraction works without any other changes. We just need to conditionally add 1 if we're in subtract mode now but... wait, we already have literally that. We just take this same "we are in subtract mode" wire and run it in as a carry-in to the rightmost bit of our adder chain. Again, if we're doing addition, that just carries in a 0 and does nothing, but if we're in subtraction, it carries in a 1, and... we're done. The explanation was a long walk, but yeah, when subtracting, just add those extra XORs, plug in that carry, and remember your negative numbers are all weird in storage. Done.

Let's do multiplication and division next!

No. We can't do that.

Well seriously, that's not a thing we can just layer on top of this relatively simple thing we have wired up. We've got this lean mean math machine will give you whatever result you need basically the instant you load values into A and B. Definitely by the time you, being conscientious about not leaving the doors to the bus open all the time, officially flag things to write out from sum and into whatever destination. Multiplying and dividing though, we need more steps, and we need scratch spaces for temporary values. I suppose if you're careful you can multiply by like, loading 0 into B, load the first number you want to multiply into A, just feed sum directly into B, and pulse the clock however many times you want to multiply, but... you probably don't want to just constantly be reading and writing like that, it's tying the whole bus up, unless you have an alternate pathway just for this, and you have to keep count. Still, I'm assuming that's how people do it when they build a dedicated function in. I'm still looking at older systems which assume you're going to do most of your multiplication one step at a time, running through some code.

There's one big exception though. If you multiply any number by 10, you just add a 0 onto the end of the number... and guess what? I'm not using "10" specifically to mean "ten" here. Whatever base you're doing your math in, that still works. So in binary, if you just want to specifically multiply by 2, it is super easy to just shift every bit to the left. Like, have some sort of "shift left/multiply by 2" wire come in, set up logical conditions so that when its set, all we do is have the bit that we are feed into the carry flag, then for the sum ignore everything but the carry flag. 00011001 turns right into 00110010. I picked that out of a hat, but that's binary for 25 getting doubled to 50 as I eyeball it here. Dead simple to do as a single operation. Shifting everything to the right, AKA dividing by 2 is similarly simple... and hey, you might notice that in say... very old games, there's a whole lot of numbers doubling. Like ghosts in Pacman? Each is worth twice the points as the last? Yeah that's because that's easy to do fast.

Other math though takes more steps, and tends to involve extra hardware design to make it work. Like if you're doing division where you aren't guaranteed to have a whole number at the end, so, most division? Suddenly you need to have decimal points in all of this, and work out where they go, and this is why you hear people talk about "floating point processors" as this whole special thing that we just did not have for decades. For now at least, that's beyond the scope of what I'm teaching. Might get there eventually.

A final bit about bits...

So hey, we need to pick some arbitrary bit count for how wide we make our bus and our registers, and also some number for memory registers, command codes, maybe other stuff. And you just kinda want to pick a nice round number. You can't pick ten though, because ten isn't a round number in binary. It's 1010. So usually, we round down to 8, nice and simple, or we round up to 16. And then if we're like filling out charts of values, it's easier to count in those bases. Counting in base 8 is easy enough. 0 1 2 3 4 5 6 7 10. With base 16 though, we need 6 more symbols in there, so we go with 0 1 2 3 4 5 6 7 8 9 A B C D E F 10. And sometimes people make a point of making the B and D lowercase, because if you want to display those on the sort of 7-segment display you still see on cheap clocks or things going for an 80s look, B and 8 are too similar, and D and 0. Base 16 is also called hexidecimal. People will shorten that to "hex" and you see it a ton when people are looking at raw data and don't want to get thrown by long binary numbers, and it particularly gets out to the general public when we're talking about like, 8-bit color values. 8 bits gives you a number from 0-63, hey that's just 2 digits in base 16, so like, for HTML color codes, you can use 2 digits each for red green and blue values, and technical artists just kinda memorize stuff like "right so FFFFFF is white, 700080 is a pretty bright, slightly blue-ish purple, etc."

We tend to go with 8 bits in most places though, or some multiple of 8 anyway, and someone randomly decided to call 8 bits a byte, and that's kind of just our standardized unit for measuring data now. Well mostly standardize. Because people will say, like, 1 kilobyte is 1000 bytes, but in practice people actually round things off to binary values and they're going to actually be off a little.

Anyway, linguistic trivia! Whatever number of bits it is we store in a register/load to the bus is called a "word" and we talk about how many bits long our words are, because once you design the architecture, you're stuck with it and all. And sometimes you want to be space efficient and not use a whole word, so you do some logic gate trickier to chop off whatever portion you don't need when reading it and not change what parts you aren't trying to when writing it and just kinda store multiple variables in a single value. One common thing that happens as a result of this is that you'll break up an 8-bit value because you just want like two values from 0-15 instead of one from 0-255. And when we're working with one of those half-bytes, because puns, the actually term for that is "a nibble." No really. And if we're using a single bit for a variable a lot of the time we call that a flag. Common to see a byte used to hold 8 flags.

For now let me just point anyone following along with this at this first post of me talking about the game console I'm designing. That's a pretty similar topic to this one.

Let me also point you again at my patreon, too.

CONTINUED IN PART 5

[auberylis]

20250308 Major ALICE update!

For a couple months i've been working on a bunch of new stuff and improvements for Aubery's Logic Integrated Circuit Emulator (ALICE), and yesterday i concluded the works that have been planned! I am very happy to tell everyone that ALICE now crashes much less, the circuit tracing GUI became much more usable, and even more high-level devices were programmed!~

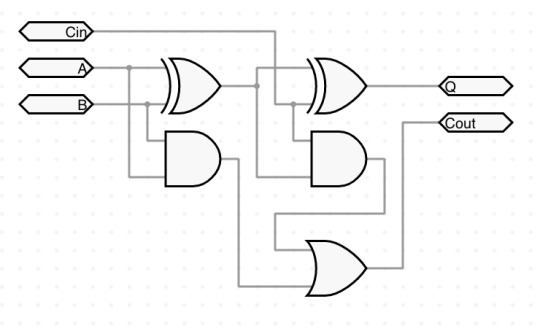
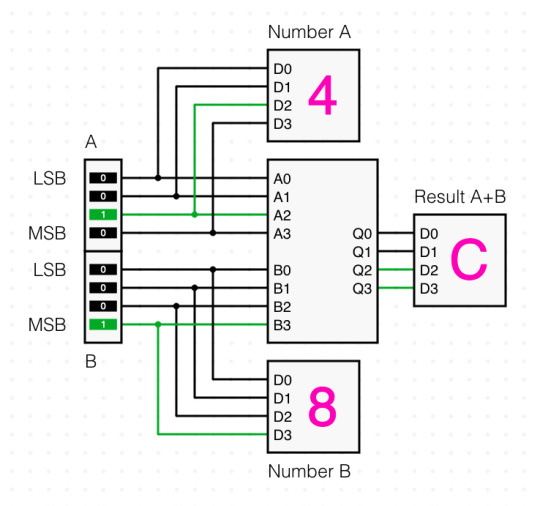
Circuit integration now works in full - watch me go from a basic logic gate based single-bit full adder to a 4-bit adder IC with a whole demo setup to test it, inside the same project!

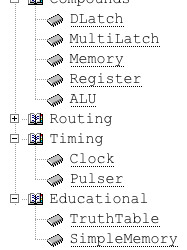
Some high-level devices were added: everything but the ALU seems to be working correctly. TruthTable allows you to build a circuit and then compose its truth table in realtime! Using the pre-made compounds can be easier on the CPU than user-made ICs, even though i'm working on making everything run even faster. Oh, and now there's a "text" device to leave notes right on top of the circuit!

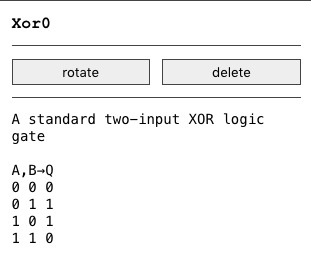
All devices now show a memo on what they do when selected, and a cohesive (although still and forever lacking) manual was started!

Finally, there are now demo projects! They and the manual are bundled within ALICE itself, so no need to download them separately from anywhere. I will work on adding more to them, with the general goal of one day having a "full basic 8-bit CPU" on the list!

Aside from these novelties, i worked real hard and made the GUI run smoother and explode less. Frankly, the code was pure spaghetti before this overhaul, and now it's at least meatballs with a side of spaghetti. It became better, i promise. Along with this, a bunch of minor bugs were eliminated, and i'm slowly ridding the project from depending on my old bmco.js utility library, which would make it run smoother.

There's a lot of plans for this project, and seeing people using it at all would greatly increase my motivation to implement them. Not like i am not motivated.. but you could make things happen faster! So! Use the thing, tell me when it explodes in your face - with saves and bug error texts preferrably - and show me what you made with it!

And one last thing: ALICE is now hosted on Gitea because i am tired of github's copilot bullshit. I will shut down the github repository soon enough -- nothing to lose, since there are no open issues out there or anything. If you feel like digging through my caverns of nonsense, or run ALICE locally, go ahead and download the source code from the Gitea repo!

[moose-mousse]

What is half-adder and full-adder combinational circuits?

So this question came up in the codeblr discord server, and I thought I would share my answer here too :3

First, a combinational circuit simply means a circuit where the outputs only depends on its input. ( combinational means "Combine" as in, combining the inputs to give some output )

It is a bit like a pure function. It is opposed to circuits like latches which remembers 1 bit. Their output depends on their inputs AND their state.

These circuits can be shown via their logic gates, or truth tables. I will explain using only words and the circuits, but you can look up the truth tablet for each of the circuits I talk about to help understand.

Ok, so an in the case of electronics is a circuit made with logic gates ( I... assume you know what they are... Otherwise ask and I can explain them too ) that adds 2 binary numbers, each which have only 1 character. 

So one number is 1 or 0

And the other number is 1 or 0

So the possible outputs are are 0, 1 and 2.

Since you can only express from 0 to 1 with one binary number, and 0 to 3 with 2, we need to output 2 binary numbers to give the answer. So the output is 2 binary numbers

00 = 0

01 = 1

10 = 2

11 = 3 // This can never happen with a half adder. The max possible result is 2

Each character will be represented with a wire, and a wire is a 0 if it is low voltage (usually ground, or 0 volts) and a 1 if it is high voltage (Voltage depends. Can be 5 volts, 3.3, 12  or something else. )

BUT if you only use half adders, you can ONLY add 2 single character binary numbers together. Never more.

If you want to add more together, you need a full adder. This takes 3 single character binary numbers, and adds them and outputs a single 2 character number.

This means it have 3 inputs and 2 outputs.

We have 2 outputs because we need to give a result that is 0, 1, 2 or 3

Same binary as before, except now we CAN get a 11 (which is 3)

And we can chain full adders together to count as many inputs as we want.

So why ever use a half adder? Well, every logic gate cirquit can be made of NAND (Not and) gates, so we usually compare complexity in how many NAND gates it would take to make a circuit. More NAND gates needed means the circuit is slower and more expensive to make.

A half adder takes 5 NAND gates to make

A full adder takes 9 NAND gates.

So only use a full adder if you need one.

Geeks for Geeks have a page for each of the most normal basic cirquits:

I hope that made sense, and was useful :3

[piratesexmachine420]

I think we're solidly into "incomprehensible" territory now.

(This is a 5-trit-wide adder, made by simply smashing five of my most recent full-adder prototypes together and binding the carries and sync lines together with vertical repeaters. An additional set of vertical repeaters are used to copy the output from the bottom of the circuit back up to the top for display purposes. Yes, it's glacially slow. It takes about seven or eight minutes to calculate a single sum. There is room to improve that, but it's not a lot of room.)

[a-comedy-blog-but-its-not-funny]

In the debate of whether computers “think”, nobody ascribes intelligence to a computer performing basic arithmetic. A binary full adder is such a simple circuit that you can easily replicate it with physical objects like marbles. The claims of intelligence surround things like LLMs, and before them, CNNs. As the process and output of a computer becomes more complex, there’s some line that it crosses where “math” becomes “thinking”, and from what I see, that line is simply the point where people stop understanding what the machine is doing. The fundamental processes have not changed—it’s still just adding and multiplying numbers together with logic gates—but because the complexity has ballooned past the point where we can understand how the machine works, we ascribe intelligence to its actions. I’m sure you could also convince a 16th century scholar that your car is alive since it moves and makes noise, because they don’t understand how engines work.

The fact that LLMs produce variable output from a given prompt is because a number (a “seed”) is provided to randomize the output. If you lock the seed, the output is deterministic. The range of text/images it can produce expresses no more creativity than you would express rolling a die to choose what’s for dinner. It isn’t “thinking”, it’s randomizing.

I understand that our own brains are also just an immensely complex web of circuits, yet we clearly have sentience and can make decisions. I’m not going to claim that I understand the nature of sentience. No one does, so we have no basis to claim it originates solely from the brain’s complexity. Therefore, you cannot assume that endlessly increasing the complexity of a computer will eventually lead to it developing sentience.

[kainsword17]

Here is the whole character-roster for a made-up fighting-game I've come up with called SEGA vs. Capcom: Clash of Heroes, featuring both heroes and villains from both the SEGA & Capcom universes that would be like the Marvel vs. Capcom and Capcom vs. SNK series. It has a roster of 14 SEGA-characters for SEGA and 14 characters for Capcom, 2 bosses and 8 DLC-characters (4 from each world)

Here's the basic story of the game idea: Sigma (from Megaman X) and Infinite the Jackel (from Sonic-Forces) have joined forces, combing their powers to conquer both worlds while hosting a fighting tournament in which many heroes and villains battle it out to see who well be the ultimate winner of their worlds, while also either helping or stopping the villains evil plan to take over the multiverse.

Now here is the main cast for the game: SEGA-Side: 

Sonic the Hedgehog (from Sonic the Hedgehog)

Amy Rose (from Sonic the Hedgehog)

Axel Stone (from Streets of Rage)

Cyclic (from Cosmic-Carnage)

Jack Caymen (from MadWorld and Anarchy Reigns)

Death-Adder (from Golden-Axe)

Nights (from NiGHTS into Dreams)

The Hermit (from House of the Dead).

Ulala (from Space-Channel 5)

Joe Masashi (from Shinobi)

Juggernaut (from Kid Chameleon)

Knuckles the Echidna (from Sonic the Hedgehog).

Zygrunt (from Fighting-Masters)

Astal (from Astal)

Capcom-Side:

Ryu (from Street-Fighter II)

Morrigan Aensland (from Darkstalkers)

Ken (from Street-Fighter II)

Jedah Dohma (from Darkstalkers 3)

Magma Dragoon (from Megaman X4)

UVA-02 Helion (from Cyberbots: Full Metal-Madness)

Zelkin Fiskekrogen (from Star-Gladiator and Plasma-Sword)

Cyber-Samurai (from Battle-Circuit)

Angelo-Agnus (from Devil-May Cry 4)

Ayame (from Power-Stone)

Hydron (from Warzard)

Chun-Li (from Street-Fighter II)

Gill (from Street-Fighter III)

Deathtanz Mantisk (from Megaman-Zero3)

Now here is the DLC characters for the game: SEGA-Side:

Akira Yuki (from Virtua Fighter)

Tails (from Sonic the Hedgehog)

Honey the Cat (from Sonic the Fighters)

Segata Sanshiro (from the Sega Saturn adverts)

Capcom-Side:

Zangief (from Street-Fighter II)

Alien-Green (from Battle-Circuit)

Kuwagust Anchus (from Megaman Zero2)

Ruby Heart (from Marvel vs. Capcom 2)

Now for the final Bosses:

Infinite the Jackel (from SEGA's Sonic Forces)

Sigma (from Capcom's Megaman x series)

[programmingandengineering]

CS223 Laboratory Assignment 2 Full adder, full subtractor and 2-bit adder on FPGA

Location: EA Z04 (in the EA building, straight ahead past the elevators) Each student should attend the time block depending on their student id. Preliminary Report (30 pts) In the previous lab, you implemented half adder and subtractor using gates on the bread board. In this lab you will implement very similar circuits, but this time on FPGA. Today’s lab needs considerable advance preparation.…

[codeshive]

Solved COMP4300 Lab Exercise One

Objective This lab is aimed at getting you familiar with using the ModelSim simulator. The circuits you will be simulating should be familiar to you from ELEC2200. Instructions Write a VHDL program consisting of a single entity whose architecture is a single process that implements a one-bit full adder . That is, a circuit which behaves as specified in the following truth table. You…

[codingprolab]

COMP4300 Lab Exercise One solved

Objective This lab is aimed at getting you familiar with using the ModelSim simulator. The circuits you will be simulating should be familiar to you from ELEC2200. Instructions Write a VHDL program consisting of a single entity whose architecture is a single process that implements a one-bit full adder . That is, a circuit which behaves as specified in the following truth table. You…

[rupasriymts]

Exciting Electronic projects for your Academic Projects

At Takeoff Edu Group, we merge creativity with skill to work electronic wonders. Here, we are passionate to helping everyone get into cool Electronic projects. Whether you're really good at engineering or just starting to learn, we have plenty of stuff to help you out and keep your ideas coming. We've got something for everyone, whether you like making your own gadgets or working on fancy robots. Our community is full of people who love creating things. Come with us as we explore, try things out, and come up with cool ideas in the fun world of electronic projects.

Here are the Takeoff Edu group titles for Electronic projects:

Latest:

High-Precision and Low-Power Offset Cancelling Tri-State Sensing Latch in NAND Flash Memory

Trendy:

Performance Analysis of 4-Bit Multiplier using 90nm Technology

An Accurate Low-Power Power-on-Reset Circuit in 55-nm CMOS Technology

Low Power and High-Performance Associative Memory Design

Low Power, High Performance PMOS Biased Sense Amplifier

Low-Power Retentive True Single-Phase-Clocked Flip-Flop With Redundant-Recharge-Free Operation

Design and Analysis of Low-Power High Performance 4-Bit Parallel Shift Register using Retentive True Single Phase Clocked D-Flip Flop

Standard:

Optimizing Ternary Multiplier Design with Fast Ternary Adder

High Efficient GDI-CNTFET-Based Approximate Full Adder for Next-Generation of Computer Architectures

Design and Implementation of a Low Power Ternary Content Addressable Memory (TCAM)

Accounting for Meritor I-V Non-linearity in Low Power Memristive Amplifiers

Optimizing Ternary Multiplier Design with Fast Ternary Adder

The Above Electronic project are the example titles of Takeoff Edu Group. Here we not only provide Electronic projects, but also furnishes all kind of project to upgrade your skills and improve your innovation levels for Students as well as hobbyists. Takeoff Edu Group gives you a proper guidance and support to those peoples who are eager to learn more about these projects with step-by-step instructions and detailed explanations.

[prakashymtsdm]

Best final year engineering projects

Welcome to our webpage dedicated to engineering projects! We are a team of experienced engineers and developers who specialize in creating innovative and cutting-edge projects for students and professionals.

Our goal is to provide individuals with the opportunity to showcase their skills and knowledge while working on real-world engineering projects that have the potential to make a positive impact on society. Our projects are designed to help individuals develop their technical and professional skills and to prepare them for successful careers in their chosen fields.

Reversible Logic-Based 1-bit Comparator using QCA

Heat and energy dissipation are the immense problems in today's processor design. These problems can be overcome if reversible logic is used for the design implementation. In this paper, the 1-bit comparator based on reversible logic is proposed. Further, the reversible logic gates used in the proposed design are implemented using "Quantum-dot Cellular Automata (QCA) nanotechnology". QCA is a viable technology among various nanotechnology through which reversible logic can be implemented at the device level with low energy, less area and high speed. The simulation is backed by the QCA Designer tool. The proposed design is single-layered which is also optimized for area, energy and delay.

Efficient Design of Vedic Square Calculator Using Quantum Dot Cellular Automata QCA

Vedic mathematics is now being realized to have a large potential in recent times which can be used to design digital circuits using the Vedic formulas. Vedic mathematics is a new trend in quantum-dot cellular automata (QCA) technology. However, an efficient coplanar design and a complete performance analysis are still desired. This brief presents the coplanar QCA architecture of a 2-bit square calculator (proposed design-1 or PD1) using the Vedic sutra 'Urdhva Tiryagbhyam'. Furthermore, based on the E-shaped XOR gate and majority gate (MV) an optimized architecture (proposed design-2 or PD2) is presented. The PD2 architecture exhibits notable improvement compared to the previous architecture. It is worth mentioning that the comprehensive performance analyses are carried out using the QCADESINER.

A Cost-Efficient QCA XOR-XNOR Topology for Nanotechnology Applications

A quantum-dot cellular automaton (QCA) is an inventive Nano-level computation that suggests fewer dimensions, and less power consumption, with more speed and premeditated as an amplification of the scaling obstacle. with the CMOS methodology. One of the newest and rising nanotechnologies used today is QCA based on the repulsion of Coulomb. One of the newest and rising nanotechnologies is The QCA based on the repulsion of Coulomb is used today. Surmised computing is a successful paradigm for energy-efficient hardware design at the Nano-scale. In this project, We proposed a proficient, low-complex 2-bit & 3-bit XOR, XNOR, 2-bit An XOR/NOR gate has been suggested in QCA technology. Next, using those proposed A 4:2 encoder and a 4:1 encoder are designed in QCA technology.

Area Efficient Multilayer Arithmetic Logic Unit Implementation in Quantum-dot Cellular Automata

Quantum-dot Cellular Automata (QCA) is a new nano-scale technology that due to making significant improvements in the design of electronic circuits can be considered as an appropriate alternative to CMOS technology. The Arithmetic Logic Unit (ALU) is a fundamental component of the Central Processing Unit (CPU) to carry out the arithmetic and logical operations the multiplexer and full adder plays an important role in its operations. In this paper, a QCA multiplexer is proposed based on the cell interaction with less number of cell count. Likewise, a QCA multilayer ALU structure is designed to perform both arithmetic and logical operations.

Binary Coded Decimal Seven Segment Circuit Designing using Quantum-dot Cellular Automata

Quantum-dot Cellular Automata (QCA) is new due to making significant improvements in the design of electronic circuits can be considered as an appropriate alternative to CMOS. technology. It is an alternative nanotechnology that keeps scaling down. The technology is further It can do scaling beyond to a level where complementary Metal oxide semiconductor (CMOS) scaling is the issue. QCA is seen as an emerging solution for nano-architectures.

Conclusion: Engineering projects play a pivotal role in addressing societal needs and driving progress. By harnessing technology, innovation, and sustainable practices, these projects offer solutions to complex problems. From enhancing urban infrastructure to revolutionizing healthcare and space exploration, they exemplify the transformative potential of engineering. As we continue to invest in these endeavors, we move closer to a more sustainable, efficient, and interconnected world. More Info

[myprogrammingsolver]

Laboratory Assignment 2 Full adder, full subtractor and 2-bit adder on FPGA

Location: EA Z04 (in the EA building, straight ahead past the elevators) Each student should attend the time block depending on their student id. Preliminary Report (30 pts) In the previous lab, you implemented half adder and subtractor using gates on the bread board. In this lab you will implement very similar circuits, but this time on FPGA. Today’s lab needs considerable advance preparation.…

[taperwolf]

Thrift store find, and a project:

Got this Alesis QX25 MIDI controller in as-is condition for $12. The most obvious problems when I got it were that the fader cap and one rotary encoder knob were missing, and one of the black keys was broken. In addition, there were solfege stickers on the keys, implying the previous owner was pretty young; that impression was backed up when I opened it to find maybe half a container of assorted glitter inside.

The fader cap I haven't come up with yet, and I've put a temporary knob on the encoder — the one at the far right — and I was able to partially disassemble the keybed and glue the key back together. (I'm using Gorilla Glue's superglue formulation, which is supposed to be better than usual cyanoacrylates at bonding plastics; if this doesn't hold, I know where to order replacements.) From a quick once over, the current status is that some of the tact switches are broken somehow — the ones, at least, for octave up and transpose down don't work. I've only given those the most cursory inspection, so I don't know if it's the switches themselves or something in the wiring; I'll have to see if my big box of tact switches has anything I can swap in for them.

But the "project" part is the part that has me enthused. Unlike a lot of more recent MIDI controllers, this one has both a USB jack for connecting to a computer and a 5-pin DIN jack for traditional MIDI instruments. It's also got a lot of spare room inside the case. So I'm looking at taking an Arduino or a Teensy and some little digital-to-analog converters and adding the ability to output CV and gate signals for modular synthesizers. Basically the Arduino will listen to the MIDI signal and interpret that; the minimal feature set is a single note off channel 1, just the CV and gate corresponding to the most recently struck key, but may expand to multiple notes and/or handling the drum pads as their own gate/trigger outs, and probably an extra CV out that can follow the mod wheel or pitch bend.

I'm debating which DACs to use. I have some lying around — the spoils of a time when Linear, Analog Devices, and Maxim were separate companies, and they, Microchip, and Texas Instruments would give out free samples if you had a plausible-sounding company name — but a lot of them aren't particularly well-suited for this. I want to run everything off the existing 5V supply — either a wall wart or USB — and not need elaborate external analog circuits to do things. I'm looking at the MCP4811, a single-channel 10-bit device, which has the advantage of an internal voltage reference at 2.048V, and a ×2 output, for a full range of 0V-4.096V that's very reliable even when run off a unreliable 5V power supply, like the keyboard's USB power input.

(In an ideal world, I'd have a perfect 1v reference, and a precision adder, so that the full precision of the part, all the bits, could be applied to just the 0-1V range, and then I could add single volts as needed to specify the octave. If we're calling 0V C0, then with the 10-bit setup over the 4.096V spread, you have to use value 396 to get G1, and you're imperceptibly sharp; with ten bits over a single volt, you'd use value 597 and add an extra volt and you'd be... slightly closer but flat this time. So the ideal world can fuck itself, and I'll see how the thing I actually have works.)

[floydsmp]

Application of Logic Gates

Now we can understand the different types of gates and their outputs, we can put them together and build what is called a circuit. A circuit is a connection of gates that we can use to create outputs that depend on the values that we input. For example, a type of circuit we can build is an adder, which adds numbers together. There are two types of adders: half and full.

A half adder is used to add two single bit numbers, outputting the sum, or added result of the inputs, and a carry bit, which can be used to help us calculate the next digits of the equation if more calculation is required. A full adder is able to add three single bit binary numbers.

We can make a half adder using one XOR gate and one AND gate. This is represented in Minecraft below:

We can create a full adder using one OR gate, two AND gates, and two XOR gates. It’s easy to see how the half adder and full adder structures are similar.

Below is a full adder with an automatic carry:

Note: This carry is always active and follows the process of a half-adder carry (Only when both inputs are 1 then the carry is active; otherwise, it is not)

Then we also have a full adder with a manual carry:

[coralstarlightfun-blog1]

What we are going to discuss? Design of Half Adder – Different ways of implementation Design of Full Adder – using two half adders, using only NAND or using only NOR gates Design of Half Subtractor Design of Full Subtractor-using two half subtractors Construction of 2-bit, 4-bit parallel binary adders, 4-bit parallel binary subtractors, 4 bit parallel binary adder/subtractor circuits Construction of Carry lookahead adder BCD addition – Design of 8421 BCD adder circuit

[jack-andthestalk]

Stuck on you, Jealous, Chapter.

I enjoy hearing what @balfeheughlywed thinks when I send her a draft just as much as I love writing it. Moodboard credit to @balfeheughlywed she is the cats pyjamas.

       There was a steady beat humming through the apartment, the place was filling up nicely and Rupert’s lovely belly laugh was bouncing from group to group welcoming guests.

 My body was still thrumming, I hated it but I couldn’t stop watching the door waiting for Jamie, a dangerous giddiness at seeing him seemed to be becoming a habit.

I had spotted Cathal slip in to the apartment a few minutes earlier; Rupert had intercepted him and guided Cathal to a group in the far corner of the room. A breathable distance between us, but he had glanced over a few times trying to catch my eye. The most prominent emotion when I looked at Cathal was guilt, and the selfish realization that if I could avoid him I wouldn’t feel as guilty, especially giving the building desire coursing my body from another mans touch.

The idea of Cathal and Jamie being in the same room filled me with dread but Rupert had insisted he couldn’t leave Cathal out, they had become friendly during the time we were together and obviously for Rupert there was never a question that Jamie wouldn’t be there.

Deciding to bite the bullet I approached Cathal uneasily, a quick embrace where our hands touched fleetingly, Cathal’s palms were clamy, his movements fidgety.Cathal’s demeanor wasn’t helped by my cursory thank you for coming, Cathal folded his arms defensively

 “I hear you have turned into quite the chef de patisserie?” he asked,  eyes narrowed, “Well I wouldn’t say that” I began, Cathal looked thoroughly disintrested and threw his drink back in one shot,  “Rupert said you had help?”

I realized where he was going with the questioning which unfortunately made me blush a furious shade of red, as the image of me pressed against the kitchen counter by Jamie and my hands slipping into the front of his trousers. Cathal blew out through his cheeks and said “I could do with another drink.”

 “Absolutely” I said a little too spritely,  “Let me get you one…” Rupert shot me a calm down look, giving Cathal no chance to respond, I scurried towards the kitchen, stuffing my whole head in the fridge in the hope it would calm the color in my face.

A warm big hand landed on the small of my back, I knew instinctively it was Jamie.

I turned to face him; he looked so handsome, smelling even better wearing a crisp white tee and blue jeans, hair still slightly damp from his shower. It was hard not to smile.  “Are ye sniffing me Sassenach?”

“I am not” I replied indignantly. He didn’t seem to take offence either that or wasn’t paying attention to a word I was saying instead he looked down at my body appraisingly “Ye have gorgeous legs…did I ever tell you that before?” his eyes ran up and down my body, a contented smile on his face. “I am sure you mentioned it…” I said trying to pull the hem of my dress down over my thighs, a useless task as my dress was mid-thigh and not budging.

“they are endless…” I rolled my eyes at him. “Will you stop.” Jamie gave me a huge grin, “Canna help it…”  I returned to the fridge rummaging for the forgotten drink for Cathal and Rupert.

Jamie braced his hand on the fridge door locking me into position, he leaned in close to my ear, steadying the full of his body against my back, “I wanted a quick word with ye?” “oh ya?” I remarked distractedly.

“I ken that ye are fretful about me and yer ex being in the one room.” “Ex” emphasized clearly.

 “And I just wanted ye to ken…that I…”

Before he had a chance to carry on I turned quickly to face him and quipped “Which ex?”

I underestimated his proximity and was now boxed in very cozily between Jamie and the fridge.

He gave me a distasteful look, “yer more recent one” his tone officious.

I nodded demurely and smiled. ”Anyway as I was saying” he continued “ye need not worry I willna do anything to stress ye or make this anyway more awkward than it has to be.” He blinked twice which I assumed was meant as a wink. “Why thank you Mr. Fraser, it is most gallant of you…and generous….can I ask what has caused this change of attitude?”

 He smiled broadly, eyes twinkling in mirth. “Well Sassenach I can still taste yer sweet mouth on mine and feel the shape of yer arse on my hands, I am hopeful ye have not treated Cathal to the same welcome, so aye ye can say I am feeling generous.” He flashed me a dazzling toothy smile, bitting his bottom lip thoughtfully before turning on his heel, leaving me feeling hotter than I was before with the added distraction of a delightful tightening in my tummy. Smug bastard.  

 After a cooling off period I meandered my way into my overcrowded living room, I busied myself between the various groups checking for top ups, Cathal’s laugh was getting consistently louder each time I did a circuit of the room, it was hard to ignore the glass of whiskey in his hand. He never drank spirits always a beer man, watching, I felt a pang of what he might be feeling being here, I knew him. The man laughing obnoxiously in my living room wasn’t him.

 It was hard not to notice the contrast between the two of them being in such close proximity, Jamie’s heritage was a huge part of him, he drew people in with his stories but also his ability to listen and show an interest in those around him.  Jamie’s ancestors were Lairds, when I looked at him I could see that direct lineage seeping from Jamie’s stance, he was a large proud beautiful scot and I couldn’t take my eyes off him. I had forgotten how much I enjoyed him work a room.

Thinking Cathal too far gone to notice whose company I kept, I slipped in beside Jamie, he was chatting to a gang of Rupert’s work mates, his broad arms moving animatedly to illustrate the story, his audience in raptures.

 Jamie noticed my presence at his side stopped his story momentarily, eyeing me tenderly “Did ye no get anything to drink for yerself Sassenach?” I looked at my empty hands and realised he was right, I was so tightly wound that I hadn’t bothered to get myself one, he nodded at his group of admirers apologetically, “Sorry lads, il be back in a minute” and disappeared into the kitchen. A sea of impatient faces stared at me while we waited awkwardly for Jamie. On his return he handed me a large glass of wine and recommenced his story. However this  time his hand fell on the small of my back, drawing me into him.

  I was guiltily conscious of his touch at first, worried that Cathal would notice but after a time it was like it was meant to be there and I slowly edged closer so that we stood hip to hip. It was easy to be hypnotized by his stories forgetting everyone else in the room. Jamie caught me gazing up at him, a contented smile brightening his face. We stood there for a minute grinning stupidly at each other before I heard one of Rupert’s friends clear his throat. “As I was asking ye Jamie…”. Jamie blushed a little and muttered “Sorry I was distracted what is it ye were saying?”

Out of the corner of my eye, I could see Gellis moving towards us at a determined pace, she slided up on the other side of Jamie extraditing us from the rest of the group. “Claire" she breathed hurriedly….I need a favour...” I looked at her curiously, her tone was rather urgent and Jamie looked positively enthralled. "Off course what do you need?"

“Can ye lend me a pair of yer wee lacy knickers? Ya ken the ones ye keep for good occasions” Jamie’s eyes went wide as stalks. “Gellis” I said scandalized.

 She sighed heavily “Claire I dinna have time for ye to pretend ye dinna own any cause ye ken fine well I have seen them.” I was fairly sure my face was a purple colour Jamie’s eyes ran from me to Gellis and back, mouth slightly agape. “Why the hell do ye need panties?” he blurted out suddenly, and I realized his face might actually be redder than mine.

 She looked at him as if he was half mad and said “Cause I dinna have any on!”

Jamie’s mouth hung slightly agape and I could see his eyes work furiously trying to decipher where to take his questioning. I however knew my friend. “I presume not having any on was a deliberate decision?” I asked cautiously,

Gellis head bobbed up down rapidly. “And why the sudden urgency for a pair then?” Jamie asked eyebrows furrowed in confusion.

 Gellis sighed again exasperatingly “Because….do ye see that fella over there?”  Jamie’s head snapped around to look and she hissed “dinna make it so obvious

 for Christ’s sake… rolling her smokey eyes at us, “well he wants me to go home with him…and I dinna want him thinking I came out looking for it aye?”

 Jamie’s eyebrows furrowed even deeper before he croaked “Why did ye come out without them so?”

 Gellis pressed her lips together and narrowed her eyes, “because I did come out looking for it but I dinna want him to ken that…he is too timid…I dinna want to scare him, Jesus fox did Claire teach ye nothing in yer time together?” I was about to tell her not to drag me into her sordid affairs but Jamie interrupted “Claire” he said through gritted teeth “taught me everything and she dinna go around without her panties on to do it!”

 “well that is a shame with her sweet wee bum, I can only imagine ye would have preferred easier access to it aye?”, Gellis flashed him a wicked smile.

 “Christ woman ye have a mouth like an adder” Jamie hissed but I noticed the hand on my back was dropping lower and lower. Gellis fluttered her eyelashes as if he had just paid her a huge compliment, turned to me and said “will ye lend me those red ones ye ken the ones ye bought in Victoria secret a couple of months back?”

 Jamie raked his hand through his hair “I dinna want to hear anymore…well ye get her the panties for the love of god Claire!”

 I smiled sweetly and dragged Gellis by the hand in the direction of my room.

   Closing the door behind me, I quickly rummaged in my drawers and threw Gellis the little frilly number she had in mind. She pulled  them up and on her without any preamble or need for privacy, I was making for the door again when she whispered   “what is happening with yerself and the fox ye seem on the chummy side…have ye been clashing tongues again? I gave her a dirty look knowing she was referring to the night of the gala. Gellis I think would have guessed had I not confessed a few days later, her only complaint had been she had missed the two ‘Cocks sparring over ye”

“Something happened earlier but Rupert came home” I admitted. “fuck’n Rupert” she said shaking her head.

I was about to continue my tale when I head Cathal’s slurred voice on the corridor outside, “well well if it aint the fucking Scottish warrior…? I could imagine the swagger on Cathal without having to see him.

I was about to open the door when Gellis halted me. “wait” she whispered.

Jamie’s clear but slightly calmer voice replied “look I am glad I have the chance to speak to ye…I wanted to apologize ye had every right to be spit’n fire and I shouldna have reacted…”

Cathal’s voice cut across “I had every right did I?….you fucking prick…I’d fucking hit you again only it would make her even more sorry for you…and right now mate that is all you have got going on …her pity.”

“What it is between me and Claire isna pity, if it was ye wouldn’t be so rattled now would ye?”

There was shuffling and for a minute I thought they were fighting again but just as I was about to open the door Cathal continued.

 “she told me about you when we first met…that her ex fucked her up…even then she was making excuses for ya…said you were a mess…? I googled ya mate…lost your brother ya? That must have been tough…. Nasty accident and you were there right? ….that kind of thing fucks up your mind…no wonder she left”

My hand shot for the handle but Gellis halted me, “it will be harder for Jamie to know you are hearing this…just wait Claire…hear what he is saying for yourself..”

 My heart was beating so fast I was afraid they would hear it, I was fit to hit Cathal myself.

Jamie growled “dinna mention my brother ye ken nothing about him or what happened.”

“sympathy fucking that is all it is mate… …I’v told her il be here waiting when she gets bored of that shit and wants a proper man in bed…because me and her never had a problem in that department.”

Cathal’s laugh was cut short when I heard a body being thrown up against the wall; nothing held me back this time.