#mysteriousquantumphysics

[crabrat]

hell yeah kite man hell yeah even :D

@merlin @where-is-vivian @bugzb1tess @wistfulenchantress @giraffes-and-crystal-meth-blog @mysteriousquantumphysics @neonpanichour @goopy-gunky-guy @ilovebeesbutifearthem

𝑇ℎ𝑒 𝑟𝑢𝑙𝑒𝑠 𝑎𝑟𝑒 𝑠𝑖𝑚𝑝𝑙𝑒: 𝑔𝑜 𝑡𝑜 𝑝𝑖𝑛𝑡𝑒𝑟𝑒𝑠𝑡, 𝑠𝑒𝑎𝑟𝑐ℎ "𝑦𝑜𝑢𝑟 𝑛𝑎𝑚𝑒 + 𝑐𝑜𝑟𝑒," 𝑝𝑜𝑠𝑡 𝑠𝑖𝑥 𝑝𝑖𝑐𝑡𝑢𝑟𝑒𝑠. 𝑇ℎ𝑒𝑛 𝑡𝑎𝑔 𝑠𝑖𝑥 𝑝𝑒𝑜𝑝𝑙𝑒.

thanks @ghosts-and-blue-sweaters and @cbuttonduo for the tag!! <3

wow i’m obsessed with this and i feel it’s fairly accurate!!

tags (no pressure): @thewildballyntynesgrow @bronzetomatoes @cloverstellar @clingyduoapologist @seeking-elsewhither @thoughts-of-caly

[mysteriousquantumphysics]

Updates from my Quantum Journey

It's been silent on my blog for a while now - the past year has been a busy time for me since I was working on my Master's thesis as well as working as a research assistant at Fraunhofer in parallel. Both were great experiences but it became so time-consuming that I totally lost track of posting any content on this blog!

In April 24 I finished my Master's Thesis in Physics in which I was mainly working on tensor networks. We tried to make DMRG (Density Matrix Renormalization Group) for Quantum Chemistry-like setups more efficient by lifting degeneracies in the symmetry sectors of the tensor network structure. Besides from what I learned on the physics-side of this project, it helped me to foster my fascination for method-development.

My work at Fraunhofer was very rewarding as well - I did not only learn a lot, I also had the chance to contribute in two publications in the area of quantum circuit cutting. In case you are interested, I could write a blog entry for one or both of the papers(:

During all this hard work and (to be honest) frustration and exhaustion in the past year I had this optimistic hope of doing a PhD after finishing my Master's degree. Now, this dream has become a reality and I started my PhD at the Technical University of Munich this month. I am really grateful for this oppurtunity in which I can work full-depth in the field of quantum computing - with a strong focus on software/method development. I am excited about what this journey has to offer and I am very much looking forward to it!

[mysteriousquantumphysics]

I'm just mindblown.

Astronomers Capture First Image of a Black Hole

The Event Horizon Telescope (EHT) — a planet-scale array of eight ground-based radio telescopes forged through international collaboration — was designed to capture images of a black hole. Today, in coordinated press conferences across the globe, EHT researchers revealed that they have succeeded, unveiling the first direct visual evidence of a supermassive black hole and its shadow. The image reveals the black hole at the centre of Messier 87, a massive galaxy in the nearby Virgo galaxy cluster. This black hole resides 55 million light-years from Earth and has a mass 6.5 billion times that of the Sun. Supermassive black holes are relatively tiny astronomical objects — which has made them impossible to directly observe until now. As the size of a black hole’s event horizon is proportional to its mass, the more massive a black hole, the larger the shadow. Thanks to its enormous mass and relative proximity, M87’s black hole was predicted to be one of the largest viewable from Earth — making it a perfect target for the EHT.  The shadow of a black hole is the closest we can come to an image of the black hole itself, a completely dark object from which light cannot escape. The black hole’s boundary — the event horizon from which the EHT takes its name — is around 2.5 times smaller than the shadow it casts and measures just under 40 billion km across.

Credit: ESO

[mysteriousquantumphysics]

How to Use Quantum Computing as a Tool for Philosophy of Science

Recently, I attended the MCQST 2023 Conference on which Lídia del Rio presented the research with her collaborators about quantum thought experiments in a quantum computer. They wrote a whole package to do this and describe the ideas in detail in [1]. It's definitely worth checking out the paper and the package - to make you curious let us look at an illustrative example [1, p.4-10].

Example Setting

Let us consider the following setting (as depicted in the image above): Alice has some two-level quantum system R (e.g. a qubit) in the state written in blue. Thus, the probability of obtaining a=0 in a measurement is 1/3 while the result a=1 will be obtained with a probability 2/3. Depending on the outcome, Bob receives the a system in state |0> (if Alice's result was a=0) or in state |+> ~ |0>+|1> (if Alice's result was a=1). In turn, Bob measures his system in the computational basis and can receive the outcome b=0 or b=1. What conclusions can Bob draw about Alice's measurement outcomes based on his? It is assumed that Bob knows the rules upon which Alice sends him the different systems. Thus, if his outcome is b=0 he cannot make any retrodiction since the outcome b=0 could stem from both possible states |0> and |+>. However, if he measures b=1 he knows that his state must have been in |+> and thus he can retrodict that Alice's outcome must have been a=1. Therefore, in one of both cases Bob can draw a deterministic conclusion about Alice's outcome.

So far so good, at this point I'd like to mention that even though this setup seems to be motivated by the Frauchiger-Renner Thought Experiment, we will not talk about apparent paradoxes or fundamental questions in foundations of quantum mechanics themselves. Instead the setting is supposed to be easy to grasp and can therefore neatly serve the purpose to illustrate how a thought experiment can be formalized in terms of quantum circuits. Hence, we will discuss a tool which can be used for quantum thought experiments in general by using a simple example.

Alice's and Bob's Brains in a Quantum Circuit

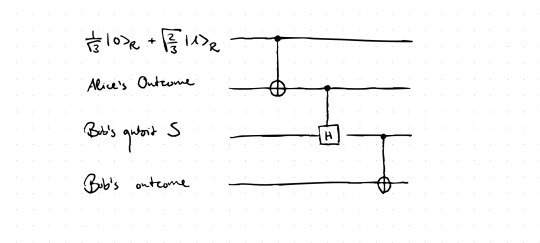
Next, we will translate this specific setting as a quantum circuit - by going through the above illustration of the resulting circuit. The first qubit is initialized in the state of Alice's system R. Even though this seems to be the only true quantum system at hand, we will act as if there was an external observer who looks at both Alice and Bob and their respective systems. Imagine you are in the position of this external observer and set the Heisenberg cut at this point: You are classical while both Alice and Bob are quantum (as it is done in Neo-Copenhagen interpretations). Then, one also has to model the "brains"/"memory" of both Alice and Bob. We start with Alice first: we assign a wire of the circuit to Alice's reasoning which basically means that somehow the possible measurement results are stored in this respective qubit. The wire representing her memory is initialized in state |0> and is connected to her system R via a CNOT gate. This means that if the system R was in state |0>, the qubit representing Alices would stay in |0>. However, if R was in |1>, Alice's state of memory would be in |1> as well. This way, one can model different measurement outcomes and also Alice's memory in a unitary manner without explicitly including measurements in the circuits yet. This is necessary since from our external perspective everything about Bob and Alice is considered to be quantum, i.e. must be modelled unitarily. Now, we can look at the third wire: It is again initialized in state |0> and remains in this state if Alice's memory is in state |0>. However, the controlled Hadamard will act on the third wire if Alice's memory is in state |1>, hence it would be turned into state |+>. Thus the controlled Hadamard models the system S which Bob receives - conditioned on Alice's measurement outcome of R. Finally, the last wire is again initialized in |0> and is supposed to model Bob's memory. Exactly as Alice's memory, also the relation between Bob's memory and his system S is modeled via a CNOT gate.

As a result we now have a quantum circuit which represents the setup from above from an external perspective. I think already at this point one can see the beauty of this approach - while one needs quite a lot of sentences to explain the simple setup, it can very easily be grasped by the neat quantum circuit. What is left to do now is to model Bob's reasoning regarding his retrodiction on Alice's outcome. We found that Bob can draw a deterministic conclusion about Alice's measurement outcome if his outcome is b=1, in the other case he cannot draw such a conclusion. How can this be mapped into a quantum circuit?

Modelling Bob's reasoning

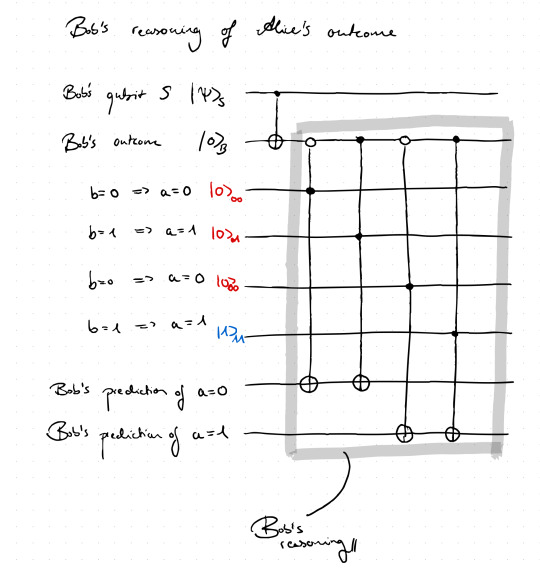
In the above circuit we added a couple of additional wires. One set represents the four possible logical inferences in this case, and the last two wires will show what Bob's prediction will be based on the initialized inferences. Let's go through this step by step: There are four possible inferences on the measurement outcomes a and b, but only one of them is assumed to hold, namely (b = 1 -> a=1), which is why only the wire corresponding to this inference is initialized in state |1>. The other three inferences, which are assumed not to hold, are initialized in |0> and since there are control nodes from the nonlocal Toffoli-type on those wires, they will not really contribute as long as one does not change the initialization. Those Toffoli-type gates have two control nodes each as well as a NOT at the lower end. One control node is placed on Bob's memory qubit, acting dependently on the outcome b and represents the antecedent of each possible inference. If the inference of a wire assumes b=1 the corresponding Toffoli node on Bob's memory will be black, while it will be white for b=0. The second control node of each Toffoli gate is black in order to be activated according to which inference is initialized with state |1>. The consequent of those inferences is modeled by the lowest two wires. The NOT of each Toffoli is placed on the corresponding wires representing the consequent. Looking at the Toffoli for the inference b=1 -> a=1, one can see that if Bob's memory is in |1> and simultaneously the wire of the corresponding inference is initialized as |1> as well, the NOT on the lowest wire will turn the respective state to |1> (the prediction wires are initialized in |0>). Thus, Bob's prediction can be read off by the states of the prediction wires. Finally, one can also run this circuit and check its consistency - how?

Consistency Checks

In the above image we have put together all we got so far: Alice's actions from before, as well as bob's actions and his reasoning as discussed right above. The consistency of such a model can be checked by measuring the prediction wires as well as Alice's memory qubit. In this case, the only deterministic inference will show itself if Bob's prediction wire for a=1 will be |1> and this will coincide with Alice's memory being in |1>. For the other case, no inference can be done. This way one can check the consistency of the model and if the results show paradoxical outcomes one knows that something went wrong, that something in the logical reasoning / adopted interpretation of quantum theory is getting problematic. Having everything formalized as a quantum circuit will make the analysis of the issues easier.

Final Remarks

It appears to me that Quantum Circuits are not used here because one expects some computational advantage by running them on a Quantum Computer - instead they are used to neatly formalize subsystems and possible inferences of thought experiments. This way, thought experiments can be made more clear and transparent as well as it is easier to see the problem if the outcomes are not consistent. Therefore, their work shows that quantum circuits have a much broader field of application - it is not only about striving for some kind of quantum advantage for specific decision problems, instead they can also be used to formalize concepts in foundations of quantum mechanics; and this is something I have never thought about before, which is why I am so fascinated by the idea.

---

References: [1] Nurgalieva, Mathis, del Rio, Renner - Thought experiments in a quantum computer. arXiv:2209.06236

[mysteriousquantumphysics]

Happy Pi Day 2024!

Happy Pi Day 2023!

[mysteriousquantumphysics]

I couldn’t resist to post this on Valentine’s Day, haha(:

[mysteriousquantumphysics]

Slowly finishing my preparations for my last exam this summer term...

[mysteriousquantumphysics]

Data Science meets the Many Body Problem

Since the machine learning course I did this semester at Tsinghua university was mainly focused on typical data science applications, I was curious in how far those methods can be applied in physics. Of course it is nothing new that neural networks can in principle also be used for physical applications - however, tensor network methods still seem to be dominant in the field of numerical many body physics. Thus, I decided to dive in a little into the literature about the usage of Restrictive Boltzmann Machines (RBM) in many body physics.

What are RBMs?

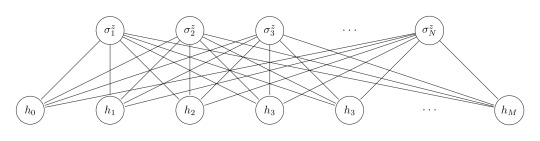
Usually, RBMs are used for instance for recommendation tasks (e.g. video recommendations on video platforms) and many more. In general, it is a unsupervised learning technique which makes use of minimizing its "energy". Thus, the intuition behind RBMs is, despite their data science applications, already related to physics: We will see that it is no surprise that "Boltzmann" is part of the name of this method. An RBM utilizes input data, tries to extract meaningful features from it and wants to find the probability distribution over the input. This follows the physical intuition as follows: The RBM is a neural network with two layers, a hidden and a visible layer, where each node can adopt binary values. An example network looks like:

where the x denote the visible nodes, the h the hidden nodes and W denotes the weights between both layers. Note that there are no links in between the nodes of a single layer; this is why these networks are called restricted Boltzmann machines.

The network is governed by a corresponding energy function as:

where we also have the offsets of the single nodes (a for the visible nodes and b for the hidden nodes). Given this energy function, one can determine the probability distribution by the Boltzmann distribution where Z is a partition function, as familiar from classical statistical physics. As usual, the energy is supposed to be minimized, what is done by the learning algorithm of the RBM but this should not explained here since it would go beyond the scope of a brief blog entry. At this point I'd only like to mention that there are some difficulties determining e.g. the partition function (which is intractable in general) and that this requires some sophisticated algortihms. If you're interested in this and how the RBMs work exactly, a neat and far more rigorous introduction into RBMs can be found here.

One side note at this point: RBMs were introduced by Geoffrey Hinton after John Hopfield (a physicist) invented the so-called Hopfield networks which are also such an energy based mechanism, based on the physical intuition of Ising models.

Note that so far we only talked about the RBMs as they are used in data science - despite their physical intuition, they had so far nothing to do with neither quantum mechanics nor the many body problem. This is what comes next.

How can this be linked to condensed matter?

As introduced in [1], an RBM that can represent a quantum many body state would look like this:

In comparison to the previous network we changed the labels from x to σ, where the σ's denote e.g. spin 1/2 configurations, bosonic occupation numbers and so on. For them one has to choose a basis, e.g. the σ^z basis. This configuration can be summarized in the set S. Hence, the visible nodes are the N physical nodes of the system. The M hidden nodes h play the role of auxiliary (spin) variables. The authors describe the understanding of such a neural-network quantum state as follows: "The many-body wave function is a mapping of the N−dimensional set S to (exponentially many) complex numbers which fully specify the amplitude and the phase of the quantum state. The point of view we take here is to interpret the wave function as a computational black box which, given an input manybody configuration S, returns a phase and an amplitude according to Ψ(S)" [1, p.2]. Thus, one gives a certain spin configuration as input and the RBM generates the state, in the following form:

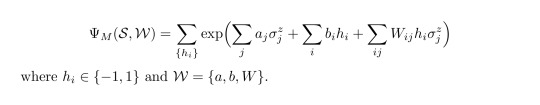
Thus, once can recognize that the form of such a neural-network quantum state adopts a similar form as the aforementioned Boltzmann distribution (exponential of energy function). However, there is additionally a sum over all possible hidden configurations which specifies the full state. After setting a state up in this form, one aim could be to find the ground state corresponding to a certain Hamiltonian, and according to the authors of [1], their RBM method gives decent results for this task!

Similarity to tensor networks

Interesting is, that this framework (even though it appears very different) has some analogous quantities as tensor network states. For example, the representational quality of a neural-network quantum state can be increased by increasing the number of hidden states: Thus, the ratio M/N plays a similar role as the bond dimension of a tensor product state! There are many more similarities, which should not be discussed here but can be found in [3].

Nevertheless, I'd like to mention an important distinction, which is also crucial for tensor network states, because some algorithms (DMRG etc.) can only handle area law states properly. While volume law states have an entanglement entropy which scales with the volume of the partitions of a state, an area law state has a scaling only proportionally with the area of the cut. Area law states can be handled better numerically, because the bond dimension of tensor network states explode for volume law states (more on tensor networks and area law can be found in [4]). According to [2] the difference between area law states and volume law states can be captured in a neat way with RBM states: While volume law states must have full connections between the hidden and physical nodes, an area law state has fewer links - this imposes locality in a sense. The RBM states thus give a neat intuition between the differenece of both kinds of states.

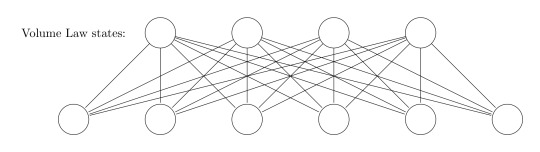
All in all, RBMs seem to be an interesting approach to connect both data science methods and many body physics. It may be that they have strengths which the usual tensor networks approaches lack: for instance, the authors of [2, p.888] claim that it might be possible that RBMs might be able to handle volume law states better than usual tensor network approaches do, which would be of course a major benefit. Since I haven't heard of this approach within the condensed matter framework before, I'm very curious how the importance of this method will evolve in future research!

--- References:

[1] Carleo, Troyer, Solving the Quantum Many-Body Problem with Artificial Neural Networks, arXiv:1606.02318

[2] Melco, Carleo, Carrasquilla, Cirac, Restricted Boltzmann machines in quantum physics, https://doi.org/10.1038/s41567-019-0545-1

[3] Chen, Cheng, Xie, Wang, Xiang, Equivalence of restricted Boltzmann machines and tensor network states, arXiv:1701.04831

[4] Hauschild, Pollmann, Efficient numerical simulations with Tensor Networks: Tensor Network Python (TeNPy), arXiv:1805.00055

[mysteriousquantumphysics]

Hi, sorry for being so inactive currently! This winter term I'm pursuing an online exchange at Tsinghua University and since my subjects there are rather related to computer science than to physics it has been difficult so far to find sufficient time to dive into nice physics topics suitable for this blog! But I hope I'll be more active again soon!:)

[mysteriousquantumphysics]

Quantum Circuit Cutting - with Randomly Applied Channels

Recently, I briefly introduced what circuit cutting is, why it is an advisable thing to do with current quantum hardware (NISQ devices) and what additional costs the cutting is causing. However, I did not go into detail how such a circuit cutting method can look like in detail - this is what this entry will be about. In particular, we will have a look on the circuit cutting procedure proposed by Lowe et. al. [1] in which randomly applied channels are able to cut a circuit.

Identity on Cut Circuits

As mentioned in the previous entry, circuit cutting requires to find a proper identity channel on the cut wires which has reasonably low sampling overhead - the definition of the identity is thus the heart of every circuit cutting procedure. In general, such an identity has the form

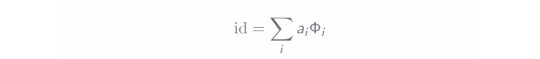
where Φ_i is some properly chosen quantum channel. The corresponding cost depends on the value κ

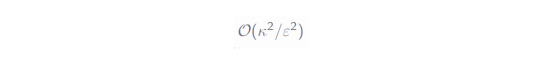
which is the L1 norm of the real coefficients of the identity channel above:

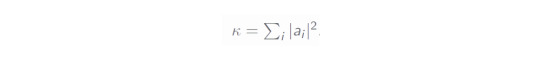
Thus, we see that the main possibility to reduce the sampling overhead is to reduce this value. One possibility with small sampling overhead is the following (however, it is not minimal! The method described in [2] has a lower overhead, but we will not go into detail of this).

The identity channel used in [1] looks like

Here, d=2^k is the dimension of the subspace governing the qubits of the cut. The variable z denotes a Bernoulli random value where z=1 appears with probability d/(2d+1). Later, we will derive this form of the identity channel and will see how this probability and also the expectation E_z emerges. Since, there are two values of z, there are also two quantum channels which can be applied. The first one, Ψ_0, is a measure-and-prepare channel:

The unitaries which are applied on the state prior to measurement have to comprise a 2-design (at least) because otherwise the derivation would not work. Such a design is formed by e.g. Clifford gates but there are many possibilities, one could also rely on approximate designs. Since the form of a quantum channel is not so pictorially, you can see in the following how this channel looks like in "circuit-language":

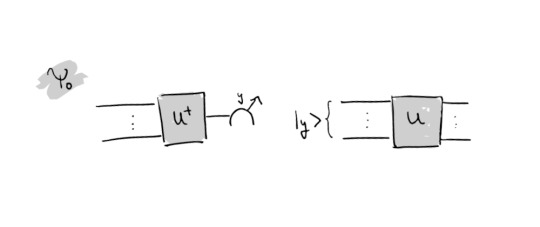
This means, one applies U^\dagger on the k cut wires, measures in z-basis and retrieves a bitstring y. A state in computational basis corresponding to this bitstring gets initialized and then U is applied. All of this is repeated many times. Note that applying such a circuit in the middle of a larger circuit destroys entanglement of the global state and this is also the reason why cutting requires a lot of sampling (quantified by the sampling overhead): The effects of entanglement in the final result must be regained somehow by repeating the procedure numerous times.

The other channel, Ψ_1, is a simpler one. It is the so-called fully depolarizing channel in which all of the information within the cut (within a sample) is lost:

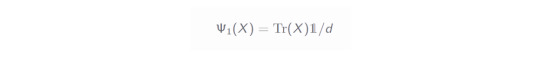
In practice, the action on the cut part of the circuit is as follows: First one measures the k cut wires in the computational basis. Afterwards one takes a uniformly sampled bitstring x and initializes it on the wires - as in the following circuit snippet:

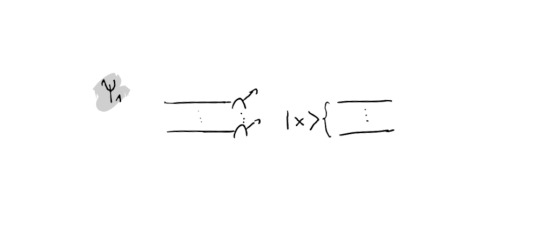
Guiding through the Derivation

Now, as we have settled the definitions, let's go through the derivation of this identity channel! At first, we need an equation which we shall not prove as this would be more involved (based on Haar measure etc.). It is called Werner Twirling Channel:

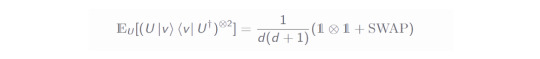
This equation is particularly nice because the right hand side is much much simpler than the left hand side, which requires all of the unitaries in the design. At the same time, the right hand side could be quickly written out by hand for e.g. d=1. This will come in handy in deriving the identity channel.

The idea of the proof is to start with one channel Ψ_0 and massage it a little to find an expression of Ψ_1 within it and then massaging it a little further and finding an expression for the identity channel.

Hence, start with the channel Ψ_0:

A lot is going on here, thus let's go through the equalities step by step: From the first to the second line the only thing happening is that we insert an identity (using completeness of the computational basis). Going to the next line, the two scalar factors are swapped and the states with index i can be used to rewrite the expression into a Tr. By exploiting the properties of tensor products and the trace, one can draw outside the sum a partial trace expression in the last line. This shape is nice, because we can recognize the left hand side of the above equation and can simplify the underbraced expression:

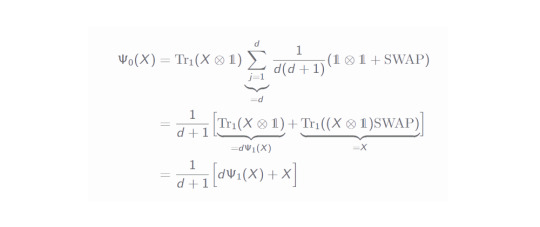
Since the expression within the sum does not depend on the index j anymore, this sum merely gives a factor d. In the second line we draw the partial trace factor into the brackets and recognize the Ψ_1 channel! Additionally, the part with the SWAP operator can be simplified as well (you can easily prove this by checking it with a 4x4 SWAP matrix and using a general matrix X). All of this helped us immensely in relating both channels to each other. Reshaping this equation a little gives us:

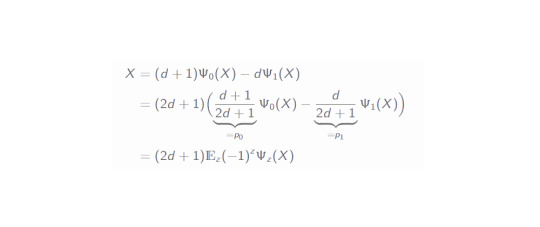
In the second line, we draw a factor outside in order to retrieve the Bernoulli probabilities we have defined previously and then, by respecting the additional sign, this can be easily rewritten as an expectation value in the last line.

What about the cost?

Now as we have both defined and derived the identity circuit expression, let's relate it to the introducing sentences about the sampling overhead. The value of κ can be easily computed:

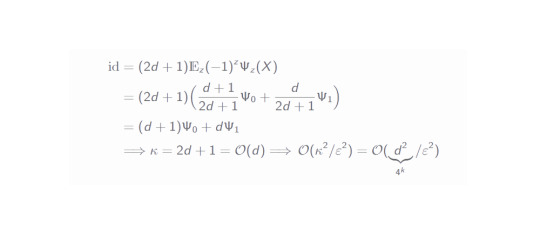
As we can see, the sampling overhead is exponential in the number of cut qubits - this is a deficit in practice. Even though, there are slightly better circuit cutting procedures, the overhead always scales exponentially in the number of cut qubits. Although unfortunate, this makes perfect sense intuitively: The cutting destroys part of the quantum properties of the system and these must be reproduced classically (by sampling). Mostly everything quantum which is simulated classically scales exponentially (since the Hilbert space dimension grows exponentially with growing number of particles).

Overall, circuit cutting is an interesting new field in quantum computing which might help to go beyond the capabilities of current NISQ devices - nevertheless, there is always a price to pay and it will become evident in future research whether circuit cutting will be a common method or not.

--- References: [1] Angus Lowe, Matija Medvidović, Anthony Hayes, Lee J. O'Riordan, Thomas R. Bromley, Juan Miguel Arrazola, Nathan Killoran. Fast quantum circuit cutting with randomized measurements. 2022. arXiv:2207.14734

[2] Hiroyuki Harada, Kaito Wada, Naoki Yamamoto. Optimal parallel wire cutting without ancilla qubits. arXiv:2303.07340

[mysteriousquantumphysics]

ZX Calculus - Another Perspective on Quantum Circuits. Part I

Recently, stumbled across a tensor network-type framework which was completely new to me - the ZX Calculus. The ZX Calculus is not only a neat way of representing possibly complicated mathematical equations, it also gives explicit rules to alter and simplify those expressions. The ZX Calculus is particularly suited to describe matters in quantum information, which is why I'd like to provide a neat example of how to use this framework. As you might already know, quantum circuits can be fully analysed and understood with the help of tensor networks (actually, they are tensor networks) [1]. However, the ZX Calculus is a specific framework which gives a very illustrative graphical way of understanding quantum circuits, while the typical tensor network approaches are mostly tailored for many body problems. All of the following is taken from [2], a very comprehensive introduction to the ZX Calculus and I fully recommend to go through this paper if the following glimpse into the topic made you curious.

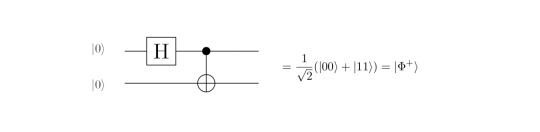
In the following we will set up the very basic set of definitions and rules in order to understand how to evaluate the outcome of the well-known Bell circuit which creates a maximally entangled Bell state:

Basic Definitions: Spiders and Vectors

The most fundamental definition in the ZX Calculus is the spider. The Z-Spider has n inputs and m outputs and is defined as follows:

Thus, such a spider is simply a way of representing a specific kind of 2^n x 2^m matrices. Here, the |0> and |1> denote the basis states of the Pauli Z operator. Similarily, an X-Spider can be defined in terms of another basis, the eigenstates of the Pauli X operator, |+> and |- >:

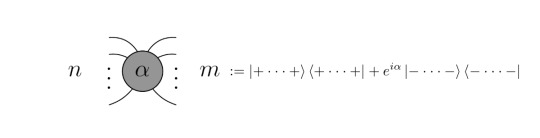
Thus, the color of the dot encodes information about the basis. The usage of the basis states of both Pauli X and Pauli Z is eponymous for the ZX Calculus. One could have chosen the Pauli Y basis as well, however the choice of X and Z results in nice symmetry properties [2, p.22]. From this, we can already conclude the first identity which we will need to evaluate the Bell circuit: Set n=m=1 as well as α=0. With these parameters, the spides become plain 2x2 identity matrices (just look at the definitions!). While α=0 is denoted with an empty dot, this observation can be represented as:

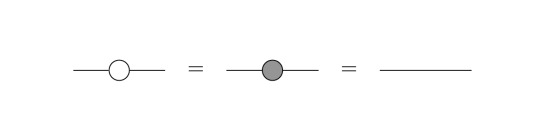
Thus, as soon as we encounter single, plain dots with one incoming and one outgoing leg, we can remove them. Additionally, we will need to know, how to represent simple basis vectors in this diagrammatic language. This is simply done by using dots with a single leg and the following simple consideration according to the definitions of the spiders:

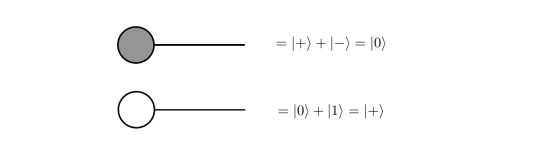
Of course, one can also describe |- > and |1> states, just apply α=π respectively. Note that we omit global phases here; thus using a simple equality sign is actually a delicate matter.

The Hadamard Gate

The Hadamard gate is a unitary gate which simply transforms between the X and Z basis; e.g. applying the Hadamard gate to a |0> state will result in |+>. Its graphical representation is just a plain box with one outcoming and one incoming leg - its action on the basis vectors is as follows:

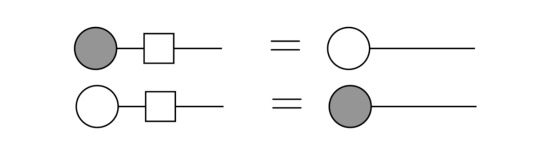
Actually, this is one special case of the more general rule, that the application of Hadamards changes colors as follows:

This of course also holds if the colors are inversed. In general, all ZX rules hold under coherent exchange of colors.

The CNOT Gate

Another central gate in quantum computing is the CNOT gate, which is a controlled NOT gate, i.e. the target qubit is only flipped if the control qubit is |1>, otherwise nothing happens. This 2-qubit-gate can be represented as

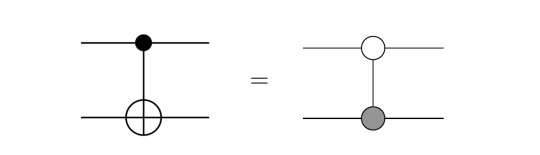
The equality sign should be taken with care as well, because the left is in the quantum circuit notation, while the right is in ZX calculus notation. Its construction is explicitly explained in [2, pp. 11]. Since it is a bit lengthy to go through it by representing the diagrams as matrices, I leave it to you to check it in the reference in case you are interested.

The Fusion Rule

In general, it is possible to "fuse" dots of the same color, while adding their phases. Note that it is addition mod 2π because α and  β are the exponents of e.

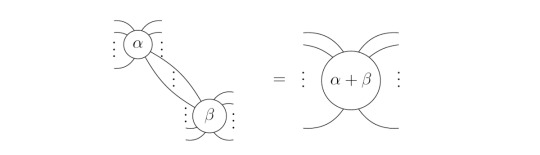
Later, we will only use a special case of this, namely that we can fuse dots of the same color which are connected by one line.

Now, we have finally settled the rough framework for analyzing the Bell circuit, which will do in the next part!

--- References: The ZX graphics were created with tikzit.github.io. Furthermore, you can find a lot of valuable information on zxcalculus.com. [1] Tensor Networks in a Nutshell - Biamonte, Bergholm. 2017. arXiv:1708.00006 [2] ZX-calculus for the working quantum computer scientist - Wetering. 2020. arXiv:2012.13966

[mysteriousquantumphysics]

Quantum Mechanics Itself as Emergent 'Phenomenon'?

Recently, we've been talking about emergence - more explicitly about emergent phenomena in many body systems. But what if the concept of emergence would not only apply 'within' quantum mechanics but also 'outside' the theory? What if quantum mechanics itself is an emergent theory from a classical-type underlying 'reality'? This is exactly the approach of an interpretation of quantum mechanics, called emergent quantum mechanics (EmQM).

Where is EmQM located in the 'zoo' of interpretations?

The 'zoo' of interpretations and alternative theories of quantum mechanics can be classified by their answers to the violation of Bell's inequalities. Bell's Theorem is a theory-independent result and therefore must hold for any possible approach which reproduces the results of standard quantum mechanics. Roughly speaking, the theorem's consequences are that one either has to give up the traditional understanding of realism, or the idea of locality. E.g. Rovelli's approach and QBism belong to the camp which gives up traditional realism and adheres to locality, whereas Bohmian Mechanics sticks to realism and therefore embraces nonlocality. In general, hidden variable theories belong to this 'realist' camp.

EmQM suspects a locally deterministic theory from which standard quantum mechanics emerges. Walleczek and Groessing (p. 2, [1]) suppose that instead of "absolute quantum randomness" there might be "quantum interconnectedness" - indicating the presence of some kind of nonlocality, e.g. nonlocal causality. Hence, this approach seems to belong to the above called 'realist' camp, in which a traditional understanding of realism is embraced and the price to pay is nonlocality, more neatly called "quantum interconnectedness".

Why EmQM?

Walleczek and Groessing [1] argue that a metaphysical fundament is needed in order to unify general relativity and quantum mechanics. Since general relativity is strictly deterministic and standard quantum mechanics inherently indeterministic, the metaphysical fundament of each theory starkly opposes each other such that the lack of unification seems inevitable. However, setting a microscopically causal fundament for both branches of physics, as well as the focus onto emergent phenomena, might yield a solution. For instance, the theory of quantum gravity already relies on the idea of emergent spacetime - together with EmQM it may be possible to lay a metaphysical framework of 'all physics'. Nevertheless it might be questionable, in my view, how this is supposed to work with an approach as EmQM in which nonlocality is a cornerstone, i.e. possibly causing trouble with causality as we know it from relativity.

EmQM and Bohmian Mechanics

Since EmQm and Bohmian Mechanics (BM) belong to the same, 'realist' camp, both seem to be related. Both claim to describe the underlying 'reality' beneath standard quantum mechanics. Both approaches share the belief that standard textbook quantum mechanics does not have descriptive character regarding the nature of reality, even though the theory is empirically successful. Then, standard quantum mechanics is regarded as an 'effective' theory.

However, two approaches can be well compared by regarding how they attempt to reproduce standard quantum mechanics. One main aspect in this respect is the appearance of randomness. Both approaches claim to be fundamentally deterministic and therefore have to explain why we experience the randomness of standard quantum mechanics in our laboratories. Bohmians do this by introducing so called "absolute uncertainty" [3], which is a consequence of the quantum equilibrium hypothesis. Effectively, this means that a universe in which Bohmian Mechanics governs the dynamics, it is impossible to gain knowledge about the configuration of a system beyond the probability distribution determined by the wave function ρ=|ψ|^2. Hence, the complete configuration of point particles, their positions and velocities do exist, but there is no experimental access to it. This limited knowledge is supposed to be the source of randomness and uncertainty that we encounter in standard quantum mechanics:

"This absolute uncertainty is in precise agreement with Heisenberg's uncertainty principle. But while Heisenberg used uncertainty to argue for the meaninglessness of particle trajectories, we find that, with Bohmian mechanics, absolute uncertainty arises as a necessity, emerging as a remarkably clean and simple consequence of the existence of trajectories." (p.864 [3])

Instead of making use of a (more or less ad-hoc) hypothesis, the appearance of randomness in EmQM seems a bit more natural: Only because the underlying dynamics is supposed to be deterministic, this does not imply pre-determination. This is something one can already observe in purely classical systems: The more complex a system is, the more uncertain is the outcome (often referred as "deterministic chaos"). A minor change in the boundary conditions can cause a huge change in the result. Thus, the central point is emergence:

"Critical in this context is that emergent phenomena are subject to unpredictability as a consequence of the intrinsically self-referential nature of the governing dynamics [...]." (p.5 [1])

In comparison, BM formulates its theory in a rather rigid manner. It formulates postulates from which the theory can be deduced. The issue with this is that these postulates have kind of an ad-hoc character. In my view, EmQM circumvents these problems by being less strict/definite. This approach does not seem to have a fixed formalism yet (at least I haven't found analyses on the same level of rigor as there are for BM), while the research seems to be more focused on exploring how emergence can enter the picture - as e.g. 't Hooft does in [2], where he describes explicit examples of possibly emergent symmetries. (Disclaimer: maybe my impression is incorrect, since I have only superficial knowledge about EmQM.)

Regardless of this point, both approaches seem to be interconnected in the end. Walleczek and Groessing (p.2 [1]) claim that a future EmQM would include BM. Hence, in my view, it might be possible that EmQM might support BM in the sense that it lifts the necessity of possibly ad-hoc appearing postulates as formulated in BM. Thus, any theory of quantum mechanics (orthodox or unorthodox) might not only yield emergent phenomena within the theory but quantum mechanics might unravel itsel as an emergent 'phenomenon'.

---

References:

[1] Walleczek, Groessing, Is the World Local or Nonlocal? Towards an Emergent Quantum Mechanics in the 21st Century, arXiv:1603.02862, 2016

[2] 't Hooft, Emergent Quantum Mechanics and Emergent Symmetries, arXiv:0707.4568, 2007

[3] Dürr, Goldstein, Zanghí, Quantum equilibrium and the origin of absolute uncertainty. J Stat Phys 67, 843–907 (1992). https://doi.org/10.1007/BF01049004

[mysteriousquantumphysics]

ZX Calculus - Another Perspective on Quantum Circuits. Part II

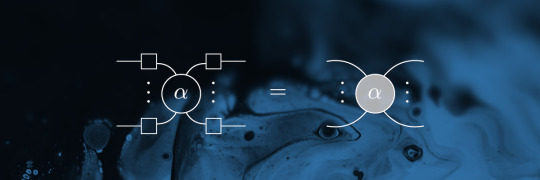
Last time we introduced basic definitions and a small set of rules of the ZX calculus. While our aim is to analyze the Bell circuit in terms of this framework, you can find more sophisticated examples in [2, pp. 28]. For the Bell circuit we only need one further ingredient:

Cups and Caps

Cups and Caps are the ZX-type representations of the Bell State |Φ^+>. As you surely know, this state "lives" in a four dimensional Hilbert space, and can be represented as a vector with four entries - and in the ZX calculus this means:

In more complicated circuits it is neat to know that this Bell state actually acts as a bended piece of wire, which introduces a lot of flexibility in one's modifications of an expression. The cups and caps are merely vectorizations of the 2x2 identity matrix.

Application to the Bell Circuit

A brief reminder about the Bell circuit: It just applies a Hadamard and a CNOT on the input qubits. The outcome is supposed to be the Bell state |Φ^+>, i.e. a cup, as desribed above.

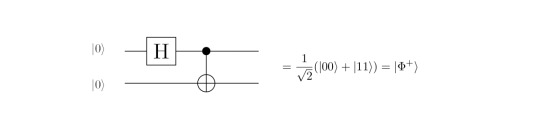
First, start by translating the circuit into ZX-language, by using the definitions we found in the previous entry. The circuit becomes:

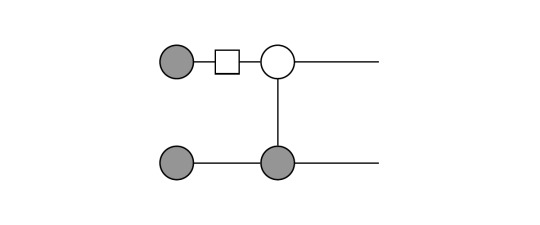
Here, we simply expressed the |0> vectors as grey dots on the left, then applied a Hadamard on the first and afterwards a CNOT. Application of the Fusion rule on the two grey dots on the bottom yields:

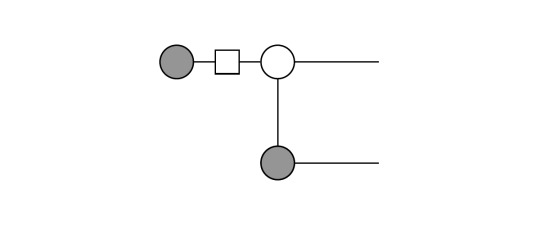
Then, we apply the Hadamard on the grey dot (|0>) which changes its color:

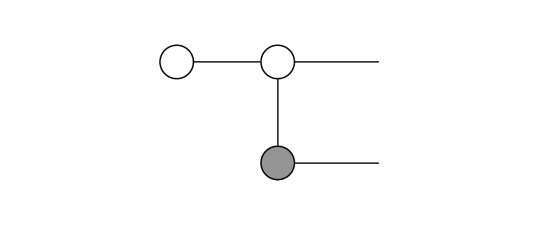
Thus, we can again fuse two dots, in this case the two white dots above:

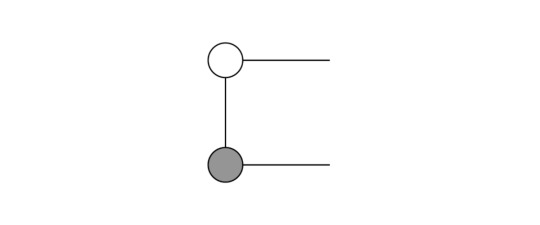
Then, we know that dots with a single income and outcome leg are actually just identities! As a result, our expression simplifies:

And this is exactly the cup we desired! Translating the circuit into ZX-language and applying the rules led us to the result that we have a Bell state in the end. Of course one could have evaluated this circuit easily by hand with the help of the matrix representations of the gates - nevertheless, I think it is a neat example to see the simplicity and beauty of the ZX-calculus. Check out [1] for more sophisticated examples!

Conclusion

Similar as tensor networks in general, the ZX calculus is a neat and beautiful framework which gives rise to a rich variety of applications - even though they resemble a lot, both are specifically tailored for different applications. A nice property of the ZX calculus is that it is universal: it can represent all 2^n x 2^m matrices and simultaneously it is a very intuitive and pictorial description [1, p.18]. As a final note: If you're familiar with condensed matter and tensor networks, you know that the AKLT state is of particular importance. It can also be described with the help of ZX Calculus and the framework is able to reveal its interesting properties as e.g. the string order [2].

--- References: The ZX graphics were created with tikzit.github.io. Furthermore, you can find a lot of valuable information on zxcalculus.com. [1] ZX-calculus for the working quantum computer scientist - Wetering. 2020. arXiv:2012.13966 [2] AKLT-States as ZX-Diagrams: Diagrammatic Reasoning for Quantum States - East, Wetering, Chancellor, Grushin. 2021. doi.org/10.1103/PRXQuantum.3.010302

[mysteriousquantumphysics]

"More is different" - how the increase of complexity leads to the emergence of new physics. Part I

Often a certain hierarchy of sciences is taken for granted, e.g. physics is regarded as being more fundamental as chemistry, chemistry more fundamental than biology and so on. Such a narrative often implies a kind of reductionist thinking which means that there is a certain set of the most fundamental laws - from these fundamental laws one is then supposed to be able to derive all concepts which are less fundamental, e.g. from physics one can infer chemistry etc. However, such a view might be very misleading as Philip Warren Anderson (who is known for a ton of important findings in quantum many-body theory, e.g. the Anderson-Higgs-Mechanism) describes in his article "More is different": "Instead, at each level of complexity entirely new properties appear, and the understanding of the new behaviours requires research which I think is as fundamental in its nature as any other." (p. 393 [1])

Just as a disclaimer, I will not reproduce Anderson's full argument here, but I rather take the quoted passage as a starting point for a presentation of some important concepts I encountered in the past winter term:

A very interesting point is that such emergence cannot only be observed between the different sciences, but already within the sciences themselfes. In our context, physics serves as our example, in particular quantum many-body theory. If you're a physics student you will encounter primarily single particle physics in your first quantum mechanics courses - the postulates of quantum mechanics, the basics of single particle dynamics and so on. However, if one regards more particles and in particular by taking the so called thermodynamic limit (i.e. regarding infinitely many particles) the picture changes drastically, even though it remains in the quantum realm. Not only the calculations become more tedious and complicated, rather new phenomena emerge which simply had no meaning in the simpler, "more fundamental" case. Hence, the mere application of single particle quantum mechanics cannot yield the richness of many-body theory - instead it "requires research which is [...] as fundamental in its nature as any other".

Phase Transitions and Symmetry Breaking as new phenomena

To make this point more specific and easy to grasp, let us consider one particular example: Phase transitions. As one knows from everyday life, water appears in different phases - however, these phases simply have no meaning if one considers a single water molecule. One water molecule cannot be a liquid, gas or a solid. The term of different phases of matter do only acquire meaning as soon as one regards a large number of particles.

One central term which appears in particular in the discussion of phase transitions is symmetry. Anderson even states that "It is only sligthly overstating the case to say that physics is the study of symmetry." (p. 394 [1]). A large part of the study of (classical and quantum) phase transitions relies on the idea of symmetry breaking. To grasp this idea we have to discuss first what a symmetry is in this context. E.g. a sphere is highly symmetric because no matter from which angle one looks at it, it looks the same - a cube is also symmetric because one can rotate it by 90 degrees around an axis and again it looks the same. However it is "less" symmetric than the sphere. Hence, one can roughly determine that symmetry is related to the self similarity an object possesses. Now, let's connect this idea to phase transitions: If one considers the phase transition from liquid water to a solid, it is easy to see that the translation and rotation invariance of a liquid is "larger" than the one of the crystalline structure of ice. Still one can rotate the ice around certain angles and ends up with the same appearance, however the translation and rotation symmetry of the liquid is broken and the symmetry of the ice is more limited (In more rigorous terms, all of this can be described in terms of group theory, which I spare you at the moment since it's about the main idea).

This particular discussion of symmetries only acquires meaning if one considers a large number of particles. Thus, one can see that, qualitatively new phenomena emerge as soon as the complexity of a system rises - and one does not even need maths to grasp the basic idea. Nevertheless, this discussion about symmetry was of course oversimplified - in the next part we will look at the symmetry breaking of the Bose Einstein Condensate, which is going to be more technical but also far more concrete and specific.

---

References:

[1] Anderson, P. W. (1972). More Is Different. Science, 177(4047), 393–396. http://www.jstor.org/stable/1734697

[mysteriousquantumphysics]

How iMPS Can Shed Light on the Distinction between Symmetry Protected Topological Phases. Part II

Previously we introduced some notions from representation theory and how infinite chains can be usefully represented via infinite matrix product states (iMPS). Now, the actually exciting part comes: We connect both parts, symmetries and iMPS. First, we start by checking how symmetries, i.e. their (projective) representations act on an iMPS.

Symmetries in iMPS

Given a system which is invariant under a certain internal symmetry with matrix representation Σ, the corresponding transformation of the Γ tensors must leave the whole iMPS invariant. This action works as

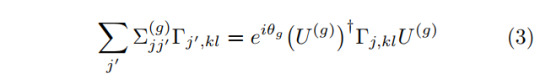
at a single Γ tensor. The diagrammatic representation looks as follows:

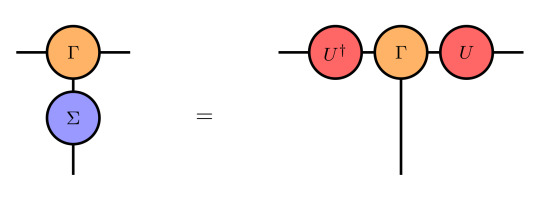
One can see that there is only a single contracted leg on the left hand side which is the reason why we only sum over j' in Equ. (3).

The elements of the symmetry group are denoted by g (which are omitted in the diagrammatic representation). Hence, by acting on one site with the symmetry representation, one gets a set of phases e^(i θ_g) and one of unitary matrices U_g if one regards all elements g of the symmetry group. The phases form a 1D representation (character) of the symmetry group, while the U_g form a projective representation, i.e. their homomorphism property is expanded by a phase, as we introduced in the previous entry. The resulting factor set can distinguish between different symmetry protected topological phases of the system. How can one practically retrieve the U matrices? By applying iTEBD or iDMRG one can retrieve the ground state of a given system, which will be provided as an iMPS in canonical form. Then, one knows that transforming a state by the symmetry should leave it invariant. Thus, the overlap between the original and transformed state has to remain <ψ|ψ'>=1. This inner product consists of several ``generalized'' transfer matrices:

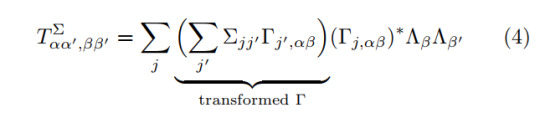
Due to the required normalization, the largest eigenvalue of this generalized transfer matrix must be η=1, otherwise the state is not invariant under the given symmetry. We denote the corresponding eigenvector X_αα' (which is actually a matrix but can be shaped into a vector by vectorization). This gives us the anticipated U matrix, which is related to the eigenvector as

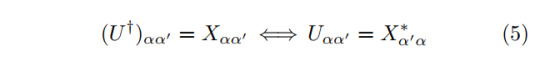
which can be explained by how the symmetry representation Σ acts on the Γ tensors as described in Equ. (3). Due to the fact that the U are unitary, only one U^† will effectively remain in the expression. This sole U^† can then be related to the eigenvector X from the fact that the iMPS is in canonical form. A diagrammatic representation of this computation works as follows:

First, we have a fraction of the generalized transfer matrix (Equ. (4)). Afterwards, we apply Equ. (3) and this yields:

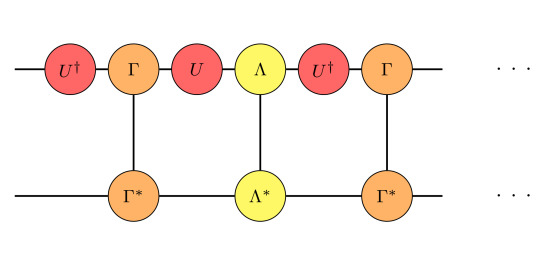
From the fact that the U are unitary and commute with Λ, one can simplify the expression as:

The remaining U^† can be related to the left eigenvector of the transfermatrix via Equ. (5). How this helps us to numerically distinguish the phases will be regarded in the next section, where we regard a specific example.

Application to the Spin-1 Chain

Let us consider a spin-1 system evolving under the Hamiltonian

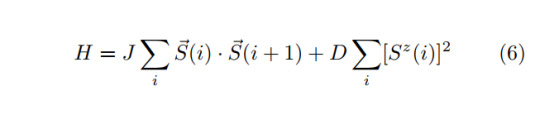
which gives rise to a symmetry protected topological phase. Note that the first term describes the usual Heisenberg model, while the second is an anisotropy of the system. Even though one can study more symmetries of this system, let us focus on the Z_2 x Z_2 symmetry. The representations Σ are given as

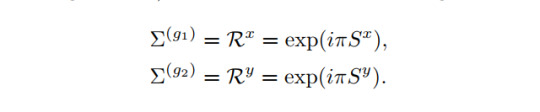
Previously, we mentioned that the factor set of a projective representation can be linked to a distinction of topological phases. In the present case this works as follows. Note that the Z_2 x Z_2 symmetry is abelian, i.e. the group elements commute. For a general projective representation U with group elements g and h, this means:

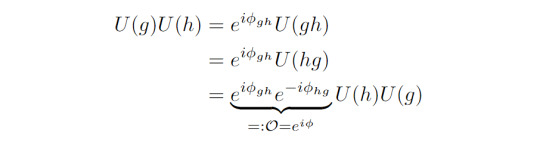
where we used the homomorphism property of the projective representation twice.

Applying this to the present Hamiltonian one will end up with two different values of the curly O which can distinguish the phases:

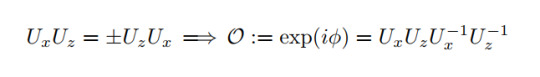
Here, ϕ can either be 0 or π, leading to O=+1,-1.

Having said this, the practical, numerical method to find the phases according to the Z_2 x Z_2 symmetry in the present system is the following: First, one implements the Hamiltonian such that it suits iTEBD. Then, one finds the corresponding ground state and applies the symmetry matrices R_x and R_y in order to retrieve the overlap in the form of the generalized transfer matrices. Afterwards, one takes one of the transfer matrices and diagonalizes it (via sparse matrix methods, e.g. Lanczos). Having implemented this, one can check for which parameters of D and J the largest eigenvalue is indeed 1 (if it is smaller than 1, the symmetry is not conserved in this phase, i.e. O=0). After this step, one can find the U_x and U_y by Equ. (5) and one can determine the phase as described above and find two distinct phases preserving the symmetry: a trivial, O=+1, and a topological, so-called Haldane phase, O=-1.

Now, the overall result we achieved is that we found values which are capable of characterizing a topological phase. This is important, since topological phases do not obey the Landau paradigm and can therefore not be distinguished by spontaneous symmetry breaking. Hence, it is remarkable that one can find a way to distinguish these new phases by combining representation theory and MPS methods. There are even more methods to distinguish the symmetry protected phases in such 1D chains - in case you're interested, have a look on the remainder of [1].

---

References

[1] Pollmann, Turner. Detection of symmetry-protected topological phases in one dimension. Phys. Rev. B 86, 125441. 2012.

[mysteriousquantumphysics]

"More is different" - how the increase of complexity leads to the emergence of new physics. Part II

In the previous part we did see that some concepts only obtain meaning if the level of complexity of a system rises. I considered the example of phase transitions and their relation to symmetry breaking - now, let's regard what symmetry breaking means in the particular case of Bose Einstein condensation:

What is a Bose Einstein Condensate (BEC)?

A Bose Einstein Condensate describes a system of bosons where a macroscopic amount of the particles occupies the ground state. As you might recall such a condensation cannot be possible for fermions, because they obey the Pauli exclusion principle, what bosons do not. Hence, in the case of high temperature, a large number of bosons can be in an unordered phase where the particles occupy more or less random energy levels. If one cools the bosons below a certain critical temperature, the phase transition takes place: The system becomes a Bose Einstein Condensate where a considerable fraction of particles can be found in the ground state.

Bose Einstein Condensate and its Broken Symmetry

Now, how is this phase transition connected to a broken symmetry? This can be seen by regarding the action S of the bosonic system first

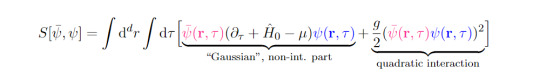
where d is the spatial dimension, τ the imaginary time, μ the chemical potential and g the interaction between the bosons. The fields are colored in magenta and their conjugates in blue - this emphasizes the symmetry of the action: Since each term pairs up a field and its conjugate, their potential phases obviously cancel and therefore this particular action is invariant under phase multiplications, i.e. obeys a U(1) symmetry.

In the current context, a symmetry can be roughly defined as the following:

This means that the symmetry transformation Σ can be applied on the field but it leaves the resulting action invariant. Note that the symmetry is global and has to be continuous. How is a broken symmetry indicated then? As soon as the ground state of a system is not invariant under the original symmetry, then one says that the symmetry is broken. Simultaneously, this indicates the phase transition.

Now, let's look at the system and let's take the condensation into account explicitly. The ground state is ψ_0 and as stated above, the BEC is characterized by the fact that a macroscopic amount of particles occupies the groundstate. Then, one can simplify the expression of the action by assuming that the ground state forms the leading contribution to the action.

One can obtain a solution for the explicit form of the ground state by regarding the saddle point approximation:

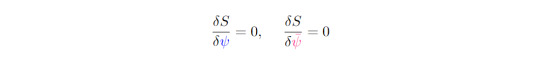
Explicitly computing the functional derivatives and setting them to zero gives us one trivial solution (ψ_0=0) as well as one non trivial solution:

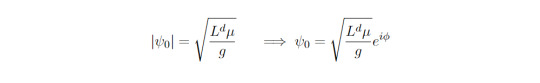
Since the solution only depends on the modulus, the nontrivial solution is infinitely degenerate because of the necessary phase factor. This degeneracy exactly shows that the U(1) symmetry is broken: Applying the symmetry transformation of U(1) will not leave the ground state invariant. Instead, it will transfrom between the infitinetly many degenerate ground states. Hence, we see that the original symmetry is indeed broken and the bosons did undergo a phase transition!

This degeneracy is illustrated in the plot below. The value of the action is the vertical direction and the horizontal plane depicts the real and imaginary part of the field. One can directly see the minimum (blue) which is the solution of the saddlepoint approximation. It has an obvious rotation symmetry which neatly shows the degeneracy of the ground state with respect to rotations, i.e. multiplications by exp(iϕ).

This finishes our discussion: Single particle physics does not give rise to the richness of many-body theory; if one considers a lot of particles, new phenomena occur which would not have meaning in a single particle case - in particular, phase transitions are such a phenomenon and they additionally neatly show us how important symmetries in physics are.

More detailed discussions of the BEC with and without interactions can be found in e.g. Chapter 2.3 of [2] and [3].

---

References:

[1] Anderson, P. W. (1972). More Is Different. Science, 177(4047), 393–396. http://www.jstor.org/stable/1734697

[2] Altland, A., & Simons, B. (2010). Condensed Matter Field Theory (2nd ed.). Cambridge: Cambridge University Press. doi:10.1017/CBO9780511789984

[3] Coleman, P. (2015). Introduction to Many-Body Physics. Cambridge: Cambridge University Press. doi:10.1017/CBO9781139020916