#paul adrien maurice dirac
Explore tagged Tumblr posts
Text
Un uomo entrò in un negozio di tecnologia per comprare un’Intelligenza Artificiale
Il commesso gliene mostrò subito alcune.
La prima sapeva rispondere a poche domande e costava 100 dollari. La seconda sapeva cantare e raccontare storie e costava 200 dollari. Un modello ancora più avanzato, con un design spettacolare, era venduto a 500 dollari perché poteva interagire in diverse lingue.
L’ultima invece, era un’AI apparentemente anonima e dal design piuttosto spartano, aveva un prezzo di 10.000 dollari. “Diecimila dollari?!” esclamò l'acquirente. “Deve essere un sistema straordinario. In quante lingue comunica?” “Parla solo inglese,” rispose il negoziante. “Ah... be’, forse avrà allora un vocabolario incredibilmente vasto!” Il negoziante scosse la testa. “Sa almeno cantare o creare contenuti eccezionali?” “No, anzi, la maggior parte del tempo rimane in silenzio.” “Beh, farà qualche cosa di formidabile, no? Cosa diavolo ha di così prezioso questa Intelligenza Artificiale?” “Signore, questa Intelligenza Artificiale pensa.”
Parafrasando la storiella del pappagallo che Rutherford usò per spiegare a Bohr cosa avesse Dirac di tanto eccezionale, nonostante fosse un tipo particolarmente silenzioso (*).
#ai#agi#artificial intelligence#intelligenza artificiale#storiella#ernest rutherford#niels bohr#paul adrien maurice dirac#futuro
2 notes
·
View notes
Text
(∂ + m) ψ = 0 (∂ + M) ψ = ❤
#Dirac#Matemática#Paul Adrien Maurice Dirac#Espín#Ecuacion#Ecuación de amor#Amor#Ingeniero#Ingenieria#Fisico teorico#Fisica#Teorias#Fisica Cuantica#Probabilidad#Electron#Particulas#Preducción#Tiempo#Transformacion#Distancia#Formula#Formula del amor#Sistemas#Interaccion#Entrelazamiento#Entrelazamiento cuantico#conexion
26 notes
·
View notes
Text

✍️Paul Adrien Maurice Dirac (1902-1984), est un mathématicien et physicien britannique.
etude-generale.com
#citationdujour#quote#beautiful quote#citation#quoteoftheday#citation du jour#quotes#francais#french#french quote#citation française#francaise#paul dirac#progrès#progrèsscientifique#courage#intelligence#réussite
0 notes
Text
Paul Adrien Maurice Dirac fue uno de esos personajes que marcó la historia de la ciencia. Coronándose como uno de los físicos más importantes del siglo XX, Dirac desempeñó un papel esencial en el avance de la mecánica cuántica y de la electrodinámica cuántica. De hecho, la formulación de la ecuación de Dirac representó un antes y un después en el estudio del comportamiento de las partículas subatómicas. Además, fue el primer científico en predecir la existencia de la antimateria, es decir, la materia formada por antipartículas.
En el año 1933 recibió el distintivo de alzarse como uno de los pocos científicos de la historia en ser homenajeados con el Premio Nobel, galard��n que compartió con Erwin Schrödinger por sus contribuciones al descubrimiento de nuevas formas productivas en la teoría atómica.
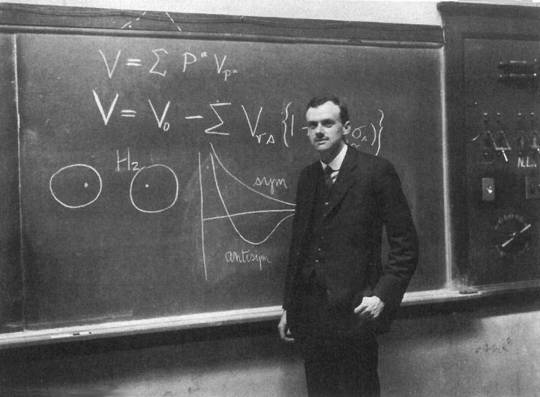
1 note
·
View note
Text
Paul Adrien Maurice Dirac, quantum mechanics ,quantum electrodynamics.
Paul Adrien Maurice Dirac, quantum mechanics ,quantum electrodynamics.
Pick a flower on Earth and you move the farthest star. … (8 August 1902 – 20 October 1984) was an English theoretical physicist considered one of the most important physicists of the 20th century. He was a Lucas Professor of Mathematics at Cambridge University, a Professor of Physics at Florida State University and the University of Miami, and won the 1933 Nobel Prize in Physics. God used…

View On WordPress
#bossesmademen#Motivational#Paul Adrien Maurice Dirac#Paul Dirac#Personal development#quantum electrodynamics.#quantum mechanics
0 notes
Quote
Le mathématicien joue à un jeu dont il invente lui-même les règles alors que le physicien joue à un jeu dont les règles sont données par la Nature mais, au fur et à mesure, il apparaît de plus en plus évident que les règles intéressantes pour le mathématicien sont en fait celles que la Nature a choisies.
Paul Adrien-Maurice Dirac
5 notes
·
View notes
Text

L’equazione di Dirac:
la cosiddetta equazione dell’Amore...
La Fisica Quantistica incontra i Sentimenti Umani.
Il grande fascino dell’Equazione di Dirac.
È la cosiddetta equazione dell’Amore,
una delle più belle della storia della fisica, perché dietro quei simboli di Paul Adrien Maurice Dirac, fisico britannico, ci sarebbe un messaggio profondo.
Nel 1928, Dirac (Premio Nobel per la Fisica nel 1933), studente del prestigioso
St John’s college di Cambridge, formula la sua equazione fatta di simboli e numeri:
(∂+m)ψ=0
“Se due sistemi interagiscono tra loro per un certo periodo di tempo e poi vengono separati, non possono più essere descritti come due sistemi distinti, ma diventano un unico sistema.”
4 notes
·
View notes
Text
TAFAKKUR: Part 287
SYMMETRY AND BEAUTY
When visiting Moscow University, Paul Adrien Maurice Dirac, the famous physicist and the founder of Quantum Mechanics, as well as being the fifteenth Lucasian Professor of Mathematics at Cambridge University, was asked about his philosophy in physics and he wrote on a blackboard “physical laws should have mathematical beauty.” This phrase remains preserved on the same blackboard today. As Sir Michael Berry said at the opening of Dirac House in 1997, “he showed that the simplest wave satisfying the requirements was not a simple number but consisted of four components. This seemed like to complicate matters, especially for those minds that were still reeling from the unfamiliarity of “ordinary” quantum mechanics. Four components! Why should anybody take Dirac’s theory seriously? Foremost and above all for Dirac was the fact that the logic leading to the theory was, although deeply sophisticated, in a sense beautifully simple. Much later, when someone asked him “what do you think of the equation?” he is said to have replied: “I think that it is beautiful.” In fact, Professor Dirac knew that very significant mathematical equations occur in all created things. Even though these consist of deeply sophisticated matters, at the same time they occur with a beautiful simplicity and are a clear description of the action of creation of the Eternally Besought of All. When we examine his quotation in this light, we are better able to understand what he meant.
Be they physical or chemical, many attributes of beings are dependent on mathematical laws and their appearances are also shaped along mathematical principles. When we observe creation from this standpoint, we can perceive the perfection as well as the spectacular beauty that is inherent in every being. As reflections of the Attributes of the Names of God Almighty, Jamil (The Owner of Beauty), Bari (The One Who Creates from nothing), Sani (The Maker of All) and Musawwir (The Designer), this beauty found in the external appearance of beings is dependent on more than one factor coinciding. The most important factor here is “symmetry,” which is described as “an exact correspondence and beautiful balance among the parts of an object.” Beings are created with various symmetrical attributes and with great artistic beauty.
The most common symmetry type is the bilateral symmetry; this creates a mirror effect which is an exact correspondence between the right and left sides. An object forms an exact symmetry with its reflection in the mirror. A perfect symmetry that is very similar to the mirror effect can be found in the human body. The left and right sides of our body are symmetrically corresponding. Imagine a dividing line that passes from the middle of the forehead, through nose, chin and down the chest, we can see a perfect symmetry on both sides of the body. Our arms, legs, eyes, ears, nose and lips are designed with a bilateral symmetry. The same symmetrical structures can also be seen in most other creatures. All mammals, reptiles and birds are symmetrically created.
Another type of symmetry is rotational (radial) symmetry. Imagine a metal object that is in the shape of an equilateral triangular placed on the sand. If we will rotate this object 120o around an axis that passes through its center, the new position of the object will fit exactly into its original mark left on the sand. The reason for this is that the radial symmetry for equilateral triangles is 120 degrees. In the same way, a square has a radial symmetry of 90o and a regular polygon with n number of sides has a radial symmetry of 360/n degrees.
The beautiful symmetry of snow flakes, with their regular hexagonal shape are a beautiful natural phenomenon. In addition to these there are shapes in nature that have a three-dimensional radial symmetry. The most significant of these shapes are regular polyhedrons. An example of such polyhedrons is the salt crystalline elements that have cubical structures. Until recently, the fact that there is a creature in nature that has a regular polyhedral shape, consisting of twenty sides, was unknown. However, when a type of adenovirus that causes infections and hepatitis in dogs was discovered, it was found that there is a creature with twenty regular sides in nature.
One of the most beautiful samples of radial symmetry in nature is the daisy. Symmetrical structures do not only exist in the normal world and in the micro worlds, but also can be found in the macro world, like all the huge celestial objects, the Sun, the Moon, galaxies, star clusters in the sky . . . . All planets move around the Sun in a symmetrical manner, whereas galaxies have a spiral symmetry. It is interesting that the symmetrical structure of living beings is overwhelmingly apparent externally, rather than internally. For example, the internal organs in the human body, like the lungs, liver, stomach and intestines are not symmetrical and we have only one heart in one side of our chest cavity. Moreover, the lobes of the brain are not symmetrical either. However, all the metabolic processes in human body function properly. Does this mean that the mathematical beauty found in our external appearance is merely for aesthetical reasons? God does not create things for only one reason or purpose, on the contrary, He creates them to serve many motives and in relation with many functions. For example, if we did not have two eyes and if they were not symmetrically placed on our faces, we would not be able to see objects three-dimensionally. In the same way, if our ears were not symmetrically placed on our heads, then we would have great difficulty in determining the direction and source of sounds. If we did not have symmetrical feet and legs, we would not be able to walk well, and if our arms were not symmetrical, we would not be able to balance our body’s center of gravity while walking. If birds did not have symmetrical wings, they would not be able to fly, and if the fins of fishes were not symmetrical, they would not be able to swim smoothly.
Symmetry is also closely related to physical and mental robustness. According to one study, women who suffer from an infectious disease during pregnancy are more likely to have babies with asymmetrical features. The same study claims that asymmetrical babies are more susceptible to heart disease than symmetrical babies.
Another study shows that people with asymmetrical teeth are more likely to have more harmful microorganisms in their mouth than those who have symmetrical teeth. It is interesting that there tends to be a greater difference between the fingerprints on the left and right hands of schizophrenic people than on those of normal people.
Symmetry is a phenomenon that is used by animals and insects. For example, an experiment showed that bees prefer flowers that are symmetrical. Actually, flowers with perfectly symmetrical shapes produce more nectar than those that are asymmetrical. In one investigation, a symmetrical flower was made asymmetrical with a pair of scissors. The flower had been attractive to bees before its shape was changed; after made asymmetrical, the flower became unattractive to bees, even though it had just the same amount of nectar as before.
All these facts reveal that there is much wisdom and beauty hidden within the symmetry that the Almighty Designer uses to shape all beings. We take symmetry for granted. To have two eyes placed equidistance and two ears on each side of the head is the norm. Anything else strikes us as strange. But if we just take a few moments to think about why our eyes are where they are, and why our ears are placed on the sides of our heads, the answer is obvious. God’s mercy is infinite; in even the simplest example of symmetry there is a reason. We should not take this world for granted, but rather use every opportunity to dwell upon and be thankful for the wonderful world that has been created for us.
#allah#god#prophet#Muhammad#quran#ayah#sunnah#hadith#islam#muslim#muslimah#hijab#help#revert#convert#religion#reminder#dua#salah#pray#prayer#welcome to islam#how to convert to islam#new muslim#new convert#new revert#revert help#convert help#islam help#muslim help
2 notes
·
View notes
Text
Einstein, Albert (1879-1955) Matematikteki zorluklarınız için endişelenmeyin, sizi temin ederim ki benimki daha büyük.
Dirac, Paul Adrien Maurice (1902-1984) Matematik, her türden soyut kavramlarla uğraşmak için özellikle uygun bir araçtır ve bu alandaki gücünün sınırı yoktur.
Egrafov, M. Matematikçilere ne yaptıklarını sorarsanız, her zaman aynı cevabı alırsınız. Onlar düşünür. Zor ve alışılmadık sorunları düşünüyorlar. Sıradan sorunlar hakkında düşünmezler: sadece cevapları yazarlar.
2 notes
·
View notes
Text
Check out this post… "Paul Dirac : The Mozart of Science 🔼".
1 note
·
View note
Text
What is a positron
What is a positron
Positrons were discovered in 1932 by Carl David Anderson in his cloud chamber studies of the composition of cosmic rays. The discovery of the positron provided an explanation for a theoretical aspect of electrons predicted by British physicist Paul Adrien Maurice Dirac. The Dirac wave equation revealed an abundance of negative energy states that had not been observed before. In 1931, Dirac…
View On WordPress
0 notes
Photo

Probably the most intelligent photo ever taken Group of the scholars who attended the fifth Institute International de Physique Solvay, which was held in Brussels, Belgium, from October 23-29, 1927 ➡️ (First Row): Irving Langmuir, Max Planck, Marie Curie, Hendrik Antoon Lorentz, Albert Einstein, Paul Langevin, Charles-Eugène Guye, Charles Thomson Rees Wilson, Owen Willans Richardson ➡️ (Second Row): Peter Joseph William Debye, Martin Knudsen, William Lawrence Bragg, Hendrik Anthony Kramers, Paul Adrien Maurice Dirac, Arthur Holly Compton, Louis de Broglie, Max Born, Niels Bohr ➡️ (Back Row): Auguste Piccard, Emile Henriot, Paul Ehrenfest, Edouard Herzen, Théophile de Donder, Erwin Schrödinger, Jules Emile Verschaffelt, Wolfgang Pauli, Werner Heisenberg, Ralph Howard Fowler, Léon Brillouin https://www.instagram.com/p/CNXHCeHB6TY/?igshid=34mw2sm7waf7
0 notes
Text
Paul Dirac Kimdir?
Paul Dirac Kimdir? Paul Dirac Richard Feynman ile birlikte Paul Adrien Maurice Dirac 8 Ağustos 1902’de Bristol İngiltere’de doğdu.Babası geçimini Fransızca öğretmenliği yaparak sağlıyordu.Babasının otoriter tavırlarından dolayı çocukluğu pek iyi geçmedi.Önce Bishop İlkokuluna başladı.Ardından babasının da öğretmenlik yaptığı Merchant Venturers’ Teknik Kolejine devam etti.Daha sonra Bristol…

View On WordPress
0 notes
Photo

008 - Física – Fichas (101-114) -
HISTORIA
101 - En el siglo XIX se produjeron avances fundamentales en la electricidad y el magnetismo, principalmente de la mano de Charles-Augustin de Coulomb, Luigi Galvani, Michael Faraday y Georg Simon Ohm, que culminaron en el trabajo de James Clerk Maxwell en 1855, que logró la unificación de ambas ramas en el llamado electromagnetismo.
102 - Además, se producen los primeros descubrimientos sobre radiactividad y el descubrimiento del electrón por parte de Joseph John Thomson en 1897.
103 - Durante el siglo XX, la física se desarrolló plenamente. En 1904, Hantarō Nagaoka había propuesto el primer modelo del átomo, el cual fue confirmado en parte por Ernest Rutherford en 1911, aunque ambos planteamientos serían después sustituidos por el modelo atómico de Bohr, de 1913.
104 - En 1905, Einstein formuló la teoría de la relatividad especial, la cual coincide con las leyes de Newton al decir que los fenómenos se desarrollan a velocidades pequeñas comparadas con la velocidad de la luz.
105 - En 1915 extendió la teoría de la relatividad especial, formulando la teoría de la relatividad general, la cual sustituye a la ley de gravitación de Newton y la comprende en los casos de masas pequeñas.
106 - Max Planck, Albert Einstein, Niels Bohr y otros, desarrollaron la teoría cuántica, a fin de explicar resultados experimentales anómalos sobre la radiación de los cuerpos.
107 - En 1911, Ernest Rutherford dedujo la existencia de un núcleo atómico cargado positivamente, a partir de experiencias de dispersión de partículas.
108 - En 1925 Werner Heisenberg, y en 1926 Erwin Schrödinger y Paul Adrien Maurice Dirac, formularon la mecánica cuántica, la cual comprende las teorías cuánticas precedentes y suministra las herramientas teóricas para la Física de la materia condensada.
109 - Posteriormente se formuló la teoría cuántica de campos, para extender la mecánica cuántica de acuerdo con la Teoría de la Relatividad especial, alcanzando su forma moderna a finales de la década de 1940, gracias al trabajo de Richard Feynman, Julián Schwinger, Shin'ichirō Tomonaga y Freeman Dyson, los cuales formularon la teoría de la electrodinámica cuántica.
110 - Esta teoría formó la base para el desarrollo de la física de partículas. En 1954, Chen Ning Yang y Robert Mills desarrollaron las bases del modelo estándar. Este modelo se completó en los años 1970, y con él fue posible predecir las propiedades de partículas no observadas previamente, pero que fueron descubiertas sucesivamente, siendo la última de ellas el quark top.
111 - Los intentos de unificar las cuatro interacciones fundamentales han llevado a los físicos a nuevos campos impensables.
112 - Las dos teorías más aceptadas, la mecánica cuántica y la relatividad general, que son capaces de describir con gran exactitud el macro y el micromundo, parecen incompatibles cuando se las quiere ver desde un mismo punto de vista.
113 - Por eso se han formulado nuevas teorías, como la supergravedad o la teoría de cuerdas, donde se centran las investigaciones a inicios del siglo XXI.
114 - Esta ciencia no desarrolla únicamente teorías, también es una disciplina de experimentación. Sus hallazgos, por lo tanto, pueden ser comprobados a través de experimentos. Además, sus teorías permiten establecer previsiones sobre pruebas que se desarrollen en el futuro.
0 notes
Quote
Le mathématicien joue à un jeu dont il invente lui-même les règles alors que le physicien joue à un jeu dont les règles sont données par la Nature mais, au fur et à mesure, il apparaît de plus en plus évident que les règles intéressantes pour le mathématicien sont en fait celles que la Nature a choisies.
Paul Adrien-Maurice Dirac
14 notes
·
View notes