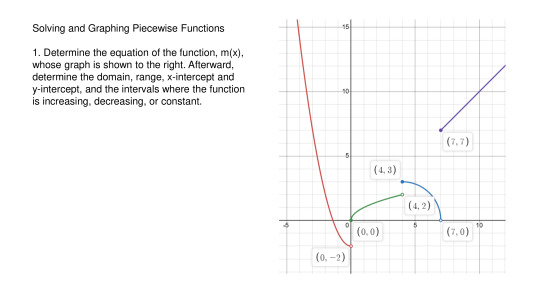
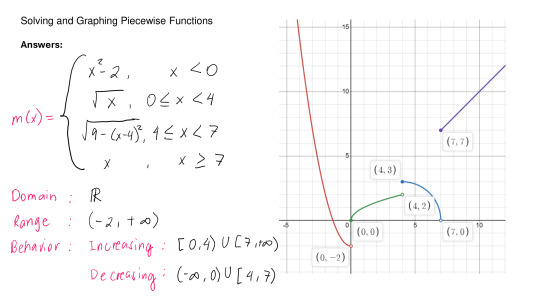
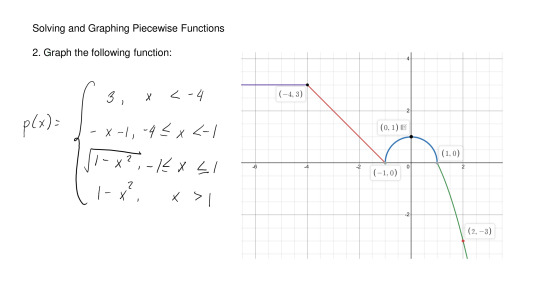
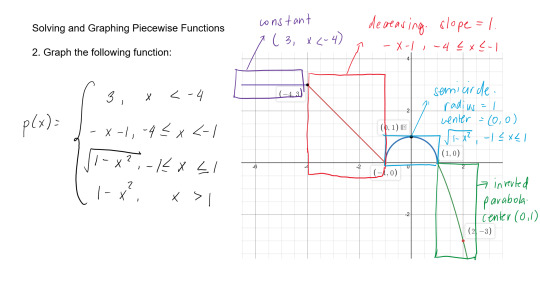
#polynomial application problem

[math-journal2]

<— Unit 3: Part 4 —>

Polynomials

Sum & Difference of Squares

Sum & Difference of Cubes

Factor Polynomial

Page 8

[anremithrl]

I work in formal methods and computational mathematics. I spend a lot of time working on SAT solvers and CAS engines and the like.

Today, I happened to be working on a SAT solver. And noticed the sat solver had another sat solver inside of it. In retrospect, that should have been obvious.

Now, for those who don't know, here is what a SAT solver does, and what its applications are:

A SAT solver takes a statement made of negations, conjunctions, disjunctions, and atomic statements and then returns an assignment of the atomic statements that makes the statement true.

For example: A or B, this can be satisfied as A = True and B = False.

This is the quintessential NP-complete problem. All the others can actually be reduced to it. So for the list of problems that a SAT solver can solve, see link below.

Modern methods have been trying to make it really really fast. Unfortunately, we haven't been able to beat the polynomial time barrier. Most people think it's impossible, but no one has actually shown that it is impossible.

I'm really naive, perhaps, in that I think P=NP. I may just believe that because it'd be so cool if it were true. So far no one has proved me wrong.

Now, whilst working on one of these SAT solvers, I realised something: the input for the solver has to be in conjunctive normal form, and there's a preprocessor that converts the statement into conjunctive normal form, that is

Anding a bunch of ors of atomic statements and their negations.

(a or b) and (c or (not a)) and (a or c) and ((not a) or c or f)

To get them there, the preprocessor system that converts things into conjunctive normal form has several rules about manipulation of these statements. As it happens, it is robust enough to do the same, but into disjunctive normal form, which in this case happens to be:

(b and c) or (a and c)

Which does actually accomplish what the SAT solver set out to do.

Now, does this system run slower and less effectively than the actual system? Yes. But I find it funny that there's a SAT solver in my SAT solver.

[gemkun]

@luckquartzed said : “Negative b, plus or minus, the square root of b squared… minus 4ac over 2a…” Aventurine flips through the textbook and scoffs. “This is what they teach kids in school? Man, I’m glad I never went. How come there’s nothing in here about voting, opening a credit account, buying a house or first aid? Who thought this belonged in public academics instead of specialized university?” He drops the book in the trash. “What a waste of 500 credits.” “It’s all inductive anyways, can’t really prove anything, watch out for the giant teapot orbiting the sun. Also moons are all made of cheese.” Aven is just being an add at this point and he knows it. “How come no matter what colour the liquid, the froth is always white?”

      ⸻       this   was   to   be   absolutely   expected.   though   ,   it   is   not   the   fault   of   the   avgin   ,   but   rather   the   education   system   and   its   failure   to   indicate   applications   relevant   to   the   livelihoods   of   others.   ❝   it   is   one   aspect   ,   but   there   are   plenty   of   other   topics   that   are   covered   within   prescribed   syllabi.   ❞   he   eyes   the   discarded   purchase   —   identifying   the   precious   publication   being   laid   to   waste.

  still   ,   his   subsequent   reasoning   ,   borders   absurdity.   in   fact   ,   it   is   explicitly   nonsensical.   ❝   what   you   have   a   listed   are   essentials   ,   no   doubt   ,   but   you   severely   underestimate   the   capabilities   of   the   quadratic   formula.   ❞   outstretched   ,   he   is   thankful   that   the   fallen   text   is   not   marred   by   assorted   scraps   ,   and   for   that   ,   his   retrieval   follows.   he   dusts   it   then   ,   to   remedy   its   bruised   state   ,   before   he   passes   it   to   its   respective   owner   ,   both   former   and   returned.

  ❝   it   is   a   consolidation   that   allows   the   ability   to   solve   the   simplest   type   of   polynomial   equations   that   can   be   used   to   study   complex   systems   within   certain   limits.   they   appear   routinely   in   all   facets   of   mathematics   and   if   you   do   not   appreciate   this   formula   ,   you   will   surely   struggle   as   you   venture   further   into   arithmetic   problems.   ��   flipping   open   the   educational   tool   ,   he   exposes   the   strategist   to   the   mediocre   explanation   across   glossy   pages.   to   assist   his   elaboration.   ❝   what   you   fail   to   comprehend   ,   is   this   concept   ,   is   applicable   to   countless   conditions   in   everyday   life   ,   including   your   dice   throws.   ❞

  and   perhaps   ,   one   he   employs   when   he   faces   these   roulettes   with   the   stoneheart.   ❝   in   its   most   basic   form   ,   it   determines   the   area   of   figures   —   by   expressing   the   area   with   a   quadratic   equation   ,   we   can   seamlessly   calculate   this   unknown.   if   we   take   this   further   ,   another   example   is   a   projectile   :   the   place   where   it   lands   ,   the   distance   travelled   and   the   time   it   takes   to   reach   its   vertex   can   be   established.   have   you   worked   out   its   use   yet   ?   ❞

  raised   brow   curls   ,   prompting   the   elite   in   a   manner   that   spells   ❛   this   should   be   obvious   ❜.   and   yet   ,   the   questions   persist   ,   coaxing   a   launch   of   spaced   out   sighs   ,   but   the   doctor   answers   nevertheless.   ❝   it   proves   plenty   ,   gambler.   i   should   assign   you   to   not   only   completing   this   section   in   your   book   ,   that   you   must   take   greater   care   of   ,   but   i   should   also   task   you   to   understand   its   application   in   your   daily   conventions.   ❞

  finality   falls   in   his   next   conviction   ,   with   piercing   gaze   to   deter   the   director   from   bothering   any   longer.   since   ,   well   ,   they   both   have   more   pressing   matters   to   attend.   ❝   to   correct   you   ,   not   all   foam   is   white.   however   ,   in   the   case   you   speak   of   ,   the   froth   is   white   due   to   light   refraction.   since   it   is   made   of   bubbles   ,   which   are   pockets   of   air   ,   light   that   enters   must   pass   through   a   number   of   surfaces   ,   which   scatter   it   in   different   directions   that   produces   this   white   colour.   ❞

  certainly   ,   this   must   sate   the   liquidation   specialist.   though   ,   if   not   ,   he   has   no   more   minutes   left   to   spare.

[govindhtech]

Quantum Recurrent Embedding Neural Networks Approach

Quantum Recurrent Embedding Neural Network

Trainability issues as network depth increases are a common challenge in finding scalable machine learning models for complex physical systems. Researchers have developed a novel approach dubbed the Quantum Recurrent Embedding Neural Network (QRENN) to overcome these limitations with its unique architecture and strong theoretical foundations.

Mingrui Jing, Erdong Huang, Xiao Shi, and Xin Wang from the Hong Kong University of Science and Technology (Guangzhou) Thrust of Artificial Intelligence, Information Hub and Shengyu Zhang from Tencent Quantum Laboratory made this groundbreaking finding. As detailed in the article “Quantum Recurrent Embedding Neural Network,” the QRENN can avoid “barren plateaus,” a common and critical difficulty in deep quantum neural network training when gradients rapidly drop. Additionally, the QRENN resists classical simulation.

The QRENN uses universal quantum circuit designs  and ResNet's fast-track paths for deep learning. Maintaining a sufficient “joint eigenspace overlap,” which assesses the closeness between the input quantum state and the network's internal feature representations, enables trainability. The persistence of overlap has been proven by dynamical Lie algebra researchers.

Applying QRENN to Hamiltonian classification, namely identifying symmetry-protected topological (SPT) phases of matter, has proven its theoretical design. SPT phases are different states of matter with significant features, making them hard to identify in condensed matter physics. The QRENN's ability to categorise Hamiltonians and recognise topological phases shows its utility in supervised learning.

Numerical tests demonstrate that the QRENN can be trained as the quantum system evolves. This is crucial for tackling complex real-world challenges. In simulations with a one-dimensional cluster-Ising Hamiltonian, overlap decreased polynomially as system size increased instead of exponentially. This shows that the network may maintain gradients during training, avoiding the vanishing gradient issue of many QNN architectures.

This paper solves a significant limitation in quantum machine learning by establishing the trainability of a certain QRENN architecture. This allows for more powerful and scalable quantum machine learning models. Future study will examine QRENN applications in financial modelling, drug development, and materials science. Researchers want to improve training algorithms and study unsupervised and reinforcement learning with hybrid quantum-classical algorithms that take advantage of both computing paradigms.

Quantum Recurrent Embedding Neural Network with Explanation (QRENN) provides more information.

Quantum machine learning (QML) has advanced with the Quantum Recurrent Embedding Neural Network (QRENN), which solves the trainability problem that plagues deep quantum neural networks.

Challenge: Barren Mountains Conventional quantum neural networks (QNNs) often experience “barren plateau” occurrences. As system complexity or network depth increase, gradients needed for network training drop exponentially. Vanishing gradients stop learning, making it difficult to train large, complex QNNs for real-world applications.

The e Solution and QRENN Foundations Two major developments by QRENN aim to improve trainability and prevent arid plateaus:

General quantum circuit designs and well-known deep learning algorithms, especially ResNet's fast-track pathways (residual networks), inspired its creation. ResNets are notable for their effective training in traditional deep learning because they use “skip connections” to circumvent layers.

Joint Eigenspace Overlap: QRENN's trainability relies on its large “joint eigenspace overlap”. Overlap refers to the degree of similarity between the input quantum state and the network's internal feature representations. By preserving this overlap, QRENN ensures gradients remain large. This preservation is rigorously shown using dynamical Lie algebras, which are fundamental for analysing quantum circuit behaviour and characterising physical system symmetries.

Architectural details of CV-QRNN When information is represented in continuous variables (qumodes) instead of discrete qubits, the Continuous-Variable Quantum Recurrent Neural Network (CV-QRNN) functions.

Inspired by Vanilla RNN: The CV-QRNN design is based on the vanilla RNN architecture, which processes data sequences recurrently. The no-cloning theorem prevents classical RNN versions like LSTM and GRU from being implemented on a quantum computer, however CV-QRNN modifies the fundamental RNN notion.

A single quantum layer (L) affects n qumodes in CV-QRNN. First, qumodes are created in vacuum.

Important Quantum Gates: The network processes data via quantum gates:

By acting on a subset of qumodes, displacement gates (D) encode classical input data into the quantum network. Squeezing Gates (S): Give qumodes complicated squeeze parameters.

Multiport Interferometers (I): They perform complex linear transformations on several qumodes using beam splitters and phase shifters.

Nonlinearity by Measurement: CV-QRNN provides machine learning nonlinearity using measurements and a quantum system's tensor product structure. After processing, some qumodes (register modes) are transferred to the next iteration, while a subset (input modes) undergo a homodyne measurement and are reset to vacuum. After scaling by a trainable parameter, this measurement's result is input for the next cycle.

Performance and Advantages

According to computer simulations, CV-QRNN trained 200% faster than a traditional LSTM network. The former obtained ideal parameters (cost function ≤ 10⁻⁵) in 100 epochs, while the later took 200. Due to the massive processing power and energy consumption of big classical machine learning models, faster training is necessary.

Scalability: The QRENN can be trained as the quantum system grows, which is crucial for practical use. As system size increases, joint eigenspace overlap reduces polynomially, not exponentially.

Task Execution:

Classifying Hamiltonians and detecting symmetry-protected topological phases proves its utility in supervised learning.

Time Series Prediction and Forecasting: CV-QRNN predicted and forecast quasi-periodic functions such the Bessel function, sine, triangle wave, and damped cosine after 100 epochs.

MNIST Image Classification: Classified handwritten digits like “3” and “6” with 85% accuracy. The quantum network learnt, even though a classical LSTM had fewer epochs and 93% accuracy for this job.

CV-QRNN can be implemented using commercial room-temperature quantum-photonic hardware. This includes powerful homodyne detectors, lasers, beam splitters, phase shifters, and squeezers. Strong Kerr-type interactions are difficult to generate, but nonlinearity measurement eliminates them.

Future research will study how QRENN can be applied to more complex problems, such as financial modelling, medical development, and materials science. We'll also investigate its unsupervised and reinforcement learning potential and develop more efficient and scalable training algorithms.

Research on hybrid quantum-classical algorithms is vital. Next, test these models on quantum hardware instead of simulators. Researchers also seek to evaluate CV-QRNN performance using complex real-world data like hurricane strength and establish more equal frameworks for comparing conventional and quantum networks, such as effective dimension based on quantum Fisher information.

[ncogofficial]

Post Quantum Algorithm: Securing the Future of Cryptography

Can current encryption meet the quantum future? With the entry of quantum computing, classical encryption techniques are under the immediate threat of compromise. There has come a new age with the post quantum algorithm as a vital solution. Having the capability to shield data from being vulnerable to quantum attacks, this fascinating technology promises digital security for the future decades. Different from classic crypto schemes, such algorithms resist even sophisticated quantum attacks. But how do they work, and why are they important? In this article, we’ll explore how post-quantum algorithms are reshaping the cybersecurity landscape — and what it means for the future of encryption.

What is a Post Quantum Algorithm?

A post quantum algorithm is an encryption technique implemented to secure sensitive information from the vast processing power of quantum computers. In contrast to the classic encryption method, which can be cracked using the help of algorithms like Shor’s by quantum computers, this new method takes advantage of maths problems that are difficult for both quantum and classical systems to calculate. Quantum computers employ qubits to process information at new rates, endangering the current state of encryption, such as RSA or ECC.

To counter this, post-quantum solutions employ methods such as lattice-based encryption, code-based cryptography, and hash-based signatures. These are long-term security frameworks that keep data safe, even when there are vast numbers of quantum computers available for cryptographic algorithms.

Why We Need Post Quantum Algorithms Today

Although quantum computers are not yet available, post-quantum implementation of the algorithms in the initial stages is unavoidable. Encryption is not for today — it’s for tomorrow’s data too. A cyberthief will tap encrypted data today and crack it when there’s quantum technology in the future.

The application of a post quantum algorithm nowadays assures long-term secure information protection. Government agencies, banks, and medical providers are already transitioning to quantum-resistant systems.

Types of Post Quantum Algorithms

There are various kinds of post quantum algorithms, and each one has special strengths-

Lattice-based Cryptography: Lattice-based cryptography holds most hope. It relies on lattice problems upon which to build security that even a highly capable quantum computer possesses no way of solving quickly. They do digital signatures and encryption, and are relatively fast. They are quite general, hence are in line for standardization.

Hash-based Cryptography: Hash-based cryptography is primarily digital signature-based. They enjoy the security of traditional cryptographic hash functions and are safe against known quantum attacks. Very secure and grown-up, but generally not employed for encryption due to their size and slow performance, these schemes are only suitable to protect firmware and software patches.

Multivariate Polynomial Cryptography: Multivariate Polynomial Cryptography: Multivariate polynomial cryptography consists of complex mathematical equations involving numerous variables. They provide compact signature generation and verification, which is advantageous in resource-limited settings such as embedded systems.

Code-based Cryptography: Code-based cryptography research has been conducted for many decades and employs error-correcting codes for encrypting and protecting information. It provides very good security against quantum attacks and is particularly suitable for encryption applications. Although code-based cryptosystems have large public key sizes, their long history of resistance makes them a popular selection for protecting information in the long term.

How Post-Quantum Algorithms Work

A post quantum algorithm relies on the concept of using mathematical problems that are hard to break through quantum computers. They are resistant to both classical and quantum attacks. One of them, lattice-based cryptography, uses vectors in high-dimensional space. It is still very hard to solve the lattice problems even for highly powerful quantum processors.

All of the suggested algorithms test extensively for performance, key size, and resistance against any known quantum attacks. The National Institute of Standards and Technology (NIST) coordinates the worldwide effort in testing and standardizing the algorithms. They will work on new cryptographic systems used to replace current systems that are vulnerable and offer long-term security of information in a world where quantum computers are readily available and extremely powerful.

Real-World Applications of Post-Quantum Algorithms

Post quantum algorithm application is not a theory. Many companies have already started using them-

Finance: Organisations in the finance sector employ quantum-resistant cryptography to protect confidential financial transactions and customer data. Financial information is confidential for decades, and quantum-safe encryption protects it from hacking in the future. Banks and payment processors are piloting and implementing post-quantum approaches into core security solutions.

Healthcare: The integrity and confidentiality of medical records form the basis of the healthcare business. Healthcare organizations and hospitals have been using quantum-secure encryption to secure patients’ data for decades. Health information is retained for many years, and post-quantum methods provide guarantees that such information will not be vulnerable to future computing breakthroughs.

Government: Government departments manage national security information that may be useful for many decades. Therefore, they are leading the adoption of post-quantum technologies, primarily for secure communication and sensitive documents. Military, intelligence, and diplomatic operations are investing in quantum-resistant technologies to prepare for the future.

Cloud Services: Cloud service providers deploy Quantum-resistant encryption. As cloud infrastructure is responsible for everything from document storage to software services, they have to ensure data protection both in transit and at rest. Cloud giants are experimenting with hybrid approaches that involve classical and post-quantum encryption to protect data even further.

Post Quantum Security in the Modern World

Security does not only mean encrypting information; it means expecting it. That is where post quantum security comes in. With billions of devices connected and more data exchanges taking place, organizations need to think ahead. One quantum attack will reveal millions of records. Adopting a post-quantum algorithm today, companies construct tomorrow-proof resilience.

Transitioning to Post Quantum Algorithms: Challenges Ahead

The transition to a post quantum algorithm presents a sequence of challenges for contemporary organizations. The majority of today’s digital architectures depend on outdated encryption algorithms such as RSA or ECC. Replacing those systems with quantum-resistant technology requires a lot of time, capital, and extensive testing. Post-quantum techniques have greater key lengths and increased computational overhead, affecting performance, particularly on outdated hardware.

To control this transition, companies have to start with proper risk analysis. Companies have to tag the systems handling sensitive or long-term data and have them upgraded initially. Having a clear migration timeline guarantees the process will be seamless. With early execution and adopting hybrid cryptography, companies can phase their systems gradually while being in advance of the quantum attack without sacrificing the security level.

Governments and Global Efforts Toward Quantum Safety

Governments across the globe are actively engaging in countering quantum computing risks. Governments recognize that tomorrow’s encryption must be quantum-resistant. Organizations such as the National Institute of Standards and Technology (NIST) spearhead initiatives globally by conducting the Post-Quantum Cryptography Standardization Process. The process is to identify the best post quantum algorithm to implement worldwide.

Parallely, nations finance research, sponsor academic research, and engage with private technology companies to develop quantum-resistant digital infrastructures. For the effectiveness of these breakthroughs, global cooperation is necessary. Governments need to collaborate in developing transparent policies, raising awareness, and providing education on quantum-safe procedures. These steps will determine the future of secure communications and data protection.

Understanding Post Quantum Encryption Technologies

Post quantum encryption employs post-quantum-resistant methods to encrypt digital information. This is in conjunction with a post quantum algorithm, which protects encrypted information such that no individual, even quantum computers, can access it. Whether it is emails, financial data, or government documents being protected, encryption is an essential aspect of data protection. Companies embracing quantum encryption today will be tomorrow’s leaders.

The Evolution of Cryptography with Post Quantum Cryptography

Post quantum cryptography is the future of secure communication. Traditional cryptographic systems based on problems like factorization are no longer efficient. Post quantum algorithm…

[xaltius]

Beyond the Buzzword: Your Roadmap to Gaining Real Knowledge in Data Science

Data science. It's a field bursting with innovation, high demand, and the promise of solving real-world problems. But for newcomers, the sheer breadth of tools, techniques, and theoretical concepts can feel overwhelming. So, how do you gain real knowledge in data science, moving beyond surface-level understanding to truly master the craft?

It's not just about watching a few tutorials or reading a single book. True data science knowledge is built on a multi-faceted approach, combining theoretical understanding with practical application. Here’s a roadmap to guide your journey:

1. Build a Strong Foundational Core

Before you dive into the flashy algorithms, solidify your bedrock. This is non-negotiable.

Mathematics & Statistics: This is the language of data science.

Linear Algebra: Essential for understanding algorithms from linear regression to neural networks.

Calculus: Key for understanding optimization algorithms (gradient descent!) and the inner workings of many machine learning models.

Probability & Statistics: Absolutely critical for data analysis, hypothesis testing, understanding distributions, and interpreting model results. Learn about descriptive statistics, inferential statistics, sampling, hypothesis testing, confidence intervals, and different probability distributions.

Programming: Python and R are the reigning champions.

Python: Learn the fundamentals, then dive into libraries like NumPy (numerical computing), Pandas (data manipulation), Matplotlib/Seaborn (data visualization), and Scikit-learn (machine learning).

R: Especially strong for statistical analysis and powerful visualization (ggplot2). Many statisticians prefer R.

Databases (SQL): Data lives in databases. Learn to query, manipulate, and retrieve data efficiently using SQL. This is a fundamental skill for any data professional.

Where to learn: Online courses (Xaltius Academy, Coursera, edX, Udacity), textbooks (e.g., "Think Stats" by Allen B. Downey, "An Introduction to Statistical Learning"), Khan Academy for math fundamentals.

2. Dive into Machine Learning Fundamentals

Once your foundation is solid, explore the exciting world of machine learning.

Supervised Learning: Understand classification (logistic regression, decision trees, SVMs, k-NN, random forests, gradient boosting) and regression (linear regression, polynomial regression, SVR, tree-based models).

Unsupervised Learning: Explore clustering (k-means, hierarchical clustering, DBSCAN) and dimensionality reduction (PCA, t-SNE).

Model Evaluation: Learn to rigorously evaluate your models using metrics like accuracy, precision, recall, F1-score, AUC-ROC for classification, and MSE, MAE, R-squared for regression. Understand concepts like bias-variance trade-off, overfitting, and underfitting.

Cross-Validation & Hyperparameter Tuning: Essential techniques for building robust models.

Where to learn: Andrew Ng's Machine Learning course on Coursera is a classic. "Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow" by Aurélien Géron is an excellent practical guide.

3. Get Your Hands Dirty: Practical Application is Key!

Theory without practice is just information. You must apply what you learn.

Work on Datasets: Start with well-known datasets on platforms like Kaggle (Titanic, Iris, Boston Housing). Progress to more complex ones.

Build Projects: Don't just follow tutorials. Try to solve a real-world problem from start to finish. This involves:

Problem Definition: What are you trying to predict/understand?

Data Collection/Acquisition: Where will you get the data?

Exploratory Data Analysis (EDA): Understand your data, find patterns, clean messy parts.

Feature Engineering: Create new, more informative features from existing ones.

Model Building & Training: Select and train appropriate models.

Model Evaluation & Tuning: Refine your model.

Communication: Explain your findings clearly, both technically and for a non-technical audience.

Participate in Kaggle Competitions: This is an excellent way to learn from others, improve your skills, and benchmark your performance.

Contribute to Open Source: A great way to learn best practices and collaborate.

4. Specialize and Deepen Your Knowledge

As you progress, you might find a particular area of data science fascinating.

Deep Learning: If you're interested in image recognition, natural language processing (NLP), or generative AI, dive into frameworks like TensorFlow or PyTorch.

Natural Language Processing (NLP): Understanding text data, sentiment analysis, chatbots, machine translation.

Computer Vision: Image recognition, object detection, facial recognition.

Time Series Analysis: Forecasting trends in data that evolves over time.

Reinforcement Learning: Training agents to make decisions in an environment.

MLOps: The engineering side of data science – deploying, monitoring, and managing machine learning models in production.

Where to learn: Specific courses for each domain on platforms like deeplearning.ai (Andrew Ng), Fast.ai (Jeremy Howard).

5. Stay Updated and Engaged

Data science is a rapidly evolving field. Lifelong learning is essential.

Follow Researchers & Practitioners: On platforms like LinkedIn, X (formerly Twitter), and Medium.

Read Blogs and Articles: Keep up with new techniques, tools, and industry trends.

Attend Webinars & Conferences: Even virtual ones can offer valuable insights and networking opportunities.

Join Data Science Communities: Online forums (Reddit's r/datascience), local meetups, Discord channels. Learn from others, ask questions, and share your knowledge.

Read Research Papers: For advanced topics, dive into papers on arXiv.

6. Practice the Art of Communication

This is often overlooked but is absolutely critical.

Storytelling with Data: You can have the most complex model, but if you can't explain its insights to stakeholders, it's useless.

Visualization: Master tools like Matplotlib, Seaborn, Plotly, or Tableau to create compelling and informative visualizations.

Presentations: Practice clearly articulating your problem, methodology, findings, and recommendations.

The journey to gaining knowledge in data science is a marathon, not a sprint. It requires dedication, consistent effort, and a genuine curiosity to understand the world through data. Embrace the challenges, celebrate the breakthroughs, and remember that every line of code, every solved problem, and every new concept learned brings you closer to becoming a truly knowledgeable data scientist. What foundational skill are you looking to strengthen first?

[alicemark0087]

ACT Math Practice Tips for Mastering Every Section

The ACT Math section can feel like a high-pressure sprint: 60 questions in 60 minutes, covering everything from basic arithmetic to trigonometry. Whether you’re a math whiz or someone who breaks into a sweat at the sight of equations, strategic ACT Math practice is the key to boosting your confidence and score. This guide will walk you through the test’s structure, the topics you need to master, actionable strategies, and the best resources to help you prepare—without any fluff or sales pitches. Let’s dive in!

Understanding the ACT Math Section: What You’re Up Against

The ACT Math test is a 60-minute, 60-question marathon designed to assess skills you’ve learned up to the start of 12th grade. It’s multiple-choice, calculators are allowed (with some restrictions), and there’s no penalty for guessing—so always answer every question! Here’s what you need to know about the content and structure:

Content Breakdown

The test focuses on six core areas, weighted by approximate percentage:

Pre-Algebra (20–25%) involves fractions, ratios, percentages, and basic number operations. These topics form the foundation of many questions on the test.

Elementary Algebra (15–20%) covers solving linear equations, inequalities, and simplifying expressions. A strong grasp of these concepts is essential for handling more complex algebraic problems.

Intermediate Algebra (15–20%): includes quadratic equations, functions, and systems of equations. This section tests your ability to solve more advanced equations and interpret complex algebraic relationships.

Coordinate Geometry (15–20%) focuses on graphing lines, circles, and understanding slopes and distance formulas. Mastering these concepts is key to solving geometry problems on the coordinate plane.

Plane Geometry (20–25%) involves the properties of shapes, angles, and geometric proofs. Understanding these concepts is essential for geometry-based questions on the test.

Trigonometry (5–10%) involves right triangles, sine/cosine/tangent functions, and basic trigonometric identities. While this section is smaller, it's still important to understand these concepts well.

You’ll also receive three subscores (Pre-Algebra/Elementary Algebra, Intermediate Algebra/Coordinate Geometry, and Plane Geometry/Trigonometry), which help pinpoint strengths and weaknesses.

Key Logistics

No formula sheet: You won’t get a formula sheet, so make sure to memorize essential formulas like the quadratic formula and the area of a circle before the test.

Calculator policy: Most graphing calculators are allowed, but avoid models with a computer algebra system (CAS). Double-check your calculator ahead of time to ensure it meets ACT guidelines.

Pacing: Aim for one minute per question. Prioritize easier problems first, quickly solving them and returning to more difficult ones later to maximize your score.

Key Topics to Focus On During ACT Math Practice

While the ACT covers a broad range of math concepts, certain topics appear frequently. Here’s what to prioritize:

Pre-Algebra & Elementary Algebra

These foundational topics make up nearly 40% of the test. Focus on:

Word problems involving ratios, percentages, and proportions, which are often framed in real-life scenarios.

Solving linear equations and inequalities, with an emphasis on real-world contexts such as determining the cost of items after tax or finding the time required for a journey.

Basic statistics, including mean, median, mode, and probability, and their applications in everyday situations like analyzing data or predicting outcomes.

Intermediate Algebra & Coordinate Geometry

These sections test your ability to solve more complex equations and interpret graphs:

Quadratic equations especially through factoring, completing the square, and applying the quadratic formula, which are essential for understanding more advanced mathematical concepts.

Functions including linear, polynomial, and logarithmic types, which are key in analyzing real-world trends such as growth patterns, financial models, and scientific data.

Graphing lines and circles, along with analyzing slopes, midpoints, and distances between points, which will test your spatial reasoning and understanding of coordinate geometry.

Plane Geometry & Trigonometry

Though trigonometry is the smallest category, it’s often the trickiest for students:

Area and volume calculations for two-dimensional and three-dimensional shapes like triangles, circles, spheres, and pyramids.

Understanding triangle properties such as the Pythagorean theorem, and the principles of similar and congruent triangles.

Basic trigonometric ratios such as sine, cosine, and tangent (SOH-CAH-TOA) along with unit circle concepts.

Top Strategies to Maximize Your Score

Knowing the content isn’t enough—you need smart test-taking tactics. Here’s how to practice effectively:

Simulate Real Test Conditions

Taking timed practice tests weekly will help build your stamina and pacing for the ACT. Using official ACT tests provides the most accurate experience and prepares you for the real exam. After each test, review your mistakes thoroughly. Reflect on whether the error was due to a calculation mistake, a misread question, or a gap in your knowledge.

Master Time-Saving Tricks

For algebra, try plugging in answer choices instead of solving from scratch. Eliminate obviously wrong answers to improve guessing odds. Use your calculator only for complex calculations, like trigonometry.

Avoid Common Pitfalls

It’s important not to over-rely on your calculator, as some problems can be solved faster mentally or with scratch work. Always double-check the units and wording of questions, especially if they involve measurements. For example, a question asking for the "radius" but giving the "diameter" is a common trap to watch out for.

The Best Resources for ACT Math Practice

You don’t need to spend a fortune to prepare well. Here are trusted free and paid tools:

Free Resources

Official ACT Practice Tests are the best for realistic questions and can be downloaded from the ACT website. Khan Academy offers free video tutorials on algebra, geometry, and trigonometry. Varsity Tutors provides diagnostic tests and concept-specific drills.

Paid Resources

The Official ACT Prep Guide includes six full-length practice tests with detailed explanations. PrepScholar offers an online course that adapts to your strengths and weaknesses. Barron’s ACT Math Workbook focuses on problem-solving strategies and high-yield topics.

Pro Tip: Build a Study Schedule

Start early with 2–3 months of consistent practice. Mix content review with practice tests, spending about 30% on learning concepts and 70% on applying them. Track progress weekly to note improvements in speed and accuracy.

Final Thoughts: Turning Practice Into Progress

The ACT Math section isn’t about being a human calculator—it’s about strategy, pacing, and knowing where to focus your energy. By targeting high-impact topics, practicing under timed conditions, and using mistakes as learning tools, you’ll build the skills to tackle even the toughest questions. Remember, consistency is key: Even 20–30 minutes of daily practice can lead to significant improvements. Now grab that calculator, hit the books, and get ready to crush this test!

[renatoferreiradasilva]

Research Problem: Construction and Validation of a Spectral Operator for the Riemann Hypothesis Integrating Quantum Computing, Machine Learning, and Differential Methods

General Description

The Riemann Hypothesis (RH) states that all nontrivial zeros of the Riemann zeta function have a real part equal to ( \frac{1}{2} ). The Hilbert-Pólya conjecture suggests that these zeros correspond to the eigenvalues of a Hermitian operator ( H ). The central challenge is to explicitly construct a differential operator ( H ) whose eigenvalues align with the zeros of the zeta function, ensuring that it is self-adjoint and statistically compatible with Random Matrix Theory (RMT).

Previous studies indicate that 12th-order differential operators, adjusted via polynomial interpolation, can generate eigenvalues consistent with the zeros of the Riemann zeta function. However, fundamental questions remain unresolved:

Mathematical justification for the choice of the differential order of the operator.

Formal proof of the self-adjointness of ( H ) in a suitable functional space.

Refinement of the potential function ( V(x) ) to ensure higher spectral precision.

Generalization of the model to ( L )-automorphic functions.

Development of a robust computational framework for large-scale validation.

This research problem seeks to integrate quantum computing, machine learning, and advanced spectral methods to address these issues and significantly advance the formulation of a spectral model for the RH.

Objectives of the Problem

The objective is to construct, validate, and test a spectral operator ( H ) that models the zeros of the zeta function, ensuring:

Mathematical Construction of the Operator ( H )

Rigorously determine the differential order of the operator and justify the theoretical choice.

Explore alternatives such as pseudo-differential operators for greater flexibility.

Formalize the Hermitian and self-adjoint properties of ( H ) using functional analysis.

Refinement of the Potential ( V(x) )

Move beyond pure polynomial interpolation and integrate hybrid methods such as:

Fourier-Wavelet transformations to capture local spectral structures.

Deep learning (neural networks) for iterative refinement of ( V(x) ).

Quantum Variational Methods to minimize deviations between eigenvalues and zeta function zeros.

Statistical Validation and RMT Comparison

Test whether the eigenvalues of ( H ) follow the distribution of the Gaussian Unitary Ensemble (GUE).

Apply statistical tests such as Kolmogorov-Smirnov, Anderson-Darling, and two-point correlation analysis.

Expand computational testing to ( 10^{12} ) zeros of the zeta function.

Generalization and Applications

Extend the methodology to ( L )-automorphic functions and investigate similar patterns.

Explore connections with noncommutative geometry and quantum spectral theory.

Implement a scalable computational model using parallel computing and GPUs.

Formulation of the Problem

Given a differential operator of order ( n ):

[ H = -\frac{d^n}{dx^n} + V(x), ]

where ( V(x) ) is an adjustable potential, we seek to answer the following questions:

What is the optimal choice of ( n ) that provides the best approximation to the zeros of the zeta function?

Evaluate different differential orders (( n=4,6,8,12,16 )).

Test pseudo-differential operators such as ( H = |\nabla|^\alpha + V(x) ).

Can the operator ( H ) be rigorously proven to be self-adjoint?

Demonstrate that ( H ) is Hermitian and defined in an appropriate Hilbert space.

Use the Kato-Rellich theorem to ensure ( H ) has a real spectrum.

How can the refinement of the potential ( V(x) ) be improved to better capture the zeta zeros?

Apply neural networks to optimize ( V(x) ) dynamically.

Use Fourier-Wavelet methods to smooth out spurious oscillations.

Do the eigenvalues of ( H ) statistically follow the GUE distribution?

Apply rigorous statistical tests to validate the hypothesis.

Can the model be generalized to other ( L )-automorphic functions?

Extend the approach to different ( L )-functions.

Methodology

The solution to this problem will be structured into four phases:

Phase 1: Construction and Justification of the Operator ( H )

Mathematical modeling of the differential operator and exploration of alternatives.

Theoretical demonstration of self-adjointness and Hermitian properties.

Definition of the appropriate functional domain for ( H ).

Phase 2: Refinement of the Potential ( V(x) )

Development of a hybrid model for ( V(x) ) using:

Polynomial interpolation + Fourier-Wavelet analysis.

Machine Learning for adaptive refinement.

Quantum Variational Methods for spectral optimization.

Phase 3: Computational and Statistical Validation

Computational implementation for calculating the eigenvalues of ( H ).

Comparison with zeta function zeros up to ( 10^{12} ).

Application of statistical tests to verify adherence to GUE.

Phase 4: Generalization and Applications

Testing for ( L )-automorphic functions.

Exploring connections with noncommutative geometry.

Developing a scalable computational framework.

Expected Outcomes

Mathematical formalization of the operator ( H ), proving its Hermitian and self-adjoint properties.

Optimization of the potential ( V(x) ) through refinement via machine learning and quantum methods.

Statistical confirmation of the adherence of eigenvalues to the GUE, strengthening the Hilbert-Pólya conjecture.

Expansion of the methodology to other ( L )-automorphic functions.

Development of a scalable computational model, allowing large-scale validation.

Conclusion

This research problem unifies all previous approaches and introduces new computational and mathematical elements to advance the study of the Riemann Hypothesis. The combination of spectral theory, machine learning, quantum computing, and random matrix statistics offers an innovative path to investigate the structure of prime numbers and possibly resolve one of the most important problems in mathematics.

If this approach is successful, it could represent a significant breakthrough in the spectral proof of the Riemann Hypothesis, while also opening new frontiers in mathematics, quantum physics, and computational science.

[drmikewatts]

Soft Computing, Volume 29, Issue 1, January 2025

1) KMSBOT: enhancing educational institutions with an AI-powered semantic search engine and graph database

Author(s): D. Venkata Subramanian, J. ChandraV. Rohini

Pages: 1 - 15

2) Stabilization of impulsive fuzzy dynamic systems involving Caputo short-memory fractional derivative

Author(s): Truong Vinh An, Ngo Van Hoa, Nguyen Trang Thao

Pages: 17 - 36

3) Application of SaRT–SVM algorithm for leakage pattern recognition of hydraulic check valve

Author(s): Chengbiao Tong, Nariman Sepehri

Pages: 37 - 51

4) Construction of a novel five-dimensional Hamiltonian conservative hyperchaotic system and its application in image encryption

Author(s): Minxiu Yan, Shuyan Li

Pages: 53 - 67

5) European option pricing under a generalized fractional Brownian motion Heston exponential Hull–White model with transaction costs by the Deep Galerkin Method

Author(s): Mahsa Motameni, Farshid Mehrdoust, Ali Reza Najafi

Pages: 69 - 88

6) A lightweight and efficient model for botnet detection in IoT using stacked ensemble learning

Author(s): Rasool Esmaeilyfard, Zohre Shoaei, Reza Javidan

Pages: 89 - 101

7) Leader-follower green traffic assignment problem with online supervised machine learning solution approach

Author(s): M. Sadra, M. Zaferanieh, J. Yazdimoghaddam

Pages: 103 - 116

8) Enhancing Stock Prediction ability through News Perspective and Deep Learning with attention mechanisms

Author(s): Mei Yang, Fanjie Fu, Zhi Xiao

Pages: 117 - 126

9) Cooperative enhancement method of train operation planning featuring express and local modes for urban rail transit lines

Author(s): Wenliang Zhou, Mehdi Oldache, Guangming Xu

Pages: 127 - 155

10) Quadratic and Lagrange interpolation-based butterfly optimization algorithm for numerical optimization and engineering design problem

Author(s): Sushmita Sharma, Apu Kumar Saha, Saroj Kumar Sahoo

Pages: 157 - 194

11) Benders decomposition for the multi-agent location and scheduling problem on unrelated parallel machines

Author(s): Jun Liu, Yongjian Yang, Feng Yang

Pages: 195 - 212

12) A multi-objective Fuzzy Robust Optimization model for open-pit mine planning under uncertainty

Author(s): Sayed Abolghasem Soleimani Bafghi, Hasan Hosseini Nasab, Ali reza Yarahmadi Bafghi

Pages: 213 - 235

13) A game theoretic approach for pricing of red blood cells under supply and demand uncertainty and government role

Author(s): Minoo Kamrantabar, Saeed Yaghoubi, Atieh Fander

Pages: 237 - 260

14) The location problem of emergency materials in uncertain environment

Author(s): Jihe Xiao, Yuhong Sheng

Pages: 261 - 273

15) RCS: a fast path planning algorithm for unmanned aerial vehicles

Author(s): Mohammad Reza Ranjbar Divkoti, Mostafa Nouri-Baygi

Pages: 275 - 298

16) Exploring the selected strategies and multiple selected paths for digital music subscription services using the DSA-NRM approach consideration of various stakeholders

Author(s): Kuo-Pao Tsai, Feng-Chao Yang, Chia-Li Lin

Pages: 299 - 320

17) A genomic signal processing approach for identification and classification of coronavirus sequences

Author(s): Amin Khodaei, Behzad Mozaffari-Tazehkand, Hadi Sharifi

Pages: 321 - 338

18) Secure signal and image transmissions using chaotic synchronization scheme under cyber-attack in the communication channel

Author(s): Shaghayegh Nobakht, Ali-Akbar Ahmadi

Pages: 339 - 353

19) ASAQ—Ant-Miner: optimized rule-based classifier

Author(s): Umair Ayub, Bushra Almas

Pages: 355 - 364

20) Representations of binary relations and object reduction of attribute-oriented concept lattices

Author(s): Wei Yao, Chang-Jie Zhou

Pages: 365 - 373

21) Short-term time series prediction based on evolutionary interpolation of Chebyshev polynomials with internal smoothing

Author(s): Loreta Saunoriene, Jinde Cao, Minvydas Ragulskis

Pages: 375 - 389

22) Application of machine learning and deep learning techniques on reverse vaccinology – a systematic literature review

Author(s): Hany Alashwal, Nishi Palakkal Kochunni, Kadhim Hayawi

Pages: 391 - 403

23) CoverGAN: cover photo generation from text story using layout guided GAN

Author(s): Adeel Cheema, M. Asif Naeem

Pages: 405 - 423

[math-journal2]

<— Unit 5: Part 3 — Unit 6 —>

Tricks

Strategy

Application Problem

Page 14

[mitchi-witch]

‘Obvious’ is the most dangerous word in mathematics. — Eric Temple Bell, Scottish mathematician

ABOUT ME

Hello everyone! I am Mitzi V. Resuello, a grade-9 student from Philippine Science High School (PSHS-CARC). Today, it is my great pleasure to share with you my Math 3 Learning Journey for the second quarter. Here, I will share my insights, advice, and most especially my journey filled with highs and lows.

QUESTION #1: HOW WOULD I DESCRIBE MY MATH 3 2ND QUARTER LEARNING JOURNEY?

Never was much of a math genius, just a normal student who gets neutral grades in Math.  Every Monday, Tuesday, and Friday or Wednesday, the class I belong to has Math in its schedule. Well, if I were to describe my Journey in Math 3 second quarter, I would say that this quarter is full of topics on a rollercoaster that is moving on broken racks. The first Long Test for this Quarter is tough like the typhoons that conquered the first half of the quarter. The topics covered in this portion have appeared to be too complex for me to carry on easily.  On the other hand, my performance for the other half of the quarter is better than the last one. For me,  the topics here are much easier compared to the last topics. I wouldn’t say that it’s easy, for me, it’s still hard. Overall, I would describe this quarter as tough as a rock like the story of Sisyphus.

QUESTION #2: WHICH TOPIC DID YOU FIND MOST ENJOYABLE? WHAT MADE IT ENJOYABLE FOR YOU? PROVIDE CLEAR IMAGES OF YOUR SOLUTIONS TO SAMPLE PROBLEMS OR EXERCISES ON THE TOPIC.

Even though this quarter has not been good for me, I would still say that I have enjoyed learning various topics. I wouldn’t include some of the lessons that I have already tackled from previous grade levels and that we “re-learned” this quarter such as the synthetic and long division of polynomials. Anyway, I enjoyed learning about piecewise functions.  I don’t know, but I enjoyed and found this lesson super fun. I guess it would have been because they’re fun to graph, you just have to familiarize yourself with what the graph of a certain function looks like.  For me, knowing the domain and range of the function based on its given conditions is really a game-changer.

Sample Problem #1:

Solution:

Sample Problem #2:

Solution:

QUESTION #3: WHAT CONCEPTS DID YOU FIND EASY TO LEARN? WHAT DO YOU THINK MADE IT EASY FOR YOU? 

As I mentioned earlier, learning about piecewise functions is enjoyable and I would say that it’s pretty much easy due to being knowledgeable of how the graph of different functions looks like. It is also a big help if you know how to get the domain and range of the function. Another concept that I found easy was step functions since I've already put into my mind that if its a floor function, the value will be rounded down, if it's a ceiling function, the value will be rounded up. 

QUESTION #4: WHAT CONCEPTS DID YOU FIND THE MOST INTERESTING /INSPIRING? WHY DO YOU THINK SO? 

The concepts I found the most inspiring is the Transformations of Functions. For me, this concept doesn't only teach us a new math information but also a life lesson on how any person will have a noticeable effect for every factor that affects them. Additionally, I find signum functions really interesting. It is very intricate but amazing at the same time. I think it's because it's kind of similar to piecewise function but the values of x just revolves around zero and it's value also centers only on a given number, the negative of that number, and zero.

QUESTION #5: WHAT CONCEPTS HAVE YOU MASTERED MOST? WHY DO YOU THINK SO?PROVIDE CLEAR IMAGES OF YOUR SOLUTIONS TO SAMPLE PROBLEMS OR EXERCISES ON THE TOPIC.

My most mastered concepts are Transformations of Functions and Piecewise Functions. I think I have mastered these concepts because I've already found the what-to-do's and what-not-to on answering these problems. These shortcuts and game-changers are applicable on any type of situations or problems in the field of these topics.

Sample Problems:

Solutions:

QUESTION #6: WHAT CONCEPTS HAVE YOU MASTERED LEAST? WHY DO YOU THINK SO?PROVIDE CLEAR IMAGES OF YOUR SOLUTIONS TO SAMPLE PROBLEMS OR EXERCISES ON THE TOPIC.

I am really struggling on the topic of Rational Zero Theorem and Descartes Rules of Signs. I think it's a really complex topic for me. I know how to factor to find the value of x but I just get really confused and empty when it comes to this topic. For me, it's because there are so many test-values that you have to try.

Sample Problem #1:

Solution:

Sample Problem #2:

Solution:

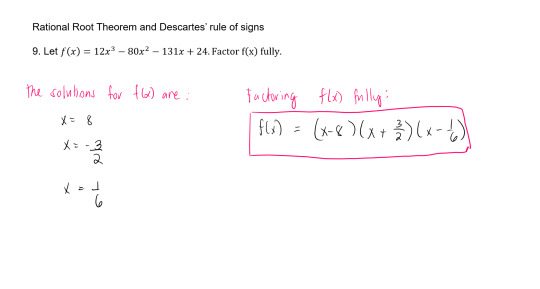
QUESTION #7: WHAT QUICK NOTES I HAVE FOR:

a. Your teacher;

For my Math 3 teacher, sir Joseph, I would say that he had accomplished on demonstrating the topics to us. He made sure that we really understood it by giving board works and individual assessments. He's really approachable and helpful.

b. Your classmates;

I think it's really inspiring that some of us are willing to help and tutor others. For me, that really shows our relationship with one another. I'd say that we should keep it up! On the other hand, I think that some of us relies too much on other people that we don't even review when there's an upcoming test because we know someone out there will teach us. Although it's good, I don't think that those amount of information that is just taught in a short span of time will be remembered throughout the whole examination.

c. Myself;

I know that this quarter isn't the best for me. I am deeply held down by a lot of setbacks but that doesn't really explain and makes up 90% of my performance, therefore, I can't blame it on external factors because it's very clear that it's on me. I don't take this as a grudge against myself but a chance for improvement and it's an opportunity for me to assess myself. The biggest piece of advice I can give to myself is to seek immediate help if I don't get the lesson. I should've never kept it for too long that it led to last-minute learning of all the concepts from the very start. I think I just tortured myself for this since I will have to focus on Math subject during exams week and I would also need to allocate a lot of time into this subject.

That ends my learning journey for Math 3 second quarter. I hope my story had inspired you and and gave you new learnings about Math 3. Thank You!

[govindhtech]

ColibriTD Launches QUICK-PDE Hybrid Solver On IBM Qiskit

ColibriTD

The  IBM Qiskit Functions Catalogue now includes ColibriTD's quantum-classical hybrid partial differential equation (PDE) solution QUICK-PDE. Based on IBM's H-DES (Hybrid Differential Equation Solver) technique, QUICK-PDE lets researchers and developers solve domain-specific multiphysics PDEs via cloud access to utility-scale quantum devices.

QUICK-PDE

QUICK-PDE was developed by quantum-powered multiphysics simulation company ColibriTD. IBM Qiskit Functions Catalogue lists it as an application function. QUICK-PDE is part of ColibriTD's QUICK platform.

The function lets researchers, developers, and simulation engineers solve multiphysics partial differential equations using IBM quantum computers in the cloud. For domain-specific partial differential equation solutions, it simplifies and makes development easier.

It works

ColibriTD's unique H-DES algorithm underpins QUICK-PDE. To solve differential equations, trial solutions are encoded as linear combinations of orthogonal functions, commonly Chebyshev polynomials. The function is encoded using $2^n$ Chebyshev polynomials, where $n$ is the number of qubits.

Variable Quantum Circuit (VQC) angles parametrise orthogonal functions.

The function is embedded in an ansatz-created state and evaluated by observable combinations that allow its assessment at any time.

Loss functions encode differential equations. By altering the VQC angles in a hybrid loop, trial solutions are brought closer to real solutions until a good result is achieved.

A solution can use many optimisers. You can chain optimisers to follow a gradient by using a global optimiser like “CMAES” (from the cma Python package) and then a fine-tuned optimiser like “SLSQP” from Scipy for the Material Deformation scenario.

Noise reduction is built into the algorithm. The noise learner strategy can mitigate noise during CMA optimisation by stacking identical circuits and assessing identical observables on various qubits within a larger circuit, reducing the number of shots needed.

Different qubits can encode each variable's function. The function may choose appropriate default values, but users can change them. The ansatz depth per function can also be changed. Adjustable variables include the number of shots needed per circuit. Since there are several optimisation processes, the shots parameter is a list whose length matches the number of optimisers used. Computational Fluid Dynamics and Material Deformation have preset shot values.

Users can choose “RANDOM” or“PHYSICALLY_INFORMED” for VQC angle initialisation. “PHYSICALLY_INFORMED” is the default and often works, but “RANDOM” can be used in other cases.

Use cases and multiphysics capabilities

QUICK-PDE solves complex multiphysics problems. We cover two key use cases:

Computational fluid dynamics

The inviscid Burgers' equation and fundamental CFD model are issues. This equation simulates non-viscous fluid flow and shockwave propagation for automotive and aerospace applications.

The Navier-Stokes equations for fluid motion have an inviscid Burgers' equation at zero viscosity ($\nu = 0$). $fracpartial upartial t + ufracpartial upartial x = 0$1117, where $u(x,t)$ is the fluid speed field

When $a$ and $b$ are random constants and $u(t=0, x) = axe + b$, the current implementation only allows linear functions as initial conditions. Change these constants to see how they affect the solution.

The CFD differential equation arguments are on a fixed grid: space ($x$) between 0 and 0.95 with 0.2375 step size and time ($t$) with 30 sample points. The dynamics of new reactive fluids for heat transfer in tiny modular reactors can be studied using QUICK-PDE.

MD: Material Deformation

Second is Material Deformation (MD), which studies 1D mechanical deformation in a hypoelastic regime like a tensile test. Simulation of material stress is crucial for manufacturing and materials research.

Problem: a bar with one end dragged and one fixed. This system of equations includes a strain function ($\sigma$) and a stress function ($u$).

A surface stress boundary condition ($t$) represents the labour needed to stretch the bar in this use case.

MD differential equation arguments use a fixed grid ($x$) between 0 and 1 with a 0.04 step size.

Future versions of QUICK-PDE will include the H-DES algorithm to handle higher-dimensional problems and additional physics domains like electromagnetic simulations and heat transport.

Usability, Accessibility:

IBM Quantum Premium, Dedicated Service, and Flex Plan users can use QUICK-PDE.

The function must be requested by users.

The quantum workflow is simplified by application functions like QUICK-PDE. They use classical inputs (such physical parameters) and return domain-familiar classical outputs to make quantum approaches easier to integrate into present operations without needing to build a quantum pipeline.

This allows domain experts, data scientists, and business developers to study challenges that require HPC resources or are difficult to solve.

The function supports “job,” “session,” and “batch” execution modes. The default mode is “job”. A dictionary contains input parameters.

Use_case (“CFD” or “MD”) and physical_parameters specific to the use case (e.g., a, b for CFD; t, K, n, b, epsilon_0, sigma_0 for MD) are crucial. Users can adjust nb_qubits, depth, optimiser, shots, optimizer_options, initialisation, backend_name, and mode using optional arguments.

The function's output is a dictionary of sample points for each variable and its computed values. For instance, the CFD scenario provides u(t,x) function values and t and x samples. In MD, x samples and function values for u(x) and sigma(x) are presented. The resulting array's structure matches the variables' alphabetic sample points.

Benchmarks for Inviscid Burgers' equation and Hypoelastic 1D tensile test show statistics like qubit usage, initialisation method, error ($\approx 10^{-2}$), duration, and runtime utilisation.

A tutorial on modelling a flowing non-viscous fluid with QUICK-PDE covers setting up starting conditions, adjusting quantum hardware parameters, performing the function, and applying the results. The manual provides MD and CFD examples.

In conclusion, QUICK-PDE can be used to investigate hybrid quantum-classical algorithms for addressing complex multiphysics problems, which may enhance modelling precision and simulation time. It is a significant example of quantum value in scientific computing and a step towards opening doors previously inaccessible with regular instrumentation.

[amourion-bahrain23]

IBDP Tutoring Support: A Key to Scoring 7/7 in Functions and Equations

The International Baccalaureate Diploma Programme (IBDP) is known for its rigor and the high expectations it sets for students. One of the subjects that often presents challenges for IBDP students is Mathematics, particularly when it comes to Functions and Equations. This area of study plays a crucial role in the curriculum, and achieving a top score of 7/7 requires not only consistent effort but also the right kind of support. At Amourion Training Center, Bahrain, we believe that specialized IBDP Tutoring Support is essential for students aiming to master these concepts and achieve their highest potential.

Why Functions and Equations are Critical in IBDP Math

Functions and Equations are foundational topics in the IBDP Mathematics curriculum. Students are expected to understand a wide array of concepts, including:

Types of functions (linear, quadratic, exponential, logarithmic)

Graphical representations

Solving equations involving polynomials, rational functions, and inequalities

Applications of functions in real-world problems

These concepts not only test a student’s mathematical ability but also their problem-solving skills, logical thinking, and ability to apply mathematical principles to unfamiliar situations. As part of the IB Math SL/HL syllabus, Functions and Equations account for a significant portion of the assessment, making it crucial for students to have a strong grasp of these topics.

The Challenge: Why Many Students Struggle with Functions and Equations

Despite its importance, many IBDP students find Functions and Equations particularly challenging. There are several reasons for this:

Abstract Nature of Functions: The abstract concept of a "function" itself can be difficult for many students to grasp. Understanding how different types of functions behave, and how to manipulate equations algebraically, requires a deep level of comprehension.

Complex Problem-Solving: Solving complex equations, whether linear or non-linear, demands not just formulaic knowledge but also a strategic approach to problem-solving. The range of problems encountered can be overwhelming without proper guidance.

Time Management and Exam Pressure: With limited time during exams, students must be able to quickly recognize the most efficient approach to solving equations, a skill that comes with practice and expert guidance.

Interdisciplinary Connections: The mathematical concepts learned in Functions and Equations often connect to other subjects, such as Physics and Economics, requiring students to see the broader picture and apply mathematical knowledge in context. This integration is challenging but essential for achieving high marks.

Why IBDP Tutoring Support is Essential

To achieve a score of 7/7 in Mathematics, particularly in the area of Functions and Equations, students need personalized support that can address their specific challenges. Here’s why IBDP Tutoring is a game changer:

Personalized Instruction: Every student has different learning needs. IBDP tutors can assess the areas where a student is struggling and provide targeted lessons that focus on these weaknesses. For Functions and Equations, this could mean revisiting foundational concepts or teaching more advanced techniques to help students overcome their challenges.

Expert Guidance: IBDP tutors at Amourion Training Center are trained to help students navigate the complexity of Functions and Equations. Tutors with experience in the IBDP curriculum understand the nuances of the program and are well-equipped to explain concepts in a way that makes sense to students, ensuring they feel confident in applying these concepts during exams.

Practice and Reinforcement: One of the key elements to mastering Functions and Equations is practice. A dedicated IBDP tutor provides students with ample opportunities to work through problems, from basic to advanced, and learn the most efficient solving techniques. This regular practice helps students internalize the material and boosts their exam performance.

Strategic Exam Preparation: Achieving a 7/7 in IBDP requires not only understanding the material but also mastering the exam format. Tutors can guide students through past papers, teaching them how to identify recurring question types and develop time-saving strategies that work best for them. With effective exam preparation, students can perform confidently under time pressure.

Developing Critical Thinking: IBDP Mathematics is designed to foster critical thinking, and a skilled tutor can help students develop this skill by encouraging them to think beyond formulas and focus on the reasoning behind each step. This type of learning helps students retain information long-term and apply it effectively in both exams and real-life situations.

How Amourion Training Center Supports IBDP Students

At Amourion Training Center, Bahrain, we understand the importance of high-quality, personalized tutoring for students aiming to excel in the IBDP curriculum. Our tutors specialize in IB Mathematics and are trained to deliver targeted support in areas like Functions and Equations. Here’s how we ensure our students are prepared for success:

One-on-One Tutoring: Tailored sessions that focus on the specific areas students find challenging.

Expert Tutors: Our tutors are experienced in the IBDP syllabus and are equipped with strategies to tackle even the toughest topics.

Comprehensive Resources: We provide students with comprehensive study materials, including practice problems and mock exams, to reinforce learning.

Flexible Schedules: We understand that IBDP students have busy schedules, so we offer flexible tutoring hours to accommodate their needs.

Conclusion

In today’s competitive academic environment, scoring a 7/7 in IB Math, particularly in the area of Functions and Equations, is a significant achievement. The right IBDP tutoring support can make all the difference in helping students overcome challenges and master the material. By providing expert guidance, personalized attention, and plenty of practice, Amourion Training Center, Bahrain is committed to helping students achieve their academic goals and excel in the IBDP program.

To learn more about our IBDP tutoring services and how we can support you in mastering Functions and Equations, contact Amourion Training Center today!

[xaltius]

What Are the Regression Analysis Techniques in Data Science?

In the dynamic world of data science, predicting continuous outcomes is a core task. Whether you're forecasting house prices, predicting sales figures, or estimating a patient's recovery time, regression analysis is your go-to statistical superpower. Far from being a single technique, regression analysis encompasses a diverse family of algorithms, each suited to different data characteristics and problem complexities.

Let's dive into some of the most common and powerful regression analysis techniques that every data scientist should have in their toolkit.

1. Linear Regression: The Foundation

What it is: The simplest and most widely used regression technique. Linear regression assumes a linear relationship between the independent variables (features) and the dependent variable (the target you want to predict). It tries to fit a straight line (or hyperplane in higher dimensions) that best describes this relationship, minimizing the sum of squared differences between observed and predicted values.

When to use it: When you suspect a clear linear relationship between your variables. It's often a good starting point for any regression problem due to its simplicity and interpretability.

Example: Predicting a student's exam score based on the number of hours they studied.

2. Polynomial Regression: Beyond the Straight Line

What it is: An extension of linear regression that allows for non-linear relationships. Instead of fitting a straight line, polynomial regression fits a curve to the data by including polynomial terms (e.g., x2, x3) of the independent variables in the model.

When to use it: When the relationship between your variables is clearly curved.

Example: Modeling the trajectory of a projectile or the growth rate of a population over time.

3. Logistic Regression: Don't Let the Name Fool You!

What it is: Despite its name, Logistic Regression is primarily used for classification problems, not continuous prediction. However, it's often discussed alongside regression because it predicts the probability of a binary (or sometimes multi-class) outcome. It uses a sigmoid function to map any real-valued input to a probability between 0 and 1.

When to use it: When your dependent variable is categorical (e.g., predicting whether a customer will churn (Yes/No), if an email is spam or not).

Example: Predicting whether a loan application will be approved or denied.

4. Ridge Regression (L2 Regularization): Taming Multicollinearity

What it is: A regularization technique used to prevent overfitting and handle multicollinearity (when independent variables are highly correlated). Ridge regression adds a penalty term (proportional to the square of the magnitude of the coefficients) to the cost function, which shrinks the coefficients towards zero, but never exactly to zero.

When to use it: When you have a large number of correlated features or when your model is prone to overfitting.

Example: Predicting housing prices with many highly correlated features like living area, number of rooms, and number of bathrooms.

5. Lasso Regression (L1 Regularization): Feature Selection Powerhouse

What it is: Similar to Ridge Regression, Lasso (Least Absolute Shrinkage and Selection Operator) also adds a penalty term to the cost function, but this time it's proportional to the absolute value of the coefficients. A key advantage of Lasso is its ability to perform feature selection by driving some coefficients exactly to zero, effectively removing those features from the model.

When to use it: When you have a high-dimensional dataset and want to identify the most important features, or to create a more parsimonious (simpler) model.

Example: Predicting patient recovery time from a vast array of medical measurements, identifying the most influential factors.

6. Elastic Net Regression: The Best of Both Worlds

What it is: Elastic Net combines the penalties of both Ridge and Lasso regression. It's particularly useful when you have groups of highly correlated features, where Lasso might arbitrarily select only one from the group. Elastic Net will tend to select all features within such groups.

When to use it: When dealing with datasets that have high dimensionality and multicollinearity, offering a balance between shrinkage and feature selection.

Example: Genomics data analysis, where many genes might be correlated.

7. Support Vector Regression (SVR): Handling Complex Relationships

What it is: An adaptation of Support Vector Machines (SVMs) for regression problems. Instead of finding a hyperplane that separates classes, SVR finds a hyperplane that has the maximum number of data points within a certain margin (epsilon-tube), minimizing the error between the predicted and actual values.

When to use it: When dealing with non-linear, high-dimensional data, and you're looking for robust predictions even with outliers.

Example: Predicting stock prices or time series forecasting.

8. Decision Tree Regression: Interpretable Branching

What it is: A non-parametric method that splits the data into branches based on feature values, forming a tree-like structure. At each "leaf" of the tree, a prediction is made, which is typically the average of the target values for the data points in that leaf.

When to use it: When you need a model that is easy to interpret and visualize. It can capture non-linear relationships and interactions between features.

Example: Predicting customer satisfaction scores based on multiple survey responses.

9. Ensemble Methods: The Power of Collaboration

Ensemble methods combine multiple individual models to produce a more robust and accurate prediction. For regression, the most popular ensemble techniques are:

Random Forest Regression: Builds multiple decision trees on different subsets of the data and averages their predictions. This reduces overfitting and improves generalization.

Gradient Boosting Regression (e.g., XGBoost, LightGBM, CatBoost): Sequentially builds trees, where each new tree tries to correct the errors of the previous ones. These are highly powerful and often achieve state-of-the-art performance.

When to use them: When you need high accuracy and are willing to sacrifice some interpretability. They are excellent for complex, high-dimensional datasets.

Example: Predicting highly fluctuating real estate values or complex financial market trends.

Choosing the Right Technique

The "best" regression technique isn't universal; it depends heavily on:

Nature of the data: Is it linear or non-linear? Are there outliers? Is there multicollinearity?

Number of features: High dimensionality might favor regularization or ensemble methods.

Interpretability requirements: Do you need to explain how the model arrives at a prediction?

Computational resources: Some complex models require more processing power.

Performance metrics: What defines a "good" prediction for your specific problem (e.g., R-squared, Mean Squared Error, Mean Absolute Error)?

By understanding the strengths and weaknesses of each regression analysis technique, data scientists can strategically choose the most appropriate tool to unlock valuable insights and build powerful predictive models. The world of data is vast, and with these techniques, you're well-equipped to navigate its complexities and make data-driven decisions.

[khanncert]

NCERT Books for Class 9: A Comprehensive Guide to Building a Strong Academic Foundation

Class 9 is a crucial stage in a student’s academic journey, as it lays the foundation for higher classes and introduces more complex concepts across all subjects. The National Council of Educational Research and Training (NCERT) books are widely recognized as the primary study material for students in India, especially those enrolled in schools affiliated with the Central Board of Secondary Education (CBSE). These books are meticulously designed to provide in-depth knowledge while ensuring clarity and accessibility for students of varying abilities. This article delves into the significance of NCERT books for Class 9, their unique features, and how they contribute to academic success.

Why Are NCERT Books Important for Class 9?

NCERT books are considered the gold standard for academic study in Indian schools, and this is particularly true for Class 9. Here's why they hold such importance:

Conceptual Clarity: NCERT books emphasize a strong understanding of fundamental concepts. Rather than overloading students with unnecessary details, the content is streamlined to focus on essential ideas. This clarity is crucial in Class 9, as students encounter new topics that form the base for Class 10 and beyond.

Aligned with CBSE Curriculum: These books strictly adhere to the CBSE syllabus, ensuring that students study only what is required for their examinations. This alignment also makes NCERT books the most reliable source for CBSE board exams.

Wide Acceptance in Competitive Exams: NCERT books are highly recommended for competitive exams like JEE, NEET, and UPSC. Class 9 concepts, especially in subjects like Mathematics and Science, form a significant portion of the syllabus for these exams.

Cost-Effective and Accessible: NCERT books are affordable and widely available in print and digital formats. The NCERT’s initiative to provide free e-books on their official website has further improved access to quality education materials.

Features of NCERT Books for Class 9

Structured Presentation: The chapters in NCERT books are well-organized and presented systematically. Each chapter begins with an introduction to the topic, followed by examples, illustrations, and exercises that reinforce the concepts discussed.

Language Simplicity: The language used in NCERT books is straightforward and easy to understand. This ensures that students grasp complex concepts without feeling overwhelmed.

Inclusion of Practical Knowledge: NCERT books often provide real-life examples and applications of theoretical concepts. For instance, Science books include experiments and activities to make learning more engaging and interactive.

Illustrations and Diagrams: Visual aids like diagrams, charts, and tables are extensively used to simplify complex topics, especially in subjects like Science and Geography.

End-of-Chapter Exercises: NCERT books include a variety of questions at the end of each chapter, ranging from objective-type to descriptive questions. These exercises are crucial for exam preparation and help students test their understanding of the topics.

Subject-Wise Overview of NCERT Books for Class 9

1. Mathematics

The NCERT Mathematics book for Class 9 introduces concepts like Polynomials, Coordinate Geometry, and Linear Equations. It emphasizes problem-solving skills and logical reasoning, preparing students for advanced topics in higher classes. Each chapter includes solved examples, practice questions, and summaries for better comprehension.

2. Science

The Science textbook is divided into three sections: Physics, Chemistry, and Biology. Topics such as Motion, Atoms and Molecules, and Diversity in the Living World are presented in a simple yet engaging manner. Practical experiments and activities are included to enhance conceptual understanding.

3. Social Science

Social Science comprises History, Geography, Political Science, and Economics. The books provide a detailed exploration of topics like the French Revolution, Natural Vegetation, Electoral Politics, and Poverty as a Challenge. The use of case studies and maps makes these subjects more relatable and interesting.

4. English

The NCERT English books for Class 9, including "Beehive" and "Moments," focus on language development, comprehension, and creative writing skills. Through prose, poetry, and supplementary stories, these books encourage students to appreciate literature while improving their communication abilities.

5. Hindi and Sanskrit

For language subjects like Hindi and Sanskrit, NCERT books introduce students to grammar, vocabulary, and literary works. These books aim to strengthen linguistic skills while fostering an appreciation for India’s rich literary heritage.

Conclusion

NCERT books for Class 9 are invaluable resources that provide a solid foundation for academic success. Their focus on conceptual clarity, simplicity, and relevance ensures that students are well-prepared for both school exams and competitive exams. By thoroughly studying NCERT books and utilizing their exercises effectively, Class 9 students can achieve a deeper understanding of their subjects and build confidence for future challenges. Embracing these books as a primary study resource is a step toward academic excellence and holistic learning. Originally Published: Blogspot.com