#regular polyhedra

[dat-physics-gal]

I'm so embarrassed, i don't know if that first one is a stellated dodecahedron or a stellated icosahedron, or either of the greatenings.

One in 4, could someone tell me which one it is before i go insane?

Demiromantic defaults ✅

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 5 (Finals)

Propaganda

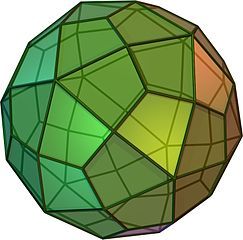
Truncated Icosidodecahedron:

Also called the Rhombitruncated Icosidodecahedron, Great Rhombicosidodecahedron, Omnitruncated Dodecahedron, Omnituncated Icosahedron

Archimedean Solid

Semiregular

Dual of the Disdyakis Triacontahedron

It has 12 regular decagonal faces, 20 regular hexagonal faces, 30 square faces, 180 edges, and 120 vertices.

It has the most edges and vertices of all platonic and archimedean solids.

Of the vertex-transitive polyhedra, it fills up the most of the volume of the sphere it fits in (89.80%).

It is not actually the shape you get when you truncate an icosidodecahedron, although it is topologically equivalent.

It is the mod's favorite three-dimensional shape.

They made a void truncated icosidodecahedron and it's glorious. I had one for a while, it's hard to turn because of alignment issues, especially the decagonal sides. Fun puzzle tho, never did figure out how to permute the last layer...

Image Credit: @anonymous-leemur

Regular Icosahedron:

Platonic Solid

Regular

Dual of the Regular Dodecahedron

It has 20 regular triangular faces, 30 edges, and 12 vertices.

Image Credit: @etirabys

[art-of-mathematics]

Quick friend-shapes needed to be made.

(meaning: I was bored and needed to do something with my hands and brain.)

[wouldyourfavepaychildsupport]

Would the mathematical set of all 18 finite regular polyhedra pay child support?

[sunless-not-sinless]

the great icosahedron is platonic! im in a qpr with it!

Hey bro would you do me a platonic solid

[flyingsoup]

Small Stellated Dodecahedron :33

[tanadrin]

I love the lists of regular polyhedra on Wikipedia

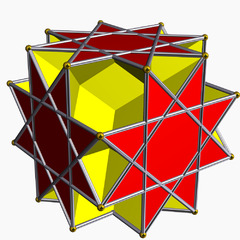
behold, the deltoidal hexecontahedron:

the great rhobihexahedron:

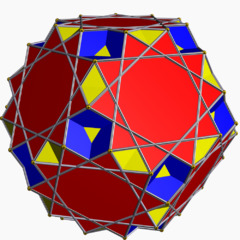
here we have the ditrigonal dodecicosidodecahedron:

the great retrosnub icosidodecahedron:

the beautiful twins, the sixteenth stellation of the icosidodecahedron, and her sister, the seventeenth stellation of same:

they look like some kind of mysterious and terrible Pokemon to me.

and lastly, her royal majesty, the final stellation of the icosahedron:

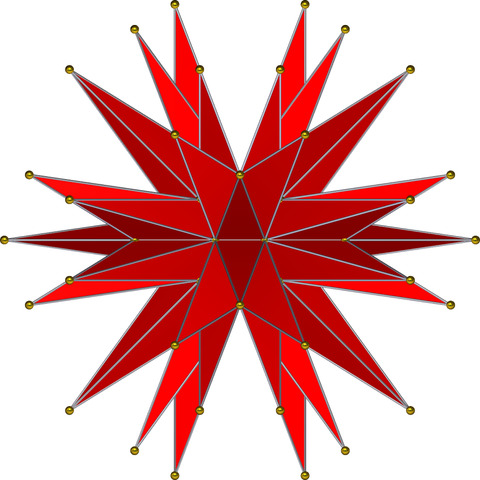
once when i was a child, i had a terrible earache that afflicted my dreams with nightmares of acute geometry. i think i saw her there, bloody and majestic, hovering above my bed.

[janmisali]

i've watched multiple of your videos and seen a few of your tumblr posts, all without knowing any of them were by the same person, and only right now are my worlds colliding. you made the 48 regular polyhedra video?? i fucking love that video it changed my life in 10th grade

oh no....... the passage of time.......

[thegneurshk]

After much study and research, I have found that the gneursk is a Great Icosahedron, which is a kepler-poinsot regular polyhedra

dat me :3

[aorish]

Realizing the etymology of the word "Elements" to refer to earth, air, water, fire, etc. is probably derived from the mathematical term that Euclid's book is titled, not the other way around.

Of course the connection between the two senses of the same Greek word (στοιχεῖον) to begin with is that the regular polyhedra, which are constructed in the final book of Euclid, are matched up with the four classical "elements" (and then messily a fifth is tacked on in what's probably a gloss) in Plato's Timaeus.

[dailypolyhedra]

Polyhedron of the Day #196: Biscribed propello dodecahedron

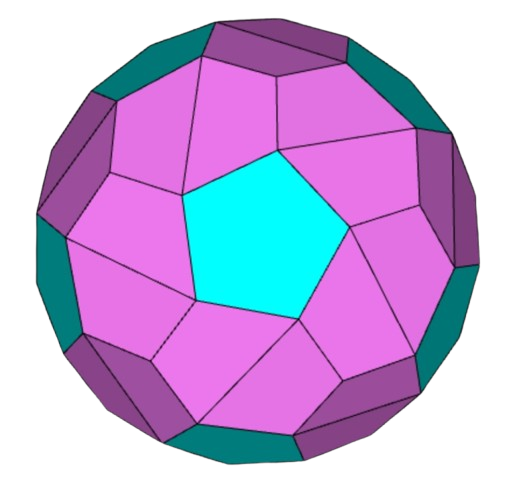
The biscribed propello dodecahedron is a convex polyhedron. It has 72 faces (60 irregular tetragons, 12 regular pentagons), 150 edges, and 80 vertices. It has chiral icosahedral symmetry. Its dual is the biscribed propello icosahedron.

Images taken as screenshots from David I. McCooey's Visual Polyhedra website.

[cheacegirl]

@foxapult aka my wonderful girlfriend (much prettier in real life!) and her accompanying Muoctahedeon form (yeah my girlfriend is an infinitely large regular polyhedra now yeah sorry yeah well she's only one piece of it but yeah sorry there's nothing we can do)

I love you so muchhhh @foxapult

Oh also huge credit to my also girlfriend @peppermints-and-lemon-zest for the drawing I used for reference, I love you as welll!!!

[best-shapes]

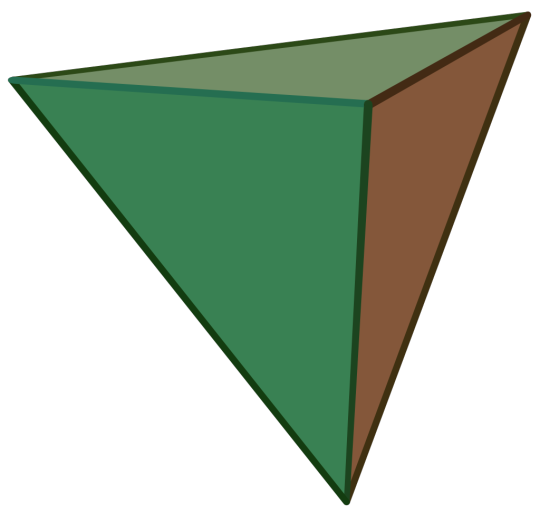
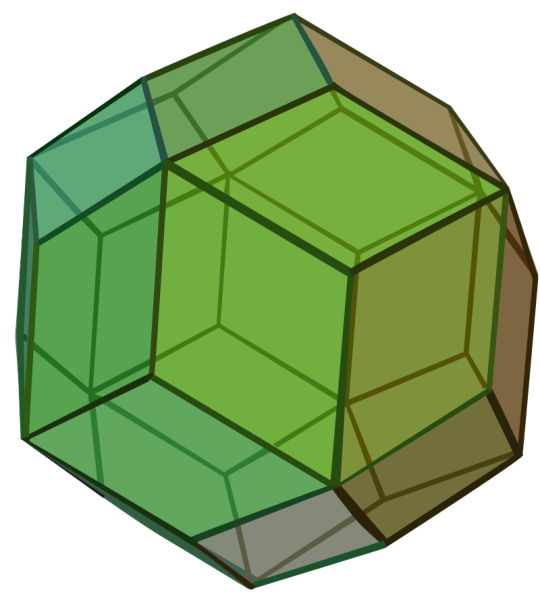
Regular-ish Convex Polyhedra Bracket — Round 3

Propaganda

Regular Tetrahedron:

Also called the Triangular Pyramid

Platonic Solid

Regular

Dual of the Regular Tetrahedron

It has 4 regular triangular faces, 6 edges, and 4 vertices.

Self-Dual

Image Credit: Cyp

Rhombic Triacontahedron:

Also called the Triacontahedron

Catalan Solid

Dual of a quasiregular polyhedron

Dual of the Icosidodecahedron

It has 30 rhombic faces, 62 edges, and 32 vertices of two types.

One of the 9 edge-transitive convex polyhedra along with the 5 Platonic Solids, the 2 Quasiregular Convex Polyhedra, and the Rhombic Dodecahedron.

Image Credit: Maxim Razin based on Cyp

[httpsoftbunni]

✧ What Are the Platonic Solids?

The Foundations of Sacred Geometry

Platonic Solids are among the most revered and significant shapes. These five perfect polyhedra not only serve as the building blocks for understanding the geometric framework of the universe but also embody deep metaphysical principles that link the material and spiritual worlds. Known to philosophers, mathematicians, and mystics alike, these solids symbolize a profound connection between form, function, and the very fabric of existence.

What are the Platonic Solids?

A Platonic Solid is a three-dimensional shape that exhibits two defining characteristics:

Identical Faces: All faces of the shape are congruent, regular polygons.

Identical Angles and Edges: All the edges and angles of the polygons are equal.

In addition to this geometrical perfection, Platonic Solids share the remarkable trait that the same number of faces meet at each vertex. The harmony between these properties makes them unique, and only five solids meet these criteria. These five solids are:

Tetrahedron – 4 triangular faces

Cube (Hexahedron) – 6 square faces

Octahedron – 8 triangular faces

Dodecahedron – 12 pentagonal faces

Icosahedron – 20 triangular faces

The Role of the Platonic Solids in the Cosmos

These solids are not only geometrically important but were also infused with profound symbolism by ancient thinkers. The most significant influence comes from Plato, the Greek philosopher who first associated these shapes with the classical elements of Earth, Water, Air, Fire, and Aether. In his dialogue Timaeus, Plato posits that the elements of the physical world are composed of these perfect shapes, each associated with a different fundamental force or substance. Plato’s integration of geometry and cosmology would have far-reaching effects on subsequent philosophical and spiritual systems.

The Platonic Solids and their elemental associations are:

Tetrahedron – Fire

Cube (Hexahedron) – Earth

Octahedron – Air

Dodecahedron – Aether (Spirit)

Icosahedron – Water

Plato believed that these shapes represented the foundational substances from which all physical reality is derived. According to him, the Tetrahedron’s sharp edges were suited to represent Fire, the Cube’s stability mirrored the solid, grounded nature of Earth, and the Icosahedron’s fluidity corresponded to Water. The Octahedron, with its balanced symmetry, represented the breath of life, Air, while the Dodecahedron, with its celestial geometry, symbolized the etheric substance that filled the heavens.

Beyond Plato: The Platonic Solids in Ancient Mysticism

While Plato may have first outlined the connections between the Platonic Solids and the elements, the belief in their metaphysical properties goes back much further. The Pythagoreans, a religious and philosophical school that preceded Plato, already recognized the mystical importance of geometry and numbers in the divine order. The Pythagoreans believed that mathematics and geometry were not just tools for understanding the physical world but were the very means by which the cosmos expressed harmony and order.

The Platonic Solids also had an important role in alchemy, theosophy, and other esoteric systems. Alchemists used these shapes in their pursuit of transmutation and spiritual transformation, believing that by understanding the geometry of the elements, they could unlock hidden truths about the soul and the universe. For example, the Dodecahedron, often referred to as the "heavenly" shape, was associated with the fifth element—the Aether—and was believed to be the shape that structured the cosmos. It was the geometric representation of the heavens themselves, the divine ether from which all things emanated.

In the context of Kabbalah, the Platonic Solids are also integrated into the teachings of sacred geometry. The Tree of Life, which serves as the primary symbol in Kabbalistic teachings, can be thought of as a geometric model composed of spheres, lines, and, notably, polyhedral shapes that mirror the Platonic Solids. These solids reflect the interaction between the spiritual and material worlds, with each solid representing a particular level of consciousness or divine emanation.

The Platonic Solids as "Sacred" Geometry

The term Sacred Geometry refers to the use of geometric shapes and proportions to symbolize spiritual truths. The Platonic Solids are considered "sacred" because of their mathematical perfection and their association with cosmic principles. In a world full of imperfect, irregular forms, the Platonic Solids stand as idealized representations of divine order.

These shapes are also seen as fundamental archetypes that govern the physical and metaphysical realms. The belief that all matter and energy are derived from geometric patterns or forms is deeply rooted in many mystical and philosophical traditions. Modern-day spiritual practitioners continue to use the Platonic Solids in meditation, visualizations, and other metaphysical practices to align with divine proportions and cultivate harmony.

Why Are These Shapes So Important?

The symmetry and mathematical precision of the Platonic Solids point to an underlying principle of cosmic order. They represent the divine blueprint that structures the universe, offering a glimpse into how geometry reflects the divine laws that govern creation. The fact that these shapes are perfectly balanced—with equal faces, edges, and angles—symbolizes harmony and unity.

Moreover, each Platonic Solid corresponds to different aspects of human experience. For example, the Cube reflects the grounded and material aspects of existence, while the Icosahedron reflects the fluidity and adaptability of the emotional world. The Dodecahedron, as the most complex and spiritually significant, represents the connection between the physical and spiritual realms.

By studying the Platonic Solids, one begins to understand how the physical world and spiritual principles intertwine, making them essential for anyone interested in sacred geometry and its relationship to universal laws.

[illegal-prime]

*chilling in the skinner petrial half mucube*

You all are stuck in a Skinner box while I am resting luxuriously in a Skinner tetrahedron.

[sheltiechicago]

grahamshellswell

Stockholm Metro: World’s Longest Art Exhibit

Tekniska Högskolan Station

Kungliga Tekniska Högskolan, the Royal Institute of Technology, was founded in 1827 and got its metro station in 1973. The station’s decor, created by Lennart Mörk, celebrates scientific advances, technology, the laws of nature, etc. The station is full of quotations from famous events in science history and representation of scientific and mathematical formulas/equations etc. The most famous piece is probably the five regular polyhedra which represents Plato’s five elements.

vintergatanphotography