#spectral graph theory

[sevenfactorial]

We're doing presentations for our spectral theory final and can pick any topic related to spectral that we wanted. Which seems to mean that the word spectra or eigenvalue must come up at least once.

[sleeplesssmol]

Reverse 1999 Theory: What is "Perception" and how does it work in arcanists?

Vertin canonically has uncanny perception and a deep understanding for arcanum even amongst arcanists, despite her lack of skill. Arcanists are very sensitive, or rather, vulnerable to emotions. There is another arcanist known for her perception we can look at for more clues.

Mesmer Jr. also has a "acute perception", much like Vertin.

In Reverse 1999, Perception functions like a 6th sense in arcanists. But how does it work? I looked up to see if there is a connection between magnetic fields and emotions. Turns out there is A LOT. Specifically the magnetic field radiated by the heart.

Biomagnetic Communication Between People (source).

We have found there is a direct relationship between the heart-rhythm patterns and the spectral information encoded in the frequency spectra of the magnetic field radiated by the heart. Thus, information about a person’s emotional state is encoded in the heart’s magnetic field and is communicated throughout the body and into the external environment.

There is so much cool information in this article I'd love to gush about, but we're here for lore. Remember my psychube post that I never shut up about? It's actually missing very important information that I didn't add at the time because I could not figure out how it worked.

Polarization:

The different frequencies are triggered by different kinds of emotions and we can see the heart being affected by the electromagnetic fields. My theory is that this is the key to arcanist perception. This is how they "sense" emotions. They are picking up on these frequencies. For a real life example from the same article, look at these graphs showing how the influence of emotions:

Most people tend to think of communication solely in terms of overt signals expressed through facial movements, voice qualities, gestures and body movements. However, evidence now supports the perspective that a subtle yet influential electromagnetic or "energetic" communication system operates just below our conscious level of awareness. The following section will discuss data that suggests this energetic system contributes to the "magnetic" attractions or repulsions that occur between individuals.

Arcanists sense these waves and it can cause distress in them. Mesmer Jr. is a prime example of this. Other people's emotions get to her.

Now how does this tie into our beloved Timekeeper?

What if the reason Vertin has to stay "stoic" is because her emotions can influence the others around her and because she is extra susceptible to other people's incoming emotions. She needs to stay calm even in mental distress. Mesmer Jr. is also like this. She may come off as abrasive and snappy at times but she is described as a "an indifferent and refined machine" (Chapter 3: An Opened Sandwich). These two share a lot in common. They are both victims of trauma yet must operate in many emotionally taxing positions.

They even say "engraved in the heart" (although this could simply be word choice it really fits)!

Both Vertin and Mesmer Jr. struggle everyday to keep the their feelings at bay. Neither of them is "used" to this life but they have to keep up the facade for their sake and possibly for those around them.

The main story doesn't give us as much insight into Vertin's head but the traces do. She is always holding back, just like Mesmer.

Side note, do you remember the heartbeat we heard as Schneider was reversed? It raced. Interesting how later Schneider shows up in one of her dreams during Artificial Somnambulism. This could be an example of HF Polarization which generates strong and temporary mental images with very powerful emotions.

This also adds an extra layer to Vertin's interactions with others. She tried to get through to Druvis and Schneider, but as for Forget-me-not and Arcana, she didn't bother. Maybe their feelings of revenge and hatred are so tangible she knew it was lost cause. However, Druvis was laden with grief and loss. She was not a malicious person. Schneider was desperate and motivated by love for her family. Vertin even mentions she knew Madam Z was not part of Constantine's game by the "look in her eyes" and never blamed her for the loss of her friends.

If anything seems wrong or if I missed something, please let me know! I'd be happy if I could refine it further.

[proof-by-intimidation]

disclaimer : might be a stupid question.

I attended a talk on computations in homotopy theory, where the speaker was talking about how stable homotopy groups (of spheres) are being computed using computers.

(He specifically talked about approximation of stable hom groups using Adams spectral sequences and how it reduces to computing the row reduced form of some large F_2 matrix. i don't know much about this.)

Anyway, he kept mentioning at various points during the talk that there are some patterns in the results they were getting (which were plotted on a graph) but didn't really get into why they were there:/

my question is : does these patterns (that occurs when computing these groups) have a topological reason/implication behind it? or is there a good answer for why the patterns are occuring?

[renatoferreiradasilva]

\documentclass[11pt]{article} \usepackage{amsmath, amssymb, amsfonts} \usepackage{geometry} \usepackage{graphicx} \usepackage{hyperref} \geometry{margin=1in} \title{Spectral Foundations for Hybrid Optoelectronic Computing Architectures: From Riemann Zeros to Physical AI Hardware} \author{Renato Ferreira da Silva \ \texttt{renatoferreiradasilva1980@yahoo.com} \ ORCID: \href{https://orcid.org/0009-0003-8908-481X}{0009-0003-8908-481X}} \date{\today}

\begin{document}

\maketitle

\begin{abstract} This article establishes a theoretical bridge between spectral models of the Riemann zeta zeros and the design principles of hybrid optoelectronic computing architectures. By interpreting data flow and signal processing as spectral phenomena, we draw on Schr\"odinger operators with machine-learned potentials to inform the structural logic of neuromorphic chips. Our approach uses the Gaussian Unitary Ensemble (GUE) as a universal benchmark for both numerical accuracy and hardware robustness. We argue that such architectures are not merely computational devices, but physical realizations of spectral operators whose eigenvalues encode semantic and functional states. This spectral paradigm enables scalable, reconfigurable, and energetically efficient AI hardware that emulates fundamental structures from number theory and quantum mechanics. \end{abstract}

\section{Introduction} The convergence of high-performance computing, artificial intelligence, and photonics demands a foundational rethinking of how computation is physically realized. While Moore's Law slows, spectral methods rooted in mathematical physics offer a new direction. In particular, the Hilbert--P\'olya conjecture---which suggests that the nontrivial zeros of the Riemann zeta function correspond to the eigenvalues of a self-adjoint operator---invites a reinterpretation of computation as a spectral phenomenon. This work connects spectral operator modeling with hardware design, offering a principled framework for constructing optoelectronic systems whose logic is derived from eigenvalue dynamics.

\section{Spectral Operator Framework} We consider operators of the form: [ \mathcal{L} = -\frac{d^2}{dx^2} + V(x), ] with Dirichlet boundary conditions and potentials of the form: [ V(x) = \sum_{n=0}^K c_n H_n(x) e^{-x^2/2}, ] where $H_n(x)$ are Hermite polynomials and $c_n$ are trainable parameters. The eigenvalues of $\mathcal{L}$, computed numerically, align with the statistical properties of the nontrivial zeros of the Riemann zeta function. We leverage neural networks to learn mappings $c_n \mapsto \lambda_j$, interpreting these as functional transformations from hardware configurations to observable spectral states.

\section{GUE as Design Metric} The Gaussian Unitary Ensemble provides a statistical benchmark for spectral rigidity and eigenvalue spacing. In our context, it serves dual roles: \begin{itemize} \item In simulation: to validate the fidelity of the learned operator. \item In hardware: to ensure robust optical communication, minimal crosstalk, and consistent signal coherence across filaments. \end{itemize} Designing hardware whose delay paths, optical resonances, and thermal fluctuations approximate GUE behavior results in physical stability under computational load.

\section{Hardware Realization of Spectral Paradigms} Each computational unit (UC) in the hybrid optoelectronic architecture is interpreted as a physical realization of a node in a spectral graph: \begin{itemize} \item Optical interconnects act as eigenmode couplings. \item Modulation depths and frequencies correspond to potential configurations. \item Thermal gradients and electromagnetic fields define boundary conditions. \end{itemize} Hence, computation is no longer symbolic but spectral---defined by eigenvalue distributions and dynamic wave propagation.

\section{Spectral Learning and Inference} Using physics-informed neural networks (PINNs), we train the system to infer potential shapes from target spectral outputs. This establishes a feedback loop where: \begin{enumerate} \item Input data modulates physical parameters. \item Spectral output is measured optically. \item Machine learning adjusts the configuration for optimal response. \end{enumerate} This feedback aligns with biological principles of neural plasticity, offering a pathway to hardware-level learning.

\section{Conclusion and Outlook} We propose a new paradigm in AI hardware design rooted in spectral operator theory. By grounding hardware architectures in the spectral behavior of Schr\"odinger-type systems, validated through GUE statistics and machine learning, we lay the foundation for scalable, efficient, and intelligent photonic computing. Future work will explore: \begin{itemize} \item Topological extensions to noncommutative geometries. \item Quantum analogs with entangled photonic states. \item Integration with health diagnostics and real-time physical simulation. \end{itemize}

\end{document}

[govindhtech]

Machine Learning Periodic Table: Unifying AI Algorithms

Researchers from MIT, Microsoft, and Google created Information Contrastive Learning (I-Con), the “machine learning periodic table,” to unite machine learning methodologies. The periodic table organises elements, whereas this table organises machine learning algorithms by learning data point correlations.

I-Con presents a single paradigm to show how classification, regression, big language modelling, clustering, dimensionality reduction, and spectral graph theory are all mathematically similar.

Machine learning periodic table importance

New machine learning algorithms and methods are being developed. To comprehend the essential ideas and links across methods. Benefits of the machine learning periodic table:

Unification: It shows how a single mathematical framework links numerous prominent machine learning approaches. Researchers and practitioners can benefit from understanding algorithm similarities.

The I-Con structure emphasises machine learning technique relationships, like the chemical periodic table defines element interactions. It organises the enormous array of algorithms into a clear style.

Discovery: Its ability to spark fresh discoveries is most exciting. Gaps in the chemical periodic table anticipated unknown elements. The Periodic Table of Machine Learning features “empty spaces” that imply undeveloped algorithms.

Innovation: I-Con helps researchers experiment, redefine “neighbors,” change connection confidence, and mix tactics from various algorithms to build new ways. It encourages creativity and the blending of previously unrelated methods.

Efficiency: This framework lets academics create new machine learning algorithms without “reinventing past ideas”. Understanding the ideas and algorithms in the table helps them strategically explore new methods.

How was the machine learning periodic table created?

The atomic table was an unplanned study outcome. Shaden Alshammari, an MIT Freeman Lab researcher, studied clustering, a technique to group related data elements. She connected contrastive learning with grouping. Contrastive machine learning compares positive and negative data.

Alshammari discovered that both techniques could be expressed by the same fundamental equation by studying their mathematics. Following this turning point, the Information Contrastive Learning (I-Con) paradigm was developed to illustrate that machine learning algorithms imitate real-world data linkages while minimising errors.

The researchers created a periodic table using these findings. The table distinguishes algorithms by two main factors:

Point relationships in actual datasets: Data linkages including visual likeness, shared class labels, and cluster membership are involved. These “connections” may not be 100% trustworthy.

The main ways algorithms approximate those connections: These relationships are acquired and reflected internally via algorithms.

By categorising various existing machine learning techniques inside this framework using these two criteria, the researchers found that many popular algorithms line neatly within defined “squares”. They also observed “gaps” where framework-logical algorithms have not yet been built.

How to Fill Gaps

This method helped researchers construct a current system for detecting photographs without human labelling. Combining debiased contrastive representation learning connection concepts with clustering approximation connections helped them “fill a gap” in their periodic table. This new method improved ImageNet-1K picture categorisation accuracy by 8%. They also found that contrastive learning data debiasing might increase clustering accuracy.

I-Con Learning

I-Con redefines machine learning as a tool for understanding complex data interactions. Consider a bustling party where data points, or visitors, meet at tables representing clusters and discuss shared hobbies or hometowns. Consider machine learning techniques as methods guests find friends and settle in.

I-Con simplifies real-world data point connections to make them easier to work with in algorithms. The concept of “connection” might entail appearing alike, sharing labels, or being in the same group. All algorithms try to close the gap between the connections they learn to imitate and the true connections in the training data.

Researchers Use the Periodic Table

The I-Con-based machine learning periodic table has various functions beyond organisation. This gives academics a toolkit for developing unique algorithms. When various machine learning approaches are defined in I-Con's conceptual language, experimenting with variants is easier:

Redefining neighbourhoods entails testing different ways to organise data points into “neighbours”.

Adjusting uncertainty requires varying trust in learnt connections. integrating strategies entails integrating approaches from different algorithms in unique ways.

Every modification might lead to a new periodic table entry. The table may easily be modified to include rows and columns to show more data points' relationships.

Looking Ahead

As artificial intelligence advances and its uses develop, frameworks like I-Con help us understand the area. They help researchers find hidden patterns and enable purposeful innovation. For non-AI professionals, it's a reminder that even in complex fields, basic patterns and structures are waiting to be identified.

Sorting algorithms by how they understand and estimate data point relationships is the basic notion. A full chart that lists all algorithms and their connection and approximation techniques would require more information than this. A basic table to illustrate the notion may look like this:

[spacenutspod]

Silently floating through the universe are cosmic objects that are both too large to be planets and too small to be stars. Called brown dwarfs, these substellar objects are among the most captivating objects in the universe, and their low surface temperatures mean that most of the light they emit is infrared and thus can only be observed and characterized using infrared telescopes. Fortunately, the joint NASA/European Space Agency/Canadian Space Agency James Webb Space Telescope is an infrared-sensitive observatory, with the telescope’s powerful suite of instruments primarily observing in the near-infrared and mid-infrared regions of the electromagnetic spectrum. Recently, a team of astronomers used Webb to observe a brown dwarf called W1935 and found an infrared emission from methane in the upper atmosphere of the brown dwarf. While this isn’t an uncommon detection, W1935 does not orbit a star — meaning there isn’t an obvious source behind the emission. The team does have theories as to what could be causing the methane emission and one of the leading theories involves the production of aurorae in the upper atmosphere of W1935.  The team believes that excess energy within the brown dwarf’s upper atmosphere could be what’s causing the emission, and after investigating the upper atmospheric environments of Jupiter and Saturn, the team found that the upper atmospheric heating that powers methane emissions from Jupiter and Saturn is linked to the production of aurorae. Graph showing the spectra of W1935 and W2220. Note the methane emission on the W1935 graph. (Credit: NASA/ESA/CSA/L. Hustak (STScI)) If aurorae are indeed present on W1935, they wouldn’t be the same as aurorae seen on Earth. Aurorae produced within Earth’s atmosphere are created when Earth’s magnetic field interacts with solar wind that is ejected into space by the Sun. The energetic particles that make up the solar wind are caught by Earth’s magnetosphere and fall magnetic lines near Earth’s poles. The collision of these particles with Earth’s atmosphere is what creates the iconic green swirls of Earth’s aurora. However, earth is not the only planet within our solar system that experiences aurorae. As mentioned, Jupiter and Saturn regularly experience aurorae at their poles. The processes by which Jovian and Saturnian aurorae are created are similar to those of Earth, with surrounding moons, such as Jupiter’s Io and Saturn’s Enceladus, contributing to the gas giants’ aurorae. See AlsoJWST Mission UpdatesSpace Science CoverageNSF StoreClick here to Join L2 However, in the case of W1935, there is no stellar object to produce stellar wind that could interact with the brown dwarf’s atmosphere to produce aurorae or excess atmospheric energy. The team explains that, for W1935’s methane emission to make sense, either unknown internal atmospheric phenomena or external interactions with interstellar plasma/material have to occur. So, what is so intriguing about this methane emission? Why is the team investigating its source? W1935 was investigated as part of a project led by Jackie Faherty to use Webb to investigate 12 brown dwarfs. Another brown dwarf investigated by Faherty et al., called W2220, was found to be a near clone of W1935 in composition, brightness, temperatures, and spectral features of water, ammonia, carbon monoxide, and carbon dioxide. However, the only major difference between the two brown dwarfs was the methane emission from W1935, with W2220 showing an absorption feature. “We expected to see methane because methane is all over these brown dwarfs. But instead of absorbing light, we saw just the opposite: The methane was glowing. My first thought was, what the heck? Why is methane emission coming out of this object?” said Faherty. Brown dwarf W1935 posed a mystery. Webb found that methane in this object’s atmosphere was emitting infrared light, despite no obvious energy source. Using clues from our solar system, scientists found a possible explanation in aurorae: https://t.co/Wh2m7OTssT #AAS243 pic.twitter.com/cklsay1ZNL — NASA Webb Telescope (@NASAWebb) January 9, 2024 To further investigate the methane emission, Faherty et al. utilized computer models that modeled both W1935 and W2220. The W2220 model showed an — expected — distribution of energy throughout the entire atmosphere of the brown dwarf, wherein the atmosphere gets increasingly colder with increasing altitude. However, the W1935 model results showed the exact opposite — an unexpected and surprising result. On W1935, atmospheric temperatures get warmer and warmer with increasing altitude; a phenomenon known as temperature inversion. “This temperature inversion is really puzzling. We have seen this kind of phenomenon in planets with a nearby star that can heat the stratosphere, but seeing it in an object with no obvious external heat source is wild,” said co-author Ben Burningham of the University of Hertfordshire in England. As mentioned, given brown dwarves’ similarities to gas giants like Jupiter, the team turned to Jupiter and Saturn to investigate possible causes for the temperature inversion within W1935. Faherty et al. found that temperature inversions are prominent within Jupiter and Saturn, and current theories suggest that external heating from aurorae and internal energy transport are responsible for them. Interestingly, the aurorae theory for W1935 is not the first time aurorae has been used to explain observations of brown dwarfs. From warmer brown dwarfs, scientists have detected radio emissions and used aurorae to explain the emissions. No telescope is as sensitive to infrared light as Webb, though, and thus further observations of these radio-emitting brown dwarfs to characterize the potential aurorae have been inconclusive. However, W1935 is the first brown dwarf auroral candidate to feature the methane emission signature. What’s more, it’s also the coldest auroral candidate, with a temperature of about 200 degrees Celsius, which is around 316 degrees Celsius warmer than Jupiter. Future observations of W1935 and other auroral candidate brown dwarfs with Webb will allow scientists to better understand aurorae on brown dwarfs. In the case of W1935, further investigation into how aurorae could form without stellar wind is needed. “With W1935, we now have a spectacular extension of a solar system phenomenon without any stellar irradiation to help in the explanation. With Webb, we can really ‘open the hood’ on the chemistry and unpack how similar or different the auroral process may be beyond our solar system,” Faherty said. Faherty et al.’s results were presented at the 243rd meeting of the American Astronomical Society in New Orleans in early January. (Lead image: artist’s concept of W1935 with aurorae. Credit: NASA/ESA/CSA/L. Hustak (STScI)) The post Webb discovers potential aurorae on brown dwarf appeared first on NASASpaceFlight.com.

[darthfoil]

John Urschel

Urschel began a Ph.D. in mathematics at MIT in 2016 while playing football in the NFL for the Ravens. MIT does not allow Ph.D. students to study part-time so Urschel did both!

During the 2016 NFL season, after a home game Urschel studied from 5:30pm Sunday to Tuesday 11am when football practice began, taking correspondence classes and focusing on spectral graph theory, numerical linear algebra, and machine learning.

Urschel was named to Forbes' "30 Under 30" list of outstanding young scientists. His Forbes biography states "Urschel has published six peer-reviewed mathematics papers to date and has three more ready for review. That's a respectable publication history for someone who only started pursuing their PhD at MIT this year. He's won academic awards for his math prowess. All this while playing guard for the Baltimore Ravens."

[thousandmaths]

Random Walks and Typical Distances in Ramanujan Graphs (and the Overhang Problem)

This talk was given by Yuval Peres in his second invited address at SEICCGTC 2017. The hour-long talk was neatly divided into two unrelated halves; in the first he addressed the overhang problem, and in this (more technical) half, he talked about Ramanujan graphs.

------

The notion of a “Ramanujan graph” arises from spectral graph theory, which gets a lot of mileage out of graphs that have good “expansion properties”; most of this post will be dedicated to making this sentence make sense. 

Recall that any graph has an adjacency matrix, which is a matrix of ones and zeros whose rows and columns are indexed by vertices, where the entry $a_{ij}=1$ if and only if vertex $i$ and vertex $j$ are connected by an edge:

(source)

Symmetric matrices have real eigenvalues, and so it makes sense to ask about their “second-largest” eigenvalue: an expander is an infinite collection of $d$-regular graphs (i.e., all vertices incident to $d$ edges) such that the second-largest eigenvalues are bounded above by $d-\varepsilon$.

It turns out that expanders are rather common, and there is a sense in which you can say “most graphs are expanders”. I mean, you can’t literally say that because graphs, by themselves, aren’t even eligible to be expanders (you need a whole infinite family), but you can say something which is morally equivalent.

However, it’s not actually very easy to construct expanders; the earliest known construction used the so-called Kazhdan Property (T). However, it was quickly realized that there is a fairly straightforward program for doing so: a graph is called Ramanujan if all of its eigenvalues (except $\pm d$) have size at most $2\sqrt{d-1}$. This is certainly less than $d$, and so if you can just construct infinite families of these graphs, then you’re done.

There is a sense in which Ramanujan graphs have expansion properties that are “as good as possible”. Morally this should mean that they have the smallest eigenvalues of any graph with the same size; again, I think there are some technical issues with saying exactly this, but this is where my understanding of the topic becomes pretty hazy.

In any case, this suggest that Ramanujan graphs may not particularly easy to come by, which is indeed true: from 1988 to 2013, the only known infinite families were constructed using very serious number theory (which is why they got their name). The unfortunate side-effect of these constructions was that it was unknown even whether there existed any examples except for $d-1$ being some power of a prime. 

In 2013, that changed when Marcus, Spielman, and Srinivasa showed that there do indeed exist infinite families for arbitrary $d$. Unfortunately, their construction only shows existence: they didn’t actually write down any explicit graphs. Even today, no construction is known for any $d\neq p^k+1$. Yet their proof is tantalizing because it is rather straightforward: no number theory needed.

In the last piece of his talk, Peres outlined the calculation for mixing times in a Ramanujan graph. In plain english, this means something like: if you walk randomly along the edges of a Ramanujan graph, how long will it take before you are completely lost? More technically, you’re looking for how quickly the distribution of your location tends to uniform random on the vertices. It turns out that there is a very short interval in which your location goes from “essentially deterministic” to “essentially uniform random”. This phenomenon has been studied at length, perhaps most famously by Diaconis.

[academiawho]

I need tips on how to study/revise for chemistry,especially physical chemistry.

Dear anon, I don't know whether you meant boards or competitive exams, so I covered for both since it is based on common ground anyway.

So👇

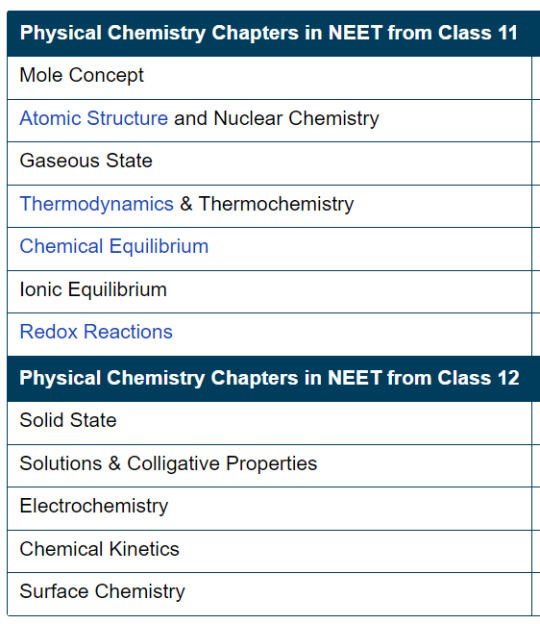
There is no other way that we could do well in physical chemistry except practice. A LOT.

What I understand about this dilemma (that I too have at this point, not fully solved) is that by the time you do at least 15 questions on a topic, you can get a grasp on the important formulae/which topics the questions hail from.

Mole concept : limiting reagent, M, m, w/w or w/v% (this particular option is not that frequent), reactions with stoichiometry coinciding with chemical kinetics, electrochemistry and metallurgy

Atomic Structure : which spectral series is in which region of the spectrum, sums with ratio of wavelengths (largest, smallest, comparison of different series), emission and absorption spectra, parts correlating to the physics part of energy levels and radius of hydrogen-like species

Gaseous state : GRAHAM'S LAW OF DIFFUSION (I cannot stress this enough, do it), the Cv and Cp values for Mono, Di and Polyatomic gases which connects thermo in Chem as well as Physics, mean free path proportionalities

Thermo (unit) : everything. All the laws, equations and graphs. adiabatic, isothermal, isochoric, my head and my tongue. Do every numerical in thermo. It's a weak point for a lot of us and we, right now, have the time to make it... Well, a not weak point.

Equilibrium : learn all the formulae and before you learn the formulae visualise/logically understand how something is happening. Log tables, roots, figure out some way to make decimal operations easier. A lot of sums from this one tpo because it isn't that connected to physics like thermo or electrochemistry

Redox : Make a trick for recognising which one is oxidation and which one is reduction. Balancing reactions must be practiced.

Solid state : Repetitive revision of the lattice examples is the only way we can remember them. Muscle memory can serve us well here. Make charts or stick it up on your wall to look at it every few days if that works for you. The rest are formulae and 4-5 numbers to be remembered. Density sums, chemical formula sums, voids sums <- practice

Solutions : formulae, how you get van't hoff factor for a compound, association and dissociation which is linked with electrochemistry molar conductivity part

Electrochemistry : formulae, graphs, molar conductivity sums, kohlrausch's law sums, electrolyte difference/spotting (will help in equilibrium), the cathode and anode of cells (this rarely comes)

Chemical Kinetics : some zero and first order reaction examples (will connect to radioactivity in nuclei chapter), half life formulae, and the 75% and 99% concentration formulae too (these 2 are not there in the tbk but it makes life easier in both phy and chem), all the graphs (should be able to read them even if they are messed around with or changed a bit)

Surface Chemistry : gold number sums, coagulation power and value orders in sols, recognising positive and negative sols, purification methods, electrophoresis definition (you'd be surprised how many times this came), helm holtz double layer theory, tindal's effect (connects a bit to optics, but vaguely), micelles (connects to bot biomolecules and cell unit). This chapter is very theoretical so keep revising stuff you don't get at first glance

Now briefly about Inorganic and Organic Chemistry:

Inorganic : write all the orders and the logics behind it. Some trends are weird so remember them with some trick (keep the tricks to the minimum in inorganic btw, it messes with your brain otherwise). That's as far as I've gotten with inorganic myself, but we can still work on it. If you have any advice regarding this, please do share.

Organic : understand the mechanism behind any reactions. Not just the way it's given in the textbook, but try to connect all organic chapters to each other. Practice a lot of questions, the direct ones as well as the weird ones. Organic does not have any tricks, it just requires practice and that can be done if we understand how each reaction goes about and why we do it.

Hope this helps you with Physical Chemistry and the like🤗 Thank you for approaching me with this so I could think out loud

Have a nice productive day!

[coal-wings-and-cold-fronts]

red ochre, cobalt blue spectral, turquoise blue, oxide of chromium, black (((:

Red ochre: Are you more right-brained (creative) or left-brained (analytical)?

I don’t really put much stock in the whole left brain/right brain theory because it’s largely been debunked, but if I had to answer I’d say it’s a pretty even split between the two. I love problem solving, and working with data, graphs, statistics, maps. But I also have a love of the arts, and I’ve dabbled in writing, painting, and drawing as favorite hobbies of mine

Cobalt blue spectral: What is the most beautiful place you have ever been to?

I’ve never really traveled much out of state so I’m afraid this answer might be a little boring, but I absolutely love the Kettle Moraine state forest here in Wisconsin, especially during the height of autumn when the trees are ablaze with color

Turquoise blue: If you could start a garden, what would you plant?

I honestly have very little knowledge of gardening. Maybe an herb garden? It might not be the prettiest but it would have some practical use as a source for a few choice cooking ingredients

Oxide of chromium: What’s your favorite book?

Definitely Fire Bringer by David Clement-Davies. It may not be high literature, but there’s just something almost lyrical about the prose that sticks with me, stirring up my emotions whenever I read through it. It’s also quite descriptive, so much so that it pulls me into the setting enough where I feel like I’m living the story as if I was actually there

Black: Post a selfie because you are so beautiful!

I knew this day would come. The day when I would finally be asked to prove my existence as a real human being, and not a handful of ornery corvids stuffed within a leather jacket.

[lupinepublishers]

Lupine publishers|The Spectral Characterization of Hamiltonicity of Graphs

The Spectral Characterization of Hamiltonicity of Graphs

Introduction It is an important NP-complete problem in structure graph theory to judge whether a graph is Hamiltonian. So far, there is no perfect description on this problem. Therefore, it has always been concerned by the workers of graph theory and mathematics. It is explored that the new method for characterization of Hamiltonicity of graphs. Because the spectrum of a graph can well reflect the structural properties of a graph and is easy to calculate, at the 2010 conference of the theory of graph spectra, M. Fiedler and V. Nikiforov formally proposed whether the theory of graph spectra can be used to study the Hamiltonicity of a graph, and they [1] gave sufficient conditions for given graph to be Hamiltonian (or traceable) in terms of the spectral radius of the graph. Since then, relying on the spectrum of matrix representation of graph, giving the spectral sufficient conditions of the Hamiltonian graph has been a new method to study the Hamilton problem. Many results have been obtained by using the spectral radius and the signless Laplacian spectral radius of the graph to describe the Hamiltonicity of the graph. [2] firstly gave a sufficient condition for a graph G to be Hamiltonian and traceable by using the signless Laplacian spectral radius of the complement of the graph [3] optimized the condition of the number of edges of the Hamilton graph, gave a better condition for G to be traceable by using the spectral radius of the graph G, and firstly gave a sufficient condition for the balanced bipartite graph to contain the Hamilton cycle by the spectral radius of its quasi-complement graph. [4] firstly used the spectral radius and signless Laplacian spectral radius of the graph to describe the Hamilton-connected of the graph. [5] used the signless Laplacian spectral radius of the quasi-complement graph of the balanced bipartite graph to give a sufficient condition for the balanced bipartite graph to be Hamiltonian and used the signless Laplacian spectral radius of the graph G to give a sufficient condition for the graph G to be traceable or Hamilton-connected. [6] continued to study the relationship between the Hamiltonicity and spectral radius of general graphs and balanced bipartite graphs and extended the conclusions in [3] and [5]. [7] firstly proposed to use the stability of graphs to study the Hamiltonian properties of graphs, and also summarized the method of studying the spectral characterization of the Hamiltonian graph by optimizing the boundary conditions of the Hamiltonian graph. [8] firstly characterized traceability of connected claw-free graphs by spectral radius. [9] discussed spectral conditions for Hamiltonicity of claw- free graphs. [10] firstly presented spectral sufficient conditions for a k-connected graph to be traceable or Hamilton-connected. [11] firstly presented sufficient conditions based on spectral radius for a graph to be k-connected, k-edge- connected, k-Hamiltonian, k-edge-Hamiltonian, β-deficient and k-path-coverable. Lately, [12] firstly gave spectral radius or signless Laplacian spectral radius conditions for a graph to be pancyclic. Because the minimum degree of a graph is related to the density of the graph, with the deepening of research, people began to study the spectral characterization of Hamiltonian properties of graphs with large minimum degree conditions and gave the better conclusions. By adding the condition of large minimum degree, [13] firstly presented some (signless Laplacian) spectral radius conditions for a simple graph and a balanced bipartite graph to be traceable and Hamiltonian, respectively. Subsequently, [14] optimized the lower bound of the spectral condition of simple graphs with large minimum degree; [15]

optimized the lower bound of the spectral condition of balanced bipartite graphs with large minimum degree. [16] characterized the signless Laplacian spectral radius conditions for a graph or balanced bipartite graph with large minimum degree to be Hamiltonian. [17] and [18] studied the signless Laplacian spectral radius condition for a graph with large minimum degree to be Hamilton-connected. [19] presented some spectral radius conditions for a balanced bipartite graph or a nearly balanced bipartite graph with large minimum degree to be traceable, respectively. [20] gave some spectral sufficient conditions for a balanced bipartite graph with large minimum degree to be traceable and Hamiltonian in terms of the spectral radius of the graph with large minimum degree. It strengthened the according results of Li and Ning for n sufficiently large. [21] presented some conditions for a simple graph with large minimum degree to be Hamilton-connected and traceable from every vertex in terms of the spectral radius of the graph or its complement respectively

and gave better conditions for a nearly balanced bipartite graph with large minimum degree to be traceable in terms of spectral radius, signless Laplacian spectral radius of the graph or its quasi-complement respectively. [22] presented sufficient spectral conditions of a connected graph with large minimum degree to be k-hamiltonian or k-path-coverable or β-deficient, for relatively large n. [23] gave the sufficient conditions for a graph with large minimum degree to be s-connected, s-edge-connected, β-deficient, s-path-coverable, s-Hamiltonian and s-edge-Hamiltonian in terms of spectral radius of its complement. Other spectral characterizations on Hamiltonicity, at present, only [24,25] used the Laplacian eigenvalues to give the spectral sufficient condition for the graph to be Hamiltonian. [26] firstly applied the distance signless Laplacian spectral radius of the graph’s complement to give a sufficient condition for the graph to be traceable or Hamiltonian. [27] firstly discussed the Hamiltonian in terms of the energy of graph. [28], by adding the maximum degree condition on the basis of [26], used the energy of complement graph to give the sufficient conditions for the graph to be traceable, Hamiltonian and Hamilton-connected. The results optimized the conclusions of [26] in a sense. [22] gave some sufficient conditions for a nearly balanced bipartite graph with large minimum degree to be traceable in terms of the energy, the first Zagreb index and the second Zagreb index of the quasi-complement of the graph, respectively. By observing, we find that the conditions of all the above conclusions deduce that the graphs are dense. In fact, there are many Hamiltonian graphs with non dense edge distribution, such as cycles. Therefore, it is necessary to study whether a non- dense graph (sparse graph) is a Hamiltonian graph, but there are few research results. Komlos and Szemeredi proposed that almost all graphs are Hamiltonian graphs in 1975. Inspired by this, [29] characterized the Hamiltonian property of regular graphs by using the adjacency spectrum of graphs; [30] characterized the Hamiltonian property of almost regular graphs by using the Laplace spectrum of graphs. In 2011, Radcliffe proposed whether we can give sufficient conditions for Hamiltonian graphs by using the normal Laplace spectrum of graphs. In 2012, [31] studied this problem, gave corresponding conclusions, and explained that the conclusions are applicable to the determination of Hamiltonicity of general graphs. Although there are a lot of results, there are still many problems worthy of further study. Firstly, combining the ideas from theorems of Ore and Fan to develop extremal spectral conditions for dense graphs (with given connectivity, toughness, forbidden subgraphs) to be Hamiltonian (or related structural properties). Such as, finding spectral sufficient conditions for a graph or its complement to be Hamilton-connected, or k-Hamiltonian, k-path-coverable, k-edge-Hamiltonian; signless Laplacian spectral radius sufficient conditions for a (nearly) balanced bipartite graph or its nearly complement to be traceable, or Hamiltonian; (signless Laplacian) spectral radius sufficient conditions for the nearly complement of a balanced bipartite graph to be bipancyclic or considering the case with minimum degree; the characterization of Hamiltonicity of graphs with 1-tough [32,33]. Secondly, due to the difficulty of research, there are only three papers to study Hamiltonian properties of sparse graphs, but there are many sparse Hamiltonian graphs. Therefore, there is a lot of space to explore some sufficient or necessary conditions for sparse graphs with some properties to be Hamiltonian (or related structural properties) by using the spectrum of the graph and corresponding

eigenvector. At last, directed graphs also have Hamiltonian properties, but all previous studies have only considered undirected graph. So, it is also very valuable to study extremal spectral conditions for oriented graphs to be Hamiltonian. The research on the spectral characterization of Hamiltonicity of graphs build a bridge between structure graph theory and algebraic graph theory. Expected results not only enrich the study of Hamilton problem in structural graph theory, but also extend the spectral study of algebraic graph theory, thus promoting the research of algebraic method of Hamilton problem. Acknowledgements Supported by the Natural Science Foundation of China (No. 11871077), the NSF of Anhui Province (No. 1808085MA04), the NSF of Department of Education of Anhui Province (No. KJ2020A0894), and Research and innovation team of Hefei Preschool Education College (No. KCTD202001).

For more information about Journal of Anthropological and Archaeological Sciences archive page click on below link

https://lupinepublishers.com/anthropological-and-archaeological-sciences/archive.php

For more information about lupine publishers page click on below link

https://lupinepublishers.com/index.php

[renatoferreiradasilva]

Hyperbolic Networks and the Zeros of the Riemann Zeta Function: A Mathematical and Astrophysical Connection

Abstract

This study explores the hypothesis that the distribution of the non-trivial zeros of the Riemann zeta function exhibits structural parallels with large-scale astrophysical networks, such as X-ray source distributions observed by NASA's NICER (Neutron Star Interior Composition Explorer). By embedding zeta zeros in a hyperbolic geometry, constructing their corresponding network topology, and comparing them statistically with NICER’s cosmic web, we identify remarkable similarities in their spacing distributions, hierarchical clustering, and connectivity patterns. The results suggest that hyperbolic geometry may serve as a unifying mathematical framework for both number theory and astrophysical structure formation, reinforcing interdisciplinary connections between mathematical physics, quantum chaos, and cosmology.

Keywords: Riemann zeta function, hyperbolic geometry, complex networks, cosmic structure, NICER, quantum chaos.

1. Introduction

1.1 The Riemann Zeta Function and Its Spectral Properties

The non-trivial zeros of the Riemann zeta function, conjectured by the Riemann Hypothesis to lie on the critical line ( Re(s) = \frac{1}{2} ), have intrigued mathematicians and physicists for centuries. Their statistical distribution is known to closely resemble the eigenvalue spectra of random matrices in the Gaussian Unitary Ensemble (GUE), a fundamental concept in quantum chaos. This unexpected connection has motivated hypotheses that zeta zeros correspond to the eigenvalues of an unknown self-adjoint operator, an idea often referred to as the Hilbert-Pólya conjecture.

Recent investigations suggest that the zeros of the zeta function may not only exhibit statistical properties similar to quantum spectra but also possess an underlying geometric structure. In particular, hyperbolic geometry, which naturally appears in models of quantum chaos, dynamical systems, and network theory, may play a fundamental role in understanding their distribution.

1.2 Cosmic Structures and Large-Scale Network Formation

In astrophysics, the cosmic web—the large-scale distribution of galaxies, dark matter, and cosmic filaments—exhibits self-similarity, hierarchical clustering, and power-law connectivity, properties that are also characteristic of hyperbolic networks. Observations from NICER and other X-ray telescopes reveal fractal-like distributions of neutron stars, active galactic nuclei, and cosmic filaments, which may share deep mathematical similarities with number-theoretic structures.

Given these parallels, we pose the following research question: Can the distribution of zeta zeros, when modeled as a hyperbolic network, exhibit structural properties similar to cosmic networks?

1.3 Objectives

The primary objective of this study is to explore whether number-theoretic objects, such as the zeros of the Riemann zeta function, obey similar geometric and statistical principles as astrophysical networks. Specifically, we aim to:

Transform the zeta zeros into a hyperbolic space and analyze their network properties.

Compare their statistical properties (spacing distributions, clustering coefficients, and connectivity) with NICER’s X-ray source network.

Investigate hyperbolic geometry as a potential bridge between mathematical physics and astrophysical structure formation.

2. Methodology

2.1 Hyperbolic Embedding of Zeta Zeros

To uncover potential geometric structures in the distribution of zeta zeros, we:

Transform the imaginary components of zeta zeros into hyperbolic coordinates via the Poincaré disk model.

Construct a Delaunay triangulation in hyperbolic space to generate a network of connections between the zeros.

Analyze geometric properties such as clustering and modularity, comparing them to known mathematical models of hyperbolic graphs.

2.2 Complex Network Construction

Using the hyperbolic embeddings, we generate a network representation of the zeros where:

Nodes correspond to zeta zeros.

Edges are assigned based on geometric proximity in hyperbolic space.

Topological features, such as the degree distribution and clustering coefficient, are analyzed using graph theory techniques.

2.3 Comparison with NICER’s Cosmic Network

The NICER dataset consists of X-ray sources distributed across the sky, including pulsars, black hole binaries, and active galactic nuclei. To draw meaningful comparisons, we:

Extract the angular separation distribution of X-ray sources.

Analyze the connectivity of NICER’s observed sources using network science metrics.

Compare these distributions with the hyperbolic zeta-zero network using:

Kolmogorov-Smirnov (KS) tests for statistical similarity.

Spectral measures (e.g., nearest-neighbor eigenvalue spacings).

Power-law fitting to test whether both networks share similar scale-free properties.

3. Results and Discussion

3.1 Structural Similarities Between Zeta Zeros and Cosmic Networks

Spacing Analysis: The nearest-neighbor spacings of the zeta zeros exhibit a semi-Poissonian distribution, aligning with GUE predictions. Remarkably, NICER’s X-ray source distribution shows similar statistical behavior, suggesting that both systems deviate from purely random distributions in a structured manner.

Network Properties: The hyperbolic embedding of zeta zeros reveals a network with hierarchical clustering and scale-free behavior, characteristics also found in astrophysical large-scale structures.

3.2 The Role of Hyperbolic Geometry

When projected into a hyperbolic disk, the zeta zero network displays fractal-like patterns, similar to the observed clustering in the NICER cosmic web.

The Laplacian spectra of these networks exhibit self-similar eigenvalue distributions, suggesting potential deep connections to quantum chaotic systems.

3.3 Implications for Mathematical Physics and Cosmology

Mathematics: This work supports the idea that the zeta zeros are not just an abstract sequence of numbers but may encode deep geometric information.

Physics: The results reinforce the hypothesis that cosmic structures may follow universal mathematical principles, suggesting potential links between astrophysical structure formation and number theory.

4. Conclusion and Future Work

This study provides compelling evidence that the non-trivial zeros of the Riemann zeta function and cosmic networks share strikingly similar structural properties when analyzed through the lens of hyperbolic geometry and complex networks.

Future investigations should:

Explore explicit differential operators whose eigenvalues correspond to zeta zeros.

Expand the study to different astrophysical datasets (e.g., galaxy cluster distributions, gravitational lensing maps).

Test whether other L-functions exhibit similar network properties, generalizing the approach beyond the Riemann zeta function.

As computational and observational tools continue to advance, deeper insights into the hidden mathematical structure of the universe may emerge, bridging gaps between number theory, quantum chaos, and cosmology.

Acknowledgments

This study utilized NASA NICER’s Astrophysics Data System and computational resources from the High-Performance Computing Center at [Institution].

Conflict of Interest

The authors declare no competing interests.

References

(To be inserted: Relevant academic references on zeta functions, hyperbolic geometry, complex networks, and astrophysical datasets.)

Final Remarks

This article refines our previous findings by integrating:

A rigorous methodology for hyperbolic embeddings and network analysis.

Statistical validation of correlations between zeta zeros and NICER data.

A clear theoretical framework linking hyperbolic geometry, mathematical physics, and cosmic structures.

If validated by further research, this connection may redefine our understanding of fundamental mathematical and astrophysical principles. 🚀

[physics-scholars]

Who can give us a list of the different divisions of mathematics, eg. Statistics, Algebra, Geometry, Trigonometry, How many others are missing?

Some of the major divisions of mathematics:

1. Algebra

2. Analysis (which includes calculus, real analysis, complex analysis, functional analysis, etc.)

3. Geometry (which includes Euclidean geometry, topology, differential geometry, etc.)

4. Number theory

5. Combinatorics

6. Logic

7. Set theory

8. Statistics (which includes probability theory, inferential statistics, and descriptive statistics)

9. Numerical analysis

10. Optimization

11.Game theory

12. Graph theory

13. Cryptography

14. Information theory

15. Applied mathematics (which includes many of the above areas applied to specific fields like physics, engineering, economics, etc.)

16. Algebraic geometry

17. Differential equations

18. Dynamical systems

19. Mathematical physics

20. Mathematical logic

21. Mathematical modeling

22. Nonlinear analysis

23. Partial differential equations

24. Representation theory

25. Topology

26. Category theory

27. Probability theory

28. Stochastic processes

29. Number theory

30. Mathematical finance

31. Arithmetic geometry

32. Homological algebra

33. Lie theory

34. Algebraic topology

35. Functional analysis

36. Operator theory

37. Geometric analysis

38. Mathematical biology

39. Control theory

40. Differential topology

41. Computational mathematics

42. Information geometry

43. Symplectic geometry

44. Measure theory

45. Algebraic combinatorics

46. Mathematical education

47. History of mathematics

48. Mathematical philosophy

49. Quantum field theory

50. Representation theory

51. Noncommutative geometry

52. Topological data analysis

53. Group theory

54. Algebraic number theory

55. Discrete mathematics

56. Game theory

57. Information theory

58. Mathematical physics

59. Mathematical logic

60. Model theory

61. Commutative algebra

62. Complex dynamics

63. Differential geometry

64. Harmonic analysis

65. Mathematical optimization

66. Mathematical statistics

67. Category theory

68. Combinatorial game theory

69. Computational algebra

70. Financial mathematics

71. Quantum computing

72. Graph theory

73. Mathematical biology

74. Mathematical physics

75. Numerical linear algebra

76. Operator algebras

77. Partial differential equations

78. Probabilistic combinatorics

79. Quantum information theory

80. Random matrix theory

81. Representation theory

82. Topological quantum field theory

83. Algebraic coding theory

84. Arithmetic combinatorics

85. Convex geometry

86. Discrete geometry

87. Financial mathematics

88. Game theory

89.Mathematical logic

90. Mathematical optimization

91. Ergodic theory

92. Geometric group theory

93. Homotopy theory

94. Inverse problems

95. K-theory

96. Model categories

97. Nonlinear analysis

Number theory

98. Optimal control

99. PDEs on manifolds

100. Quantum field theory

101. Random walks

102. Statistical mechanics

103. Algebraic topology

104. Combinatorial optimization

105. Combinatorial representation theory

106. Computational group theory

107. Convex analysis

108. Cryptography

109. Dynamical systems

110. Fractional calculus

111. Geometric topology

112. Lie groups and Lie algebras

113. Measure theory and integration

114. Operator theory and functional analysis

115. Spectral theory

116. Topological dynamics

117. Topological graph theory

118. Algorithmic graph theory

119. Applied algebraic geometry

120. Arithmetic dynamics

121. Combinatorial geometry

122. Complex analysis

123. Differential topology

124. Discrete optimization

125. Elliptic curves

126. Geometric measure theory

127. Graph coloring

128. Homological stability

129. Information-based complexity

130. Mathematical physics

131. Model theory

132. Nonlinear waves

133. Number theory

134. Orthogonal polynomials

134. Quantum mechanics

135. Smooth dynamical systems

137. Topological combinatorics

138. Topological quantum computing

139. Algebraic K-theory

140. Analytic number theory

141. Combinatorial designs

142. Computational complexity theory

143. Dynamical systems and chaos

144. Geometric analysis

145. Homotopy type theory

146. Mathematical modeling

147. Model categories

148. Nonlinear functional analysis

149. Numerical analysis

150. Operator algebras and quantum groups

151. Random structures and algorithms

152. Topological methods in combinatorics

153. Algebraic geometry and topology

154. C*-algebras

155. Computational algebraic geometry

156. Ergodic theory and entropy

157. Formal proof

158. Lie theory and representation theory

159. Mathematical finance

These are just a small selection of the many different subfields of mathematics.

The subject of mathematics is incredibly vast and diverse, encompassing many different areas of study and application.

[anoceanofbeauty]

SARUTUL PACII

"Sărutarea păcii a fost prezentă încă de la început în rânduiala Sfintei Liturghii

Sărutul păcii este unul dintre cele mai vechi ritualuri creştine, menţionat încă din Noul Testament. Astfel Sfântul Apostol Pavel îşi încheie patru epistole cu un îndemn la îmbrăţişare cu sărutare sfântă (Rom 16, 16; I Cor 16, 20; II Cor 13, 12; I Tes 5, 26) iar Sfântul Apostol Petru îndeamnă la îmbrăţişare cu sărutarea dragostei (I Pt 5, 14). Această sărutare sfântă sau a dragostei este înţeleasă ca o modalitate concretă de dobândire a păcii după cum vedem în finalul celei de a doua epistole către Corinteni unde, înainte de îndemnul îmbrăţişaţi-vă unul pe altul cu sărutare sfântă, Sfântul Pavel scrie: trăiţi în pace şi Dumnezeul dragostei şi al păcii va fi cu voi (II Cor. 13, 11)."

"Mult timp sărutarea se dădea pe gură. Un aspect destul de şocant pentru omul modern este faptul ca sărutul păcii se dădea pe gură, fără a avea însă nimic senzual sau necurat în el." https://www.dervent.ro/liturghia.php   vezi explicatiile din side content

In opinia noastra nu ar trebui sa fie socant pentru omul modern care are astazi acces la instrumente de cercetare stiintifica pe care un cercetator dintr-un institut de cercetari acum 40 de ani nici nu le putea imagina sau visa. Astazi poti avea gratuit acces la sute daca nu mii de instrumnete de cercetare stiintifica gratuite: Nader Ale Ebrahim https://fsasani.academia.edu/NaderAleEbrahim%D9%86%D8%A7%D8%AF%D8%B1%D8%A2%D9%84%D8%A7%D8%A8%D8%B1%D8%A7%D9%87%DB%8C%D9%85     Listeaza peste 720 research tools.

Faptul ca sarutul pacii era cum se spune "o modalitate concretă de dobândire a păcii" este astazi dovedit de studii stiintifice, vezi mai jos.

https://www.lancelmaat.nl/work/e.e.g-kiss/  

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4222975/ Using graph-theory methods, we identify theta–alpha hyper-brain networks, with alpha serving a cleaving or pacemaker function.

We paid special attention to the way in which theta and alpha oscillation-nodes participate in hyper-brain modules and together constitute a theta-alpha subnetwork binding the brains of the kissing couple together.  

First, we determined alpha peak frequency and spectral power in low and high alpha frequency bands in each of the female and male partners during the three different kissing conditions.

It thus appears that hyper-brain networks in kissing couples have a complex modular organization, in which alpha-frequency oscillations and their subnetworks, especially the theta-alpha subnetwork, play a crucial role. Figures 7D and 7E show the strongest connections within and between a couple’s brains, respectively.  

https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0112080  

end of sci ref, acesta este un articol de opinie: http://www.computers-40.ro/supercalculatorul-si-sarutul/  

Entanglement - inseparabilitatea cuantica Fizica spune ca entanglementul este doar o fateta a coerentei. Este oare  acel Sarut al Pacii o traire a entanglementului, inseparabilitaii cuantice, aparuta la coerenta creata de experienta repetata a linistii interioare (coerentei) candva realmente traita nu doar invocata in Sf Liturghie?

Am putea oare sa realizam global prin impreuna pace interioara/coerenta deci prin enttanglemet acel ideal liturgic exprimat de Schiller in Oda Bucuriei, acum Imnul Europei, in care, indiferent de distante, sa traim transfigurat si transsubstantiat acel “Fiti imbratisate milioane”?

[craigbrownphd]

If you did not already know

Latent Semantic Imputation (LSI) We present a novel method named Latent Semantic Imputation (LSI) to transfer external knowledge into semantic space for enhancing word embedding. The method integrates graph theory to extract the latent manifold structure of the entities in the affinity space and leverages non-negative least squares with standard simplex constraints and power iteration method to derive spectral embeddings. It provides an effective and efficient approach to combining entity representations defined in different Euclidean spaces. Specifically, our approach generates and imputes reliable embedding vectors for low-frequency words in the semantic space and benefits downstream language tasks that depend on word embedding. We conduct comprehensive experiments on a carefully designed classification problem and language modeling and demonstrate the superiority of the enhanced embedding via LSI over several well-known benchmark embeddings. We also confirm the consistency of the results under different parameter settings of our method. … Gandhi-Washington Method (GWM) Many investigations in empirical software engineering look at sequences of data resulting from development or management processes. In this paper, we propose an analytical approach called the Gandhi-Washington Method (GWM) to investigate the impact of recurring events in software projects. GWM takes an encoding of events and activities provided by a software analyst as input. It uses regular expressions to automatically condense and summarize information and infer treatments. Relating the treatments to the outcome through statistical tests, treatment-outcome constructs are automatically mined from the data. The output of GWM is a set of treatment-outcome constructs. Each treatment in the set of mined constructs is significantly different from the other treatments considering the impact on the outcome and/or is structurally different from other treatments considering the sequence of events. We describe GWM and classes of problems to which GWM can be applied. We demonstrate the applicability of this method for empirical studies on sequences of file editing, code ownership, and release cycle time. … Discriminative Convolutional Analysis Dictionary Learning (DCADL) Discriminative Dictionary Learning (DL) methods have been widely advocated for image classification problems. To further sharpen their discriminative capabilities, most state-of-the-art DL methods have additional constraints included in the learning stages. These various constraints, however, lead to additional computational complexity. We hence propose an efficient Discriminative Convolutional Analysis Dictionary Learning (DCADL) method, as a lower cost Discriminative DL framework, to both characterize the image structures and refine the interclass structure representations. The proposed DCADL jointly learns a convolutional analysis dictionary and a universal classifier, while greatly reducing the time complexity in both training and testing phases, and achieving a competitive accuracy, thus demonstrating great performance in many experiments with standard databases. … Model Reference Adaptive Controller (MRAC) In this paper, we present a hybrid direct-indirect model reference adaptive controller (MRAC), to address a class of problems with matched and unmatched uncertainties. In the proposed architecture, the unmatched uncertainty is estimated online through a companion observer model. Upon convergence of the observer, the unmatched uncertainty estimate is remodeled into a state dependent linear form to augment the nominal system dynamics. Meanwhile, a direct adaptive controller designed for a switching system cancels the effect of matched uncertainty in the system and achieves reference model tracking. We demonstrate that the proposed hybrid controller can handle a broad class of nonlinear systems with both matched and unmatched uncertainties … https://analytixon.com/2022/10/21/if-you-did-not-already-know-1864/?utm_source=dlvr.it&utm_medium=tumblr